Abstract
Human interactions have led to the emergence of a higher complexity of urban metabolic networks; hence, traditional natural- or agriculture-oriented biogeochemical models might not be transferred well to urban environments. Increasingly serious environmental problems require the development of new concepts and models. Here, we propose a basic paradigm for urban–rural complex nitrogen (N) metabolic network reconstruction (NMNR) by introducing new concepts and methodologies from systems biology at the molecular scale, analyzing both local and global structural properties and exploring optimization and regulation methods. Using the Great Hangzhou Areas System (GHA) as a case study, we revealed that pathway fluxes follow a power law distribution, which indicates that human-dominated pathways constitute the principal part of the functions of the whole network. However, only 1.16% of the effective cycling pathways and an average hamming distance of only 5.23 between the main pathways indicate that the network lacks diverse pathways and feedback loops, which could lead to low robustness. Furthermore, more than half of the N fluxes did not pass through core metabolism, causing waste and pollution. We also provided strategies to design network structures and regulate system function: improving robustness and reducing pollution by referring to the characteristics of biochemical metabolic networks (e.g., the bow-tie structure). This method can be used to replace the trial-and-error method in system regulation and design. By decomposing the GHA N metabolic network into 4398 metabolic pathways and the corresponding fluxes with a power law distribution, NMNR helps us quantify the vulnerability in the current urban nitrogen cycle. The basic ideas and methodology in NMNR can be applied to coupled human and natural systems to advance global sustainable development studies, and they can also extend systems biology from the molecule to complex ecosystems and lead to the development of multi-scale unified theory in systems biology.
1. Introduction
Urban areas intensively affect surrounding areas and now emerge as a unit that integrates a city core and peripheral wild lands [1,2,3] (Keil, 2017; Krugman, 1992; Woods & Heley, 2017), an urban–rural complex (URC) [4,5] (Chang et al., 2021; Chang & Ge, 2005), through ecological footprints, technological exports, and economic relationships. With accelerating urbanization, URCs have been widely recognized as the basic units of the globally coupled human and natural systems [5] (Chang & Ge, 2005). Intensive biogeochemical metabolism improves the well-being of all human beings, but it also causes serious environmental problems, such as nitrogen (N) pollution [6,7] (Kanter, 2018; Kanter et al., 2020). More than 50% of total N inputs in terrestrial ecosystems are controlled by humans [8] (Tilman et al., 2002), and in urban areas, in a more extreme manner, the proportion of nitrogen inputs controlled by humans is higher than in the natural or agricultural areas. The anthropogenic influence on the N process is dramatic [9] (Grimm et al., 2008); for example, fertilizer can provide food for humans and animals, while considerable N leaches through soil to surface water and subsurface water, where it validates the atmosphere and is then deposited back to almost all components in the system, forming a complex network.
The complex networks play a central role in studies of both URC biogeochemical and molecular-scale biochemical metabolism: the motion and transformation of materials in networks, the harmony between structures and functions, and regulation. The common characteristics between the two levels of metabolic systems include (Figure 1a): (i) networks: both systems demand a complex network to represent the global relationships of matter flows; (ii) pathways: both networks can be decomposed into a series of pathways, which represent a specially functional subset; (iii) conversions: a pathway in both systems consists of a group of connected conversions, including transportation and chemical reactions, and can be described by stoichiometric equations; and (iv) constraints: both systems are limited by different constraints, where the two fundamental types are balance (the conservation of mass) and bounds (constraining the values of individual variables, e.g., the flux range of a conversion or pathway). In fact, ecological theory might benefit from the use of analogies among multi-scale biosystems to accelerate the development of new concepts (e.g., ‘urban metabolism’) and apply it to coupled human and natural systems [10,11] (Collins et al., 2000; Lokatis et al., 2023). However, the current application of analogies is still limited at the conceptual level; thus, we developed PMBR to advance the interdisciplinary research.
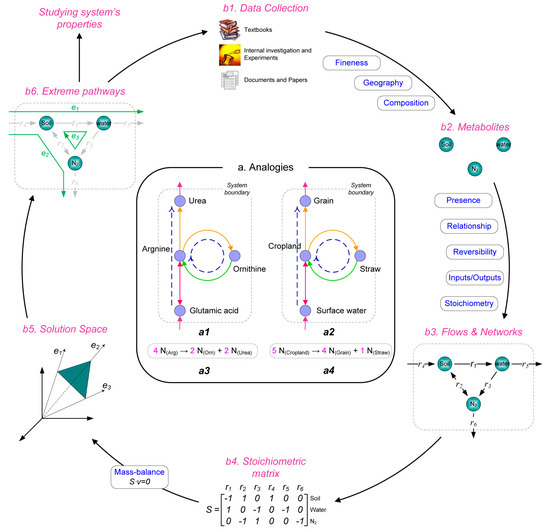
Figure 1.
Framework and reconstruction processes. (a) Structural analogies between a URC and a cell involve conversions, pathways, and networks. (a1) is a sample biochemical metabolic network, and (a2) is a sample biogeochemical network. Solid lines represent reactions/conversions and different colors mean different reactions/conversions, and dashed lines mark two pathway types (linear and cycle) in both networks. (a3,a4) are reaction and conversion equations, respectively. (b) Reconstruction process from original data to networks and extreme pathway analysis. The reconstruction is a non-automated decision-making process for establishing metabolites and conversions ((b1–b3); see Section S1 in Supplementary Materials). The reconstructed network can be described by a stoichiometric matrix (b4), from which a steady-state space and its basis vectors and the extreme pathways can be calculated (b5,b6). Extreme pathways can be used to study ecological properties and refine the data collection.
2. Methods
NMNR imitates the methodology and skills used in the reconstruction of a molecular-scale biochemical metabolic network and includes the use of metabolites and stoichiometric reactions to define network models and the use of a stoichiometric matrix, steady-state equation, and convex cone to describe the network states. Based on NMNR, extreme pathway (EP) analysis was used to explore both the local and global characteristics of the URC N metabolism. The calculation of EPs was performed using CellNetAnalyzer (CNA) [12,13] (Klamt et al., 2007; Thiele et al., 2022), which is a toolbox of MATLAB version 2014a or higher. We consider a series of EP properties in this study, including the type, number, length, flux participation, and hamming distance.
2.1. Part I. Metabolites of Great Hangzhou Areas System
Hangzhou has a history of more than 2000 years. Hangzhou is the capital of Zhejiang Province and is located at latitude 29°11′–30°34′ N and longitude 118°20′–120°37′ E. It is situated in the northern part of Zhejiang Province, adjacent to Hangzhou Bay, to the east. The largest river in the province, Qiantang, flows through most parts of the city from southwest to northeast, with a total coverage area of 16,596 km2. The terrain of Hangzhou is complex and diverse. The western, central, and southern parts of Hangzhou belong to the hilly region of western Zhejiang, whereas the eastern part belongs to the plain of northern Zhejiang. The terrain is low and flat, with an altitude of only 3–6 m and dense river networks and lakes.
Among the total land area of the city, mountains and hills account for 65.6%, plains account for 26.4%, and various types of water bodies account for a total of 8%, hence the saying ‘Seven mountains, two rivers, and two fields’. Hangzhou has a subtropical monsoon climate, with an obvious alternation of winter and summer monsoons, four distinct seasons, abundant precipitation and sunshine, an annual average temperature of approximately 16 °C, and an annual precipitation of 1300 mm. Hangzhou has experienced rapid urban development, with the built-up area of the district increasing from 69 km2 in 1990 to 801 km2 in 2023; thus, it is nearly 12 times larger; from 1.1 million in 1990 to 12.52 million in 2023, the GDP increased from RMB 20.8 billion to RMB 2006 billion.
The Great Hangzhou Areas System (GHA) system was divided into four functional groups according to their roles in N biogeochemical cycling: each functional group contained one or more subsystems. The consumer group represents the service target of the urban nitrogen flow and includes two subsystems: humans (Hm) and pets (Pt).
The processor group can process the input of fixed N into food and other useful N-containing products and then support the nutrients and materials needed by consumers. The subsystems of the processor group include agriculture (Ag), aquiculture (Aq), livestock (Ls), forest–grassland (FG), and urban lawn (Lw).
The remover group comprises artificial facilities to treat waste N with processes converting active N (NR) into N2, including only the wastewater treatment (WTF) subsystem.
The life-supporter group is closely related to almost all the other subsystems, including the surface water (SW), near-atmosphere (NA), subsurface water (SsW), and solid waste (Swst) subsystems.
Based on the subsystems, there are four types of metabolites: (A) those for processors and consumers, except for the forest–grassland subsystem, and those metabolites that were the inner components of subsystems. (B) All removers, life supporters, and forest–grassland subsystems were treated as a single metabolite. (C) Additional metabolites were considered to construct a complete network, including the outer atmosphere (the source of wet deposition), N2 (we divided it into two metabolites: N2In for the source of biological fixation and N2Ot for the target of denitrification), and accumulation (an abstract metabolite for maintaining mass balance). (D) Five external metabolites were added to the system to simplify the expression of conversions and the representation of inputs/outputs. External metabolites do not change the structural properties of the network, and we did not consider them when calculating the pathway length. The naming rule of a metabolite is as follows: for types A and D, the name of a metabolite (four letters) is the combination of its subsystem name (two letters in the abbreviation) and its component name (two letters in the abbreviation); for types B and C, the name of a metabolite just is the name of the abbreviation of the corresponding subsystem name (to 2–4 letters).
2.2. Part II. Definition
Network-based definitions of the biochemical pathways have emerged in recent years. These pathway definitions insist on the balanced use of an entire network of biochemical reactions [14,15] (Papin et al., 2003; Wang et al., 2017). Two related definitions, elementary modes and extreme pathways, have generated novel hypotheses regarding the biochemical network functions. Here, we imported extreme pathways to analyze the reconstructed UBN. Extreme pathways are a minimal set of elementary modes, and when all the exchange fluxes are constrained to be irreversible (e.g., in our model), the extreme pathways and elementary modes effectively result in the same set of pathways [16] (Klamt & Gilles, 2004).
Extreme pathways are a mathematically defined unique and minimal set of generating vectors that describe the conical steady-state solution space for the flux distribution through an entire stoichiometric network [17] (Schilling et al., 2000). For any stoichiometric network, we created an m-by-n stoichiometric matrix S, where m is the number of metabolites, n is the number of conversions, and S (x, y) is the stoichiometric coefficient of metabolite x in conversion y (Figure 1(b4)). At a steady state, the mass balance in a network can be represented by the flux balance equation:
The solution of Equation (1) forms a convex cone, and the extreme pathways are the edges of the convex cone (Figure 1(b5)). Any steady-state flux distribution v can be described as a non-negative linear combination of all the extreme pathways: :
where and represents the flux proportion through reaction j in ei, and the weight of ei is ci, which represents the flux capacity of ei. For the demo network in Figure 1(b3), means that only r1, r4 and, r5 participate in e1 and the fluxes, though they are the same. In this system, other pathways can be described by the linear combination of extreme pathways [14,15] (Papin et al., 2003; Wang et al., 2017), such as pathway , which can be described as . Thus, the extreme pathways represent the global properties of the system and establish a bridge between the structural and flux properties. The hamming distance between two strings or vectors of equal length is the number of positions where the corresponding symbols are different. For example, the hamming distance between e1 and p was 3. Therefore, the hamming distance can illustrate the similarity among the pathways.
2.3. Part III. Computation of Extreme Pathways
In this study, the computation of extreme pathways was performed using the CellNetAnalyzer 2023.1 (CNA) [12,13] (Klamt et al., 2007; Thiele et al., 2022), a program for the analysis of metabolic networks based on MATLAB (Mathworks, Inc., Natick, MA, USA). The core algorithm of the CNA is described by Gagneur & Klamt [18] (2004), Klamt & Gilles [16] (2004), Schuster et al. [19] (1999), and Thiele et al. [13] (2022) and is also suitable for our application.
2.4. Part IV. Characters of Extreme Pathways
There are three common characteristics for extreme pathways [14] (Papin et al., 2003): (1) non-decomposable: if an active flux in a non-decomposable pathway is restricted to zero, then the steady-state flux through the entire pathway must be zero; (2) unique: an extreme pathway set is unique for a given network; and (3) systemic independence: there are no extreme pathways that can be represented by non-negative linear combinations of other extreme pathways.
As we used the simplest form of conversions (one substrate and one product) and only considered the net quantity of nitrogen, in accordance with the principle of the law of conservation of mass, the stoichiometric coefficients of both the substrate and product in a conversion equation are equal to 1. As a result, all the extreme pathways present the simple non-branch form, including two types: linear and cyclical.
2.5. Part V. Types of Extreme Pathways
Based on the topological and ecological properties of extreme pathways, they can be divided into three types [17] (Schilling et al., 2000). In Type I, these pathways are linear pathways and are related to exchange fluxes (Figure S1a). Type I pathways are the major contributors to the decomposition of almost any steady-state flux distribution in URCs. Type II pathways are one type of cycle pathway, in which all the exchange fluxes are inactive, corresponding to internal cycles within the network that represent effective material recycling (Figure S1b). In the GHA system, all type II pathways are related to excretion recycling. Type III pathways are also cycle pathways, but they are related to life supporters (Figure S1c), causing pollution problems and representing inefficient and unmanaged material cycles. Type III cycles correspond to futile cycles in cellular metabolic networks.
2.6. Part VI. Parameters
A series of parameters were developed for the description and analysis of the properties of our network model.
Conversions participation. Conversions participation is the percentage of extreme pathways that utilize a given conversion and suggests the regulatory importance of conversion from a structural perspective [14] (Papin et al., 2003). In the demo network (Figure 1), the participation of conversions r1 and r3 is and . A subsystem can be viewed as a set of conversions; thus, we can also calculate the subsystem participation, which is the percentage of extreme pathways that utilize at least one conversion in the subsystem.
Conversions relationship. If two conversions are connected by at least one EP, they can be treated as related to each other. The conversion relationship represents the percentage of related conversions over all the conversions of a given conversion j, such that r1 is related to four other conversions; so, . Conversion relationships represent the degree of interconnection between the conversions.
EP length. The pathway length represents the number of conversions involved in an EP [14] (Papin et al., 2003). For example, the lengths of all three extreme pathways in the example network are three. In our model, we did not consider exchange conversions when calculating the pathway length. In this situation, the length of a pathway represents the number of inner processes involved in the pathway; for example, the length of the extreme pathway in Figure S1a is six. In ecology, the length of extreme pathways has useful properties (Figure S2).
EP number. The pathway number N is defined as the number of extreme pathways related to a systemic function, such as those connecting the same exchange conversions or with a certain length. In the example network, there were two pathways related to r1. Pathway number represents the complexity of the given functions in the metabolic networks (Stelling et al., 2002).
EP Flux. Based on Equation (2), we can use the simplex method to determine the value of cj for a specific flux distribution. For the demo network, we assume a flux distribution, . By solving Equation (2), we obtained and . In fact, ci represents the flux through ei, and the distribution of ci represents a significant systemic property (Figure S3). For high-dimensional systems (with a large number of extreme pathways), ci is not unique. The range of ci can be obtained by solving the following equation [20] (Wiback et al., 2003):
Hamming distance of EPs. The hamming distance [21] (Hamming, 1950) between two EPs is the number of conversions for which the corresponding coefficients differ. For example, the hamming distance between e1 = [1 0 0 1 1 0] and e2 = [0 1 0 1 0 1] was 2. The hamming distance is a mark of independence between EPs.
NUE and pollution rate. Extreme pathways can be classified into different categories based on ecological reasons. Here, we consider two important classifications. First, according to whether an extreme pathway passes through human consumption (food and N-chemicals), we obtained a classification of ‘utilization’ and ‘waste’ (Figure S4a). Second, depending on the final targets of an EP, we obtained another classification: ‘pollution’ and ‘completeness’ (Figure S4b). Considering the flux capacity of the extreme pathways, we can calculate the theoretical nitrogen use efficiency (NUE) or pollution rate (PR):
The advantage of this approach is that we can obtain theoretical utilization or pollution ratios of pathways with selected properties, such as those involved in given inputs/outputs or those with the same length.
The basic steps of the NMNR are shown in Figure 1b. Based on the collected data (b1), network nodes, which are metabolites with converter tags in URC biogeochemical cycles, can be defined. A URC system is a highly complex system with multiple hierarchies, from the molecule to the ecosystem; hence, the composition and fineness of metabolites should be carefully controlled to maintain the complexity of our network located at a moderate level (b1–b2). In the next step, a number of decisions must be made to establish the conversions and their stoichiometric equations (b2–b3). Systemic inputs and outputs are described by exchange conversions that cross the system boundaries. The technological details of decisions involved in the paradigm are discussed in Section S1 in Supplementary Materials, and the complete list of metabolites and reactions can be found in Tables S3 and S4. By linking nodes, we obtained a demo URC biogeochemical network model (b3), which holds the basic properties of biochemical metabolic network reconstruction [14] (Papin et al., 2003). This can be described by using a stoichiometric matrix and a linear equation (b4), whose solution space encompasses all valid steady-state flux distributions (a particular set of fluxes in a network to keep all metabolite quantities constant) of the network. The space, usually a convex cone (b5), is spanned by a set of basis vectors (b6), called extreme pathways (EPs) [17] (Schilling et al., 2000). All possible states in the cone can be described by a non-negative linear combination of EPs [14] (Papin et al., 2003).
3. Results and Discussions
Based on NMNR, we reconstructed a metabolic network model for N cycles in the GHA and used this real system as a case study to test the ability of NMNR. GHA integrates the Hangzhou city core and peripheral rural, within which the N cycles are calculated and analyzed by the mass balance approach (Figure S2). High-quality data provide a solid foundation for reconstructing the GHAN metabolic network model. The model consisted of 35 metabolites and 95 conversions, including 16 exchange conversions (10 inputs and 6 outputs) (Figure 2 and Figure S2). The computation resulted in 4398 EPs. Considering both structural and ecological properties, all the pathways were divided into 3 types, where 4347 were linear EPs (type I) and 51 were cycling EPs (Type II and Type III) (Section S1 in Supplementary Materials). Type I was the primary form (accounting for 98.84% of all pathways) and covered all subsystems and functional groups. Type II represented high-efficiency and controllable material recycling; however, only 11.76% of the cycling EPs accounted for only 1.16% of all pathways. This means that the probability and diversity of effective N recycling are located at low levels in the GHA. In contrast, type III represented futile cycles, which passed through life supporters and caused pollution or waste but comprised 88.24% of the cycling EPs. For example, irrigation-driven N runoff from croplands is an important source of N pollution in GHA [22] (Gu et al., 2009). However, in biochemical metabolic networks, extreme pathway analysis found that futile cycles were rare and included, for example, only 15% of cycling pathways [20] (Wiback et al., 2003); this was attributed to the bypass mechanism formed in long-term evolution. In ecology, isolating and deducing non-point pollution from cropland by adding some components (e.g., wetlands, as suggested by Tilman et al. [8] (2002)) coincided with the bypass mechanism.
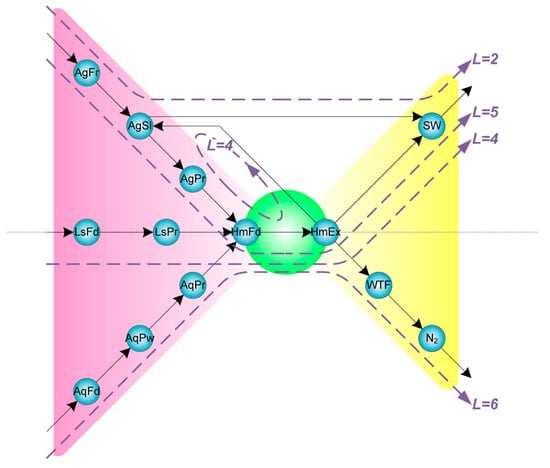
Figure 2.
A piece of the biogeochemical network of N cycles in GHA. There are 13 metabolites, AgFr (agricultural fertilizer), AgSl (agricultural soil), AgPr (agricultural product), LsFd (livestock feed), LsPr (Livestock product), AqFd (aquiculture feed and fertilizer), AqPw (aquiculture pool water), AqPr (aquiculture product), HmFd (human food), HmEx (human excretion), WTF (wastewater treatment), N2, SW (surface water), and 17 conversions (3 inputs and 2 outputs) between them. We also show 5 examples of extreme pathways with different properties. A conceptual bow tie is presented: green circle marks the core metabolism of N cycles in GHA: human food consumption; red and yellow areas are the two wings of the bow tie, which represent production and decomposition, respectively. A short extreme pathway with L = 2 means that the bow tie is faulty.
Normally, the number of EPs determines the redundancy of a system [23] (Price et al., 2002), but we found that the EPs in the stem were similar: the average hamming distance of the stem was only 5.23, which was less than half that of the random states (Section S1 in Supplementary Materials). In particular, EPs related to human-controlled inputs were outstanding; for example, the hamming distances of food import and agricultural fertilizer were 3.68 and 3.95, respectively. This means that the N metabolism network of GHA lacks independent pathways and that its robustness is low. The theoretical average flux (Cj) passing through the EPs was calculated using linear optimization. We found that the distribution of Cj followed a power law distribution (Figure 3a), which means that only a small subset of high-flux EPs played key roles in the network for the functions of the system, and a large number of low-flux EPs made the system more complex. We set a subset of EPs, whose Cj was not less than 1 GgN yr−1, to be the “stem” to represent system functions. The stem contained 617 EPs and accounted for 14% of the total pathways in the entire network, with more than 80% conversion.
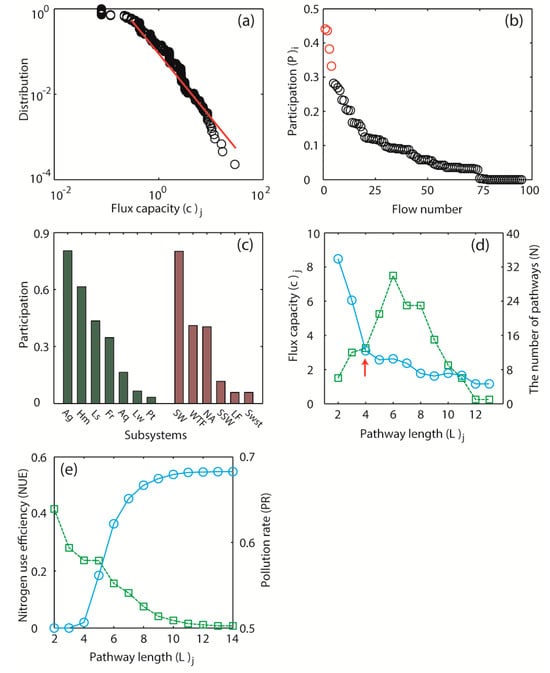
Figure 3.
Properties of N cycle in GHA. (a) Distribution of average fluxes of extreme pathways is drawn in log-log coordinate. The curve shows a power law distribution whose exponent is about −1.5. (b) The participation of conversions. Four outstanding conversions are marked by red color: human food consumption, agricultural production and irrigation, and denitrification output. (c) The participation of subsystems, shown in descending order in two groups: (i) processors and consumers and (ii) removers and life supporters. The subsystems include human (Hm), pets (Pt), agriculture (Ag), aquiculture (Aq), livestock (Ls), forest–grassland (FG), urban lawn (Lw), wastewater treatment (WTF), surface water (SW), near–atmosphere (NA), subsurface water (SsW), and solid waste (Swst). (d) Relationships among lengths, number, and average fluxes of extreme pathways. Solid curve describes the average fluxes of extreme pathways with given lengths; arrow indicates the critical point L = 4. Dash curve indicates how many extreme pathways have given lengths. (e) Nitrogen use efficiency and pollution rate (PR). We display NUE and PR calculated from extreme pathways, whose lengths are smaller than given value.
In the stem, only a few reactions frequently participated in the formation of most Eps, and the participations (Pi) of four flows were remarkable (Figure 3b): R1, human food consumption (44.1%); R2, agriculture (43.6%); R3, agricultural irrigation (38.3%); and R4, denitrification output (33.2%). This means that some basic processes closely related to human metabolism were most important in the stem. The participation of the subsystems also showed the same result: agriculture, humans, livestock, and wastewater treatment facilities all participated in more than 40% of the stem (Figure 3c). If we remove R1, there is a large drop in the number of EPs between all pairs of inputs and outputs, but the deletion of other conversions (e.g., R2 with high participation) only disturbs a part of the whole network. Thus, we defined human food consumption as the core metabolisms of N cycles from the structural perspective.
However, we found that the average fluxes of the EPs (2.11 Gg y−1 in average) passing through the core metabolism were lower than those of the EPs (2.49 Gg y−1 in average) that did not pass through the core metabolism, indicating that more than half of the N is waste and leads to pollution. In contrast, biochemical metabolic networks have evolved striking bow-tie structures [24] (Csete & Doyle, 2004), all of which are catabolized to the core metabolism to produce a handful of precursors, which then leave the core metabolism for the biosynthesis of all other metabolites. Bow-tie structures are robust, flexible, and highly efficient, and provide an excellent template to optimize global network structures.
We then set three disturbance scenarios in GHA to test the global structural optimization. The first removed the “side roads pathway”, which leads to a skip of N from the core metabolism and destroys bow-tie structures; R5, for instance, represents the conversion of fertilizer N runoff from cropland to surface water directly. This disturbance translates to an increase in the proportion of EPs passing through the core metabolism (+5%), which may quantify the fact that bow-tie structures can improve the NUE. The second scenario was to remove a node, such as the urban lawn, which is artificial and only for human well-being but does not participate in production. We found the disturbance had no obvious effect on the stem, which suggests that the lawn is an isolated component. However, the third removal of forest led to great loss of EPs (−25%). This is because the forest is an absorber of active N from the atmosphere and links fertilizer, agriculture and water bodies, and as well as fusel fuel through validation and combustion.
Decomposing the steady-state flux distribution into extreme pathways plays an increasingly important role in pathway analysis. Here, we present a method that uses ecological properties to refine the calculation of the flux capacity. In ecology, two successive conversions always maintain a proportional relationship; for example, vpre (AgFr → AgSl) and vnext (AgSl → AgPr) have: . This means that the utilization of fertilizer is no greater than 20% in agriculture; so, the flux capacity of the extreme pathway in Figure S1a appeared in . Illustratively, we imported a series of such proportion restrictions (Table S5) and obtained a narrower range of ci (Figure 4).
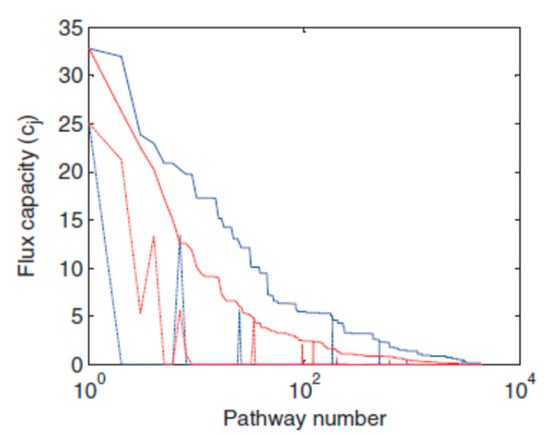
Figure 4.
The optimization of calculation of extreme pathway fluxes. Blue lines represent the distribution of the range of flux without additional restrictions, and red lines are the result with restrictions in Table S5. Solid lines indicate max fluxes and dash lines indicate min fluxes. The red range is obviously narrower than the blue range; hence, additional restrictions are effective.
Locally, the relationship between the length (Lj) and Cj of EPs provides an approach for quantifying pathway optimization. In GHA, we found that Lj = 4 was a critical length (Figure 3d,e); when Lj < 4, these EPs were “short and big”: huge fluxes of N left the processors without being utilized by core metabolisms and concentrated into life supporters (Figure 2 and Section S1 in Supplementary Materials); for example, fertilizer N runoff that went directly from cropland to surface water or to the atmosphere was represented by EPs with Lj = 2. Once Lj >= 4, N flow can complete the pathways from production to consumption (passing through the core metabolism) and decomposition. For example, to optimize the pathway from cropland to surface water, at least two additional nodes are needed to make L >= 4. The theoretical results suggest that in addition to the wetlands suggested by Tilman et al. [8] (2002) and Liu et al. [25] (2009), one more component, such as marginal cropland, which has low N availability tolerance [26] (Schmer et al., 2008), is necessary to isolate the N between cropland and surface water, and the products from the marginal cropland could return to the core metabolism.
In the case of NMNR, we found that the huge flux pathways mediated or created by humans appeared rigid and should be modified. Theoretically, the results proved that NMNR is a powerful tool for studying biogeochemical metabolism in URCs. In the future, NMNR will have great potential as a computational platform for introducing more mathematical tools, such as minimal cut sets [27] (MCS, Klamt et al., 2020), which can be used to find optimal ways to interrupt pollution, control-effective flux [28] (CEF, Stelling et al., 2002), which can be used to quantify the mutual influences among conversions, and flux balance analysis [29] (FBA, Antoniewicz 2015), which can even be used to quantitatively predict system changes. In principle, NMNR provides an opportunity to unify multi-scale metabolic systems by taking advantage of both biochemical and biogeochemical network research.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/land13081199/s1. References [30,31,32,33,34] are cited in the supplementary materials.
Author Contributions
Conceptualization, Y.M., H.L. and J.C.; Methodology, Y.M., H.L. and Y.G.; Software, Y.M. and Y.G.; Validation, H.L.; Investigation, Y.M. and Y.G.; Data curation, Y.M.; Writing—original draft, Y.M. and H.L.; Writing—review & editing, Y.M., H.L., Y.G. and J.C.; Visualization, Y.M. and H.L.; Supervision, J.C.; Funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Fundamental Research Funds for the Central Universities (1243200012), a grant from the National Natural Science Foundation of China (No. 32101337), and the National Key Technologies Research and Development Program of China “Joint Research and Demonstration for Carbon Reduction Key Technologies in Urban areas and Neighborhoods” (No. 2022YFE0208700).
Data Availability Statement
Dataset available on request from the authors: The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors thank Xiaogang Jin, Baojing Gu, and Weijun Yang at Zhejiang University; Changhui Peng at Université du Quebec à Montréal; and Yang Zhong at Fudan University for their assistance with the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Keil, R. Suburban Planet: Making the World Urban from the Outside in; John Wiley & Sons: Hoboken, NJ, USA, 2017; ISBN 0-7456-8315-0. [Google Scholar]
- Krugman, P. Geography and Trade; MIT Press: Cambridge, MA, USA, 1992; ISBN 0-262-61086-8. [Google Scholar]
- Woods, M.; Heley, J. Conceptualisation of Rural-Urban Relations and Synergies; (ROBUST Deliverable 1.1); University of Aberystwyth: Aberystwyth, UK, 2017. [Google Scholar]
- Chang, J.; Ge, Y.; Wu, Z.; Du, Y.; Pan, K.; Yang, G.; Ren, Y.; Heino, M.P.; Mao, F.; Cheong, K.H.; et al. Modern cities modelled as “super-cells” rather than multicellular organisms: Implications for industry, goods and services. BioEssays 2021, 43, 2100041. [Google Scholar] [CrossRef]
- Chang, J.; Ge, Y. Compendium for Unified Biology; Higher Education Press: Beijing, China, 2005. [Google Scholar]
- Kanter, D.R. Nitrogen pollution: A key building block for addressing climate change. Clim. Chang. 2018, 147, 11–21. [Google Scholar] [CrossRef]
- Kanter, D.R.; Bartolini, F.; Kugelberg, S.; Leip, A.; Oenema, O.; Uwizeye, A. Nitrogen pollution policy beyond the farm. Nat. Food 2020, 1, 27–32. [Google Scholar] [CrossRef]
- Tilman, D.; Cassman, K.G.; Matson, P.A.; Naylor, R.; Polasky, S. Agricultural sustainability and intensive production practices. Nature 2002, 418, 671–677. [Google Scholar] [CrossRef] [PubMed]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef]
- Collins, J.P.; Kinzig, A.; Grimm, N.B.; Fagan, W.F.; Hope, D.; Wu, J.; Borer, E.T. A new urban ecology: Modeling human communities as integral parts of ecosystems poses special problems for the development and testing of ecological theory. Am. Sci. 2000, 88, 416–425. [Google Scholar] [CrossRef]
- Lokatis, S.; Jeschke, J.M.; Bernard-Verdier, M.; Buchholz, S.; Grossart, H.-P.; Havemann, F.; Hölker, F.; Itescu, Y.; Kowarik, I.; Kramer-Schadt, S.; et al. Hypotheses in urban ecology: Building a common knowledge base. Biol. Rev. 2023, 98, 1530–1547. [Google Scholar] [CrossRef]
- Klamt, S.; Saez-Rodriguez, J.; Gilles, E.D. Structural and functional analysis of cellular networks with CellNetAnalyzer. BMC Syst. Biol. 2007, 1, 2. [Google Scholar] [CrossRef]
- Thiele, S.; von Kamp, A.; Bekiaris, P.S.; Schneider, P.; Klamt, S. CNApy: A CellNetAnalyzer GUI in python for analyzing and designing metabolic networks. Bioinformatics 2022, 38, 1467–1469. [Google Scholar] [CrossRef]
- Papin, J.A.; Stelling, J.; Price, N.D.; Klamt, S.; Schuster, S.; Palsson, B.O. Comparison of network-based pathway analysis methods. Trends Biotechnol 2004, 22, 400–405. [Google Scholar] [CrossRef]
- Wang, L.; Dash, S.; Ng, C.Y.; Maranas, C.D. A review of computational tools for design and reconstruction of metabolic pathways. Synth. Syst. Biotechnol. 2017, 2, 243–252. [Google Scholar] [CrossRef] [PubMed]
- Klamt, S.; Gilles, E.D. Minimal cut sets in biochemical reaction networks. Bioinformatics 2004, 20, 226–234. [Google Scholar] [CrossRef] [PubMed]
- Schilling, C.H.; Letscher, D.; Palsson, B.Ø. Theory for the systemic definition of metabolic pathways and their use in interpreting metabolic function from a pathway-oriented perspective. J. Theor. Biol. 2000, 203, 229–248. [Google Scholar] [CrossRef]
- Gagneur, J.; Klamt, S. Computation of elementary modes: A unifying framework and the new binary approach. BMC Bioinform. 2004, 5, 175. [Google Scholar] [CrossRef] [PubMed]
- Schuster, S.; Dandekar, T.; Fell, D.A.; Schuster, S.; Dandekar, T.; Fell, D.A. Detection of elementary flux modes in biochemical networks: A promising tool for pathway analysis and metabolic engineering. Trends Biotechnol. 1999, 17, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Wiback, S.J.; Mahadevan, R.; Palsson, B.Ø. Reconstructing metabolic flux vectors from extreme pathways: Defining the α-spectrum. J. Theor. Biol. 2003, 224, 313–324. [Google Scholar] [CrossRef] [PubMed]
- Hamming, R.W. Error detecting and error correcting codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]
- Gu, B.; Chang, J.; Ge, Y.; Ge, H.; Yuan, C.; Peng, C.; Jiang, H. Anthropogenic modification of the nitrogen cycling within the Greater Hangzhou Area system, China. Ecol. Appl. 2009, 19, 974–988. [Google Scholar] [CrossRef] [PubMed]
- Price, N.D.; Papin, J.A.; Palsson, B.Ø. Determination of redundancy and systems properties of the metabolic network of Helicobacter pylori using genome-scale extreme pathway analysis. Genome Res. 2002, 12, 760–769. [Google Scholar] [CrossRef]
- Csete, M.; Doyle, J. Bow ties, metabolism and disease. TRENDS Biotechnol. 2004, 22, 446–450. [Google Scholar] [CrossRef]
- Liu, D.; Ge, Y.; Chang, J.; Peng, C.; Gu, B.; Chan, G.Y.; Wu, X. Constructed wetlands in China: Recent developments and future challenges. Front. Ecol. Environ. 2009, 7, 261–268. [Google Scholar] [CrossRef]
- Schmer, M.R.; Vogel, K.P.; Mitchell, R.B.; Perrin, R.K. Net energy of cellulosic ethanol from switchgrass. Proc. Natl. Acad. Sci. USA 2008, 105, 464–469. [Google Scholar] [CrossRef] [PubMed]
- Klamt, S.; Mahadevan, R.; von Kamp, A. Speeding up the core algorithm for the dual calculation of minimal cut sets in large metabolic networks. BMC Bioinform. 2020, 21, 510. [Google Scholar] [CrossRef] [PubMed]
- Stelling, J.; Klamt, S.; Bettenbrock, K.; Schuster, S.; Gilles, E.D. Metabolic network structure determines key aspects of functionality and regulation. Nature 2002, 420, 190–193. [Google Scholar] [CrossRef]
- Antoniewicz, M.R. Methods and advances in metabolic flux analysis: A mini-review. J. Ind. Microbiol. Biotechnol. 2015, 42, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Francke, C.; Siezen, R.J.; Teusink, B. Reconstructing the metabolic network of a bacterium from its genome. Trends Microbiol. 2005, 13, 550–558. [Google Scholar] [CrossRef] [PubMed]
- Klamt, S.; Stelling, J. Two approaches for metabolic pathway analysis? Trends Biotechnol 2003, 21, 64–69. [Google Scholar] [CrossRef] [PubMed]
- Papin, J.A.; Price, N.D.; Wiback, S.J.; Fell, D.A.; Palsson, B.O. Metabolic pathways in the post-genome era. Trends Biochem. Sci. 2003, 28, 250–258. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Yang, L.; Yang, K.Q. Geographical effects on cascading breakdowns of scale-free networks. Phys. Rev. E 2006, 73, 036102. [Google Scholar] [CrossRef]
- Warren, C.P.; Sander, L.M.; Sokolov, I.M. Geography in a scale-free network model. Phys. Rev. E 2002, 66, 056105. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).