Abstract
Optimal flow paths obtained from percolation theory provide a powerful tool that can be used to characterize properties associated with flow such as soil hydraulic conductivity, as well as other properties influenced by flow connectivity and topology. A recently proposed scaling theory for vegetation growth appeals to the tortuosity of optimal paths from percolation theory to define the spatio-temporal scaling of the root radial extent (or, equivalently, plant height). Root radial extent measures the maximum horizontal distance between a plant shoot and the root tips. We apply here the same scaling relationship to unsteady (horizontal) flow associated with plant transpiration. The pore-scale travel time is generated from the maximum flow rate under saturated conditions and a typical pore size. At the field-scale, the characteristic time is interpreted as the growing season duration, and the characteristic length is derived from the measured evapotranspiration in that period. We show that the two scaling results are equivalent, and they are each in accord with observed vegetation growth limits, as well as with actual limiting transpiration values. While the conceptual approach addresses transpiration, most accessed data are for evapotranspiration. The equivalence of the two scaling approaches suggests that, if horizontal flow is the dominant pathway in plant transpiration, horizontal unsteady flow follows the same scaling relationship as root growth. Then, we propose a corresponding scaling relationship to vertical infiltration, a hypothesis which is amenable to testing using infiltration results of Sharma and co-authors. This alternate treatment of unsteady vertical flow may be an effective alternative to the commonly applied method based on the diffusion of water over a continuum as governed by Richards’ equation.
1. Introduction
How can one predict the complex time-dependence of the cumulative infiltration into a soil? Why do estimates of evapotranspiration (ET) at different spatial scales differ? What do infiltration and ET have in common and how do they differ? An initial attempt to answer these questions within the context of percolation theory is given here.
When rain falls upon an unsaturated porous medium such as dry soil, some runs off, some evaporates from the terrestrial surface, and some infiltrates into the medium. Of the latter, a fraction is taken up by the plants through the roots and evaporated from the stomata (a process termed transpiration), and the remainder continues downward to the water table (net infiltration or deep percolation). While the total return of water to the atmosphere includes evaporation and transpiration, known as evapotranspiration (quantities often measured together), our focus is on the plant pathway. Both transpiration and infiltration are instrumental in the drawdown of CO2 from the atmosphere, the former through photosynthesis, the latter through chemical weathering. In each case, water is critical for the chemistry: in transpiration, for transporting the CO2 from the atmosphere, plant roots and decaying organic material; in infiltration, as a reagent and as an agent to bring nutrients to plant roots, and thus facilitate nutrient uptake.
The fact that water carries reactive solutes or nutrients with it is relevant to the processes of weathering and vegetation growth, among others. The mathematical treatment of reactive solute transport is a possible source of techniques to address unsteady flow, since the majority of solute transport appears to be non-Gaussian1 [1]. Such non-Gaussian transport is generally inconsistent with the Gaussian transport predicted by the Advection–Dispersion Equation (ADE), a formulation which is echoed in the treatment of unsteady flow using the Richards’ equation [2]. Thus, particularly if infiltration experiments do not prove consistent with the Richards’ equation, there may be a motivation to address such discrepancies within the framework of non-Gaussian transport theories. While a wide range of mathematical techniques have been applied to generate non-Gaussian transport, including the Continuous Time Random Walk, or CTRW (see recent review in [3]), to our knowledge, the only technique that has also been adapted to the problem of variable infiltration is the fractional derivative, familiar from Fractional Advection Dispersion Equation (FADE) applications [4]; see [5] for application of the FADE to infiltration.
Scaling laws for solute transport based on percolation concepts, originally proposed by [6] and followed up by [7,8], have recently been applied to the growth and development of plants [9,10], as well as for chemical weathering (see e.g., [11,12]). These scaling laws treat the advective spreading of solutes into a medium that is originally fully filled with pure water, or is in the process of saturation. It is the effective “compressibility” of solutes (changing the volume of a plume as it spreads) that distinguishes solute transport from water flow under steady flow conditions, and leads to the significant non-Gaussian characteristics of the transport [11]. In unsaturated, unsteady flow, water spreads (imbibes) into a medium that is originally filled with air, in contrast to steady flow, for which the medium water content does not change. In both cases, the mass advected into the medium is presumed to preferentially follow paths of optimal flow as described in percolation theory, making a predictive approach based on analogy attractive. Importantly, both unsteady flow and solute transport are treated traditionally (in continuum mechanics) as diffusive processes [13]; however, advection of solutes into such a medium is distinctively different from diffusion [12]. The analogy between water infiltration and solute transport in terms of the concept of compressibility thus suggests that the same scaling framework that works for chemical weathering and plant growth can be applied towards unsteady water infiltration.
Therefore, the main objectives of this study are (1) to develop theoretical scaling laws for infiltration and transpiration processes in soils under unsteady flow conditions (e.g., the optimal transport distances and the most likely transport time, respectively); and (2) to compare the proposed models with experimental data. Below, we review the scaling theory of solute transport, followed by a brief discussion of scaling arguments linking vegetation growth [9] and soil formation [14].
2. Theory
In the following, we overview the classical theory of unsteady flow or solute transport only, as their results can be contrasted with the predictions of percolation theory. Since percolation theory (see e.g., [15,16]) is critical to the hypotheses tested in this manuscript, we turn to that subject first. Percolation theory comes in the three variants: site, bond and continuum (corresponding to volume fraction). Following [17,18], Hunt [19] has advocated using percolation formulas adapted to continuum percolation problems for predicting flow and transport phenomena of porous media. The reason is that, with the wide range of pore sizes and local coordination numbers, it is difficult to place such media on any kind of regular grid. Nevertheless, Sahimi [20] showed that wetting, in which water must occupy an entire pore, is a site percolation problem in principle, while drying, for which water must exit through a pore neck, should be conceptualized as a bond percolation problem. Either is more properly treated as an invasion percolation problem than as a random percolation problem while the fluid, either air or water, is incompressible at the pore scale. Such pore-scale incompressibility allows fluid to become trapped in pores rather than displaced, when a second fluid invades. Thus, wetting is invasion site percolation with trapping, drying is invasion bond percolation with trapping, and fully saturated conditions are termed random percolation. This classification scheme is important if one seeks relevant information on various percolation scaling predictions, as we do below.
One useful application from percolation theory is critical path analysis (CPA) developed to find dominant paths of charge or fluid flow through heterogeneous media [19,21,22]. The concept is most easily understood in a network model constructed of pore bodies connected through pore throats (see e.g., [23]), for which the difficulty of flow is localized along the connections between pores and discretized accordingly. Within the percolation theory framework, sites and bonds are equivalent to bodies and throats in a network of pores, respectively. The strategy of CPA is to apply the percolation threshold—the minimum fraction required to form the sample-spanning cluster and let the system percolate—to the spread of local resistance values in order to find the most resistive element on the most highly conductive (or permeable) interconnected path through the system. Sahimi [16] observed that solute transport along such optimal paths as described in percolation theory should follow the same scaling laws as solute transport through actual percolation clusters. Here, we extend that conjecture to unsteady flow as well.
Percolation Scaling Theory for Solute Transport
Percolation theory provides a promising framework that has been widely applied to study flow and transport in interconnected networks and media. Percolation theory combines microscopic characteristics of a medium with its topological properties to determine macroscopic quantities, such as conductivity, permeability, and dispersion. A full theoretical treatment of the scaling of solute transport is beyond the scope of the present work, as we are interested in distances and times such as minimum and optimal transport distances and the most likely transport time as a function of system size, rather than arrival time distributions. The most likely transport time has been found to generate transport velocities and fluxes reasonably accurately for up to five orders of magnitude of time [12]. For a comprehensive review of percolation theory applications on fluid flow and solute transport, see [16,24,25].
Percolation theory applies most simply to porous media for which flow or conduction along bonds (pore throats) between nodes (pore bodies) is either possible or impossible [26]. Here, it delivers relatively simple scaling laws for, e.g., conduction or flow properties. Such binary media can be represented by networks with resistances of value 1 or infinity, but are not characteristic of typical natural porous media, since flow is strongly pore-size dependent and pore size typically spans several orders of magnitude. Instead of bond percolation, continuum percolation has been used [17,18,19] to address flow in more realistic pore networks, with irregular lattices made of pores of different sizes and shapes. In media with a wide range of pore sizes, critical path analysis [21,22] utilizes the percolation threshold value to generate a percolating sub-network composed of all resistances less than or equal to a “critical” value, a technique which can provide effective flow parameters such as conductivity or permeability [19]. Thus, a sub-network composed of all the resistances less than or equal to a “critical” value just percolates. The importance in the present context is that Sahimi argued already more than 20 years ago [16] that solute transport in real porous media with wide ranges of pore sizes should also follow percolation scaling results because of the concentration of the flow along such critical paths. Because critical path analysis is applicable to virtually all natural soils [27], percolation theory is equally relevant to solute transport; thus, we begin by listing solute transport results from percolation theory.
Lee et al. [6] addressed the spatiotemporal scaling of solutes transported across a two-dimensional system at the percolation threshold. The authors found that for a line source of solute in a system of length x, the minimum path length, L, for particles exiting on the opposite face scales with x as , with a most likely time of , where Dmin and Db are the chemical paths exponent and the fractal dimensionality of the percolation backbone, respectively. However, when the medium is highly heterogeneous, e.g., with a wide range of pore sizes, the length L of the optimal paths that provide the most rapid transport across the system is proportional to the system length to a different exponent, Dopt, rather than to Dmin [28,29]. Dopt is the so-called optimal paths exponent, and is determined for the heterogeneous limit [30]. The values of the exponents determined by [30] are mostly accurate to five significant figures, but the optimal paths exponent only to three. The most important distinctions in porous media that affect the exponents Db and Dmin relate to the connectivity of the paths and the specific percolation conditions: (i) imbibition (wetting) conditions correspond to site invasion percolation with trapping; (ii) drying conditions to invasion percolation with trapping; and (iii) saturated flow to random percolation [20]. Following [6] the minimum path length L is (using Dmin from [30]):
where x0 is the bond length, and 2D and 3D refer to two and three dimensional systems. In the case of porous media, x0 corresponds to the inter-pore distance or a typical grain size. Numerical prefactors of order unity are less well constrained, hence omitted from Equations (1) and (2). The value of the exponent Dopt in 2D (for all conditions of saturation), 1.21, is similar to the value of Dmin for 2D imbibition or drainage, 1.21, and the optimal path lengths L scale the same as the shortest paths for imbibition or drainage, L = x0(x/x0)1.21. In 3D Dopt = 1.46. Similarly, the most likely travel time is [30]
We note that the exponent for 3D imbibition, 1.861, differs from the value for saturated conditions, 1.87 (Equation (3)). As we discuss in Section 6, such a small discrepancy actually leads to detectable differences in scaling of the cumulative infiltration. Although the conditions we address are (1) for vertical infiltration, wetting, 3D flow; and (2) for transpiration, desaturating 2D flow, we include the entire suite of values of these exponents in case conditions addressed in other investigations are different. In particular, swelling soils may develop mudcracks on drying, providing preferential flow topologies for imbibition that are constrained to two-dimensional surfaces.
In Equations (1)–(4), t0 is the time for fluid to traverse a distance x0, such that v0 = x0/t0 is the fluid flow rate at the pore scale. The contrast between the exponent 1.87 for the most likely time and 1.37 for the shortest distance (for 3D saturated conditions) helps explain why paths that do not appear to be extraordinarily tortuous (20 m in a 1 m column) can still retard the arrival of solutes by an enormous factor [11] (over 1000). Since we are interested in (1) vegetation growth and transpiration in 2D (optimal paths exponent); and (2) unsteady flow in 3D (for the wetting conditions in Philip’s infiltration theory), we select here the following exponent values (from Equations (1)–(4)): (i) Dopt (2D) =1.21 for vegetation growth, and (ii) Db (3D imbibition) = 1.861 for vertical infiltration. These two exponents are essentially the same as the two values assumed relevant [9,12] for soil formation (1.87) and vegetation growth (1.21), although as a result, our analogy to soil formation and chemical weathering is not quite precise. In [12], for example, soil was assumed to form under either saturated or saturating conditions, but only the exponent 1.87 was used. Given all the uncertainties in soil formation processes operating at time scales of up to tens of millions of years, ignoring the possibility that the appropriate exponent might, for some fraction of the time, be 1.861, seemed justified. However, in unsteady infiltration experiments, of much shorter duration and with much greater control, the exponent is constrained conceptually to be 1.861.
3. Experimental Data
Experimental data used for the analysis in this study are from three databases: (1) Falster et al. [31]; (2) Hunt [9] and (3) Sharma et al. [32]. The Biometric and Allometric Database (BAAD), in [31] includes allometric data that consist of height and age for plantation species as well as from plants growing under natural conditions. The data points from plants grown in natural conditions, i.e., 5539 out of 6650 are used to compare with the percolation theory scaling relationship. The data given in [9], the Hunt dataset, were collected from well over 100 sources, but the natural plant data were selected to include only faster growing species, notably the three sequoia species, many eucalypts, eastern cottonwoods, douglas firs, tropical dipterocarps, etc. Crop data were scarce, as most studies address total biomass, while soil data corresponded mainly to depths to the Bw horizon.
The Sharma et al. database [32] consists of experimentally measured cumulative infiltration via double-ring infiltrometers at 26 sites on a watershed, called R-5, close to Chickasha, Oklahoma. R-5 is native grassland dominated by silt loam soil texture with a slope of near 3% and an area of 9.6 ha.
4. Relevance of Percolation Scaling to Vegetation Growth and Soil Formation
The primary purposes in this section are: (1) to show the basis of the pore-scale link between vegetation growth and soil formation; (2) provide a basis for upscaling the pore-scale water flow rate controlling vegetation growth to growing season transpiration rates, as addressed in the next section. This provides both a context and a method for the following topics.
Hunt [9,14] showed that the relationship
with Db = 1.87 (for 3D flow connectivity) and x0 a typical grain diameter predicts soil depths over an extensive range of time scales (a decade to 100 Ma), where v0 = x0/t0 was taken to be the pore-scale infiltration rate. Equation (5) provides a soil formation rate of Rs = dx/dt = 0.53v0(x/x0)−0.87 or 0.53v0 (t/t0)−0.46. Furthermore, ref. [12] showed that the related scaling of solute transport rates (from the velocity of the centroid of the solute spatial distribution) could predict soil formation rates at time scales of up to 60 Ma, and that that the predicted proportionality of Rs to v0 is in accordance with the observed four orders of magnitude variability in Rs when precipitation also varied over four orders of magnitude (from the Atacama desert to the New Zealand Alps). Thus, rate of flow of water through the surface medium is responsible for much of the variability in soil formation rates.
Considering vegetation linear extent (root radial extent, RRE, or plant height), Hunt and Manzoni [9,10] showed that
with Dopt = 1.21 (2D) and x0 taken as a typical pore diameter (~10, the geometric mean plant xylem diameter, Watt [33] hold for time scales ranging from minutes to 100 kyr. In this case, x is either the plant height, or the root radial extent, which have been shown to be closely equivalent over time scales from a growing season to about 40 years [10,34,35,36,37]. Once again, v0 = x0/t0 is the pore-scale flow rate, ranging here from about 24 cm/year to 20 m/year. This is a similar, though narrower range of flow rates than those relevant for soils under typical conditions i.e., about 2.0 cm/year to 20 m/year. The soil depths and the linear extent of natural vegetation computed from Equations (5) and (6) are given in Figure 1. The vegetation data incorporate a wide range of data sets: at time scales from minutes to days, these are root tip extension rates, for weeks to hundreds of years, they are plant heights (which are a proxy for root radial extent over most of this range), and for thousands of years up, the measurements are subsurface extents of clonal organisms, such as Posidonia oceanica and various tree species, or fungi. We note that the leaf area index could also be used to characterize plant growth [38], instead of plant height. At the longest time scales, the soil data are mostly paleosols and laterites. At the shortest time scales, the soil data include primarily soil formation after disturbances, such as landslides, glacial retreat, or tree-throw. For typical pore and particle size of 10 μm and 30 μm, respectively, the presented pore scale velocities bound the data. We point out that since larger pores have a smaller retention capacity as they are easily drained, their contribution to plant growth is smaller [33]. We will apply essentially the same Equations (5) and (6) to vertical infiltration and horizontal flow associated with transpiration, respectively.
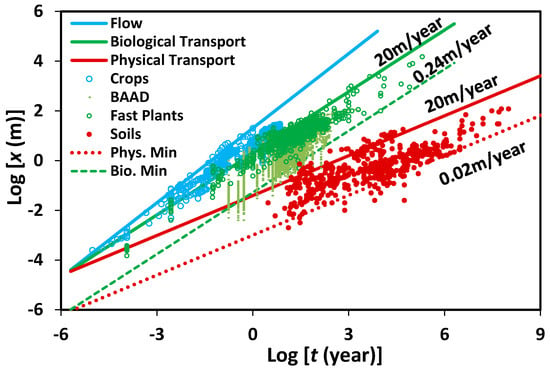
Figure 1.
Vegetation growth and soil formation as a function of time. Scaling predictions for vegetation growth, both natural (green) and intensively managed (blue), using maximum pore scale flow rates of 20 m/year, and minimum flow rates of 0.24 m/year. We assume pore and particle sizes of 10 μm and 30 μm, respectively, in accord with typical silt particle sizes and the usual assumption that pore diameters are about 30% that of particles [46]. The vegetation data are divided into crops [9], for which nitrogen and other nutrients were supplied; “fast plants” [9,10] and BAAD [31]. The sources for the soil database are referenced in [9] and [10]. The same maximum flow rate prediction (marked “Flow”), but using vertical solute transport scaling (“Physical Transport”), generates the upper bound on soil production as on plant growth (“Biological Transport”) using the horizontal optimal paths scaling. “Phys Min” and “Bio Min” are the corresponding predictions at the given lower flow rates. The lower bound for soil formation is consistent with a smaller flow velocity than for vegetation growth, in accord with the fact that soil formation, albeit at a very slow rate, can occur in regions where precipitation is insufficient to support plant growth (e.g., the Atacama desert).
5. Potential Relationship with Unsteady Flow
At spatial and temporal scales larger than the (pore) scales considered above, we hypothesize that the ratio of a transpiration depth to a transpiration time scale can take the place of the pore-scale flow velocity v0 = x0/t0. Thus, x0/t0 → xg/tg, where xg is the transpiration during a growing season (measured typically as a depth) and tg is the length of the growing season. Using this hypothesis, we rewrite the scaling for vegetation growth in Equation (6) as
Furthermore, using total ET depths xg (instead of transpiration data, which is much less abundant) that range from 0.02 m (the Namibian desert at the dry end of the scale [39]) to 1.65 m (tropical rainforests and savannahs [40]) for a growing season of tg = 0.5 year, provides x = 0.02 m (t/180 days)0.83 and x = 1.65 m (t/180 days)0.83, for a minimum and a maximum transpiration, or, equivalently, by Equation (7), for a minimum and maximum growing season plant height, respectively. As shown in Figure 2, these values of x (tg) bound the world’s plant heights [31] at a time corresponding to the length of the growing season, meaning that Equation (7) generates essentially identical scaling predictions of plant growth rates as depicted in Figure 1.
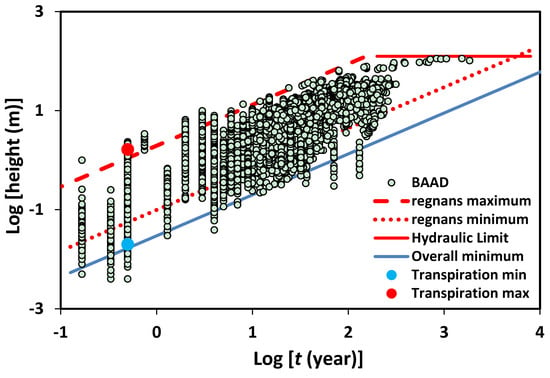
Figure 2.
Allometric data of plant height vs. time and age (5539 data points representing the unmanaged plants in the BAAD) [31] is compared with our predicted upper and lower limits on growth rates using the pore-scale flow rates discussed in the text. “Regnans maximum” is the maximum plant height of E. regnans computed from Equation (7) with 1 μm/s flow rate [9], a value which corresponds to the prediction from the analogous equation at larger scales using a corresponding ET of ~1650 mm in a growing season. “Regnans minimum” is generated from “regnans maximum” by multiplying by a factor 1/20, in general accord with the variability in precipitation to pan evaporation ratio determined in [41]. “Overall minimum” is obtained by multiplying “regnans maximum” by the ratio of smallest to largest ET values in the BAAD, 1/82.5. The hydraulic limit is postulated as a cavitation limit [47]. Note that the minimum and maximum scaling relationships could be equally expressed in terms of the limiting growing season transpiration values, 20 mm at the dry end of the spectrum [39] and 1650 mm at the wet end [40], which are plotted on the graph at the time of six months, a typical growing season. The correspondence between plant height and growing season transpiration suggests the viability of growth models in terms of growing season transpiration values.
The data of [31] Falster et al. (2015) is a compilation performed by many authors over many years of dozens of studies worldwide. Note that regnans minimum and maximum predictions are generated from the range in adult Eucalyptus regnans heights (a factor 22) across a precipitation gradient [41] together with the demonstration [10], that all Eucalyptus growth rates in the study of [42] followed the scaling of Equation (6), but with variations in the t0 values consistent with a gradation of flow rates across their study sites. Such a close correspondence between predicted upper and lower vegetation growth limits and the observed range of actual vegetation growth rates in Figure 2 (the independent meta-data set of [31]) implies the possibility of applying an analogous upscaling to the horizontal soil moisture transport associated with the plant transpiration. Further, it also suggests a close relationship between transpiration “depths” and plant heights, which is also indicated by examining record breaking crop heights [9]. For amaranth, sunflowers, hemp, and corn, these record heights all are approximately 10 m in a growing season, and for tomatoes, 20 m in a year. Such rates correspond fairly closely to some classic literature source values for the saturated hydraulic conductivity, KS. In particular, a geometric mean KS value for soils is roughly 1 μm/s [43,44] and typical saturated subsurface flow rates are of the same order of magnitude [45]. An amount of 1 μm/s corresponds to a flow distance of about 32 m in 1 year. Thus, such high transpiration rates required for growth rates on the order of 20 m/year would require the existence of very nearly saturated conditions much of the time in a typical soil. This approximate correspondence suggests that the soil saturated hydraulic conductivity may generate a rough maximum for plant growth rates, if the water (and nutrient) supply is adequate. We note that in the above we consider saturation as optimal conditions in terms of conducting water and nutrients; unsaturated conditions are optimal in terms of aerobic root metabolism.
6. Relevance of Percolation Scaling to Infiltration
Philip infiltration theory [48,49] represents cumulative infiltration I as having two terms, one a steady-state component, proportional to the time, the second a transient component proportional to the square root of time. Existence of higher order terms is also acknowledged, although these terms are mostly neglected. The two-parameter Philip’s equation is
Here, S is sorptivity, and A is a constant coefficient that depends on soil properties and initial water content. In the soil physics literature, in Equation (8) the first term represents the effect of gravity forces and the second term is due to sorptive forces. In Philip’s theory [50], A is proportional to the saturated hydraulic conductivity, KS, (), while S is proportional to the square root of KS, suggesting a dependence of S ~ A0.5, as noted (and also investigated) by [32]. However, as we show below, our treatment yields a different proportionality, S ~ A0.77.
We propose that the transient term is not governed by diffusion, but by the same scaling relationship that describes solute transport under saturated (or saturating) conditions. This transient term is suggested to correspond conceptually to the solute that is carried along with the water, with the steady-state infiltration term thus representing the advecting fluid. The cumulative infiltration is, therefore, given by
in which the first term represents the steady state infiltration, and the second term the scaling power law from percolation theory. Note that in Equation (9) we have explicitly used the value of Db = 1.861 for conditions of imbibition, rather than 1.87, appropriate for saturated conditions. Although the two resulting exponents (1/Db) of 0.5348 (saturated) and 0.537 (imbibition) are quite similar, since the medium is unsaturated by definition, one should use the latter, as in Equation (9).
Consider our Equation (9) where t0 = x0/v0, and v0 is proportional to the saturated hydraulic conductivity, KS. Most formulations (see e.g., [51]) of KS lead to a proportionality to x02 (as does the critical path analysis of [52]), such that x0/v0 is proportional to x0−1. This makes A proportional to x02 (or KS) but S proportional to x01.53, or KS0.77, suggesting a different proportionality S ≈ A0.77, than that in Philip’s theory, S ≈ A0.5.
Is there an analysis that can confirm the relevance of the exponents, 1 and 0.5? Could it distinguish between 0.5 and 0.54 (0.537 rounded up) in the transient term? The analysis proposed by [32] can reasonably confirm the approximate form of the equation, but, although the analysis does suggest that the transient-term exponent is not precisely 0.5, it cannot establish that it is actually 0.54. However, Figure 1b in [53] indicates that a much better collapse to a single curve results when infiltration data are scaled according to xt−0.55 than for xt−0.5, meaning that an exponent value of 0.537 is a better approximation than 0.5. Although the values of the exponents in [30] are exceptionally well constrained, it is known that this percolation scaling is precise only in the limit of large system sizes [15]. Systems may be considered large at upwards of 100 bonds on a side, which for typical soil particle sizes in the tens of microns means length scales of millimeters and up [25].
In the first step of their analysis (which does not address the specific form of A and S), Sharma et al. [32] consider the functions
and
These functions transform Equation (8) to β = τ + τ0.5, independent of the specific values of A and S, as stated by [32], but generate a slightly different result if I is given by Equation (9). In particular, we have
Perfect scaling, as predicted by Philip infiltration, is no longer quite developed, and a weak source of scatter is introduced (the factor t00.04), generally in conformance with the results. However, in order to determine with certainty whether the residual scatter can be attributed to the additional time factor produced by our particular theoretical description, it would be necessary to know the individual values of t0. Unfortunately, these values are not obtainable from the published data. It is clear, however, that the deviation must be due to a discrepancy in the power, because the formulation of the scaling functions [32] eliminates any scatter due to variability in the coefficients. For a first estimate of how much uncertainty is introduced by the factor t00.04, note that t0 is proportional to τ−1.06. From this, we estimate the variability in t0 using the largest and smallest τ values in the data set, 0.271 and 5.8 × 10−4, respectively, providing minimum and maximum multiplicative factors of 1.05 and 1.32. Multiplication of the second term by these values gives the lower and upper bounds, respectively, on the theoretical prediction in Figure 3. It should be noted finally that additional terms in the infiltration treatment due to Philip would also generate deviations in scaling. Interestingly, however, our lowest order theoretical treatment appears to generate just the right magnitude of scaling deviations to be compatible with experiment.
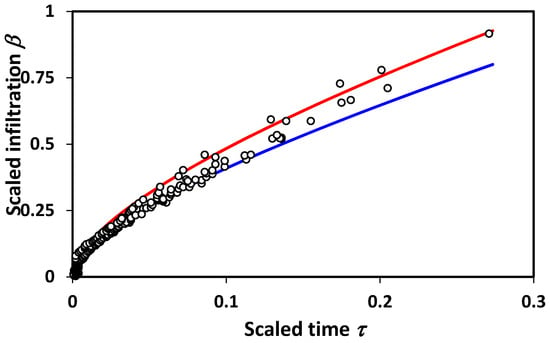
Figure 3.
Scaled parameter , determined from Equation (10) vs. scaled time , calculated from Equation (11), for 26 experiments from [32] (digitized from their Figure 2b). The infiltration data represent field measurements using double-ring infiltrometers and 26 infiltration tests carried out on a 9.6-ha grassland watershed (called R-5) near Chickasha, Oklahoma. Given that t0 is proportional to τ−1.06, we estimated the variability in t0 in Equation (12) using the largest (0.271) and smallest 5.8 × 10−4 values of τ in the dataset. This provides minimum and maximum multiplicative factors of 1.05 and 1.32. Multiplication of the second term in Equation (12) by these values gives the lower and upper bounds, respectively for the theoretical predictions. The blue and red curves are the minimum and maximum expected from the theory in this study. Philip’s infiltration theory allows no scatter, and would, to within the resolution of the graph, coincide with the blue curve.
An important point relates to the limits of applicability of percolation techniques. For very short time scales, or equivalently, very small systems, fluctuations associated with the statistical variability introduced by small system sizes will produce a wide variability in results, and, typically, overestimate the infiltration (Figure 3), while underestimating the mean [19]. In accord with these observations, we reproduce in Figure 4 a bi-logarithmic plot of the data and predictions given in Figure 3. The results are in accord with the statistical interpretation, and with previous numerical results [19] for the finite-size scaling of the hydraulic conductivity, K, which similarly had a few values of K that are much higher than predicted, and a larger number that are much lower (Figure 4). This general conclusion is also in accord with the treatment of solute transport [54], for which the simple scaling result underestimated the variability in solute dispersion at shorter distance scales, requiring calculation of the entire solute arrival time distribution for quantitative agreement with the experiment. If infiltration is analogous, the corresponding treatment of unsteady flow could introduce pore-size distribution effects into the short time (or distance) predictions.
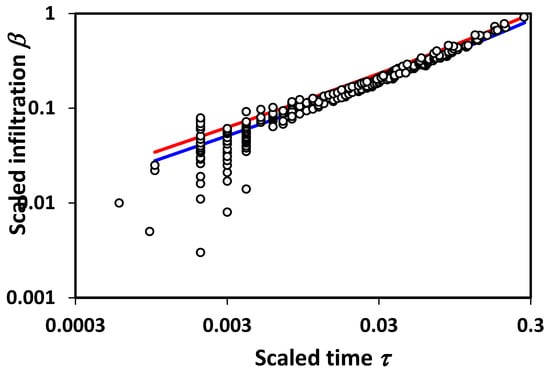
Figure 4.
Replotting the data and predictions given in Figure 3 bi-logarithmically (same color coding) demonstrates that the data agree with the statistical nature of percolation. In particular, as times and corresponding length scales increase relative to pore-scale times, the statistical constraints from percolation theory become more restrictive, and large fluctuations related to small sample size become less important.
Finally, to confirm the accuracy of our above postulate, we test in Figure 5 the prediction in [32] regarding the relationship between A and S. Fitting of the data into a power-law form yields the relationship S ~ A0.727, which is in reasonably good agreement with our prediction in the discussion following Equation (8) (0.77, 6% difference), but deviates significantly (by 45%) from the value predicted by the classical Philip’s infiltration theory, 0.5.
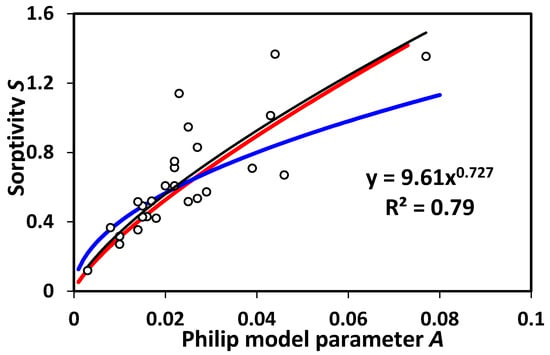
Figure 5.
Sorptivity S as a function of Philip model parameter A. Comparison of the prediction of percolation scaling (red) with the 26 experiments collected by [32], digitized from their Figure 5, for the relationship between S and A, the coefficients of the transient and steady-state terms of the infiltration equation, respectively. Note that the exponent observed from the data, 0.727 (black line), is in much closer agreement with our prediction using percolation theory, 0.77 (in red), than with the value in Philip’s infiltration theory, 0.5 (in blue).
7. Conclusions
Existing scaling predictions from percolation theory of vertical solute transport, chemical weathering and soil formation [9,11,12,14] invoke 3D imbibition (or saturated) fractal dimensionality of the backbone, relating time and distance of solute transport. Here, by comparison with an analysis of a series of experiments by Sharma et al. [32], it was shown that essentially the same scaling describes vertical infiltration. For horizontal infiltration, we adopt scaling arguments for the growth of vegetation based on the ability to find essential nutrients to the scaling of transpiration. As a consequence, we are able to express plant growth extent directly as the transpiration depth.
Overall, the above arguments support the use of percolation scaling formulations for unsteady flow in heterogeneous media such as soils, both horizontally (along layers), and vertically (through them). The implication of our approach, where percolation scaling is based on advection rather than diffusion, is that the Richards’ equation (which takes the form of a diffusive process) is not an adequate description for scaling of unsteady flow. These two results for flow bear important implications for the formation of soil and the growth of the vegetation within the soil.
Acknowledgments
The authors are grateful to the Guest Editor, Boris Faybishenko (Lawrence Berkeley National Laboratory), for the invitation to present the paper in the Special Issue “Water and Solute Transport in the Vadose Zone” in the journal “Water”. We are also thankful to Ryan Stewart, Virginia Tech, for a critical reading of the manuscript.
Author Contributions
Allen G. Hunt conceived the study, Behzad Ghanbarian did the analysis, and Ran Holtzman wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cushman, J.H.; O’Malley, D. Fickian dispersion is anomalous. J. Hydrol. 2015, 531, 161–167. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Co. Inc.: New York, NY, USA, 1972. [Google Scholar]
- Edery, Y.; Drorr, I.; Scher, H.; Berkowitz, B. Anomalous reactive transport in porous media: Experiments and modeling. Phys. Rev. E 2015, 91, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Machado, J.; Mainardi, T.F.; Kiryakova, V. Fractional calculus: Quo vadimus? (Where are we going?), Contributions to roundtable discussion held at ICFDA, 2014. Fract. Calculus Appl. Anal. 2015, 18, 495–526. [Google Scholar]
- Su, N. Mass-time and space-time fractional partial differential equations of water movement in soils: Theoretical framework and application to infiltration. J. Hydrol. 2014, 519, 1792–1803. [Google Scholar] [CrossRef]
- Lee, Y.; Andrade, J.S.; Buldyrev, S.V.; Dokholoyan, N.V.; Havlin, S.; King, P.R.; Paul, G.; Stanley, H.E. Traveling time and traveling length in critical percolation clusters. Phys. Rev. E 1999, 60, 3425–3428. [Google Scholar] [CrossRef]
- Hunt, A.G.; Skinner, T.E. Longitudinal dispersion of solutes in porous media solely by advection. Philos. Mag. 2008, 88, 2921–2944. [Google Scholar] [CrossRef]
- Hunt, A.G.; Skinner, T.E. Incorporation of effects of diffusion into advection-mediated dispersion in porous media. J. Stat. Phys. 2010, 140, 544–564. [Google Scholar] [CrossRef]
- Hunt, A.G. Spatio-temporal scaling of vegetation growth and soil formation. Vadose Zone J. 2015, 15. [Google Scholar] [CrossRef]
- Hunt, A.G.; Manzoni, S. Networks on Networks: The Physics of Geobiology and Geochemistry; Morgan and Claypool (Institute of Physics): Bristol, UK, 2015. [Google Scholar]
- Hunt, A.G.; Ghanbarian-Alavijeh, B.; Skinner, T.E.; Ewing, R.P. Scaling of geochemical reaction rates via advective solute transport. Chaos 2015, 25. [Google Scholar] [CrossRef] [PubMed]
- Hunt, A.G.; Ghanbarian, B. Percolation theory for solute transport in porous media: Geochemistry, geomorphology, and carbon cycling. Water Resour. Res. 2016, 52, 7444–7459. [Google Scholar] [CrossRef]
- Jury, W.A.; Horton, R. Soil Physics, 6th ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hunt, A.G. Soil depth and soil production. Complexity 2015, 21, 42–49. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharonoy, A. Introduction to Percolation Theory, 2nd ed.; Taylor and Francis: London, UK, 1994. [Google Scholar]
- Sahimi, M. Applications of Percolation Theory; Taylor & Francis: London, UK, 1994. [Google Scholar]
- Halperin, B.I.; Feng, S.; Sen, P.N. 1985, Differences between lattice and continuum percolation transport exponents. Phys. Rev. Lett. 1985, 54, 2391–2394. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Halperin, B.I.; Sen, P.N. Transport properties of continuum systems near the percolation threshold. Phys. Rev. B 1987, 35, 197–214. [Google Scholar] [CrossRef]
- Hunt, A.G. Applications of percolation theory to porous media with distributed local conductances. Adv. Water Resour. 2001, 24, 279–307. [Google Scholar] [CrossRef]
- Sahimi, M. Flow phenomena in rocks—From continuum models to fractals, percolation, cellular automata, and simulated annealing. Rev. Mod. Phys. 1993, 65, 1393–1534. [Google Scholar] [CrossRef]
- Pollak, M. A percolation treatment of dc hopping conduction. J. Non-Cryst. Solids 1972, 11, 1–24. [Google Scholar] [CrossRef]
- Ambegaokar, V.N.; Halperin, B.I.; Langer, J.S. Hopping conductivity in disordered systems. Phys. Rev. B 1971, 4, 2612–2621. [Google Scholar] [CrossRef]
- Fatt, I. The network model of porous media. I. Capillary pressure characteristics. Pet. Trans. AIME 1956, 207, 145–159. [Google Scholar]
- Sahimi, M. Flow and Transport in Porous Media and Fractured Rock, 2nd ed.; Wiley: Weinheim, Germany, 2011. [Google Scholar]
- Hunt, A.G.; Ewing, R.P.; Ghanbarian, B. Percolation Theory for Flow in Porous Media; Springer: Berlin, Germany, 2014. [Google Scholar]
- Berkowitz, B.; Balberg, I. Percolation theory and its application to groundwater hydrology. Water Resour. Res. 1993, 29, 775–794. [Google Scholar] [CrossRef]
- Hunt, A.G.; Ewing, R.P.; Horton, R. What’s wrong with soil physics? Invited Comment. Soil Sci. Soc. Am. J. 2013, 77, 1877–1887. [Google Scholar] [CrossRef]
- Lopez, E.; Buldyrev, S.V.; Braunstein, L.A.; Havlin, S.; Stanley, H.E. Possible connection between the optimal path and flow in percolation clusters. Phys. Rev. E 2005, 72, 056131. [Google Scholar] [CrossRef] [PubMed]
- Porto, M.; Havlin, S.; Schwarzer, S.; Bunde, A. Optimal path in strong disorder and shortest path in invasion percolation with trapping. Phys. Rev. Lett. 1997, 79, 4060–4062. [Google Scholar] [CrossRef]
- Sheppard, A.P.; Knackstedt, M.A.; Pinczewski, W.V.; Sahimi, M. Invasion percolation: New algorithms and universality classes. J. Phys. A 1999, 32, L521–L529. [Google Scholar] [CrossRef]
- Falster, D.S.; Duursma, R.A.; Ishihara, M.I.; Barneche, D.R.; Fitzjohn, R.G.; Varhammar, A.; Aiba, M.; Ando, M.; Anten, N.; Aspinwall, M.J.; et al. BAAD: A biomass and allometry database for woody plants. Ecology 2015, 96, 1445. [Google Scholar] [CrossRef]
- Sharma, M.L.; Gander, G.A.; Hunt, C.G. Spatial variability of infiltration in a watershed. J. Hydrol. 1980, 45, 101–122. [Google Scholar] [CrossRef]
- Watt, M.; Silk, W.K.; Passioura, J.B. Rates of root and organism growth, soil conditions and temporal and spatial development of the rhizosphere. Ann. Bot. 2006, 97, 839–855. [Google Scholar] [CrossRef] [PubMed]
- Kalliokoski, T.; Nygren, P.; Sievanen, R. Coarse root architecture of three boreal tree species growing in mixed stands. Silva Fennica 2008, 42, 189–210. [Google Scholar] [CrossRef]
- Stone, E.L.; Kalisz, P.J. On the maximum extent of tree roots. For. Ecol. Manag. 1991, 46, 59–102. [Google Scholar] [CrossRef]
- Phillips, C.J.; Marden, M.; Suzanne, L.M. Observations of root growth of young poplar and willow planting types. N. Z. J. For. Sci. 2014, 44, 15. [Google Scholar] [CrossRef]
- Phillips, C.J.; Marden, M.; Suzanne, L.M. Observations of “coarse” root development in young trees of nine exotic species from a New Zealand plot trial. N. Z. J. For. Sci. 2015, 45, 1–15. [Google Scholar] [CrossRef]
- Bréda, N.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Seeley, M.K. Grassland productivity: The desert end of the curve. S. Afr. J. Sci. 1978, 74, 295–297. [Google Scholar]
- Box, E.O.; Holben, B.N.; Kalb, V. Accuracy of the AVHRR vegetation index as a predictor of biomass, primary productivity, and net CO2 flux. Vegetatio 1989, 80, 71–89. [Google Scholar] [CrossRef]
- Givnish, T.J.; Wong, C.; Stuart-Williams, H. Determinants of maximum tree height in Eucalyptus species along a rainfall gradient in Victoria, Australia. Ecology 2014, 95, 2991–3007. [Google Scholar] [CrossRef]
- Walsh, P.G.; Barton, C.V.M.; Haywood, A. Growth and carbon sequestration rates at age ten years of some eucalypt species in the low to medium-rainfall areas of New South Wales, Australia. Aust. For. 2008, 71, 70–77. [Google Scholar] [CrossRef]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Bloeschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Gvirtzman, H.; Roberts, P.V. Pore scale spatial analysis of two immiscible fluids in porous media. Water Resour. Res. 1991, 27, 1165–1176. [Google Scholar] [CrossRef]
- Koch, G.W.; Sillett, S.C.; Jennings, G.M.; Davis, S.D. The limits to tree height. Nature 2004, 428, 851–854. [Google Scholar] [CrossRef] [PubMed]
- Philip, J.R. The theory of infiltration: 4. Sorptivity and algebraic infiltration equations. Soil Sci. 1957, 84, 257–268. [Google Scholar] [CrossRef]
- Philip, J.R. Sorption and infiltration in heterogeneous media. Aust. J. Soil Res. 1967, 5, 1–10. [Google Scholar] [CrossRef]
- Philip, J.R. Moisture equilibrium in the vertical in swelling soils. I. Basic theory. Soil Res. 1969, 7, 99–120. [Google Scholar]
- Bernabé, Y.; Bruderer, C. Effect of the variance of pore size distribution on the transport properties of heterogeneous networks. J. Geophys. Res. 1998, 103, 513–525. [Google Scholar] [CrossRef]
- Hunt, A.G.; Gee, G.W. Application of critical path analysis to fractal porous media: Comparison with examples from the Hanford site. Adv. Water Resour. 2002, 25, 129–146. [Google Scholar] [CrossRef]
- Gerasimov, D.N.; Kondratieva, V.A.; Sinkevich, O.A. An anomalous non-self-similar infiltration and fractional diffusion equation. Physica D 2010, 239, 1593–1597. [Google Scholar] [CrossRef]
- Hunt, A.G.; Skinner, T.E.; Ewing, R.P.; Ghanbarian-Alavijeh, B. Dispersion of solutes in porous media. Eur. Phys. J. B 2011, 80, 411–432. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).