Robust Parameter Estimation Framework of a Rainfall-Runoff Model Using Pareto Optimum and Minimax Regret Approach

Abstract

This study developed a robust parameter set (ROPS) selection framework for a rainfall-runoff model that considers multi-events using the Pareto optimum and minimax regret approach (MRA). The calibrated parameter sets based on the Nash-Sutcliffe coefficient (NSE) for two events were derived using a genetic algorithm. We generated 41 combinations for weighting values between two events for the multi-event objective function and derived 41 Pareto optimum points that were considered as the ROPS candidates. Then, two different approaches for parameter selection were proposed to determine the ROPS among the candidates: one uses NSE only and the other uses four performance measures (NSE, peak flow error, root mean square error and percentage of bias). In the NSE-only method, five events, including two events from the calibration set and three events from the evaluation set, were used, and the ROPS was selected based on the regrets of both the calibration and the evaluation sets. In the multiple (i.e., four) performance measure method, only three events from the evaluation set were used and the ROPS was determined based on the regrets of twelve different cases, including three events with four measures. As a result, while single- and multi-event optimizations produced satisfying results for the calibration events, the optimized parameters from the single-event calibration do not perform well for another event, even one with the same criteria, such as NSE. The results of this study suggest that the optimized parameter set from the well-weighted objective function can successfully simulate not only hydrographs in general but also others, such as peak flow. In addition, the ROPS can be selected by considering the multiple performance measures of multiple validation events, as well as the NSE only of multiple calibration and validation events. Note that the study provides a framework that could be performed reasonably well with a limited number of events. While the computational resources might not be a limiting factor these days, it is still valuable to have such a tool for several reasons: one could utilize it for an operational decision making support tool, as the full searches for an optimal set of parameters might not be performed in the operational facility. It could also be used in a situation where one has a limited number of good-quality observational data for some reason.

1. Introduction

Watershed models have been widely used by researchers and decision-makers to understand hydrological, ecological, and biogeochemical processes and to examine the effects of human activities and climate change or variability on water quantity and quality. However, these models require careful calibration of a large number of parameters, largely due to measurement limitations and scaling issues [1].

Rainfall-runoff models using climate data and land use and topographic information simulate the runoff from catchment basins based on a set of model parameters. Although certain model parameters can be experimentally determined, others have little or no physical meaning, and their values cannot be obtained directly from measurable quantities of catchment characteristics. Therefore, it is often necessary to calibrate the model to determine the model parameters. The process is typically performed via either manual or automatic procedures. In particular, the need for automatic calibration has been broadly recognized and increasingly emphasized for many years, and calibrations with multiple objective functions or criteria have been widely adopted [2]. Therefore, in recent years, several automatic routines that use a multi-objective formulation of the calibration problem that has been introduced to rainfall-runoff modeling [3,4,5,6,7].

The performance of the model can be evaluated using different performance measures that can quantify the goodness of fit between the simulated and observed data. For hydrological rainfall-runoff models, the critical performance measures include the runoff volume, shape of hydrograph, peak, and low-flow timing, rate, and volume [8]. To solve multi-objective functions that include multiple performance measures, calibration techniques have evolved together with advances in computational power. However, as the number of objective functions that are included in the calibration has increased, the number of exact or near-Pareto-optimal parameter sets has also increased, and thus, calibration has evolved into a decision-making problem for selecting a set of suitable model parameters from a number of Pareto sets [2].

Furthermore, great uncertainty exists in the determination of each observation site in the multi-site objective function [9,10,11] and the selection of each storm event in the multi-event optimization problem [8,12,13,14]. In both optimizations, there will be the same weighting problems on each site or for each event. Li et al. [9] used the same weight to all sites located on upstream or downstream of the river. Pierro et al. [13] developed an equal-weight summation approach consisting of formulating the model calibration problem as a multi-objective problem with m × n objective functions, where m and n are the number of performance criteria and rainfall events, respectively, that must be optimized simultaneously.

Nevertheless, as Shinma and Reis [15] have already mentioned, the equal-weighted approach is not reasonable in both multi-site and multi-event optimization problems. Therefore, they proposed the weighted sum approach, which is not necessarily as suitable for each event as the previous event-calibrated parameter values. However, these problems can be solved using a Pareto optimum, but it will still be impossible to select a parameter set for an actual rainfall-runoff simulation, because the non-linearity of the hydrological models and the objective functions leads to complex optimization problems [16]. Thus, Khu and Madsen [2] developed a multi-objective calibration procedure with Pareto preference ordering to select a more suitable and robust parameter set. It showed that Pareto-optimal points that are also Pareto optimal in different subspace combinations of the objective functions space are preferred. However, it requires tremendous calculation time and efforts and cannot be frequently used in the real application.

Therefore, this study developed an efficient and systematic procedure to select the robust parameter set (ROPS) for the hydrologic simulation model combining Pareto optimum, weighted sum approach, and minimax regret approach (MRA). MRA was used to derive the ROPS from many available optimized parameter sets based on several performance measures for multiple events [17,18,19,20]. The high uncertainty in ROPS selection is closely related to traditional decision-making problems in the operation research field; therefore, the MRA, which is one of the commonly used decision-making techniques under complete uncertainty [21], is utilized in this study. This study developed a two-step selection procedure consisting of calibration and evaluation. For the calibration, the multi-event objective function with the Nash-Sutcllife coefficient (NSE, [22]) was considered and the objective function was optimized with 41 combinations of weights between two different events. For the evaluation, the ROPS was selected out of 41 optimized parameter sets using two different approaches. One uses NSE only and the other uses four performance measures (NSE, peak flow error, root mean square error, and percentage of bias). In the NSE-only method, two events from the calibration set and three events from the evaluation set were used together, and the ROPS was selected based on the regrets of both the calibration and evaluation sets to the best NSEs. In the multiple-performance-measure method (i.e., four), only three events from the evaluation set were used, and the ROPS was determined based on the regrets of twelve different cases to the best values of four performance measures, including three events with four measures. In this study, the storm water management model (SWMM) [23] was applied in a river basin in South Korea, and the genetic algorithm (GA, [24,25]) was used to calibrate the parameter sets for the given objective function.

2. Method

2.1. Framework

Several past studies have compared all optimized parameter sets for multiple events using the aggregation index or Pareto domination approach. The aggregation approach is a commonly used method that utilizes some composite index to describe the relative superiority of solution sets [14,15], and the weighted sum method and the distance function are popularly used. The Pareto domination approach does not rely on a single comparative value but on whether one solution is dominated by the other [2]. The aggregation index needs the objective weights of the individual events, and the Pareto dominance approach is not always applicable in all cases. It is common for the optimized parameters for an event to show lower values in other performance measures.

Therefore, this study introduces MRA to select the ROPS, neglecting the significance of individual events and considering various performance measures, as shown in Figure 1. It combines two main procedures using the multi-event objective function: (1) deriving the optimized parameter sets for two rainfall events of the calibration set with GA as a calibration procedure and (2) determine the ROPS among multiple forty one calibrated parameter sets from combinations of weighting values between two events. Here, the NSE-only and the four performance measures from additional events of the evaluation set are considered for the MRA decision making. The multi-event objective function for the calibration is performed based on the NSEs of the hydrologic simulation results. For the evaluation procedure, PFE (peak flow error), RMSE (root mean squared error), and PBIAS (percent bias) are used in addition to NSE. The two-ROPS selection approach can be used: (1) to apply the NSE-only to five events, including two events from the calibration set and three events from the evaluation set and (2) to apply the NSE, PFE, RMSE, and PBIAS to three events from the evaluation set.

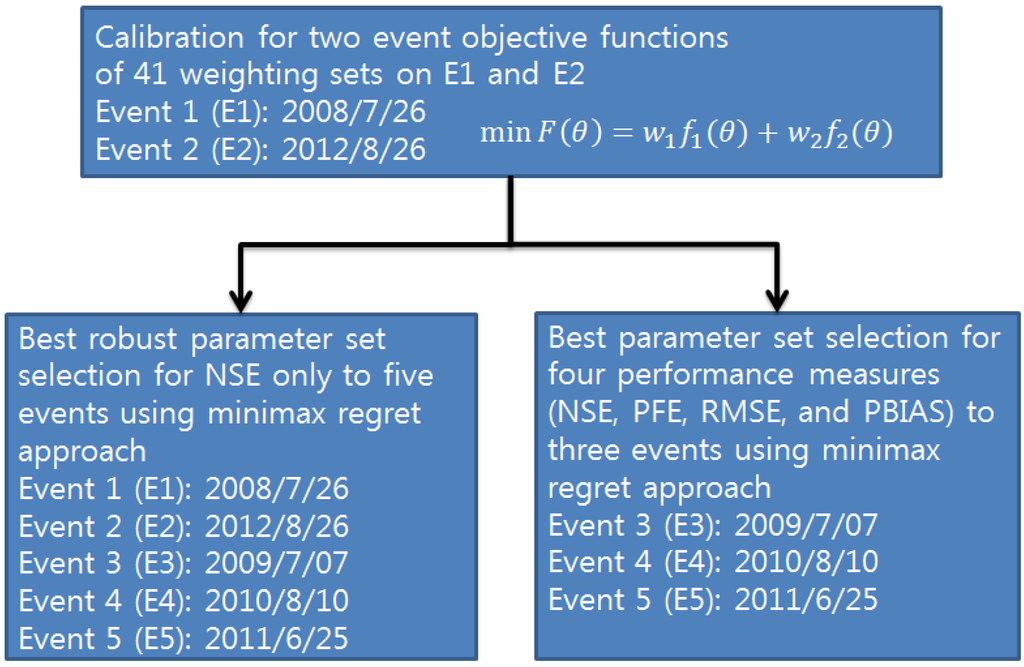
Figure 1. Parameter selection framework.

Figure 1. Parameter selection framework.

Note that this study does not focus on which selection approaches perform better than the other, rather it proposes two possible ROPS selection procedures, focusing on different aspects of the parameter selection problems (multiple events or multiple performance measures). The proposed framework can be useful because it uses a limited number of model simulations rather than the computationally intensive calibration procedures for multi-objective functions, consisting of several performance measures.

2.2. Multi-Event Objective Function

The multi-event objective function can be stated as follows:

$$\text{min} F\left(\text{θ}\right)=w_1{f}_1(\text{θ})+w_2{f}_2(\text{θ})+\cdots +w_n{f}_n(\text{θ})$$

(1)

where f_n(θ) is the objective function for the nth event to be simultaneously minimized with respect to the hydrological simulation model parameter set, θ. By randomly selecting different values for the weights allocated to the n event objectives, as many discrete optimal parameter sets as necessary can be generated to obtain an acceptable approximation of the continuous parameter set space. Alternatively, we can interactively guide the selection of weights until a satisfactory parameter set is discovered [25].

2.3. Minimax Regret Approach (MRA)

According to Loulou and Kanudia [26], the MRA is one of the more creditable criteria for selecting decisions under uncertainty, i.e., when the likelihoods of the various possible outcomes are not known with sufficient precision to use the classical expected value or expected utility criteria [18,19,20,21]. If a certain decision problem is couched in terms of a cost to minimize, the regret R(z,s)is defined as the difference between the cost incurred with the pair (z,s) and the least cost achievable under outcome perfect information on z, i.e.,:

$$R\left(z,s\right)=\text{max} C\left(\text{z},s\right)-C\left(z,s\right),\vee z\in Z, s\in S$$

(2)

where C(z,s) means the performance value of outcome z (NSE, PFE, RMSE, and PBIAS), incurred when the parameter set s is used.

A minimax regret strategy is any $s^{*}$ that minimizes the worst regret, i.e.,

$$s^{*}\in Arg \text{min}\left\{\text{max} R(z,s)\right\}$$

(3)

and the corresponding minimax regret is equal to

$$\text{MMR}=\text{min}\left\{\text{max} R(z,s)\right\}$$

(4)

2.4. Standardization

Because different units of basic indicators are employed in engineering environments, a trade-off analysis requires that the actual values be normalized using the maximum and minimum values [27]. Each score (a_ij) in the matrix is replaced with the value (s_ij) according to the following formula:

$$a_{ij}=\frac{s_{ij}-s_{i-}}{s_{i+}-s_{i-}} \text{or} a_{ij}=\frac{s_{i+}-s_{ij}}{s_{i+}-s_{i-}}$$

(5)

where s_ij is the impact of a scenario (j) with respect to a criterion (i); is the worst score of the criterion (i) with respect to all scenarios, i.e., the worst score in the row (i) of the payoff matrix; and is the “best” score of the criterion (i) with respect to all scenarios, i.e., the best score in the row (i) of the payoff matrix. This way, all scores in the payoff matrix are scaled between the values of 0.0 and 1.0 [28].

2.5. SWMM Modeling

2.5.1. Study Watershed and Rainfall Events

The proposed approach was applied to the parameter selection problem of the SWMM using five rainfall-runoff events in the Milyang Dam basin of South Korea (Figure 2). The Milyang Dam basin includes an area of 95.40 km². The study area is located in a mountainous region with the elevation ranging from 130 to 1180 m. As shown in Figure 2, the Milyang Dam is located in the outlet of the study basin with water flowing from the northeast to southwest of the basin. The basin was divided into 24 sub-basins, and the river channels were divided into the 26 sub-channels for the SWMM. The rainfall data from two telemetry (TM) stations at the Milyang Dam and Seoli were used.

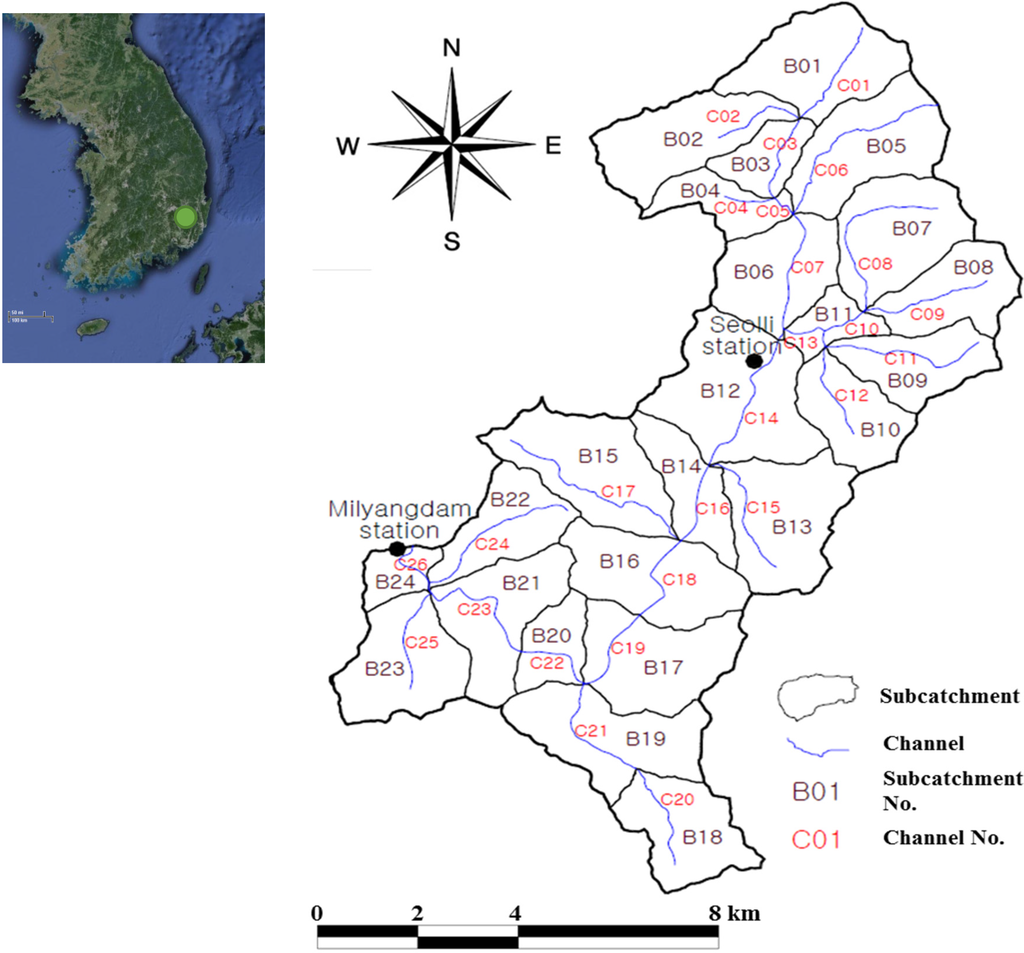
Figure 2. Study area of Milyang Dam basin.

Figure 2. Study area of Milyang Dam basin.

The five events were divided into two different sets: two events for calibration and three events for evaluation only, as shown in Table 1. We have subjectively selected one event per year during the rainy season of 2008–2012. In Korea, the most of heavy rainfall events take place during the summer monsoon (mostly in June, July and August) and therefore the flood events are observed during those months. While the selection process of rainfall events might be arbitrary, we have taken an effort to utilize various types of rainfall events in the study. The two events selected for calibration have a similar total precipitation but totally different temporal patterns, which resulted in the different peak flows. That is, E1 had a very high maximum rainfall intensity while E2 had a relatively uniform rainfall intensity. Additionally, three events for the model performance validation were selected that represent the years 2009, 2010, and 2011, respectively. E3 and E4 have spatially homogeneous rainfall because the total precipitation of the Milyang dam and Seolli stations had similar values, and E3 and E5 had a very uniform rainfall distribution because their maximum precipitation rates were under 12 mm/h.

Table 1. Description of each event.

Events		Period (mm/dd/yyyy hh:mm)	Total Precipitation (mm)		Maximum Precipitation (mm/hr)		Peak Runoff (m3/s)	Peak Time (mm/dd/yyyy hh:mm)
			Milyang Dam	Seolli	Milyang Dam	Seolli
Pareto optimality	E1 20080726	07/26/2008 01:00 ~ 07/26/2008 23:00	73	105	24	21	233.3	07/26/2008 07:00
	E2 20120828	08/28/2012 01:00 ~ 08/28/2012 23:00	64	106	6	25	119.1	08/28/2012 16:00
Performance evaluation	E3 20090707	07/07/2009 01:00 ~ 07/08/2009 12:00	121	130	9	8	223.22	07/07/2009 17:00
	E4 20100810	08/10/2010 1:00 ~ 08/12/2010 23:00	194	194	33	26	406.4	08/10/2010 11:00
	E5 20110625	06/25/2011 01:00 ~ 06/27/2011 12:00	169	249	8	12	422.4	06/26/2011 13:00

Table 1. Description of each event.

Events		Period (mm/dd/yyyy hh:mm)	Total Precipitation (mm)		Maximum Precipitation (mm/hr)		Peak Runoff (m3/s)	Peak Time (mm/dd/yyyy hh:mm)
			Milyang Dam	Seolli	Milyang Dam	Seolli
Pareto optimality	E1 20080726	07/26/2008 01:00 ~ 07/26/2008 23:00	73	105	24	21	233.3	07/26/2008 07:00
	E2 20120828	08/28/2012 01:00 ~ 08/28/2012 23:00	64	106	6	25	119.1	08/28/2012 16:00
Performance evaluation	E3 20090707	07/07/2009 01:00 ~ 07/08/2009 12:00	121	130	9	8	223.22	07/07/2009 17:00
	E4 20100810	08/10/2010 1:00 ~ 08/12/2010 23:00	194	194	33	26	406.4	08/10/2010 11:00
	E5 20110625	06/25/2011 01:00 ~ 06/27/2011 12:00	169	249	8	12	422.4	06/26/2011 13:00

2.5.2. Model Configuration

The SWMM was used here [29], as it is one of the most widely used models for simulating water quantity and quality. The SWMM allows the simulation of flows and polluting loads of urban runoff as well as their carriage through the combined sewer system. The model can be used not only for a single rainfall event but also for multiple events over a long period.

The SWMM is used to simulate the rainfall-runoff processes in the Milyang Dam basin. A 1:25,000 digital elevation model (DEM) and land-use map (2000) from the National Geographic Information Institute (NGII) of the Korean Ministry of Land, Infrastructure, and Transport (MOLIT) provide watershed topography to determine the drainage area delineation and surface slopes used in the SWMM. Storm and combined sewer infrastructure data obtained from the MOLIT are used to represent the drainage network characteristics and are combined with the watershed topography to delineate sub-watershed boundaries.

2.5.3. Model Optimization

The parameter optimization was performed with the GA, which is widely used for parameter calibration procedures in rainfall-runoff simulations because it is known as one of the most effective techniques [2,30,31]. GA is a heuristic global search algorithm based on the concept of Darwin’s evolutionary processes of natural selection and survival of the fittest. The GA is far from a particular model structure and requires only an estimate of the objective function for each decision set to proceed. The advantages of GAs over conventional parameter optimization techniques are that they are appropriate for ill-behaved problems and highly non-linear spaces for global optima and adaptive algorithms [4].

The NSEs for two events were combined with the weighting factor as follows:

$$\underset{\text{θ}}{\text{max}} w_1{f}_1(\text{θ})+w_2{f}_2(\text{θ})$$

(6)

where θ means the parameter set of the hydrologic model, f₁ and f₂ are the NSEs for the two events, and w₁ and w₂ are the weighted values for the two events for the calibration (w₁ + w₂ = 1). This study used 41 combinations of weights: (1.0 and 0.0, 0.975 and 0.025, 0.950 and 0.050, …, 0.0 and 1.0 for w₁ and w₂.

Table 2 lists the 17 model parameters subject to model optimization in this study, following the work of Kang and Lee [32]. The nine parameters related to the groundwater and channel characteristics are uniform over the Milyang Dam basin, and the eight parameters related to the basin characteristics (i.e., the percent impervious area, the characteristic width of the overland flow, and the runoff curve coefficient) differ for each sub-basin in this study.

Table 2. Search boundary of parameters for the event simulation model for the study basin.

Class	Parameters	Description	Unit	Lower Bound	Upper Bound
Basin	Pcnt. Imperv	Percent of impervious area	%	0.8*Obs. value	1.2*Obs. value
	Width	Characteristics width of the overland flow path	m	0.8*Obs. value	1.2*Obs. value
	N-Imperv	Manning’s n of impervious area	-	0.01	0.016
	N-Perv	Manning’s n of pervious area	-	0.15	0.4
	S-Imperv	Depth of depression storage on impervious area	mm	1.6	3.8
	S-Perv	Depth of depression storage on pervious area	mm	3.8	6.4
	Pct Zero	Percent of the impervious area with no depression storage	%	10	30
	CN	NRCS runoff curve coefficient	-	0.8*Obs. value	1.2*Obs. value
Channel	Manning N	Manning’s roughness coefficient	-	0.02	0.05
Ground-water	Porosity	Porosity (volume of voids/total soil volume)	Fraction	0.453	0.463
	Wilt Point	Wilting point (soil moisture content at which plants cannot survive)	Fraction	0.085	0.116
	Field Capac	Field capacity (soil moisture content after all free water has drained off)	Fraction	0.19	0.232
	Hyd Cond	Soil’s saturated hydraulic conductivity	mm/h	3.3	10.92
	Cond Slop	Average slope of log (conductivity) versus soil moisture deficit curve	-	1	10
	Tens Slop	Average slope of soil tension versus soil moisture deficit curve	mm	1,000	5000
	A1	Groundwater flow coefficient	-	0.0001	0.1
	B1	Groundwater flow exponent	-	1	5

Table 2. Search boundary of parameters for the event simulation model for the study basin.

Class	Parameters	Description	Unit	Lower Bound	Upper Bound
Basin	Pcnt. Imperv	Percent of impervious area	%	0.8*Obs. value	1.2*Obs. value
	Width	Characteristics width of the overland flow path	m	0.8*Obs. value	1.2*Obs. value
	N-Imperv	Manning’s n of impervious area	-	0.01	0.016
	N-Perv	Manning’s n of pervious area	-	0.15	0.4
	S-Imperv	Depth of depression storage on impervious area	mm	1.6	3.8
	S-Perv	Depth of depression storage on pervious area	mm	3.8	6.4
	Pct Zero	Percent of the impervious area with no depression storage	%	10	30
	CN	NRCS runoff curve coefficient	-	0.8*Obs. value	1.2*Obs. value
Channel	Manning N	Manning’s roughness coefficient	-	0.02	0.05
Ground-water	Porosity	Porosity (volume of voids/total soil volume)	Fraction	0.453	0.463
	Wilt Point	Wilting point (soil moisture content at which plants cannot survive)	Fraction	0.085	0.116
	Field Capac	Field capacity (soil moisture content after all free water has drained off)	Fraction	0.19	0.232
	Hyd Cond	Soil’s saturated hydraulic conductivity	mm/h	3.3	10.92
	Cond Slop	Average slope of log (conductivity) versus soil moisture deficit curve	-	1	10
	Tens Slop	Average slope of soil tension versus soil moisture deficit curve	mm	1,000	5000
	A1	Groundwater flow coefficient	-	0.0001	0.1
	B1	Groundwater flow exponent	-	1	5

2.5.4. Performance Measures

As previously stated, this study used four performance measures: NSE, PFE, RMSE, and PBIAS, which are explained as follows:

The NSE was used for the multi-event objective function and ROPS selection as follows:

$$\text{NSE}=1-\frac{{{\displaystyle \sum }}_{t=1}^T{\left(q_{t,obs}-q_{t,sim}\right)}^2}{{{\displaystyle \sum }}_{t=1}^T{\left(q_{t,obs}-\overline{q_{obs}}\right)}^2}$$

(7)

where $q_{t,obs}$ and $q_{t,sim}$ are the observed and the simulated discharge, respectively, at time t, and $\overline{q_{obs}}$ is the averaged observed discharge.

The PFE can be evaluated using the following equation.

$$\text{PFE}=\left|\frac{p_{obs}-p_{sim}}{p_{obs}}\right|$$

(8)

where $p_{obs}$ and $p_{sim}$ are the peak flows for the observed and simulated values, respectively.

The RMSE is a frequently used measure of the difference between values predicted by a model and the values actually observed from the environment that is being modelled. The RMSE of 0 corresponds to a perfect match between the model simulation and the observations. This varies with the variability within the distribution of error magnitudes and with the square root of the number of errors as following:

$$\text{RMSE}=\sqrt{{\displaystyle \sum }_{t=1}^n{(\frac{q_{t,obs}-q_{t,sim}}{n})}^2}$$

(9)

The PBIAS measures the average tendency of the simulated data to be larger or smaller than their observed counterparts. The optimal value of the PBIAS is 0, with low-magnitude values indicating accurate model simulation. Positive values indicate model underestimation bias, and negative values indicate model overestimation bias [25]. The PBIAS is calculated as following:

$$\text{PBIAS}=\frac{{{\displaystyle \sum }}_{t=1}^n(q_{t,obs}-q_{t,sim})}{{{\displaystyle \sum }}_{t=1}^n(q_{t,obs})}\times 100(\text{\%})$$

(10)

3. Results and Discussions

3.1. Calibration of ROPS Candidates

For the calibration, multi-event objective functions with 41 weights, as shown in Equation (6), were optimized using the GA, and the calibration results are shown in Figure 3. Figure 4 shows the derived NSEs for 41 weights (i.e., 41 different parameter sets). Although one objective function is used, the standardization process for the NSEs, as shown in Equation (7), is required because the severely different magnitudes of total runoff and peak flow can affect the importance of individual events in the calculation process.

As a result, the standardized NSEs, as shown in Figure 4b, varied dramatically according to the weighting values of the two events. The center area showed high values for the two events. Using the distance function with equal weight, the parameter sets were ranked as shown in Table 3. The optimized parameter set with weighting values (0.5, 0.5) is the best, and the adjacent weights (0.6~0.425, 0.4~0.575) showed the dominance. Weighting values (0.8, 0.2) and (0.675, 0.325) are the second and the third, respectively. The optimized parameters for just a single event showed very low NSEs when simulated. The NSEs of weights (1,0) and (0,1) showed this case. As a result, while single- and multi-event optimization lead to satisfactory results for the calibration events, the optimized parameters from the single-event calibration do not perform well for other events, even for the same NSE criteria. The results of this study suggest that the optimized parameter set from the well-weighted objective function can simulate both hydrographs and the others well.

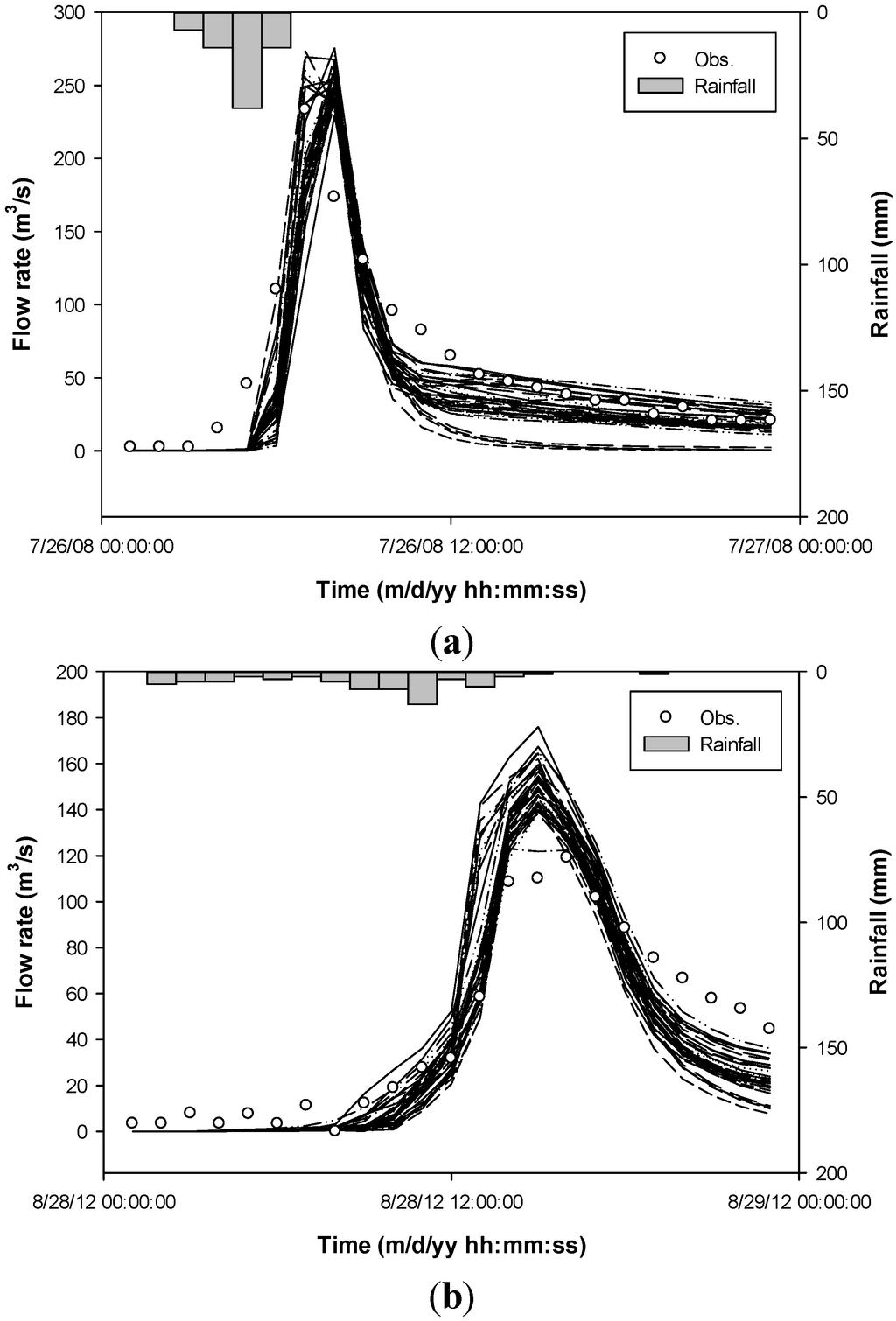
Figure 3. Calibrated hydrographs of E1 and E2 with the 41 optimized parameter sets. (a) E1; (b) E2.

Figure 3. Calibrated hydrographs of E1 and E2 with the 41 optimized parameter sets. (a) E1; (b) E2.

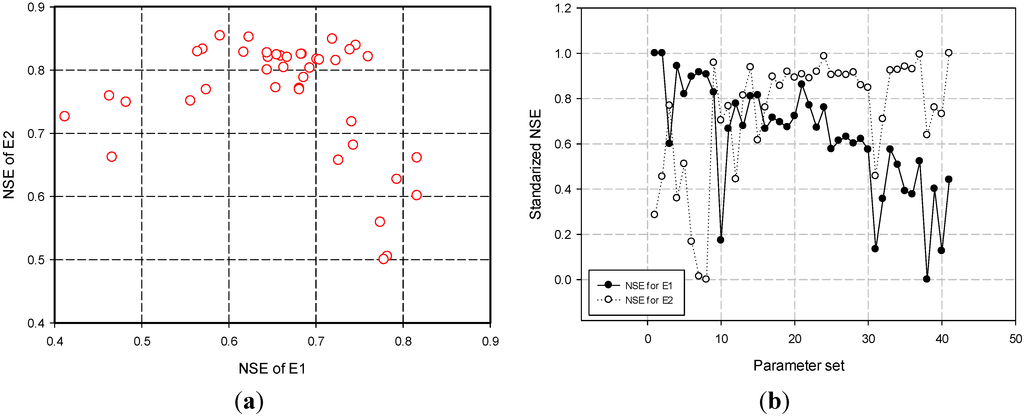
Figure 4. NSEs for E1 and E2 with 41 parameter sets: (a) scatter plot between two NSEs (i.e., Pareto optimal sets) and (b) standardized NSEs along the 41 parameter sets.

Figure 4. NSEs for E1 and E2 with 41 parameter sets: (a) scatter plot between two NSEs (i.e., Pareto optimal sets) and (b) standardized NSEs along the 41 parameter sets.

Table 3. Robust ranking based on Nash-Sutcliffe Coefficients (NSEs) of calibration and evaluation.

# of Alt.	Weights		Calibration		Evaluation		Final Rank
	E1	E2	Averaged Regret to Ideal NSEs	Rank	Averaged Regret to Ideal NSEs	Rank
9	0.8	0.2	0.173	2	0.015	2	1
11	0.75	0.25	0.334	13	0.090	9	7
14	0.675	0.325	0.191	3	0.036	5	3
15	0.65	0.35	0.384	16	0.143	10	9
19	0.55	0.45	0.327	10	0.015	2	6
20	0.525	0.475	0.277	6	0.315	23	10
21	0.5	0.5	0.139	1	0.077	8	2
22	0.475	0.525	0.230	4	0.060	7	5
24	0.425	0.575	0.240	5	0.024	4	4
33	0.2	0.8	0.426	22	0.018	3	8

Table 3. Robust ranking based on Nash-Sutcliffe Coefficients (NSEs) of calibration and evaluation.

# of Alt.	Weights		Calibration		Evaluation		Final Rank
	E1	E2	Averaged Regret to Ideal NSEs	Rank	Averaged Regret to Ideal NSEs	Rank
9	0.8	0.2	0.173	2	0.015	2	1
11	0.75	0.25	0.334	13	0.090	9	7
14	0.675	0.325	0.191	3	0.036	5	3
15	0.65	0.35	0.384	16	0.143	10	9
19	0.55	0.45	0.327	10	0.015	2	6
20	0.525	0.475	0.277	6	0.315	23	10
21	0.5	0.5	0.139	1	0.077	8	2
22	0.475	0.525	0.230	4	0.060	7	5
24	0.425	0.575	0.240	5	0.024	4	4
33	0.2	0.8	0.426	22	0.018	3	8

In this case, the Pareto-optimal parameter sets of the SWMM can be derived from Figure 4a, which represents the optimized NSEs of E1 and E2 for 41 different weights on two events. Although all different weighting values on two events were used, all NSEs from calibrated parameter sets cannot be located in the Pareto front. That is, some efficient parameter sets dominate the remaining because the NSEs for the two events obtained from some sets are much larger than those from the others. The points lying on the outskirts can be the optimal Pareto. As shown in Figure 4a, at least eight points lying the farthest from the negative ideal point and closest to the positive can be the optimal Pareto. In this study, the negative and positive ideal points for E1 and E2 are (0.412, 0.500) and (0.816, 0.854), respectively. However, it cannot be confirmed that these are always effective because they have shown the best fitness for the selected two events, E1 and E2, although they have a high possibility of fitness to all rainfall events. Therefore, all feasible candidates are included for the ROPS even though their NSEs did not lie on the outskirts in Figure 4a.

3.2. Selection of ROPS

Two different approaches are proposed to select the ROPS in this study. One assesses the NSEs with calibration and evaluation sets of events (Section 3.2.1) and the other assesses the multiple performance measures, i.e., NSE, PFE, RMSE, and PBIAS with evaluation sets only (Section 3.2.2).

3.2.1. NSE-Only with Both Calibration and Evaluation Sets

In this case, the evaluation was performed using five different events, as shown in Table 3. First, the SWMM simulations for the 3 events (E3, E4, and E5) were performed with the 41 Pareto optimal parameter sets (Figure 5), and the NSEs for E3, E4, and E5 with 41 optimized parameter sets are derived (Figure 6a). Overall, the NSEs for E4 and E5 indicated high values for all candidates. Furthermore, the standardized NSEs were calculated to consider the relativeness (Figure 6b).

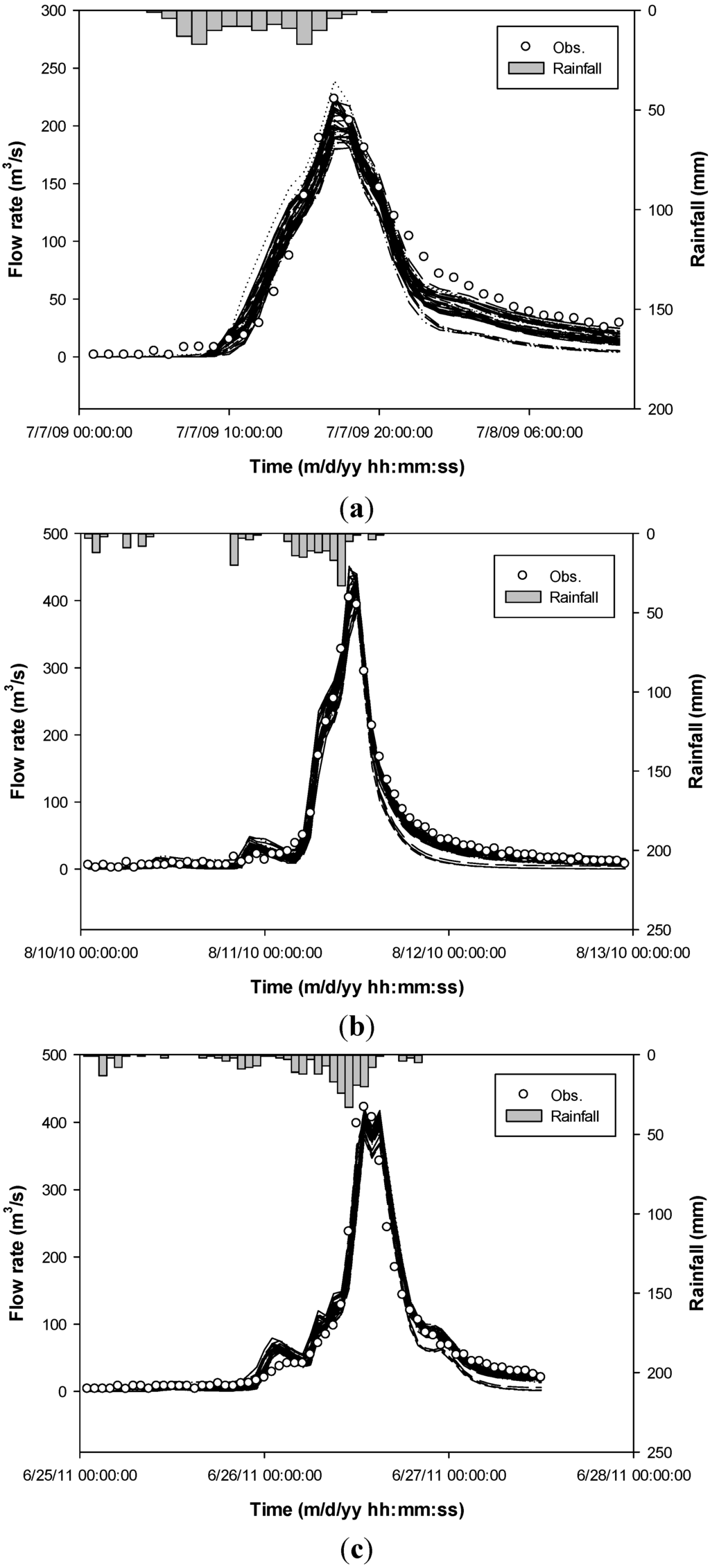
Figure 5. Simulated hydrographs of E3, E4, and E5 with 41 calibrated parameter sets. (a) E3 (20090707); (b) E4 (20100810); (c) E5 (20110625).

Figure 5. Simulated hydrographs of E3, E4, and E5 with 41 calibrated parameter sets. (a) E3 (20090707); (b) E4 (20100810); (c) E5 (20110625).

Figure 6. NSEs for E3, E4, and E5 with 41 parameter sets: (a) scatter plot between two NSEs (red circles for E3 vs. E4 and blue triangles for E3 vs. E5) and (b) standardized NSEs along the 41 parameter sets.

Figure 6. NSEs for E3, E4, and E5 with 41 parameter sets: (a) scatter plot between two NSEs (red circles for E3 vs. E4 and blue triangles for E3 vs. E5) and (b) standardized NSEs along the 41 parameter sets.

Second, the ROPS was derived using the MRA, based on the calibration and validation results (Figure 7). The minimum standardized NSEs, i.e., regrets, among E1 and E2 (calibration set) and E3, E4, and E5 (evaluation set) were calculated, respectively. Then, two regrets were aggregated into one composite regret by averaging. The NSEs of the hydrographs simulated with the most effective ten-parameter sets were calculated as shown Table 3. As a result, the calibrated parameters with (0.8, 0.2), which is the second in the application of distance function, were first, while those with (0.5, 0.5) were second. Therefore, the final determination can be changed when more events are included in the parameter selection problem using MRA.

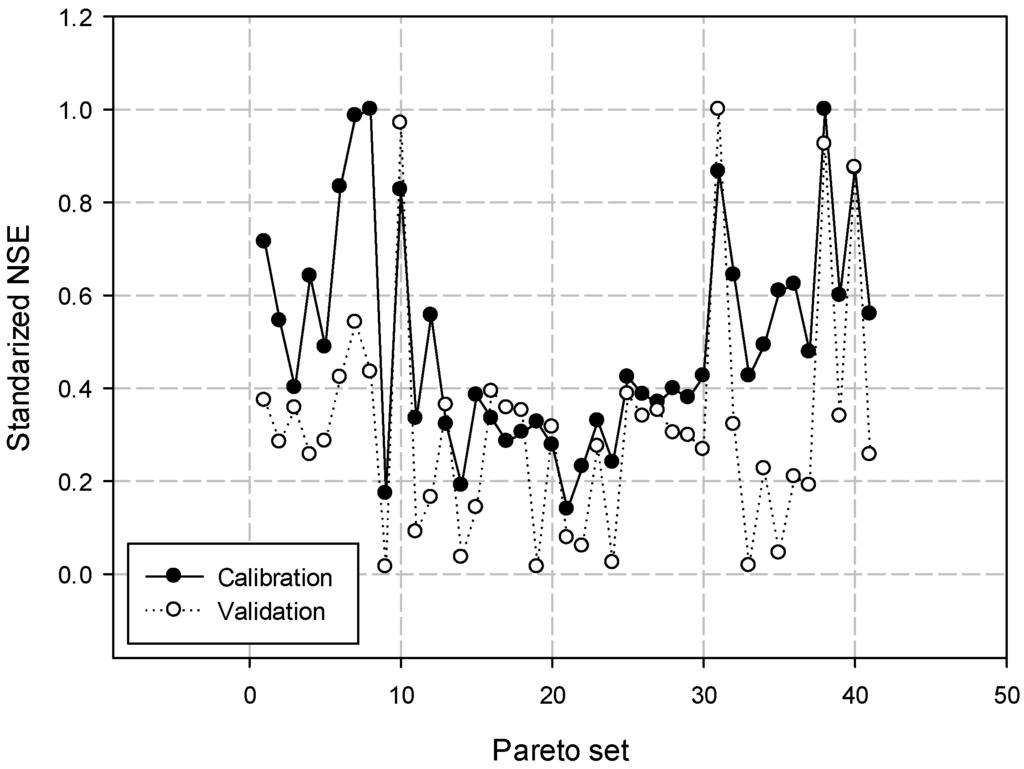
Figure 7. Standardized NSEs from calibration (E1 and E2) and evaluation sets (E3, E4 and E5).

Figure 7. Standardized NSEs from calibration (E1 and E2) and evaluation sets (E3, E4 and E5).

3.2.2. Multiple Performance Measures with Evaluation Set Only

This study introduced another method using four different performance measures for the evaluation procedure. The ROPS was determined using MRA and three events of the calibration set (E3, E4, and E5). First, four performance measures of E3, E4, and E5 were calculated (Figure 8). Then, they were standardized using the linear transformation relationship, and each regret to the maximum performance value among the three values was calculated by each performance measure. The parameter set having the minimum regret was selected. The derived rankings of all performance measures are shown in Figure 8. As shown in the rank correlations among the different measures in Table 4, it can be concluded that any particular optimized parameter set cannot always satisfy all performance measures and all events well.

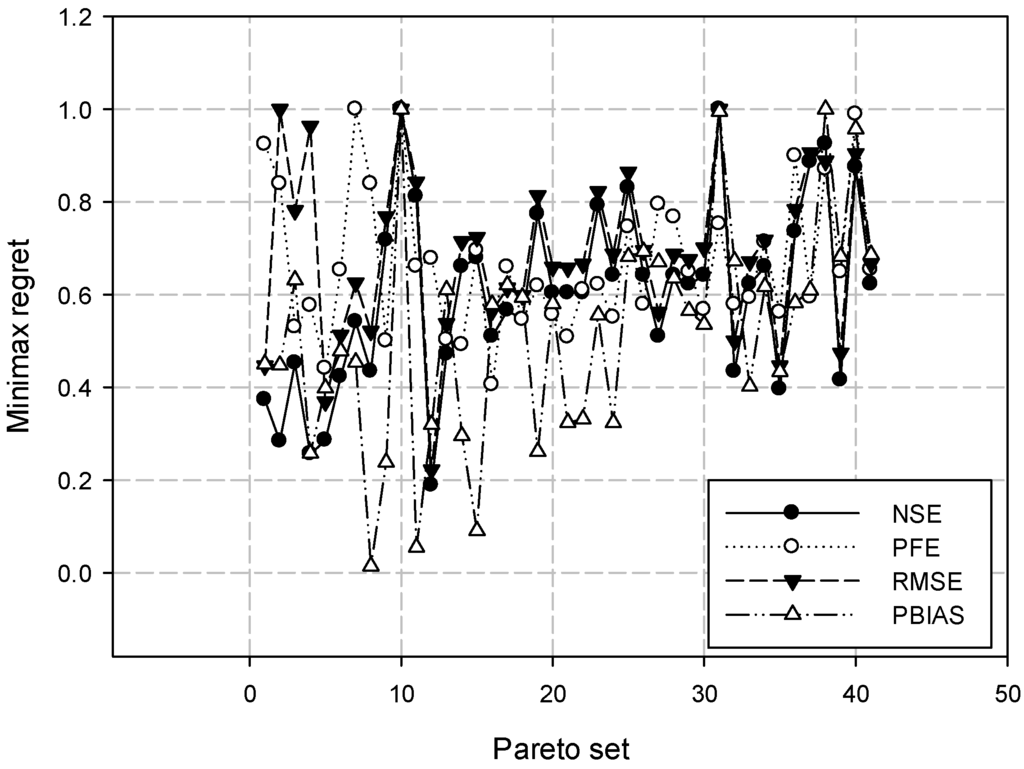
Figure 8. Values of four performance measures using minimax regret.

Figure 8. Values of four performance measures using minimax regret.

Table 4. Correlations among all rankings to four performance measures.

Performance Measures	NSE	PFE	RMSE	PBIAS
NSE	1	0.2539	0.7243	0.2719
PFE	--	1	0.2537	0.2940
RMSE	--	--	1	0.1522
PBIAS	--	--	--	1

Table 4. Correlations among all rankings to four performance measures.

Performance Measures	NSE	PFE	RMSE	PBIAS
NSE	1	0.2539	0.7243	0.2719
PFE	--	1	0.2537	0.2940
RMSE	--	--	1	0.1522
PBIAS	--	--	--	1

To derive the ROPS that can satisfy the required standard, the standardized values for each performance criteria and each event are recalculated, respectively, instead of using the weighting values of the performance criteria. Then, one or more ROPS for the hydrological simulation model can be proposed with relatively high certainty, as shown in Table 5. It is concluded that the optimized parameter set 5 that showed very high accuracies in NSE, PFE, and RMSE is the most robust ROPS. The next parameter sets are in the 35th, 12th, and 16th rows.

Table 5. Rankings based on four performance measures.

Number of Parameter Set	Weights		Performance Measures				Average Ranking	Final Ranking
	E1	E2	NSE	PFE	RMSE	PBIAS
5	0.900	0.100	4	2	2	12	5	1
35	0.150	0.875	6	11	4	14	8.75	2
12	0.725	0.275	1	27	1	8	9.25	3
16	0.625	0.375	13	1	11	22	11.75	4
21	0.500	0.500	18	6	15	10	12.25	5
8	0.825	0.175	10	34	8	1	13.25	6
13	0.700	0.300	12	5	9	27	13.25	6
6	0.875	0.125	8	23	7	18	14	8
4	0.925	0.075	2	13	38	5	14.5	9
18	0.575	0.425	16	8	12	25	15.25	10

Table 5. Rankings based on four performance measures.

Number of Parameter Set	Weights		Performance Measures				Average Ranking	Final Ranking
	E1	E2	NSE	PFE	RMSE	PBIAS
5	0.900	0.100	4	2	2	12	5	1
35	0.150	0.875	6	11	4	14	8.75	2
12	0.725	0.275	1	27	1	8	9.25	3
16	0.625	0.375	13	1	11	22	11.75	4
21	0.500	0.500	18	6	15	10	12.25	5
8	0.825	0.175	10	34	8	1	13.25	6
13	0.700	0.300	12	5	9	27	13.25	6
6	0.875	0.125	8	23	7	18	14	8
4	0.925	0.075	2	13	38	5	14.5	9
18	0.575	0.425	16	8	12	25	15.25	10

4. Conclusions

This study provides a ROPS selection framework for the hydrological simulation model utilizing the Pareto optimum for a two-event objective function and the MRA for multiple events. The calibrated parameter sets based on the NSEs for two events were derived using the GA. In this procedure, 41 different combinations of weighting values for two rainfall events were used for the two-event objective function and thus their optimized parameter sets, Pareto optimums, became the ROPS candidates. Then, two different parameter evaluation approaches were used: one uses only NSEs for a total of five rainfall events, i.e., two events for the calibration set and an additional three events for the evaluation set, and the other uses four performance measures (NSE, PFE, RMSE, and PBIAS) for an additional three rainfall events. The performance measures of the 41 ROPS candidates were evaluated with the MRA to derive the rankings of the candidates and select the most ROPS at the end.

This study indicated that the optimized parameters from the single event calibration does not perform well for another event, even for the same NSE criteria, and this led to the conclusion that the calibrated parameters, when considering two events simultaneously, could perform well on both events. In addition, even the optimized parameter sets with multiple events cannot always result in good performance when other measures and events are used. That is, more events should be included for calibration, and more performance measures should be considered for the evaluation process. Therefore, the ROPS can be selected from the multiple performance measures of multiple validation events, as well as NSE-only for multiple calibration and validation events.

Finally, the ROPS framework using the MRA can be a more useful way to determine the best among many optimized sets when considering many performance measures and multiple events. Note that this study does not focus on which selection approaches perform better than the other, rather it proposes two possible ROPS selection procedures, focusing on different aspects of the parameter selection problems (multiple events or multiple performance measures). Any approach can be used depending on the available data or personal preferences. That is, they can use one (NSE or others) or more for the selection process and then proceed to derive ROPS based on the framework proposed in this study.

Note that study provides a framework that could be performed reasonably well with a limited number of events. While the computational resources might not be a limiting factor these days, it is still valuable to have such a tool for several reasons: one could utilize it for an operational decision making support tool as the full searches for an optimal set of parameters might not be performed in the operational facility; and it could also be used in a situation where we have a limited number of good-quality observational data for some reasons.

Furthermore, this procedure could be extended or combined to incorporate multiple site observations for robust rainfall-runoff calibrations using multi-attribute decision analysis and multi-objective functions with various objective weighting derivation methods.