Abstract
In this paper, an original model-based scheme for leak location using pressure sensors in water distribution networks is introduced. The proposed approach is based on a new representation called the Leak Signature Space (LSS) that associates a specific signature to each leak location being minimally affected by leak magnitude. The LSS considers a linear model approximation of the relation between pressure residuals and leaks that is projected onto a selected hyperplane. This new approach allows to infer the location of a given leak by comparing the position of its signature with other leak signatures. Moreover, two ways of improving the method’s robustness are proposed. First, by associating a domain of influence to each signature and second, through a time horizon analysis. The efficiency of the method is highlighted by means of a real network using several scenarios involving different number of sensors and considering the presence of noise in the measurements.1. Introduction
Water Distribution Networks (WDN) are used in everyday life, whether being employed for domestic or for industrial use. They are usually large scale systems which demand continuous improvements in water loss management and new technologies to achieve higher levels of efficiency. Water losses due to leaks in distribution networks have been estimated to account up to 30% of the extracted water. The traditional approach to treat leaks in most of the cases is a passive one, i.e., a leak is repaired only when it becomes visible, which typically results in a huge loss of water. Thus, it is important to develop methods that report leaks at an earlier stage. This explains why the development of efficient leak detection and location strategies has become an essential research issue in recent years [1]. Leak detection task is about indicating the existence of a leak providing an estimation of the occurrence time. On the other hand, leak location refers to the ability to determine the place in the water network where the leak is occurring along the water system.
Several works have been published on leak detection and location methods for WDN [2,3]. Colombo et al. [4] offer a review of Transient Test Based Methods (TTBMs) for leak detection that summarizes current and past contributions. TTBMs are efficient when used in the management of the water supply systems where large pipes (corresponding to transmission mains) and less interconnected than in WDN are found due to its short duration and because they allow the use of pressure measurements. In addition, TTBMs are able to detect and locate leaks in the water system. Meniconi et al. [5] present a single transient test that shows that it is possible to find singularities in a complex system by analyzing the pressure signal in one section. In [6], a study about how the conditions of the system can affect the leak detectability is offered showing that it is important to take into account the tests conditions when selecting a leak detection method. However, the performance obtained until now is still far from allowing the detection of WDN leaks with only few sensors in a robust and fast way.
In the case where the flow measurements are available, leaks could be detected more easily since it is possible to establish simple mass balance in the pipes. In these simple cases, the leak is detected but not located in the network. See, for example the work of Ragot and Maquin [7], where a methodology to isolate leaks is proposed using a fuzzy analysis of the residuals. This method finds the residuals between the measurements with and without leaks. However, although the use of flow measurements is viable in large water transport networks, this is not the case in WDN where there is a dense mesh of pipes with only flow measurements at the entrance of each district metering area (DMA). In this situation, water companies consider as a feasible solution the possibility of equipping the DMAs with pressure sensors, because they are cheap as well as easy to install and maintain.
As an alternative, Xia and Guo-jin [8] proposed a leak detection model based on the cluster-analysis and fuzzy pattern recognition approach. Here, simulations of pipe leaks are clustered in virtual partitions. Then, a fuzzy recognition technique identifies the leak region reducing the scope for the leak detection. However, this approach still presents issues related to the size of the virtual partition that would require further improvement. Recently, acoustic instruments that allow the location of invisible leaks were developed by [9], but unfortunately, their application to a large-scale water network is very expensive and time-consuming. Another leak detection methodology based on the generation of a new class of structured residuals has been proposed in [10] and satisfactorily applied to a water distribution network. This approach allows to detect leaks in an efficient way but it may be time-consuming due to the numerical algorithm used to compute the residuals. Goulet et al. [11] proposed another original approach for the problem of leak detection and isolation as well as for optimal sensor placement. The central idea is to falsify model instances (parameter sets) for which the difference between predictions and measurements is larger than the maximum plausible error. Maximum plausible errors are determined by combining model and measurement uncertainties. However, this work is only able to find leaks of large magnitudes and needs a large number of sensors in the pipes. Recently, a new technique to address leakage has been proposed [12] using ground penetrating radars that extracts images and combines them with statistical methods to try to classify leaks.
Model-based leak detection and isolation techniques, using pressure measurements and sensitivity analysis, have been studied for two decades, since the paper by Pudar and Liggett [13], which formulates the leak detection and isolation problem as a least-squares estimation problem. However, the estimation of the parameters describing the WDN model is a difficult task since these models are non-linear. Another contribution relies on the use of binary codification of residuals proposed by [14] to compose the fault signature which can be used in binary tests to detect and isolate the leak. However, it has been shown that such approach produces a loss of information which decreases the performance.
Later, an improved method based on a model-based approach that relies on pressure measurements and leak sensitivity analysis is offered by [15]. This approach has a good efficiency under ideal conditions, but its performance decreases in presence of nodal demand uncertainty and noise in the measurements. This methodology has been extended in [16] where an analysis along a time horizon is taken into account and a comparison of several leak isolation methods is offered. In this case, the efficiency is improved despite the leak magnitude uncertainty is still affecting the performance.
Water networks are systems very too complex to model due to the huge amounts of available data and the important uncertainties regarding demand changes and noise present. However, methods that can deal with this issue have been developed in past and recent years [17,18].
Aiming to improve the efficiency of these methods, a new scheme where the leaks are identified through a specific signature minimally affected by the leak magnitude is proposed in this paper. This signature can be represented in what is called the Leak Signature Space (LSS). This representation allows to infer the location of a given leak by comparing the position of its signature with other leak signature references. Moreover, two ways of improving the method robustness are proposed. First, by associating a domain of influence to each signature and second, through a time horizon analysis.
The organization of the paper is as follows. Section 2 presents the WDN model and highlights how, under given conditions, one can approximate pressures and leaks magnitudes by means of a linear relation. Section 3 introduces the LSS representation that associates a signature and possibly a domain of influence to each leak independently of its magnitude. Section 4 shows the presented representation for the leaks in a small WDN example. Section 5 shows how the leak location is actually performed from the LSS and a complete application of the method in a real network is shown in Section 6. Section 7 offers the application in a real test scenario. Finally, Section 8 summarizes and presents potential extensions to the work presented in this paper.
2. Model Representation
This section shows the equations governing the behavior of the pressures and the water flows of a WDN under quasi-static conditions.
2.1. Water Network Model Solution
In this work, the assumption that only one leak may occur at a time in the WDN is considered. In the following, it is assumed that the behavior of the WDN follows the model described by [19] and used in most of the hydraulic simulators. Let us consider a WDN with m nodes, f pipe flows and n pressure sensors located at the nodes (typically n ≪ m). Let us also define the vectors p, p*, q, d which are respectively the vectors of pressure in the junction nodes, pressure in reservoirs, flows trough the pipes and demands:
with u corresponding to the number of reservoirs supplying water to the WDN. Then, the water network model can be formulated through the following matrix representation:
where
, i ∊ [1,⋯, f],
,
and with A21, A01 the incidence matrices obtained when only junction and reservoir nodes are considered, respectively. In A11(q), |qi| is the absolute value of the flow qi, ci is a constant parameter which depends on the diameter, the roughness and the length of the pipe, and γf is the flow exponent parameter.
The resulting water network model can then be solved numerically using a Newton–Raphson iterative scheme where the iteration k + 1 is given by the following set of equations:
where N is a diagonal matrix such that N = diag(γi), i ∊ [1,⋯, f]. It is important to note that this resolution approach is commonly employed, as e.g., in the EPANET simulator [20] where large WDN can be simulated efficiently.
The solution of the system of Equation (3) corresponds to the case without leak where an equilibrium point has been reached for the network, i.e., the flows and pressures are constant along the iterations which means pk+1 = pk = p and qk+1 = qk = q. A representation of a leak in a WDN would theoretically involve a graph structure where each possible leak could be represented by a graph node. However, a leak could possibly appear at any point of a network pipe. For this reason, the exact modeling of any possible leak becomes unfeasible in practice. To mitigate this issue, it is usually assumed that leaks only appear at existing nodes [13]. With such assumption, we can add a leak written as a vector of extra demands Δd and the new demand d′ can be expressed such as:
where Δd is a m dimensional vector with zeros everywhere except at the node’s index where the leak occurs. Now, assuming that in presence of a leak, the network flow equilibrium can also be reached, the pressure in case of leak can be expressed by:
where q′ is the flow in leak case. Then, we propose to represent the residual r (c.f. [15]) as the difference between the nominal pressure in the model without leaks and the pressure in the network in case of a leak. From Equations (3) and (5), the following approximate expression for the residual could be derived:
assuming that the leak is small compared to the non-leak flows, what allows to approximate the flow in non-leak and leak case: (q = q′). The proposed leak location approach is intended to be used for small leaks since large leaks are easily detected because usually reach the surface rapidly. In this way, it is possible to obtain an approximate linear relation between the residual (and consequently with the pressure measurement) and the leak through a matrix factor S under equilibrium assumptions that is known as the sensitivity matrix. This approximation implies an error factor εq when using the linear approximation r = S · Δd + εq. This error is not modeled when deriving Equation (6) but it will be taken into account as uncertainty in the realistic cases analyzed in the experiments. The S matrix has been used in a variety of works [15,16,21] where it has been obtained by means of simulation. However, to our knowledge it is the first time that the analytical expression Equation (6) is proposed, opening new perspectives for developing analytical methods for model based leak location.
The pressure in a network at a given time instant can be represented by a point in the m-dimensional space of the pressure measurements. In case of a leak, residual Equation (6) indicates the position of this point located on a line passing through the origin and whose direction depends on the node where the leak occurs. Moreover, the position of the point on the line depends on the leak magnitude. However, in practice, pressure measurements are available only in a limited number of nodes n, which is where the sensors are placed. Thus, the n-dimensional space of the sensors corresponds to a subspace (a projection) of the m-dimensional space of the pressure measurements. Fortunately, this linear dependency Equation (6) is also valid in this projected space.
In the following, an explanation about how these linear dependencies can be exploited to discriminate leaks is offered.
3. Leak Signature Space
Now, an original spatial representation that allows to discriminate the possible leak location is presented. The linear dependency presented above is such that for any pair of residual vectors r1 and r2 corresponding to different leak magnitudes but occurring in the same node j, it can be stated that:
with λ proportional to the leak magnitude. Thus, any residual corresponds to a direction vector of the line representing the leak at a specific node. Based on the sensors available, it is proposed to use the projection of the direction vector onto a selected hyperplane of the n-dimensional space. Then, for simplicity, let us assume for now that the last coordinate is chosen to form the hyperplane, such that for a given residual
, the projection vector
can be computed as:
Thus, there is a unique expression of such projection vector for a linear representation of the residuals. Consequently, it is possible to associate to the leak in node j and independently of its magnitude, a unique point
in this (n − 1)-dimensional hyperplane called the Leak Signature Space (LSS). In Figure 1, it can be seen the projection of the residuals for the small example when considering the three nodes equipped with sensors. Here, the last coordinate was considered, but the projection can be performed onto any hyperplane formed by taking any of the n possible coordinates equal to 1. This projected space, that allows to represent leaks independently of their magnitude, is called hereafter as the Leak Signature Space. Later on, it will be shown how to optimize the choice of the projection hyperplane.
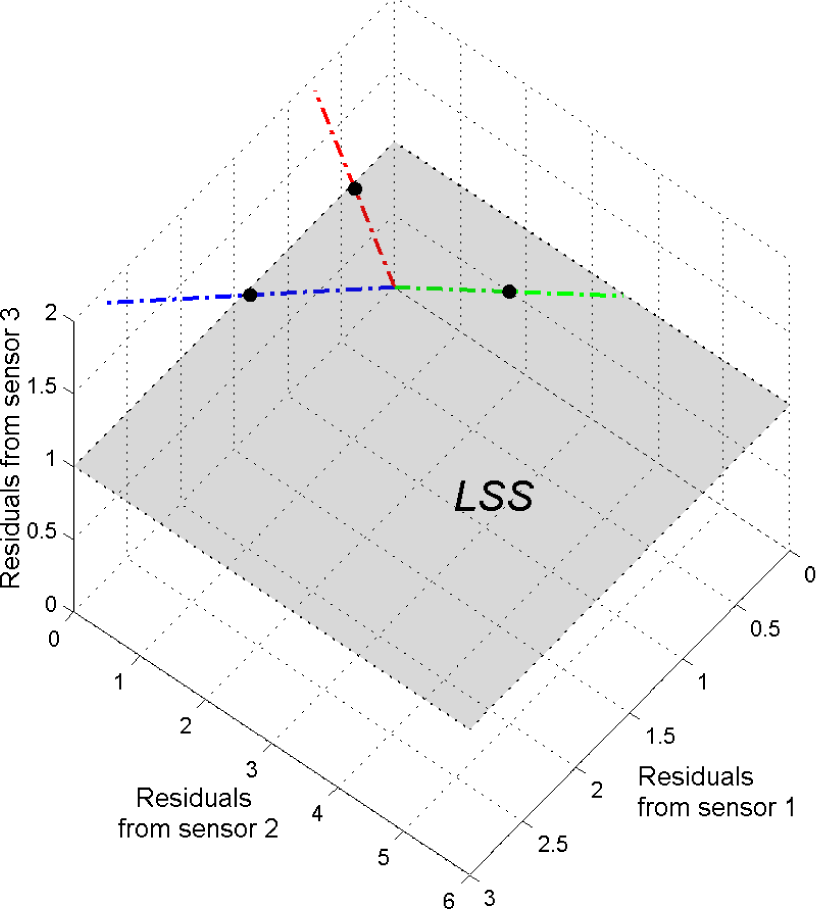
Figure 1.
The linear model approximations of the residuals for the three possible leaks are projected onto a (n − 1)-dimensional hyperplane (here a plane).
3.1. Dealing with Realistic Cases
In a real scenario, the ideal linear dependency presented in the previous section may be partially affected. First, the approximation of the studied relation should include the error factor εq as mentioned previously. Also, the model representation used is always imperfect/incomplete with respect to what is happening in a real network and the simulation based on the Newton–Raphson scheme may introduce some numerical errors. In addition, some noise is typically associated with the sensor measurements and finally, the demand may vary along the time, whereas the leak in the presented model appears as an extra demand which follows a fixed demand pattern. The problem of changes in the water demand will be considered later on. For now, it is only explained how to deal with general noise and imperfect linear dependencies.
To represent the leak associated to a given node j in the network with n sensors, s different leaks magnitudes lk are simulated, with k ∊ [1,⋯, s]. Then, the associated s residual vectors
are computed and if the projection is performed with respect to the last coordinate, their projection onto the LSS are given by the (n − 1)-dimensional points of coordinates
. Then, point
, corresponding to the leak j, is taken as the barycenter of these s partial signatures
built from the different leak magnitudes:
Computing such barycenters for the m possible leak nodes, m leak signatures
are obtained, with j ∊ [1,⋯, m], that can be used to perform leak location. It should be also remarked that when the number of sensors increases, it increases the dimension of the hyperplane in the LSS and thus increases the chances to discriminate the different leak signatures.
3.1.1. Leak Signature Domain
Each leak signature is computed as the barycenter of the partial signatures computed from different leak magnitudes simulations. Additionally, it can be determined a domain of influence to these signatures as (n − 1)-dimensional spheres whose radius corresponds to the largest Euclidean distance from the barycenter to the partial signatures. Thus, the radius for each leak signature domain is defined as:
where
are the distances between the barycenter of the node j and each of the partial signatures obtained by simulating the s different magnitudes. Then, if two domains overlap, it means that these two leak signatures are very similar and thus there is a risk of confuse one leak with the other. Such representation allows to take into account the deviations from a perfectly linear relation between leak magnitudes and residuals.
3.1.2. Choice of the Projection
The construction of the domains, associated to each signature, can be used to decide which is the most suitable projection to use in order to discriminate the leak signatures. When an intersection between two leak signature domains occurs, it means that a leak could be associated to a given node whereas it has occurred in another one. Thus, it is proposed to use the projection that minimizes the number of intersections between all the signature domains. For that, the barycenters using each of the possible sensors coordinates as hyperplane of projection are computed. Then, for each case, if the distance between two barycenters is smaller than the sum of their radii, it means their domains intersect. Finally, the number of intersections occurring for each hyperplane are counted and the one with lowest occurrence is selected.
4. Small WDN Example
In this section, the presented model representation and leak signature space will be illustrated on a small network.
4.1. Model Solution
Let us consider a small WDN example shown in Figure 2 that contains 1 reservoir, 3 demand nodes and 4 flow pipes.
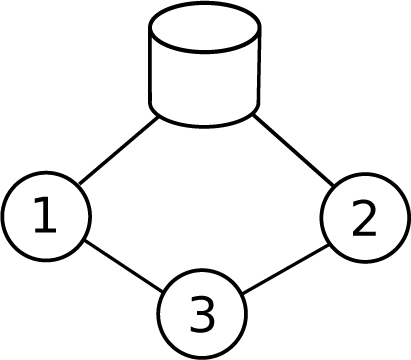
Figure 2.
Small Water Distribution Network (WDN) example. A reservoir is supplying a network composed of 3 demand nodes and 4 pipes.
Assuming that the pressure in the reservoir is known and taking into account the pipes characteristics, the matrices A11, N and S (c.f. Equation (6)) have the following numerical values:
where I is the identity matrix. Then, it is possible to compute the residuals Equation (6) for each possible leak in the network. In this example, first it is assumed that the space of the pressure measurements is 3-dimensional, i.e., all pressure nodes are measured and m = n = 3. Figure 3a illustrates this space, showing the differences of pressures for leaks in each of the three nodes for leak magnitudes varying from 1 to 5 liters per second (lps). It also shows how each node corresponds to a residual that varies linearly, according to the leak magnitude. In this figure, it is interesting to note that despite the lines representing leaks in nodes 1 and 3 are different, they have the same projection in the subspace of sensors 2 and 3.
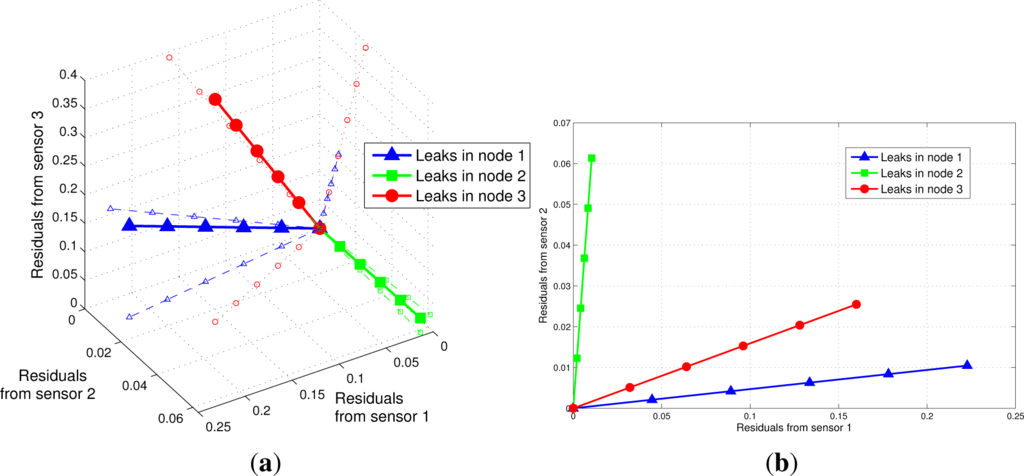
Figure 3.
3-dimensional (a) and 2-dimensional (b) space of the pressure measurements.
Figure 3b shows the case where the sensors are only installed in nodes 1 and 2 (n = 2). Thus, observations can only be made in the projected 2-dimensional space corresponding to these two sensors. In this space, the linear dependency remains.
It can be seen a linear variation of the residuals respect to the leak magnitude for leaks introduced in each of the three network nodes. The linear dependency respect to the leak magnitude also appears in the projected 2-dimensional space of two sensors installed at nodes 1 and 2.
4.2. Leak Signature
Considering that the 3 nodes of the small example are equipped with sensors (n = 3), the leak signature of each node in the LSS can be represented. For each of the 5 leak magnitudes, a Gaussian white noise with a random amplitude was added to the pressure measurements affecting the residual values. Figure 4 shows for a leak in each node j, the partial leak signatures
for each magnitude. The final signatures
obtained from the barycenter of these points and their domain appear as ellipses since axes are not normalized. The signatures are computed as the barycenter of the partial leak signatures corresponding to given leak magnitudes. The leak signature domains that appear as ellipses are only visible for node 2 since for the other two nodes the partial signatures are almost perfectly superposed.
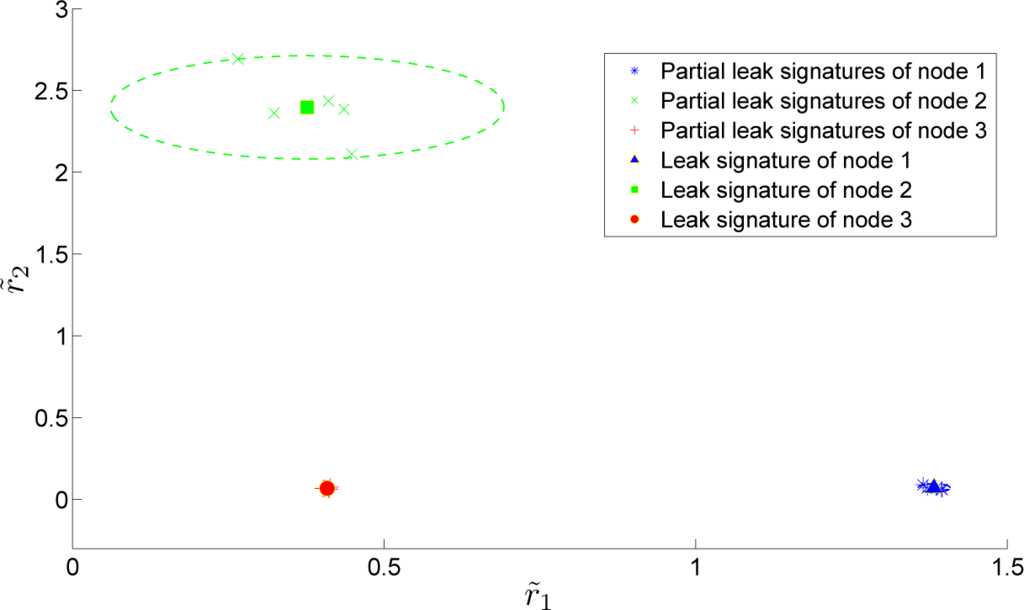
Figure 4.
Representation of leak signatures in the LSS of the small WDN, equipped with 3 sensors.
5. Leak Location Method
5.1. Basic Approach
In this section, it is explained how to estimate the leak location based on the LSS representation. First, the m leak signatures of the network nodes are computed with the method presented in the previous section. Then, when a leak occurs, its signature in the LSS is determined, i.e., the (n − 1)-dimensional point
representative of this leak from the real residual measurements is computed. Finally, the Euclidean distance ρ between
and the various leak signatures
in the LSS is computed. The leak node is estimated as the one whose signature is the closest to the current leak signature, i.e., the index id of the leak is such that:
where arg min is the argument of the minimal distance evaluated.
5.2. Exploiting Leak Signature Domains
When the leak signature domains have been computed, a more robust approach can be used for leak location. That is, the list of leak signature domains that contain the leak are sorted according to the distance of their center to the real leak. This list provides additional information regarding the leak location. If the list contains only one element (which is by definition the closest leak signature), it has a very high chance to correspond to the correct leak node. Otherwise, it provides an ordered list of additional nodes candidates for the leak, that can be checked if the nearest signature does not correspond to the correct leak location.
5.3. Time Horizon Analysis
In practice, for a given network, the demand usually varies along the time and it is important to carry out the leak location analysis taking into account a time horizon [16]. To address this point, it is proposed to record for each potential leak node j, the various signatures it has along the considered time horizon which typically corresponds to one demand pattern cycle. Since the demand varies along this pattern, the position of the leak signatures changes accordingly. Then, in presence of a leak, the positions of its signatures in the LSS along the day with the positions of the reference leak signatures are compared. This comparison is performed by summing the Euclidean distances for each time instant considered. Thus, if T instants of time are considered, there are T residuals
, t ∊ [1,⋯, T] obtained from the measured pressures. The index of the leaky node is estimated as the one that minimizes the sum of the distances between the node signature and the current leak signature along the time horizon is:
5.4. Combining Time Horizon and Leak Signature Domains
Finally, it is proposed to combine the leak signature domains with the time horizon analysis to obtain a more robust leak detection mechanism. First, the domains of the various leak signatures for each time instant considered are computed. Then, when locating a given leak, a list which includes the leak signatures whose domain contain the real leak in at least a given percentage (e.g., 90%) of the T time instances is computed. This list is also ordered according to the sum of distances between the reference signatures involved and the real leak signature, for each time instant. By means of such procedure, a list of probable leaks along a time horizon is obtained, that gives, at first rank the most probable location and next, the position of other possible locations if this first assumption is incorrect. In the following section, the leak location method based on the LSS is applied to a real network and the performance using signature domains and a time horizon is analyzed.
6. Real Network Application
The proposed method is applied to a real network (WDN of Limassol city in Cyprus) simulated in EPANET. This network consists of 1 reservoir, 197 junction nodes and 239 pipes as shown in Figure 5.
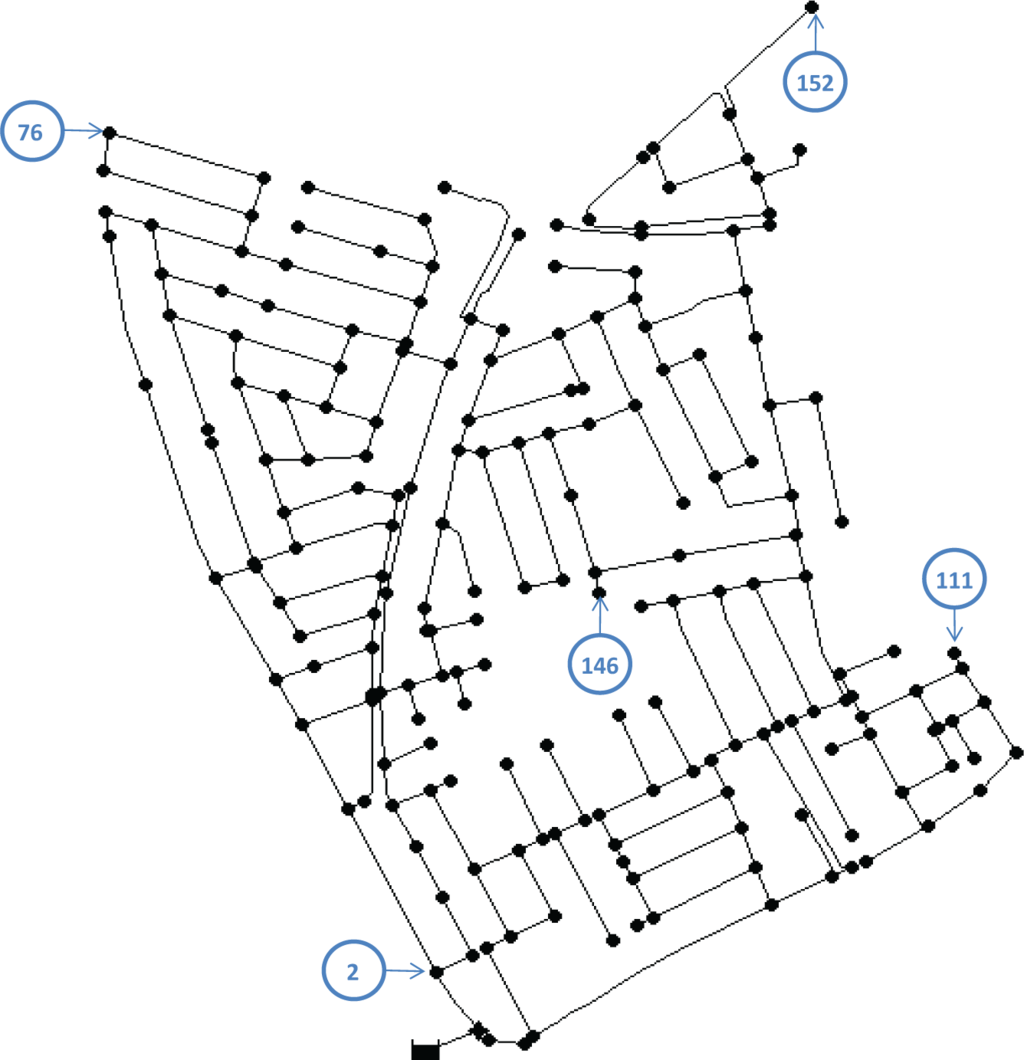
Figure 5.
Limassol water distribution network.
Leaks are simulated in a range going from 2 to 6 lps. These values are selected since, as stated before, they correspond to the leak magnitude range of interest according to the water company managing this network. To simulate individual leaks in EPANET, according to [20], it is necessary to specify an emitter coefficient (EC in lps/m1/2) based on the following expression:
where q is the flow rate, p is the fluid pressure and Pexp is the pressure exponent. Then, the EC will vary in a range going from 0.3 to 0.9 lps/m1/2 to introduce leaks in the range specified above.
It is important to remark that, whereas in the theoretical analysis part of the paper the leak is represented as an extra demand, here a different formulation is used. This difference in the way leaks are modelled will introduce some additional uncertainty. A more thorough analysis on how this different leak representation affect the proposed leak isolation method will be addressed as future work. There are some recent works that study and try to find equations for modelling leakage as a function of pressure [22,23], it is well known that the pressure exponent for the leak is commonly fixed at 0.5, being this value used in this work. However, it is very interesting to note that the leakage exponent can provide a better characterization of the pressure response when it is measured at different pressures, also, it has an important impact when different materials are tested. Also, it is important to mention that in recent studies it has been shown that the relationship between the leak discharge and the head in the pipe can be relevant for modeling leaks in WDNs. In fact, experimental evidence presented in [24] shows hysteresis behavior in a high density polyethylene pipe.
First, it is proposed to analyze how the number of sensors used in the network impacts the quality of the leak location. The sensors are distributed such that they try to cover as much as possible the various network areas and it is assumed that they are sensitive to any pressure change at their location. By experience, it has been noticed that sensors located at the edges of a network are more sensitive to changes in pressure. Thus, border nodes are arbitrarily selected trying to cover all the pressure changes (note that an optimal sensor placement has not been performed, but it will be part of the future work). The possible locations of the sensors are summed up in Table 1 and shown in Figure 5.

Table 1.
Indexes of the nodes equipped with sensors according to the total number of sensors.
6.1. Choice of Projection Hyperplane
First, the projection which optimizes the chances to detect the leak is searched. To this aim, the number of overlaps between leak signature domains for each possible projection hyperplane is counted. With the 197 nodes of the Cyprus network, and considering only one instant of time, there are for each projection, 19, 306 pairs of leaks whose leak signature domains could potentially overlap (obtained as the total of combinations of two nodes from the total of nodes, i.e.,
). Table 2 sums up the results obtained, as a function of the projection hyperplane and the number of sensors. As one can see, the number of overlaps tends to decrease with the number of sensors installed. In the case that 2 sensors are installed, the two possible projections give the same number of overlapping domains. In other cases, the most suitable projection is the one associated with sensor of index 152 which minimizes the intersections between leak signature domains.

Table 2.
Overlapping leak signature domains for a single instant of time in function of the projection hyperplane and a given number of sensors.
Analogously, the best projection when taking into account a full time horizon (in this case, a 24 h time horizon) is evaluated by averaging the sum of overlaps obtained for each single time instant. Table 3 shows the results obtained, as a function of the projection hyperplane and the number of sensors used.

Table 3.
Overlapping leak signature domains, as a function of the projection hyperplane selected and the number of sensors when considering a time horizon.
As one can see, the best choice may differ from what is obtained when considering only a single instant of time. When 2 sensors are installed, both projections give the same average number of overlaps. In the case of using 3 and 4 sensors, the most suitable projection is associated with the sensor of index 2 while in the case of 5 sensors, the best projection is based on the sensor of index 152.
6.2. Leak Location: Single Node Analysis
Here, a leak in the node of index 69 is considered with a magnitude of 3.5 lps (simulated with EC = 0.54). Figure 6 represents the leak in the LSS in case of 2, 3, and 4 sensors. Lower pictures (d,e,f) are zooms of the upper pictures (a,b,c).
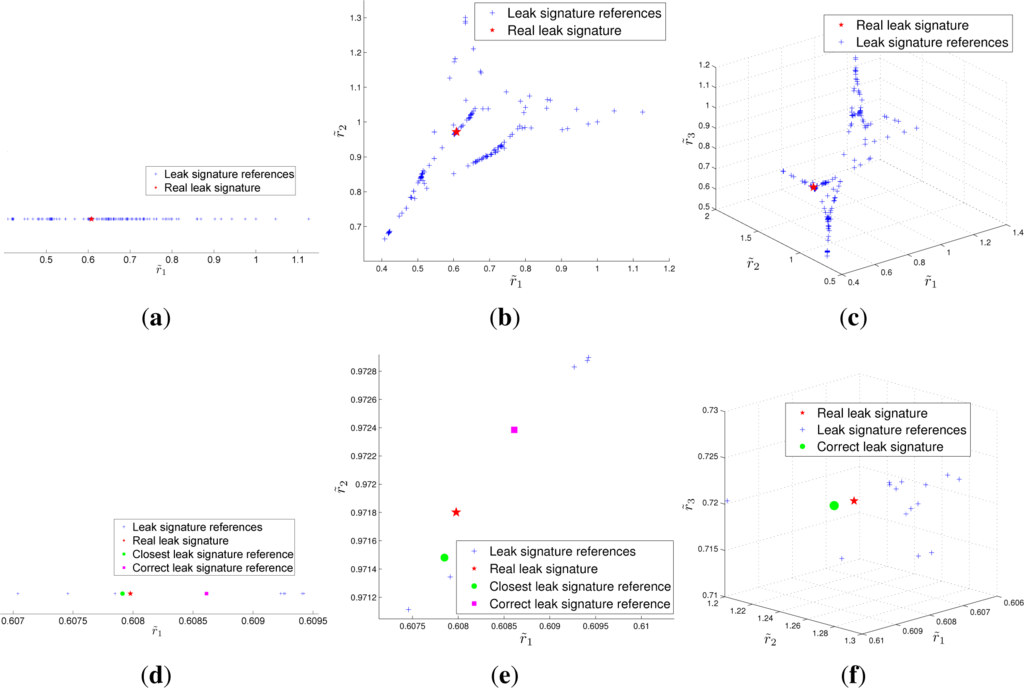
Figure 6.
View of a leak at node 69 in the LSS in case of 2 sensors (a,d); 3 sensors (b,e); and 4 sensors (c,f). Lower pictures are zooms of the upper pictures.
In the case that 2 sensors are installed in the network (Figure 6a,d), the closest leak signature corresponds to the node of index 194 which is at a topological distance of 4 nodes from the node 69. Now, if the leak signature domains are analyzed, it is possible to compute a list of probable leak nodes, which are the nodes whose domain contains the signature of the real leak. Such procedure leads to a list of 7 probable leak nodes. When the list is ordered according to the distances between the real leak signature and the reference signatures, the real leak node is ranked in the fourth position. With 3 sensors (Figure 6b,e), the leak is located at node 70 which is at a topological distance of 1 node from the node 69. In addition, the number of probable leaks with 3 sensors is reduced to 3 while the correct leak is ranked last.
Finally, with 4 sensors (Figure 6c,f), the leak can now be discriminated from any other node and it is correctly located at node 69. Moreover, when using 4 sensors, it can be seen that the only leak in the list of signature domains computed is the correct leak at node 69.
Now a test of the leak location method coupled with a time horizon analysis is proposed. In this case, a leak in the node of index 150 is considered with a magnitude of 3 lps (simulated with an EC = 0.46) with a time horizon of 24 h and sensor measurements every hour (the EC used to simulate the leak is assumed to be constant along the considered time period). Figure 7 represents the signatures in case of 2, 3, and 4 sensors in the region of the LSS where the real leak is measured. When 2 sensors are installed (Figure 7a), the node with the minimum distance summed along the time horizon is the node of index 149 two nodes away from the leak node. Considering the signature domains, an ordered list of 3 nodes of indexes (149, 150, 191) is obtained. In the case of 3 sensors, the leak is correctly located at node 150 (Figure 7b) whereas the list of probable leaks still contains three nodes but now with order (150, 149, 191). Finally, the case of 4 sensors gives almost the same results: the leak is correctly located at node 150 and the list of probable leaks contains again 3 signatures meaning that leaks are still difficult to discriminate, even with an LSS of dimension 3 (Figure 7c).
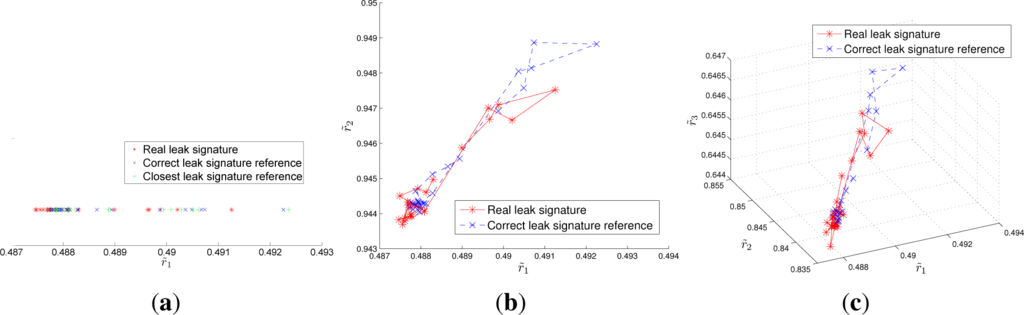
Figure 7.
View of a leak at node 150 in the LSS for a 24-hour time horizon analysis in case of 2 sensors (a); 3 sensors (b); and 4 sensors (c). The lines correspond to connections between successive time samples. The leak is correctly located when 3 and 4 sensors are present.
6.3. Leak Location: Full WDN Analysis
A global analysis of the performance locating leaks in the WDN is performed by simulating successively leaks in each of the network nodes. Here, the number of sensors may vary from 2 to 5 (see Table 1). In order to perform more realistic tests, some scenarios may include measurements noise. In these cases, Gaussian white noise with a mean amplitude corresponding to 0.5% of the expected measurements is added.
Tables 4 and 5 show the efficiency achieved for leak detection considering a single instant of time and a time horizon, respectively. The experiments were performed with or without the presence of noise. Without noise, a leak magnitude of 4 lps (EC = 0.6) is chosen whereas in presence of noise, the magnitudes are randomly taken between 2 and 6 lps (EC ∊ [0.3, 0.9]). Both tables indicate according to the number of sensors (column 1), the percentage of correct leak locations (columns 2 and 5), the average topological distance in the network in case of incorrect leak location (columns 3 and 6) and the mean rank of the real leak with the list of probable leaks (columns 4 and 7). Note that, the correct leak was always found within the list of probable leaks.

Table 4.
Leak location efficiency when considering only one instant of time.

Table 5.
Leak location efficiency with time horizon analysis.
First, comparing the two tables, it can be seen that the introduction of a time horizon clearly improves the overall robustness of the leak detection method. In addition, it can be seen as a general trend, an important improvement between 2 and 3 sensors and then between 3 and 4, whereas the relative improvement is somehow smaller when passing from 4 to 5 sensors. However, it can be observed that with the proposed method, the efficiency that is obviously affected by the presence of noise remains higher than 75% from 4 sensors when including a time horizon analysis. Moreover, the average topological distance in case of incorrect leak location is always very low, as well as the rank of the correct leak among the list of possible leaks when using signature domains. Note that another advantage of using the domains is that it indicates for a given leak if it has a risk to be confused with other nodes and which are these nodes. In particular, if the list contains only one element, there is a high probability to be the correct leak.
Table 6 show the efficiency of the leak location considering a high level of noise corresponding to values between 5% and 10% of the expected measurements. It is important to note that even when the efficiency in the correct location is affected, the nodes found by the method are in a small range from the real leak node. It means that when the measurements are more severally affected by noise in the network, the method still achieves a good location.

Table 6.
Leak location efficiency with a high level of noise.
By comparison, the method using structured residual proposed in [10] for the same Limassol network was able to correctly locate 136 of the 197 possible leaks using 3 sensors (i.e., 69%). The tests were generated using the data without noise and with leak magnitudes between 1.6 and 3.2 lps.
7. Test in a Real Leak Scenario
The proposed approach is applied to a real network that corresponds to a DMA located in Nova Icaria area in Barcelona, Spain. It is composed of 3320 nodes, where 1900 are demand nodes and the rest are street or junction nodes while 6 sensors are installed.
To test our proposed methodology in a real leak scenario, the water company provided us with data of a real leak which occurred between 00:00 on 20 December 2012 and 6:30 on 21 December 2012, i.e., 30 h and 30 min of a continuous leak. Then, in our case, we use a time horizon of 30 h taking into account data from 00:00 until 6:00 of the next day. The first stage prior to the methodology application is to detect the occurrence of a new leakage scenario in the DMA. In general, a detection procedure followed by water utilities is based on the analysis of the difference between night flows. Although leakage is pressure dependent, and at night-time pressure is lower, the reduction of the demand uncertainty makes it more reliable to analyze the night flows instead of the day flows. As shown in Figure 8a, the total DMA inflow suffered a meaningful increase on December 20th when the leak occurred with respect to the previous day. The difference between these two flows (Figure 8b) and its average value allows estimation of the size of the leakage. In this case, the estimated value of this increase (the leakage size) is 5.6 lps on average.
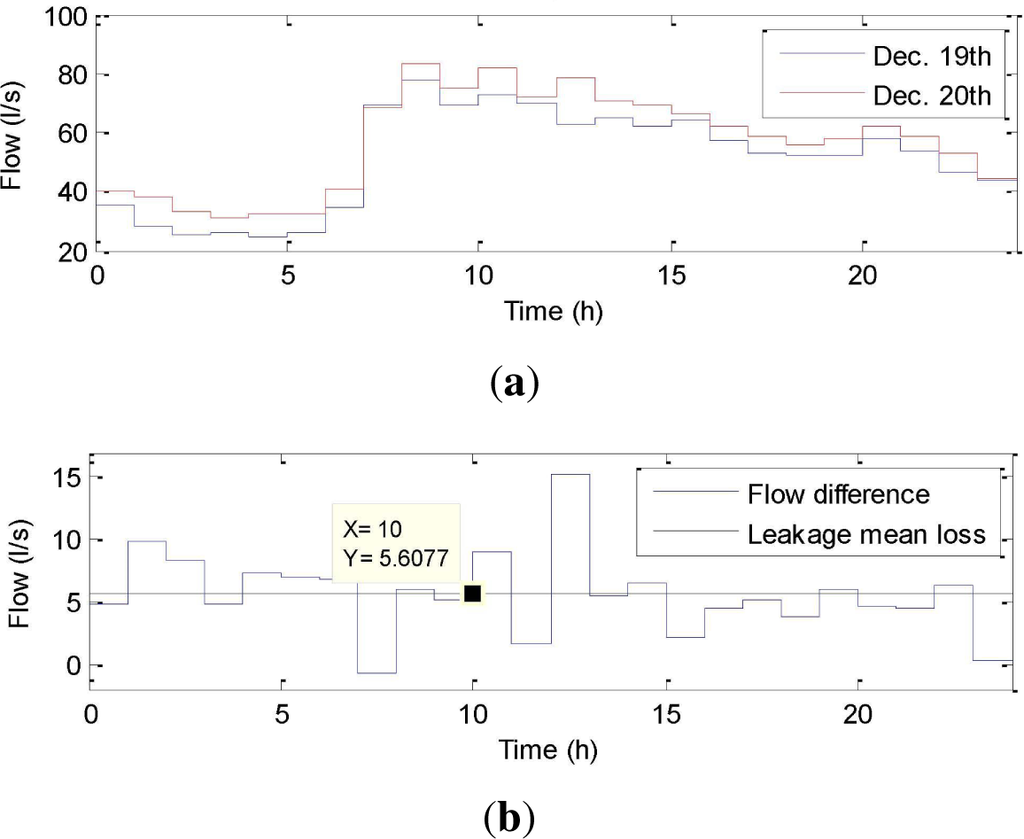
Figure 8.
Leak magnitude estimation. (a) Total input flow; (b) Leakage loss calculation.
The resolution of the sensors strongly affects the performance of the leak location. In our case, the sensors installed provide a 10 cm resolution. In order to improve the resolution, the sensors measured the pressure every 10 min along the time horizon, while the residuals were computed with an hourly average such that each hourly measure is obtained as
In a real application, some practical problems are quite common. In particular, one of the six sensors installed in the network was not working, and so the leak location was performed using only five sensors.
The hyperplane projection was performed using the projection onto the node with the less number of overlaps. To obtain the leak signatures, 6 different leak magnitudes were simulated corresponding to sizes between 2 and 6 lps approximately. In Figure 9, we can see the probability of leak. The leak node was located at 127.8 meters from the real leak. It represents an important result because it demonstrates that the proposed methodology can be applied in real cases and shows a good efficiency when using real data. It is important to note that the actual sensor placement was not based on the LSS method. Thus, with an appropriate sensor placement, is highly probable to achieve even a better leak location performance.
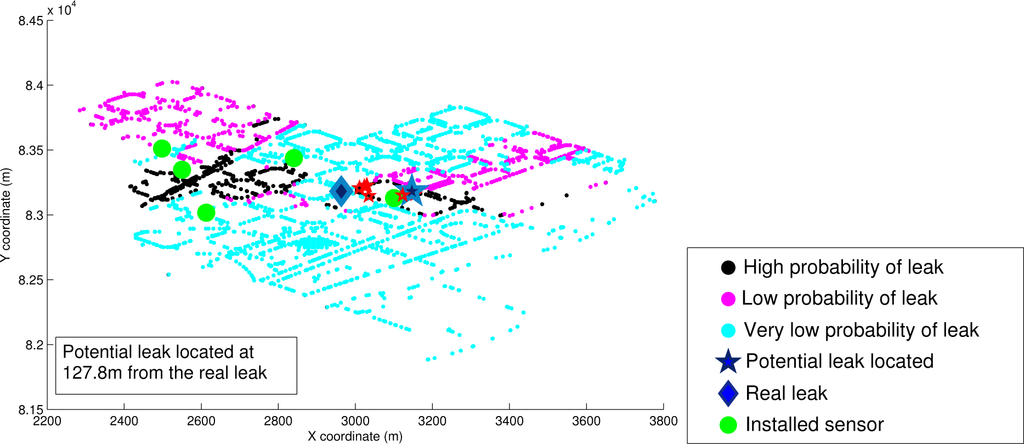
Figure 9.
Real leak scenario location using the LSS method.
8. Conclusions
In this paper, a new scheme for leak location in water distribution networks is presented. It is based on an original representation called the Leak Signature Space. In this space, a specific signature can be associated to each leak location minimizing the dependence with the leak magnitude. The distance between the measured leak and reference signatures in this space gives an estimation of the location of the leak in the network. An improvement in the robustness of the method is also proposed by considering leak signature domains and a time horizon analysis. Experiments involving simulations on a real network have shown that such method allows an interesting ratio of correct leak location which improves with the number of installed sensors, even in presence of measurements noise. In addition, when the node is incorrectly located, the topological distance between the node found and the leak node is small. Moreover, the real leak is always in the list of probable leaks, and most of the times in the upper ranks.
In future work, it could be interesting to investigate how to use the LSS representation in order to optimize the sensor placement. In this case, one possibility would be to find the best combination of sensors to optimize the distances between the leak signatures in the LSS and to minimize the number of overlapping signature domains. Finally, an extension of the methodology to address the problem of multiple leaks detection could be considered.
Acknowledgments
This work is supported by the Research Chair in Supervision and Advanced Control of Tecnológico de Monterrey, Campus Monterrey and by a CONACYT studentship. This work has been partially grant-funded by CICYT SHERECS DPI-2011-26243 and CICYT WATMAN DPI-2009-13744 of the Spanish Ministry of Education, by EFFINET grant FP7-ICT-2012-318556 of the European Commission.
Author Contributions
Myrna V. Casillas has done this work during her PhD (August 2011–December 2014). This paper is one of the outcomes of her PhD thesis. She has recently completed her PhD from Tecnológico de Monterrey. Luis E. Garza-Castañón and Vicenç Puig were Myrna’s supervisors. Adriana Vargas-Martinez was supporting this work as an expert in fault detection.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Puust, R.; Kapelan, Z.; Savic, D.A.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar]
- Wu, Z.Y.; Farley, M.; Turtle, D.; Dahasahasra, S.; Mulay, M.; Boxall, J.; Mounce, S.; Kleiner, Y.; Kapelan, Z. Water Loss Reduction. In Water Modeling and Water Loss Management; Bentley Institute Press: Exton, PA, USA, 2011. [Google Scholar]
- Almeida, F.; Brennan, M.; Joseph, P.; Whitfield, S.; Dray, S.; Paschoalini, A. On the acoustic filtering of the pipe and sensor in a buried plastic water pipe and its effect on leak detection: An experimental investigation. Sensors 2014, 14, 5595–5610. [Google Scholar]
- Colombo, A.F.; Lee, P.; Karney, B.W. A selective literature review of transient-based leak detection methods. J. Hydro-environ. Res. 2009, 2, 212–227. [Google Scholar]
- Meniconi, S.; Brunone, B.; Ferrante, M.; Massari, C. Potential of transient tests to diagnose real supply pipe systems: What can be done with a single extemporary test. J. Water Resour. Plan. Manag. 2011, 137, 238–241. [Google Scholar]
- Ferrante, M.; Brunone, B.; Meniconi, S.; Karney, B.; Massari, C. Leak Size, Detectability and Test Conditions in Pressurized PipeSystems. Water Resour. Manag. 2014, 28, 4583–4598. [Google Scholar]
- Ragot, J.; Maquin, D. Fault measurement detection in an urban water supply network. J. Process Control 2006, 16, 887–902. [Google Scholar]
- Xia, L.; Guo, J.L. Leak detection of municipal water supply network based on the cluster-analysis and fuzzy pattern recognition. Proceedings of the International Conference on E-Product E-Service and E-Entertainment (ICEEE), Henan, China, 7–9 November 2010; pp. 1–5.
- Khulief, Y.; Khalifa, A.; Mansour, R.; Habib, M. Acoustic detection of leaks in water pipelines using measurements inside pipe. J. Pipeline Syst. Eng. Pract. 2012, 3, 47–54. [Google Scholar]
- Rosich, A.; Puig, V. Model-based leakage localization in drinking water distribution networks using structured residuals. Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 410–415.
- Goulet, J.A.; Coutu, S.; Smith, I.F. Model falsification diagnosis and sensor placement for leak detection in pressurized pipe networks. Adv. Eng. Inform. 2013, 27, 261–269. [Google Scholar]
- Ayala-Cabrera, D.; Herrera, M.; Izquierdo, J.; Ocaña Levario, S.J.; Pérez-García, R. GPR-based water leak models in water distribution systems. Sensors 2013, 13, 15912–15936. [Google Scholar]
- Pudar, R.S.; Liggett, J.A. Leaks in pipe networks. J. Hydraul. Eng. 1992, 118, 1031–1046. [Google Scholar]
- Puig, V.; Schmid, F.; Quevedo, J.; Pulido, B. A new fault diagnosis algorithm that improves the integration of fault detection and isolation. Proceedings of the 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference, Seville, Spain, 12–15 December 2005; pp. 3809–3814.
- Pérez, R.; Puig, V.; Pascual, J.; Quevedo, J.; Landeros, E.; Peralta, A. Methodology for leakage isolation using pressure sensitivity analysis in water distribution networks. Control Eng. Pract. 2011, 19, 1157–1167. [Google Scholar]
- Casillas, M.V.; Garza-Castañón, L.; Puig, V. Model-based leak detection and location in water distribution networks considering an extended-horizon analysis of pressure sensitivities. J. Hydroinform. 2014, 16, 649–670. [Google Scholar]
- Lay-Ekuakille, A.; Vendramin, G.; Trotta, A. Robust spectral leak detection of complex pipelines using filter diagonalization method. IEEE Sens. J. 2009, 9, 1605–1614. [Google Scholar]
- Lay-Ekuakille, A.; Griffo, G.; Vergallo, P. Robust algorithm based on decimated Padè approximant technique for processing sensor data in leak detection in waterworks. IET Sci. Meas. Technol. 2013, 7, 256–264. [Google Scholar]
- Todini, E.; Pilati, S. A gradient algorithm for the analysis of pipe networks. In Computer Applications in Water Supply: 1—Systems Analysis and Simulation; Research Studies Press Ltd.: Taunton, UK, 1988; pp. 1–20. [Google Scholar]
- Rossman, L. EPANET 2 User’s Manual; United States Envionmental Protection Agency: Cincinnati, OH, USA, 2000. [Google Scholar]
- Casillas, M.V.; Garza-Castañón, L.; Puig, V. Extended-horizon analysis of pressure sensitivities for leak detection in water distribution networks. Proceedings of the 8th IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes, Mexico City, Mexico, 29–31 August 2012; pp. 570–575.
- Schwaller, J.; van Zyl, J. Modeling the pressure-leakage response of water distribution systems based on individual leak behavior. J. Hydraul. Eng. 2014. [Google Scholar] [CrossRef]
- Cassa, A.; van Zyl, J. Predicting the leakage exponents of elastically deforming cracks in pipes. Procedia Eng. 2014, 70, 302–310. [Google Scholar]
- Ferrante, M.; Massari, C.; Brunone, B.; Meniconi, S. Experimental evidence of hysteresis in the head-discharge relationship for a leak in a polyethylene pipe. J. Hydraul. Eng. 2011, 137, 775–780. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).