Abstract
According to the Mualem capillary model, hydraulic conductivity (HC) is integrated theoretically from the function related to soil water retention curves (SWRC). On the other hand, based on the smooth type of SWRC, the predicted HC function decreases abruptly near saturation, which often challenges the stability of numerical solutions. To improve the Mualem HC, van Genuchten’s function for SWRC was modified within the range of low matric suction. The van Genuchten-Mualem HC was then modified to integrate the proposed SWRC for each interval decomposed by a tangential curve. The analytical solutions of the modified HC were derived to prevent an abrupt decrease near saturation. The SWRC and HC data were acquired from laboratory tests for unsaturated soils sampled from five areas in Korea. The results of the HC tests were compared with the theoretical HC models using both the van Genuchten SWRCs and the modified curves. For fine grained soils, the modified model predicts a saturated HC at very small suctions. Furthermore, the modified model was shown to accurately predict the unsaturated behavior of the HC functions for Korean weathered soils.
1. Introduction
In variably saturated soils, the hydraulic conductivity is a crucial factor for understanding the hydrological behavior due to infiltration or evaporation. Experimental measurements are a very reliable way of estimating the unsaturated conductivity for various saturated conditions but the process is cumbersome. Consequently, for decades, indirect approaches have been developed to predict the hydraulic conductivity functions from the water retention characteristics [1,2,3,4,5]. Among the various soil water retention curves (SWRCs), the van Genuchten’s model can describe the normalized hydraulic behavior successfully from two parameters and provide conductivity by a closed-form equation based on Mualem theory [3].
The Mualem conductivity function, however, is extremely sensitive near saturation when smooth retention curves are used [6,7]. Small changes in the shape of the soil water retention curve near saturation can lead to significantly different results regarding the unsaturated hydraulic conductivity (HC) function based on the Mualem model. Furthermore, for fine grained soils, the HC decreases abruptly below a very small matric suction and the HC function becomes extremely steep under conditions close to saturation. From unsaturated flow analysis, the numerical solution can be highly nonlinear because of the steepness of the hydraulic conductivity [8,9]. Very steep functions in the HC can create difficulties with convergence and the solution will diverge and oscillate near saturation [10,11].
To reduce the steepness of the HC, the original fit of the van Genuchten’s curve can be modified to a non-smooth curve at a small suction [7,12,13]. Vogel et al. [7] suggested a modified SWRC to van Genuchten’s equation, in which a small capillary pressure introduces a break in the SWRC fit. On the other hand, the suggested fit of the SWRC requires additional effort to define the apparent air-entry pressure (e.g., −0.2 kPa according to Vogel et al. [7]) and replace the maximum water content with a fictitious value greater than the saturated one. In this study, to overcome such shortcomings, a modification of the SWRC is proposed near saturation, but the same parameters are used as the original fit of the van Genuchten’s model. The Mualem HC is derived as an analytical solution by integrating the proposed SWRC to preserve the stability of the solutions in infiltration analysis.
In the mountainous terrain of South Korea, the rock layer is weathered heavily and the upper layer near the surface is composed of residual soil. Consequently, the hydraulic behavior needs to be assessed frequently in geotechnical planning and construction because of rainfall infiltrating the variably saturated layers in the residual soils [11]. The modified model of the hydraulic conductivities was examined from experimental evidence obtained from residual soils in Korea. Laboratory tests on both the water retention and HC behaviors were carried out for multiple sites. Based on the fit of the water retention curves, the HC was predicted by both the van Genuchten-Mualem model and the modified model. The modified model reduced the slope of HC near saturation and also predicted the actual HC accurately.
2. The Relationship between Soil Water Retention and Hydraulic Conductivity
The soil water retention curve defines the relationship between the measures of the pore water volume and suction in the soil matrix. The matric suction p is defined as the difference between the air and water pressures in the pore. The variable for the pore water content is commonly the volumetric water content θ or effective saturation , which is defined as
where is the saturated water content and is the residual water content. According to the van Genuchten (VG) model (1980), the SWRC is defined by the relation of and p as follows:
where α is the inverse of the air-entry pressure, pb, n is the parameter on the pore size distribution and m = 1 − 1/n.
According to Mualem [2], the relative hydraulic conductivity function, , can be derived as follows:
where K is the unsaturated hydraulic conductivity function with respect to , and is the saturated hydraulic conductivity. q is an empirical parameter on the pore connectivity, which is commonly assumed to be 0.5 [2].
In the integrand of Equation (4), the inverse of p is a function of , which is obtained from the equation on the SWRC. Substituting Equation (3) into (4), the van Genuchten-Mualem (VGM) model on the hydraulic conductivity can be derived as follows [3]:
Figure 1 shows the hydraulic characteristics according to Mualem theory for a van Genuchten’s SWRC (pb = 2.43 kPa, n = 1.34, q = 0.5). As shown in Figure 1a, in the domain of a sufficiently small p, the pores are almost saturated and the water content varies insignificantly in both the SWRC data and VG fit. In contrast, the slope of the SWRCs near full saturation has a significant effect on integrating the unsaturated HC in Equation (4). As shown in Figure 1b, when Θ approaches 1, the value of 1/p increases to infinity in the smooth SWRCs, such as the VG curves. According to Equation (4), Kr (Figure 1c) is reduced abruptly in the VGM model and is much less than 1.0 (saturated value) near saturation or at very low suction. In particular, the decrease in Kr is drastic in the VGM model, when n < 1.5 for silty soils [7]. Numerical solutions using such HCs can frequently result in oscillations or divergence according to the steep gradient near saturation. Hence, the VGM model tends to estimate the HCs differently, even with extremely small variations in the shape of the SWRCs near saturation and it does not provide a unique HC for a set of SWRC data [14].
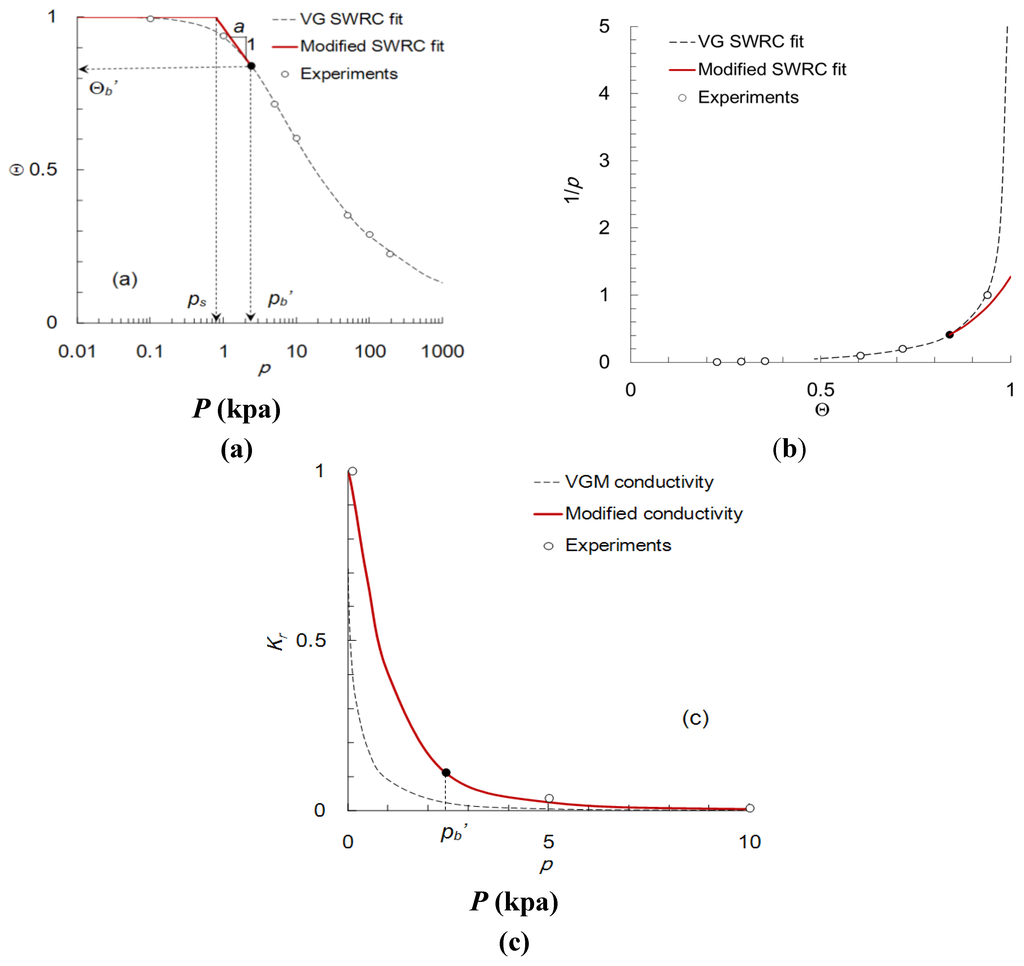
Figure 1.
Comparison of the soil water retention curves and hydraulic conductivities in both van Genuchten-Mualem theory and its modification: (a) soil water retention curves; (b) 1/p-Θ relationships; and (c) hydraulic conductivities.
To improve the VGM HC function, Vogel et al. [7] introduced a break near saturation, which serves the same purpose as ps in the non-smooth curve (Figure 1a). In the region where p > ps, the SWRC should be fitted again to the experimental results using a fictitious water content greater than the saturated one. Therefore, the parameters α and n of the SWRCs are different from those of the original fit in the VG SWRC. Furthermore, ps is determined to be a small value to retain the nonlinear form of the VG SWRC, but is difficult to assess uniquely.
pb is the inverse of α in the van Genuchten’s parametrization, which is evaluated from the curve fit of the SWRC data. In Figure 1a, pbʹ is an arbitrary estimate from which the curve is extrapolated tangentially on the log p scale to full saturation, which is less than or equal to pb. Θbʹ is the effective saturation corresponding to pbʹ in the VG fit of Equation (2). The VG curve is linearized in the logarithmic p axis by the tangential line from pbʹ to ps. ps is the value of the matric suction on the tangential line when Θ = 1. The modified VG SWRC has a partially linear shape on the logarithmic scale, where p is between ps and pbʹ and follows the VG curve smoothly in Equation (2), where p > pbʹ. The modified VG model on SWRC in Figure 1a is derived as follows:
where
Equation (8) is the same as the VG function (2b) when , and Equation (9) is a linear function in the ln p-Θ axis when . At full saturation, Θ = 1 when p ≤ ps. Θb and Θbʹ are the effective saturations at pb and pbʹ, respectively, calculated from Equation (2) of the VG model. In Equations (8–11), the modified SWRC is established by two parameters, α and n, of the VG SWRC, but it also needs to define pbʹ.
Figure 1b shows the function of 1/p with respect to Θ, in the modified SWRC according to Equations (8)–(11). For , the function is the same as the VG curve, which leads smoothly to the modified curve in the region, , according to Equation (9). When Θ = 1, the function of 1/p is a vertical line according to Equation (10) with a break of 1/ps. In the integration of Equation (4), the function of 1/p is integrated for each interval of Θ. Substituting Equations (8)–(11) into Equation (4), the relative HC is derived as follows:
where
Detailed derivation of Equations (8)–(15) is given in the Appendix. Equations (12)–(15) show the analytical solution of HC for the modified VGM model. The function of the modified SWRC is integrated to Equations (12) and (13). For full saturation (Θ = 1), Kr = 1 (Equation (14)) according to the definition of Equation (5). Figure 1c shows that the modified HC varies gradually without any abrupt decreases in the small matric suction near saturation. The difference between the SWRCs in Figure 1a is very small but the value of Kr from the modified SWRC is much greater than that of the VGM model.
According to Equations (12)–(15), the modified Kr is deduced from the parameters, α and n, of the VG SWRC. In addition, pbʹ should be determined using a sufficiently small value so that the modified SWRC can fit the actual shape of the SWRC in the experiments equivalently to the original VG model. Figure 2 shows the effect of pbʹ on the SWRCs and Kr functions (pb = 1 kPa, n = 1.2, q = 0.5), in which the maximum value of the p axis is equal to pb or 1kPa for comparison in a small p value. In Figure 2a, the modified SWRCs were compared with the VG model for three cases: pbʹ = pb (1 kPa), pb/5 (0.2 kPa) and pb/50 (0.02 kPa). Note that ps is 0.29 kPa, 0.081 kPa and 0.0087 kPa, respectively. All modified SWRCs have the same VG curve in the greater matric suction than pbʹ. As shown in Figure 2b, the Kr for the VGM model was reduced significantly, by 50%, at a matric suction of 0.001 kPa, and the overall values of Kr are less than the modified HCs. In very small matric suction, the modified VGM model prevents abrupt changes in Kr and retains the saturated Kr of 1.0. For the higher pbʹ, the value of Kr is greater than that for pbʹ = 0.02 kPa.
To compare with the Kr function of Vogel et al. [7], ps is estimated by 0.2 kPa, and α and n of the SWRCs are assumed to be the same as the original fit in the van Genuchten’s model. The modification by Vogel et al. [7] revealed a non-smooth shape at the break pressure both in the SWRC (Figure 2a) and the HCF (Figure 2b). On the other hand, the proposed Kr functions show a smooth shape, even though the modified SWRCs are not smooth.
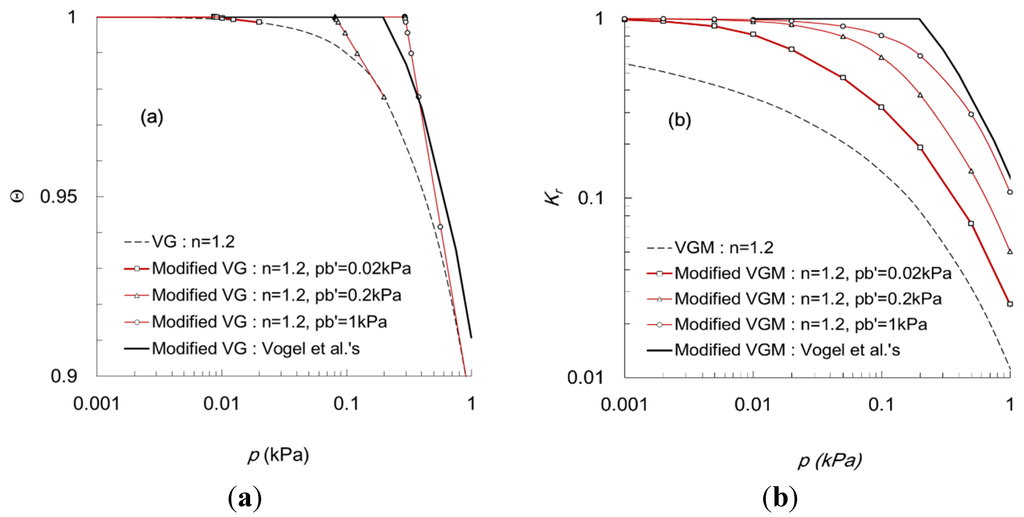
Figure 2.
Effect of linearization by the modified SWRCs on Kr functions (pb = 1 kPa, n = 1.2, q = 0.5): (a) soil water retention curves; (b) hydraulic conductivities.
As pbʹ is defined at a tangential point to extrapolate the SWRC, it is far from the physical parameter or variable, and a parametric study is examined to find pbʹ. To fit the water retention behavior equivalently to the VG model, it is better to establish a smaller pbʹ. If pbʹ is infinitesimal, Kr has the same value as that of the Mualem model based on the VG SWRC, and the numerical stability is no longer preserved. In Figure 2b, Kr at the matric suction of pb or Kr(pb) can be a measure to compare the hydraulic conductivities according to pbʹ, which decreases from 0.1–0.03 (0.01 for VGM) with decreasing pbʹ. Figure 3 shows the change in Kr(pb) as a function of pbʹ when n = 1.1 and 1.5 (pb = 1 kPa, q = 0.5). When pbʹ > pb/50 (or 0.02 kPa), Kr(pb) increases remarkably with respect to the logarithmic pbʹ. On the other hand, when pbʹ < pb/50, Kr(pb) varies steadily and converges slowly to the VGMs for very small pbʹ(<0.001 pb). Therefore, pbʹ can be assumed to be a threshold value of pb/50 to consider both the accurate fit of the experimental SWRC and the numerical stability due to the Kr function. In the case of n = 1.5, the difference in Kr(pb) between the modified and original VGM models is less than in the case of n = 1.1.
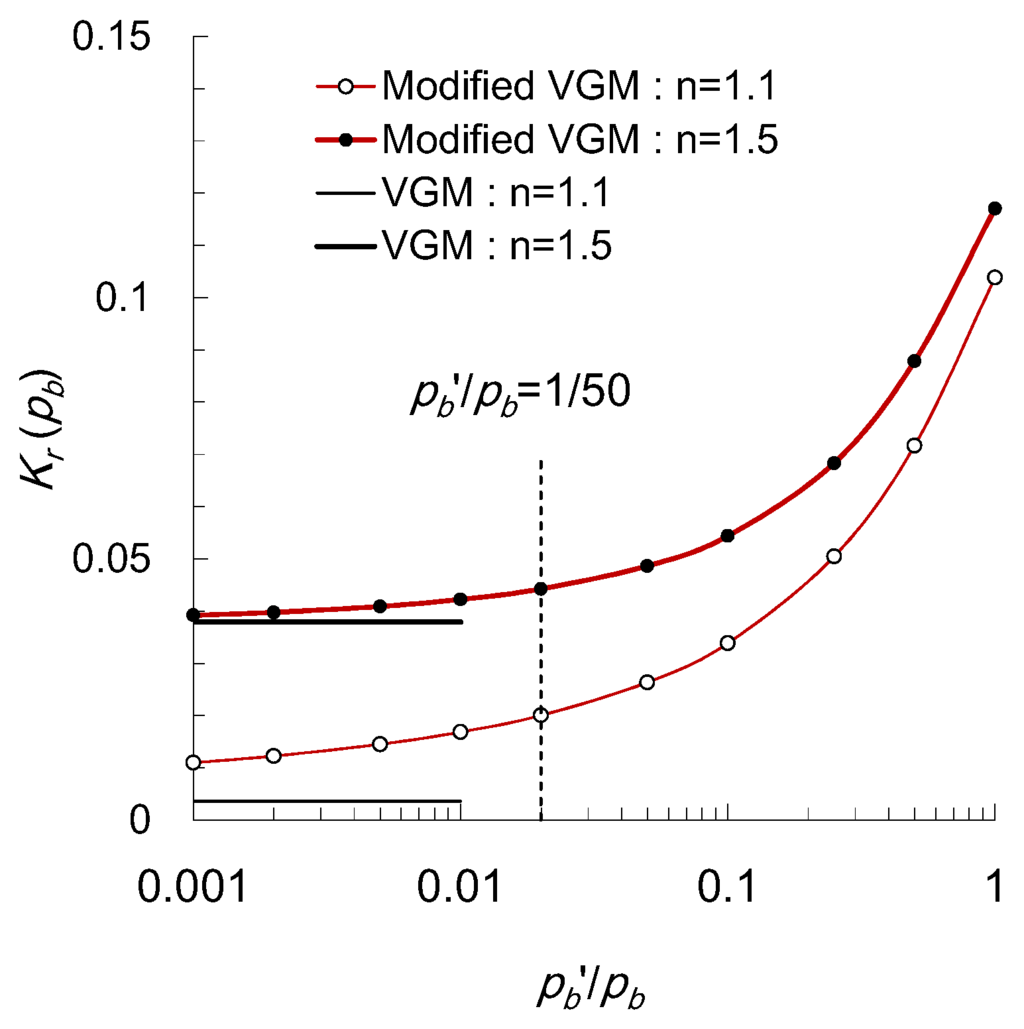
Figure 3.
Variation of Kr(pb) with respect to pbʹ for two cases of n = 1.1 and 1.5.
3. Test Procedure and Sample Conditions
Unsaturated hydraulic conductivity tests were conducted by controlling the air pressure and water pressure independently to apply matric suction into the soil sample using triaxial cell [15,16,17]. Figure 4 shows that the disks with high air entry pressure are located at both the pedestal and cap. The high air entry disk (or ceramic disk) is saturated by submerging and applying pressure in advance. In the compartments of both the cap and pedestal, a half-spiral grooved channel induces a uniform rate of water flow into or out of the soil sample, and also plays a role as a path flushing air bubble. A half-circular groove exists along the perimeter of the cap to distribute the uniform air pressure into the soil sample.
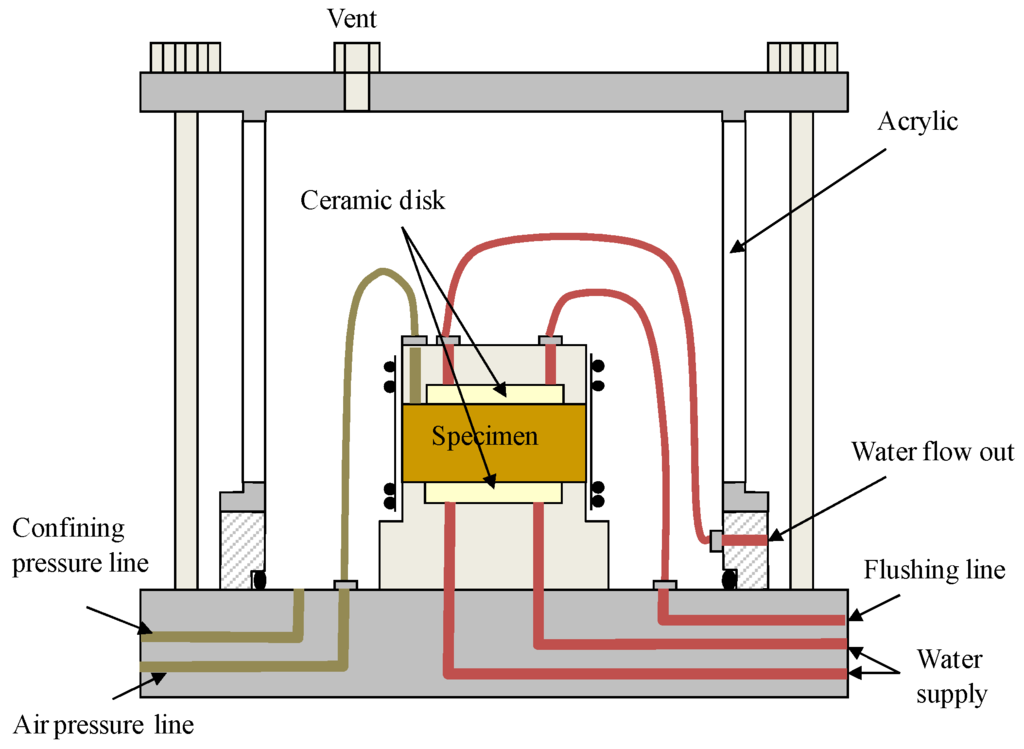
Figure 4.
Apparatus to measure the hydraulic conductivities for unsaturated soils.
To saturate the samples initially, the air is removed by suction and the water is supplied to the sample. The test is started from low matric suction values at the wetness near saturation and proceeds through a drying process. The matric suction is set to a specified value by controlling the pore air pressure, whereas the confining pressure is applied using the same air pressure for zero net stress. The difference in water pressure (10 kPa) between the pedestal and cap induces a hydraulic gradient and, hence, upward water flow within the soil sample. The pressure gradient is not so small and the test is limited by the fact that the measured conductivity is unreliable at low suctions. The matric suction in the soil is determined from the air pressure and the mean water pressure. The steady state flow condition is achieved when the outflow rate is equal to the inflow rate, and the volume of water and the period of time flowing across the soil are measured. The hydraulic conductivity is then evaluated for each matric suction according to Darcy’s law. The saturated hydraulic conductivity is obtained independently from the falling head tests [18].
In the pressure plate extractor, the soil water retention curves during the drying and wetting procedures were measured to a maximum matric suction of 200 kPa on the pre-saturated high air entry disk. The drying branch of the soil water characteristic curve was first acquired, followed by measurements of the wetting branch. The sample size for the soil-water characteristic curve was 62 mm in diameter and 15 mm in height, and that for the hydraulic conductivity was 72 mm in diameter and 30 mm in height.
The hydraulic behavior of undisturbed and remolded samples of weathered granite was examined. Two undisturbed samples were obtained, as in Asan and Kimpo. The other disturbed samples were obtained in Okcheon, Seochang and Yesan, and compacted statically by a hydraulic jack with a controlled water content and dry density, as shown in Table 1. The Yesan SP sample was obtained from different sites compared to the Yesan 1 and Yesan 2 samples. The soil samples have void ratios varying widely from 0.47 to 0.95 (Table 1). The soils in Seochang and Kimpo contain 14% and 19% fine particles (finer than #200 sieve or 75 µm in diameter), respectively. The other samples have less than 5% fine particles.

Table 1.
Geotechnical properties.
| Region | Void Ratio | Dry Unit Weight γd (kN/m3) | Initial Gravimetric Water Content w (%) | Saturated Hydraulic Conductivity Ks (m/s) | Specific Gravity Gs | Particles Less Than 75μm #200 | Unified Soil Classification System USCS ** |
|---|---|---|---|---|---|---|---|
| Asan * | 0.45 | 16.8 | – | 2.47 × 10−7 | 2.58 | 0 | SP |
| Kimpo * | 0.75 | 14.5 | – | 2.99 × 10−7 | 2.65 | 19 | SM |
| Okcheon 1 | 0.57 | 16.7 | 19.87 | 1.29 × 10−8 | 2.67 | 5 | SW |
| Okcheon 2 | 0.77 | 14.9 | 7.93 | 2.38 × 10−6 | |||
| Seochang | 0.61 | 16.3 | 20.61 | 9.13 × 10−7 | 2.64 | 14 | SC-SM |
| Yesan 1 | 0.58 | 16 | 19 | 1.39 × 10−7 | 2.63 | 2 | SW |
| Yesan 2 | 0.78 | 14.2 | 19 | 3.70 × 10−7 | |||
| Yesan SP | 0.95 | 13.5 | 13.84 | 5.00 × 10−7 | 2.68 | 1 | SP |
Notes: * Undisturbed samples; ** SP = poorly graded sand, SW = well graded sand, SM = silty sand, SC = clayey sand.
4. Comparison of the HCs of the VGM Model with a Modified Model
The parameters for SWRC (θs, θr, pb, n) were evaluated to fit the experimental data by RETC code [19] and an additional parameter q was evaluated to fit the HC data. As listed in Table 2, the hydraulic behaviors of the soils are sorted into three groups. Soils with n < 1.5 were classified as group A and the others were classified as group B. Group A was again sorted by two groups of group A-1 and group A-2, in which pb ≥ 5 kPa. The samples belong to each group due to the presence of some fine-grained soil and residual formation environments. The low values of the tortuosity factor can be related to adsorptive water retention and film conductivity [20,21], which is beyond the scope of this study. For each group, the relative hydraulic conductivity, Kr, for the modified VGM model was first compared with that of the VGM model and subsequently with the measured value.

Table 2.
Parameters of the van Genuchten-Mualem model for each SWRC and HC.
| Group | Region | θs | θr | pb (kPa) | n | q | R2 for Modified HC Fit | R2 for VGM HC Fit |
|---|---|---|---|---|---|---|---|---|
| A-1 (n < 1.5, pb ≥ 5 kPa) | Kimpo | 0.40 | 0.00 | 10.90 | 1.23 | −1.5 | 0.638 | 0.702 |
| Seochang | 0.37 | 0.00 | 9.48 | 1.24 | −2.5 | 0.968 | 0.965 | |
| Yesan 1 | 0.25 | 0.00 | 16.11 | 1.32 | −3.5 | 0.979 | 0.972 | |
| A-2 (n < 1.5, pb < 5 kPa) | Asan | 0.28 | 0.13 | 2.43 | 1.34 | −3.5 | 0.990 | 0.977 |
| Okcheon 1 | 0.37 | 0.06 | 2.01 | 1.32 | −2.7 | 0.963 | 0.951 | |
| Yesan 2 | 0.25 | 0.05 | 1.89 | 1.33 | −4.3 | 0.990 | 0.941 | |
| B (n ≥ 1.5) | Okcheon 2 | 0.33 | 0.14 | 7.86 | 1.50 | −3.7 | 0.916 | 0.880 |
| Yesan SP | 0.46 | 0.18 | 1.14 | 1.69 | −3.6 | 0.970 | 0.967 |
Figure 5 shows the SWRCs and HCs of group A-1 (n < 1.5, pb ≥ 5 kPa): Kimpo, Seochang and Yesan 1 samples. In the VG fits, n = 1.23–1.32 and pb = 9.5–16.1 kPa, while θs = 0.25–0.40 and θr = 0. The three measured SWRCs described by the effective saturation are similar because of the similar n and pb values. In the modified SWRCs, pbʹ = pb/50 or 0.19–0.32 kPa. The modified VG model fitted differently to the VG model just in the region where the matric suction is less than pbʹ. Figure 5a shows the modified VG fit when p < pbʹ. In the SWRCs of Figure 5a, the VG model fits the measured data quite accurately on three samples of group A-1 and both models have an equivalent ability to fit the experimental SWRCs.
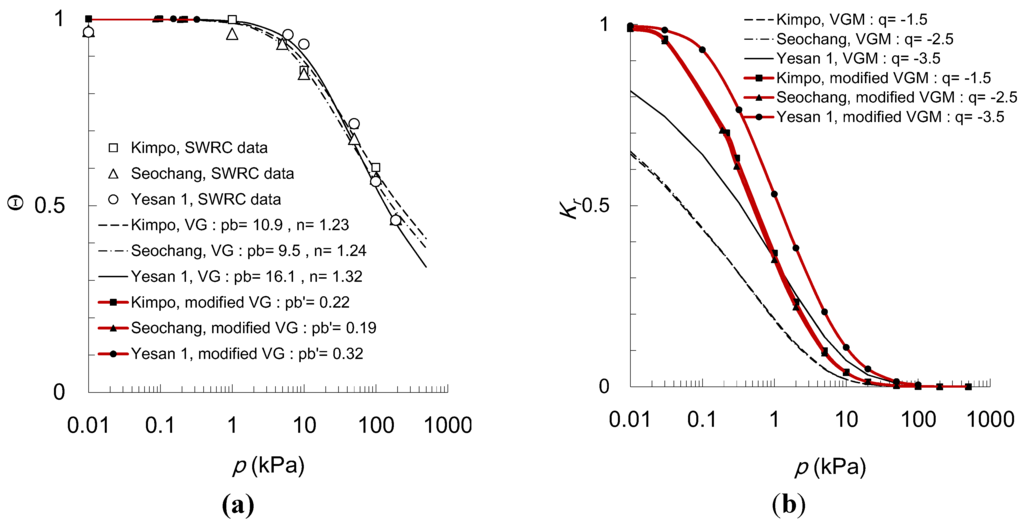
Figure 5.
Comparison of the VGM model with the modified model in Group A-1: (a) soil water retention curves (the measured data are shown by points, and the modified VG curve by lines with point when p < pbʹ); (b) hydraulic conductivities.
Kr was calculated using Equations (12)–(15), and the modified models were compared with the VGM HC models on Kimpo, Seochang and Yesan 1 samples (Figure 5b). The Kr function was calculated from the SWRC curve. The parameter q was evaluated to fit HC data as −3.5–−1.5. The SWRCs in Figure 5a incorporates the small difference in a suction less than pbʹ but Kr for the modified models is clearly greater than that for the VGM models. Near saturation, Kr = 1 in the modified VGM model, whereas Kr is reduced at a suction less than 0.01 kPa in the VGM model. The difference between the two models is 18%–37% at 0.01 kPa, which increases with decreasing n.
As shown in Figure 6, the SWRCs for group A-2 (n < 1.5, pb < 5 kPa) are used to predict the relative HC in Asan, Okcheon 1 and Yesan 2 samples. Both the VG model and the modified VG model can fit the measured SWRCs accurately, in which the parameters of the three samples to fit SWRCs are quite similar; n = 1.32–1.34, pb = 1.9–2.4 kPa and pbʹ = 0.04–0.05 kPa. θs, θr and q were evaluated to be 0.25–0.37, 0.05–0.13 and −4.3–−2.7, respectively. In Figure 6b, the VGM models for the three samples also showed an abrupt decrease in Kr, which were less than the modified VGM model by ~25% at suction of 0.01 kPa. Because pb in group A-2 is smaller than that in group A-1, the gradient of the Kr function to the matric suction in Figure 6b is greater than that in Figure 5b.
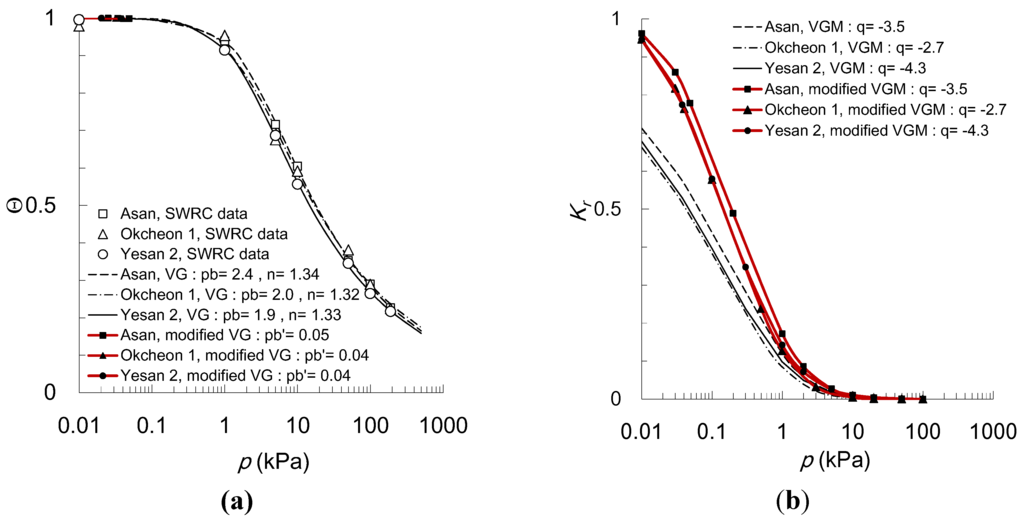
Figure 6.
Comparison of the VGM model with the modified model in Group A-2: (a) soil water retention curves (The measured data are shown by points, and the modified VG curve by lines with point when p < pbʹ); (b) hydraulic conductivities.
As shown in Figure 7, the SWRCs (Figure 7a) for group B (n ≥ 1.5 are shown with the relative HC (Figure 7b) in Okcheon 2 and Yesan SP samples. Both the VG model and the modified VG model can fit the measured SWRCs accurately; n = 1.50 and 1.69, pb = 1.1 and 7.9 kPa, θs = 0.33 and 0.46, θr = 0.14 and 0.18, and q = −3.7–−3.6, respectively. The data on the SWRCs were measured within a matric suction less than 200 kPa, which is far from the actual suction at the residual water content. Therefore, θr (Table 2) increased with increasing gradient of the SWRCs or n to optimize the SWRC fit. Near saturation, Kr ≈ 1 in both the modified VGM model and the VGM model, where Kr is reduced by 10% at most in group B. Therefore, the VGM model estimates Kr similar to the modified VGM model.
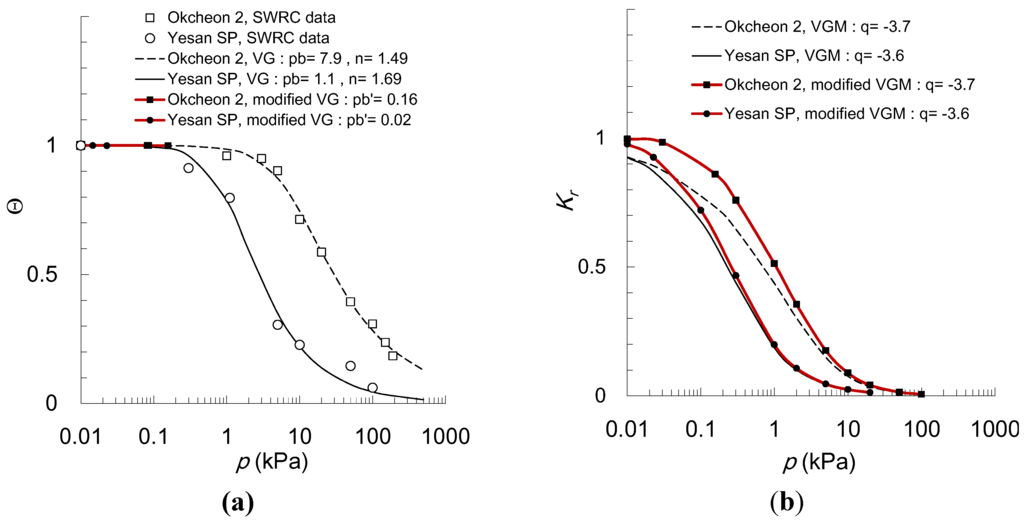
Figure 7.
Comparison of the VGM model with the modified model in Group B: (a) soil water retention curves (The measured data are shown by points, and the modified VG curve by lines with point when p < pbʹ); (b) hydraulic conductivities.
In groups A-1 and A-2, the prediction of Kr by the VGM model decreases abruptly near saturation. In such cases, the VGM model induces abnormal oscillation or divergence of the solutions in the numerical analysis near saturation. On the other hand, in group B, i.e., n > 1.5, there was a smaller decrease in Kr in the initial part of the VGM model.
5. Comparison of HCs of the Modified VGM Model with the Measured Data
Mualem’s model [2] incorporates an empirical parameter, q, accounting for the tortuosity and connectivity to predict the actual hydraulic conductivity, which is commonly assumed to be 0.5. On the other hand, many studies examined a range of values of the tortuosity parameter in the fit of the actual data [4,22,23,24], which is frequently negative [25]. The parameter, q, was estimated to be −1.5–−4.3 (−3.2 in average) in Table 2, which was obtained directly from the experimental data for Korean residual soils.
Figure 8 shows the Kr predicted by both the original and the modified VGM models for group A-1 (n < 1.5, pb ≥ 5kPa), where q was −2.5 on average. The goodness of fit of both models are compared in terms of the correlation coefficient R2 for log Kr (Table 2). Using the modified model, the measured Kr was predicted quite accurately for Yesan 1 sample (n = 1.32, R2 = 0.98 in Table 2). Because the SWRCs of Kimpo (n = 1.23) and Seochang (n = 1.24) samples are similar, as shown in Figure 5a, the measured data of the unsaturated HC were predicted well as similar curves using the modified VGM model (R2 = 0.64 for Kimpo and R2 = 0.97 for Seochang). The VGM model could predict the measured HC equivalently to the modified model (R2 = 0.70–0.97 for group A-1), but underestimated the nearly saturated Kr (~1.0) and subsequently the unsaturated part of the Kr data compared to the modified model.
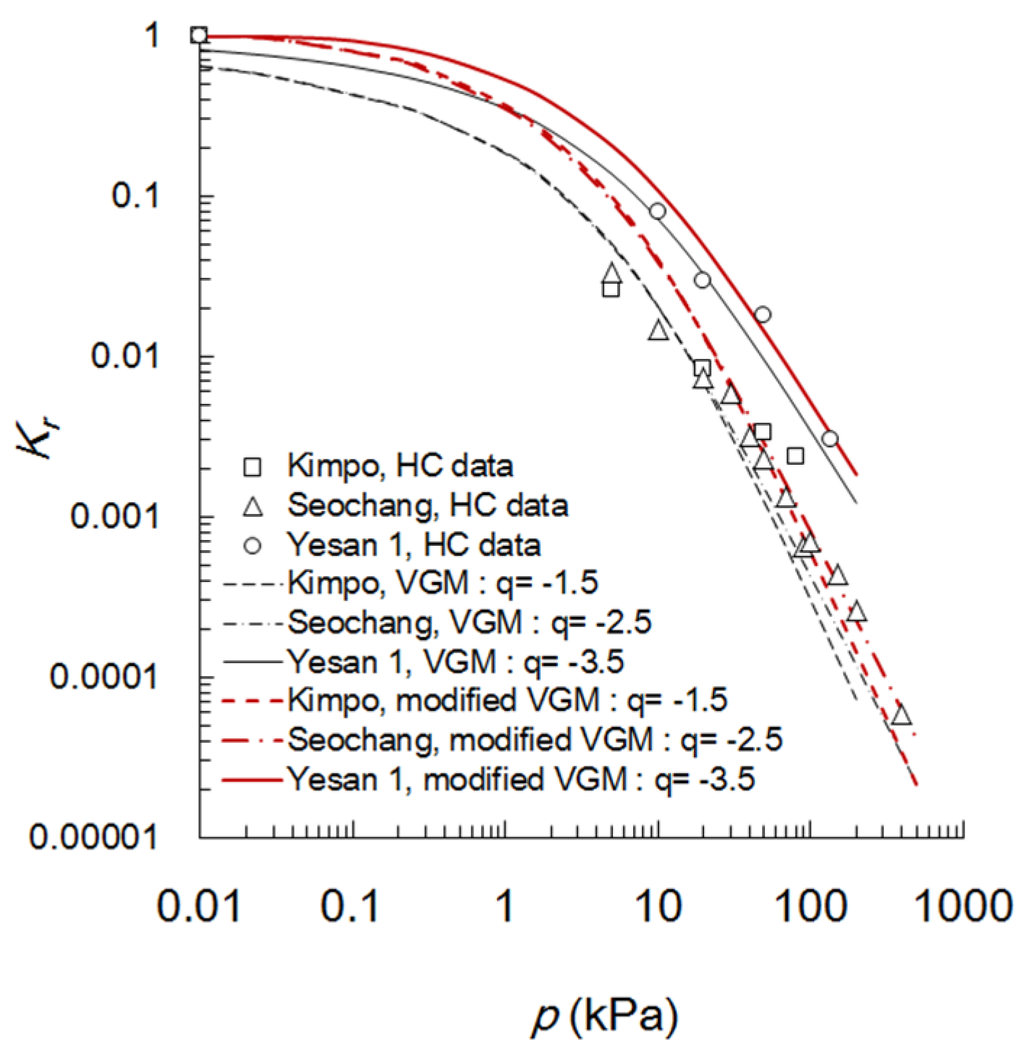
Figure 8.
Comparison of the measured hydraulic conductivities with the modified model in Group A-1.
In group A-2 (n < 1.5, pb < 5 kPa) in Figure 9, the measured Kr was also predicted quite well by the modified model for Asan (R2 = 0.99 in Table 2), Okcheon 1 (R2 = 0.96) and Yesan 2 (R2 = 0.99) samples. The VGM model could predict the measured HC fairly (R2 = 0.94–0.98 for group A-2), but underestimated the saturated and the unsaturated parts of the Kr data compared to the modified model. Regarding the effects of q on Kr, Kr increased with decreasing q. Group A-2, which has a smaller pb, q (−3.5 on average), has a much stronger effect on HC than Group A-1. Therefore, q contributes significantly to the prediction of Kr. Yesan 2 sample in Group A-2 (Figure 9) is compacted by the looser conditions and shows a higher Kr for both the measurements and predictions than the Yesan 1 sample in Group A-1 (Figure 8). Okcheon 2 sample is also looser than Okcheon 1 sample in Group A-2 (Figure 9) and belongs to Group B (Figure 10).
In group B (n ≥ 1.5) in Figure 10, the modified VGM model predicts the measured Kr reasonably well for Okcheon 2 (R2 = 0.92) and Yesan SP samples. The VGM model could predict similarly to the modified model (R2 = 0.88–0.97 for group B) because n > 1.5, and Kr ~ 1.0 in the nearly saturated state. As shown in Equation (4), Kr is multiplied by Θq, where Θ is deduced from the SWRC of each group. When q is negative, Θq > 1.0 and increases with increasing n. Group B showed the strongest effect of q (−3.6 in average) on HC than Groups A-1 and A-2, because n > 1.5.
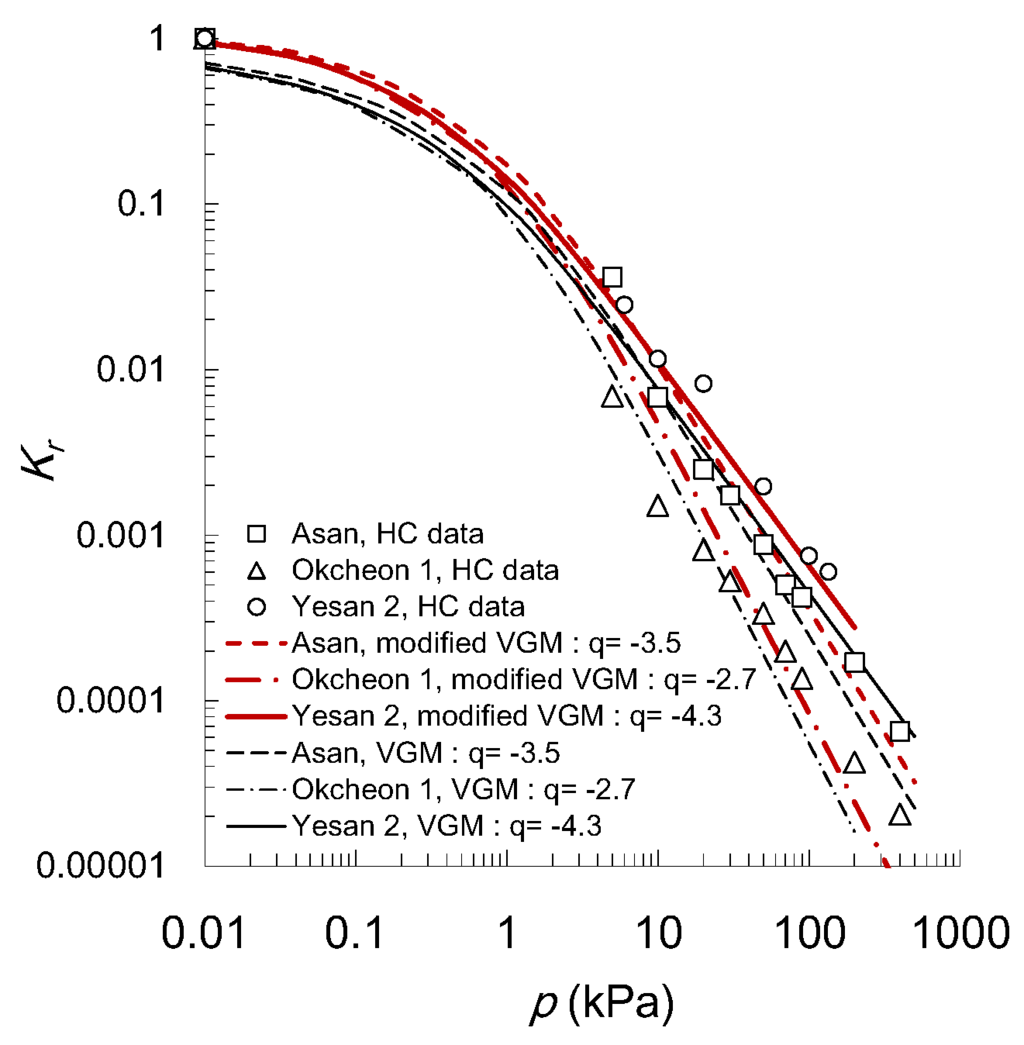
Figure 9.
Comparison of the measured hydraulic conductivities with the modified model in Group A-2.
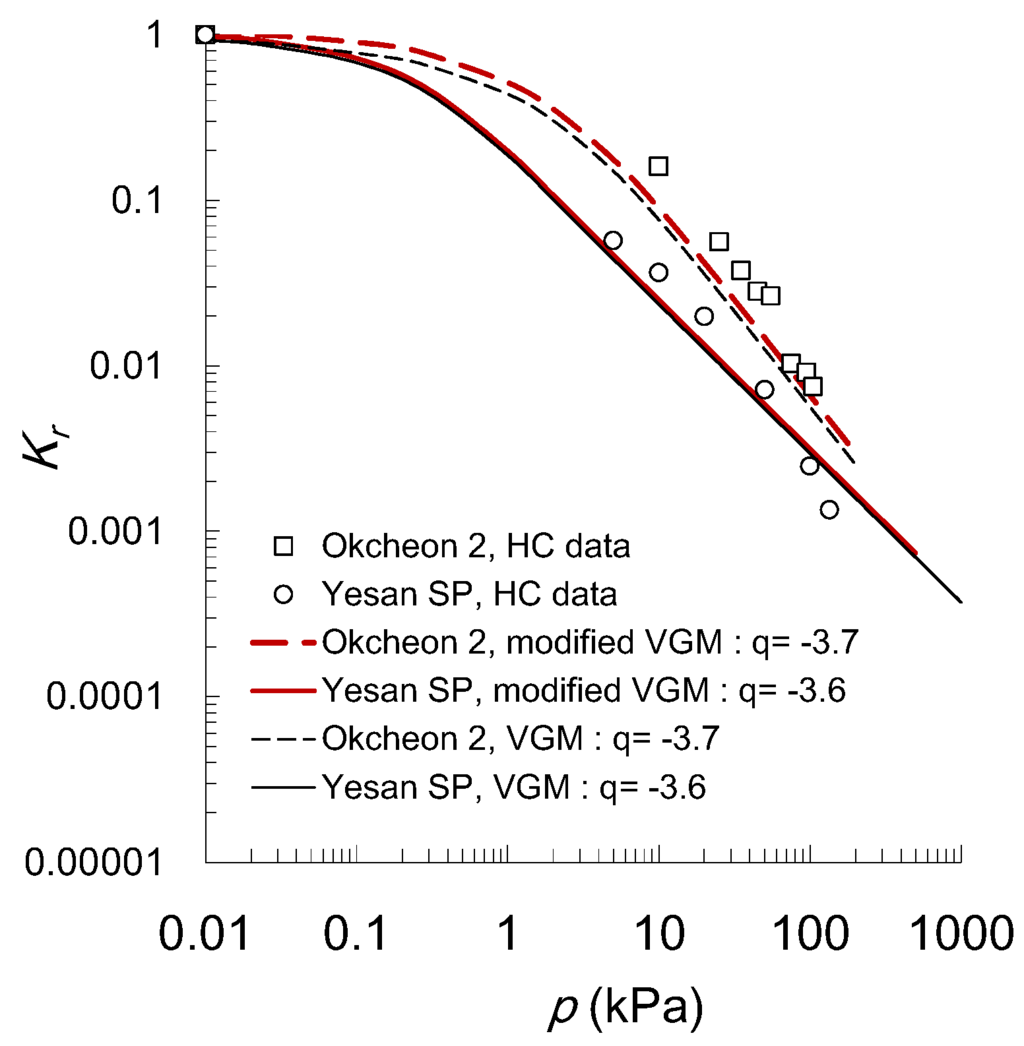
Figure 10.
Comparison of the measured hydraulic conductivities with the modified model in Group B.
6. Conclusions
The van Genuchten’s SWRC was modified near saturation and an improved model of the hydraulic conductivity was proposed by the analytical solutions based on Mualem theory. The modified model preserved both the accuracy of the SWRC fit to the measurement and the stability of the numerical solutions in infiltration analysis using the unsaturated HCs. The modified HC model included the same parameters as van Genuchten’s SWRCs (pb and n) and Mualem’s HC functions (q), but an arbitrary suction, pbʹ, was also estimated to be pb/50 to determine the tangential point in van Genuchten’s SWRC.
The experimental evidence of the SWRC and HC for a total of eight samples was examined and categorized by three groups to verify the HC model. In the SWRCs, both the VG model and the modified model fitted the measured data quite well on all samples of each group because the modified VG SWRC fitted the VG curve differently just in the region of low matric suction.
Near saturation, the calculated hydraulic conductivity in groups A-1 and A-2 when n < 1.5, was reduced abruptly in the VGM model but maintained the saturated value in the modified VGM model. The modified model could prevent the numerical instability induced by the VGM model near saturation.
The measured data of the unsaturated HC were predicted well using the modified VGM model. The tortuosity parameter q was evaluated directly using the experimental data for Korean residual soils.
Acknowledgments
This study was supported by the Yeungnam University Research Grant (214A380204), which is greatly appreciated.
Author Contributions
Seboong Oh participated in design of the study, analysis of the experimental data, and writing the manuscript. Yun Ki Kim participated in the experiments and their analysis. Jun-Woo Kim contributed to the analysis of the experimental data and preparing the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
The modified VG curve in Equations (8)–(11) was used to obtain HC by Mualem model. The slope of the tangential line in the ln p-Θ plane of Figure 1a is derived as follows:
Substituting Equation (8) of van Genuchten SWRC to (A1),
For , f() is defined by substituting Equation (8) as follows:
then,
For ,
For , g(Θ) is defined by substituting Equation (9) as follows:
then,
For ,
The HC function by the Mualem model is described by decomposition in intervals as follows:
For , Equation (A7) leads to
For , Equation (A7) leads to
Equation (12) is derived by substituting Equations (7), (A4) and (A6) into (A8). Equation (13) is derived by substituting Equations (15), (A4) and (A6) into (A9). For at saturation, Kr is not derived from Equation (A7) but Equation (14) is derived by the definition of the relative HC in Equation (5).
References
- Campbell, J.D. Pore Pressures and Volume Changes in Unsaturated Soils. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 1973. [Google Scholar]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A.; Huang, S. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 533–546. [Google Scholar] [CrossRef]
- Dourado Neto, D.; de Jong van Lier, Q.; van Genuchten, M.T.; Reichardt, K.; Metselaar, K.; Nielsen, D.R. Alternative Analytical Expressions for the General van Genuchten-Mualem and van Genuchten-Burdine Hydraulic Conductivity Models. Vadose Zone J. 2011, 10, 618–623. [Google Scholar] [CrossRef]
- Vogel, T.; Cislerova, M. On the reliability of unsaturated hydraulic conductivity calculated from the moisture retention curve. Transp. Porous Med. 1988, 3, 1–15. [Google Scholar] [CrossRef]
- Vogel, T.; van Genuchten, M.T.; Cislerova, M. Effect of the shape of the soil hydraulic functions near saturation on variably-saturated flow predictions. Adv. Water Resour. 2001, 24, 133–144. [Google Scholar] [CrossRef]
- GEO-SLOPE International. GeoStudio 2007; Calgary: Alberta, AB, Canada, 2007. [Google Scholar]
- Lu, N.; Wayllace, A.; Oh, S. Infiltration-induced seasonally reactivated instability of a highway embankment near the Eisenhower Tunnel, Colorado, USA. Eng. Geol. 2013, 162, 22–32. [Google Scholar] [CrossRef]
- Oh, S.; Kim, Y.K. A Modification of van Genuchten-Mualem Model on the Hydraulic Conductivity to Account for Numerical Stability and Empirical Connectivity in Korean Residual Soils. In Unsaturated Soils: RESEARCH & Applications; CRC Press: London, UK, 2014; pp. 1173–1177. [Google Scholar]
- Oh, S.; Lu, N. Slope stability analysis under unsaturated conditions: Case studies of rainfall-induced failure of cut slopes. Eng. Geol. 2015, 184, 96–103. [Google Scholar] [CrossRef]
- Ippisch, O.; Vogel, H.-J.; Bastian, P. Validity limits for the van Genuchten-Mualem model and implications for parameter estimation and numerical simulation. Water Resour. Res. 2006, 29, 1780–1789. [Google Scholar] [CrossRef]
- Schaap, M.G.; van Genuchten, M.T. A Modified Mualem-van Genuchten Formulation. Vadose Zone J. 2006, 5, 27–34. [Google Scholar] [CrossRef]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar] [CrossRef]
- Huang, S.; Fredlund, D.G.; Barbour, S.L. Measurement of the coefficient of permeability for a deformable unsaturated soil using a triaxial permeameter. Can. Geotech. J. 1998, 35, 426–432. [Google Scholar] [CrossRef]
- Kim, Y.K. Soil Slope Design and Stability Evaluation Methodology Considering Hydraulic Conductivity and Rainfall Characteristics. Ph.D. Thesis, Korea Advanced Institute of Science and Technology, Daejeon, Korea, 2009. [Google Scholar]
- Kim, Y.K.; Choi, K.L.; Lee, S.J.; Lee, S.R.; Kwon, H.S. Estimation of Unsaturated Permeability Function from Water Retention Characteristics for Korean Weathered Soils. J. Korean Geotech. Soc. 2010, 26, 449–460. (In Korean) [Google Scholar]
- ASTM International. Standard Test Methods for Measurement of Hydraulic Conductivity of Saturated Porous Materials Using a Flexible Wall Permeameter, D 5084. In Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2002. [Google Scholar]
- Van Genuchten, M.T.; Leij, F.J.; Yates, S.R. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; EPA 600/2–91/065; United State Environment Protection Agency (EPA): Washington, WA, USA, 1991.
- Peters, A. Simple consistent models for water retention and hydraulic conductivity in the complete moisture rang. Water Resour. Res. 2013, 49, 6765–6780. [Google Scholar] [CrossRef]
- Iden, S.C.; Durner, W. Comment on “Simple consistent models for water retention and hydraulic conductivity in the complete moisture range” by A. Peters. Water Resour. Res. 2014, 50, 7530–7534. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Improved prediction of unsaturated hydraulic conductivity with the Mualem-van Genuchten model. Soil Sci. Soc. Am. J. 2000, 64, 843–851. [Google Scholar] [CrossRef]
- Peters, A.; Durner, W. A simple model for describing hydraulic conductivity in unsaturated porous media accounting for film and capillary flow. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Salas, J.D.; Govindaraju, R.; Anderson, M.; Arabi, M.; Frances, F.; Suarez, W.; Lavado, W.; Green, T.R. Introduction to Hydrology. In Handbook of Environmental Engineering, Volume 15: Modern Water Resources Engineering; Wang, L.K., Yang, C.T., Eds.; Humana Press-Springer Science: New York, NY, USA, 2014. [Google Scholar]
- Peters, A.; Durner, W.; Wessolek, G. Consistent parameter constraints for soil hydraulic functions. Adv. Water Resour. 2011, 34, 1352–1365. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).