Hydraulic Conductivity Tests in the Triaxial Stress State: Is Peat an Aquitard or an Aquifer?
Abstract
1. Introduction
2. Materials and Methods
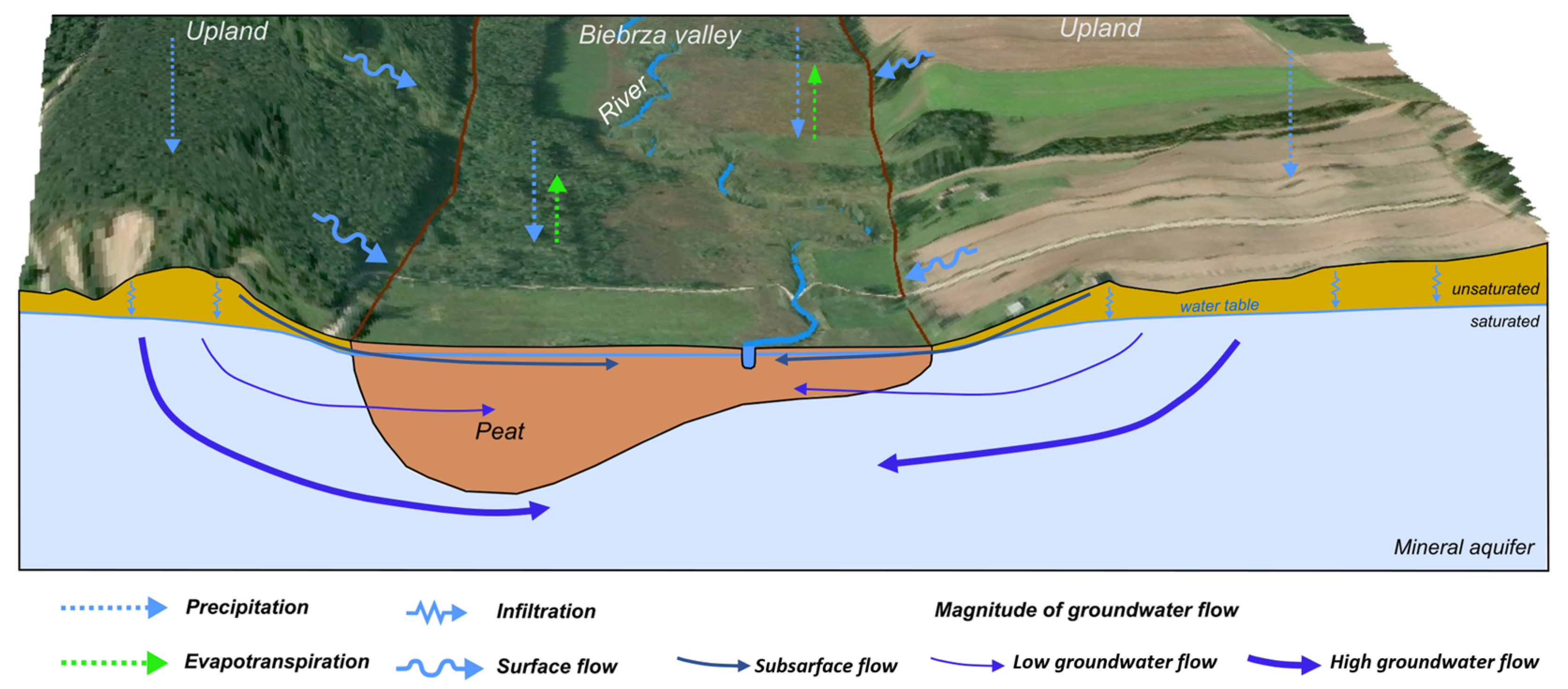
2.1. Study Area
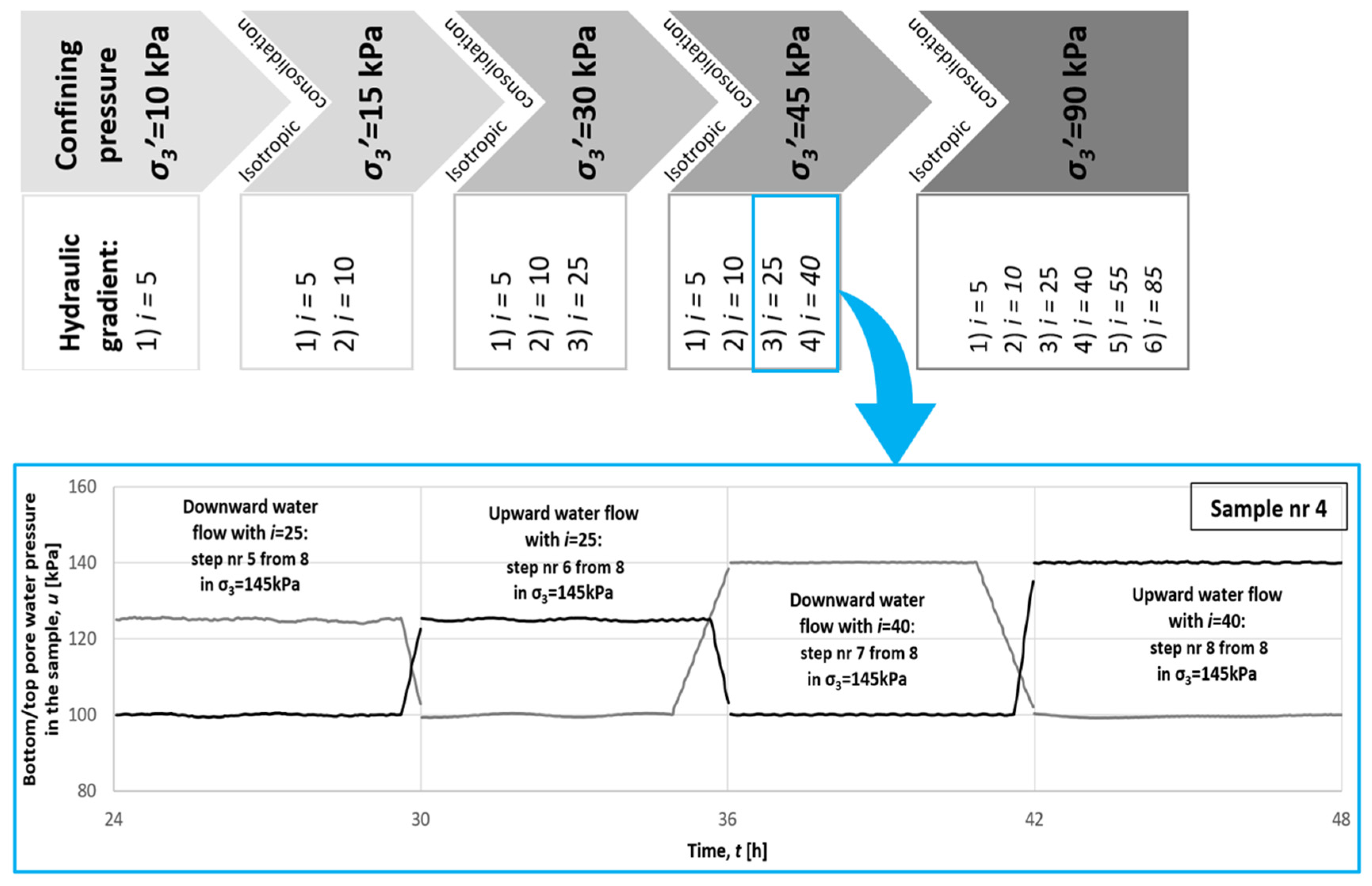
2.2. Test Procedures
- (a)
- The direction of flow (from the top to the bottom and, in the next stage, with the same gradient and radial stress but from the bottom to the top);
- (b)
- A constant hydraulic gradient (stepwise increases i = 5; 10; 25; 40; 55; 80);
- (c)
- A constant confining pressure corresponding to different triaxial stress states on the different depths (σ3′ = 10 kPa; 15 kPa; 30 kPa; 45 kPa; 90 kPa).
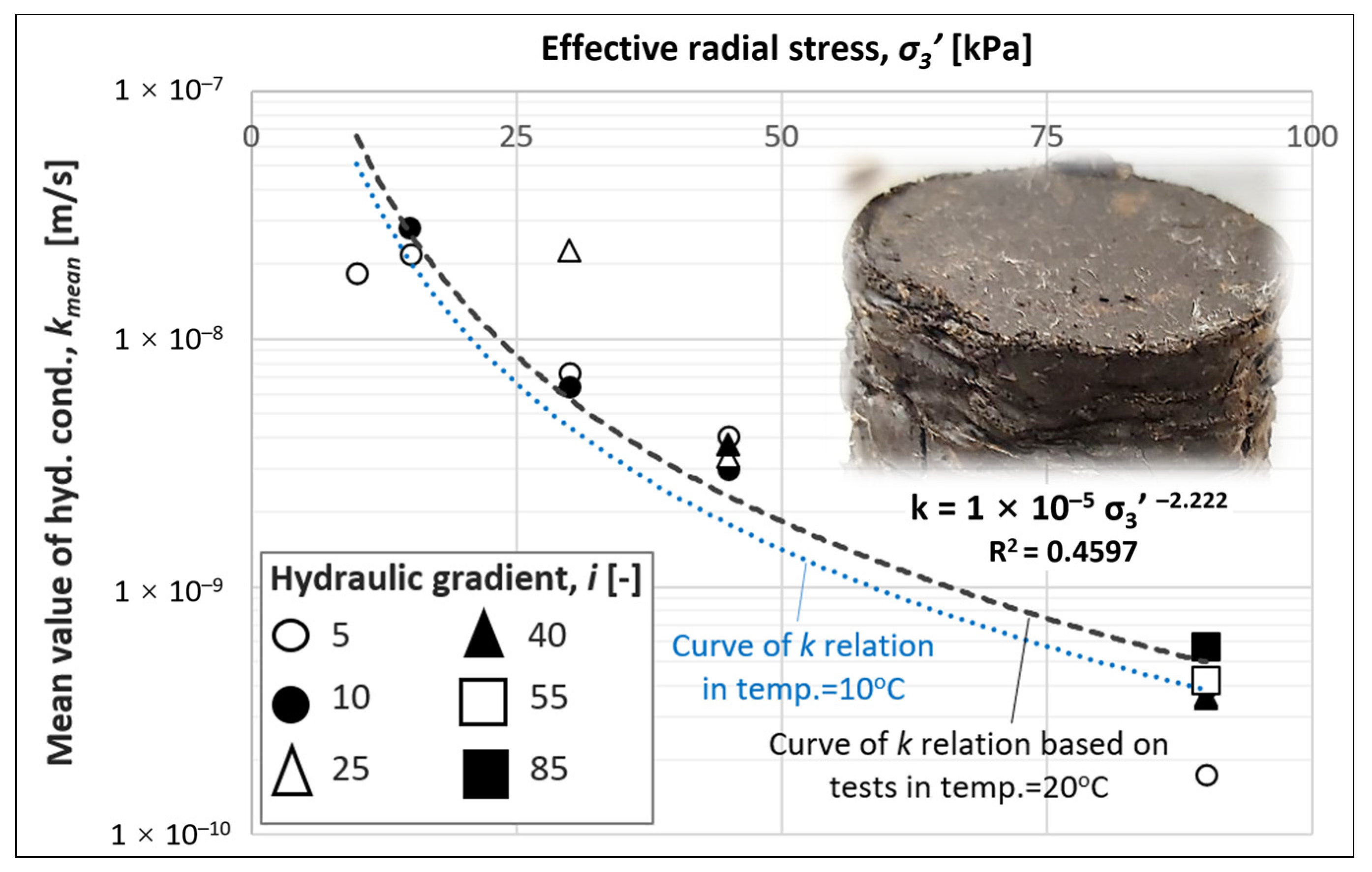
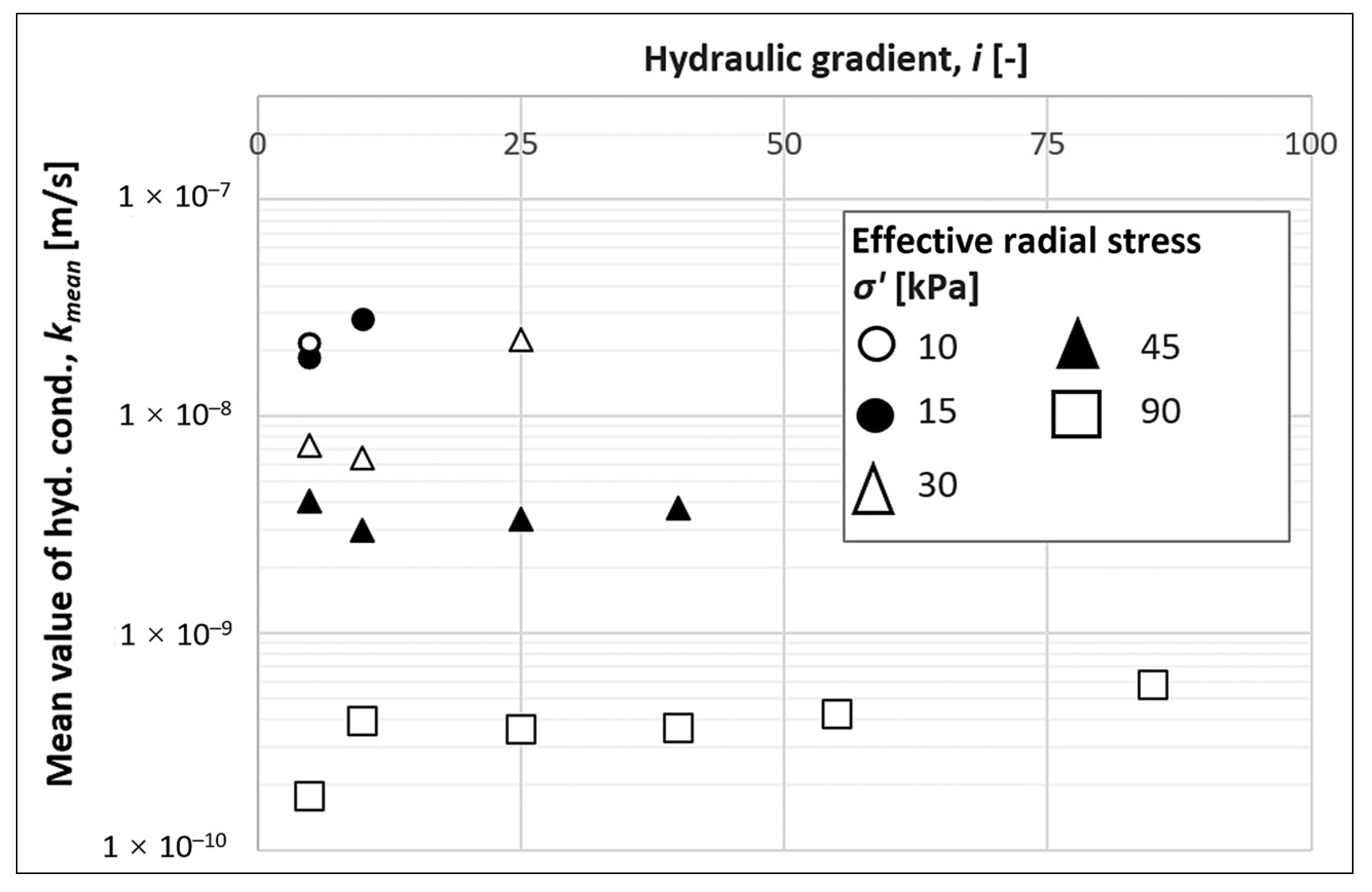
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karlsson, R.; Hansbo, S. Soil Classification and Identification; Swedish Council for Building Research: Stockholm, Sweden, 1984; 50p. [Google Scholar]
- Polish Standard PN-86/B-02480; The Building Soils—The Definitions, Symbols, the Division and Description of Soils. Polish Committee for Standardization: Warsaw, Poland, 1986; 13p.
- Haynes, R.H. The Canadian System of Soil Classification; NRC CNRC: Ottawa, Canada, 1998; 188p.
- Kaczyński, R.R. Engineering-Geological Conditions in Poland; PIG-PIB: Warsaw, Poland, 2017; 396p. [Google Scholar]
- Joosten, H.; Clarke, D. Wise Use of Mires and Peatlands; International Mire Conservation Group and International Peat Society: Totness, UK, 2002; 304p. [Google Scholar]
- Jefferson, I.; Murray, E.J.; Faragher, E.; Fleming, P.R. Proceedings of the Symposium Held at the Nottingham Trent University School of Property and Construction on 8 November 2001; Thomas Telford: London, UK, 2001; 211p. [Google Scholar]
- Kellner, R. Wetlands—Different Types, Their Properties and Functions; Uppsala University: Uppsala, Sweden, 2003; 69p. [Google Scholar]
- Labadz, J.; Allott, T.; Evans, M.; Butchr, D.; Billett, M.; Stainer, S.; Yallop, A.; Jones, P.; Innerdale, M.; Harmon, N.; et al. Peatland Hydrology; Scientific Review Commissioned by the IUCN UK Peatland Programme’s Commission of Inquiry on Peatlands: Edinburgh, UK, 2010; 52p. [Google Scholar]
- Anibas, C.; Verbeiren, B.; Buis, K.; Chormański, J.; De Doncker, L.; Okruszko, T.; Meire, P.; Batelaan, O. A hierarchical approach on groundwater-surface water interaction in wetlands along the upper Biebrza River, Poland. Hydrol. Earth Syst. Sci. 2012, 16, 2329–2346. [Google Scholar] [CrossRef]
- Grodzka-Łukaszewska, M.; Sinicyn, G.; Grygoruk, M.; Mirosław-Świątek, D.; Kardel, I.; Okruszko, T. The role of the river in the functioning of marginal fen: A case study from the Biebrza Wetlands. PeerJ 2022, 10, e13418. [Google Scholar] [CrossRef] [PubMed]
- Stachowicz, M.; Manton, M.; Abramchuk, M.; Banaszuk, P.; Jarašius, L.; Kamocki, A.; Povilaitis, A.; Samerkhanova, A.; Schäfer, A.; Sendžikaitė, J.; et al. To store or to drain—To lose or to gain? Rewetting drained peatlands as a measure for increasing water storage in the transboundary Neman River Basin. Sci. Total Environ. 2022, 829, 154560. [Google Scholar] [CrossRef]
- Morris, P.J.; Davies, M.L.; Baird, A.J.; Balliston, N.; Bourgault, M.-A.; Clymo, R.S.; Fewster, R.E.; Furukawa, A.K.; Holden, J.; Kessel, E.; et al. Saturated Hydraulic Conductivity in Northern Peats Inferred From Other Measurements. Water Resour. Res. 2022, 58, e2022WR033181. [Google Scholar] [CrossRef]
- Mesri, G.; Ajlouni, M. Engineering properties of fibrous peats. J. Geotech. Geoenvironmental Eng. 2007, 133, 850–866. [Google Scholar] [CrossRef]
- Long, M.; Paniagua, P.; Grimstad, G.; Traffor, A.; Degago, S.; L’Heureux, J.-S. Engineering properties of Norwegian peat for calculation of settlements. Eng. Geol. 2022, 308, 106799. [Google Scholar] [CrossRef]
- Herbich, P.; Ćwiertniewska, Z.; Fert, M.; Mordzonek, G.; Węglarz, D. Mapa Hydrogeologiczna Polski w Skali 1:50 000 Udostępnianie, Weryfikacja, Aktualizacja i Rozwój. Instrukcja (Hydrogeological Map of Poland on a Scale of 1:50,000 Sharing, Verification, Updating and Development. Instruction); PGI-NRI: Warsaw, Poland, 2004; 125p.
- Herbich, P.; Kapuściński, J.; Nowicki, K.; Prażak, J.; Skrzypczyk, L. Metodyka Wyznaczania Obszarów Ochronnych Głównych Zbiorników Wód Podziemnych dla Potrzeb Planowania i Gospodarowania Wodami w Obszarach Dorzeczy (Methodology for Establishing Protected Areas of Major Groundwater Reservoirs for Planning and Water Management in River Basin Districts); Polish Ministry of Environment: Warsaw, Poland, 2009; 59p.
- Baird, A.J.; Low, R.; Young, D.; Swindles, G.T.; Lopez, O.R.; Page, S.E. High permeability explains the vulnerability of the carbon store in drained tropical peatlands. Geophys. Res. Lett. 2017, 44, 1333–1339. [Google Scholar] [CrossRef]
- Suhip, M.A.A.B.H.; GÖdeke, S.H.; Cobb, A.R.; Sukri, R.S. Seismic refraction study, single well test and physical core analysis of anthropogenic degraded Peat at the Badas Peat Dome, Brunei Darussalam. Eng. Geol. 2020, 273, 105689. [Google Scholar] [CrossRef]
- Rydelek, P. Peatlands of Lubartów Upland as the potential natural geological barriers. Biul. PIG 2011, 446, 407–416. [Google Scholar]
- Chmielewska, I. Coefficient of permeability of peat. Bud. Inżynieria Sr. 2018, 9, 15–21. [Google Scholar]
- Myślińska, E. Laboratory Testing of Land and Soil, 3rd ed.; Wyd. UW: Warsaw, Poland, 2016; 280p. [Google Scholar]
- Wong, L.S.; Hashim, R.; Ali, F.H. A Review on Hydraulic Conductivity and Compressibility of Peat. J. Appl. Sci. 2009, 9, 3207–3218. [Google Scholar] [CrossRef]
- Wdowska, M.K.; Lipiński, M.J.; Jaroń, Ł. Selection of a method for determination of permeability characteristics of cohesive soils. Acta Sci. Pol. Archit. 2017, 16, 47–57. [Google Scholar]
- Liu, H.; Lennartz, B. Hydraulic properties of peat soils along a bulk denstiy gradeint—A meta study. Hydrol. Process. 2018, 33, 101–114. [Google Scholar] [CrossRef]
- Mięsiak-Wójcik, K.; Turczyński, M.; Sposób, J. Diverse Sediment Permeability and Implications for Groundwater Exchange in Closed Lake-Wetland Catchments (West Polesie, East Poland). Wetlands 2018, 38, 779–792. [Google Scholar] [CrossRef]
- Van Loon, A.H.; Schot, P.P.; Griffioen, J.; Bierkens, M.F.P.; Batelaan, O.; Wassen, M.J. Throughflow as a determining factor for habitat contiguity in a near-natural fen. J. Hydrol. 2009, 379, 30–40. [Google Scholar] [CrossRef]
- Menberu, M.W.; Marttila, H.; Ronkanen, A.-K.; Torabi Haghighi, A.; Kløve, B. Hydraulic and physical properties of managed and intact peatlands: Application of the van Genuchten-Mualem models to peat soils. Water Resour. Res. 2021, 57, e2020WR028624. [Google Scholar] [CrossRef]
- Wang, M.; Liu, H.; Lennartz, B. Small-scale spatial variability of hydro-physical properties of natural and degraded peat soils. Geoderma 2021, 399, 115123. [Google Scholar] [CrossRef]
- Gnatowski, T.; Szatyłowicz, J.; Brandyk, T.; Kechavarzi, C. Hydraulic properties of fen peat soils in Poland. Geoderma 2010, 154, 188–195. [Google Scholar] [CrossRef]
- Wierzbicki, G.; Grygoruk, M.; Grodzka-Łukaszewska, M.; Bartold, P.; Okruszko, T. Mire Development and Disappearance due to River Capture as Hydrogeological and Geomorphological Consequences of LGM Ice-Marginal Valley Evolution at the Vistula-Neman Watershed. Geosciences 2020, 10, 363. [Google Scholar] [CrossRef]
- Kossowska-Cezak, U. Climate of the Biebrza ice-margin Valley. Pol. Ecol. Stud. 1984, 10, 253–270. [Google Scholar]
- Krzywicki, T. Detailed Geological Map of Poland—Sheet Lipsk; PIG-PIB: Warsaw, Poland, 2003. [Google Scholar]
- Żurek, S. The Origin of the Biebrza Valley Wetlands; IGiPZ PAN: Warsaw, Poland, 1975; 107p. [Google Scholar]
- Pałczyński, A. Jaćwieskie Marshes. Biebrza River Valley; Annuals (Nauk Roln. Ser. D-Monografie 145); PWN: Warsaw, Poland, 1975; 252p. [Google Scholar]
- Oświt, J.; Pacowski, R.; Żurek, S. Characteristics of more important peat species in Poland. In Proceedings of the V International Peat Congress—Peatlands and Their Utilization in Poland, Poznań, Poland, 20–26 September 1976. [Google Scholar]
- Black, D.K.; Lee, K.L. Saturating laboratory samples by back pressure. J. Soils Mech. Found. Div. 1973, 99, 75–93. [Google Scholar] [CrossRef]
- Head, K.H.; Epps, R. Manual of Soil Laboratory Testing, Volume 3: Effective Stress Tests, 3rd ed.; Whittles Publishing: Dunbeath, UK, 2014; 414p. [Google Scholar]
- Romero-Ruiz, A.; Linde, N.; Keller, T.; Or, D. A review of geophysical methods for soil structure characterization. Rev. Geophys. 2018, 56, 672–697. [Google Scholar] [CrossRef]
- International Standard ISO 17892-9:2018; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 9: Consolidated Triaxial Compression Tests on Water Saturated Soils. International Organization for Standardization: Geneva, Switzerland, 2018; 25p.
- International Standard ISO 17892-11:2019; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 11: Permeability Tests. International Organization for Standardization: Geneva, Switzerland, 2019; 20p.
- Lade, P.V. Triaxial Testing of Soils; Wiley Blackwell: Chichester, UK, 2016; 500p. [Google Scholar]
- Malloy, S.; Price, J.S. Consolidation of gyttja in a rewetted fen peatland: Potential implications for restoration. Mires Peat 2017, 19, 1–15. [Google Scholar]
- Gilbert, P.A. Computer Controlled Microwave Oven System for Rapid Water Content Determination. Technical Report GL-88-21; Department of the Army Waterways Experiment Station: Vicksburg, MS, USA, 1988. [Google Scholar]
- Ilnicki, P. Peatlands and Peat; AR: Poznań, Poland, 2002; 606p. (In Polish) [Google Scholar]
- Montzka, C.; Herbst, M.; Weihermüller, L.; Verhoef, A.; Vereecken, H. A global data set of soil hydraulic properties and sub-grid variability of soil water retention and hydraulic conductivity curves. Earth Syst. Sci. Data 2017, 9, 529–543. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Estimation of saturated hydraulic conductivity with pedotransfer functions: A review. J. Hydrol. 2019, 575, 1011–1030. [Google Scholar] [CrossRef]
- Van Putte, N.; Temmerman, S.; Verreydt, G.; Seuntjens, P.; Maris, T.; Heyndrickx, M.; Boone, M.; Joris, I.; Meire, P. Groundwater dynamics in a restored tidal marsh are limited by historical soil compaction. Estuar. Coast. Shelf Sci. 2020, 244, 106101. [Google Scholar] [CrossRef]
- Rezanezhad, F.; Price, J.S.; Quinton, W.L.; Lennartz, B.; Milojevic, T.; Van Cappellen, P. Structure of peat soils and implications for water storage, flow and solute transport: A review update for geochemists. Chem. Geol. 2016, 429, 75–84. [Google Scholar] [CrossRef]

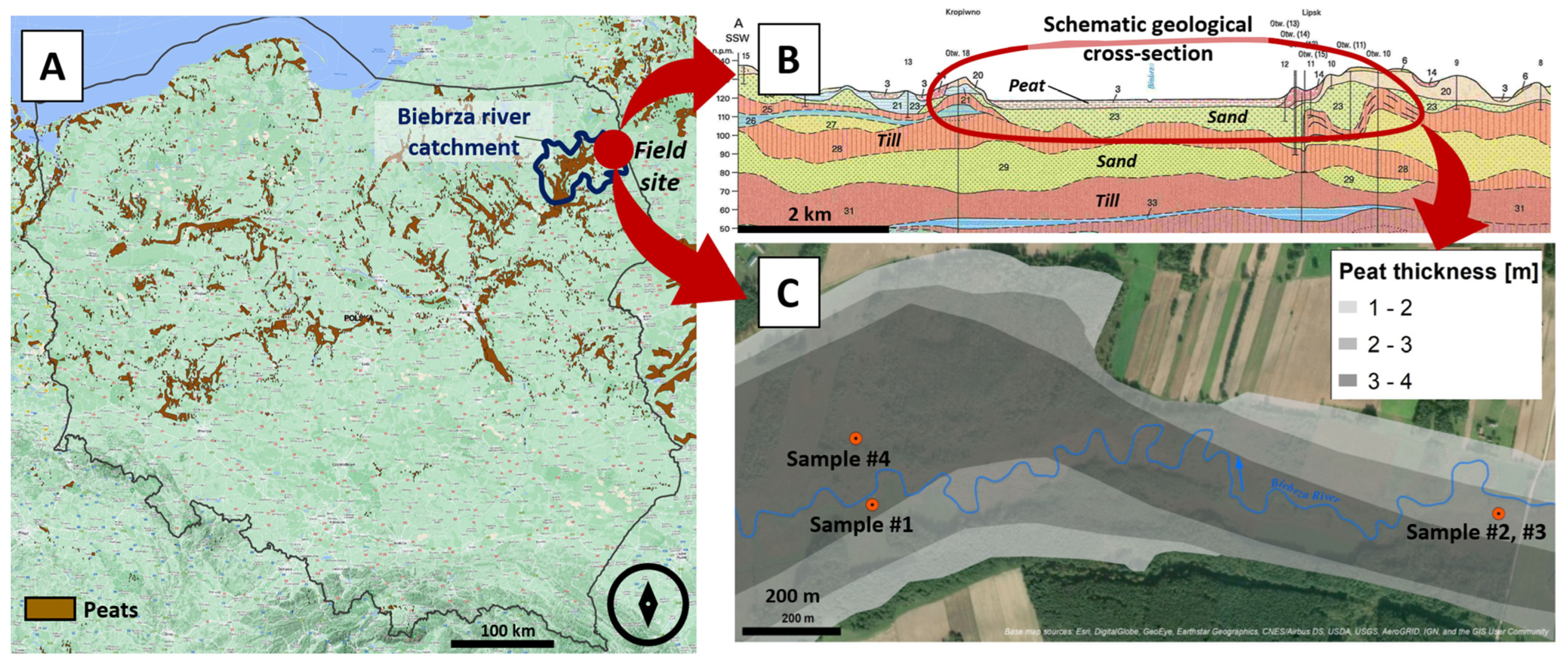


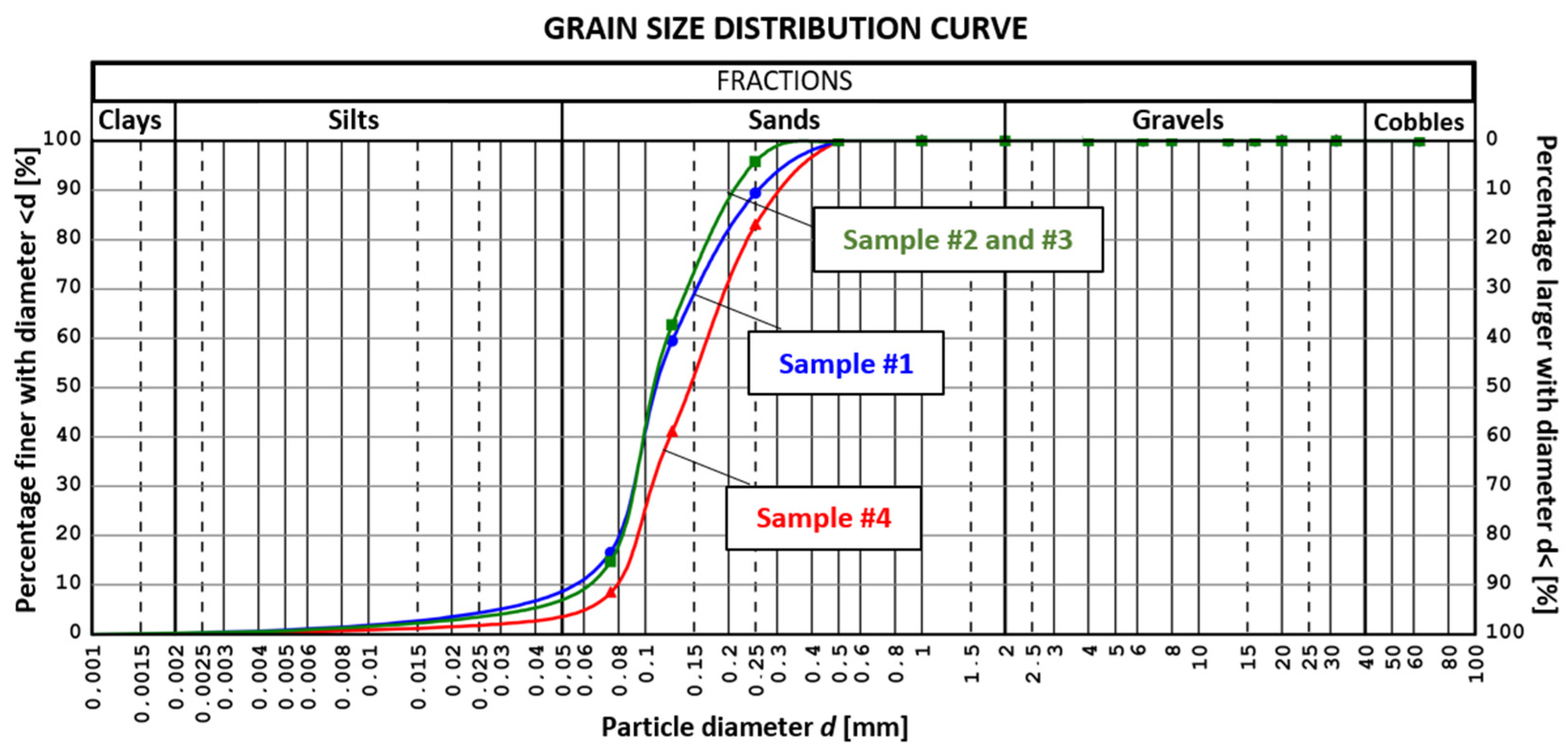


| Sample No. | Latitude | Longitude |
|---|---|---|
| 1 | 53°42′14.7″ | 23°26′43.5″ |
| 2 | 53°42′11.5″ | 23°27′53.2″ |
| 3 | ||
| 4 | 53°42′19.2″ | 23°26′42.1″ |
| Effective Confining Pressure σ3′ [kPa] | Hydraulic Gradient i [–] | Water Flow Direction | Hydraulic Conductivity k [m/s] | ||
|---|---|---|---|---|---|
| Stage Level | Mean Value | Temperature Correction α for T = 10 °C | |||
| 10 | 5 | ↓ | 3.5 × 10−8; 1.2 × 10−8 | 2.7× 10−8; 1.0 × 10−8 | 2.1 × 10−8; 7.9 × 10−9 |
| ↑ | 1.8 × 10−8; 8.1·× 10−9 | ||||
| 15 | 5 | ↓ | 1.8 × 10−8; 3.4 × 10−8; 7.7 × 10−8; 6.3 × 10−9 | 1.4 × 10−8; 2.6 × 10−8; 4.2 × 10−8; 5.4 × 10−9 | 1.1 × 10−8; 2.0 × 10−8; 3.2 × 10−8; 4.2 × 10−9 |
| ↑ | 9.9 × 10−9; 1.8 × 10−8; 7.7 × 10−9; 4.5 × 10−9 | ||||
| 10 | ↓ | 1.9 × 10−8; 3.6 × 10−8; 9.2 × 10−8; 6.3 × 10−9 | 1.7 × 10−8; 3.1 × 10−8; 5.8 × 10−8; 6.0 × 10−9 | 1.3 × 10−8; 2.4 × 10−8; 4.4 × 10−8; 4.6 × 10−9 | |
| ↑ | 1.4 × 10−8; 2.6 × 10−8; 2.3·× 10−8; 5.7 × 10−9 | ||||
| 30 | 5 | ↓ | 4.8 × 10−9; 3.0 × 10−8; 1.9 × 10−9 | 4.0 × 10−9; 1.6 × 10−8; 2.0 × 10−9 | 3.1 × 10−9; 1.3 × 10−8; 2.2 × 10−9 |
| ↑ | 3.2 × 10−9; 2.8 × 10−9; 2.1 × 10−9 | ||||
| 10 | ↓ | 4.1 × 10−9; 2.2 × 10−8; 1.8 × 10−9 | 3.6 × 10−9; 1.4 × 10−8; 1.6 × 10−9 | 2.8 × 10−9; 1.1 × 10−8; 1.2 × 10−9 | |
| ↑ | 3.1 × 10−9; 6.4 × 10−9; 1.4 × 10−9 | ||||
| 25 | ↓ | 5.2 × 10−9; 1.1 × 10−7; 2.5 × 10−9 | 5.4 × 10−9; 6.0 × 10−8; 2.3 × 10−9 | 4.2 × 10−9; 4.6 × 10−8; 1.8 × 10−9 | |
| ↑ | 5.6 × 10−9; 1.6 × 10−8; 2.1 × 10−9 | ||||
| 45 | 5 | ↓ | 2.3 × 10−9; 1.1 × 10−8; 1.7 × 10−9 | 2.0 × 10−9; 8.2 × 10−9; 1.9 × 10−9 | 1.5 × 10−9; 6.3 × 10−9; 1.5 × 10−9 |
| ↑ | 1.6 × 10−9; 5.1 × 10−9; 2.2 × 10−9 | ||||
| 10 | ↓ | 2.2 × 10−9; 9.3 × 10−9; 1.1 × 10−9 | 1.8 × 10−9; 6.0 × 10−9; 1.1 × 10−9 | 1.4 × 10−9; 4.6 × 10−9; 8.1 × 10−10 | |
| ↑ | 1.5 × 10−9; 2.6 × 10−9; 1.0 × 10−9 | ||||
| 25 | ↓ | 1.9 × 10−9; 8.8 × 10−9; 9.9 × 10−10 | 2.0 × 10−9; 7.1 × 10−9; 8.7 × 10−10 | 1.5 × 10−9; 5.5 × 10−9; 6.7 × 10−10 | |
| ↑ | 2.1 × 10−9; 5.5 × 10−9; 7.4 × 10−10 | ||||
| 40 | ↓ | 2.8 × 10−9; 1.0 × 10−8; 1.1 × 10−9 | 2.9 × 10−9; 7.4 × 10−9; 9.2 × 10−10 | 2.2 × 10−9; 5.7 × 10−9; 7.1 × 10−10 | |
| ↑ | 2.9 × 10−9; 4.3 × 10−9; 7.9 × 10−10 | ||||
| 90 | 5 | ↓ | 2.1 × 10−10; 2.1 × 10−10 | 1.9 × 10 −10; 1.6 × 10−10 | 1.4 × 10−10; 1.2 × 10−10 |
| ↑ | 1.7 × 10 −10; 1.0 × 10−10 | ||||
| 10 | ↓ | 5.2 × 10−10; 3.1 × 10−10 | 3.5 × 10−10; 4.3 × 10−10 | 2.7 × 10−10; 3.3 × 10−10 | |
| ↑ | 1.7 × 10−10; 5.5 × 10−10 | ||||
| 25 | ↓ | 4.5 × 10−10; 2.3 × 10−10 | 4.3 × 10−10; 2.8 × 10−10 | 3.3 × 10−10; 2.2 × 10−10 | |
| ↑ | 4.1 × 10−10; 3.4 × 10−10 | ||||
| 40 | ↓ | 5.6 × 10−10; 3.6 × 10−10 | 3.1 × 10−10; 4.2 × 10−10 | 2.4 × 10−10; 3.2 × 10−10 | |
| ↑ | 7.2 × 10−11; 4.8 × 10−10 | ||||
| 55 | ↓ | 5.8 × 10−10; 3.2 × 10−10 | 4.8 × 10−10; 3.6 × 10−10 | 3.7 × 10−10; 2.8 × 10−10 | |
| ↑ | 5.6 × 10−10; 4.1 × 10−10 | ||||
| 85 | ↓ | 7.5 × 10−10; 5.1 × 10−10 | 7.2 × 10−10; 4.2 × 10−10 | 5.6 × 10−10; 3.2 × 10−10 | |
| ↑ | 6.9 × 10−10; 3.3 × 10−10 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaczmarek, Ł.; Grodzka-Łukaszewska, M.; Sinicyn, G.; Grygoruk, M.; Jastrzębska, M.; Szatyłowicz, J. Hydraulic Conductivity Tests in the Triaxial Stress State: Is Peat an Aquitard or an Aquifer? Water 2023, 15, 1064. https://doi.org/10.3390/w15061064
Kaczmarek Ł, Grodzka-Łukaszewska M, Sinicyn G, Grygoruk M, Jastrzębska M, Szatyłowicz J. Hydraulic Conductivity Tests in the Triaxial Stress State: Is Peat an Aquitard or an Aquifer? Water. 2023; 15(6):1064. https://doi.org/10.3390/w15061064
Chicago/Turabian StyleKaczmarek, Łukasz, Maria Grodzka-Łukaszewska, Grzegorz Sinicyn, Mateusz Grygoruk, Małgorzata Jastrzębska, and Jan Szatyłowicz. 2023. "Hydraulic Conductivity Tests in the Triaxial Stress State: Is Peat an Aquitard or an Aquifer?" Water 15, no. 6: 1064. https://doi.org/10.3390/w15061064
APA StyleKaczmarek, Ł., Grodzka-Łukaszewska, M., Sinicyn, G., Grygoruk, M., Jastrzębska, M., & Szatyłowicz, J. (2023). Hydraulic Conductivity Tests in the Triaxial Stress State: Is Peat an Aquitard or an Aquifer? Water, 15(6), 1064. https://doi.org/10.3390/w15061064








