Discrete Analysis of Local Scour Morphology of Bridge Piers Affected by Sediment Storage Dam

Abstract

In order to solve the prediction and protection problems of local pier scour with a downstream sediment storage dam on non-uniform sand riverbeds in mountainous areas, the Xi’an Chanhe Bridge in China was taken as the research object. Through comprehensive physical model experiments, the influence of sediment storage dam layout on the surrounding water flow and local scour morphology around bridge piers was studied. The relationship between boundary conditions and local scour pit morphology was studied using a discrete analysis model. The research results showed that the inflow rate $Q$ was the most significant factor affecting local scour, and local scour generally developed rapidly within 0.5–1.0 h and then gradually reached a dynamic equilibrium. The maximum depth was located within $0.25B$ in front of the pier relative to the pier width $B$, and the impact range of local scour behind the pier was $[5B,10B]$. The recommended layout of a sediment storage dam has a distance between pier and dam $L$ of $[8B,11B]$ and a dam crest elevation $Z$ higher than that of the original riverbed elevation at the bridge pier, which is $[0.4B,0.5B]$. An improved calculation formula for the local scour depth of bridge piers $h_s$ is proposed and verified through experimental measurements to provide a reference for the design and protection of bridge piers with a downstream sediment storage dam.

1. Introduction

Bridge scour is one of the main reasons for bridge water damage. The insufficient predictions of bridge scour account for about 60% of the bridges with natural damage [1], while local pier scour accounts for 90% of the total scour [2]. Therefore, the accurate prediction of local pier scour is an important part of bridge safety assessment, which is crucial for ensuring the safety of highway and railway transportation.

The movement of water in rivers drives the movement of sediment on the riverbed, which in turn affects the water flow structure. The process of interaction between the two is called riverbed morphology evolution, and this process is always evolving [3]. Melville divides bridge scour into long-term scour, general scour, contraction scour, and local scour [4]. When piers are built on a river, the water flow is obstructed by the piers, causing water impacts and vortex actions, which lead to local scour deformation on the riverbed around the piers, known as local pier scour [5].

The complex water flow structure around the piers directly induces local scour, which includes downflow in front of the pier, blow waves in front of the pier, horseshoe vortices on the edge of the scour pit in front of the pier, and wake vortices caused by water flow separation on both sides of the pier [6]. Particle image velocimetry (PIV) [7], acoustic Doppler velocimetry (ADV) [8], and hydrogen bubble visualization technology [9] are used to study the microstructure of vortices. Dargahi observed that the horseshoe vortices were composed of five necklace-shaped vortex structures that interact with each other periodically [10]. Shen believed that unlike horseshoe vortices, tail vortices were generated by the piers themselves [11]. Sonia found that there was no obvious relationship between local scour depth and the Reynolds number [12]. Karimi studied the effect of pier inclination angle on scour processes in an experimental flume and described the water flow structure around the piers [13].

There are many factors that affect local pier scour, such as inflow rate [14], river water level [15], riverbed slope [16], sand particle size distribution [17], pier footing shape [18], etc. Diab used gravel and sand experiments and found that the scour pit depth and width of a square pier were about 1.50 times and 1.22 times that of a circular pier, respectively [19]. Breusers summarized the relationship between the relative scour depth of uniform coarse sand and fine sand and the relative flow velocity [20]. Valela studied the effect of stone pitching on local pier scour and found that specific shapes of stone pitching could reduce scour depth by 81% [21]. Grimaldi studied the effect of a submerged dam on reducing local pier scour, and when the distance between them was short, the depth, area, and volume of scour decreased [22]. Wang found that when the distance between a submerged dam and the pier was 0, the maximum scour depth of the pier decreased by 54% in a clear water scour experiment [23]. Dodaro proposed a mathematical-numerical model that uses a 3D laser scanner to obtain scour profile data at different times and used artificial intelligence methods for correction [24]. Tafarojnoruz studied the effect of six different types of structures on local pier scour [25].

The research methods for local scour mainly include field observation, physical model experiments, numerical simulations, and variable correlation analysis. Collecting data on actual bridge water damage accidents in the field is a great aid in understanding scour mechanisms, but the observation cost is high, and the recording of the process of maximum scour depth is relatively short [26]. The influencing factors studied in physical experiments are far fewer than those of natural rivers. Experiments can clearly reflect the relationship between the research variables and local scour. If the model scale is appropriate, reliable results can be obtained [27]. Numerical simulations can eliminate the interference of instruments and obtain small water flow structures that are difficult to measure in the field and in experiments. However, the selection of turbulence models, the description of water–sand coupling effects, and computational resources and efficiency are all constraints on their practical application in engineering [28].

Empirical formulas are mainly used to estimate local pier scour in engineering. Richardson revised HEC-18 and emphasized that when calculating local pier scour, the river course should be considered, and various adverse factors should be combined [29]. The Bridge Engineering Committee of the China Civil Engineering Society discussed the causes of scour, influencing factors, and physical processes of scour. Based on the principles of clear and reasonable concepts, simple structures, and high accuracy, the “65-1” and “65-2” formulas for calculating pier scour were recommended [30]. Wang Guohua and Kang Ducan proposed modifications to the “65-1” formula based on measured data to make it more suitable for practical needs [31].

Currently, there are many empirical formulas for calculating local pier scour, most of which are based on experimental results of straight flumes, single piers, and uniform sand. To solve the problem of predicting and protecting local pier scour in rivers with non-uniform sand and with a sediment storage dam downstream, physical model experiments were conducted to study the effect of sediment storage dam layout on water flow and local scour morphology around piers. A discrete analysis model was used to study the relationship between boundary conditions and local scour pit morphology. Finally, recommended sediment storage dam layouts and local pier scour formulas were obtained as references for the design and protection of piers downstream of sediment storage dams.

2. Materials and Methods

2.1. Research Object

The study object is the Chanhe Bridge in Xi’an, China. The river area where the bridge is located belongs to the hilly area with loose covering layers from the Quaternary Period, and the riverbed is covered with pebbles and gravel. The bridge is about 140 m wide and has 5 bridge spans, a net width of 25 m, a pier thickness of 2.5 m, and a pier length of 7.5 m. About 75 m downstream of the bridge pier, there is a sediment storage dam built mainly to protect the safety of the bridge pier and prevent upstream scour.

The river near the bridge is shallow and wide, and the bank is basically straight, but the main channel is winding with a width generally between 15 and 20 m. The longitudinal slope of the river is about 0.8%, and the riverbed is often not covered by water. Therefore, the riverbed is covered with weeds and bushes, as well as some orchards and vegetable gardens, with a large roughness coefficient. The roughness coefficient of the river channel is about $n=0.023-0.025$, and that of the flood plain is about $n=0.030-0.035$.

The location and morphology of the bridge and the location of the sediment storage dam are shown in Figure 1. The design flow rate of the bridge is once in a hundred years with a flow rate of 400 m³/s. There is no suspended sediment material in the river, and the transported sediment is similar to the surface bed sand. The gradation curve is shown in Figure 2, with a median diameter of the bed sand of $d_{50}$ = 6.6–7.2 mm, and the thickness of the coarse sand and gravel covering layer is about 7 m.

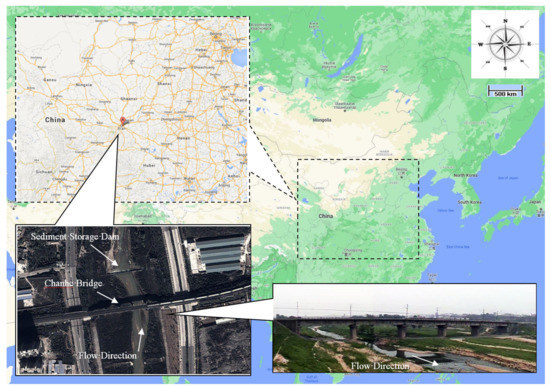
Figure 1. Location of the bridge and sediment storage dam and river channel morphology.

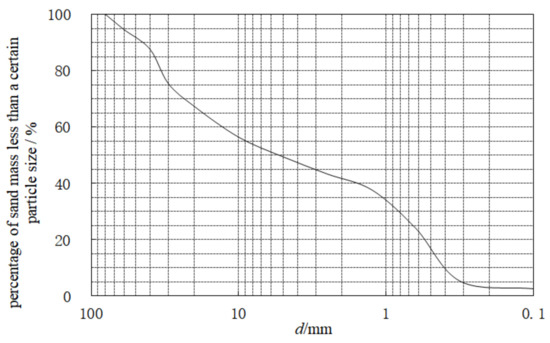
Figure 2. Grain size distribution curve of sediment near the bridge pier.

2.2. Experimental Conditions and Schemes

The experiment was conducted on a physical model using a normal distribution model with a geometric scale ratio of ${\lambda }_L=30$. The simulated length of the river section was 330 m, with 150 m upstream and 180 m downstream of the bridge, and the river width was 140 m. The model layout and cross-section of the pier and dam are shown in Figure 3. The riverbank was made of cement mortar with fine stones added to increase roughness. The main channel terrain was modeled using sand with a similar particle size distribution to the prototype. The inflow rate was controlled by an electromagnetic flow meter, and the section flow rate was measured using a photodetector propeller flow meter and a pitot tube. The tail water level was controlled by a measuring needle. The measurement of high terrain was performed using measuring needles.

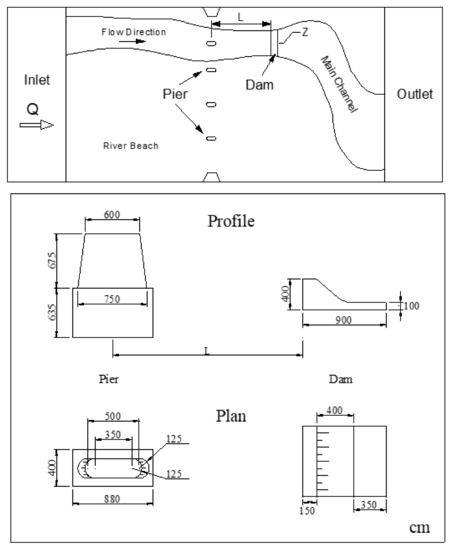
Figure 3. Model layout and cross-section of the pier and dam.

Twenty sets of experimental schemes were designed as shown in Table 1 to study the effects of five boundary conditions on local pier scour, namely inflow rate $Q$, downstream water level $H$, riverbed slope $i$, distance between pier and dam $L$, and dam crest elevation $Z$. During the experiment, the scour morphology was observed regularly, and the maximum scour depth was measured. When the scour morphology stabilized, the experiment was stopped and the scour morphology was carefully measured.

Table 1. Experimental schemes.

Experimental Scheme	Inflow Rate $\mathit{Q}$ (m3/s)	Downstream Water Level $\mathit{H}$ (m)	Riverbed Slope $\mathit{i}$	Distance between Pier and Dam $\mathit{L}$ (m)	Dam Crest Elevation $\mathit{Z}$ (m)
1	41.40	391.54	0.0067	75.00	390.00
2	41.40	391.96	0.0000	75.00	390.50
3	41.40	392.04	−0.0056	45.00	390.75
4	41.40	392.23	−0.0111	45.00	391.00
5	83.85	392.15	0.0067	75.00	390.00
6	83.85	392.73	0.0000	75.00	390.50
7	83.85	392.73	−0.0056	45.00	390.75
8	83.85	393.06	−0.0067	75.00	391.00
9	83.85	392.92	−0.0111	45.00	391.00
10	83.85	393.48	−0.0133	75.00	391.50
11	83.85	393.26	−0.0222	45.00	391.50
12	105.75	392.38	0.0067	75.00	390.00
13	105.75	392.85	0.0000	75.00	390.50
14	105.75	392.90	−0.0056	45.00	390.75
15	126.00	392.98	0.0000	75.00	390.50
16	126.00	393.16	−0.0056	45.00	390.75
17	126.00	393.53	−0.0067	75.00	391.00
18	126.00	393.49	−0.0111	45.00	391.00
19	126.00	394.09	−0.0133	75.00	391.50
20	126.00	393.95	−0.0222	45.00	391.50

3. Discrete Analysis Model

3.1. Grids and Datasets

To study the relationship between boundary conditions and local scour pit morphology, the bridge pier center was set as the coordinate origin $(0,0)$, and ($X\in \left[-10 \mathrm{m},10 \mathrm{m}\right]$, $Y\in \left[-7.5 \mathrm{m},7.5 \mathrm{m}\right]$) was selected as the research area $D$. The area $D$ was divided into 31 × 31 grid nodes. Each node served as a dataset, storing different boundary conditions and scour depth data at the corresponding $(x,y)$ location. By analyzing all node datasets, the relationship between boundary conditions and scour morphology was established. See Figure 4 for the process.

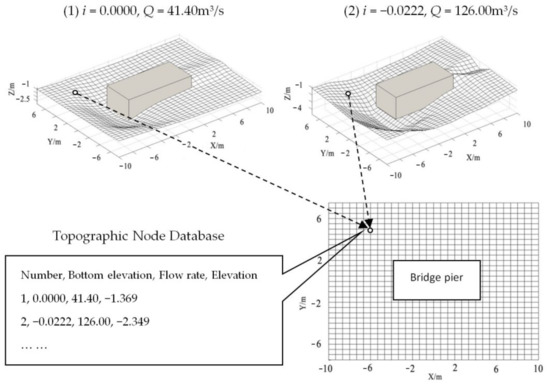
Figure 4. Grid division and establishment of node dataset.

3.2. Model Training

Three methods were used to train the model: spatial surface analysis, regression analysis, and a neural network.

(1)

Spatial Surface Analysis

Spatial surface analysis is only applicable to situations with three variables. The input variables selected were the inflow flow rate $Q$ and riverbed slope $i$, and the output variable was the scour depth data at the node. A spatial surface was constructed using cubic spline interpolation to create the response model for a single node, as shown in Figure 5.

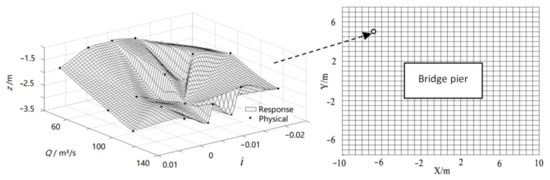
Figure 5. Construction of response model on nodes using spatial surface analysis method.

An M-function was written on the MATLAB platform. The code is shown in Table 2. Inputting the slope and flow rate can draw the simulated scour pit topography.

Table 2. MATLAB code for spatial surface analysis.

function Surface_method(Database,Slope,Flow) % Simulate the morphology of scour pits using the surface method and terrain node database by inputting the slope and flow rate  load(Database);  for i = 1:31   for j = 1:31    x = Z(i,j).ZI(:,1);    y = Z(i,j).ZI(:,2);    z = Z(i,j).ZI(:,3);    x_grid = min(x):(max(x) − min(x))/50:max(x);    y_grid = min(y):(max(y) − min(y))/50:max(y);    [XI,YI] = meshgrid(x_grid,y_grid);    ZI = griddata(x,y,z,XI,YI,‘cubic’);    NEW_Z(i,j) = interp2(x_grid,y_grid,ZI,Slope,Flow);   end  end  surf(X,Y,NEW_Z) end

(2)

Regression Analysis

Regression analysis is suitable for quantitative relationships between two or more variables. The input and output variables are the same as spatial surface analysis, and the regression equation refers to the calculation formula of local pier scour from Sundongpo [32], as shown in Equation (1).

$$h_s=K_{\xi }{K}_{\eta }{B}^{0.4}\left(1+10.98i\right){\left(1.92q\right)}^{0.6}$$

(1)

where:

• $h_s$  Local scour depth of $A,B,C,D$ bridge piers (m)
• $K_{\xi }$ Pier shape coefficient
• $K_{\eta }$ Coefficient related to bed sediment diameter
• $B$   Pier width (m)
• $i$     Riverbed slope
• $q$    Discharge per unit width (m³/s.m).

Using the regression coefficients to replace the coefficients in Equation (1), a regression equation is established, as shown in Equation (2).

$$h_{i,j}=A\left(1+Bi\right){\left(CQ\right)}^D$$

(2)

where:

• $h_{i,j}$ Depth of terrain node scour (m)
• $i$  Riverbed slope
• $Q$   Inflow rate (m³/s)
• $A,B,C,D$ Regression coefficients.

Using MATLAB’s nonlinear correlation analysis function nlinfit ( ), as shown in Equation (3), the correlation coefficient of the regression model on the terrain node is obtained.

$$r=\mathrm{nl}\inf \mathrm{it}(X,y,fun,b_o)$$

(3)

where:

• $r$   Nonlinear fitting coefficient
• $X$       Independent variable matrix
• $y$  Dependent variable
• $fun$ Nonlinear model
• $b_o$       Initial values of nonlinear model coefficients.

The results of the nonlinear fitting coefficient are greatly influenced by the initial value $b_0$. In order to make the initial $b_0$ value selection more reasonable and convenient, the optimization objective function was constructed. Assuming that the coefficient of the initial $b_0$ value is the independent variable $X_{b0}$, the regression coefficients $r_{b_0}$ under $X_{b0}$ are solved by nlinfit ( ); the obtained coefficients $r_{b_0}$ into $fun$ are used to calculate the regression model. The square sum of the difference (residual) between the predicted value and the true value of the obtained regression model is taken as the objective, and finally, the optimal solution of the objective function is obtained through a genetic algorithm (GA) as the initial value of the coefficient for inferring the nonlinear regression model. The MATLAB program code is shown in Table 3.

Table 3. MATLAB codes of regression analysis method.

function RA_method(Database,Slope,Flow)  % By using regression analysis and topographic node database, simulate the morphology of scour pits based on input of the slope and flow rate.  load(Database);  for i = 1:31   for j = 1:31    x = Z(i,j).ZI(:,1);    y = Z(i,j).ZI(:,2);    z = Z(i,j).ZI(:,3);    beta = ga(@GA2r,4);    NEW_Z(i,j) = nlin_RA(beta,[Slope,Flow]);   end  end  surf(X,Y,NEW_Z) end

function rc2 = GA2r(Beta)  % Using GA algorithm to infer initial values of nonlinear regression coefficients  load(‘temp.mat’);  [b,rc,J,COVB,mse] = nlinfit([x y],z,@nlin_RA,Beta);  rc2 = sum(rc.^2); end

function z_nlin = nlin_RA(beta_nlin,x_nlin)  % Multi-variate nonlinear fitting function  r1 = beta_nlin(1);r2 = beta_nlin(2);r3 = beta_nlin(3);r4 = beta_nlin(4);  x1 = x_nlin(:,1);x2 = x_nlin(:,2);  z_nlin = r1.*(1 + r2.*x1).*(r3.*x2).^r4; end

During the regression process, if the initial value is selected improperly, individual exceptions may occur. The corrected scour morphology is shown in Figure 6.

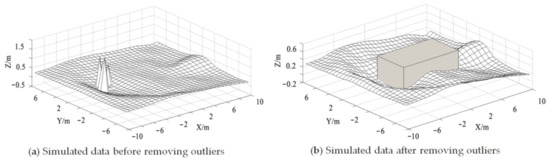
Figure 6. Simulation results of regression analysis method ($i$ = 0.0060, $Q$ = 105.75 m³/s).

(3)

Neural Network

The neural network does not need to distinguish between different nonlinear relationships. It consists of one input layer, two middle hidden layers, and one output layer. The physical model experimental data were used to train the model. The training set, validation set, and test set were 70%, 30%, and 30% of the samples, respectively. After training, the overall correlation coefficient of the model was 0.858.

The MATLAB platform was used to write a neural network analysis program, and the code is shown in Table 4.

Table 4. MATLAB codes of neural networks analysis method.

function NN_method(Database,Slope,Flow)  % Using neural network analysis and terrain node database simulation, input the slope and flow rate to simulate the morphology of scour pits.  load(Database);  for i = 1:31   for j = 1:31    x = Z(i,j).ZI(:,1);    y = Z(i,j).ZI(:,2);    z = Z(i,j).ZI(:,3);    P = [x’;y’];    T = z’;    net = newff(P,T);    net = train(net,P,T);    NEW_Z(i,j) = sim(net,[pd;ll]);   end  end  for ii = 1:31   NEW_Z(:,ii) = smooth(NEW_Z(:,ii));   NEW_Z(ii,:) = smooth(NEW_Z(ii,:));  end  surf(X,Y,NEW_Z) end

The neural network method overcomes the complexity of the traditional analysis process and reduces the difficulty of selecting model parameters; however, the disadvantage is that when the number of learning samples is insufficient, the response model has a certain degree of fluctuation, and smoothing processing is required, as shown in Figure 7.

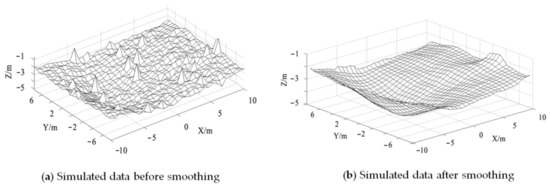
Figure 7. Simulation results of neural networks analysis method ($i$ = 0.0067, $Q$ = 126 m³/s).

3.3. Model Validation

Comparing the simulation results with physical model tests, as shown in Figure 8, it can be seen that the results simulated by the neural network method were the closest to the actual measured results of the physical model. From the depth and range of scour in front of the pier, the spatial surface method had the best simulation effect. Although the regression analysis method had a simulation effect that is relatively close to the measured results of the physical model in front of the pier, there was a certain distortion phenomenon in the overall morphology.

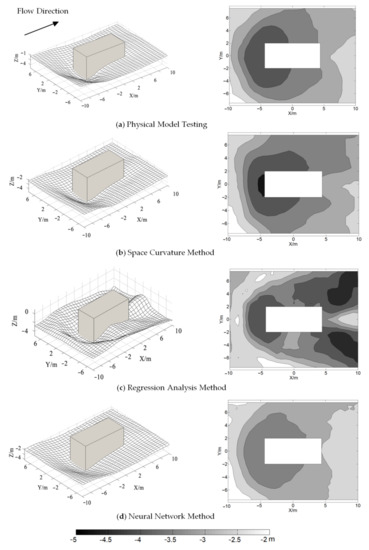
Figure 8. Comparison of simulation results using different methods.

The three methods for simulating the error distribution are shown in Figure 9. The darker the color, the greater the error. The spatial surface method mainly concentrated the error on the left side behind the pier and also had some distribution on the right side in front of the pier. The regression analysis method had a symmetrical distribution along the longitudinal axis of the bridge pier, mainly distributed on both sides behind the pier, showing a fish tail shape, and in front of the pier, showing a horseshoe shape. The neural network method mainly distributed the error in front of the pier, showing a crescent shape, and also had some distribution behind the pier.

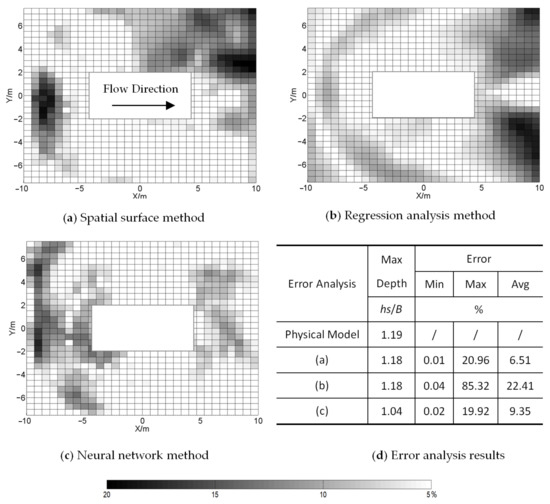
Figure 9. Simulation error analysis of different methods.

The results for the three methods for simulating error analysis are shown in Figure 9d. From the maximum penetration depth, the simulated errors of the spatial surface method, regression analysis method, and neural network method were −0.42%, −0.63%, and −12.42%, respectively. In terms of overall scour morphology, the average errors of the three methods were 6.51%, 22.41%, and 9.35%, respectively. When considering only two boundary conditions, the spatial surface method is recommended, while the neural network method is recommended for other situations.

4. Result Analysis

4.1. Flow near the Pier

(1)

The influence of riverbed slope and flow on flow pattern

Through the experiment, it can be concluded that the flow pattern and water level are mainly controlled by the riverbed slope and inflow rate. Under various flow rates, the water flow smoothly passed through the pier, and the flow pattern near the pier was relatively stable. Due to the water-blocking effect of the pier, there were surging waves in front of the pier, causing the water level upstream of the pier to rise. At both sides of the pier, eddy currents were formed, showing a local drop and rise of the water surface. The flow rate of the water on both sides of the pier increased after being squeezed, and a backflow zone was formed at the end of the pier, causing a slight decrease in the water level.

Under the same riverbed slope conditions, increasing the flow rate correspondingly raised the riverbed water level. Taking the riverbed slope value of 0 as an example, the flow rate changed from 41.40 m³/s to 126.00 m³/s. The water level at 10 m in front of the pier increased with the increase in flow rate, generally between 391.91 m and 393.13 m. The downstream water surface slope $J$ of the bridge pier (between 20 m and 45 m behind the pier) generally ranged from 0.0044 to 0.0074 under various flow rates, which is lower than the natural slope of the riverbed by 0.008.

Under the same flow rate conditions, decreasing the riverbed slope value correspondingly raised the riverbed water level. When the flow rate was 83.85 m³/s, the riverbed slope value changed from −0.0222 to 0.0067. The water level at 10 m in front of the pier increased with the increase in flow rate, generally between 392.09 m and 393.49 m. The downstream water surface slope $J$ of the bridge pier (between 20 m and 45 m behind the pier) generally ranged from 0.0024 to 0.0076 under various flow rates, which is also lower than the natural slope of the riverbed by 0.008.

(2)

The influence of distance between the pier and dam and dam crest elevation on flow pattern

Under the same flow rate and dam height, the variation in water level in front of the pier at different distances between the pier and dam was relatively small. For example, in Figure 10, for Solutions 8, 9, 17, and 18, when the distance between the pier and dam was reduced from 75 m to 45 m, the average variation was 0.12 m, which can be considered insignificant for the influence of the pier distance on the water level in front of the pier.

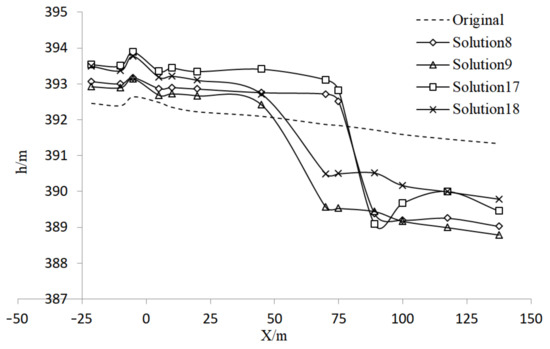
Figure 10. Influence of distance between pier and dam on water level.

Under the same flow rate and the same distance between the pier and dam, there was a significant change in water level at the first 10 m in front of the pier with different dam heights, as shown in Figure 11. For Solutions 1, 2, 12, and 13, when the dam height was increased by 0.5 m, the water level in front of the pier was raised by an average of 0.44 m. The ratio of the increase in water level in front of the pier to the increase in dam height was 0.88, indicating that the dam height has a significant impact on the water level in front of piers. Under the same flow rate, compared with the situation without a sediment storage dam, the water level in front of the piers was basically the same, just slightly lower. Since there was no obstruction from a sediment storage dam, the water level behind the piers adjusted to a natural slope.

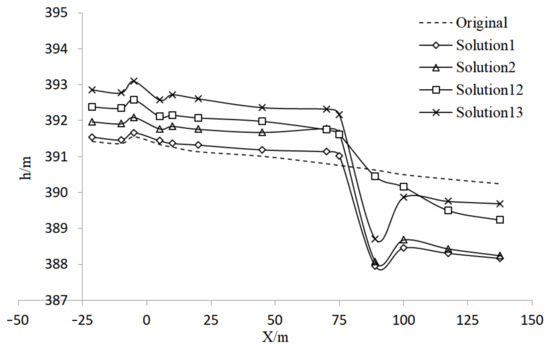
Figure 11. Influence of dam crest elevation on water level.

4.2. Local Scour Regularity

(1)

Pier scour morphology

Under the influence of a sediment storage dam, the local pier scour form showed good regularity and repeatability. The longitudinal profile of the local scour was an asymmetric triangle with a steeper upstream slope and a gentler downstream slope. The deepest point of scour generally occurred within a range of about 1 m on the upstream side of the pier platform, the plane was horseshoe-shaped, gradually narrowing from the front of the pier to the bridge pier, and the rear of the bridge pier was affected by the tail eddy current to form a tail-shaped extension. The scour morphology of the physical model test is shown in Figure 12.

Figure 12. Local scour morphology of bridge pier.

When the slope of the riverbed $i$ decreases, it will stabilize the scour base near the bridge pier, raise the water level of the river, and reduce the general scour of the downstream riverbed of the bridge pier. The general scour of the river section between the bridge pier and 45 m downstream was not significant and was proportional to the flow rate. At different flow rates, the general scour line of this section of the river was 0.3–0.5 m lower than the original riverbed. Due to insufficient upstream supply in front of the bridge pier, the actual depth was slightly larger but generally not more than 1.0 m. Under the same flow rate, as the riverbed slope $i$ decreased, the water level of the river gradually rose and the local scour depth of bridge piers correspondingly decreased. The characteristics of the local scour morphology are shown in Table 5, and the range of scour influence behind the bridge pier was $5B\le l_2\le 10B$.

Table 5. Characteristics of local scour morphology of bridge piers.

Solution	${\mathit{h}}_{\mathit{s}}$/$\mathit{B}$	${\mathit{l}}_{\mathbf{1}}$/$\mathit{B}$	${\mathit{l}}_{\mathbf{2}}$/$\mathit{B}$	${\mathit{i}}_{\mathbf{1}}$	${\mathit{i}}_{\mathbf{2}}$
1	0.69	1.25	7.75	0.5500	0.0887
2	0.58	0.95	5.75	0.6053	0.1000
3	0.60	1.13	5.63	0.5333	0.1067
4	0.59	1.23	5.50	0.4796	0.1068
5	1.03	1.30	8.38	0.7885	0.1224
6	0.93	1.18	7.88	0.7872	0.1175
7	0.81	1.28	6.63	0.6373	0.1226
8	0.66	1.28	6.13	0.5196	0.1082
9	0.91	1.20	7.38	0.7563	0.1231
10	0.90	1.25	7.38	0.7200	0.1220
11	0.80	1.20	6.13	0.6625	0.1298
12	1.11	1.33	8.50	0.8358	0.1303
13	1.00	1.23	7.38	0.8163	0.1356
14	1.03	1.28	8.63	0.8098	0.1197
15	1.06	1.50	8.63	0.7083	0.1232
16	0.99	1.45	9.13	0.6810	0.1082
17	0.84	1.38	9.25	0.6091	0.0905
18	1.06	1.33	8.63	0.8019	0.1232
19	1.08	1.43	8.63	0.7544	0.1246
20	0.95	1.45	8.00	0.6609	0.1188

Note(s): h_s represents the maximum depth of the local scour pit. l₁ and l₂ represent the distances between the deepest point of the scour pit and the edge of the upstream and downstream slope, respectively. i₁ and i₂ represent the slope of the upstream and downstream slope of the scour pit, respectively.

(2)

Local scour process

When the flow rate was 41.40 m³/s, the scour development rate developed steadily and slowly and reached equilibrium within 0.5 to 1 h or in an even shorter time. As the flow rate increased, the scour development rate increased significantly and the phenomenon of rate fluctuation appeared; the scour also reached equilibrium in about 2 h. When the flow rate reached 126.00 m³/s, the scour development rate weakened and then increased rapidly, and with the continuation of time, it finally tended to a new dynamic equilibrium of scour and deposition, and the scour reached equilibrium in about 2.5 h. The normalized scour depth development curves for different flow rates when the riverbed slope is $i$ = 0 are shown in Figure 13.

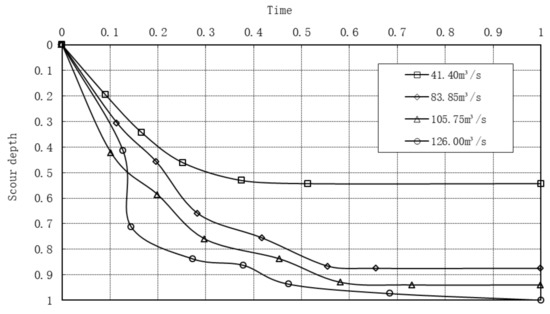
Figure 13. Development process of local scour depth.

(3)

Impact of sediment storage dam layout on scour

With the increase in flow rate, the local scour depth of the bridge pier also increased accordingly, as shown in Figure 14. When the dam crest elevation $Z$ was constant, the local scour depth $h_s$ decreased as the distance between the pier and dam $L$ decreased. The rate of change under different flow rates was similar, with the local scour depth $h_s$ decreasing by $0.01B$ when the distance between the pier and dam $L$ decreased by $1B$. When the distance between the pier and dam was $L<9B$, the local scour depth $h_s$ basically did not change, accounting for about 75.3% of the impact of not having a sediment storage dam. When the distance between the pier and dam was $L>22B$, the local scour depth $h_s$ was basically the same as the impact of not having a sediment storage dam.

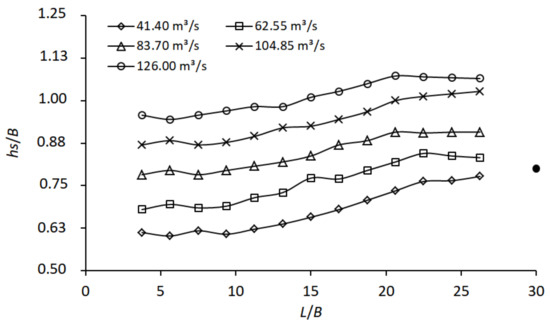
Figure 14. Influence of distance between pier and dam on maximum scour depth.

When the distance between the pier and dam $L$ was fixed, increasing the elevation of the dam crest reduced the local scour depth of the bridge pier, as shown in Figure 15. Let $Z-Z_0$ represent the relative height of the sediment storage dam and $Z_0$ represent the original riverbed elevation at the bridge pier. With the increase in flow rate, the impact of increasing the dam crest elevation became stronger. When $(Z-Z_0)/B\le 0.5$, for every 1$B$ unit increase in the dam crest elevation, the local scour depth $h_s$ decreased by 0.09$B$ when the flow rate was 41.40 m³/s, and it decreased by 0.76$B$ when the flow rate was 126.00 m³/s, which is a difference of 8.44 times. Considering the influence of flow rate, for every 100 units of flow rate increase, the dam crest elevation $Z$ increased by 1$B$ and the local scour depth $h_s$ decreased by 0.46$B$ on average. When $(Z-Z_0)/B>0.5$, the effect of increasing the dam crest elevation was no longer obvious.

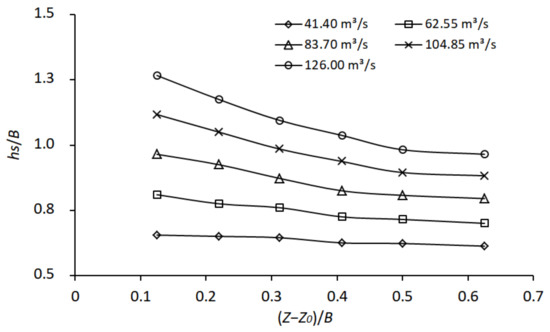
Figure 15. Influence of dam crest elevation on maximum scour depth.

4.3. Calculation of Local Scour Depth

The main factors affecting the local scour depth $h_s$ of bridge piers can be expressed as follows:

$$h_s=f(d,h_{0,}{v}_0,K_{\zeta },B)$$

(4)

In the formula, $h_{0, }{v}_0$ represent the water depth and flow velocity near the pier, respectively, $d$ represents the grain size of the bed sediment, $B$ represents the pier width, and $K_{\zeta }$ represents the shape factor of the pier.

The improved formula commonly used in the design of railway and highway bridge piers in China for calculating the local scour depth is formula 65-1:

$$h_s=K_{\xi }{K}_{\eta }{B}^{0.6}{h}^{0.15}{\left(\frac{v-v_0^{\prime }}{v_0}\right)}^n$$

(5)

Calculating the starting flow velocity $v_0$ of the riverbed material and the scour flow velocity $v_0^{\prime }$ of the bridge pier’s bed surface is a complex process, and it becomes even more complicated when the construction of a sediment storage dam is not taken into account. Therefore, we have made improvements to the formula by retaining the bridge pier shape coefficient $K_{\xi }$ and the coefficient $K_{\eta }$ related to the grain size of the bed sand. We have also added parameters such as the crest elevation $Z$ and the distance between the pier and the dam $L$. Through regression analysis, we obtained the formula for calculating the depth of local pier scour after the construction of a sand barrier:

$$h_s=2.3846K_{\xi }{K}_{\eta }{B}^{0.1}{e}^{10.447(\frac{(Z_0-Z)}{L})}{q}^{0.54}$$

(6)

where:

• $K_{\xi }$ Pier shape coefficient, usually taken as 0.9–1.0
• $K_{\eta }$ Coefficient related to the particle size, $K_{\eta }={\left(\frac{2.16}{{\overline{d}}^{0.4}}+\frac{0.11}{{\overline{d}}^{0.19}}\right)}^{1/2}$, $\overline{d}$ is set to be $d_{50}$
• $B$   Pier width (m)
• $Z_0$ Original riverbed elevation at the bridge pier (m)
• $Z$   Dam crest elevation (m)
• $L$    Distance between pier and dam (m)
• $q$    Discharge per unit width (m³/s.m).

By comparing the measured local scour depth of bridge piers with the calculated values based on the formula from [33], as shown in Figure 16, the fitting degree between the calculated values and the measured values is high, with a correlation coefficient $R$ = 0.946. This formula can be used to calculate the depth of bridge piers with downstream sediment storage dams, providing a reference basis for bridge engineering design.

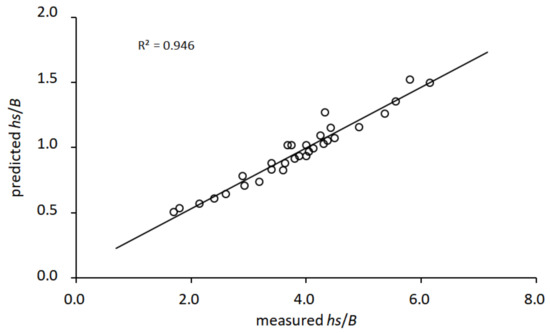
Figure 16. Comparison of measured and predicted $hs$.

5. Conclusions and Recommendations

(1)

The most significant factor affecting local pier scour with a downstream sediment storage dam was the inflow flow rate. As the inflow flow rate $Q$ increased, the water level in front of and behind the bridge pier rose, the downstream water surface level of the bridge pier was lower than the natural bed slope, the depth of local pier scour increased, and the range of scour behind the pier became longer.

(2)

The planar view of local pier scour morphology was horseshoe-shaped, gradually narrowing from the front to the bridge pier, and extending in a swallowtail shape at the back of the bridge pier. The longitudinal section was an asymmetrical triangle, with a steeper slope in front of the pier and a gentler slope behind the pier. The depth of local scour $h_s$ was within the $0.25B$ range in front of the pier base, and the influence range $l_2$ behind the pier was $5B\le l_2\le 10B$.

(3)

The development rate of local pier scour increased with the increase in the inflow flow rate. The development rate of scour was stable and slow under a low flow rate and generally reached dynamic equilibrium within 0.5–1.0 h. Under a high flow rate, the development rate of scour increased significantly, and fluctuation phenomena occurred. Scour also reached dynamic equilibrium within 2.0–2.5 h.

(4)

When $9B\le L\le 22B$, the local scour depth $h_s$ decreased with the decrease in the distance between the pier and dam $L$. The rate of change in local scour depth was similar under various flow rates, and the ratio of local scour depth to the distance between the pier and dam was $h_s/L=0.01$. When $L<9B$ or $L>22B$, the change in local scour depth $h_s$ was small. Considering the impact range of scour behind the bridge pier, it is recommended that $8B\le L\le 11B$.

(5)

As the inflow flow rate increased, the magnitude of the decrease in the local scour depth $h_s$ caused by the increase in the dam crest elevation $Z$ increased. Compared with the original riverbed elevation $Z_0$ at the bridge pier, when $(Z-Z_0)\le 0.5B$, the ratio of local scour depth to dam crest elevation was $h_s/Z=0.46$ under an average of 100 units of traffic. When $(Z-Z_0)>0.5B$, the change in the local scour depth $h_s$ was small. It is recommended that $0.4B\le (Z-Z_0)\le 0.5B$.

6. Discussion

The main innovation of this paper lies in the reasonable layout of sediment storage dams and the improved calculation formula for local scour depth $h_s$ of bridge piers, which were compared with related research results. Melville [4] believed that scour develops rapidly in the first 0.5 h, and the scour morphology basically reached equilibrium afterwards. This article demonstrated that the scour morphology develops dynamically in 0.5–1.0 h. The range of scour influence behind the bridge pier between $5B\le l_2\le 10B$ is consistent with the research results of Grimaldi [22]. The recommended distance between pier and dam $L$ in this article is $8B\le L\le 11B$, which is within the range $2B\le L\le 12B$ recommended by Wang [23]. The improved calculation formula for local scour depth $h_s$ in this article is applicable to predicting local scour around bridge piers with downstream sand barriers and with riverbeds composed of wide-graded non-uniform dispersed sand. This riverbed condition often exists in mountainous rivers. For bridge piers with local scour from cohesive soil in plain rivers, the formula in this article is not applicable. Thus, local scour morphology should be predicted by combining local measured experimental data and analyzing the most unfavorable combination of various influencing factors.