Investigating the Pressure Fluctuations of Hydraulic Jump in an Abrupt Expanding Stilling Basin with Roughened Bed

Abstract

Stilling basins with sudden expansions are one of the energy dissipation structures. In the hydraulic jump, pressure fluctuations cause significant damages in stilling basins by cavity formation, erosion, and vibration. Roughness can also lead to changes of the behavior of stream lines and vortices. Despite the large number of works on the topic, the role of roughness in spatial hydraulic jumps is not yet fully understood. Present research aimed to study the influence of rough bed on pressure fluctuations of S-jump in abrupt expanding stilling basin. Experiments were conducted in a 0.8 m width and 12 m length flume. Channel expansions ratios were 0.33, 0.5, 0.67, and 1 within the range of Froude numbers, 2 to 9.5. The results showed that roughness decreases intensity of pressure fluctuations in an abrupt expansion stilling basin. Additionally, in sudden expanding sections, the energy loss increases, and the intensity of pressure fluctuations decrease due to the formation of lateral vortices. The reduction rate of maximum pressure fluctuation was 27%, 46%, and 58% for expansion ratio of 0.67, 0.5, and 0.33, respectively. The results revealed the clear dependence of these variables on the Froude number and the distance to the hydraulic jump toe. The maximum values of extreme pressure fluctuations occur in the range 0.609 < X < 3.385, where X is dimensionless distance from the toe of the hydraulic jump, which makes it highly advisable to reinforce the bed of stilling basins in this range.

1. Introduction

Hydraulic jump is a rapidly varied flow, which represents a sudden transition from a supercritical to a subcritical flow and leads to a severe energy dissipation [1]. Transition caused a sudden increase in water level in a relatively short length [2]. The flow excess kinetic energy dissipates and converts to energy, via a hydraulic jump. Stilling basins, located at the end of the chute or channel, dissipate the destructive kinetic energy of flow and also mitigate the damaging and erosive impacts of hydraulic jump in the downstream. The most significant factors in designing the stilling basins are length, width, wall elevation, and bed level [3,4], depending on the hydraulic jump characteristics and tail water flow depth. The basic study on hydraulic jumps was performed by Belanger (1828). According to his research, the sequent depth of hydraulic jump in a smooth prismatic channel was determined by Equation (1) [5]:

$$\frac{y_2}{y_1}=\frac{1}{2}\left(\sqrt{1+8F{r}_1{}^2}-1\right)$$

(1)

where $y_2$ is the sequent depth, $y_1$ is the initial depth of flow, and $F{r}_1$ is the initial Froude number. Generally, there are three kinds of hydraulic jumps in a stilling basin with abrupt expansion, based on the tail water flow depth (Figure 1). In lower depth, the jump toe is lower than the location where the cross-wave hits the wall (point A). In this case, R-jump (repelled jump) would be created. In this type of jump, the position of toe is distant away downstream of the expansion. By increasing the tail water flow depth, the jump forms between the expansion part and point A, and S-jump (spatial jump) will be generated. The S-jump is asymmetric and similar to an oscillating jet without any surface rollers. Regarding Bremen and Hager [6], the S-jump takes place when the jump toe is located at the expansion section. With increasing depth, the jump toe would be higher than the junction part, and a T-jump will be created. Regarding the distance of jump toe and junction, T-jump can be either symmetric or asymmetric [7].

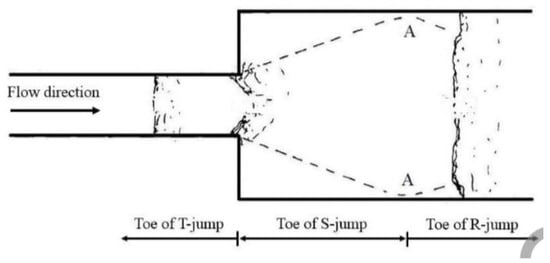
Figure 1. Different kinds of hydraulic jumps in a channel with sudden expansion [6] (Bremen 1990).

A study of Alhamid [8] showed that the S-jump has the higher efficiency and smaller conjugate depth ratio, in comparison to the classical jump. The presence of S-jump in sudden expanding basins increases the flow asymmetry and develops high-velocity jets along one side wall and a backward flow along the opposite basin side [9].

The following relationship was developed for computing the sequent depth ratio ($\alpha$) in channels with sudden expansions [10]:

$$\alpha =\frac{y_2}{y_1}\sqrt{\beta }$$

(2)

where $\beta =\frac{B_1}{B_2}$ is the ratio of upstream to downstream width. In another study, researchers assessed the impacts of a sill with various heights and locations on the of S-jump characteristics in both symmetric and asymmetric sudden expansions [11]. The hydraulic jump occurrence on the entire length of smooth bed in stilling basins is not optimum; so, using some techniques, including chute blocks and baffle blocks, and the end still can be placed in the basins [12]. The objective of these arrangements in the stilling basins decrease the hydraulic jump length. Since the baffle blocks are subjected to the inlet flow jet directly, they are exposed to corrosion and erosive damages [13,14]. If the crest of controller elements located in the stilling basin bed are at the same level as the upstream bed, they can enhance the jump characteristics, decrease the size of the stilling basin, and reduce the cavitation phenomenon. In this case, hydraulic jump on a roughened bed occurred. This kind of jump was initially studied by Rajaratnam [15]. In an experimental study, the characteristics of the hydraulic jump on a roughened bed with an adverse slope were evaluated. The results revealed that increasing height of the roughness, as well as the adverse slope leads to drop of jump length and sequent flow depth [16,17].

The impact of roughened bed on characteristics of S-jump in expanding channel was determined by [18], for the first time. It was indicated that the sequent flow depth decreased almost 53% in comparison to a classical jump on smooth bed. In a research study, it was represented that increasing the height of roughness elements caused a reduction in the S-jump length in a range of 12% to 20% and, therefore, decrease sequent depth in a range of 20% to 30.4% on roughened bed, compared with the smooth bed [19].

With topographic and economic restriction, it is not possible to excavate the stilling basin; thus, the application of cross-sectional expansion in channels would be a useful way to ensure the stabilization of the hydraulic jump in the stilling basins [20]. When the hydraulic jump occurs in a sudden expanding stilling basin, it is affected by the formation of side eddies and vortices. In some previous works, the effects of expansion on jump characteristics were investigated, while the study of the relationship between expansion ratio and pressure fluctuation parameters lacks in the literature. Hence, this study attempted to carry out the experimental research for evaluating the effects of different expansion ratios on pressure fluctuation during the spatial hydraulic jump on a roughened bed.

2. Materials and Methods

2.1. Experimental Setup

Experiments were conducted in a rectangular channel with 12 m length, 0.8 m width, and 0.7 m depth with glass side walls (Figure 2). The recirculation pump was applied in order to supply water from the storage tank to the head tank. To control the inflow conditions and subsequently prevent the outflow contraction, the sluice gate was employed. As a result, the uniform supercritical flow depth was equal to the gate opening. The narrow part of the flume was constructed using two Plexiglas boxes, which extended 0.8 m downstream to enlarge abruptly and symmetrically with the width of the main flume (Figure 2). In this study, four expansion ratios ($\frac{B_1}{B_2}$) of 1, 0.67, 0.5, and 0.33 with 0.8 m, 0.53 m, 0.4 m, and 0.27 m width were considered, respectively (where $B_1$ is the width of the approaching flume to the expansion in upstream and $B_2$ is the flume width in downstream). The tail gate was applied for controlling the toe position of the hydraulic jump at the expansion part, located at the end of the flume. The flow rate was measured by an acoustic flow meter with an accuracy of $\pm 1\%$, which was placed on the pipeline.

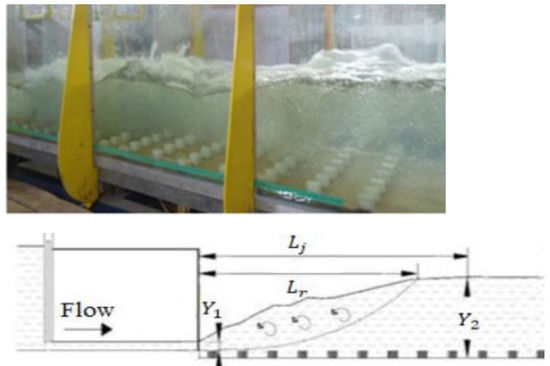
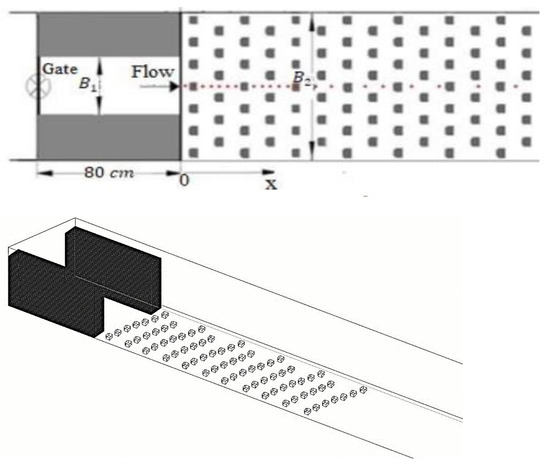
Figure 2. Schematic of the laboratory model.

The initial and sequent jump depths were measured by two methods, as follows: (1) using ultrasonic digital measuring instruments with a precision of ±0.1 mm mounted over the channel centerline for measuring the water depth during the experiments process and recording a large amount of data during the experiment helps to determine the flow fluctuations; (2) obtaining the water height with the help of a point gauge with an accuracy of $\pm$1 mm at five points of the cross-section.

In the current study, the mean values of elevation were calculated by using the two mentioned approaches to find the most appropriate profile [21].

In order to roughen the bed, the discrete elements of roughness made by polyethylene with heights of 3 cm and length of 5 cm were used. The shape and dimension of elements were chosen based on [20,22], which was effective in reducing the length of jump and the sequent depth [22]. These trapezoidal elements were located below the water jet and were not exposed to the incoming water jet directly [18]; therefore, the possibility of the cavitation will decrease [23].

Pressure fluctuations were measured by pressure transducers, Atek BCT 110 series, with accuracy of ±0.5%. A rate of 20 Hz in a period of 90 s was applied to collect 1800 samples in each test. The transducers were connected to the taps on the stilling basins through flexible tubes, and a total number of 28 were mounted at different points along the bed. Moreover, a computer was linked to the transducers via a 6-channel digital board, and the recorded data were shown by data acquisition software (Figure 3).

Figure 3. Pressure transducers and display of output results.

After designing and constructing the flume, the total of 158 experiments was carried out to measure the hydrodynamic pressure in the bed of basin. In order to investigate the impact of bed roughness on hydrodynamic pressures, experiments were performed in 2 steps. The first step, which related to smooth bed, consisted of 77 experiments with four expansion ratios, and 81 experiments were performed in the second step with roughened bed. The ranges of measured variables are indicated in Table 1. These variables include $B_1$, $B_2$, Reynolds number ($Re$), Froude number ($Fr$), and flow discharge ($Q$).

Table 1. Ranges of measured variables.

${\mathit{B}}_1$ (cm)	${\mathit{B}}_2$ (cm)	Expansion Ratio (β)	bed	${\mathit{Y}}_1$ (cm)	$\mathit{R}\mathit{e}$	$\mathit{F}{\mathit{r}}_1$	$\mathit{Q} \left(\frac{\mathit{l}}{\mathit{s}}\right)$
80	80	1			60,000–132,000	2–6.9	40–90
53	80	0.67	smooth	3–6	82,000–161,000	2.2–8.5	45–102
40	80	0.5			53,000–172,000	2.3–9.5	22–73
27	80	0.33			91,000–192,000	2.5–10.5	25–60
80	80	1			52,000–141,000	2–6.5	31–96
53	80	0.67	rough	3–6	65,000–156,000	2.3–8	32–90
40	80	0.5			62,000–153,000	2.4–9.1	26–70
27	80	0.33			74,000–242,000	3–9.5	20-70

2.2. Theoretical Expression

Due to the fact that the pressure in the stilling basin bed has random fluctuations, analyses are mainly evaluated by statistical methods. The most important pressure fluctuation parameter is a non-dimensional coefficient of $C_P{}^{\prime }$, which is defined as below [24].

$$C_P{}^{\prime }=\frac{\sigma }{V_1{}^2/2g}$$

(3)

where σ is the root mean square (RMS) value of the fluctuation and equal to $\sqrt{{P^{\prime }}^2}$, $V_1$ is the initial jump’s velocity, and g is the gravity acceleration. $P^{\prime }$ is defined as below [24]:

$$\sqrt{{P^{\prime }}^2}=\frac{1}{N}\sqrt{{\displaystyle \sum }_{n=1}^N{\left[P\left(x.y.n\Delta t\right)-\overline{P}\left(x.y\right)\right]}^2}$$

(4)

where N is the total number of recorded data, $P\left(x,y,n\Delta t\right)$ is instantaneous pressure, $\overline{P}\left(x,y\right)$ is the average pressure, and $\Delta t$ is the recording period. The positive and negative coefficients of pressure are also indicated below.

$$C^{+}p=\frac{\Delta P^{+}}{V_1{}^2/2g}$$

(5)

$$C^{-}p=\frac{\Delta P^{-}}{V_1{}^2/2g}$$

(6)

$\Delta P^{+}$ and $\Delta P^{-}$ are the maximum and minimum pressure deviations from the average pressure, in a respective order. $C^{+}p$ is defined as the maximum deviation of positive pressure from the average pressure and indicates the impacts of pressure fluctuations on the bed of the stilling basin. By contrast, $C^{-}p$ is indicative of the difference between negative pressures and the average pressure. This parameter has an important role in formation of cavitation and interaction forces under the slab.

2.3. Dimensional Analysis

A model is dynamically similar to its prototype if all non-dimensional parameters are similar, and also, all the forces acting on the corresponding points in both systems are the same. The factors affecting the hydrodynamic pressure in the stilling basin are defined below:

$$f\left(P^{\prime }.V_1.Y_1.Y_2.B_1.B_2.X.L_j.{\rho }_w.\vartheta .g\right)=0$$

(7)

where $P^{\prime }$ is related to the fluctuation pressure and equal to $P-\overline{P}$, $V_1$ is the initial velocity of jump, $Y_1$ is initial jump depth, $Y_2$ is sequent jump depth, $B_1$ is the channel width in narrow section, which is equal to 0.26 m, 0.4 m, 0.53 m, and 0.8 m for different expansion ratios, $B_2$ is the main channel width, which is equal to 0.8 m in all expansion ratios, $X$ is the distance from jump toe, $L_j$ is the hydraulic jump length, ${\rho }_w$ is water density, and $\upsilon$ is the kinematic viscosity of water.

With the help of 𝜋-Buckingham analysis and selecting $V_1$, $Y_1$, and ${\rho }_w$ as repeating parameters, the dimensionless quantities were achieved as Equation (8), after simplification:

$$f(\frac{\sqrt{{P^{\prime }}^2}}{\raisebox{1ex}{$V_1^2$}\!\left/ \!\raisebox{-1ex}{$2g$}\right.},\frac{Y_2}{Y_1},\frac{B_1}{B_2},\frac{X}{L_j},\frac{V_1{Y}_1}{\nu },\frac{V_1}{\sqrt{g{Y}_1}})=0$$

(8)

According to determination of pressure fluctuations in the stilling basin, pressure fluctuations coefficients can be defined as a function of dimensionless parameters (Equation (9)).

$$C{p}^{\prime }=\frac{\sqrt{{P^{\prime }}^2}}{\raisebox{1ex}{$V_1^2$}\!\left/ \!\raisebox{-1ex}{$2g$}\right.}=f(\frac{Y_2}{Y_1},\frac{B_1}{B_2},\frac{X}{L_j},\frac{V_1{Y}_1}{\nu },\frac{V_1}{\sqrt{g{Y}_1}})$$

(9)

3. Results and Discussions

3.1. Sequent Depth Ratio

After forming spatial hydraulic jump in different expansion ratios, it was observed that, by increasing the expansion ratio, the formation of eddies decreases. In other words, in the minimum expansion ratio, more eddies and higher flow separation were generated between the roughness elements. This observation was also revealed in other recent studies [18,25]. Figure 4 indicates the sequent depth ratio in different Froude numbers and expansion ratios.

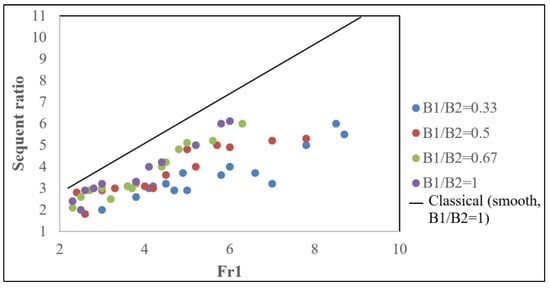
Figure 4. Sequent depth ratio in different Froude numbers and expansion ratios in the rough bed.

As is shown, the sequent depth ratio in the rough bed increased by increasing expansion ratio. Furthermore, the solid line indicates the sequent depth ratio for classical jump based on the Belanger equation. All the calculated data were below this line, which proves that roughened bed led to a drop in sequent depth of hydraulic jumps. As a result, both bed roughness and expansion ratio have a key role in a reduction in the sequent depth and an increase in the efficiency of hydraulic jumps. This is in accordance with findings of other researchers [18,26].

3.2. $C_P{}^{\prime }$ Parameter

• Without expansion ($\beta =1$)

For different Froude number, $C_P{}^{\prime }$ coefficients were computed along the hydraulic jump, and the results are presented in Figure 5 for smooth and rough bed. As indicated in the figures, $C_P{}^{\prime }$ coefficient decreases with increasing the Froude number. This result is in line with previous studies [25,27]. This result does not imply that intensity of turbulence decreases with increasing the Froude number, but by increasing the Froude number and flow rate, growth rate of kinetic energy ($V_1{}^2/2g$) was more than a pressure fluctuation rate ($\sigma$). Additionally, according to Figure 5, $C_P{}^{\prime }$ parameter has lower values in rough bed. In other words, the presence of roughness in bed caused a decrease in the pressure fluctuations due to energy dissipation between roughened elements, which is in accordance with study of [26].

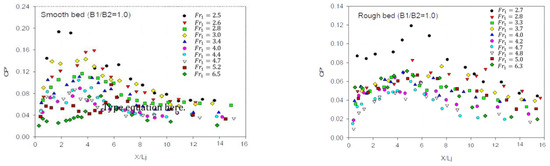
Figure 5. $C_P{}^{\prime }$ parameter in a prismatic jump.

• With abrupt expansion jump

In this section, $C_P{}^{\prime }$ parameter was calculated in both smooth and rough bed, and the results are shown in Figure 6, Figure 7 and Figure 8 for expansion ratios of 0.67, 0.5, and 0.33, respectively. As indicated in all figures, this parameter has a similar trend. The intensity of pressure fluctuations rises at the beginning of the jump and reaches its maximum value in the roller areas, where the highest turbulence occurs. Then, it decreases and becomes almost constant until the end of the jump. $C_P{}^{\prime }$ parameter also decreases by increasing the Froude number because of faster growth of kinetic energy than pressure fluctuation rate. In addition, bed roughness caused a decrease in the pressure fluctuations intensity owing to energy dissipation between roughened elements. The value of pressure fluctuations coefficient decreases by decreasing the expansion ratio ($\beta$), so this parameter in expansion ratio of 0.33 has the minimum value. Furthermore, $C_P{}^{\prime }$ values reach their maximum from the beginning of the basin to the range of $2<\frac{X}{L_j}<6$. This finding is in line with the result achieved by [28]. The distance where the $C_P{}^{\prime }$ reaches its maximum decreases by the increase in the Froude number. This issue must be considered for providing stilling basins with suitable protection against dynamic loads.

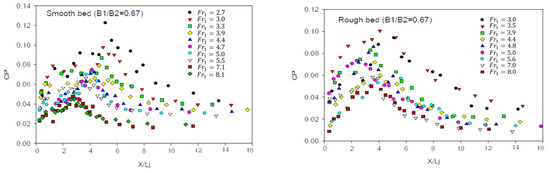
Figure 6. $C_P{}^{\prime }$ parameter for expansion ratio of 0.67.

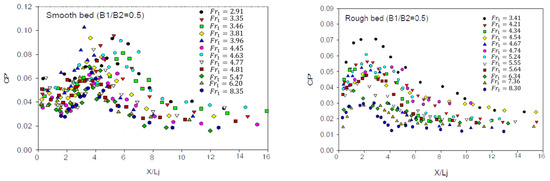
Figure 7. $C_P{}^{\prime }$ parameter for expansion ratio of 0.5.

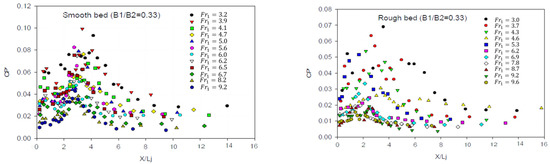
Figure 8. $C_P{}^{\prime }$ parameter for expansion ratio of 0.33.

3.3. Maximum Non-Dimensional Pressure Fluctuations Parameter ($C_P{{}^{\prime }}_{max}$)

Because of the importance of the maximum pressure fluctuations parameter ($C_P{{}^{\prime }}_{max}$) in designing the stilling basin during hydraulic jump, it is necessary to consider its changes in accordance with the Froude number. This trend is shown in Figure 9 for prismatic jump ($\beta =1$). Additionally, the results of [28] are indicated in this figure for classical hydraulic jump and the Froude number range of 4 to 10. With regard to [29], the maximum pressure fluctuation of s-jumps is higher than that of the classical jump. This occurrence can be justified by the formation of eddies near sidewalls. According to this figure, the value of $C_P{{}^{\prime }}_{max}$ decreases with increasing the Froude number in both smooth and rough bed. Due to the presence of bed roughness, $C_P{{}^{\prime }}_{max}$ decreases by an average of 20% than in smooth bed in the prismatic channel. Considering the simultaneous impact of bed roughness and expansion ratio, it can be observed that $C_P{{}^{\prime }}_{max}$ decreases by an average of 27% in expansion ratio of 0.67. Additionally, in an expansion ratio of 0.5 and 0.33, the reduction rate of $C_P{{}^{\prime }}_{max}$ achieved almost 46% and 58%, respectively (Figure 9). As a result, the presence of both factors of roughness and expansion leads to the reduction in the non-dimensional parameter of $C_P{{}^{\prime }}_{max}$. Table 2 shows the summary of the reduction rate of $C_P{{}^{\prime }}_{max}$ in different expansion ratios.

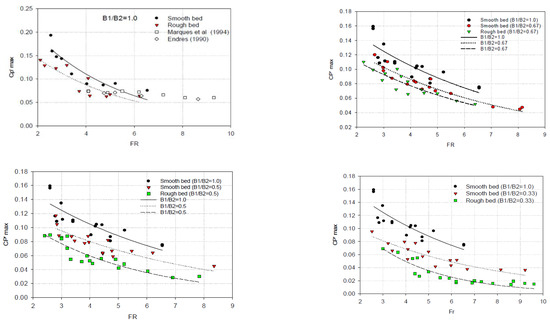
Figure 9. The values of $C_P{{}^{\prime }}_{max}$ in different expansion ratios.

Table 2. Comparison of reduction percentage of $C_P{{}^{\prime }}_{max}$ in respect to smooth prismatic jump.

Type of Jump	Reduction (%) of ${\mathit{C}}_{\mathit{P}}{{}^{\prime }}_{\mathit{m}\mathit{a}\mathit{x}}$
smooth bed and sudden expansion; β = 0.67	18
smooth bed and sudden expansion; β = 0.5	23
smooth bed and sudden expansion; β = 0.33	30
rough bed and prismatic jump; β = 1	20
rough bed and sudden expansion; β = 0.67	27
rough bed and sudden expansion; β = 0.5	46
rough bed and sudden expansion; β = 0.33	58

It is notable that the bed roughness increased the energy dissipation by creating the huge eddies and, therefore, decreased the asymmetry and stabilized the hydraulic jump. Additionally, in sudden expanding sections due to the formation of lateral vortices, the energy loss increases, and the intensity of pressure fluctuations decrease. The results of this study are compatible with previous works, in which bed roughness caused an increase in shear stress and, therefore, a decrease in pressure fluctuations [20,30].

3.4. Positive and Negative Pressure Coefficients ($C^{+}p$ ,$C^{-}p$)

The results of positive and negative fluctuations of smooth and rough bed with the Froude range of 2.5–6.5 are demonstrated in Figure 10. As indicated, the coefficients of $C^{+}p$ and $C^{-}p$ depend strongly on the distance to the hydraulic jump toe. They grow sharply near the hydraulic jump toe, reaching the maximum value at almost X = 0.3., and decrease until the end of the range. The maximum value of positive and negative coefficients in smooth bed was approximately 0.55, while it had lower value (0.35) in rough bed. Hence, roughness factor leads to a decrease in positive and negative pressure fluctuations. The similar trends are also shown for other expansion ratios in Figure 10. This finding agrees well with the presented results of [26].

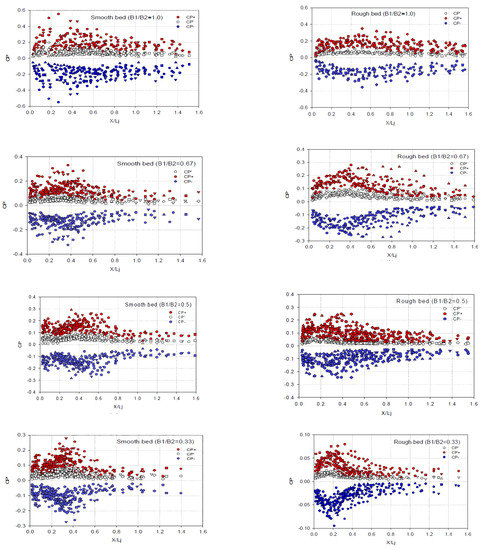
Figure 10. Positive and negative pressure fluctuations versus dimensional distance from jump toe and range of the Froude numbers.

Since the maximum values of the positive and negative pressure coefficients occur within the range of 0.06 < X < 0.35, it is advisable to reinforce the bed of the stilling basins in this area to avoid damages due to dynamic loads. This information can assist designers of hydraulic structures to adopt the most suitable and economical stilling basin setup based on the flow conditions and characteristics.

4. Conclusions

The design of stilling basins is an important issue for reducing costs of construction. In the present study, the main features of a hydraulic jump under the effects of both bed roughness and sudden expansion of basin were determined through experimental investigation. For this aim, a 12 m long and 0.8 m wide channel and four different expanding ratios of 0.33, 0.5, 0.67, and 1 were used. Non-dimensional pressure fluctuation parameter ($C_P{}^{\prime }$) and also its maximum value ($C_P{{}^{\prime }}_{max}$) were calculated for all expanding ratios. The results showed that both bed roughness and sudden expansion lead to a decrease in the pressure fluctuation intensity due to producing lateral vorticities and eddies and increasing the energy loss in the basin. As a result, the reduction rate of maximum pressure fluctuation in rough bed was 20%, 27%, 46%, and 58% for expansion ratio of 1, 0.67, 0.5, and 0.33, respectively, rather than smooth bed.