Parallel-Computing Two-Way Grid-Nested Storm Surge Model with a Moving Boundary Scheme and Case Study of the 2013 Super Typhoon Haiyan
Abstract
:1. Introduction
2. Methodology
2.1. Governing Equation of the Storm Surge Model
2.2. Discretization
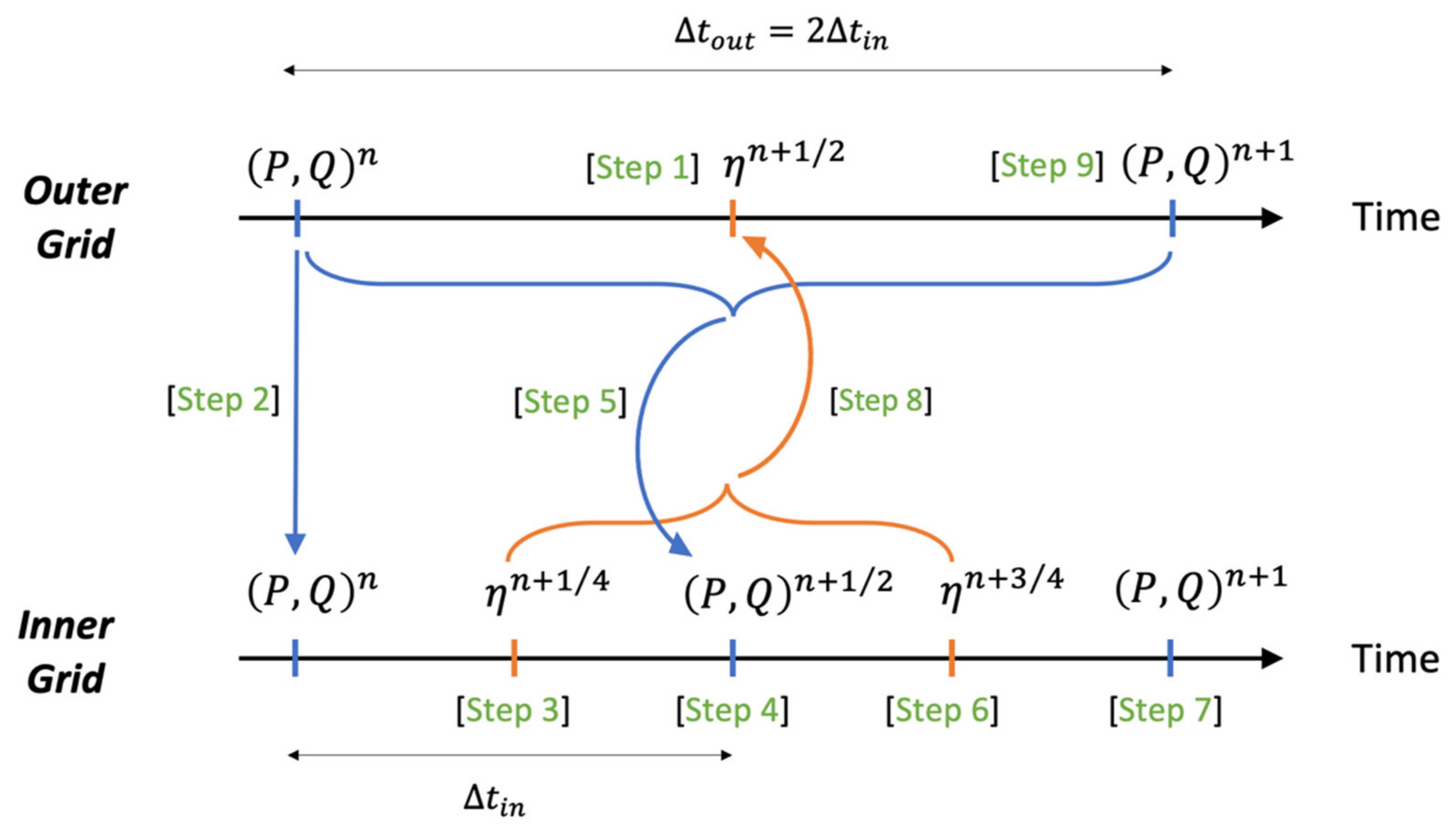
2.3. Grid Nesting in Time and Space
2.4. Moving Boundary Scheme
2.5. OpenMP Parallel Computing
3. Model Validation—Solitary Wave Runup on a Circular Island
3.1. Introduction
3.2. Computational Setting
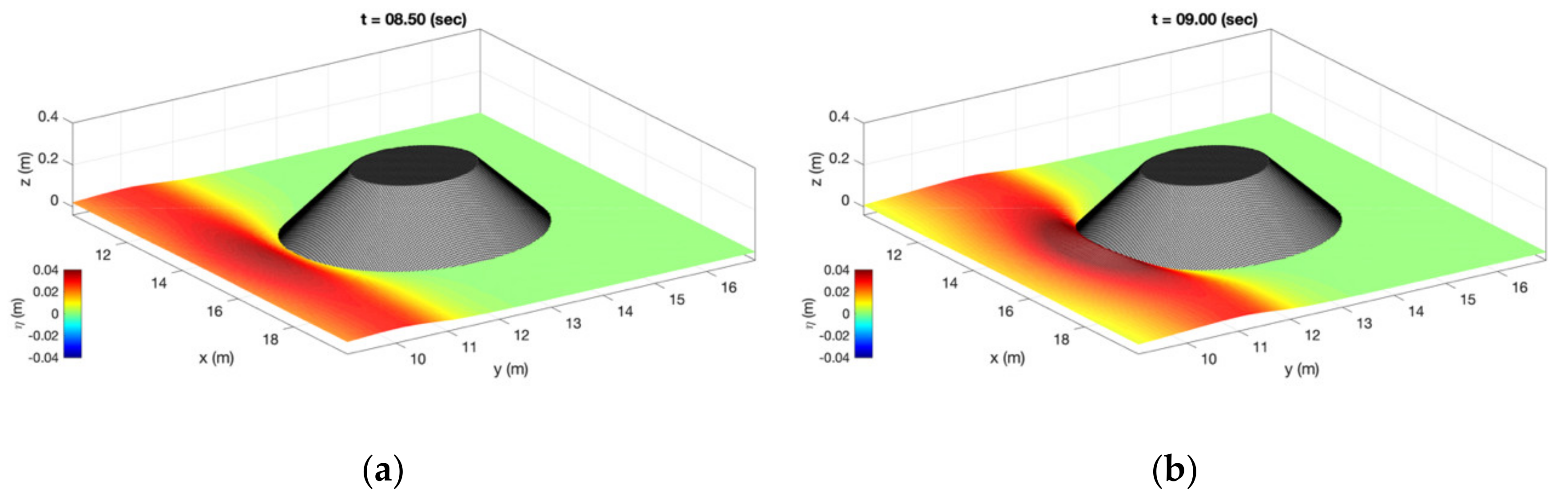
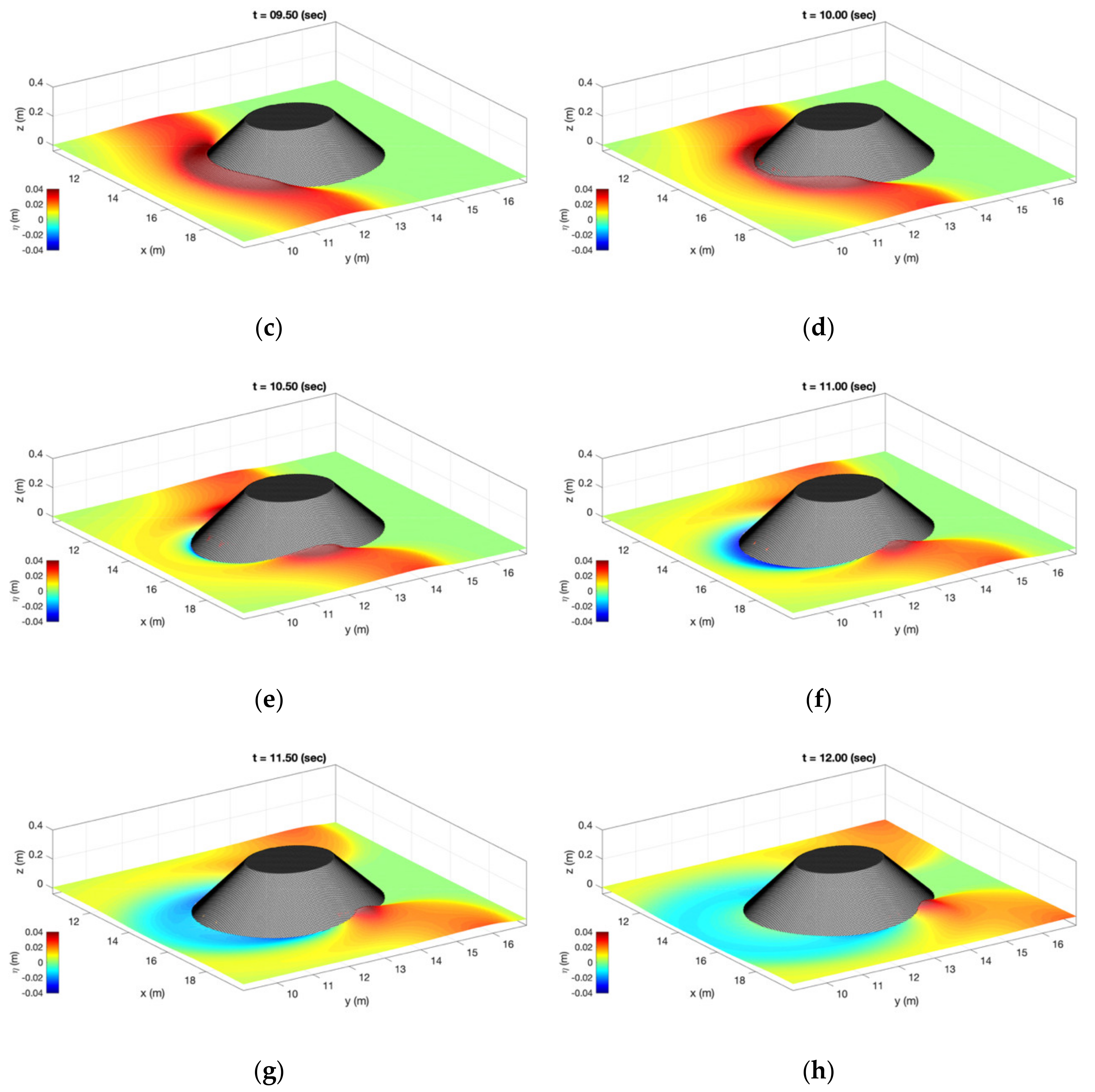
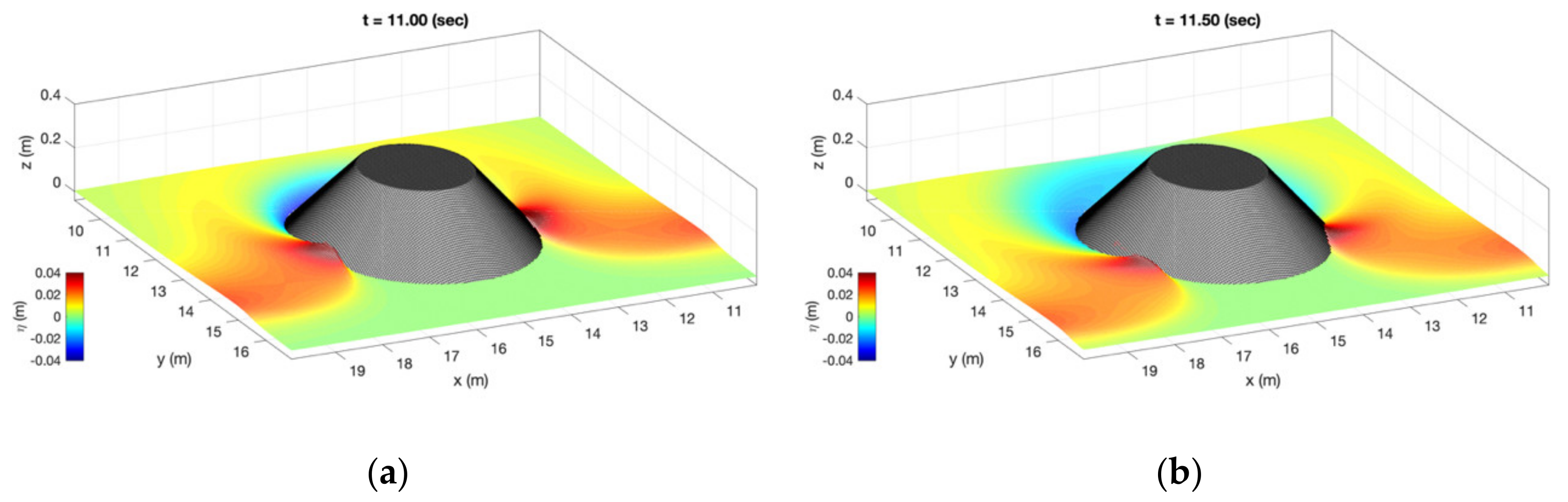
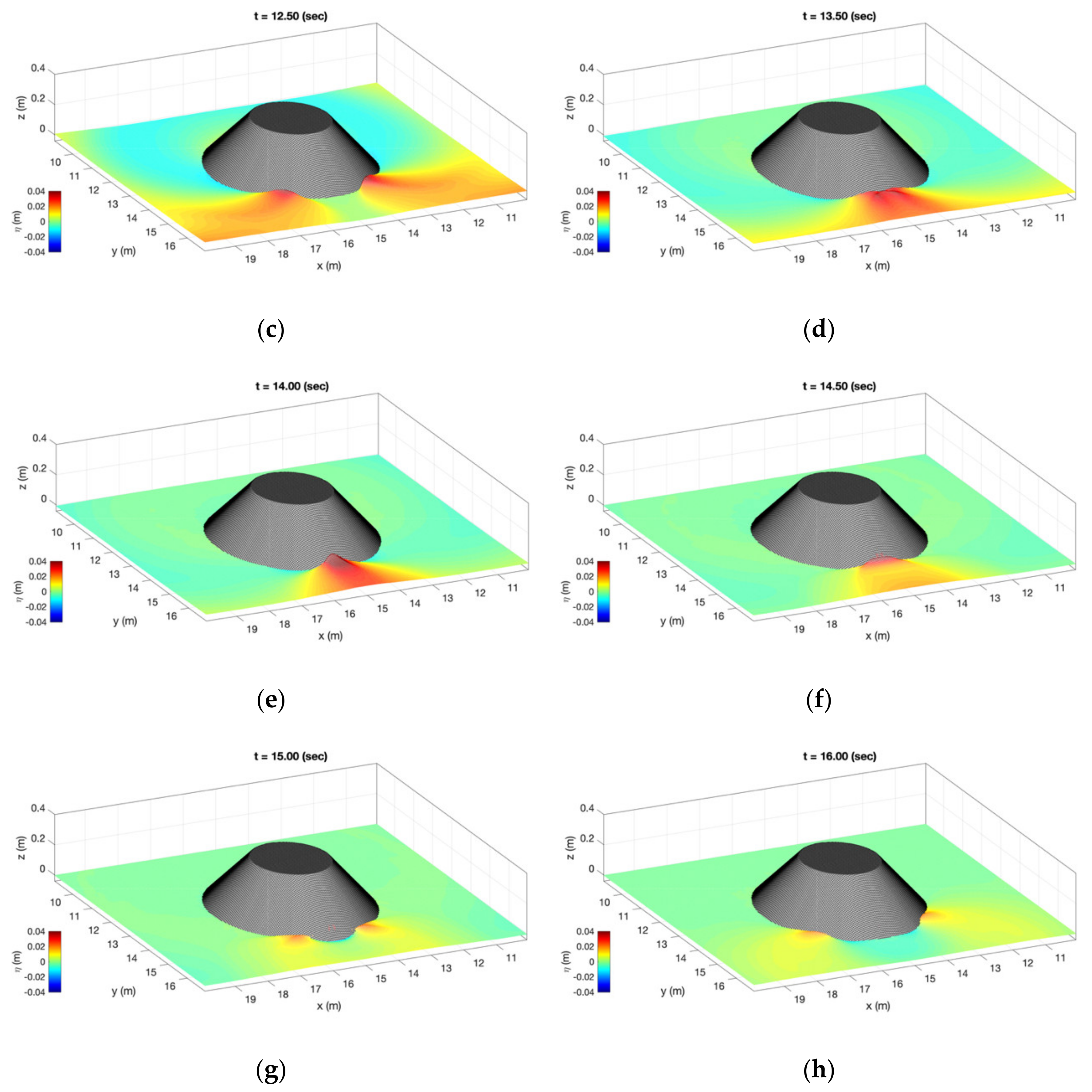
3.3. Computed Free Surface Elevations
3.4. Time History of Free Surface Elevations
3.5. Runup Height and Inundation Area
4. Case Study of Storm Surges—2013 Super Typhoon Haiyan
4.1. Introduction of 2013 Typhoon Haiyan
4.2. Computational Setting
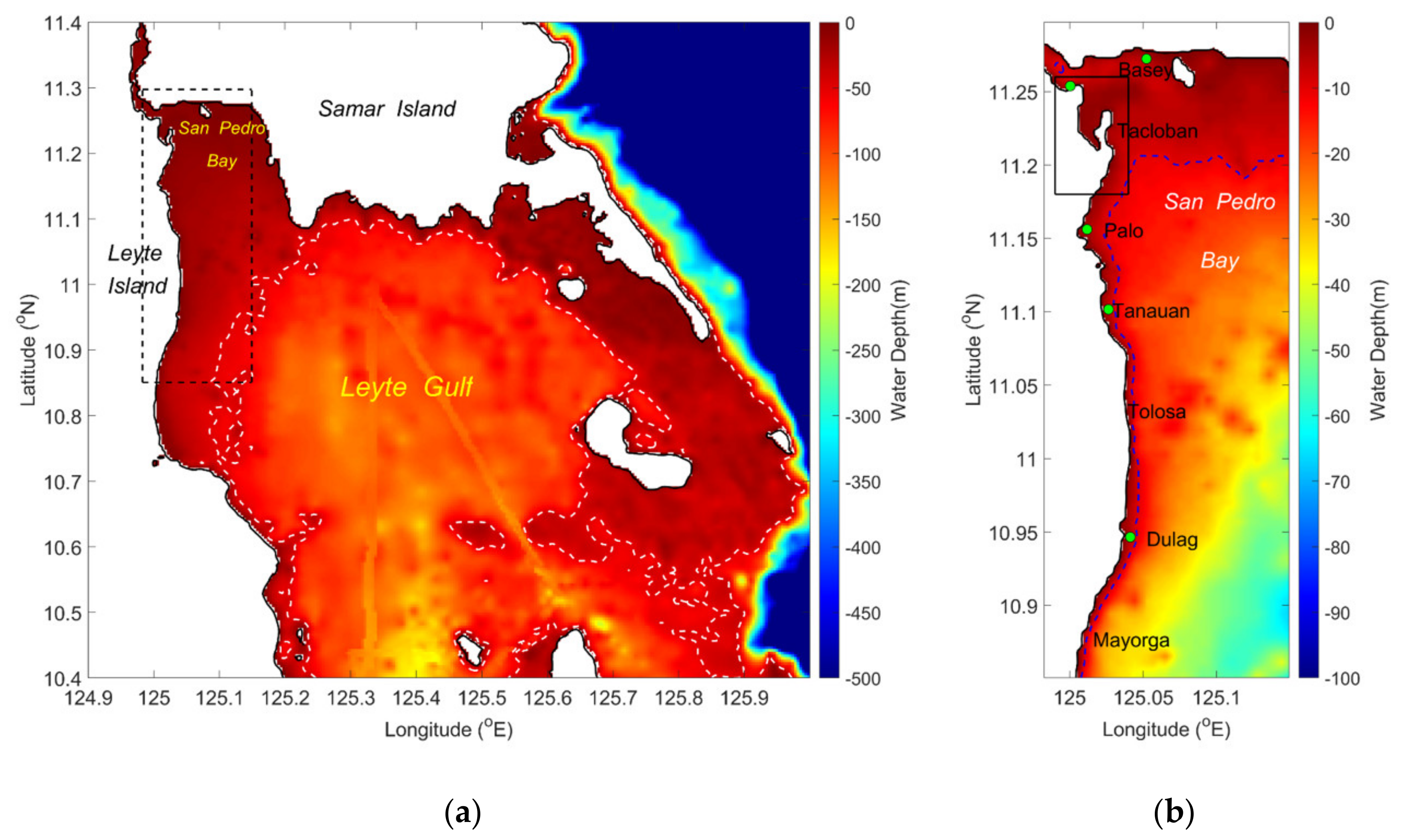
| Domain | Longitude (Unit: °E) | Latitude (Unit: °N) | (Unit: m) | (Unit: s) |
|---|---|---|---|---|
| D01 | 124.9–126.0 | 10.4–11.4 | (437.24, 445.28) | 0.4 |
| D02 | 124.98–125.15 | 10.85–11.30 | (145.66, 148.42) | 0.2 |
| D03 | 124.99–125.04 | 11.18–11.26 | (48.52, 49.48) | 0.1 |
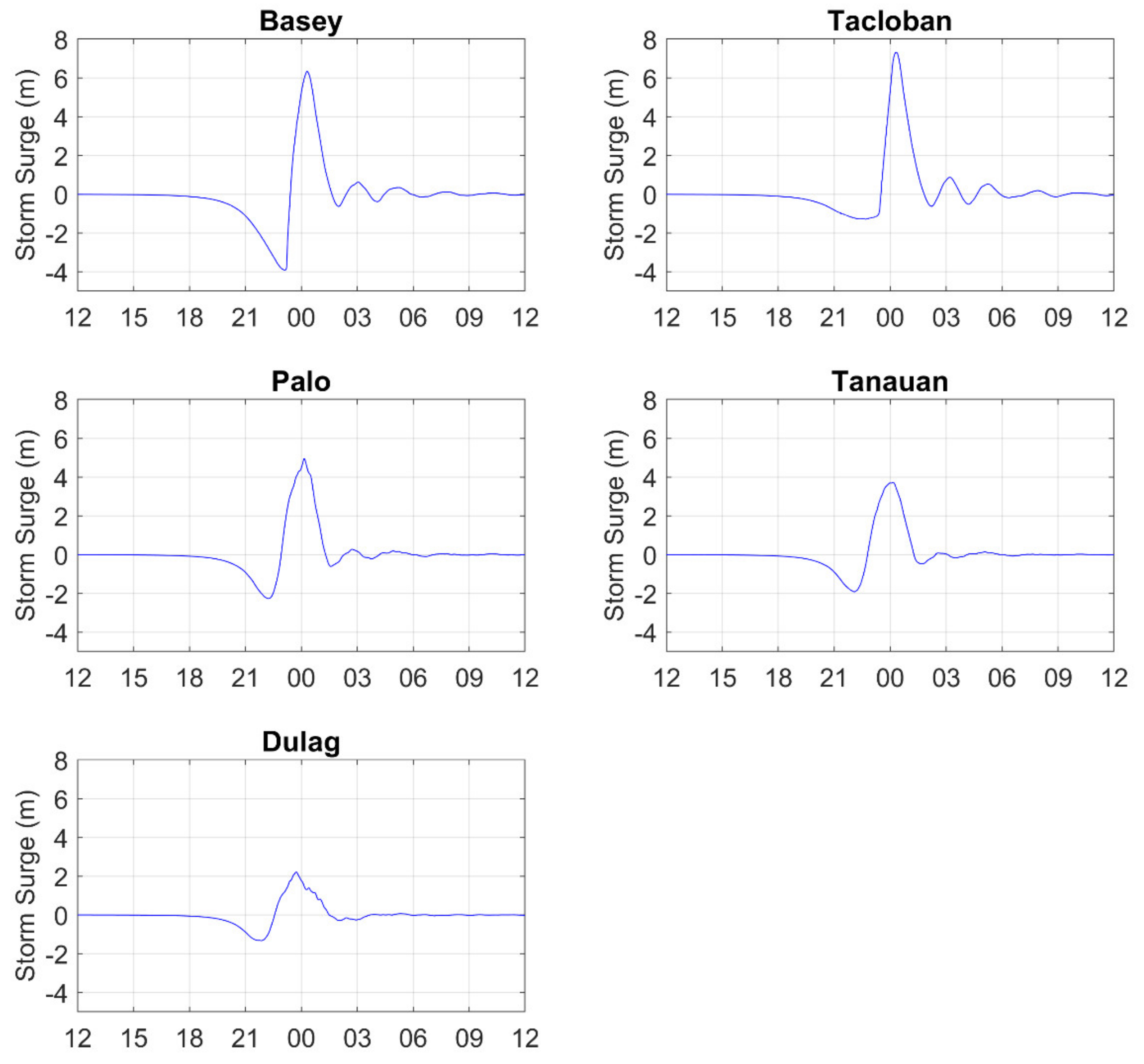
| Station Name | Longitude (Unit: °E) | Latitude (Unit: °N) | Domain |
|---|---|---|---|
| Basey | 125.0523 | 11.2723 | D02 |
| Tacloban | 125.0004 | 11.2538 | D03 |
| Palo | 125.0118 | 11.1561 | D02 |
| Tanauan | 125.0264 | 11.1016 | D02 |
| Dulag | 125.0413 | 10.9465 | D02 |
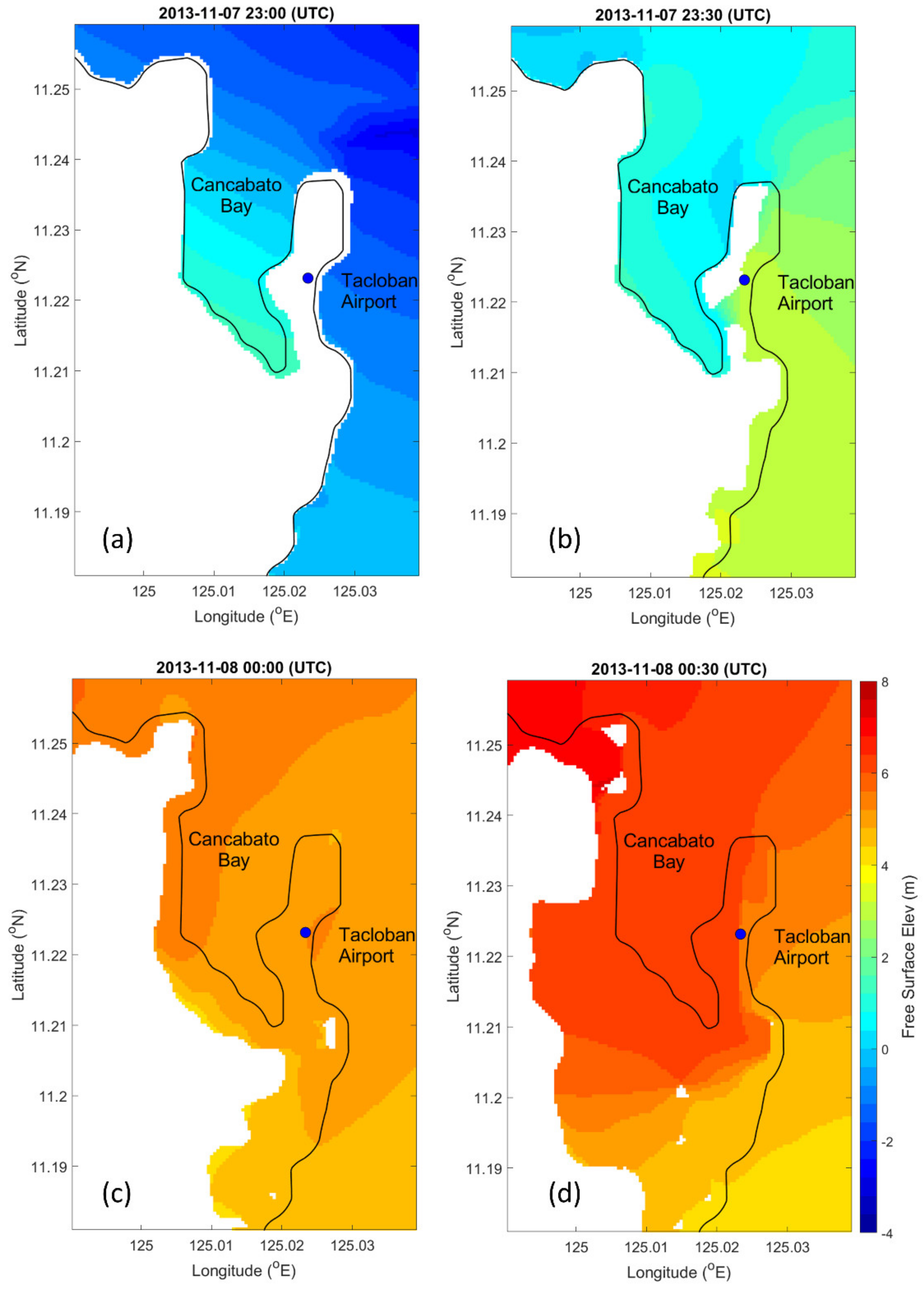
4.3. Storm Surges and Storm-Induced Currents
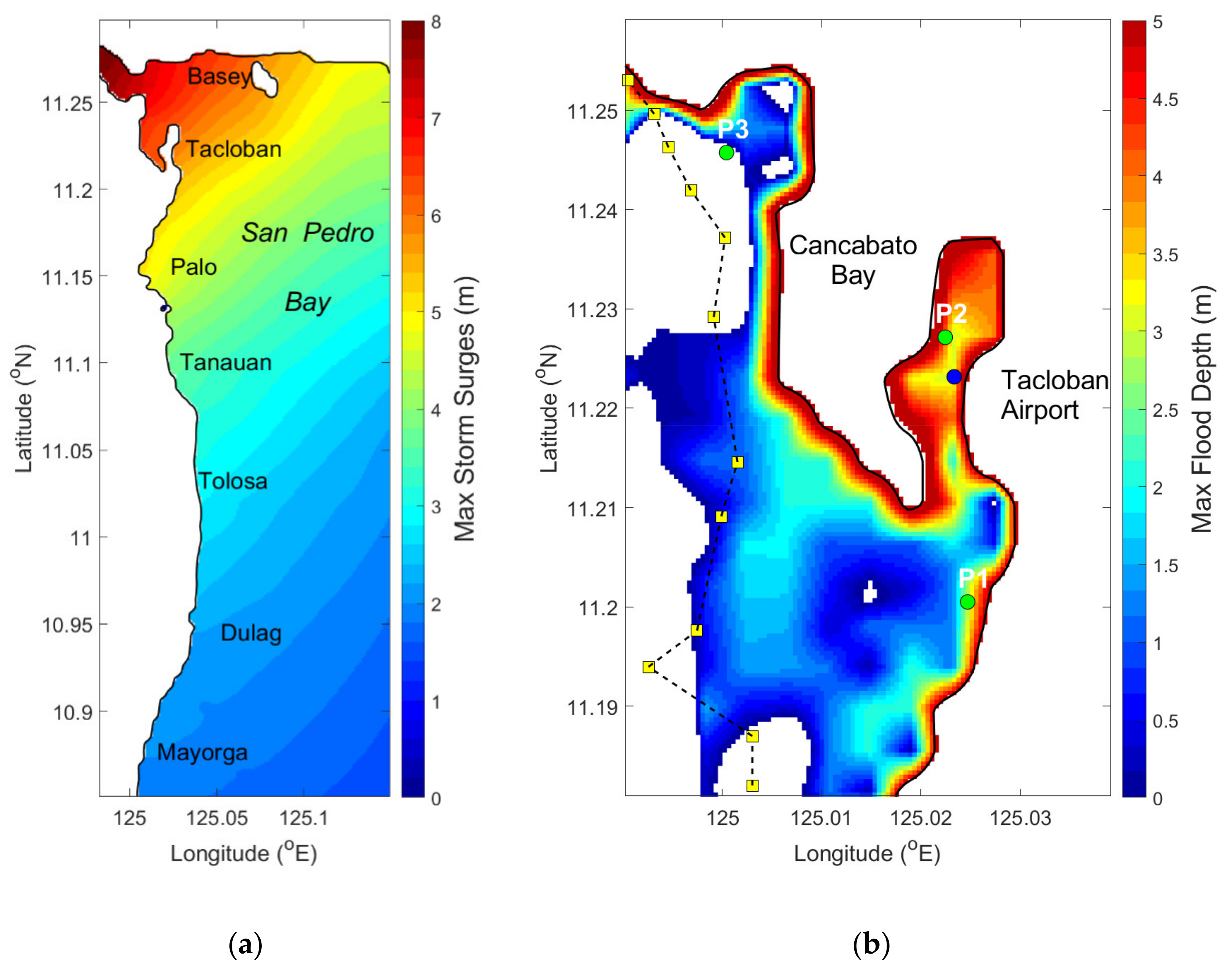
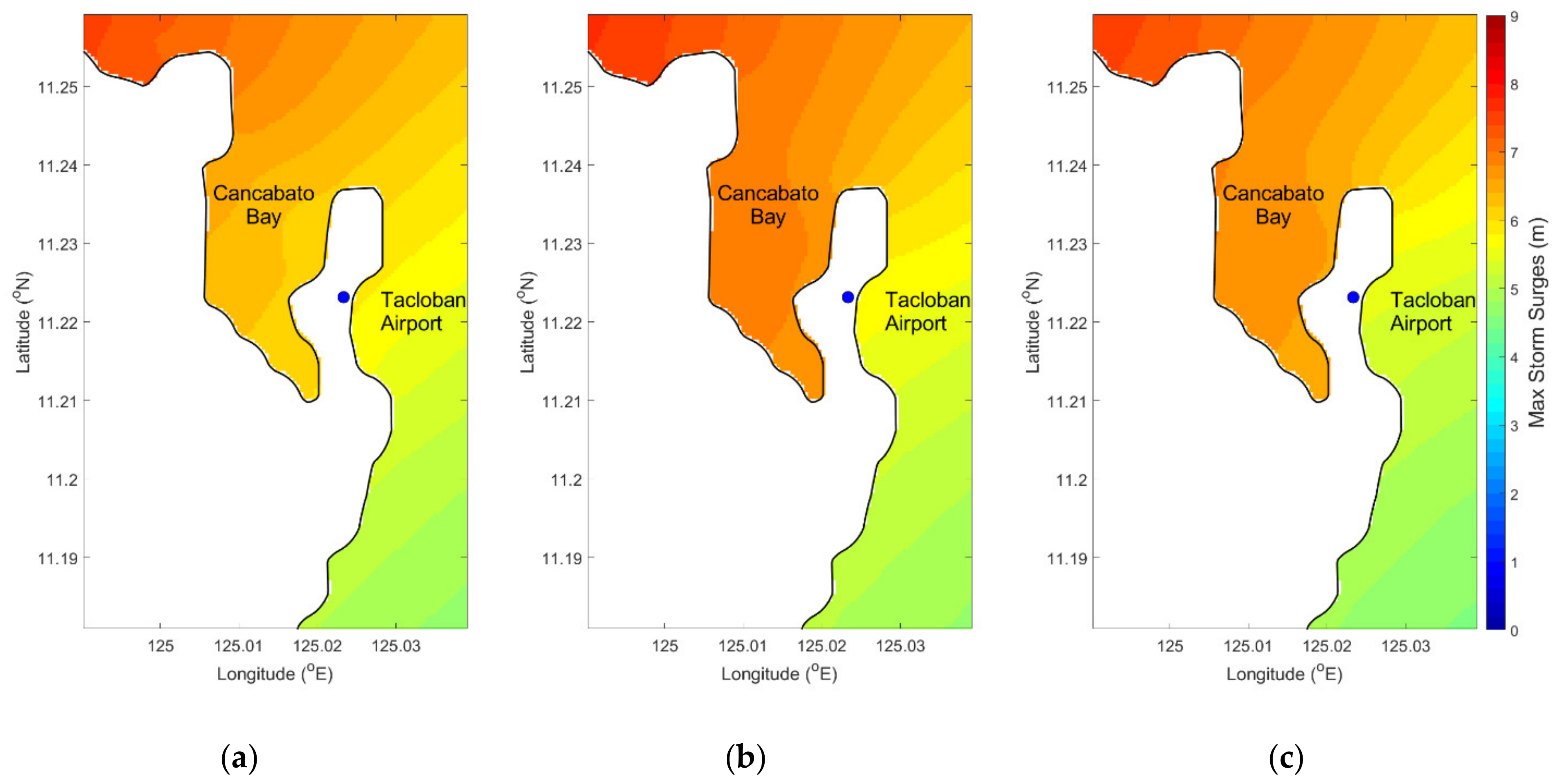
4.4. Maximum Storm Surges and Flood Depths
4.5. Time Series of Storm Surges
5. Numerical Experiments
5.1. Linear/Nolinear Equations with a Fixed or Moving Shoreline
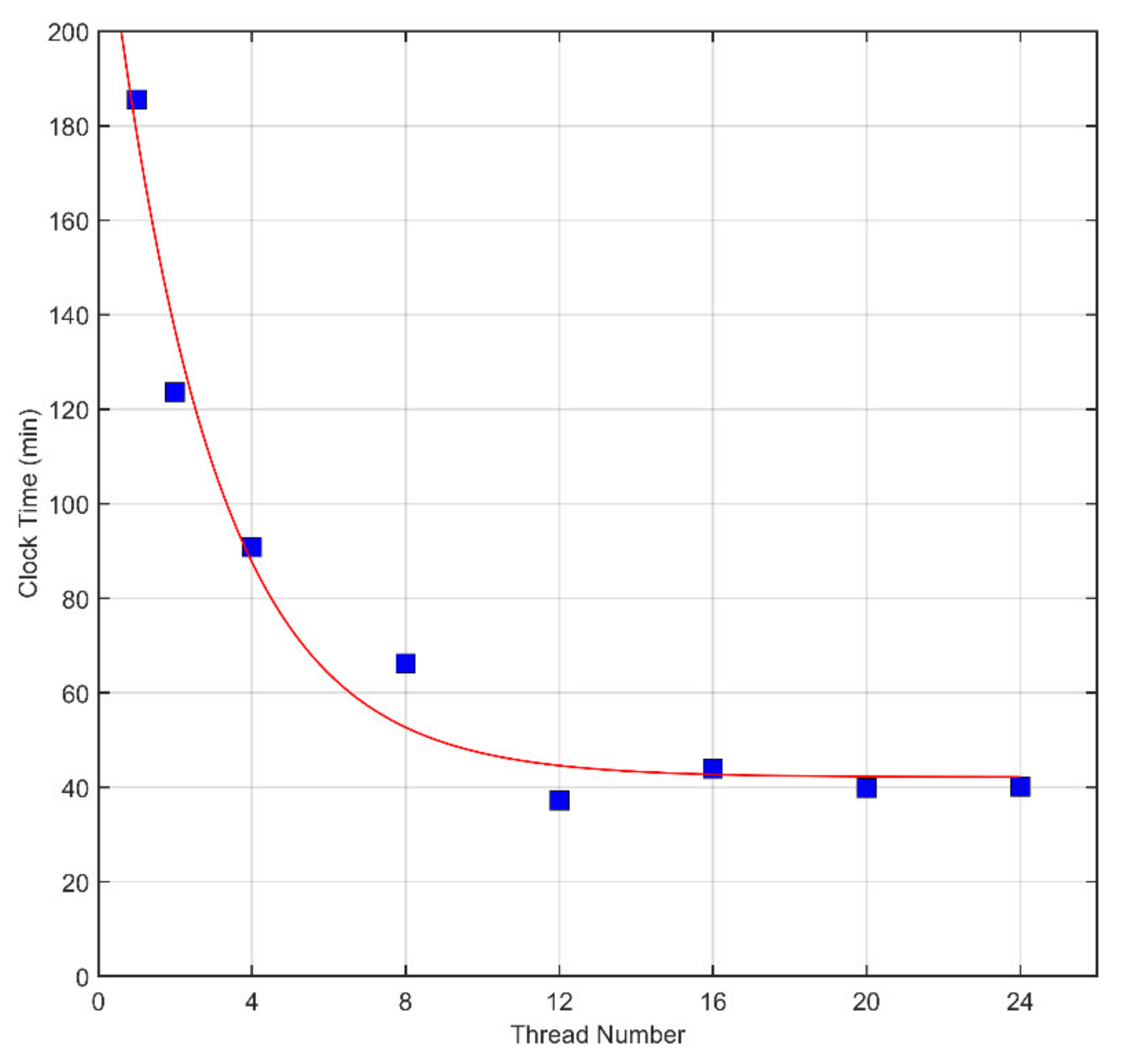
5.2. Parallel-Computing Efficiency
6. Conclusions and Future Work
6.1. Conclusions
6.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fritz, H.M.; Blount, C.; Sokoloski, R.; Singleton, J.; Fuggle, A.; McAdoo, B.G.; Moore, A.; Grass, C.; Tate, B. Hurricane Katrina storm surge distribution and field observations on the Mississippi Barrier Islands. Estuarine Coast. Shelf Sci. 2007, 74, 12–20. [Google Scholar] [CrossRef]
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Oey, L.; Xu, F.-H.; Lin, Y.-C. Sea level rise, surface warming, and the weakened buffering ability of South China Sea to strong typhoons in recent decades. Sci. Rep. 2017, 7, 7418. [Google Scholar] [CrossRef]
- Zhang, W.-Z.; Shi, F.; Hong, H.-S.; Shang, S.-P.; Kirby, J.T. Tide-surge interaction intensified by the Taiwan Strait. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.M.; Sanderson, B.; Holland, G.; Grimshaw, R. A numerical study of storm surges and tides, with application to the North Queensland coast. J. Phys. Oceanogr. 1996, 26, 2700–2711. [Google Scholar] [CrossRef] [Green Version]
- Mastenbroek, C.; Burgers, G.; Janssen, P.A.E.M. The dynamical coupling of a wave model and a storm surge model through the atmospheric boundary layer. J. Phys. Oceanogr. 1993, 23, 1856–1866. [Google Scholar] [CrossRef] [Green Version]
- Bunya, S.; Dietrich, J.C.; Westerink, J.J.; Ebersole, B.A.; Smith, J.M.; Atkinson, J.H.; Jensen, R.; Resio, D.T.; Luettich, R.A.; Dawson, C.; et al. A high-resolution coupled riverine flow, tide, wind, wind wave, and storm surge model for southern Louisiana and Mississippi. Part I: Model development and validation. Mon. Weather Rev. 2010, 138, 345–377. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, J.C.; Bunya, S.; Westerink, J.J.; Ebersole, B.A.; Smith, J.M.; Atkinson, J.H.; Jensen, R. A high-resolution coupled riverine flow, tide, wind, wind wave, and storm surge model for southern Louisiana and Mississippi. Part II: Synoptic description and analysis of Hurricanes Katrina and Rita. Mon. Weather Rev. 2010, 138, 378–404. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, A.; Gravois, U.; Zachry, B.C.; Westerink, J.J.; Hope, M.E.; Dietrich, J.; Powell, M.; Cox, A.T.; Luettich, R.A.; Dean, R.G. Origin of the Hurricane Ike forerunner surge. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Jelesnianski, C.P. SLOSH: Sea, Lake and Overland Surges from Hurricanes; U.S. Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service: Silver Spring, MD, USA, 1992; Volume 48.
- Zhang, K.; Li, Y.; Liu, H.; Rhome, J.; Forbes, C. Transition of the Coastal and Estuarine Storm Tide Model to an Operational Storm Surge Forecast Model: A Case Study of the Florida Coast. Weather Forecast. 2013, 28, 1019–1037. [Google Scholar] [CrossRef]
- Kim, S.; Mori, N.; Mase, H.; Yasuda, T. The role of sea surface drag in a coupled surge and wave model for Typhoon Haiyan 2013. Ocean Model. 2015, 96, 65–84. [Google Scholar] [CrossRef]
- Sheng, Y.P.; Alymov, V.; Paramygin, V.A. Simulation of storm surge, wave, currents, and inundation in the Outer Banks and Chesapeake Bay during Hurricane Isabel in 2003: The importance of waves. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a coupled ocean–atmosphere–wave–sediment transport (COAWST) modeling system. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef] [Green Version]
- Weisberg, R.H.; Zheng, L. Hurricane storm surge simulations comparing three-dimensional with two-dimensional formulations based on an Ivan-like storm over the Tampa Bay, Florida region. J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.J.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless cross-scale modeling with SCHISM. Ocean Model. 2016, 102, 64–81. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, J.; Zijlema, M.; Westerink, J.; Holthuijsen, L.; Dawson, C.; Luettich, R.; Jensen, R.; Smith, J.; Stelling, G.; Stone, G. Modeling hurricane waves and storm surge using integrally-coupled, scalable computations. Coast. Eng. 2011, 58, 45–65. [Google Scholar] [CrossRef]
- Cheung, K.; Phadke, A.; Wei, Y.; Rojas, R.; Douyere, Y.-M.; Martino, C.; Houston, S.; Liu, P.; Lynett, P.; Dodd, N.; et al. Modeling of storm-induced coastal flooding for emergency management. Ocean Eng. 2003, 30, 1353–1386. [Google Scholar] [CrossRef]
- Flather, R.A. Existing operational oceanography. Coast. Eng. 2000, 41, 13–40. [Google Scholar] [CrossRef]
- Hasegawa, H.; Kohno, N.; Itoh, M. Development of Storm Surge Model in Japan Meteorological Agency. In Proceedings of the 2nd JCOMM Scientific and Technical Symposium, Key West, FL, USA, 8–13 November 2015. [Google Scholar]
- Yu, Y.-C.; Chen, H.; Shih, H.-J.; Chang, C.-H.; Hsiao, S.-C.; Chen, W.-B.; Chen, Y.-M.; Su, W.-R.; Lin, L.-Y. Assessing the potential highest storm tide hazard in Taiwan based on 40-year historical typhoon surge hindcasting. Atmosphere 2019, 10, 346. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.-B.; Liu, W.-C. Assessment of storm surge inundation and potential hazard maps for the southern coast of Taiwan. Nat. Hazards 2016, 82, 591–616. [Google Scholar] [CrossRef]
- Li, N.; Yamazaki, Y.; Roeber, V.; Cheung, K.F.; Chock, G. Probabilistic mapping of storm-induced coastal inundation for climate change adaptation. Coast. Eng. 2018, 133, 126–141. [Google Scholar] [CrossRef]
- Medeiros, S.C.; Hagen, S.C. Review of wetting and drying algorithms for numerical tidal flow models. Int. J. Numer. Methods Fluids 2012, 71, 473–487. [Google Scholar] [CrossRef]
- Forbes, C.; Rhome, J.; Mattocks, C.; Taylor, A. Predicting the storm surge threat of Hurricane Sandy with the National Weather Service SLOSH Model. J. Mar. Sci. Eng. 2014, 2, 437–476. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.L.-F.; Woo, S.-B.; Cho, Y.-S. Computer Programs for Tsunami Propagation and Inundation; Cornell University: Ithaca, NY, USA, 1998. [Google Scholar]
- Liu, P.L.F.; Cho, Y.-S.; Briggs, M.J.; Kanoglu, U.; Synolakis, C.E. Runup of solitary waves on a circular Island. J. Fluid Mech. 1995, 302, 259–285. [Google Scholar] [CrossRef]
- Tsai, Y.-L.; Wu, T.-R.; Lin, C.-Y.; Lin, S.C.; Yen, E.; Lin, C.-W. Discrepancies on storm surge predictions by parametric wind model and numerical weather prediction model in a semi-enclosed bay: Case study of typhoon Haiyan. Water 2020, 12, 3326. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Fang, M.-C.; Hwung, H.-H. Transport reversal due to Typhoon Krosa in the Taiwan Strait. Open Ocean Eng. Journa 2010, 3, 143–157. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Hwung, H.-H.; Fang, M.-C. The Numerical Simulation of Storm-Surge and Coastal Flooding in Western Taiwan: A Case Study of 2007 Typhoon SEPAT. J. Shipp. Ocean. Eng. 2011, 1. [Google Scholar] [CrossRef]
- Cho, Y.-S. Numerical Simulations of Tsunami Propagation and Run-up. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1995. [Google Scholar]
- Lin, S.C.; Wu, T.-R.; Yen, E.; Chen, H.-Y.; Hsu, J.; Tsai, Y.-L.; Lee, C.-J.; Philip, L.-F.L. Development of a tsunami early warning system for the South China Sea. Ocean Eng. 2015, 100, 1–18. [Google Scholar] [CrossRef]
- Yen, E.; Lin, S.C.; Wu, T.-R.; Tsai, Y.-L.; Chung, M.-J. Knowledge-Building Approach for Tsunami Impact Analysis Aided by Citizen Science. Front. Earth Sci. 2020, 8, 315. [Google Scholar] [CrossRef]
- Wu, J. Wind-stress coefficients over sea surface from breeze to hurricane. J. Geophys. Res. Ocean. 1982, 87, 9704–9706. [Google Scholar] [CrossRef]
- WAMDI. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Power, W. COMCOT: A Tsunami Generation, Propagation and Run-Up Model; GNS Science: Lower Hutt, New Zealand, 2011. [Google Scholar]
- Briggs, M.J.; Synolakis, C.E.; Harkins, G.S.; Green, D.R. Laboratory experiments of tsunami runup on a circular island. Pure Appl. Geophys. 1995, 144, 569–593. [Google Scholar] [CrossRef]
- Titov, V.; Synolakis, C.E. Numerical modeling of tidal wave runup. J. Waterw. Port Coast. Ocean. Eng. 1998, 124, 157–171. [Google Scholar] [CrossRef]
- Lynett, P.; Wu, T.-R.; Liu, P. Modeling wave runup with depth-integrated equations. Coast. Eng. 2002, 46, 89–107. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991. [Google Scholar] [CrossRef]
- NDRRMC. Effects of Typhoon “YOLANDA” (HAIYAN); Technical Report; National Disaster Risk Reduction and Management Council: Quezon City, Philippines, 2014.
- Schiermeier, Q. Did Climate Change Cause Typhoon Haiyan? Nature 2013, 11. [Google Scholar] [CrossRef]
- Takagi, H.; Esteban, M.; Shibayama, T.; Mikami, T.; Matsumaru, R.; De Leon, M.; Thao, N.; Oyama, T.; Nakamura, R. Track analysis, simulation, and field survey of the 2013 Typhoon Haiyan storm surge. J. Flood Risk Manag. 2014, 10, 42–52. [Google Scholar] [CrossRef]
- Tajima, Y.; Yasuda, T.; Pacheco, B.M.; Cruz, E.C.; Kawasaki, K.; Nobuoka, H.; Miyamoto, M.; Asano, Y.; Arikawa, T.; Ortigas, N.M.; et al. Initial report of JSCE-PICE joint survey on the storm surge disaster caused by Typhoon Haiyan. Coast. Eng. J. 2014, 56, 1450006. [Google Scholar] [CrossRef]
- Mas, E.; Bricker, J.; Kure, S.; Adriano, B.; Yi, C.; Suppasri, A.; Koshimura, S. Field survey report and satellite image interpretation of the 2013 Super Typhoon Haiyan in the Philippines. Nat. Hazards Earth Syst. Sci. 2015, 15, 805–816. [Google Scholar] [CrossRef] [Green Version]
- Soria, J.L.A.; Switzer, A.D.; Villanoy, C.L.; Fritz, H.M.; Bilgera, P.H.T.; Cabrera, O.C.; Siringan, F.P.; Maria, Y.Y.-S.; Ramos, R.D.; Fernandez, I.Q. Repeat storm surge disasters of Typhoon Haiyan and its 1897 predecessor in the Philippines. Bull. Am. Meteorol. Soc. 2016, 97, 31–48. [Google Scholar] [CrossRef]
- Mikami, T.; Shibayama, T.; Takagi, H.; Matsumaru, R.; Esteban, M.; Thao, N.D.; Kumagaim, K. Storm surge heights and damage caused by the 2013 Typhoon Haiyan along the Leyte Gulf coast. Coast. Eng. J. 2016, 58, 1640005. [Google Scholar] [CrossRef]
- Weatherall, P.; Marks, K.M.; Jakobsson, M.; Schmitt, T.; Tani, S.; Arndt, J.E.; Rovere, M.; Chayes, D.; Ferrini, V.; Wigley, R. A new digital bathymetric model of the world’s oceans. Earth Space Sci. 2015, 2, 331–345. [Google Scholar] [CrossRef]
- Holland, G.J. An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Zu, T.; Gan, J.; Erofeeva, S.Y. Numerical study of the tide and tidal dynamics in the South China Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2008, 55, 137–154. [Google Scholar] [CrossRef]
- Jan, S.; Yang, Y.-J.; Wang, J.; Mensah, V.; Kuo, T.-H.; Chiou, M.-D.; Chern, C.-S.; Chang, M.-H.; Chien, H. Large variability of the Kuroshio at 23.75°N east of Taiwan. J. Geophys. Res. Oceans 2015, 120, 1825–1840. [Google Scholar] [CrossRef]
- Mori, N.; Kato, M.; Kim, S.; Mase, H.; Shibutani, Y.; Takemi, T.; Tsuboki, K.; Yasuda, T. Local amplification of storm surge by Super Typhoon Haiyan in Leyte Gulf. Geophys. Res. Lett. 2014, 41, 5106–5113. [Google Scholar] [CrossRef] [Green Version]
- Sepúlveda, I.; Tozer, B.; Haase, J.S.; Liu, P.L.; Grigoriu, M. Modeling uncertainties of bathymetry predicted with satellite altimetry data and application to tsunami hazard assessments. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019735. [Google Scholar] [CrossRef]
- Kowalik, Z.; Murty, T.S. Chapter III Two-Dimensional Numerical Models. In Numerical Modeling of Ocean Dynamics; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1993; pp. 105–215. [Google Scholar] [CrossRef]


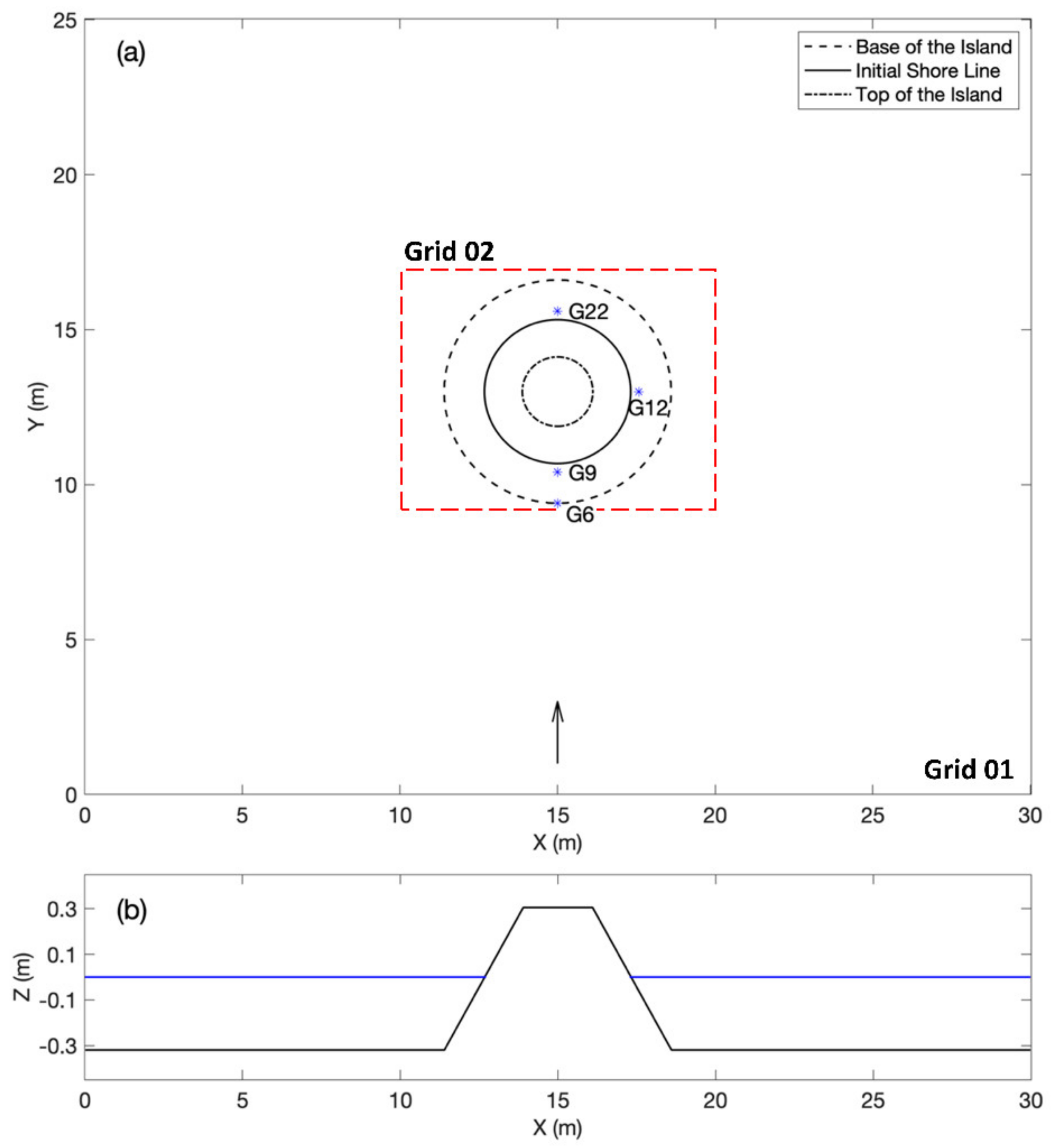



| Gauge Number | X Location (Unit: m) | Y Location (Unit: m) |
|---|---|---|
| G6 | 15.00 | 9.40 |
| G9 | 15.00 | 10.40 |
| G16 | 17.58 | 13.00 |
| G22 | 15.00 | 15.60 |
| Domain | Sea-Level Pressure/Wind Shear Stress | Advection Term | Coriolis Force Term | Bottom Friction | Horizontal Eddy Diffusion Term | Moving Boundary Scheme |
|---|---|---|---|---|---|---|
| D01 | O | X | O | O | O | X |
| D02 | O | O | O | O | O | X |
| D03 | O | O | X | O | X | O |
| Field Survey Points | Longitude (Unit: °E) | Latitude (Unit: °N) | Measured Flood Depth (Unit: m) | Predicted Flood Depth (Unit: m) |
|---|---|---|---|---|
| P1 | 125.0247 | 11.2005 | 5.9 | 3.095 |
| P2 | 125.0224 | 11.2271 | 3.5 | 3.783 |
| P3 | 125.0004 | 11.2457 | 3.5 | 0.891 |
| Thread Number | 1 | 2 | 4 | 8 | 12 | 16 | 20 | 24 |
| Clock Time (Unit: min) | 185.47 | 123.58 | 90.87 | 66.17 | 37.22 | 43.95 | 39.83 | 40.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, Y.-L.; Wu, T.-R.; Yen, E.; Lin, C.-Y.; Lin, S.C. Parallel-Computing Two-Way Grid-Nested Storm Surge Model with a Moving Boundary Scheme and Case Study of the 2013 Super Typhoon Haiyan. Water 2022, 14, 547. https://doi.org/10.3390/w14040547
Tsai Y-L, Wu T-R, Yen E, Lin C-Y, Lin SC. Parallel-Computing Two-Way Grid-Nested Storm Surge Model with a Moving Boundary Scheme and Case Study of the 2013 Super Typhoon Haiyan. Water. 2022; 14(4):547. https://doi.org/10.3390/w14040547
Chicago/Turabian StyleTsai, Yu-Lin, Tso-Ren Wu, Eric Yen, Chuan-Yao Lin, and Simon C. Lin. 2022. "Parallel-Computing Two-Way Grid-Nested Storm Surge Model with a Moving Boundary Scheme and Case Study of the 2013 Super Typhoon Haiyan" Water 14, no. 4: 547. https://doi.org/10.3390/w14040547
APA StyleTsai, Y.-L., Wu, T.-R., Yen, E., Lin, C.-Y., & Lin, S. C. (2022). Parallel-Computing Two-Way Grid-Nested Storm Surge Model with a Moving Boundary Scheme and Case Study of the 2013 Super Typhoon Haiyan. Water, 14(4), 547. https://doi.org/10.3390/w14040547







