Abstract
The research into rainfall-runoff plays a very important role in water resource management. However, runoff simulation is a challenging task due to its complex formation mechanism, time-varying characteristics and nonlinear hydrological dynamic process. In this study, a nonlinear autoregressive model with exogenous input (NARX) is used to simulate the runoff in the Linyi watershed located in the northeastern part of the Huaihe river basin. In order to better evaluate the performance of NARX, a distributed hydrological model, TOPX, is used to simulate the discharge as a reference, and runoff classification by cluster analysis is used to further improve the accuracy of runoff simulation. Based on the four statistics indexes of the Nash–Sutcliffe efficiency (NSE), correlation coefficient (CC), root mean square error (RMSE) and mean relative bias (Bias), the NARX model is capable of simulating the rainfall-runoff dynamic process satisfactorily, although there is a little underestimation of the peak flow. After runoff classification, underestimation has been improved, and discharge simulation driven by NARX based on runoff classification (C-NARX) is well consistent with the observation. It is feasible to take it as a promising method, which also can be seen as a good reference and replacement for the current rainfall-runoff simulation.
1. Introduction
The study of rainfall-runoff is a main component of hydrology research and plays a very important role in water resource management, such as controlling floods, mitigating drought, irrigating agriculture, and optimizing reservoir operation [1,2,3]. Rainfall-runoff simulation and prediction is a difficult problem because the formation mechanism and influencing factors of discharge are complex and changeable, resulting in an obvious time-varying effect of runoff sequencing.
The watershed hydrological model is an important means of hydrology research which can accurately predict hydrological dynamics and flow processes [4]. The hydrological model with a physical basis can provide solid foundations for forecasting streamflow based on historical hydrological and meteorological data. With the rapid development of information technology, some physical-mechanistic hydrology models such as System Hydrological European (SHE), Soil and Water Assessment Tool (SWAT), Variable Infiltration Capacity (VIC), Topography based Hydrological Model (TOPMODEL) and Xinanjiang Model (XAJ) have been developed and widely used in hydrological simulation, forecasting and prediction, etc. [5,6,7,8,9]. However, the hydrological process is a highly complex, random and nonlinear system which involves many uncertain factors [10,11,12]. In order to obtain more accurate results of simulation and prediction, an in-depth understanding of the model is widely sought after, such as runoff generation and concentration mechanisms, model inputs, hydrological structure, parameter optimization and watershed responses [13,14,15,16,17]. Its complex physical mechanism, the higher amount of input variables and parameter calibration limit the application of the hydrological model, especially in areas where data are scarce.
To overcome the limitations of hydrological models, hydrologists tried to simulate the hydrological processes by using new methods, such as grey systems, fuzzy mathematics and an artificial neural network (ANN) based on data-driven techniques [18,19]. With the fast development of computer technology, ANN has been successfully applied in many fields due to its unique advantages of nonlinearity, non-convexity and self-adaptability [20,21,22]. The rainfall-runoff process is a highly nonlinear, time-varying, spatially uneven and dynamically uncertain process, and therefore ANN has been widely used to handle water resource problems such as rainfall forecasting and urban drainage systems [23,24,25]. A series of researches are used to explore the applicability of static ANNs, such as typical back propagation neural networks (BPNN) and extreme learning machines (ELM) [26,27,28]. However, a static neural network might fail to predict the dynamical hydrological process because it lacks the ability of memory and association for historical input and output values and cannot reflect the characteristics of inherent tempo-spatial variations from a runoff series [29]. Consequently, the comprehensive analysis of hydrological processes remains a great challenge to overcome.
The application of the concept of signal delay in neurobiological information processing has led to the rapid development of dynamic neural networks [30]. Taking the time delay into account through feedback connections, recurrent neural networks (RNN) are more powerful and plausible than other static neural networks, can be trained to learn time-varying patterns and are regarded as an effective approach to simulate complex dynamic hydrological processes [31,32]. The Elman neural network (ENN), long short-term memory (LSTM) and the nonlinear autoregressive model with exogenous input (NARX) are widely used RNN models in hydrological time series forecasts. ENN can learn any dynamic input–output relationship arbitrarily well. However, it uses simplified derivative calculations at the expense of less reliable learning [33,34]. An LSTM network adopts memory blocks that are composed of an input gate, an output gate, a memory cell and a forget gate, and tends to do better on a volatile time series with more of a stationary component [35,36]. The NARX model adds loops to feed the previous input and output back to the network, which can be efficiently applied to the long-term prediction of a nonlinear time series for streamflow forecasting and prediction [37,38]. Rjeily et al. utilized the NARX neural network to develop a flood forecasting system with urban drainage [39]. Wei et al. established urban waterlogging pre-warning systems based on coupling RBF-NARX neural networks [40]. Di Nunno et al. used NARX to predict the spring flows in the Umbria region [41]. Yang et al. carried out a real-time reservoir operation using LSTM and NARX based on genetic algorithm (GA-NARX) neural networks and inflow forecast from a hydrological model [42]. Thapa et al. performed snowmelt-driven streamflow prediction using machine learning techniques in a Himalayan basin [43]. These results showed that the NARX neural network is effective for urban flood forecasting and waterlogging pre-warning, snowmelt-driven streamflow prediction, reservoir simulation and spring flow prediction. However, there are few applications for rainfall-runoff simulation and forecast on a hilly watershed scale, especially in daily runoff simulation throughout the year in the Huai river basin.
Compared to other machine learning algorithms, the NARX model can be efficiently applied to the prediction of nonlinear time series and allow for a simpler physical interpretation of the parameter investigated. In addition, it can also provide accurate predictions even for short time series because it considers the recursive update of predictors and model parameters. At the same time, NARX networks have faster convergence to find the proper weights than other ANN approaches because the variable slope for the sigmoidal activation function accelerates the ANN training dramatically. Although the NARX model has been successfully applied in hydrological research, flow data are rarely classified to train networks in the simulation of rainfall-runoff processes. Discharge data mined together for the training network will smooth some extreme values and result in bias errors. For example, the simulation result in the semi-humid season is generally not ideal for extreme conditions due to the large difference in runoff values in the drought season, semi-humid season and flood season. Therefore, it is necessary to classify the runoff before the training network.
In this study, we intend to investigate the reliability and accuracy of the NARX model for rainfall-runoff process simulation. Firstly, runoff values are classified based on hierarchical cluster analysis, and the NARX model is constructed by using rainfall, evapotranspiration and runoff data in the study region. Next, the effectiveness of the NARX model is verified and tested for rainfall-runoff simulation by using the distributed hydrological model TOPX as a reference. Thirdly, compared to ungrouping runoff series, the performance of the NARX model is further evaluated by using runoff classification data. The results of this study are expected to improve the accuracy of the discharge based on the NARX model and runoff classification and to further provide an effective alternative method for runoff simulation and forecast.
2. Materials and Methods
2.1. Study Area
The Linyi watershed (117°35′–118°44′ E, 34°59′–36°18′ N), located in the northeastern part of the Huaihe river basin, lies in the transition zone between the mountains of south-central and the hills of eastern Shandong. As the hydrological control station for the outlet section of the basin, Linyi station covers a drainage area of 10,152 km2, accounting for 3.7% of the total area of the Huaihe basin. The region mainly consists of plains, hills and mountains, which range from 57 m to 1125 m in elevation. The basin belongs to a typical continent monsoon climate which is cold and windy in winter, hot and rainy in summer, and mild in spring and autumn. The average annual temperature ranges from 11.8 ℃ to 13.3 ℃, and the mean annual precipitation/evaporation is approximately 830 mm and 839 mm. Precipitation also has a distinct inter-annual and seasonal distribution, which accounts for 50–80% of the annual total during May–September. Flood disasters are common in the research areas because of the large terrain slopes and rapid water flow collection, which exceeds the flood discharge capacity of the downstream rivers. The spatial distribution map of the station and elevation in the interest area is shown in Figure 1.
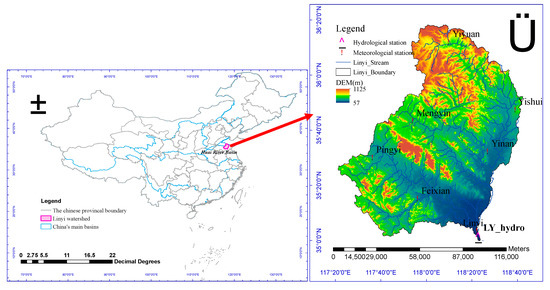
Figure 1.
Spatial map of the Linyi watershed, and meteorological stations and hydrological control station.
In this study, daily precipitation and daily evapotranspiration of the meteorological stations have been obtained from the Linyi meteorological administration. Daily discharge data of the hydrological control station are from the Linyi hydrographic bureau. Seven representative stations in the Linyi watershed have been considered in this paper. The average area’s rainfall and evapotranspiration are interpolated and estimated from rain gauges and pan data by using the ordinary Kriging interpolation method, which is an advanced geostatistical procedure based on the regionalized variable theory. The precipitation, evapotranspiration and discharge data are from 2001 to 2008. ASTER GDEM with 30 m spatial resolution can be downloaded from the website (http://www.gdem.aster.ersdac.or.jp/index.jsp/, accessed on 20 March 2022). In order to match the spatial resolution of the distributed hydrological model, a DEM with 30 m spatial resolution needs to resample to 1 km.
2.2. Methodology
2.2.1. Cluster Analysis
Cluster analysis has been widely used in the hydrological or climatological field as a classification method of statistical multivariate analysis [44]. Considering the practical convenience, the statistical characteristics of each monthly flow series are calculated in monthly units in this study. Four variables from the Linyi station, namely monthly average runoff, monthly maximum runoff, monthly minimum runoff and monthly standard deviation of runoff, are chosen to be divided into different groups based on the cluster analysis. Hierarchical cluster analysis was performed by using the Statistical Analysis System (SAS) software in this study (Table 1). Firstly, the data processing method of the normalization: taking into account the sensitivity of cluster analysis methods to the observed scales of the variables, these variables are normalized and rescaled to 0 to 1 range so that their ranges were comparable.
where is the normalized value, is the monthly runoff data at the ith month, and denote the monthly maximum and minimum runoff values, respectively.

Table 1.
The statistical characteristics based on monthly discharge in Linyi hydrological station.
Secondly, the selection of cluster method. There are two main methods in SAS software—the average linkage method and Ward’s method—which are similar and sensitive to redundant information based on the Euclidean distance. The core idea of cluster analysis tends to join clusters that contain a small number of sites and are strongly biased in favor of producing clusters containing approximately equal numbers of sites. The main difference between the two methods is the determination of distance, which are, respectively, the average Euclidean distance from the average linkage method and the squared Euclidean distance from Ward’s method [44]. Ward’s method is selected in this paper. Thirdly, the whole runoff series is divided into several groups by cluster analysis. Considering the convenience and feasibility of the practical application, the final three classifications are shown in Table 2. More details on cluster analysis can be found in [45].

Table 2.
The runoff classification based on cluster analysis.
2.2.2. NARX Model
The NARX network is a recurrent dynamic network with feedback connections enclosing several layers of the network. The NARX model is based on the linear ARX model, which is commonly used in time-series modeling. The defining equation for the NARX model is:
where t is the time, is the prediction, represent the previous observations of y; represent the external input data with any time delay n, n and m are the input delay and output delay, respectively, while m ≥ 1, n ≥ 1. The nonlinear function f (·) represents the network architecture, which is generally approximated by using a feedforward neural network, like a multi-layer perceptron network. The resulting connection architecture is called the NARX network [37].
The NARX model is composed of an input layer, hidden layer and output layer, each consisting of interlinked neurons (Figure 2). The input layer consists of the input parameters and allows the reception of the data into the network, which is presented to the hidden layers to progressively process it and gives a result in the output layer. The output is fed back to the input of the feedforward neural network as part of the standard NARX architecture. Precipitation and evapotranspiration are selected as the input parameters because the runoff is directly related to the net rainfall and discharge. Comprehensive consideration of the surface runoff routing time and model input components, precipitation P(t), P(t − 1),…, P(t − 5), evapotranspiration E(t), E(t − 1),…, E(t − 5) and discharge Q(t − 1), Q(t − 2),…, Q(t − 5) are chosen as input parameters while the output was represented by the predicted discharge Q(t). For the hidden layer, a sigmoidal activation function is selected in the NARX model, which can accelerate the ANN training. The number of hidden nodes was obtained by trial and error processes. The number of hidden neurons was determined by the empirical equation given by Wanas et al. [46].
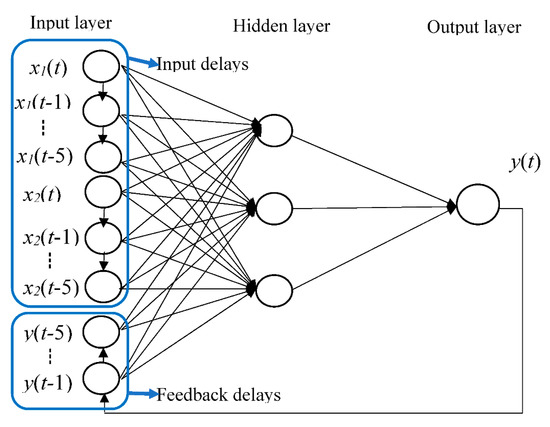
Figure 2.
The structure of the NARX model.
For the output layer, series-parallel architectures are created in which the true output is used instead of feeding back the estimated output to make the input to the feedforward network more accurate. The NARX model can be optimized based on the Levenberg–Marquardt algorithm, which combines the advantages of the Gauss–Newton algorithm and gradient descent method. The maximum number of epochs is settled to 1000, and the Levenberg–Marquardt adjustment parameter and error gradient are, respectively, settled equally to 10−10 and 10−7. If one of the above-mentioned parameters reaches the goals, the NARX process is stopped. More details can be found in [43,47]. The output variable is calculated by the following formula:
where x is the hidden layer data, w represents the weight, b is the bias, N is the number of nodes in the previous layer, and Y is the output variable.
The precipitation, evapotranspiration and discharge data from the observation were divided into three parts: 62.5% of 2922 time series are randomly selected for training, 12.5% for verification and 25% for testing. That is, data from 2001 to 2005 as training samples, data from 2006 as validation samples and data from 2007 to 2008 as test samples. Considering the faster convergence and the influence of extreme values on the training network, the input data were normalized to the range 0–1 before training and rescaled to the original values after training. The key parameter of the NARX structure has a great influence on the simulation results of the network model. In this work, from what has been studied and trained above, the optimal architecture of the NARX model was obtained by 2 input variables, 1 hidden layer, 10 hidden neurons, 5-day delays and 1 output target. The performance of the NARX model is evaluated by the mean square error.
2.2.3. Hydrological Model Introduction
The distributed hydrological model TOPX is selected to simulate the hydrological process as a reference in this paper, which is developed by professor Zhang’s and Yong’s research team [48]. The core idea of TOPX is based on the TOPMODEL’s topographic index (TI) concept and the XAJ model’s water balance. TOPX mainly includes seven parts, namely, the soil water storage curve, dynamic change of soil moisture, surface runoff and subsurface runoff, base-flow and Muskingum merge flow and discharge. The detailed theoretical basis, structure and physical parameters of the TOPX model can be found in [48,49]. Runoff, soil moisture and merge flow of TOPX will be highlighted and described as follows.
A revised SIMTOP runoff generation scheme is adopted in this study, which is more accurate in describing topographic information and the temporal and spatial distribution of intermediate variables. It is defined as follows:
where Rs and Rsb are surface runoff and subsurface runoff, respectively; Fsat is the percentage of the saturated area; is the soil moisture deficit depth; Qwat is the net rainfall; Rsb,max is the maximum subsurface runoff when equals zero; f is the attenuation coefficient of soil; Fsat is determined by the two-parameter power function, which is established by the relationship between TI and soil moisture.
The calculation of soil moisture is based on the three-layer soil evapotranspiration scheme from the XAJ model. The dynamic change process of soil moisture of each layer on a different grid can be obtained based on the iterative calculation of soil moisture and evapotranspiration. is a crucial variable connecting surface runoff and subsurface runoff, which is closely related to the dynamic change of soil moisture, which not only simplifies the calculation but also satisfies the precision required by the model. It is defined as follows:
where WM is the areal mean soil water storage capacity, which includes soil moisture in the upper, lower and deep layers; is the soil water storage capacity of the three layers at the ith grid. Finally, the surface runoff and subsurface runoff can be calculated based on the soil moisture deficit.
Runoff concentration mainly includes overland flow concentration, river network flow and subsurface flow concentration which are computed based on the empirical unit hydrograph method, Muskingum channel routing method and linear reservoir parameter method, respectively. Finally, the total discharge of the outlet is obtained by the above runoff concentration.
2.2.4. Model Performance Evaluation
Four metrics of root mean square error (RMSE), correlation coefficient (CC), mean relative bias (Bias) and Nash–Sutcliffe efficiency (NSE) are used as performance indicators of NARX and the hydrological model TOPX. NSE describes the statistical properties of the models, which are widely used to evaluate the accuracy of the hydrological model [50,51]. CC and NSE are two normalized statistical indexes and are closer to 1, indicating a better simulation. The formula of these indexes are listed as follows:
where n is the number of samples; Robs(i) and Rsim(i) are the observed and simulated discharge at the ith day; obs and sim are the mean values of the observed and simulated discharge for the time series.
3. Results
3.1. Model Performance Comparison in Runoff Simulation
The performances of the NARX and NARX based on runoff classification (C-NARX) models are summarized and evaluated by means of the indexes of NSE, CC, RMSE and bias in Table 3. Results elucidated that the precision of rainfall-runoff simulation based on the C-NARX model is better than that of the NARX model in training, validation and test periods, especially during the dry season with a significant improvement of NSE and CC from 0.435 to 0.947, and from 0.682 to 0.973, respectively, in the training period. It can be also seen from Table 3 that the accuracy of discharge simulation is better in the training period than in the test period, which may be attributed to the large difference between the training and test samples. For different seasons, as is shown in Table 3, runoff classification has the greatest influence on the drought season in this study. Take, for example, the training period and scatter plots of the daily discharge estimated by the NARX and C-NARX models; the observed values are shown in Figure 3, which is further evidence of the correlation between simulation and observation. From the CC value and the scattered data distributed on both sides of the line y = x, we can see that correlation is further improved, and the estimation is in good agreement with the observation based on the C-NARX model.

Table 3.
Performance of the NARX and C-NARX models based on the runoff classification.
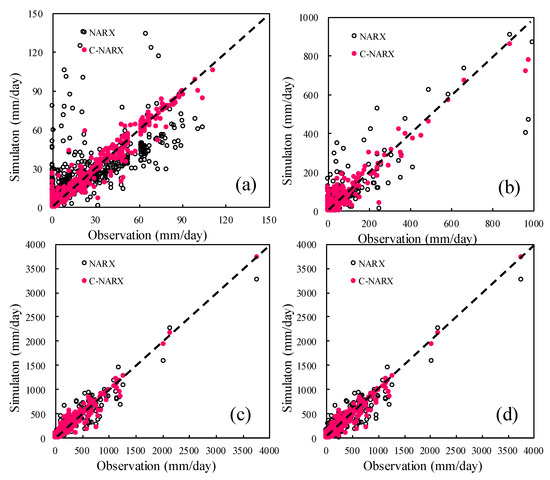
Figure 3.
Comparison of simulation and observation values between NARX and C-NARX models in training period with the dry season (a), semi-humid season (b), humid season (c) and all years (d).
To better evaluate the NARX-based rainfall-runoff models, we compare the performance of the models under different runoff classifications. The runoff simulation driven by the NARX and C-NARX models is shown in Figure 4 during the dry season, semi-humid season and humid season in this study. It can be seen from Figure 4b,c that the rainfall-runoff process line simulated by the NARX model is basically consistent with the observation in the semi-humid and humid seasons, which indicates that the NARX model performs well. As is shown in Figure 4, it further validates that the C-NARX model is more suitable and efficient for daily runoff forecasting than the NARX model, especially during the arid season, which also indicates runoff classification is helpful to improve the precision of discharge simulation. From what has been displayed above, the C-NARX model is feasible to effectively simulate the hydrological dynamic characteristic of the daily runoff and to reflect the complex nonlinear runoff regular pattern in the studied watershed.
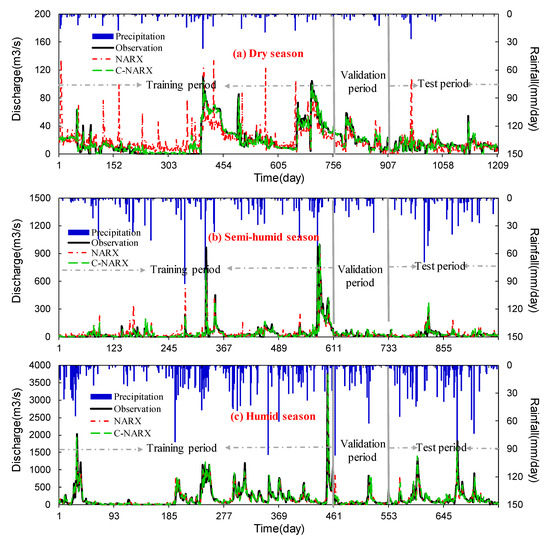
Figure 4.
Discharge results based on the NARX and C-NARX models in the (a) dry season, (b) semi-humid season and (c) humid season.
3.2. Rainfall-Runoff Simulation by TOPX Model
In order to validate the performance of the NARX model, the distributed hydrological model TOPX is used to simulate the rainfall-runoff processes as a reference in this study. In the TOPX model, the data from 2001 to 2005 are selected to calibrate the sensitive parameters in the training period, and those from 2007 to 2008 are used to validate the preformation of the model in the test period. The daily area’s precipitation can be obtained by the ordinary kriging interpolation algorithm, and the sensitive parameters of the model are determined based on parameter optimization. The optimal parameter values are listed in Table 4 during the calibration period.

Table 4.
The sensitive parameters and their optimal values in the TOPX model.
The rainfall-runoff process simulation driven by the TOPX model is shown in Figure 5 in the study watershed. As is illustrated in Figure 5, the runoff simulation by TOPX is basically satisfactory with the NSE of 0.713 in the calibration or training period, and the rainfall-runoff process line is consistent with the observation as a whole. The results indicate that the TOPX model performs well, although it has a slight underestimation of the peak flow, and the peak occurrence time captured by TOPX slightly lags behind the observation. It can be seen from Figure 5 that the simulated results are better in flood years with abundant rainfall than in drought years, especially in the rainy season. For example, TOPX can capture the peak flow from 2003, 2004 and 2005, and the peak flow does not show in the flow process line from the dry year of 2002. In order to verify the adaptability of the TOPX model in the sub-humid and semi-arid regions, the discharge is simulated by TOPX with the same calibrated parameters of Table 4 in 2007–2008. It can be shown from Figure 5 that the simulated result of the hydrologic process during the test period is similar to the calibration period, and is moreover slightly superior to the calibrated term, which may be attributed to the intermediate and uniform precipitation of a sub-humid year. From what has been shown above, TOPX distributed hydrological model can perform well and obtain a satisfying result in daily rainfall-runoff process hydrographs.
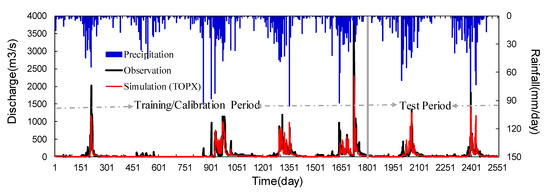
Figure 5.
Runoff simulation results driven by TOPX models in the training or calibration period.
3.3. The Comparison of Discharge Simulation by NARX and TOPX Model
The performance of the NARX, C-NARX and TOPX models are further compared and evaluated by means of the indexes of NSE, CC, RMSE and bias in Table 5. We can see from Table 5 that the above three models driven by a rain gauge perform satisfactorily in the training and test periods, and the accuracy of the runoff simulation decreases in the C-NARX, NARX and TOPX models. For example, it can be shown that during the test period, the statistical results from the TOPX model are, respectively, an NSE of 0.816, a CC of 0.897, an RMSE of 1.018, and a bias of 0.418; they are more performance-driven in the NARX model than the TOPX model and have the highest NSE (0.910) and CC (0.943), and the smallest RMSE (0.707) and bias (0.329) are obtained from C-NARX model after runoff classification.

Table 5.
Comparison of the simulation results based on the TOPX, NARX and C-NARX models.
Figure 6 and Figure 7, respectively, compare the process line of discharge simulation driven by the NARX, C-NARX and TOPX models during the training and test periods in this study. As is shown in Figure 6, the rainfall-runoff hydrological process graph simulated by the three models agrees with the observation as a whole, and the precision of simulation from C-NARX after runoff classification is the highest (NSE = 0.949) among the above models. It can also be seen from Figure 7 that the results driven by the three models are similar to those in Figure 6, and, moreover, are slightly superior to Figure 6 in the study area. As a data-driven model, NARX uses mathematical equations and the network architecture to replace the complex hydrodynamic process of physical models, which can be regarded as a parameter optimization of runoff simulation, and thus the results will obey the basic laws of physics. At the same time, taking into account the historical input and output data, and the feedback from the output, the discharge simulation results driven by NARX can perform well, especially in arid years. From what has been shown above, the C-NARX and NARX models are more efficient for daily runoff simulation than TOPX, which can also be seen as a good reference and replacement for the current rainfall-runoff simulation.
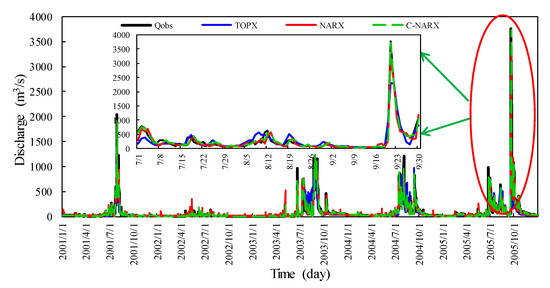
Figure 6.
The comparison of runoff simulation results driven by the NARX, C-NARX and TOPX models in the training or calibration period.
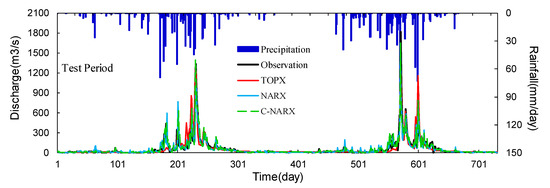
Figure 7.
The comparison of runoff simulation results driven by the three models in the test period.
4. Discussion
The results of this research are valuable for rainfall-runoff simulation and obtaining an alternative method in the study area, especially in areas where data are scarce. However, some issues may require more in-depth study in the future.
Research has shown that distributed hydrological model TOPX performs well in the study area as a whole. However, the flow does not have a good response to rainfall events in some cases. Therefore, some problems may be discussed as follows. For example, the TOPX model did not simulate the flood peak of the rainfall-runoff process from 2002 and May 2003. There are two possible reasons for this: one is attributed to the prophase soil water content. Discharge is not formed in the short term after a long drought because the rainfall is mainly used to meet the demand for evapotranspiration and soil storage, which is similar to some research [49,52]. The other reason may be related to the mechanism of saturation excess runoff of the TOPX model, which is more suitable and efficient for humid and semi-humid regions than arid and semi-arid regions, which is in accordance with previous research and theories [48,49].
On account of adding loops to feed the previous input and output back to the network, NARX can satisfactorily simulate the hydrological dynamic process, which can accurately reflect the complex nonlinear runoff generation and convergence mechanism of the watershed. Although there is a slight underestimation of the flood peak, the discharge simulation is generally consistent with the observation, which is similar to some studies in which NARX has been successfully used in many catchment areas [42]. The underestimation of peak flow may be caused by the sigmoidal activation function. For sigmoidal functions, the absolute value of the independent variable increases and the slope gradually decreases to zero, which indicates that there is an obvious deviation when a higher or lower flow is transformed by activation functions [53]. In addition, another reason may be the insufficient training of the model with a limited high and low flow series because the intermediate flow dataset is far higher than the data set at both ends. Considering the great difference in runoff generation mechanism among different rainfalls, it is necessary to extract the flow data with similar and relative homogeneity based on runoff classification, so as to construct a local network to improve the performance of the model. This is the main reason why NARX based on runoff classification can further improve the accuracy of discharge simulation.
From what has been discussed above, the results of runoff simulation driven by the NARX and TOPX models are slightly better in the test period than in the training/calibration period, which may be attributed to the large difference between the training and the test samples. In the training period, the samples mainly indicate less rainfall in the arid year of 2002, intermediate and uniform precipitation in the sub-humid years (2001, 2003 and 2004) and abundant rainfall in the flood year of 2005. In the test period, most of the samples came from sub-humid years with moderate rainfall (2006 and 2007), and the uniformity and consistency of the samples obtain good runoff simulation results. So, the adaptability of calibrated parameters is affected by the sample differences, further resulting in a slight simulation effect, which is similar to [52,54], whose findings revealed hydrological model parameters are related to the characteristics of samples such as the shape, size and number of flood peaks.
As recommended by previous studies, the model performance can be judged “satisfactory” for flow simulations if the daily CC is greater than 0.84, the NSE is greater than 0.50, −15% < bias < 15% and the RMSE is less than half of the standard deviation of the observed data for watershed-scale models [50,55,56]. According to the above-judged criterion, the performance of NARX and C-NARX is basically satisfactory, and the model can efficiently simulate the rainfall-runoff dynamic process. Although the bias is slightly larger, there is a higher NSE and CC in the NARX and C-NARX models. Therefore, the two RNN models can meet the demand for runoff simulation in the study region. At the same time, it is inevitable to have some errors due to the limited data collected in this study. So, the longer the data series, the greater the need for regional and deeper research to illustrate the superiority of this method in the future.
5. Conclusions
The major work of this study investigated the applicability of the NARX model for rainfall-runoff simulation in research watersheds. In order to better evaluate and validate the performance of NARX, the distributed hydrological model TOPX is used to simulate the discharge as a reference, and runoff classification based on cluster analysis is used to further improve the accuracy of runoff simulation driven by the C-NARX model in this study. The main conclusions are summarized as follows:
- (1)
- The NARX model is capable of simulating the rainfall-runoff process satisfactorily, capturing the flood peak flow and peak occurrence time properly and reflecting complex nonlinear hydrological dynamin rules based on the four criteria of NSE, CC, RMSE and bias in this study area. Although there is a little underestimation of the peak flow, the discharge simulation is generally consistent with the observation.
- (2)
- By the runoff classification based on cluster analysis, the accuracy of the runoff simulation is further improved due to overcoming the great difference in runoff generation mechanisms caused by different rainfalls. The performance of C-NARX is better than the NARX model, especially during the arid season. In addition, the underestimation of peak flow has also been improved by runoff classification in this study.
- (3)
- Compared with the hydrological model TOPX, the performance of daily runoff simulations driven by the NARX and C-NARX models is better and more efficient in the study watershed. It is feasible to take it as a promising method, which also can be seen as a good reference and replacement for the current rainfall-runoff simulation.
Good results are obtained for rainfall-runoff simulation through NARX based on the runoff classification in the study area. However, some issues may require more in-depth study in the future. For example, there is an underestimation of peak flood flow based on the NARX model, which may be related to the variable slope for the sigmoidal activation function. The selection of proper weights is important for NARX to perform. Therefore, improvements to the NARX algorithm such as the selection of function and proper weights must be considered in future research. At the same time, insufficient training data with the limited high and low flow series may be affected by the results of runoff simulation. So, it is hoped that more and longer data series can be collected in the next step, which will be used to illustrate the superiority of this method.
The key message we wish to convey in this study is that rainfall-runoff simulation based on the NARX model has the advantages of nonlinearity, recursive updates of predictors and faster convergence to reflect the time-varying characteristics and nonlinear hydrological dynamic processes. The NARX model is feasible to effectively simulate the hydrological dynamic characteristic of the daily runoff in the basin as a promising and efficient method. Improving the accuracy of the runoff prediction based on the NARX moded is of great significance to hydrological forecasting. The research is valuable and greatly significant for providing a new perspective on effective flood control, optimizing reservoir operation and water resource management.
Author Contributions
All authors contributed substantially and equally towards the success of this study, proofread the final manuscript, and approved it for publication. For research articles with several authors, Conceptualization, Y.S. and J.Z.; methodology, Y.S. and J.X; validation, Y.S., J.Z. and J.X.; formal analysis, A.F.; investigation, M.L.; data curation, J.Z.; writing—original draft preparation, Y.S.; writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financially supported by the Meteorological Open Research Fund in Huaihe River Basin (HRM201702), by the Special Fund for Natural Science Foundation of Jiangsu province (BK20141001), by the National Key Research and Development Program of China (No. 2021YFC3201101), by the China Postdoctoral Science Foundation (Nos. 2020T130309 and 2019M651892), Jiangsu Water Resources Science and Technology Project (Nos. 2020022 and 2021024).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors are grateful to Linyi Meteorological Bureau and Linyi Hydrographic Bureau of China for providing observation data at sites based on project cooperation. The authors would like to acknowledge the anonymous reviewers for their thoughtful comments and suggestions.
Conflicts of Interest
The authors declare that they have no conflict of interests.
References
- Liu, Y.; Bralts, V.F.; Engel, B.A. Evaluating the effectiveness of management practices on hydrology and water quality at watershed scale with a rainfall-runoff model. Sci. Total Environ. 2015, 511, 298–308. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Fu, A.; Zhao, J.; Xu, J.; Wu, J. Improving quantitative precipitation estimates by radar-rain gauge merging and an integration algorithm in the Yishu River catchment, China. Theor. Appl. Climatol. 2021, 144, 611–623. [Google Scholar] [CrossRef]
- Shi, Z.; Shen, Q.; Tan, Q.; Li, T. Development of Integrated Flooding Early Warning and Rainfall Runoff Management Platform for Downtown Area of Shanghai. Sustainability 2021, 13, 11250. [Google Scholar] [CrossRef]
- Liu, D.; Gao, J. Distributed Watershed Hydrological Simulation Method Based on SWAT Model. J. Coastal. Res. 2020, 104, 738–741. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Y. Advancing representation of hydrologic processes in the Soil and Water Assessment Tool (SWAT) through integration of the TOPographic MODEL (TOPMODEL) features. J. Hydrol. 2012, 420, 319–328. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Sun, G.; Strauss, P.; Guo, J.; Tang, Y.; Yao, A. Multi-site calibration, validation, and sensitivity analysis of the MIKE SHE Model for a large watershed in northern China. Hydrol. Earth Syst. Sci. 2012, 16, 4621–4632. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Huang, Y.; Zhang, Z.; Kong, R.; Tian, J.; Zhou, Y.; Duan, Z. Evaluation of TMPA satellite precipitation in driving VIC hydrological model over the Upper Yangtze River Basin. Water 2020, 12, 3230. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Huang, Y.; Yu, L.; Liu, S.; Ma, G. A new Xin’anjiang and Sacramento combined rainfall-runoff model and its application. Hydrol. Res. 2021, 52, 1173–1183. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, M.; Song, Y.; Lai, Y. Hydrological simulation of the Jialing River Basin using the MIKE SHE model in changing climate. J. Water Clim. Chang. 2021, 12, 2495–2514. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, H.; Xu, C.Y.; Jie, M.X.; Hou, Y.K. Feasibility and uncertainty of using conceptual rainfall-runoff models in design flood estimation. Hydrol. Res. 2016, 47, 701–717. [Google Scholar] [CrossRef] [Green Version]
- Xue, L.; Yang, F.; Yang, C.; Wei, G.; Li, W.; He, X. Hydrological simulation and uncertainty analysis using the improved TOPMODEL in the arid Manas River basin, China. Sci. Rep. 2018, 8, 452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nonki, R.M.; Lenouo, A.; Tshimanga, R.M.; Donfack, F.C.; Tchawoua, C. Performance assessment and uncertainty prediction of a daily time-step HBV-Light rainfall-runoff model for the Upper Benue River Basin, Northern Cameroon. J. Hydrol. Reg. Stud. 2021, 36, 100849. [Google Scholar] [CrossRef]
- Chargui, S.; Gharbi, H.; Slimani, M. Runoff responses at different watershed scales in semi-arid region: Exploration of a developed rainfall runoff model (Merguellil and Skhira watershed, Central Tunisia). Earth Sci. Inform. 2013, 6, 127–136. [Google Scholar] [CrossRef]
- Deb, P.; Kiem, A.S.; Willgoose, G. Mechanisms influencing non-stationarity in rainfall-runoff relationships in southeast Australia. J. Hydrol. 2019, 571, 749–764. [Google Scholar] [CrossRef]
- Muhammad, A.; Evenson, G.R.; Stadnyk, T.A.; Boluwade, A.; Jha, S.K.; Coulibaly, P. Impact of model structure on the accuracy of hydrological modeling of a Canadian Prairie watershed. J. Hydrol. Reg. Stud. 2019, 21, 40–56. [Google Scholar] [CrossRef]
- Gou, J.; Miao, C.; Duan, Q.; Tang, Q.; Di, Z.; Liao, W.; Zhou, R. Sensitivity analysis-based automatic parameter calibration of the VIC model for streamflow simulations over China. Water Resour. Res. 2020, 56, e2019WR025968. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Zhu, Z.; Xie, Y.; Cai, Y. Impacts of rainfall spatial and temporal variabilities on runoff quality and quantity at the watershed scale. J. Hydrol. 2021, 603, 127057. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Kavianpour, M.R.; Kisi, O.; Nourani, V. A new approach for simulating and forecasting the rainfall-runoff process within the next two months. J. Hydrol. 2017, 548, 588–597. [Google Scholar] [CrossRef]
- Parvinizadeh, S.; Zakermoshfegh, M.; Shakiba, M. A simple and efficient rainfall–runoff model based on supervised brain emotional learning. Neural. Comput. Appl. 2022, 34, 1509–1526. [Google Scholar] [CrossRef]
- Pan, T.; Wang, R. Using recurrent neural networks to reconstruct rainfall-runoff processes. Hydrol. Processes Int. J. 2005, 19, 3603–3619. [Google Scholar] [CrossRef]
- Cecconi, F.R.; Moretti, N.; Tagliabue, L.C. Application of artificial neutral network and geographic information system to evaluate retrofit potential in public school buildings. Renew. Sustain. Energy Rev. 2019, 110, 266–277. [Google Scholar] [CrossRef] [Green Version]
- Lees, T.; Buechel, M.; Anderson, B.; Slater, L.; Reece, S.; Coxon, G.; Dadson, S.J. Benchmarking data-driven rainfall–runoff models in Great Britain: A comparison of long short-term memory (LSTM)-based models with four lumped conceptual models. Hydrol. Earth Syst. Sci. 2021, 25, 5517–5534. [Google Scholar] [CrossRef]
- Meng, C.; Zhou, J.; Tayyab, M.; Zhu, S.; Zhang, H. Integrating artificial neural networks into the VIC model for rainfall-runoff modeling. Water 2016, 8, 407. [Google Scholar] [CrossRef] [Green Version]
- Roy, B.; Singh, M.P.; Kaloop, M.R.; Kumar, D.; Hu, J.W.; Kumar, R.; Hwang, W.S. Data-Driven Approach for Rainfall-Runoff Modelling Using Equilibrium Optimizer Coupled Extreme Learning Machine and Deep Neural Network. Appl. Sci. 2021, 11, 6238. [Google Scholar] [CrossRef]
- Gholami, V.; Sahour, H. Simulation of rainfall-runoff process using an artificial neural network (ANN) and field plots data. Theor. Appl. Climatol. 2022, 147, 87–98. [Google Scholar] [CrossRef]
- Ilunga, M. Infilling annual rainfall data using feedforward back-propagation Artificial Neural Networks (ANN): Application of the standard and generalised back-propagation techniques. J. S. Afr. Inst. Civ. Eng. 2010, 52, 2–10. [Google Scholar]
- Taormina, R.; Chau, K.W. Data-driven input variable selection for rainfall–runoff modeling using binary-coded particle swarm optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
- Alizadeh, A.; Rajabi, A.; Shabanlou, S.; Yaghoubi, B.; Yosefvand, F. Modeling long-term rainfall-runoff time series through wavelet-weighted regularization extreme learning machine. Earth Sci. Inform. 2021, 14, 1047–1063. [Google Scholar] [CrossRef]
- Cui, W.D.; Jin, B. Improved support vector machine regression model and its application to annual runoff forecast. J. Hydroel. Eng. 2015, 34, 7–17. [Google Scholar]
- Manivannan, R.; Samidurai, R.; Cao, J.; Alsaedi, A.; Alsaadi, F.E. Global exponential stability and dissipativity of generalized neural networks with time-varying delay signals. Neural Netw. 2017, 87, 149–159. [Google Scholar] [CrossRef]
- Saharia, M.; Bhattacharjya, R.K. Geomorphology-based time-lagged recurrent neural networks for runoff forecasting. KSCE J. Civ. Eng. 2012, 16, 862–869. [Google Scholar] [CrossRef]
- Ishida, K.; Kiyama, M.; Ercan, A.; Amagasaki, M.; Tu, T. Multi-time-scale input approaches for hourly-scale rainfall–runoff modeling based on recurrent neural networks. J. Hydroinf. 2021, 23, 1312–1324. [Google Scholar] [CrossRef]
- Li, C.; Zhu, L.; He, Z.; Gao, H.; Yang, Y.; Yao, D.; Qu, X. Runoff prediction method based on adaptive Elman neural network. Water 2019, 11, 1113. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, Q.; Zhang, G.; Nie, Z.; Gui, Z. A hybrid model for annual runoff time series forecasting using elman neural network with ensemble empirical mode decomposition. Water 2018, 10, 416. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Jian, S.; Li, Z.; Chen, Y.; Zhang, G.; Zhang, Z.; Wang, S. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J. Hydrol. 2022, 608, 127553. [Google Scholar] [CrossRef]
- Menezes, J.M.P., Jr.; Barreto, G.A. Long-term time series prediction with the NARX network: An empirical evaluation. Neurocomputing 2008, 71, 3335–3343. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, W.; Xie, J.; Liu, Q. A Water Consumption Forecasting Model by Using a Nonlinear Autoregressive Network with Exogenous Inputs Based on Rough Attributes. Water 2022, 14, 329. [Google Scholar] [CrossRef]
- Rjeily, Y.A.; Abbas, O.; Sadek, M.; Shahrour, I.; Chehade, F.H. Flood forecasting within urban drainage systems using NARX neural network. Water Sci. Technol. 2017, 76, 2401–2412. [Google Scholar] [CrossRef]
- Wei, M.; She, L.; You, X.Y. Establishment of urban waterlogging pre-warning system based on coupling RBF-NARX neural networks. Water Sci. Technol. 2020, 82, 1921–1931. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F.; Gargano, R.; De Marinis, G. Prediction of spring flows using nonlinear autoregressive exogenous (NARX) neural network models. Environ. Monit. Assess. 2021, 193, 350. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological mode. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Thapa, S.; Zhao, Z.; Li, B.; Lu, L.; Donglei Fu, D.L.; Xiaofei Shi, X.F.; Tang, B.; Qi, H. Snowmelt-Driven Streamflow Prediction Using Machine Learning Techniques (LSTM, NARX, GPR, and SVR). Water 2020, 12, 1734. [Google Scholar] [CrossRef]
- Fovell, R.G.; Fovell, M.Y.C. Climate zones of the conterminous United States defined using cluster analysis. J. Clim. 1993, 6, 2103–2135. [Google Scholar] [CrossRef] [Green Version]
- Hosking, J.R.M.; Walllis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Wanas, N.M.; Auda, G.; Kamel, M.; Karray, F. On the Optimal Number of Hidden Nodes in a Neural Network. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (Cat. No.98TH8341), Waterloo, ON, Canada, 25–28 May 1998; pp. 918–921. [Google Scholar]
- Foresee, F.D.; Hagan, M.T. Gauss-Newton approximation to Bayesian learning. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 12 June 1997; Volume 3, pp. 1930–1935. [Google Scholar]
- Yong, B. Development of a Land-SURFACE Hydrologic Model TOPX and Its Coupling Study with Regional Climate Model RIEMS; Nanjing University: Nanjing, China, 2008. [Google Scholar]
- Shao, Y.H. Precipitation Retrieved by Doppler Radar and Its Assimilation Study with the Improved Regional Climate Model RIEMS; Nanjing University: Nanjing, China, 2010. [Google Scholar]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Nash, J.E.; Sutclife, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Feng, K.P.; Hong, Y.; Tian, J.C.; Tang, G.Q.; Kan, G.Y.; Luo, X.Y. Evaluating runoff simulation of multi-source precipitation data in small watersheds. Arid. Land Geogr. 2020, 43, 1179–1191. (In Chinese) [Google Scholar]
- Sudheer, K.P.; Nayak, P.C.; Ramasastri, K.S. Improving peak flow estimates in artificial neural network river flow models. Hydrol. Process. 2003, 17, 677–686. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, J.H.; Luo, X.C.; Bao, J.; Zhang, M.; Yang, X.X. Research on the Runoff Forecasting of Yalong River Basin Driven by TRMM Data. China Rural. Water Hydropower 2020, 11, 8–13. [Google Scholar]
- Yang, T.; Gao, X.; Sorooshian, S.; Li, X. Simulating California reservoir operation using the classification and regression-tree algorithm combined with a shuffled cross validation scheme. Water Resour. Res. 2016, 52, 1626–1651. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).