Abstract
The hydrologic characteristic of a permeable friction course (PFC) pavement is dependent on the rainfall intensity, pavement geometric design, and porous asphalt properties. Herein, the hydrologic characteristic of PFC pavements of various lengths and slopes was determined via numerical analysis. A series of analyses was conducted using length values of 10, 15, 20, and 30 m and slope values of 0.5%, 2%, 4%, 6%, and 8% for the equivalent water flow path. The PFC pavements were simulated for various values of rainfall intensity, which ranged from 10 to 120 mm/h, to determine the time taken for water to flow over the PFC pavement surface. The results show that the time for water overflow decreased when the pavement length or rainfall intensity increased, and it increased when the slope increased. Finally, a series of design charts was developed to determine the time taken for water to flow over the PFC pavement surface for given rainfall intensities. Since this study was conducted based on numerical analysis, further studies are recommended to verify experimentally the results presented.
1. Introduction
In recent years, permeable pavements have been used widely, and they have played an essential role in controlling rainwater quantity and quality in urban areas [1,2,3]. There are different types of permeable pavements, such as porous asphalt, pervious concrete, porous turf, plastic geo-cell, open-jointed block, open-celled grid, and permeable friction course (PFC) pavement [4]. The PFC pavement or open-graded friction course pavement refers to a type of porous asphalt laid on the surface layer of conventional impermeable asphalt pavement, and it is increasingly becoming popular in many countries [5]. As the porous asphalt is designed to have a high porosity, the PFC pavement allows rainwater to infiltrate its pores and drain out laterally. As a result, PFC pavement tends to reduce the peak flow of and pollutants in rainwater compared to impermeable asphalt pavement [6,7,8].
The hydrologic characteristic of a PFC pavement depends not only on the properties of the porous asphalt material (such as porosity and permeability) but also on the geometric design of the pavement, such as the longitudinal slope (Sy), cross slope (Sx), length (L), width (W), and thickness (T) [9,10]. The intensity of rainfall (I) is also a critical factor that should be considered. Several researchers investigated the effects of these factors on the hydrologic characteristic of PFC pavement [9,10,11]. Ranieri [10] used a rainfall simulator to evaluate the hydrologic characteristic of a PFC pavement having dimensions of 1.45 × 0.75 × 0.07 m. It was tested for various longitudinal slopes (Sy) and rainfall intensities (I). Piezometers were installed within the specimen for recording the head of water flow within the body of the PFC pavement. The results of the rainfall simulation experiments were in a good agreement with those from theoretical calculations. Based on the results of the experimental tests, they provided a chart that described the relationship between the ratio of the maximum head of water flow to the pavement length (H/L) and the ratio of the rainfall intensity to the permeability (4I/k). The thickness of the PFC pavement (T) that prevents surface ponding could be determined from the chart, and the chart can be used as a preliminary design tool. Charbeneau and Barrett [12] developed a mathematical model for estimating the steady-state phreatic line in PFC during rainfall. The results of their study showed that as the rainfall intensity (I) increased, the head of water flow within the body of the PFC pavement also increased. They concluded that the hydrologic characteristic of a PFC pavement is significantly dependent on rainfall intensity (I), as well as the permeability (k) and geometric design of the PFC pavement. Tan et al. [9] used a finite element program to investigate the effect of geometric design (Sx, Sy, T, and W) and rainfall intensity (I) on the hydrologic characteristic of PFC pavements. They assumed that the permeability (k) of porous asphalt was 20 mm/s. In each analysis case, they determined the maximum allowable rainfall intensity (Ia) that prevented surface ponding over the PFC pavement. Based on the results of their study, a relationship between the ratio of the thickness to the width (T/W) of the pavement and the maximum allowable rainfall intensity (Ia) was established. The results also showed that as the cross slope (Sx) and the ratio of thickness to width (T/W) increased, the effect of the longitudinal slope (Sy) on the drainage decreased. Recently, Liu et al. [13] proposed a computational model for predicting the water flow of PFC pavements during rainfall. They presented equations for calculating the fluid motion of the water flow. The water flow within the body was estimated as a two-dimensional flow using the diffusive wave equation, whereas the water flow over the surface was estimated as a three-dimensional flow using Richard’s equation. The results indicated that the thickness (T) of the PFC pavement has a significant effect on the time at which surface ponding is initiated, but a less significant effect on the phreatic line in PFC pavement. The time at which surface ponding is initiated (tp), known as the time taken for water flow over the PFC pavement surface, is an important factor that contributes to the calculation of the peak flow [14]. In low-impact development (LID) techniques, it is called the delay time of peak flow which is one of the typical performance measures for permeable pavements [15]. According to Liu et al. [13], the time taken for water flow over the PFC pavement surface is also critical for safety in transportation. It was also studied by Park et al. [16] in the case of using it for a permeable pavement (constructed with permeable block, subbase, and subgrade) and an impermeable pavement. They were tested with a rainfall simulator. In the test, rainfall intensities of 50 and 150 mm/h were used. The results showed that the time taken for water flow over the PFC pavement surface (tp) was in a range of 16–21 minutes for the permeable pavement. However, for the impermeable pavement, this value was only 10 minutes, regardless of rainfall intensity. It could be concluded that the permeable pavement results a higher time taken for water flow over the PFC pavement surface than the impermeable pavement. Another study of Huang et al. [17] evaluated the time taken for water flow over the PFC pavement surface for three different kinds of permeable pavement systems consisting of permeable interlocking pavers, porous asphalt, and porous concrete. The authors figured that the porous asphalt and permeable interlocking paver specimens provided the same time taken results. They concluded that the time taken for water flow over the PFC pavement has a strong relationship with the removal rate of pollutants.
The literature showed that the hydrologic characteristic of PFC pavement is influenced by rainfall intensity, geometric design, and porous asphalt properties. However, there is a dearth of literature on how long it takes until surface ponding occurs or the time taken for water flow over the PFC pavement surface and how the PFC fails to accommodate the excess rainfall. The aim of this study is to determine the time taken for water flow over the PFC pavement surface and the effects of the geometric design and rainfall intensity on it using numerical analysis. PFC pavements with different geometric designs were simulated for a range of rainfall intensities to obtain the time taken for water to flow over the PFC pavement surface. Based on the results of this study, the hydrologic characteristic of the PFC pavement was evaluated and compared.
2. Water Flow in a PFC Pavement
Water flow from rainfall in a PFC pavement consists of two components: flow within the body and flow over the surface of the pavement. Generally, under the dry condition, with constant rainfall intensity, the water flow can be described as follows: water initially infiltrates the pores of the PFC pavement and then begins to flow out of the body laterally without surface ponding. The water flow within a PFC body is considered to be laminar or between laminar and turbulent [10,18]. The head of the water flow (H) in a PFC body is illustrated in Figure 1. This value is a function of the rainfall intensity and time, as well as the permeability and geometric design of the PFC. During the rainfall, the pores in the PFC pavement are filled with water, and the head of water flow increases gradually.
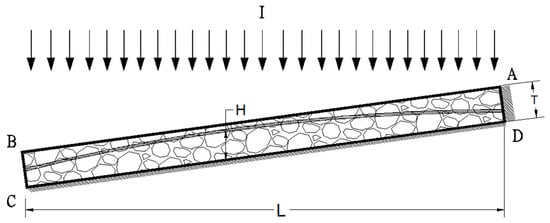
Figure 1.
Water flow in a PFC body [10].
When the head of water flow reaches the surface of the PFC pavement, i.e., when the head of water flow exceeds the thickness of the PFC pavement (H equals to T), surface ponding occurs. At this moment, water can flow over the PFC pavement surface, and the pavement tends to be almost saturated.
3. Modeling of Water Flow in a PFC Pavement and Analysis Parameters
3.1. Transient Unsaturated/Saturated Seepage
In this study, a finite element program, SV Flux 2D [19], was used to model the transient unsaturated/saturated seepage in the PFC pavement. Assuming that water has a constant volume and is incompressible, the governing equation of two-dimensional water flow is expressed in Equation (1):
where kx and ky are the hydraulic conductivities in the horizontal and vertical directions, respectively, h is the total water head, kvd is the vapor conductivity, uw is the pore water pressure, γw is the unit weight of water, is the coefficient of water storage obtained from the derivative of the soil–water characteristic curve, and t is the time.
The soil–water characteristic curve (SWCC) represents the nonlinear relationship between the volumetric water content and the suction in the soil. Van Genuchten’s equation [20,21] was used in this study to model the SWCC, as shown in Equation (2):
where θ is the volumetric water content, θs is the saturated volumetric water content, θr is the residual volumetric water content, Ψ is the soil suction, and a, n, and m are the material (fitting) parameters.
3.2. Geometric Dimensions
In a PFC pavement, a majority of the water flows along the steepest slope, which is the resultant SR of the cross slope Sx and the longitudinal slope Sy, as presented in Figure 2. The flow of water for a PFC pavement in a three-dimensional direction can be represented by the flow of water for one with a two-dimensional direction having an equivalent water flow path consisting of the length (LR) and slope (SR). These variables can be calculated from the width W, length L, cross slope Sx, and longitudinal slope Sy of the PFC pavement based on Equation (3) and Equation (4) [10]:
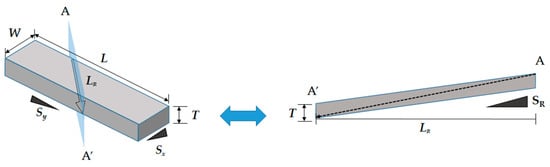
Figure 2.
Equivalent water flow path: length (LR) and slope (SR).
3.3. Boundary Conditions
Three main types of boundary conditions were applied in the analysis: climate, review, and zero-flux conditions. Figure 1 illustrates the application of the boundary conditions in modeling the PFC pavement. The surface of the PFC pavement, i.e., the AB line, along which rainfall occurred, was assigned the climate boundary condition. The outlet of the PFC pavement, i.e., the BC line, from where the water drained out of the pavement, was assigned the review boundary condition. Finally, the bottom CD line and the upper AD line, where the water could not drain out, were assigned zero-flux boundary conditions to model the impermeable characteristics.
3.4. Analysis Cases
Based on the conventional dimension of pavement in the AASHTO manual, “Policy on Geometric Design of Highways and Streets” [22], the equivalent water flow path including the length LR and slope SR of the PFC pavement was determined according to Equation (3) and Equation (4). The equivalent length LR, ranging from 10 to 30 m, and the equivalent slope SR, ranging from 0.5% to 8%, as listed in Table 1, were selected for observation since the other values are exaggerated for a PFC pavement. For each geometric model, a rainfall intensity of 10 mm/h was simulated first, and this value was increased in steps of 10 mm/h up to a maximum value of 120 mm/h. For each iteration, the time taken for water flow over the PFC pavement surface (tp) was evaluated.

Table 1.
Analysis cases.
3.5. Material Parameters
The horizontal and vertical permeabilities of the porous asphalt used in the numerical analysis were determined from the laboratory experiment. Specimens with dimensions of 0.3 × 0.3 × 0.05 m and porosity of 19.6% were tested. The horizontal permeability was evaluated according to a procedure developed by Ahn et al. [23], and the vertical permeability was examined using a constant head procedure presented in Ahn et al. [24]. A summary of the two test procedures is presented in Figure 3 and Figure 4.

Figure 3.
Horizontal permeability test for porous asphalt specimens (after Ahn et al. [23]).

Figure 4.
Vertical permeability test for porous asphalt specimen (after Ahn et al. [24]).
From the experimental results, the horizontal and vertical permeabilities were 11.1 and 9.2 mm/s, respectively. The horizontal permeability of the porous asphalt was found to be slightly higher than the vertical permeability. In this study, the permeability of the PFC pavement was assumed to be isotropic and equal to 10 mm/s.
The SWCC parameters for a pervious concrete given in Lim and Kim [25] were used for those of the PFC pavement in this study. They obtained the SWCC parameters through the equation of Fredlund and Xing [26] using Fredlund’s device [27]. These parameters were substituted in Equation (2) in this study. The SWCC parameters and curve are presented in Table 2 and Figure 5, respectively.

Table 2.
SWCC parameters for the PFC pavement (after Lim and Kim [25]).
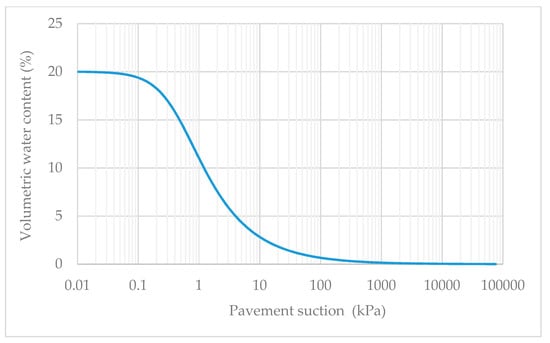
Figure 5.
SWCC curve of the PFC pavement.
According to previous studies, PFC pavements absorb the surrounding air to reduce the noise from moving vehicle tires [4]. In the case of no rainfall, PFC pavement has a suction force and a negative value for the pore water pressure [28]. Therefore, in this study, the initial pore water pressure was set to a negative value within the range of the residual zone.
In the numerical analysis, it was noted that the pore water pressure values within the range of the residual zone had no significant effect on the allowable rainfall intensity and time taken for water flow over the PFC pavement surface. Based on Figure 5, −200 kPa was selected as the initial value of the pore water pressure in the PFC pavement to indicate that the pavement was completely dry before rainfall. Data for inflow and outflow volumes and degree of saturation with respect to time were continually recorded during the analysis.
4. Results and Discussion
4.1. Time Taken for Water Flow over the PFC Pavement Surface
Various values of rainfall intensity, which ranged from 10 to 120 mm/h, were considered in the numerical analysis to evaluate the time taken for water flow over the PFC pavement surface. The results are presented in Table 3. The cells with no numerical values indicate that at that given rainfall intensity, surface ponding did not occur, i.e., the rainfall intensity was not large enough to trigger surface ponding in these cases.

Table 3.
Time taken for water flow over the PFC pavement surface (tp).
PFC pavements with different equivalent water flow paths (lengths LR and slopes SR) resulted in various times taken. Generally, as the rainfall intensity increased, the time taken for water flow over the PFC pavement surface decreased. This finding confirms that the hydrologic characteristic is dependent on rainfall intensity and geometric design.
4.2. Effect of Geometric Design
The relationships between the time taken for water flow over the PFC pavement surface and the rainfall intensity according to the different geometric designs are depicted in Figure 6. Based on the results, it is observed that tp decreases with the increase in the length of LR. For instance, for I = 40 mm/h and SR = 8%, as LR increased by 20 m (from 10 to 30 m), tp decreased by 9 min (from 26 to 17 min). These results indicate that surface ponding occurred earlier for the PFC pavement that had a longer length LR.
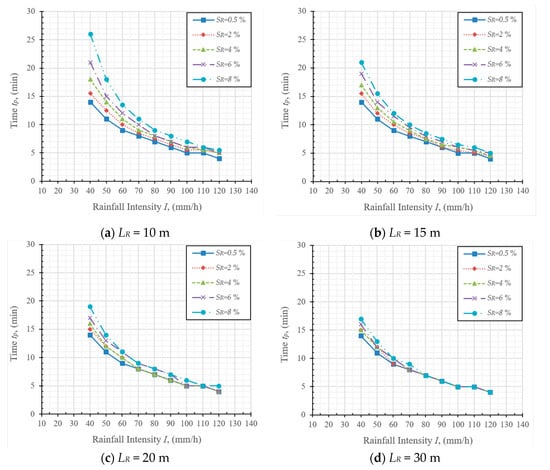
Figure 6.
Relationship between the time taken for the water flow over the PFC pavement surface (tp) and rainfall intensity (I) with different slope (SR) values.
In this study, it was also found that the slope had a significant effect on the time taken for water flow over the PFC pavement surface. The increase in SR results in a corresponding increase in tp, as reported by Tan et al. [9]. For example, for LR = 10 m and I = 40 mm/h, tp increases by 12 min (from 14 to 26 min) when SR increases by 7.5% (from 0.5% to 8%).
In Figure 6d, it is noticed that as LR = 30 m, different values of SR result in correspondingly similar values of tp. The finding highlights that the hydrologic characteristic of the PFC pavement is less sensitive to the slope SR when it has a longer length LR. Furthermore, it can be seen that the PFC pavements with different geometric designs have close results in the time taken for water flow over the PFC pavement surfaces at high rainfall intensities. It can be concluded that PFC pavements at high rainfall intensity have a similar hydrologic characteristic, regardless of the geometric design.
4.3. Allowable Rainfall Intensity for the PFC Pavement
In this study, the allowable rainfall intensity Ia for the PFC pavement, which is the maximum rainfall intensity for which the water flow would remain only within the PFC pavement body, was estimated. In other words, this value of the rainfall intensity allows the head of water flow H inside the PFC pavement to be equal to its thickness T, regardless of the rainfall duration. The results are displayed in Table 4.

Table 4.
Allowable rainfall intensity, Ia.
In Figure 7, the allowable rainfall intensities Ia according to the slope SR and length LR are presented. It can be seen that when SR increases, there is an upward trend in Ia. This observation is consistent with that of Tan et al. [9]. In addition, Ia decreases when LR increases, which supports the results reported by Ranieri [29]. This observation implies that a PFC pavement with a shorter LR and longer SR exhibits higher drainage capacity.
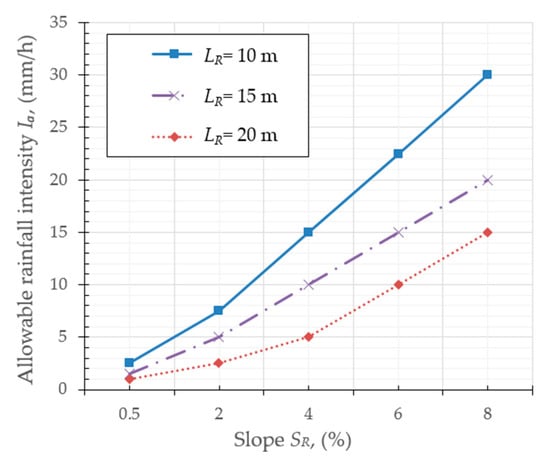
Figure 7.
Allowable rainfall intensity Ia according to the slope SR and lengths LR.
A PFC pavement with a shorter length LR is more sensitive to variations in the slope SR. For example, when the value of SR increases from 0.5% to 8%, for LR = 10 m, Ia significantly increases by 27.5 mm/h (an increase from 2.5 to 30 mm/h), but for LR = 15 m, I¬¬a increases by only 19 mm/h. However, for LR = 20 m, Ia slightly increases by 5 mm/h.
4.4. Effects of Thickness and Porosity
The effects of the thickness T and porosity n of the PFC pavement on its hydrologic characteristic were investigated. Observations were made for PFC pavements with T = 0.05 m and 0.1 m, and n = 10% and 20%. All the PFC pavements had the same water flow path of LR = 10 m and SR = 2%. The results are displayed in Table 5 and Table 6.

Table 5.
Time taken for water flow over the PFC pavement surface (tp) for I = 50 mm/h, LR = 10 m, and SR = 2%.

Table 6.
Time taken for water flow over the PFC pavement surface (tp) for I = 100 mm/h, LR = 10 m, and SR = 2%.
From the Tables, it can be seen that the thickness T and porosity n have a significant effect on the hydrologic characteristic of a PFC pavement. As the thickness T and porosity n increase by a factor of two, the time taken for the water flow over the PFC pavement surface tp doubles. According to Hou et al. [11], this could be attributed to the storage capacity of the PFC pavement, a PFC pavement with a higher porosity n has a higher water storage capacity.
4.5. Design Charts for PFC Pavement
Five variables, namely, rainfall intensity I, length LR, and slope SR for the water flow path, the time taken for the water flow over the PFC pavement surface tp, and the permeability of porous asphalt k, were used to develop design charts in terms of the hydrologic characteristic for the PFC pavement. For each value of , the values of are presented as a function of . Table 7 below gives the values of the five variables.

Table 7.
Normalized variables for PFC pavement design.
It is possible to estimate the time taken for water to flow over the PFC pavement tp at the design rainfall intensity I using the design charts in Figure 8. The use of these charts is described in the following example. A PFC pavement with an equivalent water flow path has a length LR = 10 m, a thickness T = 0.05 m, and LR/T = 200. Assuming that the permeability k = 6.6 mm/s = 24,000 mm/h, at a design rainfall intensity I = 50 mm/h, the results of the time taken for the water flow over the PFC pavement surface tp for different slopes SR can be determined as follows (Equation 5):
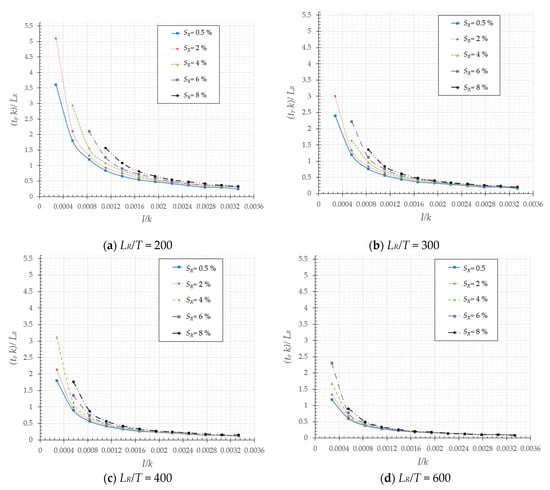
Figure 8.
Design charts.
The values of are defined in Figure 8. Consequently, the values of tp were calculated and are listed in Table 8. The results from the design charts demonstrate that the time taken for the water flow over the PFC pavement surface (tp) can be determined efficiently.

Table 8.
Results of the time taken for water flow over the PFC pavement surface, tp.
5. Conclusions
In this study, the hydrologic characteristic of PFC pavements of various lengths and slopes was determined via numerical analysis. A series of analyses was conducted using length values of 10, 15, 20, and 30 m and slope values of 0.5%, 2%, 4%, 6%, and 8% for the equivalent water flow path. The PFC pavements were simulated for various values of rainfall intensity, which ranged from 10 to 120 mm/h, to determine the time taken for water to flow over the PFC pavement surface. The following conclusions are drawn:
The hydrologic characteristic of a PFC pavement significantly depends on the rainfall intensity and geometric design of the pavement. PFC pavements with different equivalent water flow paths resulted in different times for water overflow. Generally, as the rainfall intensity increases, the time for water to flow over the PFC pavement surface decreases.
The observation of the effect of the geometric design on the hydrologic characteristic demonstrates following. As the length of the water flow path increases, the time for water overflow decreases. However, when the slope increases, it increases significantly. Based on these results, it appears that the hydrologic characteristic of the PFC pavement that has a longer water flow path is less sensitive to variations in the slope. In addition, a PFC pavement having a shorter water flow path or steeper slope exhibits higher drainage capacity. Thickness and porosity have significant effects on the hydrologic characteristic of a PFC pavement. As the thickness and porosity increase by a factor of two, the time for water overflow is doubled.
A series of design charts was developed based on the results of the numerical analysis of the PFC pavement. These charts can be used to determine the time for water overflow over the PFC pavement surface at specified rainfall intensities. Since this study was conducted based on numerical analysis, sequential experimental studies are necessary to verify the results presented.
Author Contributions
Conceptualization, T.H.N. and J.A.; methodology, J.A.; software, J.A.; validation, J.A. and T.H.N.; formal analysis, T.H.N.; investigation, T.H.N.; resources, J.A.; data curation, J.A.; writing—original draft preparation, T.H.N.; writing—review and editing, J.A. and T.H.N.; visualization, J.A.; supervision, J.A.; project administration, J.A.; funding acquisition, J.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (Grant 21CTAP-C152124-03).
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Ministry of Land, Infrastructure, and Transport of the Korean government for the grant from the Technology Advancement Research Program (Grant Number 21CTAP-C152124-03).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chu, L.; Tang, B.; Fwa, T. Evaluation of functional characteristics of laboratory mix design of porous pavement materials. Constr. Build. Mater. 2018, 191, 281–289. [Google Scholar] [CrossRef]
- Wu, H.; Yu, J.; Song, W.; Zou, J.; Song, Q.; Zhou, L. A critical state-of-the-art review of durability and functionality of open-graded friction course mixtures. Constr. Build. Mater. 2020, 237, 117759. [Google Scholar] [CrossRef]
- Zhang, L.; Ye, Z.; Shibata, S. Assessment of Rain Garden Effects for the Management of Urban Storm Runoff in Japan. Sustainability 2020, 12, 9982. [Google Scholar] [CrossRef]
- Ferguson, B.K. Porous Pavements; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Manrique-Sanchez, L.; Caro, S. Numerical assessment of the structural contribution of porous friction courses (PFC). Constr. Build. Mater. 2019, 225, 754–764. [Google Scholar] [CrossRef]
- Eck, B.J.; Winston, R.J.; Hunt, W.F.; Barrett, M.E. Water quality of drainage from permeable friction course. J. Environ. Eng. 2011, 138, 174–181. [Google Scholar] [CrossRef]
- Berbee, R.; Rijs, G.; De Brouwer, R.; van Velzen, L. Characterization and treatment of runoff from highways in the Netherlands paved with impervious and pervious asphalt. Water Environ. Res. 1999, 71, 183–190. [Google Scholar] [CrossRef]
- Roseen, R.M.; Ballestero, T.P.; Houle, J.J.; Avellaneda, P.; Briggs, J.; Fowler, G.; Wildey, R. Seasonal performance variations for storm-water management systems in cold climate conditions. J. Environ. Eng. 2009, 135, 128–137. [Google Scholar] [CrossRef]
- Tan, S.; Fwa, T.; Chai, K. Drainage considerations for porous asphalt surface course design. Transp. Res. Rec. 2004, 1868, 142–149. [Google Scholar] [CrossRef]
- Ranieri, V. Runoff control in porous pavements. Transp. Res. Rec. 2002, 1789, 46–55. [Google Scholar] [CrossRef]
- Hou, L.; Feng, S.; Huo, Z.; Ding, Y.; Zhang, S. Experimental study on rainfall-runoff relation for porous pavements. Hydrol. Res. 2008, 39, 181–190. [Google Scholar] [CrossRef]
- Charbeneau, R.J.; Barrett, M.E. Drainage hydraulics of permeable friction courses. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Shen, C. Coupled two-dimensional surface flow and three-dimensional subsurface flow modeling for drainage of permeable road pavement. J. Hydrol. Eng. 2016, 21, 04016051. [Google Scholar] [CrossRef]
- NRCS, U. Urban Hydrology for Small Watersheds-Technical Release 55; US Department of Agriculture Natural Resources Conservation: Washington, DC, USA, 1986. [Google Scholar]
- LeFevre, N.-J.B.; Watkins, D.W., Jr.; Gierke, J.S.; Brophy-Price, J. Hydrologic performance monitoring of an underdrained low-impact development storm-water management system. J. Irrig. Drain. Eng. 2010, 136, 333–339. [Google Scholar] [CrossRef]
- Park, D.-G.; Sandoval, N.; Lin, W.; Kim, H.; Cho, Y.-H. A case study: Evaluation of water storage capacity in permeable block pavement. KSCE J. Civil Eng. 2014, 18, 514–520. [Google Scholar] [CrossRef]
- Huang, J.; Valeo, C.; He, J.; Chu, A. Three types of permeable pavements in cold climates: Hydraulic and environmental performance. J. Environ. Eng. 2016, 142, 04016025. [Google Scholar] [CrossRef]
- Kovács, G. Seepage Hydraulics; Elsevier: Amsterdam, The Netherlands, 2011; Volume 10. [Google Scholar]
- Thode, R.; Gitirana, G. Theory Manual of Saturated/Unsaturated Finite Element. 2D/3D Seepage Modeling; SVFlux, SoilVision Systems Ltd: Saskatoon, SK, Canada, 2014. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils 1. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, M. User’s Manual for SVFlux, Saturated-Unsaturated Numerical Modeling; SoilVision Systems: Saskatoon, SK, Canada, 2010. [Google Scholar]
- AASHTO, A. Policy on geometric design of highways and streets. Am. Assoc. State Highw. Transp. Off. Wash. DC 2001, 1, 158. [Google Scholar]
- Yoo, J.; Nguyen, T.H.; Lee, E.; Lee, Y.; Ahn, J. Measurement of Permeability in Horizontal Direction of Open-Graded Friction Course with Rutting. Sustainability 2020, 12, 6428. [Google Scholar] [CrossRef]
- Ahn, J.; Marcaida, A.K.; Lee, Y.; Jung, J. Development of Test Equipment for Evaluating Hydraulic Conductivity of Permeable Block Pavements. Sustainability 2018, 10, 2549. [Google Scholar] [CrossRef]
- Lim, B.K.; Kim, Y.T.; (Department of Ocean Engineering, Pukyong National University, Busan, Korea). Personal Communication, 2012.
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- GCTS Testing System. Available online: https://www.gcts.com/ (accessed on 23 June 2020).
- Si, C.; Chen, E.; You, Z.; Zhang, R.; Qiao, P.; Feng, Y. Dynamic response of temperature-seepage-stress coupling in asphalt pavement. Constr. Build. Mater. 2019, 211, 824–836. [Google Scholar] [CrossRef]
- Ranieri, V.; Colonna, P.; Sansalone, J.J.; Sciddurlo, A. Measurement of hydraulic conductivity in porous mixes. Transp. Res. Rec. 2012, 2295, 1–10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).