Abstract
This paper presents the calculation of the hydrodynamic forces exerted on an oscillating circular cylinder when it moves perpendicular to its axis in infinitely deep water covered by compressed ice. The cylinder can oscillate both horizontally and vertically in the course of its translational motion. In the linear approximation, a solution is found for the steady wave motion generated by the cylinder within the hydrodynamic set of equations for the incompressible ideal fluid. It is shown that, depending on the rate of ice compression, both normal and anomalous dispersion can occur in the system. In the latter case, the group velocity can be opposite to the phase velocity in a certain range of wavenumbers. The dependences of the hydrodynamic loads exerted on the cylinder (the added mass, damping coefficients, wave resistance and lift force) on the translational velocity and frequency of oscillation were studied. It was shown that there is a possibility of the appearance of negative values for the damping coefficients at the relatively big cylinder velocity; then, the wave resistance decreases with the increase in cylinder velocity. The theoretical results were underpinned by the numerical calculations for the real parameters of ice and cylinder motion.
1. Introduction
As is well known, a significant proportion of the world’s oil and gas reserves (up to 80% according to some estimates) are concentrated on shelves of the surrounding oceans and seas. In recent years, the volume of hydrocarbon production in the shelf zone has been growing rapidly; the increased volume stimulates the rapid growth of onshore and offshore engineering construction. In many countries, offshore projects are developing intensively. One of the priority areas for the development of the energy sector is the exploration of the Arctic and, possibly, Antarctic oil and gas fields. Progress in the development of natural resources of the sea shelf is inextricably linked with the study of hydrodynamic processes on the shelf and the ability to effectively describe and predict them. This is especially important in relation to the study of extreme events. Due to the specifics of the circumpolar regions, the development of research in the oceans and seas covered by ice is of great importance. Large sea areas where research, energy production or the construction of hydraulic structures (platforms, oil and gas pipelines) are conducted, may be covered with pack ice, broken ice or solid ice, which is in a stress state due to wind influences or pressure from outside mainland ice. According to available data, up to 12% of the oceans and seas are covered with ice. Most of the ice cover is found in the circumpolar regions, but, during particularly cold winters, the ice cover can deviate significantly south in the Northern Hemisphere or north in the Southern Hemisphere. The up-to-date review of the problem of interaction of ocean waves with ice cover at the destructive influence of global climate change is presented in the review by Ref. [1], which includes the results of theoretical, laboratory and fieldwork studies.
In many cases, there are currents in the ocean beneath the ice cover. The currents can cause vibrations of pipelines leading to wave motion in the ice. In certain conditions, instability can arise, resulting in the simultaneous growth of pipeline oscillations and flexural-gravity wave (FGW) amplitude in the ice cover. Therefore, the problem of the description of such a phenomenon is both topical and important from the practical point of view. It is also important to calculate the hydrodynamic loads exerted on the pipelines in the current in the seas or oceans covered by ice.
Many works have been devoted to the problem of studying waves in an ocean with an ice cover, among which the pioneering publications dating back to the 1960s can be mentioned [2,3]. Since that time, joint systems of equations describing wave disturbances in water and in an infinite homogeneous ice plate have been studied by many authors (see, e.g., the reviews [4,5,6] and references therein). In addition, FGWs in the ice cover generated by underwater sources were studied for both stationary and moving fluid of finite or infinite depth [7,8,9,10,11,12,13]. Effective direct mathematical methods for studying wave interactions with floating flexible structures have been developed by many authors and are described in the book by Sahoo [4]. The detailed review of interactions of fluid/structure/ice was presented by Ref. [14]. In this paper, various analytical and numerical results are presented on the interaction of a uniform current with a circular cylinder submerged below an ice sheet in water of a finite depth. In particular, the properties of the dispersion equation for the different current speeds, resistance and lift forces, ice sheet deflection for the different regimes of flow, etc. are presented. However, the calculations are performed for the uncompressed ice plate of the fixed thickness m; the ice plate inertia is neglected.
Under natural conditions, an ice sheet on the water can undergo compression or tension due to wind stress and pressure from other ice areas, for example, due to the sliding of continental ice into the ocean. As a result, the study of FGWs in oceans covered by compressed ice is a topical and important problem. However, this problem becomes rather complex from the theoretical point of view since it leads to a wide variety of possible cases due to a rather complex dispersion relation for this type of waves (see, e.g., [15,16,17,18]). The recently published work by the current authors [18] contains a study of FGWs generated by a dipole moving horizontally at some depth under the ice and oscillating along the direction of motion. Neglecting the effects of viscosity in water and in an ice plate, the basic equations of wave motion for a fluid of finite depth are derived. The wave patterns generated by a cylinder of a finite radius in an infinitely deep ocean are also analysed in detail. The added mass coefficients and the damping coefficients acting on the cylinder are found. In the same work, it is shown that the wave motion created by a cylinder of the finite radius can be modelled with the reasonable accuracy by the motion of a point dipole. The problem studied represents a particular case of the well-known general problem when, in the process of translational motion of a body oscillating along and perpendicular to the motion, the body experiences action of radiative hydrodynamic forces. This problem has been thoroughly investigated in the linear approximation for a submerged cylindrical body moving under a free surface in a homogeneous or two-layer fluid (see, e.g., [19,20,21] and references therein).
In this paper, which continues our previous study [18] and further develops the results of Ref. [14], we examine in detail the effect of compressed floating ice cover on the hydrodynamic loads exerted on the translationally moving and oscillating circular cylinder submerged in water. In the linear approximation, we derive a solution for the steady wave motion generated by the cylinder within the hydrodynamic set of equations for the incompressible ideal fluid of infinite depth. It is shown that, depending on the rate of ice compression, both normal and anomalous dispersion can occur in the system. In the latter case, the group velocity is opposite to the phase velocity in a certain range of wavenumbers. The dependences of hydrodynamic loads (the added mass, damping coefficients, wave resistance and lift force) exerted on the cylinder on the translational velocity and frequency of oscillation are investigated. It is shown that there is the possibility of the appearance of negative values of the damping coefficients at the relatively big cylinder velocity; then, the wave resistance decreases with increasing of the cylinder velocity. The theoretical results are underpinned by the numerical calculations for the real parameters of ice and cylinder motion.
2. Governing Equations and Boundary Conditions
Let us consider a circular cylinder of a radius a (e.g., a pipeline) flowing around by a uniform current with the velocity in an ideal incompressible fluid of the density (see Figure 1). The cylinder oscillates in the horizontal and vertical directions with the frequency . We assume that the water is infinitely deep and contains an ice cover on the top, which can be modelled by a thin elastic plate. The main set of hydrodynamic equations and boundary conditions describing FGWs in the linear approximation is as follows. For the velocity potential , we have the Laplace equation:
where the fluid velocity .

Figure 1.
Sketch of the flow around a rigid cylinder in a deep water covered by a flexible ice cover.
It is assumed that the lower boundary of the ice plate is always in contact with the water. By denoting as the vertical displacements of the ice cover from the undisturbed flat position, the kinematic and dynamic conditions at the upper boundary of the fluid (at ) can be written as [18]:
where , , E is the Young’s modulus of elastic plate, Q is the longitudinal stress ( corresponds to compression and to stretching), is the Poisson ratio, is the thickness of the ice plate and g is the acceleration due to gravity. The first term in Equation (3) describes the elastic property of the ice plate; the second term represents a horizontal stress or strain of the plate; and the term with the coefficient M describes the inertial property of the ice plate. All perturbations vanish in the bulk of the fluid so that for the vertical component of fluid velocity we have:
The dispersion relation of FGW relating the frequency of harmonic waves of infinitesimal amplitude with the wavenumber k is (see, e.g., [2,18,22]):
The phase and group velocities of FGW are:
As is known, the dispersion relation (5) imposes a restriction on the maximal value of the compression force. The stability of oscillations of a floating ice plate is guaranteed by the condition , whereas at the buckling occurs—the ice plate shatters (see, e.g., [2,22]). There is one more critical value of the parameter Q such that for the group velocity of FGW is positive for all wavenumbers . Such a case when is called normal dispersion in contrast to the case of anomalous dispersion for , which is characterised by the presence of a wavenumber interval within which the group velocity is negative (details can be found in [18]). Both critical values and , as well as the corresponding wavenumbers and , can be determined from the solution of two simultaneous equations and .
In this paper, we study a steady regime of fluid motion caused by the translationally moving and oscillating cylinder. In this case, the total potential of fluid velocity can be presented in the form:
where is the velocity potential corresponding to the uniform motion of the body with the unit velocity, () are the radiation potentials due to the cylinder oscillation in the horizontal () and vertical () directions and are the amplitudes of cylinder vibrations in these directions. Similar to Equation (8), the vertical displacements of the ice plate can be presented as:
The stationary part of the total potential satisfies the Laplace equation in the fluid:
with the boundary conditions at of
The boundary conditions far from the source are as follows:
where functions are equal to zero if the current speed U is less than the minimal phase speed of FGWs. If , then functions represent wave disturbances oscillating in x when .
On the circular contour , which represents the surface of the rigid cylinder, the impermeability condition is posted:
where = is the inner normal to the contour S and h is the distance of the cylinder centre from the upper boundary of the fluid .
The components of radiation potentials also satisfy the Laplace equation:
and the boundary conditions at are
where the operator .
The boundary condition on the cylinder circular contour is:
where .
In the far-field zone, when , wave perturbations consist of superposition of several periodic waves (the details are clarified below).
Hydrodynamic forces exerting on the cylinder, are determined by integrating the fluid pressure (less the hydrostatic term) along the contour S. It is convenient to replace this integral by the sum
where are the stationary force components (the wave resistance and lifting force) acting on a body in a stationary uniform flow, while are the radiation forces, which are usually written in the matrix form (for more details, see, e.g., [23]): . The quantities () represent a complex force acting in the j-direction and caused by sinusoidal oscillations of a body with a unit amplitude in the k-direction; they can be represented as . The real quantities and are known as the added mass and damping coefficients, respectively.
Let us introduce polar coordinates with the origin in the centre of the contour S, , . Then, taking into account that the components of the unit vector normal to the circular cylinder are
we obtain (see, e.g., [20]):
where symbol stands for complex conjugate.
In the next sections, we present solutions of stationary problem for the potential and non-stationary problem for the radiation potentials .
3. Solutions of the Stationary Problem
A solution to the stationary problem of the flow around a circular cylinder has been obtained by the method of multipole expansions by Li et al. [14]. Here, we present only the main results of this solution that are required further for the study of the radiation problem in Section 4. According to Ref. [14], the solution to Equation (10) with the boundary conditions (11)–(14) can be represented in the form:
with the unknown coefficients to be determined.
Using the well-known relation
and taking into account conditions (11) and (12) on the upper boundary of the fluid, we obtain a representation for the function in the form:
To take into account the boundary condition on the surface of the cylinder (14), we use the relationship:
Then, the stationary potential in the vicinity of the cylinder can be presented up to an insignificant constant in the form:
To calculate , let us do the following transformation:
The denominator in the integrand, which is the fourth-degree polynomial in k, can be represented as:
where are the roots of the polynomial. Then, we use the following expansion:
where the coefficients can be readily calculated from the solution of the corresponding system of linear algebraic equations obtained from the requirement of equality of the numerator on the right- and left-hand sides of Equation (31).
The polynomial on the left-hand side of Equation (30) can be presented in the form:
As was noted by Ref. [18], the equation
has real positive roots only for . The value of the minimum phase velocity of FGW is , where is defined as the real positive root of the equation:
According to Equation (32), all four roots in Equation (33) are complex if , whereas, when , there are two real positive roots and () and two complex roots and .
We further use the recurrent formulae to calculate the integrals arising in Equation (29) with the help of Equation (31). Let us denote
Before going ahead, let us take into account the Sommerfeld radiation condition at the big distances from the cylinder centre (in the far-field zone). This condition presumes that there are only outgoing waves generated by the moving cylinder, i.e., a wave with the wavenumber propagates co-current (counter-current), since its phase velocity is greater (less) than the group velocity. Then, for the real roots , we obtain:
Here, , and the symbols PV stands for the principal value of the integral. There is a recurrent formula for [24]:
where Ei is the exponential integral of a real argument.
For complex roots , Equation (35) reduces to:
where
and is the exponential integral of a complex argument [24]. Therefore, the integral term in Equation (29) can be presented as:
Differentiating Equation (28) with respect to r and using the boundary condition (14) with the relations (20), as well as the orthogonality of trigonometric functions, we obtain a system of linear algebraic equations for determining the coefficients in Equation (23):
where is the Kronecker symbol.
Substituting expression (29) in Equation (28) for and differentiating with respect to , we obtain for :
After that, the expressions for the stationary forces exerting on the cylinder as follows from Equation (21) are:
4. Solutions of the Radiation Problem
Now, let us determine the coefficients of the radiation load in Equation (22). To this end, we need to find the radiation potentials in Formula (8). Let us present the solution for the radiation potentials in the form:
Here, the unknown coefficients are to be determined. Taking into account the boundary conditions (16) and (17) for the radiation potentials and performing similar manipulations as in Section 3, we obtain the following relations:
where
Now, let us take into account the boundary condition (18) on the surface of the cylinder. Using relation (27), we can write down functions in the vicinity of the cylinder up to an insignificant constant in the form:
where
We present expressions for in a form similar to (29):
Functions in the denominator of the integrand in Equation (52) are fifth-degree polynomials; by analogy with Equation (30), they can be written in the form:
Then, one can use the decomposition:
where the coefficients are calculated from the solution of the corresponding systems of linear algebraic equations obtained from the requirement of equality of the numerator on the right- and left-hand sides of Equation (54).
The analysis of the real positive roots is performed separately for and . Below, we briefly present some information about the properties of these roots (for more details, see [18]). As follows from Equation (49) for , the roots must satisfy one of the equations:
The first equation in (55) defines the stationary points of function in the notation of the paper by Ref. [18]; it has at most two roots and () only at certain restrictions on the flow velocity U. The second equation in (55), which determines the stationary points of function in the notation of Ref. [18], always has one positive root; however, it can have two additional roots at certain restrictions on the magnitude of ice compression Q. We denote these roots by . As follows from the form of function in (48), it is easy to see that the roots must satisfy the equation:
This equation defines the stationary points of function in the notation of [18].
Equation (56) always has one positive root and, possibly, two additional roots at certain restrictions on the frequency of cylinder oscillation and flow velocity U. Let us denote these roots .
The direction of wave propagation determined by stationary points of functions and depends on the sign of the expression and, for function , on the sign of the expression , where k should be replaced by the wave numbers corresponding to the stationary points of each function . Waves with the positives value of these expressions propagate downstream (), whereas waves with the negative values of the expressions propagate upstream (). Therefore, the expressions of in Equation (52) can be transformed to the form:
Here, as in Equation (36), for the real roots , an additional term must be introduced such that for waves propagating downstream and for waves propagating upstream.
Let us return now to constructing a system of linear algebraic equations for determining the unknown coefficients in Equation (44). For calculating the second derivatives in the boundary conditions (18), we use the following relations [20]:
where .
Differentiating Equation (44) with respect to r and taking into account Equation (50) and the boundary conditions (18), we obtain the following systems of linear equations for the determining :
where
The quantities are given in Equation (57), where the recurrence Formulars (37) and (39) are used to calculate for the real and complex roots , respectively.
On the surface of the cylinder at , the values of the radiation potentials are:
5. Numerical Results
To investigate quantitatively the effect of ice plate cover on cylinder oscillation in infinitely deep water and the hydrodynamic forces exerting on the cylinder, we undertook numerical calculations with the following set of parameters:
Several ice-plate thicknesses were chosen to study its influence on FGWs and the hydrodynamic characteristics of the cylinder.
Calculations of wave resistance and lift force of a uniform flow around a circular cylinder submerged in a fluid of finite depth covered by ice were studied by Ref. [14]. Figure 6 of that work shows the dependence of the stationary forces on the current velocity for different fluid depths and, in particular, for an infinitely deep fluid. The following dimensionless values of hydrodynamic forces were used:
Note that, in the cited paper [14], the calculations were performed for the uncompressed ice plate () with the neglected inertia of the plate (); the thickness of the ice plate was chosen to be fixed, m, and the gravity constant was set to be m/s. Other parameters were the same as in Equation (65). In Figure 2, we present a comparison of the results obtained in [14] (solid black curve) with our calculations (red dots for and blue lines for kg/m). As one can see, the results of these studies agree very well for the same set of parameters. The influence of the inertial parameter M is small and can be neglected in most cases. The dimensionless value of the minimum phase velocity of the FGW is for and is for kg/m. The effect of the ice thickness on the characteristics of stationary hydrodynamic loads was studied in detail by Li et al. [14].

Figure 2.
(Color online.) The wave resistance and lift force as functions of the dimensionless velocity . Solid black lines (1) represent the results shown in Figure 6 of [14] for the infinitely deep fluid; red dots are the results of this work for ; blue lines (2) are the results of this work for kg/m.
Subsequent calculations presented below were performed for the ice thickness m and different values of the compression parameter . The following dimensionless parameters for the Froude number and frequency of cylinder oscillations are used below (the Froude number is determined here in terms of the cylinder radius):
For the used parameters, the critical dimensionless compression parameter, above which the anomalous dispersion of FGW occurs, is . When the numerical calculations were performed, the infinite sums in Equations (23) and (44) were replaced by finite sums which contained only the first terms. A further increase of N does not change the value of the first five significant figures of the hydrodynamic loads. Figure 3 shows the dependence of stationary hydrodynamic forces (43) for . The dimensionless values of the critical Froude numbers for the used values of are given in Table 1. Note that there are several definitions of a Froude number in the literature and their critical values, respectively (see, e.g., [5,14]). The Froude number can be defined through the total fluid depth H: , through the depth of a submerged body h: or through the radius of a submerged cylinder a, as in our case (see Equation (67) where index a is omitted for the sake of simplicity). In the fluid of a finite depth covered by ice, two critical values of the Froude number can be considered. One of them relates to the water speed exceeding the velocity of long linear waves , whereas the other relates to the water speed exceeding the minimal phase velocity of FGWs, . In our case of infinitely deep water, there is only one critical Froude number related to the minimal phase speed of FGWs as defined above.
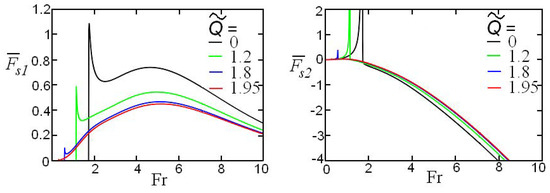
Figure 3.
(Color online.) The wave resistance and lift force as functions of the Froude number for different values of the compression parameter

Table 1.
Dependences of the parameters , and on the normalised compression parameter .
According to the kinematic properties of FGWs, the excitation of wave motion in the infinitely deep water can occur only for in the so-called super-critical regime. Therefore, the wave resistance is identically zero if (in the sub-critical regime). When the compression parameter is relatively small, the wave resistance sharply increases from zero to some finite value when the Froude number increases and passes through the critical value . Then, when the Froude number further increases, the wave resistance smoothly but non-monotonically decreases. The lift force in the sub-critical regime is positive and increases sharply when approaches ; then, it sharply decreases when and becomes negative. When the compression parameter increases, the jumps of wave resistance and lift force decreases in the vicinity of the critical value . For big Froude numbers, the effect of compression of the ice cover on the wave resistance decreases (see Figure 3, left).
To determine the hydrodynamic loads for the radiation problem, it is necessary to determine a number of generated waves in the far-field zone at the big distance from the cylinder centre. To this end, it is convenient to construct the ()-plane and determine regions in this plane where the number of generated waves is different. Examples of such diagrams are given in [18] for the thickness of ice plate m.
Figure 4 shows the configurations of the regions with the different number of generated waves for the thickness of the ice cover m and several values of the compression parameter . In the case of normal dispersion, the ()-plane is divided into four regions (see Figure 4a,b), whereas, in the case of the anomalous dispersion, into six regions (see Figure 4c,d). Small vertical arrows on the horizontal axis show the values of , and small horizontal arrows on the vertical axis show the values (see Table 1) where , and is such that the group velocity of FGWs, in Equation (7), has a minimum at .
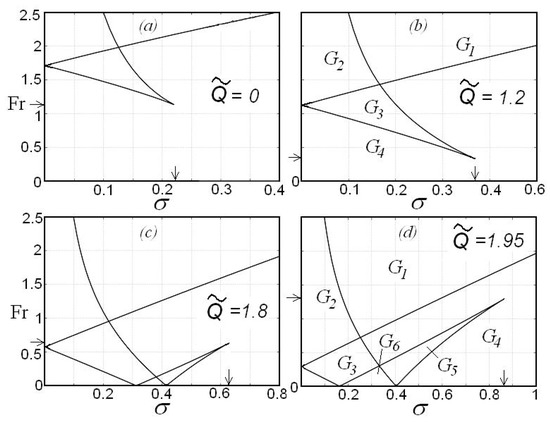
Figure 4.
Configuration of the domains for different values of the compression parameter . The thickness of the ice plate was m.
Table 2 shows the number of waves in the far-field zone and their direction of propagation for each region shown in Figure 4 ( pertains to the downstream propagating waves and to the upstream propagating waves).

Table 2.
The number of waves in the far-field zone.
The values of radiation loads (the added mass and damping coefficients) calculated by using Equations (22) and (64) for the Froude number and various values of the compression parameter are shown in Figure 5 (for ) and Figure 6 (for ). The dimensionless values of these quantities are defined as follows:
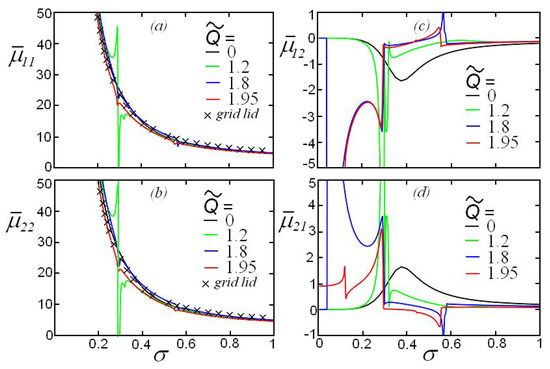
Figure 5.
(Color online.) The dependence of the added mass coefficients: on the dimensionless frequency of cylinder oscillation for and fixed Froude number . Crosses show the values of and for the fluid covered by a rigid lid.
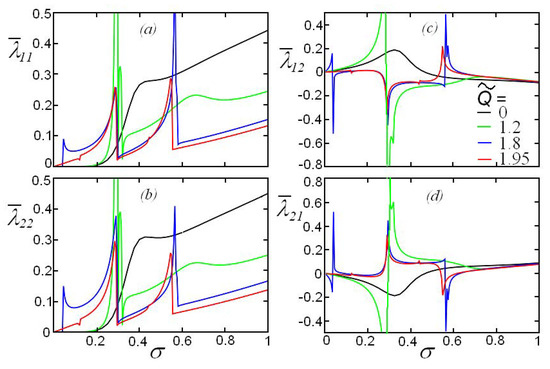
Figure 6.
(Color online.) The dependence of the added damping coefficients: on the dimensionless frequency of cylinder oscillation for and fixed Froude number .
As shown in Figure 5 and Figure 6, the hydrodynamic loads smoothly depend on the oscillation frequency only when since, in this case, for all frequencies and fixed Froude number , the boundaries of the regions are not crossed (see Figure 4a). In all other investigated cases of the compression parameter , there are sharp changes in the values of the hydrodynamic loads in the vicinity of the frequencies corresponding to the boundaries of the regions . The hydrodynamic loads in the vicinity of these frequencies can significantly exceed the corresponding values for the uncompressed ice when . For a given Froude number , the diagonal coefficients of the added mass matrix in the cases of uncompressed ice and rigid cover practically coincide; they are indistinguishable in Figure 5a,b.
Similar dependences of the hydrodynamic loads on the oscillation frequency are shown in Figure 7 and Figure 8 for the Froude number . In Figure 7a,b, the values of the added mass coefficients are practically indistinguishable for and . When the Froude number increases, the frequency dependences of hydrodynamic loads notable change even in the case of . In the vicinity of the frequency , there is a sharp change in the coefficients, since the considered value of the Froude number is close to the value of for (see Table 1).
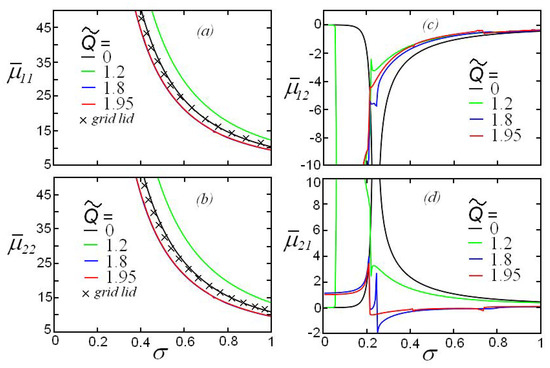
Figure 7.
(Color online.) The dependence similar to those shown in Figure 6 but for .
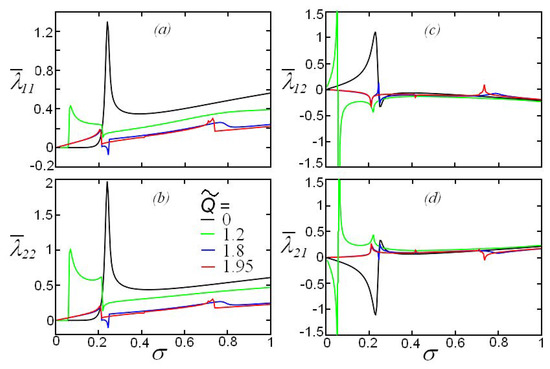
Figure 8.
(Color online.) The dependence similar to those shown in Figure 6 but for .
As is well known, at the superposition of the slow translational and oscillatory motion of a circular cylinder in a water with the free surface, the Timman–Newman symmetry conditions are satisfied [25]:
In the considered problem of cylinder motion under a compressed ice cover, the fulfillment of these conditions is observed for and , as well as for and .
An interesting feature of the considered problem is the possibility of appearance of negative values for the diagonal damping coefficients and for the Froude numbers corresponding to the decrease in the wave resistance with increasing cylinder velocity (the so-called falling wave resistance section). According to Figure 3, this phenomenon of wave resistance is observed when for all considered compression parameters. For the illustration, we show in Figure 9 the diagonal damping coefficients for .
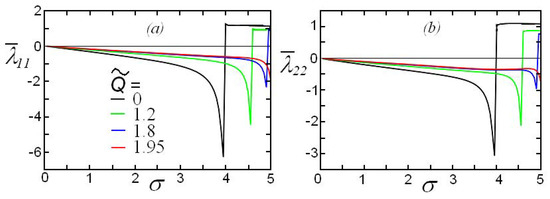
Figure 9.
(Color online.) The dependences of the diagonal damping coefficients (a) and (b) on the dimensionless frequency and Froude number .
Negative damping coefficients, apparently, were obtained for a first time by Newman [26] when he calculated the hydrodynamic loads exerting on an ellipsoid uniformly moving under the free surface of a homogeneous fluid and simultaneously oscillating along one of six degrees of freedom. It was noted that this phenomenon occurs only at high speeds of motion. Usually, the wave resistance increases when the speed increases at relatively low speeds, but then, when the speed becomes high enough, the wave resistance decreases when the speed of a body further increases. In this range of the velocities, the motion of an oscillating body in a fluid can be accompanied by the radiation instability when the amplitude of oscillations increases with time due to the pumping of energy into the oscillatory mode from the kinetic energy of the translational motion. The physical analysis of this phenomenon was carried out by [27] with the example of the motion of a small-radius sphere in a two-layer fluid. The complete solution of the linear radiation problem for a circular cylinder in a uniform flow of an infinite two-layer fluid made it possible to determine the dependences of hydrodynamic loads on the speed of the body and frequency of oscillations. Using these results, a system of ordinary differential equations was derived to describe the motion of a cylinder with two degrees of freedom, and the possibility of onset of non-decaying oscillations of the body was shown [21].
As the particular case of the radiation problem, let us consider radiation caused by the submerged oscillating cylinder without a translational speed, . In this case, the solution presented above significantly simplifies. In the expression for the radiation force in Formula (22), only the diagonal terms are non-zero, . The detailed solution to this problem is presented in [18]. The effect of ice compression on the hydrodynamic loads is illustrated in Figure 10. In this figure, one can see the frequency dependences of the added mass (Figure 10, left) and damping coefficient (Figure 10, right) for a few values of the parameter . In the first two cases, the normal dispersion of FGWs takes place, whereas, in the latter case, the dispersion is anomalous so that FGWs with the negative group velocities appear in the range of dimensionless frequencies (see Figure 4c). As shown in Figure 10, in the presence of ice compression, the extreme values of hydrodynamic loads significantly increase in the vicinity of frequencies where the group velocity of FGWs becomes very small or changes its sign.
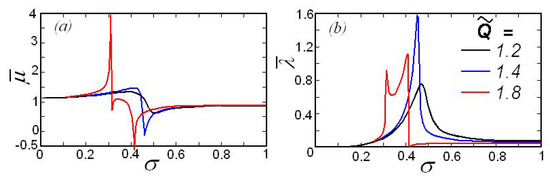
Figure 10.
(Color online.) The frequency dependences of the added mass (a) and damping coefficient (b) for a few values of the parameter .
6. Conclusions
As shown in this paper, ice cover provides a significant influence on the hydrodynamic loads of a cylinder in a uniform current. Even in the case when there is no mean flow and the cylinder experiences only oscillations, the added mass and damping coefficient can significantly differ from those values when there is no ice cover. Moreover, ice compression plays an important role by providing an increase in hydrodynamic loads within certain intervals of frequency of cylinder oscillation. The dependences of the added mass and damping coefficient on frequency have a resonant character (see Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10) with the extremal values in the vicinity of such frequencies where the group velocity of FGWs becomes very small or changes its sign. Such a situation when the group velocity is opposite to the phase velocity in a certain range of wavenumbers and the anomalous dispersion of FGWs occurs is realisable when the rate of ice compression is sufficiently high. The critical values of ice compression when the anomalous dispersion arises and then the buckling phenomenon appears were evaluated.
We also investigated the dependences of hydrodynamic loads (the added mass, damping coefficients, wave resistance and lift force) exerted on the cylinder that is uniformly moving and oscillating. It was shown that there is such a regime of motion when negative values for the damping coefficients occur. Such a phenomenon is well-known in the case of a body moving with oscillations beneath a free surface [26,27]. Here, we demonstrated that a similar phenomenon can occur in the ocean covered by compressed ice and investigated the dependence of the effect on the degree of compression. As shown in Figure 9, the maximal negative value of the damping coefficients decreases with the increase of ice compression and shifts toward the high frequencies.
The results obtained can be useful in the design of underwater pipelines and other engineering constructions in the marine zones covered by ice. Tidal flows and other currents can produce significant loads on the constructions and lead to the development of instabilities with big-amplitude oscillations. Here, a rather idealised model was considered where the viscosity and nonlinearity effects were neglected. The influence of these factors on the flow around a cylinder and hydrodynamic loads deserves further study but leads to a significant complication of the problem. Solution of such a problem cannot easily be obtained by analytical methods; however, contemporary numerical packages such as ANSYS CFD can be used. It is also worth mentioning that, as shown in [28], the influence of nonlinearity in the problem of moving loads on ice sheets becomes notable for rather big-amplitude FGWs. The influence of viscosity and nonlinearity in the general problem of ocean waves and ice interaction is reviewed in [1]. When our paper was ready and submitted for publication, we become aware of an interesting preprint [29] where the two-dimensional nonlinear problem of steady flow around a body submerged in water covered by an elastic sheet is considered. Compression forces are ignored in this paper but can be considered in the future.
Any experimental work in this field is also a topical problem. To the best of knowledge, there are no publications reporting experimental data on forces exerted on a submerged and oscillating cylinder in the ice-covered ocean or sea. In a recently published paper by [30], the results of laboratory experiments of investigation of hydrodynamic forces exerted on a semi-submerged cylinder in water with a free surface under an oscillatory flow are reported. Based on the main hydrodynamic features, a novel empirical formula for the prediction of the lift forces on a cylinder is proposed. In our paper, the hydrodynamic forces are calculated numerically on the basis of the derived analytical formulae. Further experimental work in this field is highly desirable.
Author Contributions
Conceptualisation, Y.S. and I.S.; methodology, Y.S. and I.S.; software, I.S.; validation, I.S.; formal analysis, Y.S. and I.S.; investigation, Y.S. and I.S.; resources, I.S.; writing—original draft preparation, I.S.; writing—review and editing, Y.S. and I.S.; and visualisation, I.S. All authors have read and agreed to the published version of the manuscript.
Funding
Y.S. acknowledges the funding of this study provided by the grant SPARC/2018-2019/P751/SL through the Scheme for Promotion of Academic and Research Collaboration of the Ministry of Human Resource Development, Government of India, by grant No. FSWE-2020-0007 through the State task program in the sphere of scientific activity of the Ministry of Science and Higher Education of the Russian Federation, and grant number NSH-2685.2018.5 provided by the President of Russian Federation for the State support of leading Scientific Schools of the Russian Federation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data of numerical calculations are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| water density |
| ice density |
| thickness of the ice plate |
| g acceleration due to gravity |
| E Young’s modulus of elastic plate |
| Poisson ratio |
| ice rigidity |
| Q longitudinal ice stress |
| first critical value of the stress parameter when the anomalous dispersion occurs |
| second critical value of the stress parameter when the ice buckling occurs |
| parameter describing the inertial property of ice |
| phase velocity of FGWs |
| group velocity of FGWs |
| a cylinder radius |
| frequency of cylinder oscillations |
| Froude number in terms of the cylinder radius a |
| normalised wave resistance in the stationary flow |
| normalised lift force in the stationary flow |
| a complex matrix of radiation forces |
| a real matrix of added masses |
| a real matrix of damping coefficients |
| normalised added mass coefficient |
| -normalised damping coefficient |
Abbreviations
The following abbreviation is used in this manuscript:
| FGW | flexural-gravity wave |
References
- Squire, V.A. Ocean wave interactions with sea ice: A reappraisal. Annu. Rev. Fluid Mech. 2020, 52, 37–60. [Google Scholar] [CrossRef]
- Kheisin, D.Y. Dynamics of Floating Ice Cover; Technical English Translation in: FSTC-HT-23-485-69, U.S. Army Foreign Science and Technology Center; Gidrometeoizdat: Leningrad, Russia, 1967. (In Russian) [Google Scholar]
- Krasil’nikov, V.V. On excitation of flexural-gravity waves. Akust. Zhurnal 1962, 8, 133–136. (In Russian) [Google Scholar]
- Sahoo, T. Mathematical Techniques for Wave Interaction with Flexible Structures; CRC Press: New York, NY, USA, 2012. [Google Scholar]
- Squire, V.A.; Hosking, R.J.; Kerr, A.D.; Langhorne, P.J. Moving Loads on Ice Plates; Springer: Berlin, Germany, 1996. [Google Scholar]
- Sturova, I.V. Unsteady three-dimensional sources in deep water with an elastic cover and their applications. J. Fluid Mech. 2013, 730, 392–418. [Google Scholar] [CrossRef]
- Davys, J.W.; Hosking, R.J.; Sneyd, A.D. Waves due to a steadily moving source on a floating ice plate. J. Fluid Mech. 1985, 158, 269–287. [Google Scholar] [CrossRef]
- Il’ichev, A.T.; Savin, A.A.; Savin, A.S. Formation of wave on an ice-sheet above the dipole, moving in a fluid. Dokl. Phys. 2012, 57, 202–205. [Google Scholar] [CrossRef]
- Pavelyeva, E.B.; Savin, A.S. Establishment of waves generated by a pulsating source in a finite-depth fluid. Fluid Dyn. 2018, 53, 461–470. [Google Scholar] [CrossRef]
- Savin, A.A.; Savin, A.S. Ice cover perturbation by a dipole in motion within a liquid. Fluid Dyn. 2012, 47, 139–146. [Google Scholar] [CrossRef]
- Savin, A.A.; Savin, A.S. Waves generated on an ice cover by a source pulsating in fluid. Fluid Dyn. 2013, 48, 303–309. [Google Scholar] [CrossRef]
- Savin, A.A.; Savin, A.S. Three-dimensional problem of disturbing an ice cover by a dipole moving in fluid. Fluid Dyn. 2015, 50, 613–620. [Google Scholar] [CrossRef]
- Schulkes, R.M.S.M.; Hosking, R.J.; Sneyd, A.D. Waves due to a steadily moving source on a floating ice plate. J. Fluid Mech. 1987, 180, 297–318. [Google Scholar] [CrossRef]
- Li, Z.F.; Wu, G.X.; Shi, Y.Y. Interaction of uniform current with a circular cylinder submerged below an ice sheet. Appl. Ocean Res. 2019, 86, 310–319. [Google Scholar] [CrossRef]
- Das, S.; Kar, P.; Sahoo, T.; Meylan, M.H. Flexural-gravity wave motion in the presence of shear current: Wave blocking and negative energy waves. Phys. Fluids 2018, 30, 106606. [Google Scholar] [CrossRef]
- Das, S.; Sahoo, T.; Meylan, M.H. Dynamics of flexural gravity waves: From sea ice to Hawking radiation and analogue gravity. Proc. R. Soc. A 2018, 474, 2017223. [Google Scholar] [CrossRef]
- Das, S.; Sahoo, T.; Meylan, M.H. Flexural-gravity wave dynamics in two-layer fluid: Blocking and dead water analogue. J. Fluid Mech. 2018, 854, 121–145. [Google Scholar] [CrossRef]
- Stepanyants, Y.; Sturova, I. Waves on a compressed floating ice plate caused by motion of a dipole in water. J. Fluid Mech. 2021, 907, A7. [Google Scholar] [CrossRef]
- Wu, G.X. Hydrodynamic forces on a submerged cylinder advancing in water waves of finite depth. J. Fluid Mech. 1991, 224, 645–659. [Google Scholar] [CrossRef]
- Wu, G.X. Radiation and diffraction of water waves by a submerged circular cylinder at forward speed. J. Hydrodyn. Ser. B. 1993, 5, 85–96. [Google Scholar]
- Sturova, I.V. Radiation instability of a circular cylinder in a uniform flow of a two-layer fluid. J. Appl. Math. Mechs. 1997, 61, 957–965. [Google Scholar] [CrossRef]
- Bukatov, A.E. Waves in the Sea With a Floating Ice Cover; Marine Hydrophys. Inst.: Sebastopol, Ukraine, 2017; Available online: http://mhi-ras.ru/news/news201802151133.html (accessed on 12 March 2021). (In Russian)
- Newman, J.N. Marine Hydrodynamics; The MIT Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Applied Mathematics Series. 55 (Ninth Reprint with Additional Corrections of Tenth Original Printing with Corrections; National Bureau of Standards; Dover Publications: New York, NY, USA, 1983. [Google Scholar]
- Wu, G.X.; Eatock Taylor, R. Reciprocity relations for the hydrodynamic coefficients of bodies with forward speed. Intl. Shipbuild. Prigr. 1988, 35, 145–153. [Google Scholar]
- Newman, J.N. The damping of an oscillating ellipsoid near a free surface. J. Ship Res. 1961, 5, 44–58. [Google Scholar]
- Gaponov-Grekhov, A.V.; Dolina, I.S.; Ostrovsky, L.A. The anomalous Doppler effect and radiative instability of the motion of oscillators in hydrodynamics. Sov. Phys. Docl. 1983, 28, 117–119. [Google Scholar]
- Dinway, E.; Kalisch, H.; Părău, E.I. Fully dispersive models for moving loads on ice sheets. J. Fluid Mech. 2019, 876, 122–149. [Google Scholar] [CrossRef]
- Semenov, Y.A. Nonlinear flexural-gravity waves due to a body submerged in the uniform stream. arXiv 2021, arXiv:2103.02573v1. [Google Scholar]
- Ren, H.; Fu, S.; Liu, C.; Zhang, M.; Xu, Y.; Deng, S. Hydrodynamic forces of a semi-submerged cylinder in an oscillatory flow. Appl. Sci. 2020, 10, 6404. [Google Scholar] [CrossRef]
Short Biography of Authors
 | Yury Stepanyants graduated in 1973 with the HD of MSc Diploma from the Gorky State University (Russia) and started to work as the Engineer with the Research Radiophysical Institute in Gorky. Then, he proceeded his career with the Institute of Applied Physics of the Russian Academy of Sciences (Nizhny Novgorod) taking successively the positions of Junior, Senior, and Leading Research Scientist from 1977 to 1997. In 1983 Yury obtained a PhD in Physical Oceanography, and in 1992 he obtained a degree of Doctor of Sciences in Geophysics. After immigration in Australia in 1998, Yury worked for 12 years as the Senior Research Scientist with the Australian Nuclear Science and Technology Organisation in Sydney. Since July 2009 he holds a position of Full Professor at the University of Southern Queensland in Toowoomba, Australia. Yury has published more than 100 journal papers, 3 books, several review papers and has obtained 3 patents. His major scientific interests are in: Hydrodynamics and geophysical fluid mechanics; Theory of nonlinear oscillations and waves; Exact and asymptotic solutions of nonlinear equations; Mathematical modelling and computational physics. |
 | Izolda Sturova graduated from Novosibirsk State University in 1964 and began working at the Institute of Hydrodynamics where she works until now. She took the positions of: the Intern-Researcher, Junior Scientist (since 1967), Senior Scientist (since 1976), Leading Research Scientist (since 1988), Head of a Sector (since 1991), and Chief Scientist (from 1998 to present time). In 1972 she obtained a PhD degree in Fluid Mechanics, and in 1995 the degree of Doctor of Sciences in Fluid Mechanics. Izolda is the author of over 100 scientific publications, including one monograph. Her research interests are: surface, internal and flexural-gravity waves, hydroelastic properties of ice and floating platforms. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).