Abstract
River training and river restoration often imply modifying the patterns and dimensions of bars, channels, and pools. Research since the 1980s has greatly advanced and matured our knowledge on the formation and behavior of river bars, thanks to field work, laboratory experiments, theoretical analyses, and numerical modelling by several research groups. However, this knowledge is not easily accessible to design engineers, river managers, and ecologists who need to apply it. This is mainly due to confusing differences in terminology as well as to difficult mathematical theories. Moreover, existing scientific publications generally focus on specific aspects, so an overall review of the findings and their applications is still lacking. In many cases, the knowledge achieved so far would allow minimizing hard engineering interventions and thus obtaining more natural rivers. We present an integrated review of the major findings of river bar studies. Our aim is to provide accessible state-of-the-art knowledge for nature-based bar management and successful river training and river restoration. To this end we review the results from analytical, numerical, experimental, and field studies, explain the background of bar theories, and discuss applications in river engineering and river restoration.
1. Introduction
River bars are large sediment deposits, separated by channels, emerging during low flows. The presence and dynamics of these deposits are at the heart of many river engineering problems, since bars may block water intakes, hinder navigation, and reduce the water conveyance under bridges (Figure 1). Bars are also associated with local scour and bank erosion, which may undermine bridge piers and hydraulic structures, such as groynes. Finally, bars form important fluvial or riparian habitats, and for this reason the restoration of bars is a common goal in river rehabilitation projects (e.g., [1]). However, despite their great practical importance, no general treatise on how to deal with bars is available.

Figure 1.
(a) Gravel-bars under a bridge, Tagliamento River, Italy (courtesy of Paolo Reggiani); (b) sediment sorting on a bar in the River Adige, at Castelvecchio Bridge, Verona, Italy.
Bar studies include theoretical analyses [2,3,4,5,6,7,8,9,10,11], field observations [12,13,14], numerical modelling [3,15,16,17,18,19,20,21], as well as experimental investigations [22,23,24,25,26]. A comparative analysis integrating the results of these works is still lacking, so practitioners are confronted with publications treating only specific aspects of the overall picture. The use of different terminologies to distinguish different types of bars adds confusion, some terminologies related to mechanistic explanations (e.g., free bars, steady bars, forced bars, spatial bars, hybrid bars, migrating bars, central bars, braid bars), other terminologies to shapes (e.g., longitudinal bars, diagonal bars, transverse bars, crescentic bars, medial bars [27]).
In this paper, we seek to integrate the results from theoretical analyses, numerical simulations, laboratory experiments, and field observations by different research groups, and to translate those results in an accessible way for applications. We propose practical definitions to clearly distinguish the different types of bars and describe the factors influencing their formation. We summarize the insights gained and discuss applications of the present knowledge in river engineering.
2. Summary of Bar Studies
2.1. Bar Classification and Terminology
Bars have horizontal sizes that scale with the width of the main river channel and heights that scale with the bankfull water depth [28]. Bars can appear as single or periodic alternations of shoals, accompanied by deeper pools.
Single bars form at geometrical features or discontinuities of the river channel causing a permanent flow perturbation or “forcing,” such as structures, exposed bedrock, confluences, bends, or bankline irregularities. Classic examples of these “forced bars” are the point bars that form inside a river bend (Figure 2a) and the central bar that forms in locally wider sections (Figure 2b).

Figure 2.
(a) Rhine River, the Netherlands. Point bar inside a river bend, forced by channel curvature, hinders navigation. Flow direction from top to bottom. (b) Cauca River, Colombia. Compound central bar forced by a local width expansion. Flow direction from bottom to top.
Periodic bars develop from an instability phenomenon that arises as a response to water flowing over loose material under certain hydraulic and sediment mobility conditions. They appear as double-harmonic waves of the riverbed surface (Figure 3), i.e., with transverse and longitudinal wavelengths, and are either steady or migrating. The periodic bars that form in straight channels without any forcing are indicated as “free bars” and are typically migrating in downstream or sometimes upstream direction [29]. The presence of forcing, causing a permanent flow configuration at a certain location, fixes the location of the bars, at least for a certain distance, which then become steady. These periodic bars are called “hybrid bars”, because they depend on both morphodynamic instability and forcing (Figure 4). There is a relation between bar celerity and bar size so that migrating bars are generally shorter than steady bars [26].

Figure 3.
Tagliamento River, Italy. Multiple free bars have merged into large compound bars.
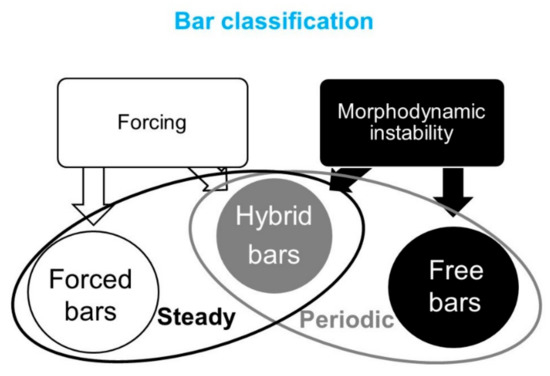
Figure 4.
Bar classification after Duró et al. [19].
The presence of hybrid bars in alluvial rivers was first recognized from a large oscillation in the longitudinal profile of point bars inside river bends, and for this reason these bars were first recognized as an “overshoot” [3] or “overdeepening” phenomenon [4,9]. They were later named “forced bars” to distinguish them from the “free bars,” highlighting their dependency on forcing. However, this term did not allow distinguishing them from the single bars that arise close to the source of forcing which do not originate from morphodynamic instability but from local perturbation. This ambiguity was discussed by Eekhout et al. [13] and Rodriguez et al. [14] and was resolved by Duró et al. [19], who introduced the term “hybrid bars.”
Alluvial rivers present different bar patterns, ranging from alternate bars that alternatingly form at the left and the right bank, central bars that form in the middle of the channel, and multiple bars that appear as several bars in each cross-section (Figure 3). The terms “mid-channel bar” and “braid bar,” often encountered in the literature, refer to bars in the middle of the channel and to a single component of a multiple-bar system, respectively.
2.2. Linear Bar Theories
Mathematical theories on river bars are generally based on depth-averaged and turbulence-averaged equations for the motion of water and sediment. The motion of water is represented by hydrodynamic equations, expressing conservation of mass and momentum, along with relationships for hydraulic resistance and the effects of curvature-induced helical flows. The motion of sediment is represented by a sediment mass balance, as well as by relationships for sediment transport rate and direction. The averaging over depth implies that the equations are inaccurate close to the banks where vertical flow components are significant. It also implies that detailed flow features around smaller bedforms, such as flow separation, are not represented explicitly but accounted for by tuning the parameters of the relationships for resistance and sediment transport. The averaging over turbulence implies that sediment transport capacity depends on the mean flow features, without any influence from variations in turbulence intensity. The resulting set of equations and relationships has been implemented in numerical models, but it cannot be solved analytically. Analytical solution requires further simplification and, hence, involves further simplifying assumptions that limit the validity of the model. The art of mathematical analysis consists of introducing simplifications that do not compromise the essential behavior of the physical system while keeping track of the validity limits in applications and interpretation. Theoretical results are nonetheless also useful beyond their strict limits of validity, as reasonable estimates for rapid assessment or as qualitative indicators for the effects of changed conditions.
A first major simplification is linearization. The formal procedure for this is expansion into Taylor series, but the principle is explained more easily as follows. Suppose that the flow depth, h, can be decomposed into a constant average value, h0, and a deviation from this value, h′, that varies in time and space: . The average flow depth corresponds to a flat riverbed without bars. The deviation, or perturbation, corresponds to a superimposed pattern of bars and pools. Suppose that the square of the flow depth, h2, appears somewhere in the equations. This can then be elaborated as: . The key assumption of linearization is that the perturbation is much smaller than the average value, also called “basic state”: h′ << h0. This justifies neglecting (h′)2. The remaining is then substituted for h2 in the equations, along with similar substitutions for other nonlinear terms. The basic state, however, is already known to be a solution of the set of equations. Subtracting the corresponding basic-state equations for h0 from the perturbed equations results in a set of equations for the perturbation, h′, only. These are the equations that describe the pattern of bars and pools.
The next step consists of assuming that all perturbations can be represented by harmonic functions (exponential functions, sines, and cosines). This assumption rests on the Fourier theorem that any arbitrary function can be represented by a sum of harmonic functions. Not explaining this explicitly has been a source of reservations against linear bar theories. For instance, Rhoads and Welford [30] question the postulation of such a harmonic perturbation instead of a random perturbation. The Fourier theorem implies, however, that random perturbations are composed of harmonic perturbations. The one with the fastest growth rate emerges as the dominant initial pattern of bars.
The simplifications and assumptions result in a characteristic system of equations describing the relation between bar wavelength, migration speed (celerity), and rates of growth or damping in time and space. The final bar amplitude is not a part of this but requires a nonlinear approach, since it cannot be described by a small perturbation of the local water depth. Figure 5 shows that the bar pattern is periodic in longitudinal and transverse direction. In theory, the transverse bar wavelength is equal to an integer m times two channel widths, where m is the “bar mode.” Different ratios between transverse wavelength and channel width result in different bar patterns: alternate, central, and multiple. The bar mode corresponds to the number of parallel rows of alternate bars that can be distinguished in the channel (Figure 5) and thus m can be used to represent the bar pattern.
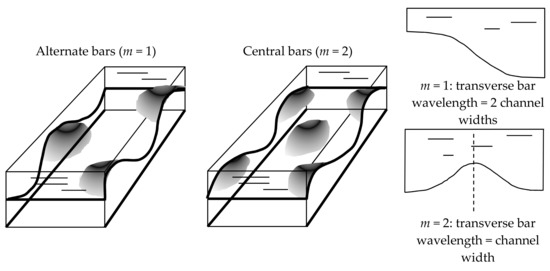
Figure 5.
Longitudinal and transverse bed oscillations caused by the presence of alternate and central (periodic) bars. Alternate bars: one row of alternate bars in the channel (m = 1). Central bars: two parallel rows of alternate bars in the channel (m = 2).
The characteristic system of equations has been analyzed further in two different approaches, which Parker and Johanneson [4] termed “Genoa approach” and “Delft approach.” The Genoa approach assumes that the channel is infinitely long without any irregularities in the bank lines. The bar amplitude can then be assumed constant in longitudinal direction. The resulting stability analysis reveals the conditions for incipient growth of free bars without forcing, following the approach developed by Hansen [31] and Engelund [32]. These conditions are represented by marginal stability curves, one for each bar mode, m, indicating the limits of stable-bed conditions, intended as channel beds without m-mode bars. Above these curves, incipient m-mode bars grow with time. Below these curves, incipient bars decay, and no m-mode bar pattern forms [33]. Mode, longitudinal wavelength, growth rate, and celerity of free bars mainly depend on flow width-to-depth ratio, with higher bar modes forming at larger width-to-depth ratios. It is particularly important to consider that no free bars form on the riverbed below a critical value of the width-to-depth ratio (critical value for bar formation), which defines the limit for stable alluvial channels (i.e., channels without any bars). This means that bars are expected to form only if the flow width-to-depth ratio is larger than the critical value. Since bars depend also on sediment mobility, represented by the Shields number, and to a minor extent on other parameters too, the critical value of width-to-depth ratio varies from river to river.
Combining the bar stability analysis with the bend stability analysis of Ikeda et al. [34], Blondeaux and Seminara [2] identified a resonance point for which free alternate bars with constant amplitude have zero celerity, enabling the forcing of channel bend growth. Zolezzi and Seminara [29] found that this point separates two bar regimes: sub-resonant, with width-to-depth ratios smaller than the resonant one and bars migrating in downstream direction; and super-resonant, with width-to-depth ratios larger than the resonant one and bars migrating in upstream direction.
The Delft approach focuses on the periodic steady bars that develop in unstable channels in presence of forcing hybrid bars [3,10,35]. The source of forcing can be a channel bend, a structure, a width restriction or expansion, etc. The channel is not assumed to be infinitely long, and the bar amplitude can increase or decrease in longitudinal direction. The 2D linearized system of equations describes flow velocity and water depth variations related to steady incipient bars of a specific mode. A cross-section with prescribed constant flow velocity and water depth perturbations represents a boundary that forces the system. By neglecting temporal variations, bars are assumed to be steady in the sense that they do not migrate, grow, or decay. This “equilibrium bar state” describes wavelength and longitudinal amplitude variation of incipient bars, because the linearization removes the influence of nonlinear effects on the wavelength and longitudinal amplitude variation of fully developed hybrid bars.
The two approaches of Genoa and Delft focusing on free and hybrid bars, respectively, have in common the resonance point [4,9], where free bars have zero celerity and hybrid bars have constant amplitude. All bar modes have their resonance point (Table 1).

Table 1.
Approaches in bar studies.
2.3. Nonlinear Bar Theories
Linear theories provide information on changes in bar amplitude in time and space, but they cannot predict the actual values of bar amplitude. This requires a nonlinear approach. Both weakly nonlinear and fully nonlinear theories have been developed for this. Weakly nonlinear theories [5,7] are extensions of linear theories of free bars. They also assume that perturbations of a flatbed are harmonic and much smaller than the flow depth. Here Eckhaus [36] distinguishes two levels of “small,” “infinitesimally small” amplitudes for linear analysis and “finite small” amplitudes for nonlinear analysis. River bar amplitudes, however, are not small in either of these senses and, accordingly, the results of Colombini et al. [5] show that their weakly nonlinear analysis predicts just the order of magnitude of experimentally observed amplitudes, with considerable scatter. Another limitation is that this type of analysis is formally limited to a small range of width-to-depth ratios close to the smallest width-to-depth ratio for which bars are formed, i.e., close to the minimum of the marginal stability curve [5]. Nonetheless, weakly nonlinear analyses have given useful insights in the growth toward a finite amplitude [5] and the effects of discharge variations [37] and suspended sediment transport [38].
Fully nonlinear theories have been elaborated for the shape of cross-sections in river bends, to calculate pointbar height along inner bends and pool depth along outer bends. These theories neglect variations in streamwise direction and therefore refer to the constant cross-section of an infinitely long bend. As this hypothetical condition implies a river spiraling down around a vertical axis, this approach is called “axisymmetric” [3].
2.4. Numerical Modelling
The advantage of numerical approaches lies in the full non-linearity of the equations they solve, allowing the simulation of bar development beyond their incipient state and far from their critical conditions. Struiksma et al. [3], pioneers in morphodynamic simulations, showed that a 2D model is capable of reproducing what they called “the overshoot effect”: a waving channel bed inside river bends due to the presence of hybrid bars superimposed on forced point bars. Nelson [15] studied the elongation of bars from incipient to fully developed conditions.
Numerical models have also the advantage of allowing analyzing the morphodynamic processes of river channels with spatially varying characteristics and non-uniform sediment. Including bank erosion, Jang and Shimizu [39] studied the effects of irregular bank strength on free alternate bar processes, finding that channel widening slows down the celerity and reduces the height of free bars. This is in agreement with the results of the linear analysis of Zolezzi and Seminara [29] if the bar regime is sub-resonant. Duró et al. [19] analyzed the effects of groynes and other types of channel restrictions or expansions on hybrid bar formation, showing that the intensity of forcing exerted by groynes of different lengths determines the growth rate and the location where hybrid bars form. But the intensity of forcing does not affect their wavelength and amplitude, which are determined by the morphodynamic characteristics of the system. Duró et al. also showed that imposing a symmetric flow forces central bar formation and that imposing an asymmetric flow forces alternate bars even beyond their linear instability range, but just for a limited distance. After that distance, hybrid bars acquire the mode that pertains to local morphodynamic characteristics, described by width-to-depth ratio, sediment size, and mobility, etc. Singh et al. [20] studied the effects of sediment heterogeneity on bar mode in gravel-bed braided rivers, indicating the limits of assuming uniform sediment. Cordier et al. [21] analyzed sediment sorting in straight channels with series of free or hybrid bars, showing that coarser sediment accumulates on bar tops if bars are migrating, but accumulates in deeper parts if bars are steady.
The evolution of bars from incipient to fully developed conditions has been simulated with 2D and 3D models, visualizing the merging phenomenon that occurs in broad shallow channels with multiple bars. Merging gradually decreases the bar mode through the formation of compound bars e.g., [18,20,40].
2.5. Laboratory Investigations
Bar processes have been studied in laboratory flumes since the 1970s [41]. Based on his experimental results, Ikeda [42] developed an empirical method to assess the wavelength and the amplitude of free alternate bars. Fujita and Muramoto [22] studied the free-bar evolution in a straight flume, showing that these bars elongate with time until they attain a stable length. Crosato et al. [26] showed that free alternate bars might present an unstable behavior, as they observed them to flatten suddenly repeatedly all together and then to reform. This was attributed to a forcing from the boundaries. Lanzoni performed long series of experiments in a straight channel with uniform [23] and non-uniform [24] sediment, observing that non-uniform sediment results in bars with smaller amplitude and that bars tend to become steady if the coarser fraction is only partly mobile. The formation of hybrid alternate bars has been generally obtained in the laboratory by adding some forcing, created by placing a transverse plate at the upstream boundary. Generally forming in the upstream half of the flume close to the source of forcing, hybrid bars were found to have wavelengths two to three times longer than those of the free bars that formed in the second half of the flume [23,25,35]. In general, hybrid bars were found to have wavelengths on the order of 10–15 times the channel width, but shorter wavelengths are also possible [35].
Kinoshita and Miwa [41] studied the interaction between free alternate bars and point bars, finding that free bars can migrate through sinuous channels but that a critical curvature exists that prevents their migration. Whiting and Dietrich [43] performed laboratory experiments in mildly to strongly sinuous channels to study migrating bar stabilization by channel bends and tested existing linear theories.
The effects of vegetation on river pattern and bars were studied in the laboratory by Tal and Paola [44], who observed that riparian vegetation reduces the channel width, and consequently also the bar mode, and thus the degree of river braiding. Later, Vargas-Luna et al. [45], showed that riparian vegetation shortens alternate hybrid bars and that further colonization of bar tops tends to elongate them.
2.6. Field Observations
Field observations show that free alternate bars are common in channelized river systems whereas in natural rivers hybrid bars are more common than free bars. This is due to the forcing by numerous long-lasting geometrical features and discontinuities, such as spatial width variations, structures protruding in the river channel, meanders, tributaries, bedrock, bridge piers, etc.
Leopold [46] made quantitative measurements of migrating and hybrid alternate bars, including migration rates and wavelengths, in the channelized reach of the Colorado River and in straight reaches between channel bends of Baldwin Creek and East Fork. Jaeggi [47] studied the alternate bars in the straightened and narrowed Rhine River at the border between Switzerland and Liechtenstein. Ferguson et al. [48] analyzed alternate bar processes in an almost straight channelized river, providing their geometry and migration rates. Eekhout et al. [13] monitored the formation and evolution of bars in a 600 m long reach of a recently restored stream in the Netherlands. In the first three years after restoration alternate bars appeared and then gradually elongated during high-flow events. Because of their low dynamics, Eekhout et al. classified these bars as steady. Rodrigues et al. [14] studied the dynamics of bars in a channel expansion of the Loire River, showing the alternating formation of central and lateral bars as a response to discharge variations. Adami et al. [49] analyzed the long-term dynamics of the alternate bars that characterize the morphology of the channelized Rhine River in the same reach as studied by Jaeggi [47]. They provide a detailed description of bar and river characteristics and their evolution with time. Multiple-bar dynamics in gravel-bed braided rivers were observed, among others, by Ham and Church [50].
Caruso et al. [51] studied the effects of vegetation on the braided Ahuriri River in New Zealand and found that vegetation correlates with the frequency of occurrence of high flows, showing that by reducing the flood intensity, river damming would promote the colonization of bar tops and riverbanks by vegetation. The interactions between free bars and colonizing vegetation has been recently analyzed on the dammed Isère River by Serlet et al. [52], who found that colonization by vegetation transforms free migrating alternate bars in much longer and steady hybrid bars.
3. Summary of Insights Gained
The following insights have been gained from combining the results of linear and nonlinear bar theories with the results of laboratory experiments, numerical modelling, and field observations:
- (1)
- Fluvial bars can be divided into forced bars, occurring locally, and periodic bars, occurring as rhythmic sequences of more or less similar bars.
- (2)
- Forced bars are generated by local geometry or discontinuity. Examples are point bars at inner bends, confluence bars at tributary junctions, and eddy bars at locations of flow separation.
- (3)
- Periodic bars result from morphodynamic instability of the riverbed. The influence of physical parameters on their features can be understood from linear and nonlinear theoretical analyses of the fundamental mathematical equations for the motion of water and sediment.
- (4)
- Periodic bars can be divided into free bars, migrating through the river, and hybrid bars, which have fixed positions because at least one of the bars in the sequence is forced locally.
- (5)
- The river pattern can be characterized by the bar mode, which represents the number of bars in cross-sections. Alternate bars are typical of meandering rivers whereas multiple bars characterize braided rivers.
- (6)
- The major parameter governing bar length, bar growth rate, bar migration speed (celerity), and bar mode is the width-to-depth ratio of the flow. Periodic bars do not develop if the width-to-depth ratio is below about 10. Channels become braided at width-to-depth ratios larger than about 50. Forced bars do not depend on morphodynamic instability and can occur at width-to-depth ratios below the critical value for the formation of periodic bars.
- (7)
- The wave lengths of hybrid alternate bars are 10–15 times the channel width. The wave lengths of free bars at the same width-to-depth ratio are two to three times smaller.
- (8)
- The longer the bar, the smaller the migration speed.
- (9)
- Observed bar migration is not necessarily associated with free bars. It can also result from elongation during the development of a pattern of hybrid bars, as observed experimentally [26], numerically [15], and in the field [14]. Bars forced during floods at locations of overbank flows migrate too after the fall of the flood, while being eroded away gradually.
- (10)
- Migrating bars can be distinguished from non-migrating bars by their shape. They present a clear migration front and tend to be triangular (Figure 6).
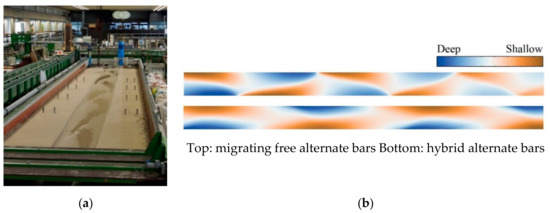 Figure 6. (a) Free bars migrating in downstream direction in the laboratory. Flow direction from bottom to top (courtesy of Andrés Vargas-Luna). (b) Comparison between the shape and size of free bars migrating in downstream direction (channel above) and of steady hybrid bars (channel below) obtained with identical boundary conditions in a 2D numerical model constructed with the Delft3D code (courtesy of Le Thai Binh). Flow direction from left to right.
Figure 6. (a) Free bars migrating in downstream direction in the laboratory. Flow direction from bottom to top (courtesy of Andrés Vargas-Luna). (b) Comparison between the shape and size of free bars migrating in downstream direction (channel above) and of steady hybrid bars (channel below) obtained with identical boundary conditions in a 2D numerical model constructed with the Delft3D code (courtesy of Le Thai Binh). Flow direction from left to right. - (11)
- The intensity of the forcing determines the location of hybrid bars, but it does not alter the bar mode. The type of forcing (symmetric in cross-sectional direction or antisymmetric) can impose the presence of symmetric (such as central bars) or antisymmetric bars (such as alternate bars) for a certain distance and thus locally influence the bar mode. For instance, imposing an asymmetric flow to a central-bar system has been found to force the formation of compound alternate bars [19].
- (12)
- Linear theories provide fair predictors of bar mode, bar length, and bar migration (Section 4.1 and Section 4.2). Neither linear nor nonlinear theories, however, provide reliable predictors for bar height and pool depth (Section 4.3). The latter inevitably require numerical modelling or empirical estimates.
- (13)
- Bars may have a simple shape, or a compound shape crossed by smaller channels. Compound bars may arise from discharge variability [53] and from forcing (see point 11).
- (14)
- Fully developed bars assume a lower mode if incipient bars have modes higher than 2. This occurs through a process of merging into larger compound bars. This means that linear theories, strictly speaking valid for incipient bar characteristics, tend to overestimate the bar mode at larger width-to-depth ratios.
- (15)
- The development of an initially straight channel with erodible banks into a meandering alignment can be explained from the formation of non-migrating bars, either hybrid bars [54] or free bars with zero celerity [2]. However, meandering requires accretion of the opposite bank too. Otherwise the bank erosion merely results in a pattern of width expansions and constrictions as in Figure 7.
 Figure 7. Alternate bars enhance opposite bank erosion (courtesy of Andrés Vargas-Luna).
Figure 7. Alternate bars enhance opposite bank erosion (courtesy of Andrés Vargas-Luna). - (16)
- Discharge variations affect bar characteristics. Tubino [37] finds that bars grow during falling stages of floods, and that bar geometry is controlled by the duration of the active part of flood waves, i.e., the part capable of reworking bed sediment. Hall [55] finds that the mere presence of flow variations can produce non-migrating bars.
- (17)
- Sediment transport in suspension changes bar characteristics if it exhibits significant spatial lags in its adaptation to changing flow conditions [56]. Talmon [57] finds that sediment suspension makes hybrid bars longer and higher. Extending analyses by Bolla Pittaluga and Seminara [58] and Federici and Seminara [59], Bertagni and Camporeale [38] find that suspension has the same effect on free alternate bars. Comparing experimental findings with theoretical and numerical results, Talmon [57] infers that gravity pull along transverse bed slopes affects not only bedload but also part of the suspended load.
- (18)
- Riverbeds composed of mixtures of different grain sizes lead to other bar characteristics than beds composed of uniform sediment. Horizontal and vertical sorting because of bar migration and selective transport interact with the formation and evolution of bars. Free bars are higher and longer for mixed-size sediment than for uniform sediment [21]; hybrid bars, however, are lower [21,24]. Their lengths were shorter compared to bars in uniform sediment in experiments with weakly bimodal mixtures [24] but longer in numerical simulations for more strongly heterogeneous mixtures [21]. Imposed spatial patterns of grain size variations suppress the occurrence of free bars and force the bed into a pattern of steady bars [60]. Sediment heterogeneity appears to influence also river braiding, since higher heterogeneity was found to increase the braiding degree while decreasing the length of braid bars in numerical simulations [20].
4. Applications
4.1. Managing Bar Modes
The simplified version of the linear model of Struiksma et al. [3] for hybrid bars allows predicting the bar mode, m, as a function of morphodynamic parameters and channel geometry (longitudinal slope and width), assuming uniform flow [10]:
in which m is the bar mode; g is the acceleration due to gravity (m/s2); b is the degree of non-linearity of the sediment transport law expressed as a function of flow velocity (-), for which Crosato and Mosselman [10] suggest b = 10 for gravel-bed rivers (low sediment mobility) and b = 4 for sand-bed rivers (high sediment mobility). In our experience, b = 10 holds for laboratory experiments with low-mobility sand too. B is the channel width (m); i is the longitudinal bed slope (-); ∆ is the relative submerged mass density of sediment (-); D50 is the median sediment grain size (m); C is the Chézy coefficient for hydraulic resistance (m1/2/s) and QW is the water discharge (m3/s), suggested as bankfull [10], but in general to be chosen depending on the situation. The Chézy coefficient, C, can be derived from the Manning coefficient, n, and flow depth, h, through C = h1/6/n.
The bar mode must be an integer number, but Equation (1) returns a real number. The correct integer mode, denoted by , is derived as the integer number closest to the calculated real value of m. If = 0 (m < 0.5), the river is expected to be morphodynamically stable, i.e., without any periodic bars. However, forced bars that do not depend on morphodynamic instability might always form close to the sources of forcing, such as point bars inside river bends. If = 1 (0.5 ≤ m < 1.5), the channel is expected to present alternate bars; if = 2 (1.5 ≤ m < 2.5), the channel is expected to present central bars; and if > 2 (m ≥ 2.5), the channel is expected to present multiple bars. The “fluvial style” or “channel pattern” of the river, meandering vs. braided, can be characterized by the bar mode e.g., [31,61,62]. Meandering can be expected for ≤ 1, transition between meandering and braiding for = 2, and braiding for > 2. Being based on a linear approach, the theory overestimates the bar mode for width-to-depth ratios larger than 100. For such a large value of this ratio one can expect a braided river pattern [10], so even if the bar mode is overestimated, the bar pattern is correctly predicted.
Bars could cause intake obstruction, enhance opposite bank erosion, and create problems to bridges. Bars could hinder river navigation. River interventions are thus often aimed at bar removal, but mere excavation or dredging would only have a temporary effect as bars would grow again. Equation (1) shows that the bar mode primarily depends on channel width, B, so an effective intervention to decrease the bar mode, or even to eliminate bars, in this case by reaching the condition = 0, is channel narrowing (if the associated increased flow velocities do not pose problems to navigation). A well-documented example is the disappearance of bars by narrowing to avoid ice jams and improve navigability of the river Waal in the Netherlands [63]. River restoration is becoming a common practice in Europe [64] and in the United States [65], as well as in other parts of the world where trained rivers are given more space to regain some dynamics and improve their ecological value [66]. In many cases, restoration projects include the removal of bank protection works or the setback of dikes, enlarging the river channel for entire river reaches (e.g., [67]). One of the goals is the development of bars, often multiple bars, to achieve a less uniform bed topography that allows different aquatic habitats. This can indeed be obtained by channel widening (Equation (1)). Examples are the widening to enhance habitat heterogeneity in the Thur River [68] and the widening to create a more beautiful riverscape of the Aire River [69], both in Switzerland.
Usually three questions arise: (1) What is the new channel width to be imposed to the river channel? (2) How long should the river reach involved be? (3) What is the reference discharge?
- (1)
- Equation (1) is a useful tool to assess the new river width as a function of discharge, riverbed slope, sediment characteristics. This formula derived for hybrid bars was found to provide good predictions for migrating free bars too [10]. However, its application should be restricted to channels having width-to-depth ratio smaller than 100. Considering that the channel roughness, represented by Chézy’s coefficient, is a bulk parameter incorporating the effects of many factors on flow and sediment processes, it is advised to use several values of this coefficient, selected within a realistic range, and not a single value to compute the bar mode.
- (2)
- Duró et al. [19] showed that it is sufficient to narrow a river for a distance of about 10 times the channel width to free a location in the center of the narrowed reach from alternate bars.
- (3)
- Equation (1) was successfully applied using the bankfull discharge. However, it can also be used to assess the different bar modes that are likely to appear in a river channel as a result of discharge variations [70]. The relation between bar mode and discharge, QW, is inverse: a larger discharge decreases the bar mode, and vice versa. In practice discharge variations produce compound bars that are a combination of different bar modes of which the dominant one pertains to bankfull conditions.
4.2. Managing Bar Length and Migration Rates
The simplified linear theory by Struiksma et al. (1985) [3] allows predicting the wavelength of hybrid bars of mode m:
where LP is the m-mode bar wavelength and
with h0 being the reach-averaged water depth and θ0 the reach-averaged Shields parameter. The function for the effect of gravity pull, , can be expressed as [71]:
with E being a calibration coefficient.
The same theory allows deriving the damping coefficient, 1/LD, which defines the longitudinal damping of hybrid-bar amplitude:
Equations (2)–(6) are only valid for hybrid bars, which are the most common bars in natural rivers. As strictly speaking the equations hold for incipient bars and bars have been observed to elongate during further development [15,22], Equation (2) tends to underestimate the bar wavelength. Finally, colonization by vegetation shortens the length of hybrid bars (Vargas Luna et al. [45]), whereas at the same time vegetation transforms free bars in longer hybrid bars [52].
Bars can be stabilized by introducing a forcing that transforms free migrating bars into longer steady hybrid bars [19], at least over a certain distance. The length of this distance depends on the value of the longitudinal damping coefficient computed with Equation (6). The higher the damping coefficient, the shorter the distance in which bars are stabilized.
A popular river restoration intervention is re-meandering of previously straightened river reaches (e.g., [64,72]) to stimulate the development of a sinuous channel with point bars inside the river bends. The associated increased curvature suppresses the occurrence of free migrating bars [41,43,73]. Tubino and Seminara [74] developed a theoretical predictor for the minimum curvature required for this suppression, but this predictor is not easily translated into simple formulas for practical designs.
4.3. Managing Bar Height and Pool Depth
Bar height and pool depth depend on the amplitude of bars. Linear theories predict how a given amplitude of hybrid bars attenuates along the river, but they cannot predict this given amplitude itself. Weakly nonlinear theories would predict bar height and pool depth if these were small with respect to flow depth, but this is not the case. These theories thus merely explain how bar height and pool depth depend on width-to-depth ratio, sediment grain size, and sediment mobility in a relative way. Quantitative predictions require a fully non-linear approach.
A fully nonlinear solution does exist for the cross-sectional shape of river bends, with a forced point bar at the inner bend and a deep pool at the outer bend. It is based on the transverse bed slope for which the outward gravitation along this slope balances the inward drag by the helical flow driven by the centrifugal forces and pressure gradients [3]:
where is the transverse bed slope; is a coefficient weighing the intensity of helical flow; is a function of local Shields parameter representing gravity pull along the slope (Equation (5), substituting θ0 with θ); is the local water depth and is the radius of depth-averaged streamline curvature. Theoretically, for curved channels with uniform width and well away from the banks, depends on Chézy coefficient, , and Von Kármán coefficient, (= 0.4), according to
This fully nonlinear solution is called “axisymmetric” because it refers to the idealized but unrealistic situation of an infinitely long river bend, spiraling down around a vertical axis. Bends have a finite length and hence channel curvature varies spatially. This variation generates hybrid bars as predicted by the linear theory of Section 4.2. Superimposition of these hybrid bars on the forced point bar causes an overshoot in transverse bed slope, bar height, and pool depth [3], known as “overdeepening” [4]. Both the linear theory and the axisymmetric nonlinear theory, however, ignore bank roughness and the significant vertical flow components in the vicinity of banks. This means that these theories have little practical value for the prediction of near-bank bend scour, relevant for the design of bank protection. Empirical predictors for bend scour [75,76,77] perform better. These empirical predictors, however, hold for well-defined bends without significant planimetric changes. At least three more effects need to be accounted for when stabilizing banks along rivers with actively shifting channels. First, channels along a stabilized bank tend to become narrower and deeper because inner-bank accretion continues after arresting the outer-bank erosion [78]. Second, forced scour areas near bank protection structures pose less resistance to the flow. This attracts more flow, eroding the riverbed in such a way that also channels are directed toward the scour area along the alignments that exacerbate the conditions for scouring [79]. Third, these exacerbating alignments create sharp bends at the points where they impinge on the protected bank. This gives rise to complex 3D flows that separate and generate extra turbulence at the associated mixing layers [80,81]. This scours the bed even further.
5. Conclusions and Recommendations
We presented an overview of studies on fluvial bars, integrating results from theoretical analyses, laboratory experiments, numerical modelling, and field observations. We primarily distinguished forced bars (Figure 2), free bars (Figure 3 and Figure 6), and hybrid bars (Figure 6). We summarized the key insights gained from these studies in a way accessible to practitioners in river training and river restoration. We translated these insights into guidance for practical applications, providing simple formulas for rapid assessment and design. These are the formulas for hybrid bars, not free bars, for two reasons. First, hybrid bars are the most common bars in natural rivers, whereas free bars occur primarily in straightened channelized streams. Second, the richer information of theories for free bars, which includes predictions for bar growth and migration, is not easily translated into simple formulas.
We recommend applying the presented formulas straightforwardly only to small and medium-sized rivers and streams. Our practical guidance is insufficient for expensive interventions in larger rivers. Training and restoration of larger rivers require specialist expertise, supported by numerical modelling. The latter are better suited for analyzing and solving bar problems than physical models, because the geometrical distortion needed for sufficient model flow depth and proper reproduction of the Shields parameter conflicts with the requirement of properly reproducing the width-to-depth ratios that govern bars [82]. Physical models are thus fraught with scale effects. Notwithstanding our recommendation of numerical modelling, the insights presented can help in first assessments of promising interventions to reach river training or river restoration objectives in large rivers too.
Author Contributions
Conceptualization, A.C. and E.M.; methodology, A.C. and E.M.; formal analysis, A.C. and E.M.; writing—original draft preparation, A.C. and E.M.; writing—review and editing, A.C. and E.M.; visualization, A.C. All authors have read and agreed to the published version of the manuscript’.
Funding
This research received no external funding.
Acknowledgments
The authors wish to thank Aronne Armanini for the fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rohde, S.; Schütz, M.; Kienast, F.; Englmaier, P. River widening: An approach to restoring riparian habitats and plant species. River Res. Appl. 2005, 21, 1075–1094. [Google Scholar] [CrossRef]
- Blondeaux, P.; Seminara, G. A unified bar-bend theory of river meanders. J. Fluid Mech. 1985, 157, 449–470. [Google Scholar] [CrossRef]
- Struiksma, N.; Olesen, K.W.; Flokstra, C.; de Vriend, H.J. Bed deformation in curved alluvial channels. J. Hydraul. Res. 1985, 23, 57–79. [Google Scholar] [CrossRef]
- Parker, G.; Johanneson, H. Observations on several recent theories of resonance and overdeepening in meandering channels. In River Meandering; Water Resour. Monograph 12; Ikeda, S., Parker, G., Eds.; AGU: Washington, DC, USA, 1989; pp. 379–415. [Google Scholar]
- Colombini, M.; Seminara, G.; Tubino, M. Finite-amplitude alternate bars. J. Fluid Mech. 1987, 181, 213–232. [Google Scholar] [CrossRef]
- Colombini, M.; Tubino, M.; Whiting, P. Topographic expression of bars in meandering channels. In Dynamics of Gravel-Bed Rivers; Billi, P., Hey, R.D., Thorne, C.R., Tacconi, P., Eds.; Wiley & Sons: New York, NY, USA, 1992; pp. 457–474. [Google Scholar]
- Schielen, R.; Doelman, A.; de Swart, H.E. On the nonlinear dynamics of free bars in straight channels. J. Fluid Mech. 1993, 252, 325–356. [Google Scholar] [CrossRef]
- Federici, B.; Bolla Pittaluga, M.; Seminara, G. On the convective nature of bar instability: The effect of suspended load. In Proceedings of the 3rd IAHR Symposium on River, Coastal and Estuarine Morphodynamics (RCEM2003), Barcelona, Spain, 1–5 September 2003; Sánchez-Arcilla, A., Bateman, A., Eds.; IAHR: Madrid, Spain, 2003. [Google Scholar]
- Mosselman, E.; Tubino, M.; Zolezzi, G. The overdeepening theory in river morphodynamics: Two decades of shifting interpretations. In Proceedings of the River Flow 2006, Lisbon Portugal, 6–8 September 2006; Ferreira, R.M.L., Alves, E.C.T.L., Leal, J.G.A.B., Cardoso, A.H., Eds.; Taylor & Francis: London, UK, 2006; Volume 2, pp. 1175–1181. [Google Scholar]
- Crosato, A.; Mosselman, E. Simple physics-based predictor for the number of river bars and the transition between meandering and braiding. Water Resour. Res. 2009, 45, W03424. [Google Scholar] [CrossRef]
- Southgate, H.N.; Crosato, A. Non-Linear Evolution of Steady and Migrating Alternate Bars in a Straight Channel. In Proceedings of the 8th Symposium of RCEM River, Coastal and Estuarine Morphodynamics, Santander, Spain, 9–13 June 2013. [Google Scholar]
- Welford, M.R. A field test of Tubino’s (1990) model of alternate bar formation. Earth Surf. Process. Landf. 1994, 19, 287–297. [Google Scholar] [CrossRef]
- Eekhout, J.P.C.; Hoitink, A.J.F.; Mosselman, E. Field experiment on alternate bar development in a straight sand-bed stream. Water Resour. Res. 2013, 49, 8357–8369. [Google Scholar] [CrossRef]
- Rodrigues, S.; Mosselman, E.; Claude, N.; Wintenberger, C.L.; Juge, P. Alternate bars in a sandy gravel bed river: Generation, migration and interactions with superimposed dunes. Earth Surf. Process. Landf. 2015, 40, 610–628. [Google Scholar] [CrossRef]
- Nelson, J.M. The initial stability and finite-amplitude stability of alternate bars in straight channels. Earth Sci. Rev. 1990, 29, 97–115. [Google Scholar] [CrossRef]
- Nicholas, A.P. Reduced-complexity modeling of free bar morphodynamics in alluvial channels. J. Geophys. Res. Earth Surf. 2010, 115, F04021. [Google Scholar] [CrossRef]
- Nicholas, A.P. Modelling the continuum of river channel patterns. Earth Surf. Process. Landf. 2013, 38, 1187–1196. [Google Scholar] [CrossRef]
- Schuurman, F.; Marra, W.A.; Kleinhans, M.G. Physics-based modeling of large braided sand-bed rivers: Bar pattern formation, dynamics and sensitivity. J. Geophys. Res. Earth Surf. 2013, 118, 2509–2527. [Google Scholar] [CrossRef]
- Duró, G.; Crosato, A.; Tassi, P. Numerical study on river bar response to spatial variations of channel width. Adv. Water Res. 2015, 93, 21–38. [Google Scholar] [CrossRef]
- Singh, U.; Crosato, A.; Giri, S.; Hicks, M. Sediment heterogeneity and discharge variability in the morphodynamic modeling of gravel-bed braided rivers. Adv. Water Res. 2017, 104, 127–144. [Google Scholar] [CrossRef]
- Cordier, F.; Tassi, P.; Claude, N.; Crosato, A.; Rodrigues, S.; Pham Van Bang, D. Numerical study of alternate bars in alluvial channels with nonuniform sediment. Water Resour. Res. 2019, 55. [Google Scholar] [CrossRef]
- Fujita, Y.; Muramoto, Y. Studies on the process of development of alternate bars. Bull. Disaster Prev. Res. Inst. Kyoto Univ. 1985, 35, 55–86. [Google Scholar]
- Lanzoni, S. Experiments on bar formation in a straight flume; 1. Uniform sediment. Water Resour. Res. 2000, 36, 3337–3349. [Google Scholar] [CrossRef]
- Lanzoni, S. Experiments on bar formation in a straight flume; 2. Graded sediment. Water Resour. Res. 2000, 36, 3351–3363. [Google Scholar] [CrossRef]
- Crosato, A.; Mosselman, E.; Desta, F.B.; Uijttewaal, W.S.J. Experimental and numerical evidence for intrinsic nonmigrating bars in alluvial channels. Water Resour. Res. 2011, 47, W03511. [Google Scholar] [CrossRef]
- Crosato, A.; Desta, F.B.; Cornelisse, J.; Schuurman, F.; Uijttewaal, W.S.J. Experimental and numerical findings on the long-term evolution of migrating alternate bars in alluvial channels. Water Resour. Res. 2012, 48, W06524. [Google Scholar] [CrossRef]
- Church, M.; Jones, D. Channel bars in gravel-bed rivers. In Gravel-Bed Rivers: Fluvial Processes, Engineering, and Management; Hey, R.D., Bathurst, J.C., Thorne, C.R., Eds.; Wiley & Sons: New York, NY, USA, 1982; pp. 291–338. [Google Scholar]
- Wright, N.; Crosato, A. The Hydrodynamics and Morphodynamics of Rivers. In Treatise on Water Science; Wilderer, P., Ed.; Elsevier: Oxford, UK, 2011; Volume 2, pp. 135–156. [Google Scholar]
- Zolezzi, G.; Seminara, G. Upstream influence in erodible beds. Phys. Chem. Earth. Part B-Hydrol. Ocean. Atmos. 2001, 26, 65–70. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Welford, M.R. Initiation of river meandering. Prog. Phys. Geogr. 1991, 15, 127–156. [Google Scholar] [CrossRef]
- Hansen, E. On the Formation of Meanders as a Stability Problem; Basis Research; Progress Report 13; Coastal Engineering Laboratory; Technical University of Denmark: Lyngby, Denmark, 1967; p. 9. [Google Scholar]
- Engelund, F. Instability of erodible beds. J. Fluid Mech. 1970, 42, 225–244. [Google Scholar] [CrossRef]
- Seminara, G. Stability and morphodynamics. Meccanica 1998, 33, 59–99. [Google Scholar] [CrossRef]
- Ikeda, S.; Parker, G.; Sawai, K. Bend theory of river meanders. Part 1: Linear development. J. Fluid Mech. 1981, 112, 363–377. [Google Scholar] [CrossRef]
- Struiksma, N.; Crosato, A. Analysis of a 2-D bed topography model for rivers. In River Meandering; Water Resources Monograph; Ikeda, S., Parker, G., Eds.; AGU: Washington, DC, USA, 1989; Volume 12, pp. 153–180. [Google Scholar]
- Eckhaus, W. Studies in Non-Linear Stability Theory; Truesdell, C., Ed.; Springer Tracts Natural Philosophy; Springer: New York, NY, USA, 1965; Volume 6, ISBN 978-3-642-88319-4. [Google Scholar]
- Tubino, M. Growth of alternate bars in unsteady flow. Water Resour. Res. 1991, 27, 37–52. [Google Scholar] [CrossRef]
- Bertagni, M.B.; Camporeale, C. Finite amplitude of free alternate bars with suspended load. Water Resour. Res. 2018, 54. [Google Scholar] [CrossRef]
- Jang, C.L.; Shimizu, Y. Numerical simulations of the behavior of alternate bars with different bank strengths. J. Hydraul. Res. 2005, 43, 596–612. [Google Scholar] [CrossRef]
- Enggrob, H.G.; Tjerry, S. Simulation of morphological characteristics of a braided river. In Proceedings of the IAHR Symposium on River, Coastal and Estuarine Morphodynamics, Genoa, Italy, 6–10 September 1999; Springer: New York, NY, USA, 1999; Volume I, pp. 585–594. [Google Scholar]
- Kinoshita, R.; Miwa, H. River channel formation which prevents downstream translation of transverse bars. Shinsabo 1974, 94, 12–17. (In Japanese) [Google Scholar]
- Ikeda, S. Prediction of alternate bar wavelength and height. J. Hydraul. Eng. 1984, 110, 371–386. [Google Scholar] [CrossRef]
- Whiting, P.J.; Dietrich, W.E. Experimental constraints on bar migration through bends: Implications for meander wavelength selection. Water Resour. Res. 1993, 29, 1091–1102. [Google Scholar] [CrossRef]
- Tal, M.; Paola, C. Effects of vegetation on channel morphodynamics: Results and insights from laboratory experiments. Earth Surf. Process. Landf. 2010, 35, 1014–1028. [Google Scholar] [CrossRef]
- Vargas-Luna, A.; Duró, G.; Crosato, A.; Uijttewaal, W.S.J. Morphological adaptation of river channels to vegetation establishment: A laboratory study. J. Geophys. Res. Earth Surf. 2019. [Google Scholar] [CrossRef]
- Leopold, L.B. Other quantitative measurements of migrating and steady bars in natural rivers. In Gravel-Bed Rivers: Fluvial Processes, Engineering and Management; Hey, R.D., Bathurst, J.C., Thorne, C.R., Eds.; Wiley & Sons: New York, NY, USA, 1982; pp. 359–388. [Google Scholar]
- Jaeggi, M.N.R. Formation and effects of alternate bars. J. Hydraul. Eng. 1984, 110, 142–156. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Bloomer, D.J.; Church, M. Evolution of an advancing gravel front: Observations from Vedder Canal, British Columbia. Earth Surf. Process. Landf. 2011, 36, 1172–1182. [Google Scholar] [CrossRef]
- Adami, L.; Bertoldi, W.; Zolezzi, G. Multidecadal dynamics of alternate bars in the Alpine Rhine River. Water Resour. Res. 2016, 52. [Google Scholar] [CrossRef]
- Ham, D.; Church, M. Morphodynamics of an extended bar complex, Fraser River, British Columbia. Earth Surf. Process. Landf. 2012, 37, 1074–1089. [Google Scholar] [CrossRef]
- Caruso, B.S.; Edmondson, L.; Pithie, C. Braided River Flow and Invasive Vegetation Dynamics in the Southern Alps. New Zealand Environ. Manag. 2013, 52, 1. [Google Scholar] [CrossRef]
- Serlet, A.J.; Gurnell, A.M.; Zolezzi, G.; Wharton, G.; Belleudy, P.; Jourdain, C. Biomorphodynamics of alternate bars in a channelized, regulated river: An integrated historical and modelling analysis. Earth Surf Process. Landf. 2018, 3, 1739–1756. [Google Scholar] [CrossRef]
- Cordier, F.; Tassi, P.; Claude, N.; Crosato, A.; Rodrigues, S.; Pham Van Bang, D.; Pham Van Bang, D. Bar pattern and sediment sorting in a channel contraction/expansion: Application to the Loire River at Bréhémont (France). Adv. Water Res. 2019. submitted for publication. [Google Scholar]
- Olesen, K.W. Alternate bars in and meandering of alluvial rivers. In River Meandering, Proc. Conf. Rivers 1983; Elliott, C.M., Ed.; ASCE: New York, NY, USA, 1984; pp. 873–884. [Google Scholar]
- Hall, P. Alternating bar instabilities in unsteady channel flows over erodible beds. J. Fluid Mech. 2004, 499, 49–73. [Google Scholar] [CrossRef]
- Mosselman, E. Basic equations for sediment transport in CFD for fluvial morphodynamics. In Computational Fluid Dynamics; Applications in Environmental Hydraulics; Wiley& Sons: New York, NY, USA, 2005; Chapter 4; pp. 71–89. [Google Scholar]
- Talmon, A.M. Bed topography of River Bends with Suspended Sediment Transport. In Communications on Hydraulic and Geotechnical Engineering; Delft University of Technology (TU Delft): Delft, The Netherlands, 1992. [Google Scholar]
- Bolla Pittaluga, M.; Seminara, G. Depth-integrated modeling of suspended sediment transport. Water Resour. Res. 2003, 39, 1137. [Google Scholar] [CrossRef]
- Federici, B.; Seminara, G. Effect of suspended load on sandbar instability. Water Resour. Res. 2006, 42, W07407. [Google Scholar] [CrossRef]
- Mosselman, E.; Hassan, K.I.; Sieben, A. Effect of spatial grain size variations in two-dimensional morphological computations with uniform sediment. In Proceedings of the IAHR Symposium River Coastal and Estuarine Morphodynamics, Genova, Switzerland, 6–9 September 1999; Sánchez-Arcilla, A., Bateman, A., Eds.; IAHR: Madrid, Spain, 2003; pp. 236–246, ISBN 90-805649-6-6. [Google Scholar]
- Parker, G. On the cause and characteristic scales of meandering and braiding in rivers. J. Fluid Mech. 1976, 76, 457–479. [Google Scholar] [CrossRef]
- Fredsøe, J. Meandering and braiding of rivers. J. Fluid Mech. 1978, 84, 609–624. [Google Scholar] [CrossRef]
- Schoor, M.M.; Wolfert, H.P.; Maas, G.J.; Middelkoop, H.; Lambeek, J.J.P. Potential for floodplain rehabilitation based on historical maps and present-day processes along the River Rhine, The Netherlands. In Floodplains: Interdisciplinary Approaches; Marriott, S.B., Alexander, J., Eds.; Geological Society: London, UK, 1999; Volume 163, pp. 123–137. [Google Scholar]
- Rinaldi, M.; Johnson, P.A. Characterization of Stream Meanders for Stream Restoration. J. Hydraul. Eng. 1997, 123, 567–570. [Google Scholar] [CrossRef]
- Small, M.J.; Doyle, M.W. Historical perspectives on river restoration design in the USA. Prog. Phys. Geogr. Earth Environ. 2012, 36, 138–153. [Google Scholar] [CrossRef]
- Vaughan, I.P.; Diamond, M.; Gurnell, A.M.; Hall, K.A.; Jenkins, A.; Milner, N.J.; Naylor, L.A.; Sear, D.A.; Woodward, G.; Ormerod, S.J. Integrating ecology with hydromorphology: A priority for river science and management. Aquat. Conserv. Mar. Freshw. Ecosyst. 2009, 19, 113–125. [Google Scholar] [CrossRef]
- Piégay, H.; Darby, S.E.; Mosselman, E.; Surian, N. A review of techniques available for delimiting the erodible river corridor: A sustainable approach to managing bank erosion. River Res. Appl. 2005, 21, 1–17. [Google Scholar] [CrossRef]
- Rachelly, C.; Weitbrecht, V.; Vetsch, D.F.; Boes, R.M. Morphological development of river widenings with variable sediment supply. In Proceedings of the River Flow 2018, Ninth International Conference on Fluvial Hydraulics, Lyon, France, 5–8 September 2018. [Google Scholar] [CrossRef]
- Atelier Descombes Rampini Superposition Renaturation River Aire 2016. Landezine Landscape Architecture Platform. Available online: http://landezine.com/index.php/2016/06/renaturation-of-the-river-aire-geneva/ (accessed on 20 February 2020).
- Jaballah, M.; Camenen, B.; Pénard, L.; Paquier, A. Alternate bar development in an alpine river following engineering works. Adv. Water Res. 2015, 81, 103–113. [Google Scholar] [CrossRef]
- Talmon, A.M.; Struiksma, N.; Van Mierlo, M.C.L.M. Laboratory measurements of the direction of sediment transport on transverse alluvial-bed slopes. J. Hydraul. Res. 1995, 33, 495–517. [Google Scholar] [CrossRef]
- Kondolf, G.M. River restoration and meanders. Ecol. Soc. 2006, 11, 42. [Google Scholar] [CrossRef]
- Miwa, H.; Nagayoshi, T. Suppression limit of alternate bar migration through sine-generated meander channels. J. Nat. Disaster Sci. 1999, 21, 1–10. [Google Scholar]
- Tubino, M.; Seminara, G. Free-forced interactions in developing meanders and suppression of free bars. J. Fluid Mech. 1990, 214, 131–159. [Google Scholar] [CrossRef]
- Watanabe, Y.; Hasegawa, K.; Houjyou, K. Influence of hydraulic factors on river bed scour. J. Hydrosci. Hydraul. Eng. 1990, 8, 53–63. [Google Scholar]
- Thorne, C.R.; Abt, S.R.; Maynord, S.T. Prediction of near-bank velocity and scour depth in meander bends for design of riprap revetments. In Rever, Coastal and Shoreline Protection; Barends, F.B.J., Maynord, S.T., Pilarczyk, K.W., Eds.; Wiley & Sons: New York, Ny, USA, 1995; pp. 115–133. [Google Scholar]
- Maynord, S.T. Toe-scour estimation in stabilized bendways. J. Hydraul. Eng. 1996, 122, 460–464. [Google Scholar] [CrossRef]
- Mosselman, E.; Shishikura, T.; Klaassen, G.J. Effect of bank stabilization on bend scour in anabranches of braided rivers. Phys. Chem. Earth 2000, 25 Pt B, 699–704. [Google Scholar] [CrossRef]
- Mosselman, E.; Sloff, C.J. Effect of local scour holes on macroscale river morphology. In River Flow 2002: Proceedings of the International Conference Fluvial Hydraulic, Louvain-la-Neuve, Belgium, 4–6 September 2002; pp. 767–772. [Google Scholar]
- Leeder, M.R.; Bridges, P.H. Flow separation in meander bends. Nature 1975, 253, 338–339. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Parsons, D.R.; Lane, S.N.; Hardy, R.J. Flow in meander bends with recirculation at the inner bank. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Mosselman, E. Modelling in applied hydraulics: More accurate in decision-making than in science? In Advances in Hydroinformatics: SimHydro 2017-Choosing the Right Model in Applied Hydraulics; Gourbesville, P., Cunge, J., Caignaert, G., Eds.; Springer: Singapore, 2018; Chapter 53; pp. 741–749. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).