Abstract
Many calibration techniques have been developed for the Soil and Water Assessment Tool (SWAT). Among them, the SWAT calibration and uncertainty program (SWAT-CUP) with sequential uncertainty fitting 2 (SUFI-2) algorithm is widely used and several objective functions have been implemented in its calibration process. In this study, eight different objective functions were used in a calibration of stream flow of the Pursat River Basin of Cambodia, a tropical monsoon and forested watershed, to examine their influences on the calibration results, parameter optimizations, and water resources estimations. As results, many objective functions performed better than satisfactory in calibrating the SWAT model. However, different objective functions defined different fitted values and sensitivity rank of the calibrated parameters, except Nash–Sutcliffe efficiency (NSE) and ratio of standard deviation of observations to root mean square error (RSR) which are equivalent and produced quite identical simulation results including parameter sensitivity and fitted parameter values, leading to the same water balance components and water yields estimations. As they generated reasonable fitted parameter values, either NSE or RSR gave better estimation results of annual average water yield and other water balance components such as annual average evapotranspiration, groundwater flow, surface runoff, and lateral flow according to the characteristics of the river basin and the results and data of previous studies. Moreover, either of them was also better in calibrating base flow, falling limb, and overall the entire flow phases of the hydrograph in this area.
1. Introduction
Several distributed hydrological models have been increasingly and widely employed, which are extremely essential to simulate hydrological phenomena, to manage and plan water resources, to investigate sedimentation and water quality, and to forecast the impact of universal climate and land-use changes. The Soil and Water Assessment Tool (SWAT) is one of the most well-known and has demonstrated its strengths in the above aspects with a large and growing number of model application in various studies ranging from catchment to continental scales [1,2,3,4,5]. It is open source software developed by the U.S. Department of Agriculture (USDA) Agricultural Research Service and Texas A&M. This physically based, watershed-scale, continuous model is commonly applied for measuring the impact of land-use and climate changes and for determining the different watershed management activities on hydrology, sedimentation, and water quality [6,7,8,9,10]. However, proper calibration/validation and uncertainty analysis are required to improve the model simulation and analysis for the watershed.
Calibration and uncertainty analysis are intimately linked, and no calibration results should be presented without quantification of the degree of uncertainty of the model prediction [11]. To run a physically based distributed hydrological model, such as SWAT, various parameters must be calibrated because of measurement difficulties. Calibration is performed by carefully selecting values with their respective uncertainty ranges and by comparing the simulation output for a given set of measured data [7]. Several calibration techniques have been developed for SWAT, including manual and automated calibration procedures using the shuffled complex evolution method and other common methods. The SWAT calibration and uncertainty program (SWAT-CUP) links sequential uncertainty fitting 2 (SUFI-2), generalized likelihood uncertainty estimation (GLUE), parameter solution (ParaSol), Markov chain Monte Carlo (MCMC), and particle swarm optimization (PSO) algorithms to SWAT [12] and has been widely used for calibration and uncertainty analysis [13,14,15].
Among these algorithms, SUFI-2 has gained the most popularity among users for carrying out parameterization, sensitivity analysis, calibration, validation, and uncertainty analysis of hydrological parameters [16]. This is due to the availability of many parameters regarding water balance modeling, the easier calibration process to carry out within realizable time bounds, better accountability for uncertainties, and the smallest number of computational runs to achieve good prediction uncertainty bands and model performance [17,18,19]. However, many objective functions have been incorporated into the SUFI-2 calibration procedure, but most studies have not considered the influence of the choice of objective functions on the calibration results, the calibrated parameter values/ranges, or the estimated water balance components. One study conducted in two Iranian watersheds by Kouchi et al. [20] was likely the only one thus far that has compared the choice of objective functions during the calibration process in SUFI-2. That study showed that all objective functions used in the calibration had a similar performance; however, each produced notably different parameter ranges and consequently led to significant differences in the water resource estimates.
Thus in this study, the objectives were to examine the influences of eight different objective functions in the calibration process of SWAT-CUP using the SUFI-2 algorithm on the calibration results, parameter optimizations, and water balance component estimations when simulating the stream flow of the tropical monsoon and forested watershed of the Pursat River Basin of Cambodia. Those objective functions include the coefficient of determination (R2), modified coefficient of determination (bR2), Nash–Sutcliffe efficiency (NSE), modified Nash–Sutcliffe efficiency (MNS), ratio of standard deviation of observations to root mean square error (RSR), ranked sum of squares (SSQR), Kling–Gupta efficiency (KGE), and percent bias (PBIAS). We also aimed to identify a proper objective function which produced reasonable calibration results, calibrated parameter sets, and water resources estimations which reflected the characteristics of this river basin.
2. Study Area
The Pursat River Basin, located in Pursat Province of Cambodia, is one of the Tonle Sap sub-basins and drains an area of 5955 km2 [21] (Figure 1a). The river flows for approximately 150 km from the Southwest at the Cardamom Mountains to the Northeast direction until the Tonle Sap Lake with a basin elevation ranging between 6 and 1717 m above sea level. There is an operating hydrological station named Bak Trakuon with a drainage area of 4245 km2 [22] where this study focused on (Figure 1b). More than 75% of the river basin encompasses a hilly terrain, with an elevation greater than 30 m above sea level and is covered by forested land of varying density, while the remaining low-lying land is occupied by agriculture [23]. Those over 75% of the forest cover are mainly concentrated in Bak Trakuon drainage boundary (Figure 1b) where the major soil types are Dystric Leptosols and Dystric Leptosols/Dystric Cambisols (LPd and LPd/CMd) and Gleyic Acrisols/Plinthic Acrisols (ACg/ACp) [22]. The climate in Pursat River Basin is influenced by tropic monsoon systems with distinct wet and dry seasons. The wet season, which extends from May to November, receives approximately 90% of the total annual rainfall. The dry season, which extends from December to April, is characterized by the prevalence of hot and dry air [22]. The rainfall in the area increases with elevation, but the annual totals vary considerably from year to year with the average ranging from 1200 to 1700 mm [24]. Daily maximum temperatures vary between 36 °C during the hottest months (April–May) and 32 °C during the coldest months (December–January). Daily minimum temperatures vary between 25 and 17 °C. The annual average temperature is approximately 28 °C. The monthly mean relative humidity ranges from 66% in the dry season to 71% in the wet season with a mean annual humidity of 70% [22].
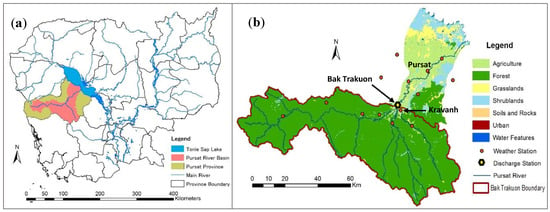
Figure 1.
(a) Location of the Pursat River Basin and (b) land-use map in 2003 with monitoring stations.
3. Materials and Methods
Figure 2 shows the workflow diagram for this study. To simulate hydrological processes in the river basin using the SWAT model, input data, such as DEM, soil type, land-use map, and climate data, were required. The simulation output of the model without any calibration is called the default/initial result. The initial result was checked by using the SWAT Check program to identify any potential model problems, and the simulated discharge was compared with the observed data. If there was a problem or a huge difference between the simulated and observed data, the model inputs (e.g., spatial data, rainfall) need to be focused on, and if there were no problems, model calibration/uncertainty analysis was performed. SWAT-CUP with SUFI-2 algorithm was employed to conduct the model calibration/uncertainty analysis. This process started with parameterization in which several parameters were selected with indication of their value ranges. This was based on the difference between the simulated and observed data, watershed characteristics, and literature reviews. The next step involved applying different objective functions before beginning the calibration and validation. The results of the calibration and validation were evaluated. If the criteria was not satisfied, parameterization was rechecked; then, the model was recalibrated and revalidated. After the calibration and validation process using different objective functions, each objective function was evaluated based on its calibration result, calibrated parameters, the estimation of discharge processes, and the simulation of the hydrograph components. The details of each step are described in the following sections.
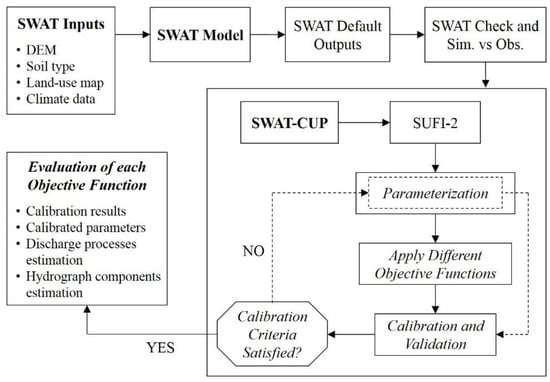
Figure 2.
Workflow diagram.
3.1. SWAT Input Datasets
Input data, such as topography, land-use map, soil type, and weather data, were collected from different sources and agencies, as listed in Table 1. The digital elevation model (DEM) was from the Shuttle Radar Topography Mission (SRTM) Global with a 30 m raster resolution and downloaded from OpenTopography (https://www.opentopography.org/). The land-use and soil maps from 2003 were obtained from Cambodia National Mekong Committee (CNMC) with a 250-m raster resolution. Weather and hydrological data were collected from the Pursat Provincial Department of Water Resources and Meteorology. There are several rainfall stations nearby and within the river basin, but one station, Kravanh, was selected because it is the only station that has lengthy data recorded from the 1990s and is located in the drained area of the Bak Trakuon outlet (discharge monitoring station used for model evaluation) (Figure 1b). Because of this limitation, a uniform distribution of rainfall in the Kravanh station was applied to the model simulation. For minimum and maximum air temperatures, the dataset in Pursat station located downstream of the river basin was used because it was the only available temperature station in the study area. Other climate data, such as relative humidity, wind speed, and solar radiation, were not available and were simulated by a weather generator. In this study area, the daily river discharge data were the only available hydrological data and were used for model calibration and evaluation.

Table 1.
Description of data used in this study.
3.2. SWAT Model Setup
In this study, the ArcSWAT 2012 interface was used to setup the model. With a threshold drainage area of 5000 ha, the basin was discretized into 60 sub-basins, and by classing the slope below and above 5%, the sub-basins were further subdivided into 667 HRUs (Hydrologic Response Units). The model then required the inputs of weather data before it could be run. For this study, the model was run in a monthly time step for a total simulation period of 26 years from 1990 to 2015 in which the period from 1990 to 1994 was treated as the warm-up period to mitigate the initial conditions and was not included in the analysis.
3.3. SWAT-CUP with the SUFI-2 Algorithm
Calibration can be difficult and is almost infeasible for many large-scale applications [7]. A number of auto-calibration and uncertainty analysis tools for SWAT have been developed to solve this problem and are currently available to assist the optimization process. In this study, SWAT-CUP with the SUFI-2 algorithm was used to calibrate the model. SWAT-CUP is an auto-calibration and uncertainty analysis module program developed for SWAT [12,25]. SWAT-CUP allows the use of several algorithms for the calibration or validation procedure. Among them, the SUFI-2 algorithm [16,26], which is a semi-automated approach used for model calibration, validation, sensitivity, and uncertainty analysis, was used in this study. In SUFI-2, all sources of parameter uncertainties are assigned to parameters. The range of input parameters is assumed to be a uniform distribution, while the model output uncertainty is quantified by the 95% prediction uncertainty (95PPU) determined at the 2.5% and 97.5% levels of the cumulative distribution of output variables obtained via Latin hypercube sampling. The details of the SWAT-CUP program and SUFI-2 algorithm are in the SWAT-CUP user manual [12].
3.3.1. Parameterization
Parameterization is a process of selecting parameters and setting their initial value ranges for calibration. Based on previous studies on the region [27,28,29] and literature on SWAT calibration/validation [7,11], nine parameters were selected, and then, their initial value ranges were defined. Two methods, Relative and Replace, were used for different parameters. When Relative is reported this means that a percentage relative change is applied to original parameters, and only when Replace the min and max range values allowed for calibration are reported. The descriptions of each parameter along with their minimum and maximum values are presented in Table 2.

Table 2.
Parameters used for the calibration and their initial ranges.
3.3.2. Objective Functions
Eleven objective functions are currently allowed in the SUFI-2 algorithm. Eight of the eleven were selected to evaluate their impacts on the calibration results, calibrated parameters, and the overall discharge processes simulation owing to their popularity and available details on accessibility. For the remaining three objective functions such as the multiplicative form of the square error, the summation form of the square error, and the Chi square, we have no or very little knowledge about them and will not be able to make any discussion and evaluation for their performances. The selected eight objective functions include the coefficient of determination (R2), modified coefficient of determination (bR2), Nash–Sutcliffe efficiency (NSE), modified Nash–Sutcliffe efficiency (MNS), ratio of the standard deviation of observations to the root mean square error (RSR), ranked sum of squares (SSQR), Kling–Gupta efficiency (KGE), and percent bias (PBIAS). The equations and references for these objective functions are presented in Table 3. For NSE and RSE, it is expected that their simulation results are similar as they are equivalent objective functions given that NSE = 1 − RSR2 according to their equations in Table 3.

Table 3.
List of objective functions used in this study.
Here, is a variable (e.g., discharge), stands for the measured value, stands for the simulated value, represents the ith measured or simulated data, is the mean measured data of variable , is the mean simulated data of variable , is the coefficient of the regression line between the measured and simulated data, is the modified Nash–Sutcliffe efficiency factor (= 1 was used in this study), is the total number of measured or simulated data, represents the rank, and is the linear regression coefficient between the simulated and measured variables, and and , where and are the standard deviations of the simulated and measured data, respectively. Additionally, and are the means of the simulated and measured data, respectively.
3.3.3. Model Calibration, Validation, and Evaluation
Model calibration involves fitting parameter values by comparing the predicted output and measured data until a satisfactory standard for an objective function is achieved [36], whereas validation is an evaluation of whether the calibrated model has the ability to predict for later periods. In this study, the model was run in a monthly time step. The measured discharge data at the Bak Trakuon station during the 1995–2008 and 2009–2015 periods were used for model calibration and validation, respectively.
The strengths of the calibration and validation of each objective function were evaluated. The evaluation was based on statistical indices of all objective functions used in this study. The detailed descriptions and equations are presented in Table 3, and their statistical ranges, optimal values, and satisfactory values are shown in Table 4. The satisfactory threshold values for bR2 and MNS were considered greater than or equal to 0.4, which was adopted from Kouchi et al. [20], who introduced measures based on the results of the studies of Muleta [37], Mehdi et al. [38], and Akhavan et al. [39]. For the SSQR, a satisfactory value could not be specified because the measured and simulated variables were independently ranked, and the value depends on the magnitude of the variables being investigated. Satisfactory values of the other indices were based on Moriasi et al. [32] and Thiemig et al. [40].

Table 4.
Performance evaluations for the monthly discharge simulation [20,32,40].
3.4. Evaluation of Each Objective Function
To identify a better objective function when calibrating the discharge in this study area, the simulated result of each objective function was graphically compared with the observed data, and the performance evaluation criteria (as shown in Table 4) was also taken into consideration. Additionally, characteristics of this tropical monsoon river basin were analyzed, and based on these characteristics, estimated results of water balance components, such as evapotranspiration, surface runoff, lateral flow, groundwater flow, estimated results of the water yield, and calibrated values of the best parameter sets obtained from all objective functions during the calibration process, were also evaluated.
Additionally, the MOD16A2 Version 6 Evapotranspiration/Latent Heat Flux product with an 8-day composite dataset produced at 500 m pixel resolution from MODIS (Moderate Resolution Imaging Spectroradiometer) was used to confirm the actual evapotranspiration amount of the Pursat River Basin [41]. MODIS ET data was obtained for 2001 to 2015 period through R package “MODIStsp” and analyzed using R 4.0.2 version software (The R Foundation for Statistical Computing, Vienna, Austria) [42].
For further evaluation of the hydrological characteristics of this watershed, simulated discharges of the best calibrated parameter sets of the different objective functions were categorized into the base flow, rising limb, peak flow, and falling limb phases and then compared with the observed data at the respective flow phases from 1995 to 2008 (calibration period) using scatter plots. Then, the coefficient of determination (R2) and root mean squared deviation (RMSD) were used for the evaluation. The R2, which was calculated as shown in Table 3, determines how much variance the two variables share, and its value varies between 0 (no correlation) and 1 (perfect correlation). However, when the model systematically over- or under-predicts all the time, the R2 value is still close to 1. To cope with this problem, the slope and intercept of the regression on which R2 is based were taken into account. For a good agreement, the slope and intercept should be close to 1 and 0, respectively. The RMSD represents the mean deviation of the predicted values with respect to the observed values [43,44] and can be calculated as
where is the total number of observations, is the measured discharge, is the simulated discharge, and is the ith measured or simulated data. The unit of the RMSD is the same as the unit of and . The RMSD is always positive, and a value of 0 (almost never achieved in practice) indicates a perfect fit of the data. Generally, a lower RMSD is better than a higher one.
4. Results
4.1. Simulation Results
Figure 3 graphically represents the best simulated discharges on the monthly time step (calibrated from 1995 to 2008 and validated from 2009 to 2015) of different objective functions compared with the observed data. The simulated discharges corresponded well with the rainfall data. With the R2 objective function, the calibrated model usually overestimated peak flows. When bR2 was used, the peak flow estimation became even more overestimated compared to the observed data. This originated from the equations of these objective functions. Both are defined by a minimization of total errors from a linear regression model and the length from the average value, which are not direct errors of measured and estimated data and could have the effect on the calibrated parameters. According to Legates and McCabe [45], owing to the squared differences in their equations, they are oversensitive to high extreme values and insensitive to additive and proportional differences between model predictions and measured data.
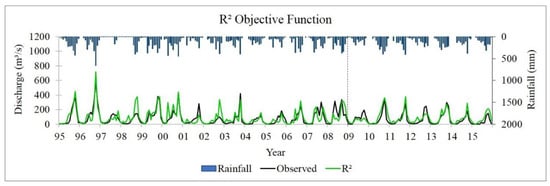
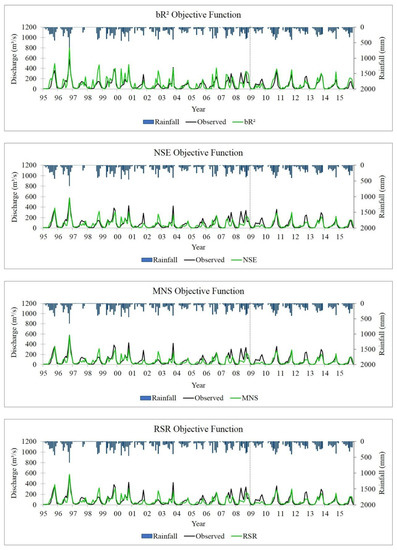
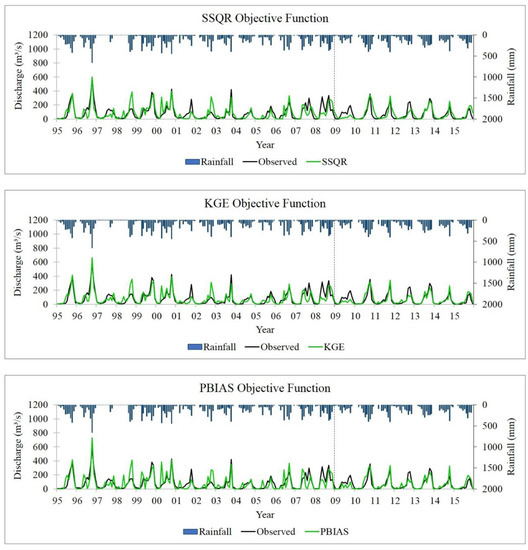
Figure 3.
Monthly simulated and validated discharges of different objective functions compared with observed data.
For the choice of NSE, MNS, and RSR objective functions, their calibrated results were similar, especially the NSE and RSR objective functions. In addition to increasing the fitness between the simulated and observed base flows and recession curves, the simulated peak flows were also significantly reduced with considerable correspondence to the observed data. Similarly, when we used the SSQR and KGE objective functions, the simulation results could also capture well the distribution of the observed flow, although the simulated peak flows were slightly high. Those objective functions focus on errors between the measured and estimated data. Then, optimization of these objective functions reduces the errors.
The PBIAS objective function, however, gave a different calibration result. Compared to the calibration results of the other objective functions, the simulated peak flows were occasionally overestimated when we used the PBIAS objective function, whereas the simulated base flows were occasionally underestimated. This is the result of the characteristics of this objective function. When the model overpredicts as much as it underpredicts, PBIAS can still provide a deceptive rating of model performance [35,46].
4.2. Model Performance
The model performances of the calibrated parameter sets obtained from different objective functions were evaluated and compared by using the statistical indices of all objective functions (Figure 4). Many objective functions performed better than satisfactory in terms of calibration and validation for most of the criteria described in Table 4. The simulated results of the fitted parameter sets from the NSE, MNS, RSR, and KGE objective functions satisfied all statistical indices, whereas the results of the parameter set by the R2 objective function failed to satisfy the PBIAS statistical index during the validation period. For the result of the parameter set by SSQR, it failed to satisfy the MNS statistical index during both calibration and validation periods. Of the worst, the result of the parameter set by the bR2 objective function failed to satisfy NSE, MNS, and RSR statistical indices during the calibration period, whereas the SSQR statistical value of this objective function during the calibration period was quite high compared to that of other objective functions. For the PBIAS objective function, the result of the parameter set during the calibration period failed to satisfy the NSE, MNS, and RSR statistical indices.
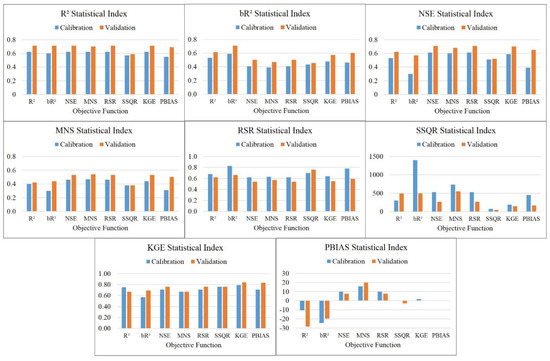
Figure 4.
Results of model performance indices of different objective functions.
In this study, as mentioned earlier, the calibration period was defined longer (1995–2008). The purpose of this was to cover all the magnitudes of discharge pattern which included not only the normal years but also the wettest year in 1996 and the driest year in 2002 (Figure 3) in the calibration process. On the contrary, the validation period, which was shorter from 2009 to 2015, included mostly normal years only. As the result, the performance of the validation as measured by the statistical indices was better than that of the calibration in many cases (Figure 4).
5. Discussion
5.1. Discharge Process Estimations
The results of annual average water balance components and water yields estimated by different objective functions using the best parameter sets in the calibration process are shown in Figure 5. The results showed that the estimated water balance components and water yields differed by the types of objective functions used. The estimated annual average evapotranspiration (ET) by different objective functions ranged from 656.60 to 756.30 mm (48.99% to 56.42% of the total rainfall), whereas the estimated annual average surface runoff (SurQ) ranged from 116.27 to 560.05 mm (8.67% to 41.78% of the total rainfall) (Figure 5a). The ratios of estimated annual average lateral flow (LatQ) and groundwater flow (GWQ) to the total rainfall generated by those objective functions ranged from 0.51% (6.83 mm) to 26.02% (348.76 mm) and 0.31% (4.17 mm) to 13.18% (176.7 mm), respectively. Additionally, the ratios of estimated annual average deep aquifer recharge (DAR) and amount of water moving from the shallow aquifer to plant/soil profile (Revap) to the total rainfall generated by those objective functions ranged from 0.26% (3.51 mm) to 0.89% (11.92 mm) and 0.86% (11.54 mm) to 11.84% (158.66 mm), respectively. For the estimated annual average water yield (Figure 5b), with the MNS objective function, the model generated the lowest annual average water yield of 456.49 mm, whereas the highest annual average water yield of 679.79 mm was given by the model when we used the bR2 objective function. The result showed that the estimated water balance components and water yields of the NSE and RSR objective functions were the same.
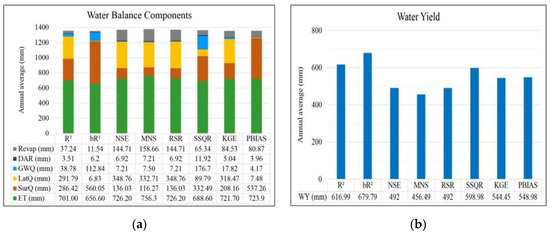
Figure 5.
(a) Results of the water balance components and (b) water yields of different objective functions using the best parameter sets from the calibration process.
In a study conducted by Shimizu et al. [47], almost all mountainous regions of west Cambodia (where this study area was also located) had annual renewable freshwater resources (water yield) of 500 mm. Thus, NSE and RSR objective functions provided closer annual average water yield estimations than other objective functions at the same value of 492 mm, followed by the MNS, KGE, and PBIAS objective functions, which generated water yields of 456.49, 544.45, and 548.98 mm, respectively. For the results of the water balance components estimation, of the objective functions used in this study, the MNS, NSE, RSR, PBIAS, and KGE objective functions provided the most reasonable estimation results of annual average evapotranspiration (ET) of 756.3, 726.2, 726.2, 723.9, and 721.7 mm, respectively. These results closely corresponded to the ET value obtained from MODIS ET of 745 mm on average annually (Figure 6) and the findings in the study conducted by JICA [48] in southern Cambodia with an estimated annual average ET of 743.9 mm. The goodness of the ET simulated by these objective functions were also confirmed by the linear regression with the ET obtained from MODIS ET as shown in Figure 7. Again, the PBIAS, NSE, RSR, MNS, and KGE objective functions provided relatively small estimated values of groundwater flow (GWQ), and these objective functions, except for the PBIAS objective function, generated a small proportion of surface runoff (SurQ) compared to a proportion of lateral flow (LatQ), which reflected the flow characteristics of this study area. A detailed description of the discharge characteristics and physiographic condition of the river basin is presented in Section 5.4.
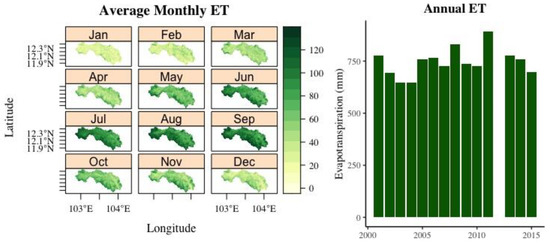
Figure 6.
Average monthly (left) and annual evapotranspiration (right) in Pursat River basin (drainage area at Bak Trakuon outlet) from 2001 to 2015 obtained from MODIS ET.
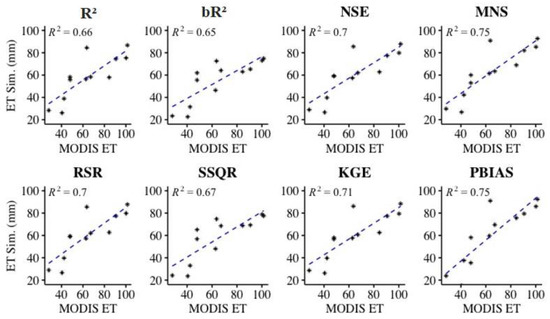
Figure 7.
Linear regression between monthly average evapotranspiration obtained from the simulation results (ET Sim.) of different objective functions and monthly average evapotranspiration obtained from MODIS ET.
5.2. Best Parameter Sets and Sensitivity Rank
Table 5 shows the fitted parameter values and sensitivity rank of the parameters used in this study obtained from different objective functions during the calibration process. Besides the NSE and RSR objective functions, different objective functions generated different values of best parameter sets and sensitivity rank. The fitted parameter sets of the NSE, RSR, and MNS objective functions were in a reasonable range in this study. When we used the R2 objective function, the relative value of the parameter change for CN2 was high (+13%), whereas the existing parameter value of CN2 of the initial model was (between 55 and 92) approximately 78 on average, which was already high for the land-use and soil types of this study area. This led to a big runoff (surface and lateral flow) amount, as shown in Figure 5a, and high simulated peak flows, as shown in Figure 3. This objective function produced a small threshold value of GWQMN of 1680.42 mm, which led to more groundwater flow, and a small coefficient of GW_REVAP of 0.03, which generated a lower evapotranspiration rate and revap because of the limitation of movement of water from the shallow aquifer to the root zone. Moreover, these three parameters were among the five most sensitive parameters, which highly controlled the simulation results of the R2 objective function. Even worst, the bR2 objective function produced a higher relative value of the parameter change for CN2 of +15%, a smaller threshold value of GWQMN of 291.86, a low coefficient of GW_REVAP of 0.07, and a large value of ESCO, which then led to a large runoff, greater groundwater flow, smaller evapotranspiration, and lower revap (Figure 5a). Consequently, this objective function highly overestimated the peak flows as shown in Figure 3. Furthermore, while the value of the initial model of SOL_AWC was small between 84 and 371 mm (approximately 186 mm on average), the fitted value of the relative change was still underestimated at +16%, and also, the fitted value of SLSUBBSN was overestimated at 68.03 m. As a result, a huge surface runoff and a neglected lateral flow occurred for this objective function. Additionally, the calibrated value of the average slope steepness (HRU_SLP) of bR2 was small. However, this parameter was the least sensitive, which may not have as a considerable effect as the earlier mentioned six parameters (they were the top six sensitive parameters).

Table 5.
Fitted values and sensitivity ranks (values in parentheses) of the calibrated parameters obtained from different objective functions during the calibration process.
Regarding the SSQR objective function, the problems were that the fitted value of the relative change of SOL_AWC was small (18%), whereas the fitted value of SLSUBBSN was large (37.25 m), which were the fifth and seventh most sensitive parameters, respectively. This resulted in a large surface runoff and small lateral flow (Figure 5a). Moreover, the large value of ESCO (0.95), which was the third most sensitive parameter, led to a low evapotranspiration; the small value of GW_REVAP (0.04), which was the second most sensitive parameter, led to big groundwater flow and small revap; and the small value of REVAPMN (5.75), which was the sixth most sensitive parameter, contributed to a slightly high deep aquifer recharge. Regarding the KGE objective function, the problems included the calibrated parameter set being slightly large for the relative change of CN2 (8%), which was the fifth most sensitive parameter, the slightly small value of GWQMN (1731.04), which was the third most sensitive parameter, and the slightly small value of GW_REVAP (0.07), which was the most sensitive parameter. As the result, runoff (surface and lateral flow) and groundwater flow generated by this objective function were slightly large, and the revap was relatively small (Figure 5a). For the PBIAS objective function, the calibrated parameter value of the relative change of CN2, which was the most sensitive parameter, was huge (+14%), whereas the value of the relative change of SOL_AWC, which was the second most sensitive parameter, was negative (−10%) and the value of SLSUBBSN, which was the fourth most sensitive parameter, was too long (118.23 m). Consequently, the runoff obtained from this objective function was large with a huge surface runoff and a very small lateral flow (Figure 5a). This is shown in Figure 3 as an overestimation of the peak flows. This objective function also produced a very small value for ESCO, which was the third most sensitive parameter, which should produce a large evaporative demand from the soil. However, owing to the limited available plant water (small SOL_AWC), evaporative demand from the soil was also restricted, leading to an evapotranspiration restriction.
5.3. Hydrograph Components Estimation
To evaluate how different objective functions performed the simulation of each hydrological process, the monthly calibrated results of discharge and observed data were classified into base flow, rising limb, peak flow, and falling limb phases. Based on the monthly average hydrograph in Section 5.4, base flow, which is the period of low flow, was considered from January to March. Then, the rising limb or concentration curve, the ascending portion of the hydrograph, was considered from April to August. Peak flow or crest segment, the inflection point on the rising limb to the falling limb, was considered from September to October; and the falling limb or recession curve, the descending portion from the point of inflection at the end of the crest segment to the base flow, was considered from November to December for each year of the calibration period from 1995 to 2008. In this section, the results of RSR objective function was not further presented and discussed as it is equivalent to and produced the same results with NSE objective function.
Figure 8 presents the scatter plots of the simulated versus observed discharge of base flow period for different objective functions. All of the objective functions generally overestimated the base flows. This behavior can be explained by the small fitted parameter values of GWQMN below 3000 mm as generated by many of the objective functions and the small fitted parameter values of GW_REVAP below 0.05 as defined by some of the objective functions (Table 5). A study conducted by Rafiei Emam et al. [49] in central Vietnam, which is also predominant by forest, defined the final range for GWQMN between 3133 and 3756 mm. However, among them, NSE and MNS objective functions produced better simulation results for the base flows with higher R2 values, better slope (optimum value of 1) and intercept (optimum value of 0), and smaller RMSD value. The simulated base flows of the MNS objective function achieved an R2 of 0.45, slope of 0.48, intercept of 3.59, and RMSD of 7.78, whereas the simulation results of the NSE objective function provided a value of R2 of 0.48, slope of 0.41, intercept of 2.84, and RMSD of 10.76.
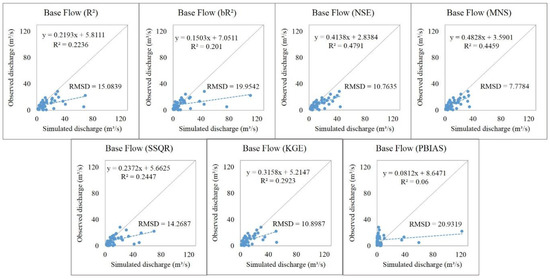
Figure 8.
Scatter plots of simulated versus observed base flows for different objective functions.
For the rising limb estimation, none of the simulation results of these objective functions showed a reasonable correlation with the observed data with an R2 of 0.21 at most and large intercepts; however, the correlation slopes of some of them reached a value that was greater than 0.6. Again, NSE objective function provided the closest simulation results (Figure 9) with R2, slope, intercept, and RMSD values of 0.21, 0.67, 35.16, and 63.97, respectively.
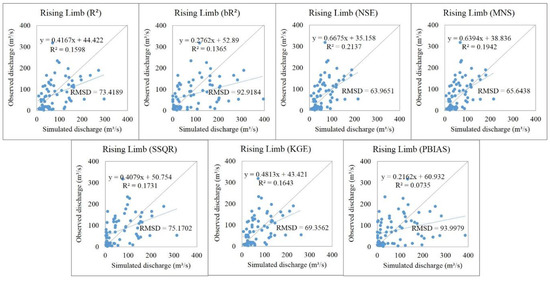
Figure 9.
Scatter plots of simulated versus observed rising limb for different objective functions.
Conversely, the simulated peak flows of these objective functions gave a reverse performance result (Figure 10). The simulated peak flows of the PBIAS, bR2, R2, and KGE objective functions attained slightly higher R2 values compared to the results of the other objective functions at slightly larger than 0.50, whereas those of the remaining objective functions were a little less than 0.50. However, the regression slopes of the results obtained from the NSE and MNS objective functions reached a satisfactory value of above 0.70, and those obtained from the other objective functions were between 0.54 and 0.64. The intercepts obtained from all objective functions were between 76.82 and 102.54, and the RMSD values were between 106.67 and 127.61.
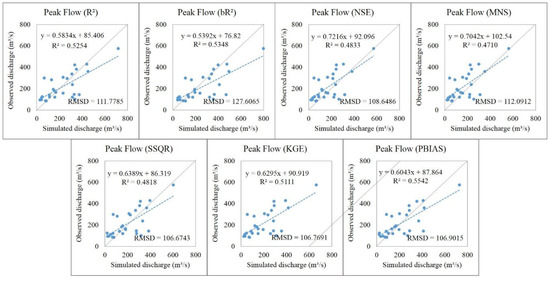
Figure 10.
Scatter plots of simulated versus observed peak flows for different objective functions.
For the falling limb estimation, the performances of most objective functions were good (Figure 11). The MNS objective function performed well in simulating the falling limbs with an R2 of 0.79 with a good slope of 1.01, a small intercept of −9.62, and a RMSD of 37.38. The NSE and KGE objective functions performed similarly but were lower with an R2 of approximately 0.78 and RMSD of approximately 41. However, the regression slope and intercept obtained from the NSE objective function were at 0.97 and −14.46, respectively, whereas those obtained from KGE were 0.90 and −5.52, respectively.
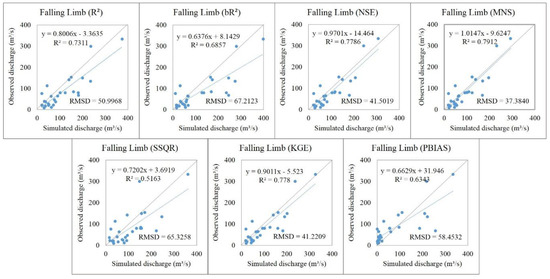
Figure 11.
Scatter plots of the simulated versus observed falling limbs for different objective functions.
The results showed that the NSE and MNS objective functions provided overall better estimation results for all the components of the hydrograph for this river basin. However, KGE, R2, bR2, SSQR, and PBIAS were among the more poor objective functions, especially for the simulation during low flow periods. For NSE, the differences between the observed and predicted values were calculated as squared values. As a result, larger values in a time series are strongly overestimated, whereas lower values are neglected [45]. Additionally, runoff peaks will tend to be underestimated when NSE is used in the optimization [34]. However, NSE is good for use with continuous long-term simulations and can be used to determine how well a model simulates trends for the output response of concern [46,50]. Because the calibration duration of this study was 14 years, it is likely that the NSE objective function could capture this long-term trend of the discharge. For the MNS objective function, which was the modified form of NSE with the modified factor of p = 1 used in this study, it can be expected that the modified forms are more sensitive to significant over- or under-prediction than the squared forms [30]. However, in this study, the performance of the MNS objective function was only slightly better than the performance of the NSE objective function when we simulated the falling limbs, but it always slightly performed worse than the NSE objective function when we simulated the other components of the hydrograph.
Another objective function used in this study, KGE, is a decomposition of NSE. Similar to NSE, the runoff peaks will tend to be underestimated, but when the KGE optimization is used, the underestimation will not be as severe [34]. As a result, the simulated peak flows of KGE exhibited a slightly better correlation than that of NSE. However, the slope of the regression line for NSE was better (Figure 10), which was because of the suitability of NSE in regressing the observed against the simulated values [34]. The R2 objective function is widely used in hydrological modeling studies, but it is oversensitive to high extreme values and insensitive to additive and proportional differences between model predictions and measured data [45]. For the bR2 objective function, the under- or over-predictions are quantified together with the dynamics, which results in a more comprehensive reflection of model results [30]. The SSQR objective function aims at fitting the distribution of the flows, ensuring that the full range of the flows is represented but without considering the time of occurrence of a given value of the flows [33]. Perhaps due this characteristic, the estimated recession curves (falling limbs) were typically flatter than the observed data, and the estimated base flows were shortened (Figure 3). As a result, the simulation performances of the falling limbs (Figure 11) and base flows (Figure 8) of this objective function were relatively low. For the PBIAS objective function, it is useful for continuous long-term simulations and can be used to determine how well the model simulates the average magnitudes for the output response of interest [46]. PBIAS can provide a deceptive rating of model performance when the model over-predicts as much as it under-predicts, in which case PBIAS will be close to zero even though the model simulation is poor [46]. This may be why there were several sudden peak and drop points of the simulated result of this objective function during the base flow and rising limb periods (Figure 3), leading to poor model performances in simulating the base flows and rising limbs, as shown in Figure 6 and Figure 7, respectively.
5.4. Objective Functions Corresponding to the Characteristics of the River Basin
Figure 12 shows the monthly average hydrograph of the observed flow at Bak Trakuon Station and rainfall at Kravanh Station during the calibration period from 1995 to 2008 (data between 1997 and 1998 were excluded due to missing data). The validation period was not included because this study focused on the effect of different objective functions on model calibration. Because the dry season, which extends from December to April, is influenced by the northeast monsoon system [22], the river discharge is relatively low, approaching zero between January and March. This indicated that groundwater from the upstream area did not contribute considerably to the river discharge. However the river discharge begins to rise from April when the wet season starts, and the first peak occurs in May as the monsoon rain travels north [22]. This peak is followed by a period of lower rainfall between June and August. The greatest peak occurs between the months of September and October and is caused by a southerly shift in the monsoon circulation pattern, which is characterized by heavy rainfall. This indicated that the flow characteristic in this river basin is highly controlled by the monsoon rainfall pattern, especially during the wettest period from August of November when the correlation between the monthly discharge and the monthly rainfall was so high.
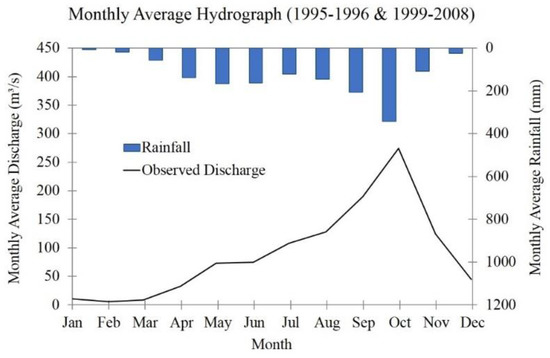
Figure 12.
Monthly average hydrograph at Bak Trakuon Station during the calibration period from 1995 to 2008 (excluding 1997 and 1998 when rainfall data were missing).
Additionally, the physiographic condition likely influences the hydrological process as well, particularly at beginning of the rainy season from April to July when the correlation between the monthly discharge and the monthly rainfall was low as the result of a lag time in the hydrograph. With the size of the drainage area at Bak Trakuon Station, the elongated shape, the forested land cover with varying densities, and the textures of Dystric Leptosol and Cambisol may also contribute to this broad rising limb in the hydrograph (concentration curve of the hydrograph from April to September) owing to retardation of overland flow and the increase of infiltration and storage capacities of the soils [51]. However, the sharp slope of the falling limb of the hydrograph (recession curve of the hydrograph from late October to December) is likely due to the hilly terrain topography of the drainage area that form a large stream and valley slopes, which result in quick depletion of storage [51].
Compared to other land covers, a forested watershed has some unique features. Mature forests have relatively large aboveground (i.e., over-story and under-story layers) and belowground (i.e., roots) biomass [52,53]. They generally have a higher canopy surface roughness, higher leaf area index, and deeper roots compared to crops and/or grass [54], which result in a relatively high ET [55] and soil infiltration capacity. Forest soil permeability would be maintained by defoliation and organic matter supply from the biomass and considerably reduce the potential for surface flow, lower the total stream flow, and lower the peak flow [56]. Generally, forest stream flow originates from subsurface flow (lateral flow) or groundwater discharge at headwater streams.
Based on the hydrograph and physiographic characteristics of this study area, the NSE, RSR, and MNS objective functions in addition to their goodness of fits for simulating the discharge (Figure 3 and Figure 4) were found to be among the better objective functions for estimating hydrological components, such as a higher ET, lower surface runoff, larger lateral flow, smaller groundwater flow, greater revap, and lower water yield (Figure 5). Moreover, their performances in simulating hydrograph components were overall better than other objective functions, especially the NSE and RSR objective functions, when simulating the base flow, rising limb, and falling limb (Figure 8, Figure 9 and Figure 11).
6. Conclusions
The SWAT model was employed to simulate the stream flow of Pursat River Basin. Eight different objective functions were used in the calibration process of SWAT-CUP with the SUFI-2 algorithm to examine their influences on the calibration results, parameter optimizations, and water resources estimations. Many objective functions performed better than satisfactorily for calibrating the SWAT model. However, different objective functions defined different fitted values and sensitivity ranks of the calibrated parameters, resulting in different estimations of water balance components and water yield. Among the objective functions used in this study, the Nash–Sutcliffe efficiency (NSE) and ratio of standard deviation of the observations to root mean square error (RSR) are equivalent and produced identical simulation results, including the parameter sensitivity and fitted values of the calibrated parameters, leading to the same water balance components and water yields estimation results. By taking results and data of previous studies and according to the characteristics of the river basin, either NSE or RSR objective functions gave the best estimation results of annual average water yield and other water balance components, such as annual average evapotranspiration (ET), groundwater flow (GWQ), surface runoff (SurQ), and lateral flow (LatQ), because these equivalent objective functions generated reasonable fitted values of the calibrated parameters. Moreover, either of them was also better at calibrating the base flow, falling limb, and overall the entire flow phases of the hydrograph for this area.
Author Contributions
Conceptualization and methodological framework, D.S. and T.K.; investigation and data collection, D.S. and P.T.; SWAT model setup, calibration and validation, D.S. and L.H.T.; MODIS ET analysis, A.F. and T.K.; result analysis and visualization, D.S.; writing—original draft preparation, D.S.; writing—review and editing, T.K., C.O., L.H.T., P.T., A.F. and D.S.; supervision, T.K. and C.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by JSPS KAKENHI Grant Number JP18H02295.
Acknowledgments
The authors also would like to thank Enago (www.enago.jp) for the English language review.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gosain, A.K.; Rao, S.; Basuray, D. Climate change impact assessment on hydrology of Indian river basins. Curr. Sci. 2006, 90, 9. [Google Scholar]
- Rostamian, R.; Jaleh, A.; Afyuni, M.; Mousavi, S.F.; Heidarpour, M.; Jalalian, A.; Abbaspour, K.C. Application of a SWAT model for estimating runoff and sediment in two mountainous basins in central Iran. Hydrol. Sci. J. 2008, 53, 977–988. [Google Scholar] [CrossRef]
- Huang, T.; Lo, K. Effects of Land Use Change on Sediment and Water Yields in Yang Ming Shan National Park, Taiwan. Environments 2015, 2, 32–42. [Google Scholar] [CrossRef]
- Näschen, K.; Diekkrüger, B.; Evers, M.; Höllermann, B.; Steinbach, S.; Thonfeld, F. The Impact of Land Use/Land Cover Change (LULCC) on Water Resources in a Tropical Catchment in Tanzania under Different Climate Change Scenarios. Sustainability 2019, 11, 7083. [Google Scholar] [CrossRef]
- Cambien, N.; Gobeyn, S.; Nolivos, I.; Forio, M.A.E.; Arias-Hidalgo, M.; Dominguez-Granda, L.; Witing, F.; Volk, M.; Goethals, P.L.M. Using the Soil and Water Assessment Tool to Simulate the Pesticide Dynamics in the Data Scarce Guayas River Basin, Ecuador. Water 2020, 12, 696. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment, Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool—Theoretical Documentation (Version 2005); Agricultural Research Service: Temple, TX, USA, 2005.
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute Technical Report No. 406; Texas A&M University System: College Station, TX, USA, 2011. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute of Aquatic Science and Technology: Zurich, Switzerland, 2015. [Google Scholar]
- Ha, L.T.; Bastiaanssen, W.G.M.; van Griensven, A.; van Dijk, A.I.J.M.; Senay, G.B. SWAT-CUP for Calibration of Spatially Distributed Hydrological Processes and Ecosystem Services in a Vietnamese River Basin Using Remote Sensing. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–35. [Google Scholar] [CrossRef]
- Roth, V.; Nigussie, T.K.; Lemann, T. Model parameter transfer for streamflow and sediment loss prediction with SWAT in a tropical watershed. Environ. Earth Sci. 2016, 75, 1321. [Google Scholar] [CrossRef]
- Gholami, A.; Habibnejad Roshan, M.; Shahedi, K.; Vafakhah, M.; Solaymani, K. Hydrological stream flow modeling in the Talar catchment (central section of the Alborz Mountains, north of Iran): Parameterization and uncertainty analysis using SWAT-CUP. J. Water Land Dev. 2016, 30, 57–69. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Vejdani, M.; Haghighat, S. SWAT-CUP Calibration and Uncertainty Programs for SWAT; Modelling and Simulation Society of Australia and New Zealand: Christchurch, New Zealand, 2007; pp. 1596–1602. [Google Scholar]
- Khoi, D.N.; Thom, V.T. Parameter uncertainty analysis for simulating streamflow in a river catchment of Vietnam. Glob. Ecol. Conserv. 2015, 4, 538–548. [Google Scholar] [CrossRef]
- Shivhare, N.; Dikshit, P.K.S.; Dwivedi, S.B. A Comparison of SWAT Model Calibration Techniques for Hydrological Modeling in the Ganga River Watershed. Engineering 2018, 4, 643–652. [Google Scholar] [CrossRef]
- Sloboda, M.; Swayne, D. Autocalibration of Environmental Process Models Using a PAC Learning Hypothesis. In Environmental Software Systems. Frameworks of eEnvironment; IFIP Advances in Information and Communication Technology; Springer: Berlin/Heidelberg, Germany, 2011; Volume 359, pp. 528–534. ISBN 978-3-642-22284-9. [Google Scholar]
- Kouchi, D.H.; Esmaili, K.; Faridhosseini, A.; Sanaeinejad, S.H.; Khalili, D.; Abbaspour, K.C. Sensitivity of Calibrated Parameters and Water Resource Estimates on Different Objective Functions and Optimization Algorithms. Water 2017, 9, 384. [Google Scholar] [CrossRef]
- Ashwell, D.; Lic, V.; Loeung, K.; Maltby, M.; McNaughton, A.; Mulligan, B.; Oum, S.; Starr, A. Baseline Assessment and Recommendations for Improved Natural Resources Management and Biodiversity Conservation in the Tonle Sap Basin, Cambodia; Fauna & Flora International: Phnom Penh, Cambodia, 2011; 92p. [Google Scholar]
- Cambodia National Mekong Committee (CNMC). Basin Development Plan Program (Ed.): Profile of the Tonle Sap Sub-Area (SA-9C); CNMC: Phnom Penh, Cambodia, 2012. [Google Scholar]
- Japan International Cooperation Agency (JICA). Report on Examination of Impact of New Dam Plans on the West Tonle Sap Irrigation Rehabilitation Project in Pursat River Basin; Ministry of Water Resources and Meteorology (MOWRAM): Phnom Penh, Cambodia, 2011. [Google Scholar]
- Japan International Cooperation Agency (JICA). Brief Progress Report on the Water Balance Examination Study for Pursat and Baribor River Basins; Ministry of Water Resources and Meteorology (MOWRAM): Phnom Penh, Cambodia, 2013. [Google Scholar]
- Abbaspour, K.C.; van Genuchten, M.T.; Schulin, R.; Schläppi, E. A sequential uncertainty domain inverse procedure for estimating subsurface flow and transport parameters. Water Resour. Res. 1997, 33, 1879–1892. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.A.; Van Genuchten, M.Th. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Rossi, C.G.; Srinivasan, R.; Jirayoot, K.; Duc, T.L.; Souvannabouth, P.; Binh, N.; Gassman, P.W. Hydrologic Evaluation of the Lower Mekong River Basin with the Soil and Water Assessment Tool Model. Int. Agric. Eng. J. 2009, 18, 1–13. [Google Scholar]
- Ly, S.; Oeurng, C. Climate change and water governance in Stung Chrey Bak Cathment of Tonle Sap Great Lake Basin in Cambodia. In Proceedings of the 15th Annual Conference of the Science Council of Asia (SCA), Siem Reap, Cambodia, 17–19 May 2015; pp. 134–138. [Google Scholar]
- Ang, R.; Oeurng, C. Simulating streamflow in an ungauged catchment of Tonlesap Lake Basin in Cambodia using Soil and Water Assessment Tool (SWAT) model. Water Sci. 2018, 32, 89–101. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Van Griensven, A.; Bauwens, W. Multiobjective autocalibration for semidistributed water quality models: Autocalibrations for water quality models. Water Resour. Res. 2003, 39, 1348. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Automatic calibration of conceptual rainfall-runoff models: Sensitivity to calibration data. J. Hydrol. 1996, 181, 23–48. [Google Scholar] [CrossRef]
- James, L.D.; Burges, S.J. Selection, Calibration, and Testing of Hydrologic Models. In Hydrologic Modeling of Small Watersheds; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1982; pp. 437–470. [Google Scholar]
- Muleta, M.K. Model Performance Sensitivity to Objective Function during Automated Calibrations. J. Hydrol. Eng. 2012, 17, 756–767. [Google Scholar] [CrossRef]
- Mehdi, B.; Ludwig, R.; Lehner, B. Evaluating the impacts of climate change and crop land use change on streamflow, nitrates and phosphorus: A modeling study in Bavaria. J. Hydrol. Reg. Stud. 2015, 4, 60–90. [Google Scholar] [CrossRef]
- Akhavan, S.; Abedi-Koupai, J.; Mousavi, S.-F.; Afyuni, M.; Eslamian, S.-S.; Abbaspour, K.C. Application of SWAT model to investigate nitrate leaching in Hamadan–Bahar Watershed, Iran. Agric. Ecosyst. Environ. 2010, 139, 675–688. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; De Roo, A. Hydrological evaluation of satellite-based rainfall estimates over the Volta and Baro-Akobo Basin. J. Hydrol. 2013, 499, 324–338. [Google Scholar] [CrossRef]
- Running, S.; Mu, Q.; Zhao, M. MOD16A2 MODIS/Terra Net Evapotranspiration 8-Day L4 Global 500m SIN Grid V006 [Data Set]; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2017.
- Busetto, L.; Ranghetti, L. MODIStsp: An R package for automatic preprocessing of MODIS Land Products time series. Comput. Geosci. 2016, 97, 40–48. [Google Scholar] [CrossRef]
- Kobayashi, K.; Salam, M.U. Comparing Simulated and Measured Values Using Mean Squared Deviation and its Components. Agron. J. 2000, 92, 345–352. [Google Scholar] [CrossRef]
- Gauch, H.G.; Hwang, J.T.G.; Fick, G.W. Model Evaluation by Comparison of Model-Based Predictions and Measured Values. Agron. J. 2003, 95, 1442–1446. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Harmel, R.D.; Smith, P.K.; Migliaccio, K.W. Modifying Goodness-of-Fit Indicators to Incorporate Both Measurement and Model Uncertainty in Model Calibration and Validation. Trans. ASABE 2010, 53, 55–63. [Google Scholar] [CrossRef]
- Shimizu, A.; Suzuki, M.; Sawano, S.; Kabeya, N.; Nobuhiro, T.; Tamai, K.; Tsuboyama, Y.; Chann, S.; Keth, N. Water Resources Observation and Large-scale Model Estimation in Forested Areas in Mekong River Basin. Jpn. Agric. Res. Q. 2010, 44, 179–186. [Google Scholar] [CrossRef]
- Japan International Cooperation Agency (JICA). The Study on Groundwater Development in Southern Cambodia; Ministry of Rural Development: Phnom Penh, Cambodia, 2002; 309p.
- Rafiei Emam, A.; Kappas, M.; Hoang Khanh Nguyen, L.; Renchin, T. Hydrological Modeling in an Ungauged Basin of Central Vietnam Using SWAT Model. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–33. [Google Scholar] [CrossRef]
- Harmel, R.D.; Smith, P.K. Consideration of measurement uncertainty in the evaluation of goodness-of-fit in hydrologic and water quality modeling. J. Hydrol. 2007, 337, 326–336. [Google Scholar] [CrossRef]
- Subramanya, K. Engineering Hydrology; Tata McGraw-Hill: New York, NY, USA, 2008; ISBN 978-0-07-133748-9. [Google Scholar]
- Waring, R.H.; Running, S.W. Forest Ecosystems: Analysis at Multiple Scales, 3rd ed.; Elsevier/Academic Press: Amsterdam, Boston, 2007; ISBN 978-0-12-370605-8. [Google Scholar]
- Chapin, F.S.; Matson, P.A.; Vitousek, P.M. Principles of Terrestrial Ecosystem Ecology; Springer: New York, NY, USA, 2011; ISBN 978-1-4419-9503-2. [Google Scholar]
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Sun, G.; Alstad, K.; Chen, J.; Chen, S.; Ford, C.R.; Lin, G.; Liu, C.; Lu, N.; McNulty, S.G.; Miao, H.; et al. A general predictive model for estimating monthly ecosystem evapotranspiration. Ecohydrology 2011, 4, 245–255. [Google Scholar] [CrossRef]
- Sun, G.; Lockaby, B.G. Water Quantity and Quality at the Urban-Rural Interface. In Urban-Rural Interfaces; American Society of Agronomy, Soil Science Society of America, Crop Science Society of America, Inc.: Madison, WI, USA, 2012; pp. 29–48. ISBN 978-0-89118-616-8. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).