Towards Model-Free Pressure Control in Water Distribution Networks

Abstract

Pressure control in water distribution networks (WDNs) is one of the interventions commonly employed to improve the reliability and sustainability of water supply. Various approaches have been proposed to solve the problem of pressure control. However, most schemes that have been proposed rely on the accuracy of a model in order to precisely control a real WDN. Therefore, any deviation between a model and real WDN parameters could render the results of control schemes useless. As a result, this work proposes the utilisation of the reinforcement learning (RL) technique to control nodes pressure in WDNs without solving the model. Quadratic approximation emulators of WDNs and RL agents are used in the proposed scheme. The effectiveness of the proposed scheme is tested on two WDNs networks and the results are compared with the conventional optimisation scheme that is commonly used for simulation cases. The results show that the proposed scheme is able to achieve the desired results when compared to the benchmark optimisation procedure. However, unlike the optimisation procedure, the proposed scheme achieved the results without the numerical solution of the WDNs. Therefore, this scheme could be used in situations where the model of a network is not well defined.

1. Introduction

Potable water is one of the important contributors to the well-being and good health of a society. Despite this, depletion of potable water resources is of paramount concern. Ordinarily, water is supplied and distributed through water distribution networks (WDNs) from reservoirs to the consumers. Modern day WDNs operate under various adverse dynamic conditions, their management since it ensures that operation conforms with the tight requirement for reliability and dependability. WDNs operators must ensure that water is supplied to the consumers at a precise pressure and an acceptable quality [1].

Presently, it is generally accepted that proper management of pressure in WDNs leads to more reliable operation [2,3,4,5,6]. The pressure in WDNs is normally adjusted and maintained by pressure reducing valves (PRVs) [7,8]. Determination of an appropriate adjustment of pressure in PRVs has been a challenge over the past few decades. Classical, advanced, and optimal control strategies are amongst the techniques that are commonly employed to control the operation of PRVs. In [9], a PID controller is used to control a pumping system in WDNs for pressure regulation. However, the shortfall of its control precision and capability is discussed in [10]. The issue of frequency fluctuations that may lead to an unsteady pressure in a pipeline is also raised in [11].

Optimal control techniques have also been widely used to determine an appropriate setting for PRVs in WDNs. Jowitt and Xu [2] and Hindi and Hamam [12] use linearisation techniques to transform a non-linear optimisation problem (NLOP) a linear problem. In recent times, the existence of packages such as Interior-Point Optimizer (IPOPT) [6,13] has allowed for a direct solution of NLOP to determine the optimal control of WDNs. Meta-heuristic techniques have also been used to solve a rather complex non-linear optimisation problem of pressure control [4,5,14,15]. Furthermore, it is evident that all these schemes rely on the accuracy of a model to realise appropriate settings for PRVs. In [3,16,17] the utilisation of artificial neural networks (ANNs) to emulate the control process of the PRVs were proposed. Although the ANN scheme would not ordinarily rely on a model to control PRVs, it may be rendered useless should the topology of a real system be augmented [18].

Nevertheless, most of the methodologies that have been proposed in the literature have shown positive results. It is worthy to note that most of these schemes rely on the accuracy of a model in order to control real physical systems. Therefore, any discrepancy between a model and the real system could lead to an undesired operation as a model would not be an exact representation of the physical system. Elements of WDNs are exposed to various environmental conditions, hence, it is inevitable that the network parameters (i.e., hydraulic resistance) will be affected. This may result in a mismatch between model parameters and the physical system. The effect of environmental conditions on network parameters has not been accounted for previously in the literature. Consequently, this work proposes an alternative model-free pressure control for WDNs. Model-free control in this context denotes an external agent that can manipulate a network without the utilisation of its model to determine appropriate control inputs. Quadratic approximation of the WDNs is utilised in this work to mimic the operation of a network. Reinforcement learning agents are used to learn an appropriate manipulation of the network. These agents propose control inputs based on the current state of a network and receive feedback (reward) to inform the controller whether the action proposed is good or not. The controller (policy used by the agent) is updated until an optimal point is reached. The performance of the proposed is compared against the conventional optimisation process used in the literature [5,13,14] for simulation studies. Conventional optimisation in this context refers to the direct search and gradient based algorithms [19].

The rest of the paper is organised as follows: In Section 2 a review of related works that have been proposed in the literature. The mathematical representation of WDNs and the control problem formulation are presented in Section 3 and Section 4. The results of the numerical experiment and their discussions are presented in Section 5 while some conclusion remarks are given in Section 6.

2. Related Works

The problem of pressure control in WDNs was investigated in [20,21]. In the work, a scheme that uses a proportional (P)-controller that does not use model parameters was presented. Its performance was better than the classical methods.

The first set of significant works on pressure control via optimisation techniques were present in [2,22]. In the work, non-linear problems are linearised and solved as linear problems to minimise the computational burden. The separable linearisation scheme proposed in [12] was recently used in [23] in demand response scheduling for water distribution network (WDN). Ref. [24] proposes a quadratic approximation of pipes functions and formulated mathematical optimisation to solve the pressure control problem. The results obtained in [24] are compared with the popular EPANET software (United States Environmental Protection Agency, Westlake, OH, USA) [25] and up to 1% difference was observed. The utilisation of genetic algorithms to solve dual pressure control and localisation of PRVs is explored in [14]. The solution of the MINLP problem shows that the need for rehabilitation of WDNs elements may be halved by using the proposed scheme. Various mathematical formulation for pressure control in WDNs are put forward in [26]. In [27] Strictly Feasible Sequential Convex Programming is used to achieve 3.7% reduction in pressure reduction in subdivision of water distribution network. Various authors [4,5,15,28] propose the utilisation of meta-heuristic and soft-computing techniques to solve the optimisation problem formulated to optimally control the PRVs.

Notwithstanding their strengths, most of the methods rely on the solution of a model to determine the optimal settings on the PRVs. This could render the results absolute should the accuracy of the model be compromised as a result of degraded WDNs elements.

3. Water Distribution Network Modelling

A water distribution network (WDN) consists of links (pipes) and nodes (demand and source). Generally, the topology of a WDN permits utilisation of the graph-theoretic approach to define its model. Consider a WDN that consists of a $N_b$ number of links or pipes, $N_n$ number of nodes encompassing $n_s$ number of sources nodes, and $n_d$ number of demand nodes. The nodal balance equation can be expressed as

$$C_{ij}Q=I$$

(1)

where, $I\in \forall N_n$ is a vector of nodal injections and demands and $Q\in \forall N_b$ is a vector of flows in the pipes. $C_{ij}$ is $N_n\times N_b$ node-branch incidence matrix. Matrix $C_{ij}$ can be decomposed as

$$C_{ij}=\left[\begin{array}{c}{C}_s\\ C_l\end{array}\right]$$

(2)

The flow at the load nodes only can be written as

$$C_{l}Q=-L$$

(3)

In Equations (2) and (3), $C_s$ and $C_l$ are the node-branch incidence matrices for the source and load nodes respectively while L is the demand vector of the load nodes. The topological matrices defining the energy conservation of the pipes for a closed-loop water distribution network can be expressed as

$$\Delta h=\left[\begin{array}{cc}{C}_s^T& C_l^T\end{array}\right]\left[\begin{array}{c}{h}_s\\ h_l\end{array}\right]$$

(4)

where, $h_s$ and $h_l$ are vectors of pressures at sources and load nodes, respectively. For each pipe i, the pressure drop has a general form that is given in Equation (5)

$$\Delta h=k_p{Q}_i^{\alpha }=k_p{Q}_i{\left|Q_i\right|}^{\alpha -1}$$

(5)

where $k_p$ is the pipe resistance and $\alpha$ is the pressure exponent. It is important to note that for pipes with PRVs installed, the total pressure (head) loss will encapsulate the minor loss m due to the valve [25]. Rearranging Equation (4) and substituting Equation (5) in (4) yields

$$k_p{\left|Q\right|}^{\alpha -1}Q-C_s^T{h}_s-C_l^T{h}_l=0$$

(6)

Defining matrix A as $A=diag\left(k_p{\left|Q\right|}^{\alpha -1}\right)$, then

$$AQ-C_s^T{h}_s-C_l^T{h}_l=0$$

(7)

Equations (3) and (7) are the hydraulic equations that define the operation of the WDN. Their Newton’s solution yields the hydrostatic pressure h and the water flows through the pipes Q.

4. Pressure Control in Water Distribution Networks

4.1. Classical Model-Based Pressure Control Problem Formulation

The objective of the scheme is to ensure that the pressure in the system is considerably reduced. Furthermore, the problem is formulated to keep the pressure at all nodes above the minimum and below the maximum. Mathematically, the objective can be expressed as [14]

$$\min f=\sum {\omega }_i{\left(h_i{\left(t\right)}^{ref}-h_i{\left(t\right)}^{calc}\right)}^2$$

(8)

where $\omega$ is the weighing factor. The objective is subject to the following constraints.

• The continuity equation at each node expressed as

  $$C_{l}Q+L=0$$

  (9)
• The head pressure loss constraint (conservation of energy) of each pipe.

  $$\Delta h-C_s^T{h}_s-C_l^T{h}_l=0$$

  (10)
• Nodal head constraint

  $$h_i\left(t\right)\ge h_i{\left(t\right)}^{min}$$

  (11)

  $$h_i\left(t\right)\le h_i{\left(t\right)}^{max}$$

  (12)
• Pipe Flow constraint

  $$Q_{i}unrestricted$$

  (13)
• Valve opening

  $$0<u_{ij}\le 1$$

  (14)

In Equation (14), $u\in \{0:1\}$ is a diameter multiplier (control input to the PVRs) which imitate the presence of a valve [14]. The choice of $h_i{\left(t\right)}^{ref}$ and $h_i{\left(t\right)}^{min}$ is of great importance because the demand varies with time. Ordinarily, at lower demands, the pressure in the network would generally be in excess of what is required and at higher demands, the pressure falls below the required [29]. Therefore, $h_i{\left(t\right)}^{ref}$ and $h_i{\left(t\right)}^{min}$ should be adapted accordingly as the demand varies. The flow through the pipes is left unrestricted as ordinarily, the change in the valves will affect the flows in the whole system.

4.2. The Proposed Model-Free Pressure Control

Model-free control (MFC) with a reinforcement learning (RL) controller is used to learn the behaviour of WDNs (environment) and based on a given demand (state s), it determines the optimal adjustment of the PRVs (action a). RL is a subset of machine learning but unlike supervised (mapping input with outputs) and unsupervised (classification), it learns directly from data in a dynamic environment. As such, RL does not need any prior information about the structure of the model. The works of Hamam and Hindi [3] and Rao [16] indicate that one of the major challenge with supervised learning is that several thousands of simulations has to be performed in order to generate the dataset that can be used for training. An RL agent only needs the structure of the observation and the manipulated variables. The agent then determines the optimal policy ${\pi }^{*}\left(s\right)$ to decide on what actions to take given a state of the environment. For each action proposed by the agent, it is rewarded and the policy is updated based on the reward. The structure of an RL agent is shown in Figure 1.

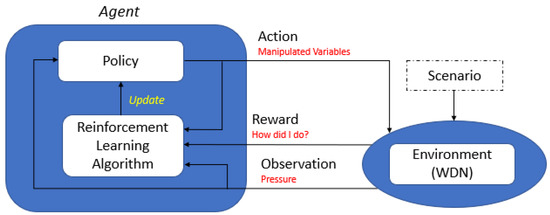
Figure 1. Reinforcement learning agent.

Given a scenario or state s and an action a, the environment produces the observation and rewards the agent for the proposed action. Equation (15) shows the reward function that is used. It can be seen that the reward is either 100 or −10. The RL agent is rewarded with 100 if the absolute value of the difference of $h-h_{ref}$ is less than the threshold or positive and less than the threshold, otherwise the agent is rewarded with −10.

$$\begin{array}{c}\hfill r=\left\{\begin{array}{c}100,\mathrm{if}|h-h_{r}ef|<threshold\mathrm{or}h-h_{r}ef>0\mathbf{and}<threshold\hfill \\ -10,otherwise\hfill \end{array}\right.\end{array}$$

(15)

The algorithm is then invoked and upon convergence, the policy is updated. In this work, the value iteration algorithm is used to update the policy. The pseudocode for the algorithm is shown in Algorithm 1.

Algorithm 1: Value Iteration Algorithm

For every scenario $s\in S$ observed by the environment in Figure 1, pressure from a critical node (CN) is obtained and fed to the RL agent. It has been shown in the literature that, the pressure in WDNs could be controlled based on the pressure observed on a critical nodes [21,30] and it is defined as a sensitive node with lowest pressure. Actions a are proposed by the RL agent (using the current policy) based on the observed pressure and manipulated variables in the environment are updated. For every action (a) and state s, $p:a\times s\to r$, obtains the reward r. As the reward function is based purely on the pressure at a critical node ($h_{CN}$), $p:a\times s\to r$ relies on the invocation of Equation (16) (interaction with the environment in Figure 1) for computing $h_{CN}$. This operation on Line 8 of algorithm 1 updates the value function $V\left(s\right)$ and compare it to the previous v given by $a\leftarrow a-1$ to computes. This operation is repeated for $s\to s+1$ to determine appropriate action for the current demand.

The environment in this work is simulated by a quadratic approximation of WDNs hydraulic operation. Ordinarily, the environment would be the solution of the WDNs model as defined by Equations (3) and (7). The solution is often computed using the open source EPANET software [25]; however, in this work, a MATLAB script was written to obtain the solution of the WDN. For a daily demand variation in [2], the pressure at a critical node ($h_{CN}$) is recorded with the corresponding vector of control inputs computed as shown in Section 4.1. The function is chosen for emulation due to the quadratic nature of the flow-pressure relationship shown in Equation (5). Equation (16) presents the quadratic formulation for the approximation of the hydraulic operation of WDN.

$$\begin{array}{cc}\hfill h_{CN}& =\left[\begin{array}{ccccc}{u}_1& \cdots & u_n& L_1& \cdots L_m\end{array}\right]\left[\begin{array}{cccccc}{a}_{11}& \cdots & a_{1n}& a_{1(n+1)}& \cdots & a_{1(m+n)}\\ ⋮& \cdots & \cdots & \cdots & \cdots & ⋮\\ a_{n1}& \cdots & \cdots & \cdots & \cdots & a_{n(m+n)}\\ a_{(n+1)1}& \cdots & \cdots & \cdots & \cdots & a_{(n+1)(m+n)}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ a_{(m+n)1}& \cdots & a_{(m+n)n}& a_{(m+n)(n+1)}& \cdots & a_{(m+n)(m+n)}\end{array}\right]\left[\begin{array}{c}{u}_1\\ ⋮\\ u_n\\ L_1\\ ⋮\\ L_m\end{array}\right]\hfill \\ & +\left[\begin{array}{cccccc}{b}_1& \cdots & b_n& b_{n+1}& \cdots & b_{m+n}\end{array}\right]\left[\begin{array}{c}{u}_1\\ ⋮\\ u_n\\ L_1\\ ⋮\\ L_m\end{array}\right]+c\hfill \end{array}$$

(16)

In Equation (16), the vector $\mathbf{U}=[u_1\cdots u_n]$ represents the control inputs to the PRVs and n is the number of the installed PRVs. $\mathbf{L}=[L_1\cdots L_m]$ is the vector of nodal withdrawal at the demand nodes and scalar $h_{CN}$ is the pressure of the critical node. The unknown coefficients of the quadratic formula are $a_1\cdots a_{m+n}$ and $b_1\cdots b_{m+n}$ while the constant term is c. If a symmetric matrix

$$\mathbf{M}=\left[\begin{array}{cccccc}{a}_{11}& \cdots & a_{1n}& a_{1(n+1)}& \cdots & a_{1(m+n)}\\ ⋮& \cdots & \cdots & \cdots & \cdots & ⋮\\ a_{n1}& \cdots & \cdots & \cdots & \cdots & a_{n(m+n)}\\ a_{(n+1)1}& \cdots & \cdots & \cdots & \cdots & a_{(n+1)(m+n)}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ a_{(m+n)1}& \cdots & a_{(m+n)n}& a_{(m+n)(n+1)}& \cdots & a_{(m+n)(m+n)}\end{array}\right]$$

(17)

and matrix

$$\mathbf{B}=\left[\begin{array}{cccccc}{b}_1& \cdots & b_n& b_{n+1}& \cdots & b_{m+n}\end{array}\right]$$

(18)

are partitioned to have the unknown coefficients as sub-matrices of M and B, Equation (16) may expressed in simple form as

$$\begin{array}{c}\hfill h_{CN}=\left[\begin{array}{cc}\mathbf{U}& \mathbf{L}\end{array}\right]\left[\begin{array}{cc}{\Lambda }_1& {\Lambda }_2\\ {\Lambda }_2^T& {\Lambda }_4\end{array}\right]\left[\begin{array}{c}{\mathbf{U}}^T\\ {\mathbf{L}}^T\end{array}\right]+\left[\begin{array}{cc}{\Lambda }_5& {\Lambda }_6\end{array}\right]\left[\begin{array}{c}{\mathbf{U}}^T\\ {\mathbf{L}}^T\end{array}\right]+c\end{array}$$

(19)

where ${\Lambda }_1$ and ${\Lambda }_2$ have the dimension $n\times n$ and $n\times m$ respectively while ${\Lambda }_4$ has the dimensions $m\times m$. ${\Lambda }_5$ and ${\Lambda }_6$ are vectors with dimensions $1\times n$ and $1\times m$ respectively. The results of the matrix operation in Equation (19) can be expressed in a compact form as

$$h_{CN}\approx A_B\delta$$

(20)

where the matrix of unknown coefficients is denoted by $\delta$ and matrix composing vectors of known demand, control inputs and constants is assigned $A_B$. To determine the unknown coefficients, the least square solution expressed as

$$\delta ={\left[A_B^T{A}_B\right]}^{-1}{A}_B^T{h}_{CN}$$

(21)

is used while the MATLAB’s backslash operation solved Equation (21).

5. Numerical Experiments

Two test cases of WDNs are used to evaluate the effectiveness of the proposed model-free control scheme. Both case studies have been used previously in the literature [31,32] and MATLAB software was used for all simulations.

5.1. Numerical Experiment 1

The first case study is shown in Figure 2, and consists of 15 nodes with 2 of them being source nodes and 21 pipes. Five (5) pressure reducing valves (PRVs) were installed in the network. Pipes 1, 9, 10, 17, and 21 were selected as the installation location for the PRVs. Parameters of the nodes and pipes are given in Table A1 and Table A2.

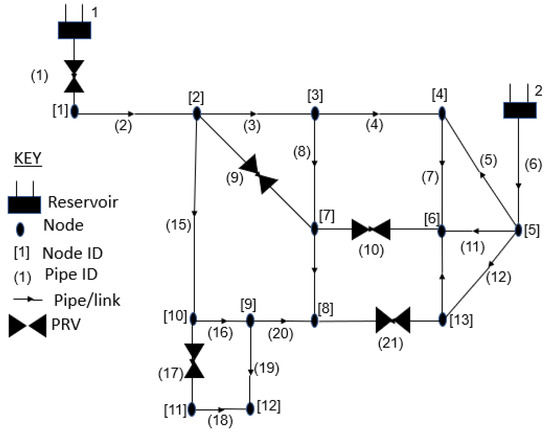
Figure 2. Schematic diagram for case study 1.

In Figure 3 and Figure 4, the impact of pressure control on the operation of the WDN is depicted. It is evident in Figure 3 that, the flow in some pipes decreased and in others increased as a result of pressure control. This is allowed by the unrestricted flow in the formulation of the control problem. Figure 4 shows an increase in pressure drop along the pipes for the demand in Table A2 (demand factor of 100%), especially those pipes with PRVs installation. This is due to the losses introduced by the valves and their subsequent adjustment. It is evident that pipes with PRVs installed (1, 9, 10, 17, and 21) experienced a significant increase in pressure drop. This is due to a minor loss of the PRVs and losses as a result of their partial closure.

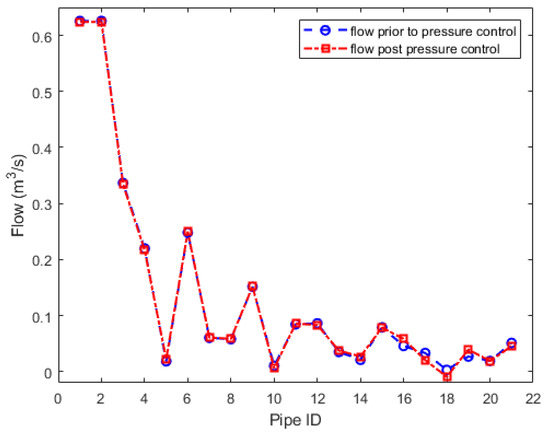
Figure 3. Pipe flows for case study 1.

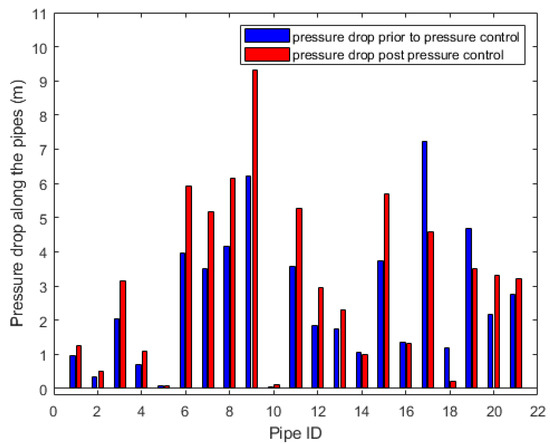
Figure 4. Nodal pressure heads for case study 1.

The head observed in the critical node (CN) of the first test case is presented in Table 1. The CN in case study 1 is marked as node 12 in Figure 2. In Table 1, the head prior to the implementation of any control scheme is presented with the observation from two of the control schemes in Section 4.1 and Section 4.2. The optimal actions from the RL agent are tested on the model and the results are also presented in Table 1. Equation (3) is used to determine the effect of the pressure control on the nodal withdrawals. Evidently, both schemes significantly reduce the pressure observed at the critical node. However, the scheme in Section 4.1 requires an explicit model, whereas, the alternative scheme proposed could achieve good results without an explicit model. Furthermore, it can be seen that the control does not affect the amount of water withdrawn at the demand nodes.

Table 1. Pressure observed on the critical node at 80%, 100% and 120% demand.

Demand	${\mathit{h}}_{\mathbf{CN}}$	${\mathit{h}}_{\mathbf{CN}}$	${\mathit{h}}_{\mathbf{CN}}$	${\mathit{h}}_{\mathbf{CN}}$ RL Output	L Prior	L Post
Factor	Prior Control	Post MBC	Post MFC	Tested on a Model
80%	52.84 m	46.04 m	45.93 m	45.89 m	699 L/s	699 L/s
100%	48.69 m	44.16 m	43.71 m	44.19 m	874 L/s	874 L/s
120%	43.76 m	41.49 m	41.95 m	41.34 m	1048.8 L/s	1048.8 L/s

$h_{CN}$ prior Control: Uncontrolled nodal pressure head. $h_{CN}$ post MBC: Model based controlled (MBC) nodal pressure head. $h_{CN}$ post MFC: Model-free controlled (MFC) nodal pressure head. $h_{CN}$ RL output tested on a model: Testing the control settings from the RL agent on the model.

In comparison, the model-based optimal controller achieved 13%, 10% and 6% pressure reduction for 80%, 100% and 120% loading respectively. Evidently, the percentage of pressure reduction achieved is reduced as the demand increases. This is a result of overall pressure decrease as the demand increase [29].

The threshold in Equation (15) was set to $0.5\mathrm{m}$. It can be seen in Table 1 that, the RL agent MFC scheme results in hydrostatic pressure of the CN being within the $0.5$ margin setout in the reward function. The PRVs settings obtained from the RL agent was tested in the model in Section 3. The results obtained via the CN showed the difference of at most $0.15\mathrm{m}$ as compared to those attained via the model-based optimisation problem.

5.2. Numerical Experiment 2

The second test case, shown ii Figure 5, consists of 70 nodes of which three (1, 69, 70) are the supply nodes and 108 pipes. Seven (7) PRVs are installed in the nominated location (1, 3, 5, 20, 46, 99, 102) of the WDN. Parameters of the nodes and pipes are given in Table A3 and Table A4.

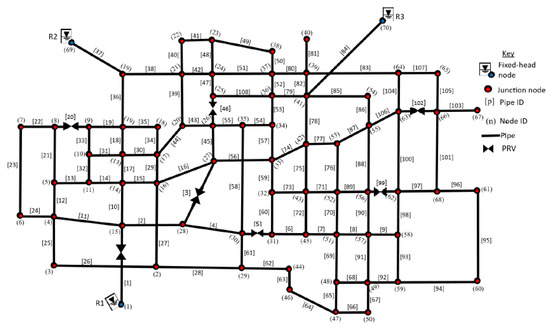
Figure 5. Case study 2.

In Figure 6 and Figure 7 it can be seen that the installation of PRVs and their subsequent adjustment results in decreased flows through the pipes, mainly, in the pipes with PRVs. Figure 7 shows consistency with Section 5.1. Pipes with PRVs installation show notably increased head drop which results in decreased pressure at the lower end of the pipe for the demand in Table A4 (demand factor of 100%). It can further be seen in Figure 7 that adjustment of head loss in some pipes affects the entire network.

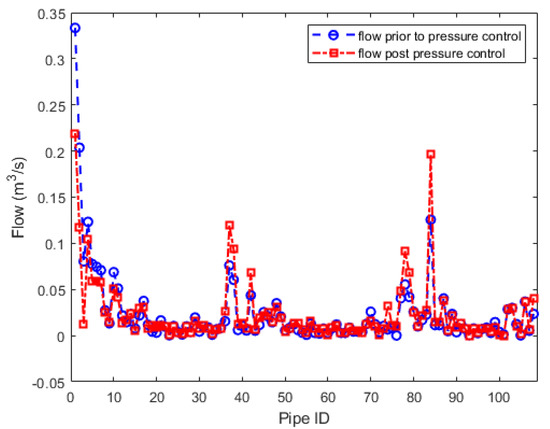
Figure 6. Pipe flows for case study 2.

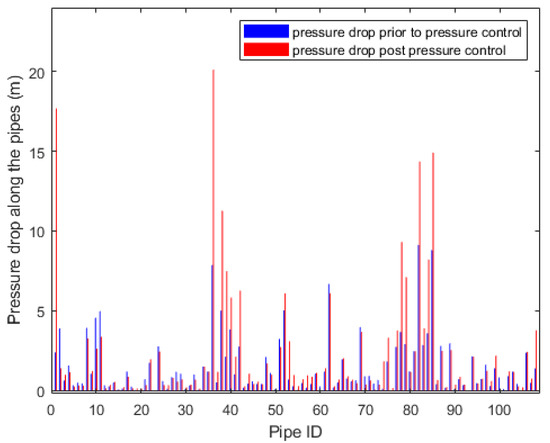
Figure 7. Nodal pressure heads for case study 2.

To further establish the effectiveness of the proposed MFC, the RL agent was tested with three (3) loading conditions for the network in Figure 5 and the results are presented in Table 2. The threshold in Equation (15) was set to $0.5$ m. Equation (3) is used to determine the effect of the pressure control on the nodal withdrawals. It can be seen from Table 2 that the proposed scheme is able to mimic the conventional optimisation procedures commonly employed. It is further evident that the actions/settings from the MFC yield valid results when tested on the model formulated. A noteworthy observation in Table 2 is that with all tested loading conditions, the MFC is able to achieve the solution without violating the threshold as tested on the WDN emulator and the model. In comparison, the MBC achieved 20.91%, 15.47% and 10.37% for 80%, 100% and 120% loading whereas the MFC achieved 20.67%, 15.08% and 10.52%. Consistent with Table 2, the decrease in the nodal head on the CN was observed as the demand increases. The CN in case study 2 is marked as node 67 in Figure 2. It is worth noting that the proposed scheme does not rely on the model and therefore it can be deployed on real networks where modelling of the system could be a challenge. It can further be observed from Table 2 that the nodal withdrawal was not affected by the pressure control as the flows were increased in other pipes to ensure that the supply is satisfied. Furthermore, the computational simplicity of the proposed scheme adds to its strength.

Table 2. Pressure observed on the critical node at 80%, 100% and 120% demand.

Demand	${\mathit{h}}_{\mathbf{CN}}$	${\mathit{h}}_{\mathbf{CN}}$	${\mathit{h}}_{\mathbf{CN}}$	${\mathit{h}}_{\mathbf{CN}}$ RL Output	$\sum \mathit{L}$ Prior	$\sum \mathit{L}$ Post
Factor	Prior Control	Post MBC	Post MFC	Tested on a Model
80%	79.47 m	62.85 m	63.04 m	62.57 m	428 L/s	428 L/s
100%	74.07 m	62.61 m	62.90 m	62.91 m	535 L/s	535 L/s
120%	67.67 m	60.65 m	60.55 m	60.49 m	642 L/s	642 L/s

$h_{CN}$ prior Control: Uncontrolled nodal pressure head. $h_{CN}$ post MBC: Model based controlled (MBC) nodal pressure head. $h_{CN}$ post MFC: Model-free controlled (MFC) nodal pressure head. $h_{CN}$ RL output tested on a model: Testing the control settings from the RL agent on the model.

6. Conclusions

The problem of pressure control in WDNs was investigated and presented in this paper. A model-free control scheme was proposed and its effectiveness was compared to the scheme commonly employed in the literature. It can be seen from the results that both schemes reduce the pressure in the WDN effectively. However, the strength of the proposed scheme lies in its ability to do so without any information about the model. This is significant because, parameters of the pipes and/or PRVs are affected over time by the environmental conditions, therefore, an inaccurate model may render results useless, unless it is continuously updated with the values of estimated parameters. Whereas with the scheme proposed, the controller is updated by the dynamics of the network in operation. Therefore, a RL based controller may be effective in a case where the parameters of the existing infrastructure are hard to estimate. In addition to its ability to determine the settings of the manipulated variables without the model of the system, a RL based controller draws its strength from the simple computational process as compared to solving the optimisation problem. However, the starting point and the quality of the randomly proposed actions becomes the key to the efficiency of the RL controller. Future research efforts would be directed towards the performance of this model under uncertain demand to test its performance under stochastic operation.