Abstract
This research introduces an inverse transient-based optimization approach to automatically detect potential faults, such as leaks, partial blockages, and distributed deteriorations, within pipelines or a water distribution network (WDN). The optimization approach is named the Pipeline Examination Ordinal Symbiotic Organism Search (PEOS). A modified steady hydraulic model considering the effects of pipe aging within a system is used to determine the steady nodal heads and piping flow rates. After applying a transient excitation, the transient behaviors in the system are analyzed using the method of characteristics (MOC). A preliminary screening mechanism is adopted to sift the initial organisms (solutions) to perform better to reduce most of the unnecessary calculations caused by incorrect solutions within the PEOS framework. Further, a symbiotic organism search (SOS) imitates symbiotic relationship strategies to move organisms toward the current optimal organism and eliminate the worst ones. Two experiments on leak and blockage detection in a single pipeline that have been presented in the literature were used to verify the applicability of the proposed approach. Two hypothetical WDNs, including a small-scale and large-scale system, were considered to validate the efficiency, accuracy, and robustness of the proposed approach. The simulation results indicated that the proposed approach obtained more reliable and efficient optimal results than other algorithms did. We believe the proposed fault detection approach is a promising technique in detecting faults in field applications.
1. Introduction
1.1. Background and Problem Statement
Water distribution networks (WDNs) in modern cities are usually large-scale, with complex systems and limited instrumentation. Water may be lost due to system aging, poor maintenance, and improper operations. The effective management of a water supply may be a serious engineering problem faced by cities, and rapid urbanization and infrastructure aging are expected to intensify in the future [1]. Faults in the pipeline system may not only cause problems in water resource management, but may also induce economic problems such as lost revenue or extensive repair times [2]. The faults in a pipeline or a WDN may be divided into three types: Leak, blockage, and deterioration, which may induce various problems. Leaks in pipelines and WDNs may cause large economic losses. Water supply networks leak an average of 20% of their water supply and lose an estimated U.S. $9.6 billion each year [3]. This may also affect environmental health and safety [4,5,6] and create water quality problems, such as equipment failure, problematic operations management, and errors in pipeline design [4,7,8,9]. If a pipeline has blockages, this will reduce the pipe carrying capacity of the system and there will be severe safety problems [10]. Pipeline deterioration may not impose imminent threats to the operation of pipeline systems, but it may reduce water transmission efficiency [11] and create water quality problems [12]. Hence, fault detection in WDNs is an important task in the community of water supply engineers.
1.2. Literature Review
Due to different data collection methods, the fault identification problem may be classified into the following two categories: Steady-state methods and transient analysis. Steady-state methods, such as vibration analysis, pulse-echo analysis, and acoustic reflectometry, were developed in previous studies for leak isolation [13,14,15,16], blockage detection [17,18,19,20], and deterioration determination [21,22,23]. These methods deliver a large number of results with high precision. However, they are usually developed based on some indispensable customized hardware with a long-term operation, which may lead to high costs [24]. In contrast, the application of the transient-based approach is simple and efficient [25,26]. In transient analysis, a pressure wave with appropriate bandwidth and amplitude is intentionally injected into the system [27]. The faults in the system, such as leakage, blockage, and deterioration can easily affect the head changes in the system when they are compared to those in a steady-state condition. The system responses can be freely obtained through a simple operation. However, this has a big drawback because the pressures created by a transient event may be too high to damage pipelines or even cause catastrophic failure in pipelines.
The heuristic algorithm is capable of searching for global optimal solutions [28]. It is therefore commonly used for detecting leaks in WDNs. Vítkovský et al. [29] combined a genetic algorithm (GA) with inverse transient analysis (ITA) to detect leaks and to calibrate friction factors in water pipelines. A GA was utilized to replace the Levenberg–Marquardt (LM) method used in Reference [30] to minimize the difference between calculated and measured heads. Vítkovský et al. [31] considered the shuffled complex evolution (SCE) algorithm to be an optimization tool in ITA for detecting single and multiple leaks in a pipeline system using laboratory observations with various errors (i.e., data errors, model input errors, and model structure errors). They indicated that a model structure error was the most possible limiting factor in field tests of ITA application. Jung and Karney [32] contrasted the performance of a GA and particle swarm optimization (PSO) in leak detection and friction factor calibration in a developed WDN model. They found that PSO provided faster convergence and produced better results than the GA. Haghighi and Ramos [33] exploited a central force optimization (CFO)-based approach as an inverse problem solver for leak detection in a benchmark leaking pipe network (reported in References [30,31]). The CFO-based approach exhibited excellent accuracy in identifying the friction factor and detecting the leaking node. Covelli et al. [34] highlighted the susceptibility of aged and high-pressure zones in leakage occurrences in WDNs and applied a GA to determine the optimal number, positioning, and setting of pressure reduction valves for reducing background leakages within the network.
Blockage detection is a crucial issue in aged pipelines and pipe networks in energy, chemical, and water industries. A blockage consists of chemical or physical depositions [26] or a valve that has only been partially reopened. It may cause system failures and an increase in water leakage due to the high-pressure redistribution within the system [35]. On the issue of blockage detection development, Wang et al. [10] detected discrete blockages in pipes by analytically using the transient damping of different frequency harmonics. However, detection of the blockage location was not mentioned in their study. Mohapatra et al. [36] developed a technique for detecting partial blockages in a single pipeline using the frequency response method. The patterns and numbers of peaks were used in the pressure frequency response of the system to detect blockage locations and estimate the effective size of two partial blockages. Lee et al. [37] numerically determined the properties of blockage-induced oscillations using the Fourier transform of the inverted peak magnitude in the frequency response diagram. Meniconi et al. [35] investigated two transient-based methods, pressure signal analysis and frequency response analysis, to detect a partial blockage in experimental pipes. The results showed that the former was more accurate in detecting the location of the blockage, while the latter was more reliable in predicting the severity of the blockage. Duan et al. [38] examined wave–blockage interactions under unsteady flow in pressurized pipelines. They revealed that an extensive blockage might change resonant frequencies and amplitudes, but a partial blockage might only affect resonant amplitudes. Lee et al. [27] used analytical, numerical, and experimental methods to investigate the importance of signal bandwidth in fault detection. They suggested that both low and high bandwidth signals should be considered in a transient-state system. A low bandwidth signal was used to identify the regions of suspected damage, while the fault’s location and properties were pinpointed by the high bandwidth signal.
The condition of the pipe wall in pressurized pipelines changes with their age or operating condition. Pipe wall deterioration may be due to corrosion, material erosion, and external pressures with system aging. At present, the transient-based approach is recognized as a potential tool for the noninvasive detection of discrete and distributed deterioration in pressurized pipelines [39]. Many previous studies have investigated deterioration detection technologies for water transmission pipelines. Stephens et al. [40,41] applied fluid transients and ITA to detect changes in the thickness of a pipe wall in a field test. They mentioned that the loss of cement mortar lining could lead to wall corrosion and significant changes in wave speed. Hachem and Schleiss [42] presented a transient-based approach to determine the stiffness of a pipe segment and identify the location of a structurally weak segment of a single pipeline. The location and length of the weak segment were identified using two mean wave speed values and the travel time of the reflections from a weak segment. Gong et al. [43] applied time-domain reflectometry (TDR) analysis to detect distributed deterioration in an experimental water transmission pipeline in a laboratory. They found that the size of the pressure wave reflection from a deteriorated section could be affected by any change in the pipeline impedance of the deteriorated section. Recently, Gong et al. [44] developed a new transient pressure wave generator using controlled electrical sparks. They provided high-frequency waves and improved the incident signal bandwidth. The location and length of thinner wall sections in an experimental pipeline system were then determined through a TDR technique.
1.3. Objective
Multiple fault detection in pipeline systems or WDNs using ITA is considered to be a troublesome issue because a large amount of input data and computation time is required. Moreover, the computation time and searching space in the optimization process may be enormous, especially for a complicated WDN with multiple faults. This paper presents a novel and efficient transient-based approach for multiple fault detection, including leak detection, partial blockage identification, and distributed deterioration determination, in a single pipeline or a WDN. An ITA-based hybrid heuristic approach called the Pipeline Examination Ordinal Symbiotic Organism Search (PEOS) was developed based on a combination of an ordinal optimization algorithm (OOA) and a symbiotic organism search (SOS). The proposed approach can simultaneously determine information on various faults via inverse calculation. Two experimental single pipeline cases and two numerical tests with different pipe network configurations were considered to examine the performance and capability of the proposed approach. The performance of PEOS was further compared to different optimization algorithms to demonstrate its accuracy and efficiency in predicting fault information. The reliability and robustness of the proposed approach for fault detection in a complicated WDN (considering data collection issues) was further validated.
2. Methodology
2.1. Pipe Network Simulation
EPANET is a widely used public software package for modeling hydraulic and water quality behavior in pressurized pipe systems. However, it needs an external functionality to model water leakage in a system in simulations [45]. Moreover, it is not easy to simulate the hydraulic behavior of a pressurized pipe system with blockages or deterioration. In order to simulate steady-state water head distribution in a network with various faults, we therefore developed a heuristic optimization algorithm called a pipe network symbiotic organism search (PNSOS) based on the algorithm for pipe network simulated annealing (SA) introduced by Yeh and Lin [46]. The SOS was adopted here to replace the SA in order to deal with a complex network for the sake of computational efficiency. The PNSOS is an efficient tool in estimating the steady-state nodal head and flow rate for a given pipe network system with faults before a transient operation. The Hazen–Williams (H–W) equation is then used to express the relationship between the flow rate and head loss for each pipe [47,48]. The modified loss coefficient (Kij(t)) in the H–W equation for a pipe at used year t is defined as
where ij is defined from node i to node j for the variable, Lij is the length (m) of the pipe, and Dij is the internal pipe diameter (m). The modified H–W coefficient (for modeling the effect of pipe aging) is defined as [49]
where t is the used year of the pipe, e0ij(t) is the initial roughness (mm) of the pipe, and aij(t) is the roughness growth rate (unique per year) in the pipe at year t. The following equations are used in the proposed approach to calculate the values of e0ij and aij [49]:
For a new installed pipe (i.e., t = 0), the value of in Equation (3) is considered to be the initial value of the H–W coefficient at the time of pipe installation (i.e., ). Thus, the modified H–W coefficient for each pipe could be iteratively obtained. On the basis of Equations (1)–(4), the flow rate Qij(t) (m3/s) in each pipe at year t could be expressed as
where ΔHij is the frictional head loss in a pipe. The equation of mass conservation at node i could be written as
where nn is the number of total neighbor nodes to node i, and QIi(t) is the demand or the source at node i. The flow rate is positive for flow out of node i and negative for flow into node i, while QIi is positive for inflow and negative for outflow. The objective function used in the PNSOS is defined as
where nd is the total number of nodes needed to estimate the nodal heads and flows in a network system.
2.2. Hydraulic Transient Model and Faults in the Pipeline
The unsteady pressurized flow in a pipe network with a known steady-state nodal head and flow rate can be described by a pair of partial differential equations, written as [50]
where g is the acceleration of gravity, A is the pipe cross-sectional area, H is the piezometric head, x is the distance along the pipe, Q is the volume flow rate, t is the time, D is the diameter of the pipe, a is the wave speed, and f is the friction factor, which can be described in steady-, quasi-steady-, or unsteady-state conditions. The friction factor was considered to be steady with a value of 0.02, since this study was numerical verification-oriented. Readers can refer to related studies regarding unsteady friction [51,52]. Equations (8) and (9) are respectively the momentum and continuity equations. By means of the method of characteristics (MOC) and the finite difference method, both equations can be solved with appropriate initial and boundary conditions. Then the hydraulic transient heads and flow rates along the pipelines are solved.
Three kinds of faults (i.e., leaks, partial blockages, and distributed deterioration) are considered and discussed. Both leaks and blockages could be described by the simple orifice equation and implemented as an internal boundary condition in the MOC analysis as [53]
where QO is the volumetric flow rate through the orifice, CdO is the discharge coefficient of the orifice, AO is the orifice area, and ΔHO is the head loss across the orifice. The leaks represent the flow loss through the offline orifice with no head loss, while the blockages represent the head loss through the inline orifice with no flow loss.
The volumetric flow rate QL through leakage is denoted as [53]
where QU and QD are the volumetric flow rates upstream and downstream of the leakage, respectively; CdLAL is the discharge coefficient of leakage times the leak area of the orifice; HP and Hout are respectively the heads at the leak and outside the leak; z is the pipe elevation at the leak; and and are respectively the heads upstream and downstream of the leak. The outside head is generally considered to be the atmospheric pressure head and is hence set to zero [53]. The initial value of CdL is set to unity, and the elevation z is assumed to be zero.
Similarly, a discrete (partial) blockage is treated as an inline valve with a constant opening area. The upstream and downstream of the blockage satisfy the continuity conditions of the head and flux. The volumetric flow rate QB through the blockage is expressed as [53,54]
where and are respectively the flow rates upstream and downstream of the blockage; and CdBAB is the discharge coefficient times the orifice area of the blockage. Note that Equation (12) is a simple model to approximate a blockage of any shape and length [53].
Deterioration (e.g., pipe wall damage or pipeline corrosion) often introduces a decrease in pipe wall thickness, which in turn introduces a change in the pipeline impedance and wave speed, defined as [39,43]
where , ai, and Ai are respectively the impedance, wave speed, and pipe cross-sectional area of ith reach. Their values are known in the MOC analysis.
2.3. Ordinal Optimization Approach (OOA)
Ho et al. [55] introduced the key cogitation of the OOA to reduce the process of searching for global optimal solutions blindly. Ordinal comparison and goal softening procedures are the major processes employed in the OOA. The approach looks for reliable and satisfactory solutions by searching through the relative rankings of each solution instead of directly evaluating the optimal solution in a complex optimization model. Thus, relatively better solutions are selected and used in the optimization process, and the best solution can be obtained without meaningless calculations and iterations of the worst solutions.
2.4. Symbiotic Organism Search (SOS)
The SOS algorithm [56] is an evolutionary metaheuristic algorithm inspired by actual biological interactions in nature, such as mutualism, commensalism, and parasitism. Like other population-based algorithms (e.g., a GA and PSO), the SOS shares the following similar features: (1) Control parameters should be properly settled before operation; (2) it has operators to enhance or improve candidate solutions via the interaction of each solution; (3) it has a selection mechanism to determine the current optimal solution in the solution domain and preserve the current best solution during the process [56,57]. Furthermore, the SOS algorithm requires no algorithm-specific parameters. Only the initial ecosystem (population) size and the maximum number of iterations are needed.
In short, the organisms (solutions) in the ecosystem are guided toward the current best organism in mutualism and commensalism states, while the parasitism state is used to prevent the organisms trapping in a local optimal solution. These three states are repeated until the stopping criterion is achieved. Details about the SOS algorithm are given in the Supplementary Materials.
2.5. Inverse Transient Analysis (ITA)
The ITA introduced by Pudar and Liggett [58] was developed by minimizing the errors between the measured and calculated system state variables (i.e., pressure or flow rates). Various potential faults with unknown parameters (fault information) are tested in a numerical simulator until the measured state variable traces match the calculated ones [4]. A heuristic algorithm is a useful tool for the numerical simulators of ITA because it can explore global or near-global optimum solutions in the search space in an affordable time [28]. However, the ITA method relies on an accurate transient model of the system. A model consisting of transient and boundary conditions with correct system parameters is needed in ITA for obtaining a reliable transient response in the system [5]. The pressure measurements are theoretically more suitable than the volume measurements (i.e., flow rate) because the response of the pressure is more sensitive than that of the flow rate in the ITA [59]. Transient flow is not easy to precisely measure in practice with a very high sampling rate, when only the pressure can be measured. The objective function F in the proposed approach for fault detection is defined as
where m is the total number of observation points in the network; n is the total amount of data at an observation point; and and represent the ith observed and simulated heads at observation point j, respectively. Thus, an ITA model was set up for a pipe network, in which head specifications were computed as a function of unknown variables (fault information), e.g., Lp, LL, CdLAL, Bp, BL, CdBAB, Dp, DL, LD, aD, and AD (listed and defined in Table 1).

Table 1.
Fault information to be determined.
2.6. Development of PEOS
The PEOS is a hybrid heuristic algorithm combining the screening procedure of OOA and the heuristic algorithm SOS to automatically determine fault information in WDNs. The overall operational architecture and steps of PEOS are briefly given below (also in Figure 1):
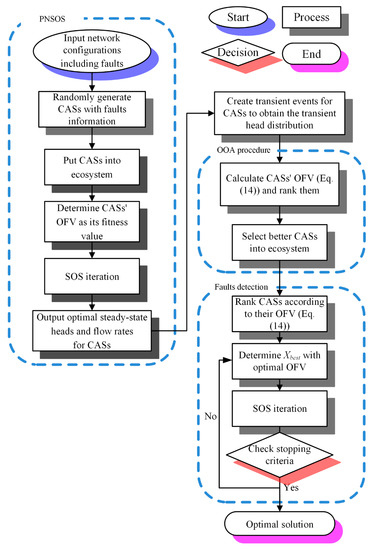
Figure 1.
Flowchart of the Pipe Examination Ordinal Symbiotic Organism Search (PEOS).
- Import the network configurations;
- Randomly generate candidate solutions (CASes) with different fault information consisting of the unknown variables listed in Table 1;
- Rearrange the network configurations, since the new fault points (leaks and blockages) and/or new fault pipe reaches (deterioration parts) are added;
- Use PNSOS to calculate the optimal steady-state nodal heads and piping flow rates within a given WDN for each CAS;
- Generate hydraulic transient events and apply the MOC to obtain the transient head distribution of each CAS;
- Utilize Equation (14) to calculate the CASes’ objective function values (OFVs) and rank them. The top 5% of CASes with smaller OFVs are selected for the next step;
- Consider the selected CASes to be initial organisms for the ecosystem of the SOS used in the pipe examination;
- Execute the fault detection procedure, in which the organisms containing fault information continually move forward to the current best solution (Xbest), with optimal fault information due to the three states of the SOS;
- Check whether the optimization process satisfies the stopping criterion. If so, the fault detection procedure is then terminated and moves to the next step. Otherwise, the searching process goes on.
The first stopping criterion is defined as the absolute difference between two successive optimal OFVs (in Equation (14)), which is always less than 10−4 within four iterations. The second criterion for fault detection is the iteration reaching the specified maximum limit.
2.7. Benchmark Evolutionary Algorithms
To validate the ability of the proposed approach in obtaining global optimal fault information, the performance of PEOS will be further compared in a later section to other evolutionary algorithm-based approaches, including a pipe examination genetic algorithm (PEGA), pipe examination particle swarm optimization (PEPSO), and a pipe examination symbiotic organism search (PESOS).
PEGA and PEPSO are benchmark pipe examination techniques that were developed based on the evolutionary algorithms of GA and PSO. A GA and PSO are employed as optimization tools to substitute the algorithm SOS uses in PESOS. PEGA uses a process involving selection, crossover, and mutation to evolve a population of potential solutions toward improved solutions. In PEPSO, the potential solutions, called particles, fly through the problem space by following the current optimum particle. Each particle’s movement is influenced by its local best-known position and is also guided toward the global best-known positions in the search space. The readers may refer to References [29,60] for detailed discussions on the use of GAs. In addition, more detail about the application of PSO can be obtained in References [32,61]. The other benchmark approach is PESOS, which is a simplified fault detection approach similar to PEOS but without the preliminary elimination procedure (i.e., the OOA) for the initial organisms. The initial solutions of PEGA, PEPSO, and PESOS are randomly generated from feasible solution domains with corresponding upper and lower bounds. The control and specific parameter settings for each algorithm are listed in Table 2.

Table 2.
Specific parameters for each algorithm, with NP = 10, 20, or 50, and Miter = 10,000 or 20,000.
3. Laboratory Experiments and PEOS Simulations
3.1. Experiment Configurations
Two cases of experimental reservoir pipe valve (RPV) systems with leaks or blockages that have been reported in the literature were adopted to verify the applicability of PEOS. The first case was carried out in a specially constructed RPV system at Imperial College (IC), London [62]. The system had a pump and tank upstream and a valve at the downstream end. The valve was a transient generation point, and pressure signals were also measured there at the same time. The IC pipe was made of high-density polyethylene (HDPE) with an inner diameter of 50.6 mm and a length of 272 m. Two leaks with different orifice sizes of 1.21 × 10−5 m2 and 1.50 × 10−5 m2 occurred at the locations of 65.95 m and 146.32 m, respectively: This was measured from upstream. These two leak orifices were very small, and the discharge coefficient was considered to be one. Thus, the CdLALs for the two leaks was respectively 1.21 × 10−5 m2 and 1.50 × 10−5 m2. The initial flow rate downstream was 1 L/s.
The second case was carried out at the Water Engineering Laboratory (WEL) at the University of Perugia, Italy [63]. A pressurized tank upstream of the system supplied the pipe, and a valve was located at the downstream end for data measurement and transient generation. The WEL pipe was also made of HDPE, with an inner diameter of 93.3 mm and a length of 164.93 m. A partial blockage was located at 88.96 m, measured from upstream. The partial blockage was simulated by an inline valve with a diameter of 38.8 m, and thus the CdBAB was 1.18 × 10−3 m2. The initial flow rate downstream was 2.57 L/s.
3.2. PEOS Simulation
In the PEOS application, the IC pipeline system was divided into six series segments with seven nodes. Each segment was assigned a pipe number from 1 to 6 from upstream to downstream. The first five segments had the same length, 50 m, and the last segment had a length 22 m. Two leaks, L1 and L2, which occurred 65.95 m and 146.32 m from the upstream end, were respectively placed in segments 2 and 3. The WEL pipeline system was partitioned into four series segments with five nodes. From upstream to downstream, the segments were given a pipe number from 1 to 4. Segments 1 to 3 had the same length, 50 m, and the last one was 14.93 m. A blockage named B1 was located at segment 2 and was 88.96 m from upstream. A valve was set at the last downstream node for measurement and transient generation for both pipeline systems. The distance interval (Δx) was considered to be 2 m to divide each segment for PEOS to search for leaks. The simulation durations for the IC and WEL pipeline systems were selected to be 15 and 5 s, respectively.
The temporal head distributions predicted by the PEOS for the IC and WEL pipeline systems were respectively displayed in Figure 2a,b. Both predicted temporal head distributions exhibited oscillatory patterns almost identical to the experimental data, indicating that the transient events in the IC and WEL pipeline systems could be precisely simulated by PEOS. Fault information was successfully identified, with the initial values listed in Table 3. In the IC pipeline system, L1 and L2 were respectively detected at 66 m in segment 2, with CdAs = 1.23 × 10−5 m2, and at 146 m in segment 3, with CdAs = 1.52 × 10−5 m2. Blockage B1 in the WEL pipeline system was identified at 88 m in segment 2, with CdBAB = 1.20 × 10−3 m2. The leak and blockage locations in both systems were accurately determined by the proposed approach. The largest relative difference (E) between the actual CdLALs/CdBAB and the predicted one was 1.69% for detecting blockage B1 in the WEL pipeline system. The relative differences were insignificant in both systems. The success of PEOS in fault detection indicated that PEOS performs excellently in a pipeline system.
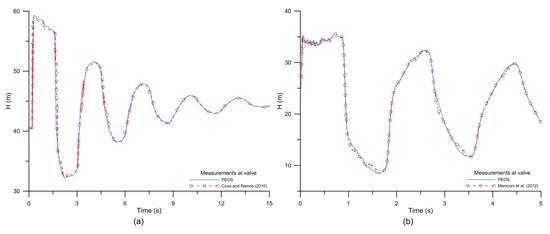
Figure 2.
The simulated head distributions at the valve for (a) the Imperial College (IC) pipeline and (b) the Water Engineering Laboratory (WEL) pipeline.

Table 3.
The predicted and actual fault information for the two pipeline systems.
4. Fault Detection in a Synthetic Pipe Network
4.1. Simulation Setup and Pipe Network Configuration
A synthetic benchmark WDN (pipe network A) was adopted from Reference [46] to test the applicability of PEOS in fault detection. The associated simulation followed the concept of district metering areas (DMAs), implying that the inflow and outflow of the pipe network system were steady and completely understood. User demands in the pipe network were considered to be constant and could be separated through continuous observation of mass conservations of flow measurements. Pipe network A, shown in Figure 3, is composed of 11 pipes, 9 nodes (with 7 in continuous outflow), 1 potential leak, 1 partial blockage, and 1 distributed deterioration reach. Notice that the characters “N”, “P”, “L”, “B”, and “D” represent the node, pipe, leak point, blockage point, and distributed deterioration reach, respectively. The properties of the pipes and nodes of pipe network A are listed in Table 4. The pipe material was considered to be cast iron with an aging effect on the material. Thus, the initial H–W coefficient CHW(0) for each pipe was 130. The H–W coefficient considering the effect of pipe aging (CHW(t)) for each pipe was calculated through Equations (2)–(4) and is given in the last column of Table 4. The initial wave speed a0 of all pipes was postulated as 1000 m/s [25], except for the faulty parts. The impedance of each pipe was calculated by Equation (13) and is given in Table 4. Node N1 was the water supply node, with a constant inflow rate of 400 L/s and a constant head of 120 m. In addition, continuous discharges at N2, N3, N4, N5, N6, N8, and N9 had rates of 80, 40, 35, 35, 40, 80, and 80 L/s, respectively. The leak L1 was located at P11, 300 m away from N3, with CdLAL = 2.50 × 10−4 m2 and QL = 3.0 L/s. A partial blockage B1 was placed at P10, 200 m away from N9. It blocked about 20% of the cross-sectional area of P10, and thus the CdBAB was 5.6 × 10−2 m2. In addition, a distributed deterioration reach, D1, occurred at a segment of P1 and was 200 m away from N2. The length and cross-sectional area of D1 were respectively designed to be 80 m and 0.071 m. Its wave speed was assumed to be 800 m/s, and thus the impedance was calculated as 1148.98 s/m2 from Equation (13). In the simulation, N8 was treated as the transient generation and data measurement point for the simulation of a sudden closure of the valve. The total transient simulation time was considered to be 30 s, with a simulation time interval (Δt) selected as 0.01 s. Thus, the initial Δx was 10 m for the nondeterioration reach and further changed with the wave speed of the deterioration reach. The transient operation was fixed to 5 s for a simulation of the complete closure of the valve.
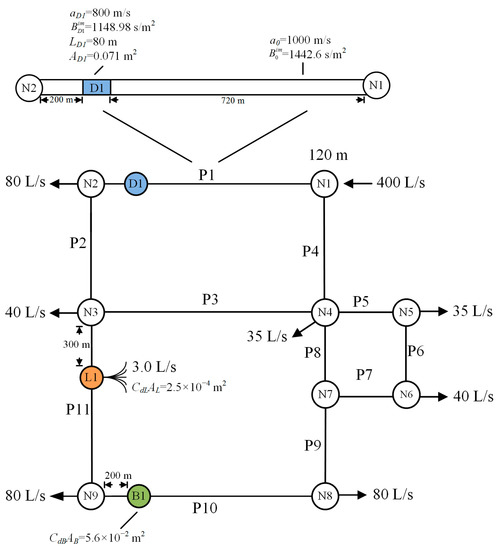
Figure 3.
Configuration of pipe network A with a sectional view of P1.

Table 4.
The characteristics of the synthetic water distribution network (WDN) (pipe network A).
In the following section, the performance of the proposed approach is validated and compared to the other evolutionary algorithm-based approaches mentioned in Section 2.7. The maximum iteration (Miter) was 10,000. Notice that all of the results presented in the following sections were performed on a personal computer with an Intel 2.8 G i5-8400 CPU and 32 GB of RAM.
4.2. Validation and Application of PEOS
The steady-state nodal heads and piping flow rates of pipe network A were solved by PNSOS in 52 s. The transient head distributions were further predicted by three benchmark algorithms and the proposed approach. Temporal transient perturbations were observed at N8 by applying different approaches with the various NP displayed in Figure 4a–d, and the predicted results are given in Table 5. The figures show that the transient perturbations fluctuated between 20 and 140 m with similar oscillatory patterns over 30 s. Figure 4a,b shows that PEGA and PEPSO overestimated the transient perturbations for the case NP = 10 due to an overestimation of the leakage area size by both algorithms. Such results reflect that the WDN contained a larger total flow rate at the beginning of transient perturbations. Moreover, the blockage at P10 was not detected by either PEGA or PEPSO. Thus, the transmission of water and pressure may not have been affected by the blockage, resulting in the accumulated volumes of water at N8 being higher than other cases when the transient operation point was closed. The predicted head was also overestimated in the case of PEGA for NP = 20. The calculations in both PEGA and PEPSO were forced to stop because they reached the maximum iteration, Miter = 10,000, in the cases of NP = 10 and 20. In contrast, the temporal transient perturbations displayed in Figure 4c,d were precisely reconstructed by two SOS-based approaches for all cases of ecosystem size. Deterioration, a blockage, and a leak were detected at P1, P10, and P11, respectively. Table 5 shows that the deterioration, blockage, and leak information was also accurately predicted by two SOS-based approaches. The results prove that those two SOS-based approaches are capable of obtaining optimal fault information even after using fewer initial organisms, reflecting that PESOS and PEOS had great abilities in obtaining the best solution even when using less input data and guessing values. This may have greatly reduced the searching process and computation times. Moreover, Figure 5a,b displays the predicted results of PEOS for impedance and wave speed along P1 and P10, respectively. Both a partial blockage and a deteriorated section can also be identified from the plots of the predicted distributions of the impedance and wave speed in Figure 5. The successful numerical simulation validated the proposed approach to detecting various faults in WDNs.
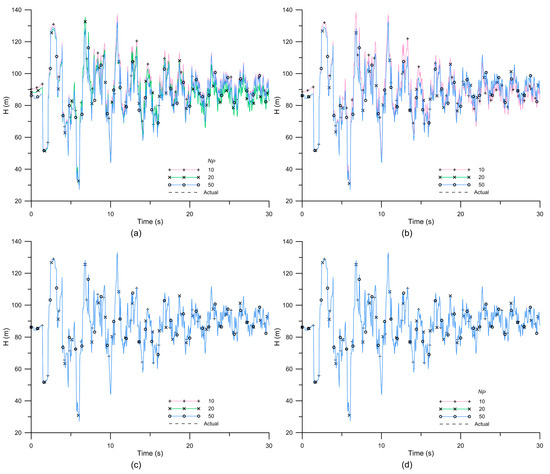
Figure 4.
Temporal transient perturbations at N8 of pipe network A predicted by (a) PEGA, (b) PEPSO, (c) PESOS, and (d) PEOS with various NP.

Table 5.
Determined fault information of pipe network A.
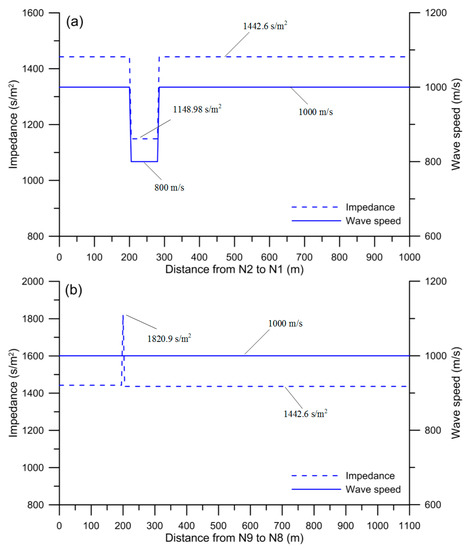
Figure 5.
Impedance and wave speed along (a) P1 and (b) P10, determined by PEOS.
The present techniques were further executed five times to guarantee the reproducibility of the predicted result and to test its efficiency, accuracy, and robustness for obtaining the optimal solution. The NP was fixed at 50 for all algorithms, and thus all approaches were ensured to deliver accurate predictions, as the results demonstrate above. Table 6 delineates the performance of PEOS and other approaches (five times) in obtaining the optimal fault information of pipe network A. PEGA, PEPSO, and PESOS took about 331.2, 302.2, and 105.4 min and 8072, 7604, and 3882 iterations, respectively, to obtain optimal results over a five-time average. In contrast, PEOS took about 50.6 min and 1382 iterations to complete the searching process and obtain the optimal result. Apparently, PEOS outperformed PEGA and PEPSO, not only in computation time but also in convergence speed. The computational efficiency of PEOS was approximately 84.7% and 83.2% better than PEGA and PEPSO. The computational efficiency of PEOS in fault detection in the WDN significantly improved as a result of using the OOA and SOS. In addition, PEOS saved about 52.8% in computing time and 64% in iterations compared to PESOS, indicating that the OOA could significantly speed up optimization computation by reasonably avoiding blind searches and unnecessary objective function evaluations in the optimization process. PEOS had superiority over the other methods in its fast convergence and effective computation. It also gave more accurate results than the other evolutionary-based algorithms.

Table 6.
The performances of the four algorithms.
5. Faults Detection in Large-scale WDN
5.1. Simulation Setup and Large-Scale WDN
PEOS further demonstrated its accuracy and robustness in fault detection on a large-scale drinking WDN by considering different data collection issues. Figure 6 displays the structure of pipe network B with various faults. Pipe network B was modified from Reference [64] with the data of the pipe characteristics listed in Table 7. The pipe network consisted of 74 pipes and 48 nodes, including 11 continual consumption nodes, 2 water supply nodes, and 2 constant-head reservoirs. All pipes were considered to be long-term used cast iron pipes. Hence, the initial H–W coefficient CHW(0) and wave speed a0 for all pipes in pipe network B were 130 and 1000 m/s, respectively. The CHW(t) for various pipes was also calculated by Equations (2)–(4) and is listed in the last column of Table 7.
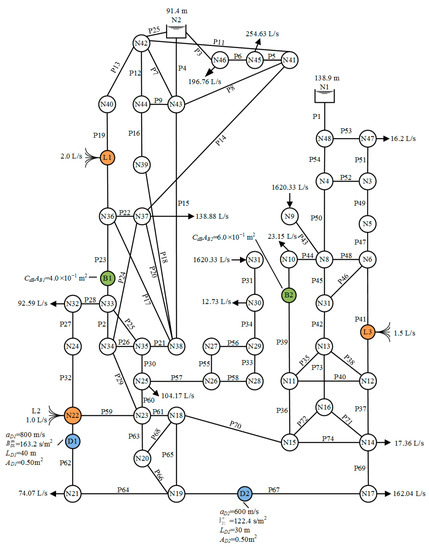
Figure 6.
Configuration of the large-scale WDN (pipe network B).

Table 7.
The characteristics of the large-scale WDN (pipe network B).
N1 was the first reservoir with a constant-head of 138.9 m, and the second reservoir N2 had a constant-head of 91.4 m. The inflow rates at nodes N9 and N31 were both 1620.33 L/s. The consumption rates at nodes N10, N14, N17, N21, N25, N30, N32, N37, N45, N46, and N47 were respectively 23.15, 17.36, 162.04, 74.07, 104.17, 12.73, 92.59, 138.88, 254.63, 196.76, and 16.2 L/s. Three leaks were separately located at different pipes. Leak L1 was at the middle of P19 and was 1150 m away from N36. Leak L2 was located at P32, 0 m away from N22, implying that leak L2 occurred exactly at N22. Leak L3 was 960 m away from N12 and was located at P41. The CdLAL values for L1, L2, and L3 were respectively 2.00 × 10−4, 1.00 × 10−4, and 1.20 × 10−4 m2. In addition, QLs was 2.0, 1.0, and 1.5 L/s for L1, L2, and L3, respectively. Two partial blockages, B1 and B2, were respectively situated at P23 and P39. B1 was 200 m away from N33 and blocked 20% of the cross-sectional area of P23, while B2 was 600 m away from N10 and blocked 15% of the cross-sectional area of P39. Hence, the CdBAB values of B1 and B2 were 4.0 × 10−1 m2 and 6.0 × 10−1 m2, respectively. Moreover, two distributed deterioration reaches, D1 and D2, occurred at P62 and P67, respectively. D1 was located at P62, 400 m away from N22, while D2 was located at P67, 600 m away from N19. The length, wave speed, impedance, and cross-sectional area of D1 were respectively 40 m, 800 m/s, 163.2 s/m2, and 0.50 m2, while those of D2 were 30 m, 600 m/s, 122.4 s/m2, and 0.50 m2. The properties of the two deterioration reaches are shown in Figure 6 as well. The outflow node N17 was considered to be the transient operation and data collection point for pipe network B. The Δt was also selected to be 0.01 s. Thus, the initial Δx was also considered to be 10 m for the intact pipe reach and was further altered with different wave speeds in the deterioration reach. Because the WDN scale was large and complicated, the transient wave may have taken more time to arrive at the fault points/parts. The total simulation time increased to 60 s. A total of 6001 data points should be collected and used in a complete simulation. Two different cases with different data collection issues were considered to test the reliability of the proposed approach for fault detection in a large-scale WDN. NP was chosen to be 50, and Miter was updated to 20,000 for possible enormous iterations. The transient excitation period was chosen as 5 or 10 s for the simulation of the complete closure of the valve.
5.2. Case Description and Error Criteria
Three cases were selected to test the capability of PEOS in fault detection in a complex pipe network such as pipe network B, considering the effects of limited observations, measurement errors, and inappropriate transient operation. Case 1 used less data, with a low frequency of 0.1 s (i.e., 10% of the original sampling frequency) to represent instrument limitations in the field survey, and thus 601 data points were collected and used in the simulation of case 1. In case 2, measurement errors were added to the 601 low-frequency data points to depict the uncertainty in data collection. Notice that the white noise was normally distributed, with a zero mean and a standard deviation of 0.01 m, which was generated as a random measurement error that was added to each data point in case 2. The observation heads with errors were defined as
Case 3 was designed under the same sampling frequency as case 1, but the transient operation time was extended to 10 s to address the effects of an inappropriate transient operation. There were 601 data points collected after 10 s of transient operation that were used in the simulations of case 3.
In order to evaluate the effects of limited observations and measurement errors on the results predicted by the proposed approach, two error criteria, the standard error of the estimate (SEE) and mean error (ME), were considered. The SEE is a measure of the accuracy of predictions, defined as the square root of the sum of squared errors between the observed and predicted heads divided by the number of degrees of freedom, which equals the number of observed data points minus the number of unknowns. The criterion ME is the average of the sum of errors between the observed and simulated heads.
5.3. Results and Error Analysis
The steady-state hydraulics of pipe network B were predicted by PNSOS in 309 s, and the transient event was then generated by closing the valve at N17. The transient head distributions for cases 1–3 were therefore measured at N17. Table 8 shows the results of fault detection for cases 1–3. In case 1, the information about deterioration reaches D1 and D2 was accurately determined with its corresponding parameters. The locations of three leaks and two blockages were also precisely detected by PEOS. It is noteworthy that leak L2 at node N22 was isolated by the proposed approach, indicating that PEOS was capable of handling the case of pipe junction leakage. In case 1, the E between the actual CdLALs/CdBAB values and the predicted ones was insignificant. Table 9 shows the values of the ME and SEE, which for case 1 were 3.41 × 10−6 m and 1.27 × 10−4 m, respectively. The results denote that the predicted heads were not affected by the use of limited observations. The results for case 1 and the small ME and SEE values indicate that PEOS had the potential to deliver moderately good results in a field survey even when only a few observations were available. The success of using fewer measurements indicates that PEOS may not be restricted by instrument limitations. In addition, the data measurement period can therefore be reduced, and the system impact due to a transient event may be slight while using PEOS.

Table 8.
The optimal fault information of pipe network B predicted by PEOS for three cases.

Table 9.
The prediction errors for three cases. ME: mean error; SEE: standard error of the estimate.
Table 8 shows that PEOS provided relatively good results for deterioration detection in case 2. The locations of the deterioration segments, determined at 390 m for P62 and 610 m for P67, deviated slightly from the actual ones, which were instead located at 400 m for P62 and 600 m for P67. The lengths of D1 and D2 were accurately determined. The impedances for D1 and D2 were respectively estimated as 162.0 and 121.5 s/m2, with corresponding wave speeds of 794.3 and 595.8 m/s. For leak and blockage detection in case 2, the predicted locations of three leaks and two blockages were close to the real locations, implying that the measurement errors may not have affected location detection. There were errors in the predictions of CdLAL and CdBAB in case 2. The relative differences between the predicted CdLAL values and the actual ones were about 6%, 2%, and 5.83% for L1, L2, and L3, respectively. The relative differences between the determined CdBAB values and the real ones were about 5.25% for B1 and 4.17% for B2. The results showed that the predicted CdLAL values and CdBAB may have been more sensitive than location to measurement errors. This was due to the fact that the OFVs used in PEOS for fault detection were directly related to the head difference (i.e., Equation (14)), which may have been directly influenced by the change in leak area and blockage area. The MEs and SEEs for case 2 are listed in Table 9 and were respectively 1.73 × 10−4 m and 6.35 × 10−2 m, which were both two orders larger than those of case 1. Such a result indicates that measurement errors may have affected accuracy in determining the leak area and blockage area. Thus, data uncertainty should be of concern as an important issue in fault detection in a large-scale pipe network or in future field applications.
In case 3, leaks, blockages, and deterioration segments were also accurately determined by PEOS, with its associated parameters listed in Table 8. The locations of various faults were precisely detected by PEOS. The sizes of leaks and blockages were slightly overestimated compared to case 1, with the largest relative difference, 2.5%, for L3. The values for the ME and SEE for case 3 were respectively 3.29 × 10−6 m and 1.12 × 10−4 m, as shown in Table 9. The results indicate that the predicted heads were not affected, while the transient operation was inadequate. Note that the concept of ITA is to minimize errors between the measured and calculated system state variables. Measurements with an unsuitable transient operation still work well based on the objective function of ITA. The results of case 3 reveal that PEOS can provide good predictions when using different transient operation durations. However, a rapid transient operation is recommended, because it produces large system response data, thus improving the performance of the ITA [31].
6. Conclusions
This paper demonstrates an inverse transient-based heuristic optimization approach called PEOS for pipe examination in a pipeline or pipe network system. The application of PEOS was verified by two experimental RPV systems in the literature, and PEOS was further applied to identify fault information in synthetic pipe networks. PEOS was used to detect faults in an experimental pipeline (carried out at Imperial College London) and in a pipeline at the Water Engineering Laboratory at the University of Perugia. The head distributions predicted by PEOS agreed well with those from the experiments reported in the literature. The leak and blockage information in both systems was accurately determined by the proposed approach. The results indicated that PEOS provided good predictions in fault detection in a real pipeline system.
The proposed approach was further compared to three evolutionary-based algorithms in fault detection in a synthetic benchmark pipe network. Temporal head distribution and fault information were accurately predicted by PEOS and agreed well with the actual ones, even when using only 10 initial input organisms. PEOS on average took about 50.6 min and 1382 iterations to obtain the optimal results, which is significantly faster than other algorithms. The results indicated that the OOA made the proposed approach avoid most unnecessary calculations of incorrect solutions and quickly converge to the optimal result via three states of SOS. In other words, PEOS not only provided predictions with better accuracy and robustness, but also performed better at computational efficiency. The proposed approach with these two advantages obviously outperformed other algorithms.
To illustrate the applicability of PEOS in fault detection in real-world problems, a large-scale WDN with three data collection statuses was considered as a field study to represent practical issues. The results indicated that PEOS performed well in solving the fault detection problem, considering the effects of limited observations and measurement errors in a complicated WDN. The effect of limited observations on the estimated result was not significant, but the measurement errors induced some inaccuracy. When the observations contained measurement errors, the predicted CdLAL and CdBAB had slight deviations compared to the actual ones, indicating that PEOS could achieve good results if the measurements were well collected. Moreover, the results revealed that inappropriate transient operation may not have affected the performance of PEOS in predicting head distribution and fault information.
In summary, we demonstrated via the simulations that PEOS has the ability to simultaneously detect various faults in a pipeline and pipe networks and can outperform other existing evolutionary-based algorithms. Another superiority of PEOS over competing algorithms is the small number of parameters that must be tuned. Fault information can be precisely predicted even when observations are collected with issues. The cases presented in this study were for relatively simple pipe system configurations and operations. Extending the current work from numerical simulations to solving the problems of real-world complicated WDNs would be an interesting direction for further research.
Supplementary Materials
The details of the SOS algorithm are available online at https://www.mdpi.com/2073-4441/11/6/1154/s1.
Author Contributions
C.-C.L. designed the numerical experiment, analyzed the data, and wrote the paper. H.-D.Y. is the supervisor of the proposed research.
Acknowledgments
The authors would like to thank the editor and three anonymous reviewers for their valuable and constructive comments, which greatly improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bartos, M.; Wong, B.; Kerkez, B. Open storm: A complete framework for sensing and control of urban watersheds. Environ. Sci. Water Res. Technol. 2018, 4, 346–358. [Google Scholar] [CrossRef]
- Scola, I.R.; Besançon, G.; Georges, D. Blockage and leak detection and location in pipelines using frequency response optimization. J. Hydraul. Eng. ASCE 2017, 143, 04016074. [Google Scholar] [CrossRef]
- Moser, G.; Paal, S.G.; Smith, I.F.C. Leak detection of water supply networks using error-domain model falsification. J. Comput. Civil Eng. 2018, 32, 04017077. [Google Scholar] [CrossRef]
- Colombo, A.F.; Lee, P.; Karney, B.W. A selective literature review of transient-based leak detection methods. J. Hydro Environ. Res. 2009, 2, 212–227. [Google Scholar] [CrossRef]
- Puust, R.; Kapelan, Z.; Savić, D.A.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Xin, K.; Li, F.; Tao, T.; Xiang, N.; Yin, Z. Water losses investigation and evaluation in water distribution system—The case of sa city in china. Urban Water J. 2015, 12, 430–439. [Google Scholar] [CrossRef]
- Al-Khomairi, A. Leak detection in long pipelines using the least squares method. J. Hydraul. Res. 2008, 46, 392–401. [Google Scholar] [CrossRef]
- Shamloo, H.; Haghighi, A. Optimum leak detection and calibration of pipe networks by inverse transient analysis. J. Hydraul. Res. 2010, 48, 371–376. [Google Scholar] [CrossRef]
- Huang, Y.C.; Lin, C.C.; Yeh, H.D. An optimization approach to leak detection in pipe networks using simulated annealing. Water Resour. Manag. 2015, 29, 4185–4201. [Google Scholar] [CrossRef]
- Wang, X.J.; Lambert, M.F.; Simpson, A.R. Detection and location of a partial blockage in a pipeline using damping of fluid transients. J. Water Resour. Plan. Manag. ASCE 2005, 131, 244–249. [Google Scholar] [CrossRef]
- Tran, D.H.; Perera, B.J.C.; Ng, A.W.M. Hydraulic deterioration models for storm-water drainage pipes: Ordered probit versus probabilistic neural network. J. Comput. Civil Eng. 2010, 24, 140–150. [Google Scholar] [CrossRef]
- Vreeburg, J.H.G.; Boxall, J.B. Discolouration in potable water distribution systems: A review. Water Res. 2007, 41, 519–529. [Google Scholar] [CrossRef] [PubMed]
- Juliano, T.M.; Meegoda, J.N.; Watts, D.J. Acoustic emission leak detection on a metal pipeline buried in sandy soil. J. Pipeline Syst. Eng. Pract. 2013, 4, 149–155. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Vibroacoustic measurements for detecting water leaks in buried small-diameter plastic pipes. J. Pipeline Syst. Eng. Pract. 2017, 8, 04017022. [Google Scholar] [CrossRef]
- Martini, A.; Rivola, A.; Troncossi, M. Autocorrelation Analysis of Vibro-Acoustic Signals Measured in a Test Field for Water Leak Detection. Appl. Sci. 2018, 8, 2450. [Google Scholar] [CrossRef]
- Yazdekhasti, S.; Piratla, K.R.; Atamturktur, S.; Khan, A. Experimental evaluation of a vibration-based leak detection technique for water pipelines. Struct. Infrastruct. Eng. 2017, 14, 46–55. [Google Scholar] [CrossRef]
- Wang, X.; Lennox, B.; Turner, J.; Lewis, K.; Ding, Z.; Short, G.; Dawson, K. Blockage detection in long lengths of pipeline using a new acoustic method. In Proceedings of the 16th International Congress on Sound and Vibration, Krakow, Poland, 5–9 July 2009. [Google Scholar]
- Lile, N.L.T.; Jaafar, M.H.M.; Roslan, M.R.; Azmi Muhamad, M.S. Blockage detection in circular pipe using vibration analysis. Int. J. Adv. Sci. Eng. Inf. Technol. 2012, 2, 54–57. [Google Scholar] [CrossRef][Green Version]
- Lile, N.L.T.; Hadi, H.; Roslan, M.R. Vibration Analysis of Blocked Circular Pipe Flow. Appl. Mech. Mater. 2012, 165, 197–201. [Google Scholar] [CrossRef]
- Duan, W.; Kirby, R.; Prisutov, J.; Horoshenkov, K.V. On the use of power reflection ratio and phase change to determine the geometry of a blockage in a pipe. Appl. Acoust. 2015, 87, 190–197. [Google Scholar] [CrossRef]
- Holley, M.; Diaz, R.; Giovanniello, M. Acoustic Monitoring of Prestressed Concrete Cylinder Pipe: A Case History. In Proceedings of the Pipeline Division Specialty conference 2001, San Diego, CA, USA, 15–18 July 2001. [Google Scholar]
- Delgadillo, H.H.; Loendersloot, R.; Akkerman, R.; Yntema, D. Development of an inline water mains inspection technology. In Proceedings of the IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016. [Google Scholar]
- Wang, X.H.; Jiao, Y.L.; Yang, J.; Niu, Y.C. The acoustic emission detection and localisation technology of the pipeline crack. Int. J. Sen. Net. 2016, 20, 111–118. [Google Scholar] [CrossRef]
- Li, R.; Huang, H.; Xin, K.; Tao, T. A review of methods for burst/leakage detection and location in water distribution systems. Water Sci. Technol. Water Supply 2015, 15, 429–441. [Google Scholar] [CrossRef]
- Chaudhry, M.H. Applied Hydraulic Transients, 3th ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Datta, S.; Sarkar, S. A review on different pipeline fault detection methods. J. Loss Prev. Process Ind. 2016, 41, 97–106. [Google Scholar] [CrossRef]
- Lee, P.J.; Duan, H.F.; Tuck, J.; Ghidaoui, M. Numerical and experimental study on the effect of signal bandwidth on pipe assessment using fluid transients. J. Hydraul. Eng. ASCE 2015, 141, 04014074. [Google Scholar] [CrossRef]
- Sheikholeslami, R.; Talatahari, S. Developed swarm optimizer: A new method for sizing optimization of water distribution systems. J. Comput. Civil Eng. 2016, 30, 04016005. [Google Scholar] [CrossRef]
- Vítkovský, J.P.; Simpson, A.R.; Lambert, M.F. Leak detection and calibration using transients and genetic algorithms. J. Water Resour. Plan. Manag. ASCE 2000, 126, 262–265. [Google Scholar] [CrossRef]
- Liggett, J.A.; Chen, L.C. Inverse transient analysis in pipe networks. J. Hydraul. Eng. ASCE 1994, 120, 934–955. [Google Scholar] [CrossRef]
- Vítkovský, J.P.; Lambert, M.F.; Simpson, A.R.; Liggett, J.A. Experimental observation and analysis of inverse transients for pipeline leak detection. J. Water Resour. Plan. Manag. ASCE 2007, 133, 519–530. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B.W. Systematic exploration of pipeline network calibration using transients. J. Hydraul. Res. 2008, 46, 129–137. [Google Scholar] [CrossRef]
- Haghighi, A.; Ramos, H.M. Detection of leakage freshwater and friction factor calibration in drinking networks using central force optimization. Water Resour. Manag. 2012, 26, 2347–2363. [Google Scholar] [CrossRef]
- Covelli, C.; Cozzolino, L.; Cimorelli, L.; Della Morte, R.; Pianese, D. Optimal location and setting of prvs in wds for leakage minimization. Water Resour. Manag. 2016, 30, 1803–1817. [Google Scholar] [CrossRef]
- Meniconi, S.; Duan, H.F.; Lee, P.J.; Brunone, B.; Ghidaoui, M.S.; Ferrante, M. Experimental investigation of coupled frequency and time-domain transient test-based techniques for partial blockage detection in pipelines. J. Hydraul. Eng. ASCE 2013, 139, 1033–1040. [Google Scholar] [CrossRef]
- Mohapatra, P.K.; Chaudhry, M.H.; Kassem, A.A.; Moloo, J. Detection of partial blockage in single pipelines. J. Hydraul. Eng. ASCE 2006, 132, 200–206. [Google Scholar] [CrossRef]
- Lee, P.J.; Vítkovský, J.P.; Lambert, M.F.; Simpson, A.R.; Liggett, J.A. Discrete blockage detection in pipelines using the frequency response diagram: Numerical study. J. Hydraul. Eng. ASCE 2008, 134, 658–663. [Google Scholar] [CrossRef]
- Duan, H.F.; Lee, P.J.; Ghidaoui, M. Transient wave-blockage interaction in pressurized water pipelines. Procedia Eng. 2014, 70, 573–582. [Google Scholar] [CrossRef]
- Gong, J.; Lambert, M.F.; Simpson, A.R.; Zecchin, A.C. Detection of localized deterioration distributed along single pipelines by reconstructive moc analysis. J. Hydraul. Eng. ASCE 2014, 140, 190–198. [Google Scholar] [CrossRef]
- Stephens, M.L.; Simpson, A.R.; Lambert, M.F. Internal wall condition assessment for water pipelines using inverse transient analysis. In Proceedings of the 10th Annual Symposium on Water Distribution Systems Analysis, American Society of Civil Engineers, Kruger National Park, South Africa, 17–20 August 2008. [Google Scholar]
- Stephens, M.L.; Lambert, M.F.; Simpson, A.R. Determining the internal wall condition of a water pipeline in the field using an inverse transient. J. Hydraul. Eng. ASCE 2013, 139, 310–324. [Google Scholar] [CrossRef]
- Hachem, F.E.; Schleiss, A.J. Detection of local wall stiffness drop in steel-lined pressure tunnels and shafts of hydroelectric power plants using steep pressure wave excitation and wavelet decomposition. J. Hydraul. Eng. ASCE 2012, 138, 35–45. [Google Scholar] [CrossRef]
- Gong, J.; Simpson, A.R.; Lambert, M.F.; Zecchin, A.C.; Kim, Y.i.; Tijsseling, A.S. Detection of distributed deterioration in single pipes using transient reflections. J. Pipeline Syst. Eng. Pract. 2013, 4, 32–40. [Google Scholar] [CrossRef]
- Gong, J.; Lambert, M.F.; Nguyen, S.T.N.; Zecchin, A.C.; Simpson, A.R. Detecting thinner-walled pipe sections using a spark transient pressure wave generator. J. Hydraul. Eng. ASCE 2018, 144, 06017027. [Google Scholar] [CrossRef]
- Cobacho, R.; Arregui, F.; Soriano, J.; Cabrera, E. Including leakage in network models: An application to calibrate leak valves in EPANET. J. Water Supply Res. Technol. Aqua 2015, 64, 130–138. [Google Scholar] [CrossRef]
- Yeh, H.D.; Lin, Y.C. Pipe network system analysis using simulated annealing. J. Water Supply Res. Technol. Aqua 2008, 57, 317–327. [Google Scholar] [CrossRef]
- Mays, L.W. Water Supply Systems Security; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Savić, D.A.; Banyard, J.K. Water Distribution Systems, 2nd ed.; ICE: London, UK, 2011. [Google Scholar]
- Seifollahi-Aghmiuni, S.; Bozorg Haddad, O.; Omid, M.H.; Mariño, M.A. Effects of pipe roughness uncertainty on water distribution network performance during its operational period. Water Resour. Manag. 2013, 27, 1581–1599. [Google Scholar] [CrossRef]
- Larock, B.E.; Jeppson, R.W.; Watters, G.Z. Hydraulics of Pipeline Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Duan, H.F.; Ghidaoui, M.; Lee, P.J.; Tung, Y.K. Unsteady friction and visco-elasticity in pipe fluid transients. J. Hydraul. Res. 2010, 48, 354–362. [Google Scholar] [CrossRef]
- Reddy, H.P.; Silva-Araya, W.F.; Chaudhry, M.H. Estimation of decay coefficients for unsteady friction for instantaneous, acceleration-based models. J. Hydraul. Eng. ASCE 2012, 138, 260–271. [Google Scholar] [CrossRef]
- Bergant, A.; Tijsseling, A.S.; Vítkovský, J.P.; Covas, D.I.C.; Simpson, A.R.; Lambert, M.F. Parameters affecting water-hammer wave attenuation, shape and timing—Part 1: Mathematical tools. J. Hydraul. Res. 2008, 46, 373–381. [Google Scholar] [CrossRef]
- Stephens, M.L.; Simpson, A.R.; Lambert, M.F. Hydraulic transient analysis and discrete blockage detection on distribution pipelines: Field tests, model calibration, and inverse modeling. In Proceedings of the World Environmental and Water Resources Congress 2007, Tampa, FL, USA, 15–19 May 2007. [Google Scholar]
- Ho, Y.C.; Cassandras, C.G.; Chen, C.H.; Dai, L. Ordinal optimisation and simulation. J. Oper. Res. Soc. 2000, 51, 490–500. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Prayogo, D. Symbiotic organisms search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Prayogo, D.; Tran, D.H. Optimizing multiple-resources leveling in multiple projects using discrete symbiotic organisms search. J. Comput. Civil Eng. 2016, 30, 04015036. [Google Scholar] [CrossRef]
- Pudar, R.S.; Liggett, J.A. Leaks in pipe networks. J. Hydraul. Eng. ASCE 1992, 118, 1031–1046. [Google Scholar] [CrossRef]
- Abhulimen, K.E.; Susu, A.A. Liquid pipeline leak detection system: Model development and numerical simulation. Chem. Eng. J. 2004, 97, 47–67. [Google Scholar] [CrossRef]
- Simpson, R.A.; Dandy, C.G.; Murphy, J.L. Genetic algorithms compared to other techniques for pipe optimization. J. Water Resour. Plan. Manag. ASCE 1994, 120, 423–443. [Google Scholar] [CrossRef]
- Jung, B.S.; Karney, B. Fluid transients and pipeline optimization using ga and pso: The diameter connection. Urban Water J. 2004, 1, 167–176. [Google Scholar] [CrossRef]
- Covas, D.; Ramos, H. Case Studies of Leak Detection and Location in Water Pipe Systems by Inverse Transient Analysis. J. Water Resour. Plan. Manag. ASCE 2010, 136, 248–257. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Ferrante, M. Water-hammer pressure waves interaction at cross-section changes in series in viscoelastic pipes. J. Fluids Struct. 2012, 33, 44–58. [Google Scholar] [CrossRef]
- Chin, K.K.; Gay, R.K.L.; Chua, S.H.; Chan, C.H.; Ho, S.Y. Solution of water networks by sparse matrix methods. Int. J. Numer. Methods Eng. 1978, 12, 1261–1277. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).