Abstract
There has been a significant rise in the use of aluminium salts (Al3+) for the chemical precipitation of phosphates in wastewater treatment plants due to growing stricter regulatory requirements for wastewater effluent release to the environment. The modelling of the settleability of the resultant Al3+ sludge in present engineering practice for design and optimisation are still based on conventional sludge settleability models. This paper describes a novel activated sludge settleability model which is designed to analyse the effects of Al3+ dosing on activated sludge settleability indicators, zone settling velocity (ZSV), and stirred specific volume index (SSVI). The impact of Al3+ dosing concentrations on ZSV and SSVI of full scale activated sludge plant were analysed in the laboratory over a three years’ period and the exponential form of the Vesilind equation was optimised and validated to include alum chemical dosing parameters. The proposed model equation was found to effectively describe the settleability of Al3+ dosed sludge for dosing concentrations range of 0 to 100 mg/L.
1. Introduction
The increasing technological advancements and sustained growth in the human population have contributed to increased discharges of phosphorus into the surrounding water bodies causing eutrophication and leading to environmental pollution and adverse human health issues [1,2,3,4]. Consequently, there are stricter effluent quality requirements for wastewater treatment plants in Europe with <1 mg/L phosphorus consents in some jurisdictions. To meet this stringent requirement for phosphorus discharge, there is an increased use of chemical phosphorus removal using metal salts for chemical precipitation. Coagulants like aluminium salts (Al3+) are increasingly being used for the precipitation of phosphates from wastewater [1,2,3]. Their use is more common in activated sludge plants (ASP) [4,5].
The activated sludge process (ASP) is a well-known suspended growth system for wastewater treatment where suspended solids (SS) is separated from clarified water by downward gravitational settling to produce a clear supernatant low in effluent suspended solid (ESS), effluent nitrogen (EN), and phosphorus (EP) concentration [6,7,8]. In order to remove suspended solids (SS) at the lowest possible cost, the solid removal process during the ASP should be done speedily and efficiently by increasing the SS removal from the sedimentation tank. This will not just increase the treatment efficiency in the tank, but also reduce the size of wastewater treatment facilities located downstream of the clarifiers since the investment costs of settling facilities accounts for one-third to one-fourth of the total cost of treatment plant construction [9]. Therefore, increasing the SS removal efficiency in sedimentation tanks to optimise activated sludge settleability is vital.
Final sedimentation tank (FST) is a critical component of the activated sludge treatment processes and contributes greatly to the overall efficiency of an ASP and determines the final effluent quality of the activated sludge [6,10]. The functions of FST includes; Thickening which maintains a continuous underflow of concentrated sludge for recirculation to the biological reactors, Clarification which ensures a clarified effluent is produced and sludge storage tank which ensures storage of sludge (under peak wet weather flow-PWWF) to prevent loss of SS and maintain the effluent quality [11,12,13].
The evaluation of zone settling velocity (ZSV) is vital in both the design and modelling of FSTs. The settling classifications are typically reliant on the nature and concentration of the sludge particulates and the interaction between the activated sludge particulates [14]. Based on the flocculation, sedimentation propensity, and concentration of sludge flocs, the settling in FST can be classified into four major types including; free, flocculent, zone, and compression settling [13]. While the free settling classification is attributed to both very low concentrations and flocculation propensity and occurs in the upper region of the FST [15]. Flocculent settling occurs in the upper mid stream region of the FST where though low solids concentration exists, the floc particles show a resilient flocculating ability and the settling velocity will equally depend on individual sludge floc properties since there is no interaction between sludge particulates. Zone settling occurs in the middle section of FST and this takes place when the concentration of particles increases, and sludge particles settle as one mass with the same velocity and in the same direction. Compression settling occurs at the bottom area of the FST and at a much higher concentration as sludge particulates come in close interaction with each other and form a compression layer.
The activated sludge settleability process is a very complex solid–liquid separation process which has made the characterisation of the complete settling process in the FST challenging [7]. The characterisation of the complete settling process in FST is not yet fully understood and this has created challenges in the optimisation of activated sludge settling in WWTPs. Several factors affect the efficiency of FSTs ranging from hydraulic and loading factors to external factors like tank configuration, surface area, depth, flow distribution, and turbulence in conveyance structures [13,16,17,18]. Also, several other factors affecting sludge settleability including; particle size, sludge particle shape, sludge floc porosity, flocculability tendency and extracellular polymeric substances (EPS) have been extensively investigated by various researchers [18,19,20]. However, the effects of chemical dosing on activated sludge settleability have been largely neglected.
Since the mass flux theory was developed by Kynch [21] various studies have been conducted [6,7,22,23], to examine the relationship between zone settling velocity (ZSV) and activated sludge concentration (X) and to also evaluate the efficiency of FSTs in an ASP, by a number of empirical models [24,25,26,27,28]. Other empirical settling velocity models were proposed due to different activated sludge settling zones and they find application in forecasting the flow field and velocity of flow and estimating the sludge blanket height [6,12,29]. They include; one-dimensional (1-D) and two-dimensional (2-D) settling models [30,31,32,33]. Among the empirical models proposed to relate the initial settling velocity to the sludge concentration is the Vesilind equation [24]. It is the most acceptable empirical model for predicting the sludge settleability behaviour within the FST. The model is expressed in Equation (1).
where,
- ZSV = zone settling velocity (m/h)
- X = activated sludge concentration (g/L)
- = sludge settleability constant (m/h)
- k = sludge settleability constant (L/g).
The vesilind parameters k and from Equation (1), can be obtained from the slopes of batch test settling curves. Likewise, the correlations between ZSV (Vesilind 1968 equation) and sludge volume index (SVI), diluted sludge volume index (DSVI), and stirred sludge volume index (SSVI) are derived from empirical equations described in Haandel & Lubbe [2]. Other reviews addressing reasons for variable sludge density and its effects on activated settleability in a full-scale secondary wastewater treatment system have been conducted [32]. In addition, further studies were reported on the effect of settling velocity within various sludge concentration and thicknesses [34]. The findings showed agreement with Vesilind [24] assertion that as biomass concentration was increased in zone settling test, settling velocities decreased but a non-linear correlation between the settling velocity and the range of buoyant density was observed but investigations have not considered the impact of chemical dosing on activated sludge settleability. A new model that included a buoyant density parameter in the Vesilind settling velocity model () was proposed, but again, this did not include a chemical dosing parameter. Further details on the proposed model are provided in Schuler and Jang [34].
The modelling of the design and optimisation of activated sludge settleability to date is based on Pitman and White settleability model. The Pitman and White [35,36] model is based on Vesilind [24] expression. The Pitman & White model is expressed in Equation (2).
where,
SSVI = Stirred sludge volume index (mL/g)
The SSVI is the volume of a unit mass of suspended solids after 30 min of settling in a measuring cylinder with the application of a gentle stirring (mL/g) and and K are sludge settleability constants.
The model was designed mainly on the settling characteristics of conventional activated sludge (CAS) but with the increasing usage of metal salts like aluminium in the precipitation of phosphates today, the overall characteristics of sludge are different from the conventional sludges on which the existing models were based. Therefore, there is a need to develop a new model that describes the settling properties of chemically dosed activated sludge (CDAS). This paper is an attempt to develop a new CDAS model that describes the effects of the varying concentration of Al3+ dosing on activated sludge settleability indicators. The proposed new model equation will address the limitation of Pitman and White model for the modelling of the settleability of CDAS.
2. Materials and Methods
2.1. Sludge Sampling and Analysis
Activated sludge was sampled regularly within a duration of three years from the Minworth Sewage Treatment Plant (an activated sludge treatment plant) in the West Midlands in the United Kingdom. The sewage treatment plant has an average flow of 450 mega litres per day (ML/D) at full flow to treatment (FFT) of 1070 ML/D. The sewage treatment plant serves a population equivalent of 1.3 million people in 24 aeration basins with a capacity of 250,000 cubic metres and 54 circular final settling tank in operation. The mixed liquor samples (MLSS concentration of the samples ranged from 2800 to 3500 mg/L, with the pH ranging from 6.5 to 7.5 and a phosphate concentration of 7 to 12 mg/L) were sampled in 32.5 L sample containers from the distribution chambers and analysed in the laboratory within 24 h of sampling. Details of the methods have been previously described [19].
2.2. Settlometer Tests
The activated sludge settleability test followed the standard Water Research Council (WRc) settling test [12,37] performed in a 3.25 L type 305 setlometer equipment (Triton Electronic Ltd., Cambridge, UK) with 100 mm diameter and 500 mm height, a slow speed stirrer (1 rev/min) used to prevent any event of sludge bridging to the walls. Batch settling tests were carried out over several sampling campaigns lasting three years. The experiments were carried out at varying MLSS dilution concentrations ranging from 1200 mg/L to 3500 mg/L. The MLSS samples were dosed with varying concentrations of alum ranging from 0 to 250 mg/L. The detailed processes have been recently described by the authors [19]. The ZSV and SSVI were computed from the results of the the batch settling tests. The mean values from the three years data were used in the model development.
2.3. Data Analysis
The results of the ZSV and SSVI data sets of batch tests were analysed using the Minitab 17 software and solver optimisation tool. The solver optimisation tool allows the solver parameter to be set for the target objective of a reduced sum of square deviation (SSD) value so that the ZSV model fits the ZSV experimental data while the minitab 17 allows the design of an experimental model for investigation of the impact of input variables on the response variable at the same time. Results were also analysed using the non-linear regression in the minitab 17 software and the F-test (F > 0.05), lack of fit test (P > 0.05), R2 (coefficient of determination), residual plot, probability plot and interval plot was used to validate how the ZSV model fits the ZSV experimental data.
3. Model Development and Model Validity for Al3+ Dosed Sludge
The most familiar approach to evaluating sludge settleability in wastewater treatment processes is using the sludge volume index (SVI) method since it gives a result very quickly in the laboratory. Based on the definition of SVI as the volume occupied per unit mass of sludge particulate (mL/g) after 30 min of settling; it implies that SVI is a function of settling velocity all through the settling column where the activated sludge vary with respect to time (t) and settling height (H). However, employing SVI as a variable in the evaluation of the real settling in FSTs is contentious since the test relies on the initial sludge concentration before it is being deduced, which contradicts the expectation of a true process parameter for sludge settleability. As FST is known to perform a unique function in the design and operation of the activated sludge process, the evaluation of ZSV in the modelling and design of the FST becomes paramount [13,14]. Given the limitations of SVI, a more robust approach was introduced called the zone settling velocity test (ZSV). The ZSV approach allows settling velocities to be evaluated over a range of activated sludge concentrations (X) to estimate the rate of zone settling in the settling column where flocs are in proximity to one another. The resultant ZSV values are then used to regulate various models relating the settling velocity and solids concentration. Although, since the mass flux theory was developed by Kynch [21], various studies have been conducted to examine the relationship between zone settling velocity and activated sludge concentration [25,28,38,39]. Dick and Young [25] showed the relationship between ZSV and sludge concentration as expressed in Equation (3). The most acceptable models are those suggested by Vesilind [24] (Equation (1)). Following previous work by White [36] and Haandel and Lubbe [2], it was revealed that these models define the correlation between zone settling velocity and sludge concentration.
The Capital and K are sludge settleability constants expression for Dick and Young [25] expression in Equation (3). The explains the effect of sludge settleability on the actual settling velocity while K explains the effect of sludge settleability on sludge compaction (sludge volume index—SVI).
Meanwhile, other researchers have utilised the empirical relationship with the sludge settleability parameters such as SVI, diluted sludge volume index (DSVI) and SSVI to obtain the Vesilind and k parameter [13,19,40,41,42]. The research conducted by Pitman [43,44] involving an analysis of six years full scale studies resulted in the development of an empirical relationship between the constants of Vesilind’s equation and SSVI. The correlation obtained was expressed in Equation (2). Further research by Ekama and Marias [45] was analysed along with that of other researchers—including Rachwall et al. [29], White [36], Koopman and Cadee [46]—and came up with the findings that Pitman’s empirical expression in Equation (2) resulted in a good description for all and that a relationship exists between and k. This was expressed as in Equation (4)
However, since the value of k is known then the value of can be computed as follows using Equations (2) and (4).
However, it is challenging to investigate the settling behaviour of activated sludge at low concentrations specifically below 1 kg/m3 due to the limit of measurement and because there is no interaction with the sludge particles and settling velocity will be a function of individual floc properties and also, since no clear relationship with the concentration of the activated sludge particle exists at low sludge concentration. This challenge was resolved by other researchers by utilising Vesilind functions in different ways to determine the settling process at low concentration namely; modelling directly the functions Takacs´ et al. [26]; Dupont and Dahl [47] and defining particles with different velocities Dupont and Henze [48]; Lyn et al. [49]; Otterpohl and Freund [50]; and Mazzolani et al. [51]. Previous studies also reported the investigation of their own data from unit processes in South Africa Smollen and Ekama [52] and numerous activated sludge processes Pitman [43] and [44]; Tuntoolavest and Grady [53]; and concluded that Vesilind’s equation gave a better description of the actual settling performance of activated sludge. Following a further result from research conducted by Catunda et al. [54,55], rearranging Equations (3) to (5) will make it possible to express k and as a function of SSVI which can be expressed as
The empirical coefficient and k are obtained by performing ZSV test over a range of mixed liquor suspended solids (MLSS) concentration for sludge samples. Upon substituting Equations (6) and (7) into Equation (2) and Equation (8) is obtained;
It can be concluded that Catunda et al. [54,55] findings agree with the earlier mentioned researchers view and that Equations (6) and (8) can be utilised to compute the constants k and directly from the values without conducting a ZSV test. Therefore, Vesilind equation has been adopted as the foundation for describing activated sludge settling in an FST.
In an earlier study by Ojo and Ifelebuegu [19], the batch settling test measurements of zone settling curve (ZSC) of ZSV reveals ZSV as a linear representation (Figure 1) of sludge height as a function of time (m/h) for 100 mg/L Al3+ dosed sludge. Also, the results as previously reported [19] showed that the ZSV increased, while SSVI decreased with increasing concentrations of Al3+ salt up to <100 mg/L. Beyond this concentration the sludge settleability disintegrated due mainly to surface charge reversal.
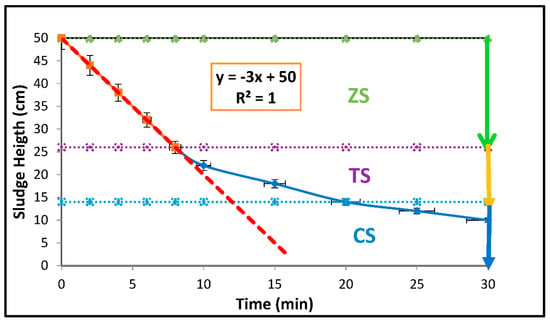
Figure 1.
Zone settling curve (ZSC) for 100 mg/L Al3+ dosed MLSS (ZS = zone settling, TS = transition settling, CS = compression settling, error bars represent the standard deviation of the mean). The ZSV was obtained from the slope of the linear graph.
Within the full range of concentrations of Al3+ used (0 to 250 mg/L), a non-linear representation of ZSV and SSVI as a function of Al3+ dosing concentrations were observed as presented in Figure 2 and Figure 3. It was additionally represented using the rate of change of ZSV and SSVI (Figure 4 and Figure 5). This provided a basis for the modification of the conventional empirical model of ZSV (Equation (1)) to include a new Al3+ dosing parameter. It further demonstrated that Al3+ dosing concentrations had a non-linear correlation with ZSV and SSVI.
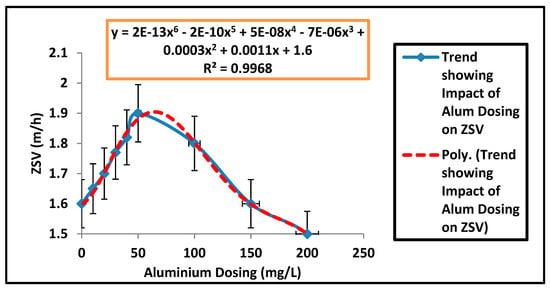
Figure 2.
Impact of Al Dosing (mg/L) on ZSV (m/h) (Error bars represent standard deviation of the mean).
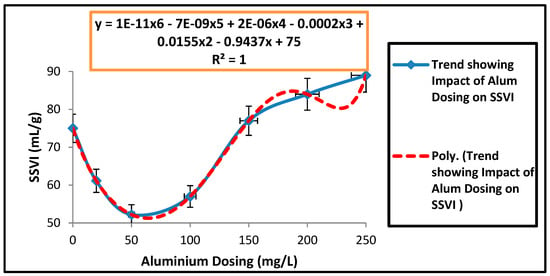
Figure 3.
Impact of Al Dosing (mg/L) on SSVI (mL/g) (Error bars represent standard deviation of the mean).
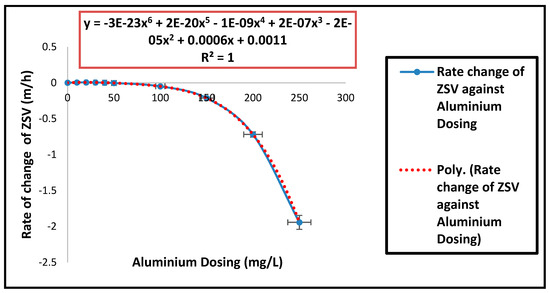
Figure 4.
Rate of Change of ZSV against aluminium dosing (error bars represent the standard deviation of the mean).
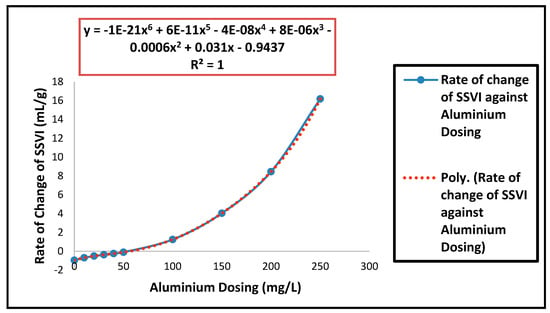
Figure 5.
Rate of Change of SSVI against aluminium dosing (the error bars represent the standard deviation of the mean).
The conventional empirical model for sedimentation in FSTs expressed as a function of solid concentration, termed Vesilind equation is illustrated in Equation (1). The empirical coefficient and k are obtained by performing ZSV test over a range of mixed liquor suspended solids (MLSS) concentration for both un-dosed and Al3+ dosed sludge as mentioned earlier and applying linear regression to the linearized form of the Vesilind equation to obtain a new expression in Equation (9).
The plot of natural log of ZSV (m/h) against un-dosed and Al3+ dosing concentration for the average data from the various batch test is shown in Figure 6. The negative of the gradient of each linear regression for the batch test is the Vesilind k value while the intercept is the Vesilind parameter. However, because we are modelling an Al3+ dosed sludge, then Vesilind and k expression becomes re-defined as and for Al3+ dosed sludge. There is a relationship between Al3+ dosing concentration and ZSV which was not accounted for in the conventional Vesilind model equation in Equation (1). To express this, it was achieved by the transformation of data in the Vesilind exponential relationship and back tracking to calculate the values of the Vesilind exponential constant parameter. Hence, the ZSV was plotted against the Al3+ dosing concentration on a natural log to a linear scale (Figure 6) and the Vesilind coefficient was Al (= −0.0045 and = 1.576 m/h). It can be inferred that the calculated and parthe ameter for Al3+ dosed sludge from the graph of ln ZSV against Al3+ concentrations is a function of the dosing concentrations.
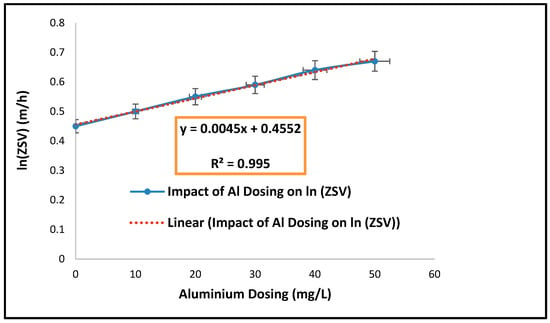
Figure 6.
Natural log of ZSV against Al3+ Concentration (the error bars represent the standard deviation of the mean).
The natural logarithm of SSVI was plotted against the Al3+ dosing concentration (Figure 7). The gradient and intercept of the curves accounted for the coefficient for Al ( = 0.0072 and = 64.78 mL/g).
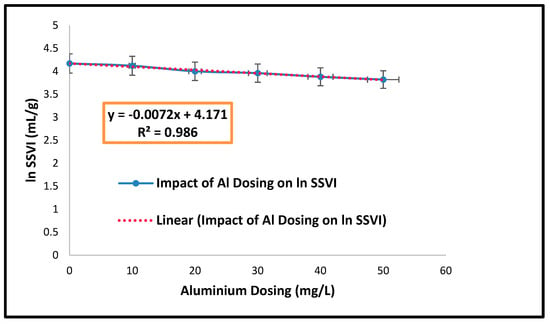
Figure 7.
ln (SSVI) against Al3+ dosing concentration (the error bars represent the standard deviation of the mean).
3.1. New Model Calibration to Include Al3+ Dosing Parameter
The simulation and control of settling in final settling tanks (FST) in wastewater treatment depends on calibrated models [56]. Model validation helps to evaluate whether or not the proposed new mathematical model describes properly the settling characteristics of Al3+ sludge. The approach is to check whether the new model fits the experimental batch test results. The exponential form of the Vesilind equation (Equation (1)) can be optimised to include chemical dosing parameter by investigating a new model equation for settling velocity. The investigated ZSVo and parameter for Al3+ dosed sludge from the graph of ln ZSV against dosed MLSS concentration () and Al3+ dosing concentration (mg/L) (Figure 6 and Figure 7) shows linearised and exponential correlation between ZSV and SSVI with Al3+ dosing concentrations. The new empirical model for settling velocity for an Al3+ dosed activated sludge can take the form of a decay equation (A = ) (Equation (10)) that obeys the exponential law of decay
where
- A = Activity (the number of unstable nuclei remaining), Bq
- = Original number of unstable nuclei, Bq
- e = Constant = 2.718
- λ = Decay constant,
- t = time, s
The new equation in Equation (11) shows the inclusion of a new dosing protocol () that follows the decay equation.
where,
- ZSV = Actual settling velocity (m/h)
- () Al = Maximum settling velocity (m/h) for Al3+ dosed sludge
- () Al = Empirical Al3+ dosed sludge settling parameter relating to sludge compaction
- () Al = Empirical Al3+ dosing constant related to stokes settling velocity
- () Al = Empirical Al3+ dosing constant related sludge compaction
- () Al = Al3+ dosing concentration (mg/L)
- (X) = Al3+ dosed MLSS concentration (mg/L)
The Equation (11) obeys the exponential law of decay and both the additive and the multiplicative rule of exponentials. The empirical coefficients in Equation (11) (ZSVo and ) are typically determined by performing zone settling velocity (ZSV) batch tests over a range of aluminium dosing concentrations (0, 10, 20, 30, 40, 50, 100, 150, 200, and 250 mg/L) and applying regression analysis and linear approximation to Equation (11) by taking the natural log.
For a better understanding of the new empirical heuristic expression for settling velocity for a dosed activated sludge, the comparison of terms in the new Al3+ dosed sludge expression (Equation (11)) and conventional decay equation becomes vital. The version of terms in Equation (10) compared with Equation (11) is as follows; = + ), λ = and t = x. This shows below that applying the additive rule with e as a common factor in Equation (11), then Equation (12) can be expressed as
On the other hand, applying the multiplicative rule with X as a common factor in Equation (11), the expression in Equation (13) is obtained.
The constants , , and helps in shifting the ZSV model to predict the observed values in aluminium dosed sludge. However, the experimentally estimated ZSV data have been universally used for regulating settling models in wastewater industry (Vesilind 1968—ZSV = ). Since it is equally common practice to deduce the Vesilind empirical constants (Vo and K) through conducting batch laboratory ZSV test over range of concentrations and applying linear regression evaluation to a linearized form of Vesilind equation (ln V = −KX + ln ), it becomes paramount to apply the same principle to the new Al3+ dosed activated sludge model.
We can consider defining and from Equation (11) as follows: = () and = ) as two functions of ZSV and this gives Equation (14)
As earlier mentioned that there exists an exponential relationship between the ZSV and Al dosing (Figure 5 and Figure 7) but because the relationship is a non-linear relationship, calculating the value of the new empirical coefficient (, , and ) of aluminium dosed activated sludge model can be evaluated by linearizing Equation (11) to become (14). Therefore, the linear approximation (Equation (15)) was obtained by taking the natural log of Equation (11) which can be expressed as
The Equation (15) also follows the equation of a straight line (Y = MX + C), M = Slope while C = Intercept and hence Equation (15) can be modified as Equation (16) by re-defining ln (ZSV) = Z; ln ( + ) = P and ( − ) = Q respectively.
Z = P − Q X
The transformation of Equations (11) to (15) allowed establishing a linear relationship between Z and X (Equation (16)) and not between ZSV and X since it is already an exponential model. This transformation allows back tracking the constant of the new model for Al3+ dosed sludge (, , and ) to predict the ZSV experimental data. Therefore, once a linear relationship is established between Z and X (Z = P − QX), the value of the Al3+ dosed settleability constants (, , and ) can be evaluated and the experimental value of ZSV and dosing concentrations () without performing a ZSV batch experiment. A new expression ((17) and (18)) was obtained from Equation (16) for calculating the value of as it relates to aluminium when the four constants (, , and ) for aluminium dosed sludge are known.
The results of the regression analysis using Equation (15) showed that the coefficient of determination (R2) was close to 1 (Figure 6). This suggests that the exponential function in Equation (11) was suitable to model the Al3+ dosed activated sludge settleability process (ZSV).
However, the SSVI expression for Al3+ dosed activated sludge can be derived from the new empirical Al3+ dosed activated sludge model for settling velocity in Equation (11). The K and Vo parameter calculated from the expression in Catunda et al. [54] in Equations (6) and (7) becomes re-written as ZSVo and parameter for Al3+ dosed sludge computed in Equations (19) and (20)
where,
- = Empirical aluminium dosed activated sludge settling parameter related to sludge compaction (L/g)
- = Maximum settling velocity for Al3+ dosed activated sludge related to stokes settling velocity (m/h)
In deriving a new expression for Al3+ dosed SSVI, Equations (19) and (20), was compared with the existing Pitman [43] and White [36] expression in Equation (2) { = 68 × e (−0.016 × SSVI3.5)} and the Equation (2) can be re-written in the form of ZSVo and parameter as
The new SSVI expression (Equation (22)) was obtained by substituting Equations (19)–(21) into Equation (11) is
The results of regression analysis for the impact of Al3+ dosing on SSVI using the experimental data in the batch test conducted showed that the coefficient of determination (R2) was close to 1 (0.986) (Figure 7). This suggests that the linearized expression in Equation (22) was suitable to model the impact of Al3+ dosing on activated sludge settleability (SSVI) process.
3.2. Validation of Novel Model for Impact of Al3+ Dosing on ZSV and SSVI
Novel ZSV Model
The heuristic expression used for the derivation of the new model for Al3+ dosed sludge expressed in Equation (21) (ZSV = + ) ) and its linear approximation is ln (ZSV) = ln ( + ) – () X. The experimental data of five batches of settling velocity tests were classified into two groups. The first group (Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5) were used to develop the model while the second group (Table 1 and Table 2 and Figure 8 and Figure 9) are used to validate the model. The model was validated using two approaches namely; Solver optimization tool and Minitab 17. Although, the batch settling test measurements revealed ZSV as a linear representation (sludge height as a function of time) (Figure 1), on the contrary a non-linear representation was observed in Figure 2 and Figure 3 showing ZSV and SSVI as a function of Al3+ dosing concentration. The transformation of the data of the parameter in the conventional Vesilind equation further allows the inclusion of a new Al3+ dosing parameter () in the existing Pitman and White model [36,43] in Equation (2) and Catunda et al. [54] in Equations (6) and (7) which are both in agreement with the Vesilind (1968) expression.

Table 1.
Model validation Minitab 17 and Solver optimisation tool result

Table 2.
ZSV experimental and ZSV model comparison using Solver optimisation and Minitab 17.
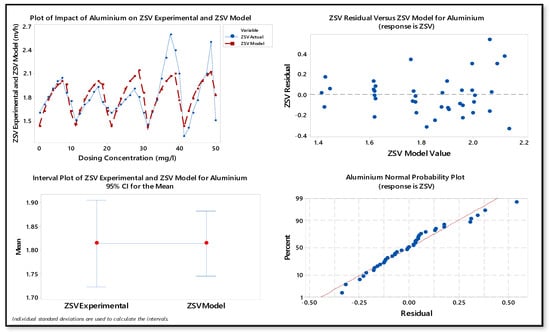
Figure 8.
Non-linear fitting, interval plot, residual plot, and probability plot.
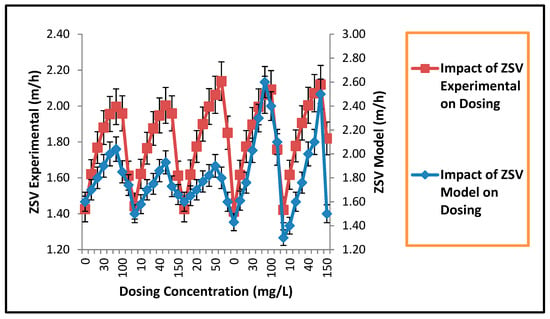
Figure 9.
Non-linear curve fitting of the impact of aluminium on ZSV (the bars represent the standard deviation of the mean).
The Solver optimisation tool and Minitab 17 were utilised to fit non-linear model data to actual experimental data through non-linear fitting method (Table 1 and Table 2). Table 1 and Figure 8 and Figure 9 shows a comparison of the experimental and predicted zone settling velocities using Equation (11). It was observed that the validation results were good enough and valid for alum concentration ranging from (0, 10, 20, 30, 40, 50, and 100 mg/L). A regression model will exhibit a lack of fit when it fails to adequately describe the functional relationship between the experimental factors and the response variable. The lack of fit test in Minitab indicates that there is no evidence that the model does not fit the data well because the P value was greater than the significance level (P Value > α) 0.675 > 0.05 (Table 1 and Figure 8 and Figure 9). This means an α of 0.05 shows that the chance of concluding that the model does not fit the experimental data when it does is only 5%. The 95%CI values for the estimated values of parameter (ZSVo, , , and ) was significantly different from zero and F-value was greater than 0.05 ( = 0.82, P = 0.675) which depicts a good fit. The non-linear fitting, interval plot, residual plot, and probability plot (Figure 9) further establishes the validity of the model using Minitab 17.
The probability plot creates estimated cumulative distribution function from sample data by plotting the value of each observation against its estimated cumulative probability and a scale transformation allows the fitted distribution to form a straight line. A good distribution fit is one where the observations are near the fitted line. The data in Figure 8 are near the fitted line hence it indicates a good distribution fit between model and experimental data. The residual shows how far is the model data from the experimental data and the residual plot in Figure 8 shows a good fit. The coefficient of determination (R2) was 0.993 in Table 1, shows that the difference between the observed experimental value and the model predicted values are small and unbiased. The interval plot (Figure 8) shows that at 95% CI, the mean value of ZSV model and experimental is significant as the 95% confidence interval bar do not overlap.
The solver optimisation tool allows the solver parameter to be set for the target objective of a reduced sum of square deviation (SSD) value so that the model fits the experimental data. In Table 2 and Figure 9, a significant SSD value of 0.334 was reported and it indicated the ZSV model fits the actual ZSV value.
The values of, , , , and (Table 1) used to validate the numerical model in Equation (23) are the same at different dosing concentration (0, 10, 20, 30, 40, 50, and 100 mg/L) and approximate to 0.026, 1.377, −0.020, and −0.0023 respectively. Therefore, the new ZSV model for aluminium dosed sludge is expressed as Equation (23).
The new SSVI expression for alum dosed activated sludge (Equation (24)) was derived from substituting the compared and ZSVo parameter calculated from the redefined expression in Catunda et al. [54] with the Pitman [43] and White [36] expression in Equation (21) { = 68 × e−0.016 × SSVI3.5} and substituting into the new alum dosed activated sludge model for settling velocity in Equation (11).
3.3. Summary and Perspectives
The results of this work demonstrated that the proposed models developed as an update of existing models based on conventional activated sludges, can be explicitly used in activated sludge plants to predict the impact of Al3+ dosing concentrations on the settleability of activated sludge. The ZSV and SSVI model equations will find applications in the design and optimisation of FSTs for the solids separation of Al3+ dosed activated sludge plants. They are valid for Al3+ concentrations in the range of 0 to100 mg/L. High surface charges associated with higher concentrations of Al3+, causes a general disintegration of the activated sludge floc structure as previously reported [19]. This will result in the Al3+ dosed sludge not fitting the proposed equation at concentrations higher than the stated range.
4. Conclusions
A novel activated sludge settleability model was designed to analyse the effects of Al3+ dosing concentrations on activated sludge settleability indicators; zone settling velocity (ZSV) and stirred specific volume index (SSVI) using linear transformation of polynomials and exponential functions to achieve replication of a non-linear correlation between the Al3+ dosing concentrations and settleability indicators (ZSV and SSVI). The new empirical model that describes the relationship between Al3+ dosing concentrations and the ZSV and SSVI were further validated using non-linear parameterization. The results showed that the settleability indicators of Al3+ dosed sludges can be described by the proposed equations which showed a good fit to the experimental data within a dose range of between 0 to <100 mg/L of Al3+. The new model equations will find application in the water industry for the modelling and optimization of Al3+ dosed activated plants.
Author Contributions
Conceptualisation, A.O.I.; Formal evaluation, P.O.; Writing original draft, P.O.; Investigation, A.O.I.; supervision, A.O.I.; review and editing, A.O.I.
Funding
This research received no external funding
Acknowledgments
The authors wish to thank Severn Trent Water Limited for their support and assistance during the sampling campaigns.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Al | Aluminium |
| ASP | Activated sludge plant |
| CI | Confidence interval |
| CDAS | Chemically dosed activated sludge |
| Empirical chemical dosing constant related to stokes settling velocity | |
| Empirical chemical dosing constant related sludge compaction | |
| DF | Degree of freedom |
| DSVI | Diluted sludge volume index, mL/g |
| Aluminium dosing concentration (mg/L) | |
| ESS | Effluent suspended solid |
| EPS | Extracellular polymeric substances |
| EN | Effluent nitrogen |
| EP | Effluent phosphorus (EP) |
| FST | Final settling tank |
| F | F-test statistics |
| FFT | Full flow treatment |
| H | Sludge height, cm |
| k | Vesilind sludge settleablity constant |
| K | Dick and Young sludge settleability constant |
| Empirical settling parameter relating to sludge compaction | |
| MLD | Mega litres per day |
| MLSS | Mixed liquor suspended solids, g/L |
| R2 | Coefficient of determination |
| SSVI | Stirred specific volume Index, mL/g |
| SVI | Sludge volume index, mL/g |
| SS | Suspended colids |
| SSD | Sum of squared deviation |
| Vesilind sludge parameter related to settling velocity (m/h) | |
| Dick and Young sludge parameter related to settling velocity (m/h) | |
| WWTP | Wastewater treatment plant |
| WRc | Water Research Council |
| X | Activated sludge concentration, g/L |
| Alum dosed MLSS concentration, g/L | |
| α | Significance level |
| ZSVO | Maximum zone settling velocity (m/h) |
| ZSV | Actual zone settling velocity (m/h) |
References
- Wilfert, P.; Kumar, P.S.; Korving, L.; Witkamp, G.J.; van Loosdrecht, M.C.M. The relevance of phosphorus and iron chemistry to the recovery of phosphorus from wastewater: A review. Environ. Sci. Technol. 2015, 49, 9400–9414. [Google Scholar] [CrossRef]
- Haandel, A.C.V.; Lubbe, J.G.M.V. Handbook of Biological Wastewater Treatment: Design and Optimisation of Activated Sludge System, 2nd ed.; IWA Publishing: London, UK, 2012. [Google Scholar]
- Ojo, P.; Ifelebuegu, A.O. The Impact of Alum on the Bulking of a Full scale Activated Sludge Plant. Environ. Eng. 2016, 3, 53–57. [Google Scholar]
- Zou, J.; Zhang, L.; Wang, L.; Li, Y. Enhancing phosphorus release from waste activated sludge containing ferric or aluminium phosphates by EDTA addition during anaerobic fermentation process. Chemosphere 2017, 171, 601–608. [Google Scholar] [CrossRef] [PubMed]
- Ge, J.; Meng, X.; Song, Y.; Terracciano, A. Effect of phosphate releasing in activated sludge on phosphorus removal from municipal wastewater. Environ. Sci. 2018, 67, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.; Yin, F.; Xu, Y.; Yu, H. A force-based mechanistic model for describing activated sludge settling process. Water Res. 2017, 127, 118–126. [Google Scholar] [CrossRef]
- Li, B.; Stenstrom, M.K. Dynamic one-dimensional modelling of secondary settling tanks and design impacts of sizing decisions. Water Res. J. 2014, 50, 160–170. [Google Scholar] [CrossRef]
- François, P.; Locatelli, F.; Laurent, J.; Bekkour, K. Experimental study of activated sludge batch settling velocity profile. Flow Measur. Instrum. J. 2016, 48, 112–117. [Google Scholar] [CrossRef]
- Heikal, H.A.M.; El Baz, A.R.; El-Hafiz, A.A.; Farghaly, S.M. Study the Performance of Circular Clarifier in Existing Potable Water Treatment Plant by Computational Fluid Dynamics; International Water Resources Association: Paris, France, 2017. [Google Scholar]
- Zhang, D.J.; Li, Z.L.; Lu, P.L.; Zhang, T.; Xua, D.Y. A method for characterizing the complete settling process of activated sludge. Water Res. 2006, 40, 2637–2644. [Google Scholar] [CrossRef] [PubMed]
- Mancell-Egala, W.A.S.K.; Kinnear, D.J.; Jones, K.L.; Clippeleir, H.D.; Takacs, I.; Murthy, S.N. Limit of stokesian settling concentration characterizes sludge settling velocity. Water Res. 2016, 90, 100–110. [Google Scholar] [CrossRef]
- Ramin, E.; Wagner, D.S.; Yde, L.; Binning, P.J.; Rasmussen, M.R.; Mikkelsen, P.S.; Plosz, B.G. A new settling velocity model to describe secondary sedimentation. Water Res. 2014, 55, 447–458. [Google Scholar] [CrossRef]
- Ekama, G.A.; Barnard, J.L.; Gunthert, F.W.; Krebs, P.; McCorquadale, J.A.; Parker, D.S.; Wahlberg, E.J. Secondary Settling Tanks, Theory, Modelling, Design and Operation; Scientific Report No 6; International Association of Water Quality (IAWQ): London, UK, 1997. [Google Scholar]
- Tchobanoglous, G.; Burton, F.L.; Stensel, H.D. Wastewater Engineering: Treatment and Reuse, 4th ed.; McGraw-Hill Science: New York, NY, USA, 2003. [Google Scholar]
- Jung, K.W.; Hwang, M.J.; Ahn, K.H.; Ok, Y.S. Kinetic study on phosphate removal from aqueous solution by biochar derived from peanut shell as renewable adsorptive media. Int. J. Environ. Sci. Technol. 2015, 12, 3363–3372. [Google Scholar] [CrossRef]
- Ghawi, A.G.; Kris, J. A Computational Fluid Dynamics Model of Flow and Settling in Sedimentation Tanks. Appl. Comput. Fluid Dyn. J. 2012, 2, 19–34. [Google Scholar]
- Ghawi, A.G.; Kris, J. Improvement Performance of Secondary Clarifiers by a Computational Fluid Dynamics Model. Slovak J. Civ. Eng. 2011, 19, 1–11. [Google Scholar] [CrossRef]
- WEF-Water Environment Federation. Clarifier Design WEF Manual of Practice No. FD-8, 2nd ed.; McGraw-Hill: New York, NY, USA, 2005; Available online: http://www.assettler.com/COKTURME%20TANKLARI%20TASARIMI.pdf> (accessed on 20 May 2015).
- Ojo, P.; Ifelebuegu, A.O. The Impact of Aluminium Salt for Chemical Phosphorus Removal on the Settleability of Activated Sludge. Environments 2018, 5, 88. [Google Scholar] [CrossRef]
- Wilen, B.M.; Jin, B.; Lant, P. The influence of key constituents in activated sludge on surface and flocculating properties. Water Res. 2003, 37, 127–2139. [Google Scholar] [CrossRef]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 148, 166–176. [Google Scholar] [CrossRef]
- Li, B.; Stenstrom, M.K. Research advances and challenges in one-dimensional modelling of secondary settling Tanks: A critical review. Water Res. J. 2014, 65, 40–63. [Google Scholar] [CrossRef]
- Torfs, E.; Balemans, S.; Locatelli, F.; Diehl, S.; Bürger, R.; Laurent, J.; François, P.; Nopens, I. On constitutive functions for hindered settling velocity in 1-D settler models: Selection of appropriate model structure. Water Res. 2017, 110, 38–47. [Google Scholar] [CrossRef]
- Vesilind, P.A. Theoretical considerations: Design of prototype thickeners from batch settling tests. J. Water Sew. Works 1968, 115, 302–307. [Google Scholar]
- Dick, R.I.; Young, K.W. Analysis of thickening performance of final settling tanks. In Proceedings of the 27th Industrial Waste Conference, Lafayette, IN, USA, 2–4 May 1972. [Google Scholar]
- Takács, I.; Patry, G.G.; Nolasco, D. A dynamic model of the clarification-thickening process. Water Res. J. 1991, 25, 1263–1271. [Google Scholar] [CrossRef]
- Dupont, R.; Dahl, C. A one-dimensional model for a secondary settling tank including density current and short-circuiting. Water Sci. Technol. 1995, 31, 215–224. [Google Scholar] [CrossRef]
- Cho, S.; Colin, F.; Sardin, M.; Prost, C. Settling velocity model of activated sludge. Water Res. J. 1993, 27, 1237–1242. [Google Scholar] [CrossRef]
- Zhang, Y.; Grassia, P.; Martin, A.; Usher, S.P.; Scales, P.J. Designing thickeners by matching hindered settling and gelled suspension zones in the presence of aggregate densification. Chem. Eng. Sci. 2015, 134, 297–307. [Google Scholar] [CrossRef]
- Guyonvarch, E.; Ramin, E.; Kulahci, M.; Plosz, B.G. ICFD: Interpreted Computational Fluid Dynamics—Degeneration of CFD to one-dimensional advection-dispersion models using statistical experimental design—The secondary clarifier. Water Res. 2015, 83, 396–411. [Google Scholar] [CrossRef] [PubMed]
- Bürger, R.; Diehl, S.; Faras, S.; Nopens, I.; Torfs, E. A consistent modelling methodology for secondary settling tanks: A reliable numerical method. Water Sci. Technol. 2013, 68, 192–208. [Google Scholar] [CrossRef] [PubMed]
- De Clercq, J. Batch and Continuous Settling of Activated Sludge: In-depth Monitoring and 1D Compression Modelling. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2006. [Google Scholar]
- De Clercq, J.G.U.; Nopens, I.G.U.; Defrancq, J.; Vanrolleghem, P. Extending and calibrating a mechanistic hindered and compression settling model for activated sludge using in-depth batch experiments. Water Res. J. 2008, 42, 781–791. [Google Scholar] [CrossRef]
- Schuler, A.J.; Jang, H. Causes of variable biomass density and its effects on settleability in full-scale biological wastewater treatment systems. Environ. Sci. Technol. 2007, 41, 1675–1681. [Google Scholar] [CrossRef]
- Schuler, A.J.; Jang, H. Microsphere addition for the study of biomass properties and density effects on settleability in biological wastewater treatment systems. Water Res. 2007, 41, 2163–2170. [Google Scholar] [CrossRef]
- White, Settling of Activated Sludge, Technical Report TR11; WRC: Stevanhage, UK, 1975.
- MCR-Process & Technology 2008 Stiro-Settlometer. Available online: http://www.mcrpt.com/english/pdf/manuel_stiro.pdf > (accessed on 10 February 2014).
- Schuler, A.J.; Jang, H. Density effects on activated sludge zone settling velocities. Water Res. J. 2007, 41, 1814–1822. [Google Scholar] [CrossRef]
- Vaerenbergh, E.V. Numerical computation of secondary settler area using batch settling data. Tribune Cebedeau 1980, 33, 369–374. [Google Scholar]
- Wahlberg, E.J.; Keinath, T.M. Development of settling flux curves using SVI. J. Water Pollut. Control Fed. 1988, 60, 2095–2100. [Google Scholar] [CrossRef]
- Giokas, D.; Diagger, G.T.; Sperling, M.V.; Kim, Y.; Paraskevas, A. Comparison and evaluation of empirical zone settling velocity parameters based on sludge volume index using unified settling characteristics database. J. Water Res. 2003, 37, 3821–3836. [Google Scholar] [CrossRef]
- Daigger, G.T. Development of refined clarifier operating diagrams using an updated settling characteristics database. J. Water Environ. Res. 1995, 67, 95–100. [Google Scholar] [CrossRef]
- Pitman, A.R. Settling properties of extended aeration sludge. J. Water Pollut. Control Fed. 1980, 52, 524–536. [Google Scholar]
- Pitman, A.R. Operation of biological nutrient removal plants: In Theory, Design and Operation of Nutrient Removal Activated Sludge Processes; Water Research Commission: Pretoria, South Africa, 1984. [Google Scholar]
- Ekama, G.A.; Marais, G.V.R. Sludge Settleability and Secondary Settling and Design Procedures. Water Pollut. Control 1986, 87, 101–113. [Google Scholar]
- Koopman, B.; Cadee, K. Prediction of thickening capacity using diluted sludge volume index. Water Res. 1983, 17, 1427–1431. [Google Scholar] [CrossRef]
- Lakehal, D.; Krebs, P.; Krijgsman, J.; Rodi, W. Computing shear flow and sludge blanket in secondary clarifiers. J. Hydraul. Eng. 1999, 125, 253–262. [Google Scholar] [CrossRef]
- Dupont, R.; Henze, M. Modelling of the secondary clarifier combined with the activated sludge model no. 1. Water Sci. Technol. 1992, 25, 285–300. [Google Scholar] [CrossRef]
- Lyn, D.A.; Stamou, A.I.; Rodi, W. Density currents and shear induced flocculation in sedimentation tanks. Hydraul. Eng. 1992, 118, 849–867. [Google Scholar] [CrossRef]
- Otterpohl, R.; Freund, M. Dynamic models for clarifiers of activated sludge plants with dry and wet weather flows. Water Sci. Technol. 1992, 26, 1391–1400. [Google Scholar] [CrossRef]
- Mazzolani, G.; Pirozzi, F.; d’Antonoi, G. A generalized settling approach in the numerical modelling of sedimentation tanks. Water Sci. Technol. 1998, 38, 95–102. [Google Scholar] [CrossRef]
- Smollen, M.; Ekama, G.A. Comparison of empirical settling velocity equations in flux theory for secondary settling tanks: South Africa. Water Sci. Technol. 1984, 10, 175–184. [Google Scholar]
- Tuntoolavest, M.; Grady, C.P.L.J. Effect of activated sludge operational conditions on sludge thickening characteristics. Water Pollut. Control Fed. 1980, 54, 1112–1117. [Google Scholar]
- Catunda, P.F.C.; Van Haandel, A.C.; Araujo, L.S.; Vilar, A. Determination of the Settleability of Activated Sludge; The 15th Congress of the Brazilian Sanitary Engineering Organisation: Belem, Brazil, 1989. [Google Scholar]
- Catunda, P.F.C.; Van Haandel, A.C. Activated sludge settling-part I: Experimental determination of settling characteristics. Water 1992, 18, 165–172. [Google Scholar]
- Bürger, R.; Careaga, J.; Diehl, S.; Ryan, M.; Zambrano, J. Estimating the hindered-settling flux function from a batch test in a cone. Chem. Eng. Sci. 2018, 192, 244–253. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).