Abstract
An integrated hydrological-hydraulic model employing the 2-D local inertial equation as the core is established for effective numerical simulation of surface water flows in a great lake and its floodplain. The model is a cascade of validated hydrological and hydraulic sub-models. The model was applied to simulating the surface water flows of the Tonle Sap Lake and its floodplain in Cambodia using the roughness coefficient value calibrated comparing with a remote-sensing data set. The resulting model reasonably handles backwater flows during the rainy season and simulates the propagations of wet and dry interfaces without numerical instability, owing to a proper setting of time step supported by a novel numerical stability analysis. Sensitivity analysis of the surface water dynamics focusing on the setting of roughness coefficient and the backwater effect was also carried out. Overall, utilizing the 2-D local inertial equation in the assessment of lake water dynamics is a new modelling approach, which turns out to be an efficient simulation tool.
1. Introduction
An effective tactic for assessing surface water flows of a freshwater body is employing mathematical models that can describe hydrological processes occurring around it and its hydrodynamics. Since such models are generally not easy to handle analytically except for very simplified cases where exact solutions are available [1,2,3,4], they have to be implemented numerically in practice. The most widely-used mathematical models in hydrological and hydraulic research areas are lumped models, distributed hydrological models, hydraulic models based on the shallow water equations (SWEs), or detailed full 3-D models based on the Navier-Stokes equations [5]. Since each model has many variants, only those with the SWEs, which are closely related to the model used in this paper, are reviewed below. The SWEs, especially the 2-D one, can potentially describe surface water dynamics for which the hydrostatic pressure assumption is valid [6], like large-scale horizontal circulation in lakes and/or inundation of floodplains. Mathematically, the SWEs are a nonlinear hyperbolic system of equations that govern horizontal mass and momentum dynamics in surface water [7]. An extensive description on the theory and applications of the SWEs is provided in Reference [8]. The SWEs have been employed in modern integrated hydrological-hydraulic models and have been applied to realistic problems [9,10,11,12,13].
It is desirable to use a simpler and computationally more efficient while still physically reasonable mathematical model for practical flood simulation. From this viewpoint, the local inertial equation (LIE) has recently gained recognition as a core of simple and efficient flood simulation [14]. The LIE is a shallow water model that is mathematically simpler and its nonlinearity is less dominant than the conventional SWEs and furthermore, it is numerically easier to handle than the diffusion-wave models [14]. Formally, the LIE is simply derived by omitting the momentum flux terms from the momentum equations of the SWEs. Further, omitting the temporal partial differential terms from the momentum equations reduces the LIE to the corresponding diffusion wave model. Omitting the momentum flux terms is physically justified when the horizontal length scale of the problem is sufficiently larger than its vertical length scale, such as shallow water flows occurring in a wide lake and its floodplain like those focused on in this paper [15,16]. Almeida and Bates [17] numerically compared solution behavior between the LIE and SWEs through numerical experiments and demonstrated that their performances are comparable for small Froude numbers, especially in the low range of subcritical flows. Even though the LIE is a simplified counterpart of the SWEs, it is potentially able to handle backwater flows reasonably owing to employing the momentum equation with inertia. This is not the case for more simplified models like the kinematic wave models that assume the water surface gradient locally equals the bed slope [18,19,20].
The finite difference scheme for discretization of the LIE proposed by Bates et al. [14] has served as a simple as well as computationally efficient numerical tool for simulating surface water flows. The scheme is based on an innovative semi-implicit treatment of the friction slope term avoiding inversion of large-size matrices that the many implicit methods for hydrodynamics models encounter. The scheme has widely been applied to the modelling and assessment of key surface water dynamics around the world; such examples include the Amazon River [21], the Ganges-Brahmaputra-Meghna Delta [22] and the Mekong River having the Tonle Sap Lake (TSL) [23,24]. Yamazaki et al. [25] implemented the 1-D LIE with the semi-implicit scheme into a global river model called CaMa-Flood (Catchment-based Macro-scale Floodplain) model and reported it has a higher computational efficiency than its diffusion wave counterpart. The LIE has recently been applied to numerical evaluation of storm surges caused by a cyclone [26]. The LIE with the semi-implicit finite difference scheme has also been applied to flood simulation in urban areas by many researchers, exhibiting its usefulness [27,28,29,30,31,32]. Almeida et al. [17] examined several semi-implicit finite difference schemes for the LIEs against 1-D test cases with analytical solutions and a 2-D realistic problem. Pontes et al. [33] developed a GIS-based software to simulate coupled hydrological-hydraulic dynamics for large floodplain river systems. Finite volume schemes based on well-balanced explicit Riemann-solvers have also been applied to numerical discretization of the 1-D and 2-D LIEs and their accuracy and stability are examined [34,35]. The finite volume scheme has also been verified in detail against the flows with wet and dry interfaces [36].
TSL in Cambodia is one of the most important shallow lakes on the earth in terms of biodiversity (containing a Ramsar site), fish production and local cultural values. This distinctive ecosystem is being maintained and characterized largely by the adjacent huge floodplains and district seasonality [37,38,39]. Many researchers [24,40,41,42,43] have thus investigated hydrological characteristics of TSL. Yet, the modelling of its inundation pattern and surface water dynamics have gained less attention. Given the hydrological and ecological importance of floodplains, however, it is critically important to develop a feasible modelling approach to describe such a dynamic inundation pattern for enhancing our scientific understanding as well as environmental management. For this purpose, sophisticated finite volume methods have been utilized [41] but numerically efficient schemes such as the LIEs have not been examined so far.
In response to such an urgent need, in this paper, we aim to establish and validate an integrated hydrological-hydraulic model for simulating surface water dynamics of TSL and its floodplain. The originality of this paper is an application of the 2-D LIE to simulating surface water dynamics in TSL and its floodplains: a new approach for analyzing surface water dynamics in and around TSL. Before the application, this study explored the mathematical background of the setting of proper time increment. The analysis shows a validity of using smaller time increment than that determined by the CDFL condition. The resulting model turns to reproduce the backwater flow in TSL during the rainy season accurately, which is an essential driver of water environment and aquatic ecosystems in and around the lake [44,45,46]. The present model can deal with the cascade of the hydrological and hydraulic phenomena only with the limited data availability across Cambodia. Sensitivity analysis of the surface water dynamics by the integrated model focusing on the setting of the roughness coefficient and the backwater effect is carried out as well for deeper comprehension on performance of the model.
2. Hydrological-Hydraulic Integrated Model
2.1. Model Structure
The present integrated model has a cascading structure that consists of the three hydrological and hydraulic sub-models, each of which has been recognized as a useful tool for flood analysis: the distributed hydrological model Geomorphology-Based Hydrological Model (GBHM) [47], the 1-D hydraulic model Mike11 [48] and the 2-D LIE. Figure 1 is the conceptual image of the present model. The GBHM computes the water budget in each watershed of tributaries of TSL, which serve as the inflow boundary conditions for both the Mike11 and the 2-D LIE. Mike11 is then used to calculate longitudinally 1-D surface water dynamics in TSL and its downstream rivers and delta, which serve as essential backwater flow driving the 2-D LIE. Finally, the 2-D LIE with the semi-implicit finite difference scheme is operated to simulate horizontally 2-D flow structures in and around TSL that Mike11 cannot reproduce solely. The flow computed with the Mike11 is utilized as the downstream outflow boundary condition for the 2-D LIE along a cross-section traversing Tonle Sap River.
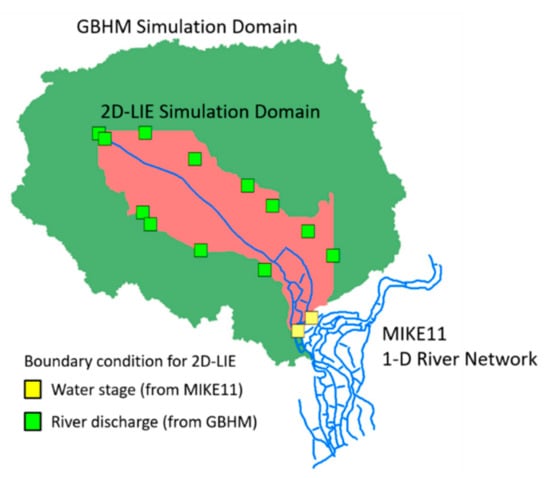
Figure 1.
A conceptual image on the model integration among GBHM, MIKE11 and 2-D LIE. The green and red areas are the simulation domains of GBHM and 2D-LIE, respectively; the blue lines are MIKE11 river network. Boundary river discharge and water stage are given by GBHM and MIKE11 as the light-green and yellow boxes, respectively.
The three sub-models, namely GBHM, Mike11 and the 2-D LIE are presented in this section. The numerical scheme for the 2-D LIE is presented in the next section and its stability analysis result in Appendix A since it is the core of the integrated model.
2.2. GBHM
The hydrological sub-model GBHM [47] solves the continuity, momentum and energy equations using the two modules: the hillslope module and the river routing module. Detailed description of each module is presented in Appendix B.
In GBHM, the target watershed is divided into grids and a digital elevation model (DEM) is used to create the associated river network. Each sub-basin is divided into flow intervals. In the sub-basins, a flow interval is defined as a function of distance from the sub-basin’s outlet. Lateral flow to the main stream is estimated by accumulating runoff at each grid in one hillslope unit. This treatment means that all hillslopes of a flow interval drain into the main stream. The flow interval-hillslope realizes a fast flow computation even in large basins [11,49,50].
In the hillslope module, each grid is divided into four layers: which are canopy, soil surface, unsaturated zone and groundwater. A central assumption in this module is that vegetation covers the surface soil and prevents direct rainfall onto the land. Vegetation coverage and leaf area index are used to calculate the deficit of canopy interception. To simulate the unsaturated zone water flow, a vertical one-dimensional Richards’ equation is used. Saturated water flow and its exchange with the river water are described using basic mass balance equations. The Pfafstetter numbering system [51] is applied to tracking water flows efficiently from upstream toward downstream.
2.3. MIKE11
The downstream outflow boundary condition for the 2-D LIE is prepared with Mike11 [48], which is a hydraulic sub-model that can compute the open channel network flow on downstream rivers of TSL. Mike11 is a versatile and fully dynamic 1-D modelling package with a map-based and highly intuitive graphical user interface. This hydraulic model has widely been applied to a variety of surface water dynamics occurring in and around open channels, such as urban drainage system [52], flash flood propagation [53], pollutant transport [54] and ecosystem assessment [55].
The basic physical model utilized in Mike11 is the cross-sectionally averaged 1-D SWEs where is the time and is the locally 1-D abscissa taken along each channel:
Here, is the discharge, is the cross-sectional area, is the lateral inflow, is the water stage, is the hydraulic radius, the momentum correction coefficient and is the Chezy’s resistance coefficient that is related to the Manning’s roughness coefficient as . The SWEs (1) and (2) are numerically solved with the implicit finite difference scheme [56].
2.4. Local Inertial Model
The 2-D LIE as the core sub-model defined in the conventional horizontal coordinates is formulated here [14]. The 2-D LIE consists of the continuity equation
and the momentum equations
Here, is the time; is the bed elevation, is the line discharge in the -direction, is the line discharge in the -direction, is the water depth, is the source term due to rainfall, is the sink term due to evaporation, and is the gravitational acceleration. The continuity Equation (3) governs the mass balance in the surface water, while the momentum Equations (4) and (5) govern the momentum balance. The continuity and momentum equations should be equipped with the appropriate initial and boundary conditions for their well-posedness. The 2-D LIE does not have the terms on the Coriolis force and wind shear, because the preliminary computational results suggest that they have negligible influences on the surface water dynamics [16].
Differences between the 2-D LIE and the conventional 2-D SWEs are briefly summarized here for self-contentedness of the paper. Both the LIE and SWEs govern surface water dynamics in shallow water bodies where the water depth is significantly smaller than the horizontal extensions of the water body of interest. They share the same continuity equation, while having different momentum equations. The momentum equations of the 2-D LIE can be seen as a simplified counterpart of those of the 2-D SWEs where the momentum flux terms are omitted. Based on the scaling analysis [15,16], this simplification can be justified when the horizontal extensions are sufficiently large and/or the flow speed is sufficiently small. This difference of the momentum equations results in the difference of the wave structures between the models [35]. More exactly, the 2-D SWEs have a genuinely nonlinear wave structure, in which shock waves and rarefaction waves possibly coexist and sub- and super-critical flow transitions are involved [7]. On the other hand, the wave structure of the 2-D LIE is much simpler: it consists of the shock waves and have neither rarefaction nor the flow transitions. Therefore, the 2-D LIE is not suitable for describing surface water flows where the flow transitions are essential, such as flows around hydraulic structures. In other words, from a practical side, the 2-D LIE potentially serves as a simpler and efficient alternative to the 2-D SWEs when simulating large-scale surface water dynamics.
3. Numerical Scheme for the 2-D LIE
3.1. Discretization
The 2-D LIE is discretized with a semi-implicit finite difference scheme [14], which is based on a spatio-temporally staggered discretization and an efficient treatment of the friction slope terms in the momentum Equations (4) and (5).
The domain of surface water flows is discretized into an orthogonal structured mesh having rectangular cells. The time increment for the temporal integration is denoted as . The spatial increments in and directions are denoted as and , respectively. The quantity evaluated at the time at the location is denoted as where , , and are integers. The quantities with half-integer sub- and/or super-scripts are defined in the same manner.
Assume , , and have already been computed at each cell. The continuity Equation (3) is discretized as
The momentum Equations (4) and (5) are discretized as
The water depths and are evaluated as
and
respectively, to avoid non-physical, negative water depths that may break down numerical computations. The initial conditions are also specified. The boundary conditions are specified if necessary.
The semi-implicit finite difference scheme presented above has been chosen for the integrated model since the scheme does not require employing iterative solvers for linear or nonlinear systems at each time step. The scheme is therefore suitable for parallel computation of the 2-D LIE. In addition, the semi-implicit treatment of the friction terms greatly improves numerical stability of computed water flows and allows for a larger time increment than those of the explicit scheme as demonstrated below. For numerical implementation of the present numerical method, we are using an Open MP environment for easily-implementable parallelization.
3.2. Stability Analysis Results
It would be useful to comprehend stability of the present semi-implicit scheme for effective operation of the present model. Conventionally, the scheme has been widely operated under the well-known CFL condition
where is the representative water depth, such as the maximum water depth in the computational domain. The CFL condition serves only as a guide for friction-less flows but not a stability condition for problems with friction but has been employed as a stability criterion for operating the semi-implicit scheme [14,16,17]. However, in preliminary computations not presented here, we found that the scheme sometimes fails when the bottom slope is relatively large. This fact has been pointed out in the literature [14,15,16,17], while its theoretical background is yet to be detailed, especially in a mathematical manner. Here, a linear stability analysis results for the LIE are briefly presented, focusing on the 1-D counterpart whose numerical discretization is more tractable. So far, explicit, semi-implicit and implicit finite difference schemes have been proposed and their stability analysis has been carried out assuming a linear friction term [57]. The stability analysis here considers a more realistic situation where a quadratic, non-linear friction term like the Manning’s one is employed. The proof of stability analysis is provided in Appendix A since it is bit long. We demonstrate that the stability condition of the present finite difference scheme actually depends on the bed slope and is strictly narrower than that of the CFL condition (11).
The stability analysis here focuses on the stability of a 1-D steady uniform flow with the water depth of along a uniform open channel with the bed slope of subject to small perturbations of the water depth. The unit flow discharge of the uniform flow is calculated with and based on the conventional Manning’s formula as . In the numerical experiments, the parameters are specified as (0.1 m, 0.001), (0.1 m, 0.005) and , and as 0.03 s/m1/3, which are realistic values encountered in applications. For different values of and , we compare the theoretical stability analysis results obtained through the procedure presented in Appendix A and the numerical computation results with the uniform flow perturbed with 0.01 % water depth fluctuations. In the numerical computation, the scheme is judged to be unstable if the computed water flow diverges or oscillates permanently since the true solutions are monotone and non-oscillatory. The representative results were summarized in Table 1, where the results for the explicit counterpart in which the friction slope terms are discretized in a fully-explicit manner are included in the table as well to highlight the wider stability region of the semi-implicit scheme. The results presented in the table indicate that the semi-implicit treatment clearly shows higher numerical stability than the explicit one and more importantly, lower stability than the CFL condition. Although it is empirically found that the CFL condition is insufficient to guarantee numerical stability of simulation, the above analysis clarified its mathematical evidence. According to this finding, we set a safety factor to regulate the time increment to be smaller than one determined by the CFL condition. Tanaka and Yoshioka [58] addressed theoretical stability analysis of the discretized 1-D LIEs with explicit, semi-implicit and implicit treatments for the friction term. Their results support that the CFL condition gives an optimistic stability conditions for flows with friction.

Table 1.
Comparison of maximum allowable time step at 500 m resolution on a slope with gradient 0.001, 0.005 and 0.01 and water depth of 0.1 m, 1.0 m and 2.0 m by the CFL conditions, one simulated using the explicit and semi-implicit treatment based on von Neumann stability analysis (see Appendix A).
4. Application
4.1. Study Site
This study is carried out in the basin of the TSL in Cambodia [39]. The basin is physiographically characterized by four distinct topographical features. The north is formed by an escarpment of the sandstone Dangrek Mountains. The southwest is dominated by the granite Cardamom Mountains which forms the watershed boundary between the rivers flowing down in the lake and the coastal area. The central flat lowland of the TSL is interrupted by isolated hills which form watershed boundary between the tributaries of the lake and the Mekong River. There were generally twelve major sub-basins around the lake. Basins of the TSL are influenced by a tropical monsoon climate which gives two distinct seasons, the dry season from December to May followed by six months of the rainy season from June to November. During the rainy season, the south-west monsoon wind comes in from the Indian Ocean and brings about 80% of the annual rainfall with it. The temperature across the basin of the TSL ranges from a mean daily minimum of 19 °C in January to a mean daily maximum of 36 °C in April. There is very little variation across the region with differences of the order of 1 °C. The mean annual temperature is 28 °C. The TSL experiences high humidity with mean annual values ranging from 69% at Pursat to 79% at Phnom Penh. The lake rarely experiences humidity below 65% throughout the year. The records indicate a variation in the mean wind speeds across the basin with the south region (Pursat) experiencing much lower wind speeds than the north (Siem Reap) and southeast (Phnom Penh) regions. Mean wind speeds range from 0.5 m/s in the south to 4.4 m/s in the southeast. Tanaka and Yoshioka [16] confirmed that actual wind speed over the lake in this range did not influence macroscopic lake water dynamics. Accordingly, wind shear was not included in the 2-D LIE in this paper.
4.2. Remote Sensing
Remote sensing data is utilized for validation of the present integrated model. Remote sensing data used here was obtained from the Terra satellite using MODIS sensor and the Landsat 7 using ETM+ sensor. The spatial resolution of MODIS images is 250 m to 500 m and the repeat cycle is 1 day. The MOD09A1 and MOD09Q1 products are eight-day composite images that are corrected for atmospheric effects. Therefore, the influence of clouds is removed to the greatest extent possible. On the other hand, the spatial resolution of Landsat 7 images is 15 m to 30 m and the repeat cycle is 16 days. MODIS images are used for time-series validations because the repeat cycle is shorter than that of Landsat 7 and Landsat 7 images are used to check the flood that cannot be captured by MODIS images.
Flood areas are identified by the enhanced vegetation index (EVI), land surface water index (LSWI) and difference between EVI and LSWI (DVEL). The equations used to derive EVI, LSWI and DVEL are as follows:
where NIR, RED, BLUE and SWIR are the reflectance values of Band 2, Band 1, Band 3 and Band 6 in the MODIS and Band 4, Band 3, Band 1 and Band 5 in the Landsat 7. Using these indexes and a specific decision tree, Sakamoto et al. [59,60] proposed flood discrimination algorithms and the approach has been applied in many regions. In this methodology, the ground surface state was classified into three stages: flood, mixture and non-flood. Certain thresholds of the decision tree were expressed as follows:
If either (15) or (16) is satisfied, then an objective pixel is classified as “flood”. On the other hand, if (17) is satisfied, then an objective pixel is classified as “mixture”. Finally, if (18) is satisfied, then an objective pixel is classified as “non-flood”.
4.3. Model Setup in the Tonle Sap Lake
4.3.1. Hydrological Model GBHM
The simulation domain in this paper is shown in Figure 2. The watershed, flow directions and surface steepness in the TSL basin was arranged using the Shuttle Radar Topography Mission (SRTM), provided by the American National Geospatial-Intelligence Agency and the National Aeronautics and Space Administration (http://www2.jpl.nasa.gov/srtm/). The land cover and soil type for the basin were obtained from Global Land Cover 2000 (http://edc2.usgs.gov/glcc/eadoc2_0.php) and the FAO soil map of the world [61], respectively. Daily precipitation and air temperature data from 80 weather stations (blue and green circles in Figure 2) were obtained from the Mekong River Commission [62,63] (MRC) (see Figure 2).
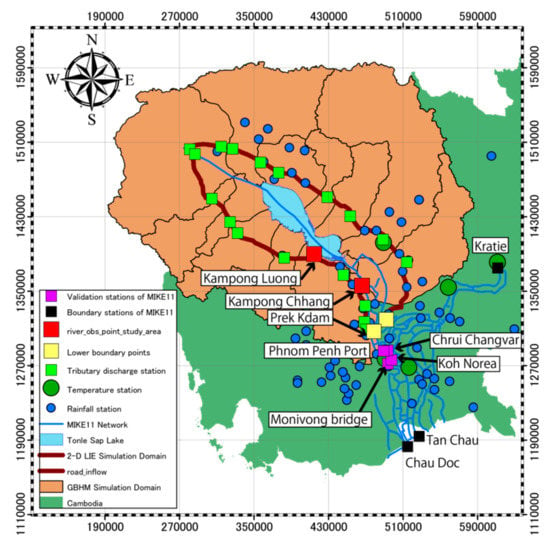
Figure 2.
Simulation domain and cascade system among GBHM, MIKE 11 and 2D-LIE. Brown area: simulation domain for the GBHM, blue lines: 1-D flow network for MIKE11 and brown line: boundary of simulation domain for the 2-D LIE. Rainfall and temperature are observed at blue and green circles, respectively, which are given to the GBHM and 2-D LIE. MIKE11 receives upstream tributary discharge from GBHM and observed upstream/downstream boundary water stage at light-blue and black rectangular points, respectively. Observed water stages at red points are used for the validation of the 2-D LIE.
The estimated basin-averaged annual rainfall, based on the available weather stations, is 1541 mm/year on average during 1998–2003, which is not the same as, but not significantly far from, the 1290 mm/year reported by Kummu et al. [64]. Evapotranspiration was calculated with the Thornthwaite method with a monthly air temperature of 1667 mm/year, which is comparable to the 1627 mm/year reported by Kummu et al. [64]. Therefore, the collected meteorological data, which can be potentially a source of error, is considered to be reasonably accurate as an input for the present model.
Daily discharges were simulated for ten years and compared with the observations at the evaluation sites for the Chinit River and the Sen River (Figure 3). The parameters were calibrated for observed discharge from 1997 to 2003 and validated from 2004 to 2006. In Chinit River, the water discharge NSE of 0.66 and 0.71 were obtained for the calibration and the validation, respectively. Similarly, in Sen River, NSE of water discharge accounted for 0.68 and 0.65 for the calibration and validation period, respectively.
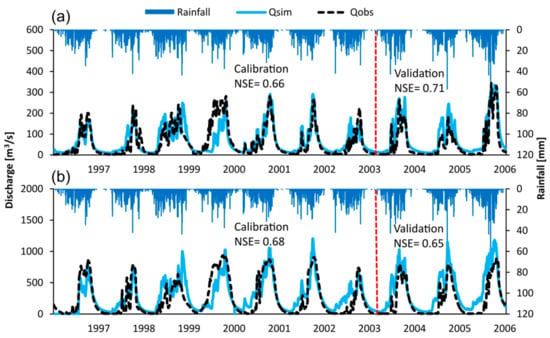
Figure 3.
Observed (black-dot) and simulated (light blue-line) discharges at the gauging sites. (a) Chinit River, (b) Sen River.
4.3.2. 1-D River and Lake Routing Model MIK11
Mike11 in this model was established based on Fujii et al. [47] as follows. The simulation domain is the Mekong-Bassac-Tonle Sap and the Great Lake system from Kratie to Tan Chau and Chau Doc including the surrounding floodplains. At the Kratie (upstream boundary) and the Than Chau (downstream boundary) stations on the Mekong River and the Chau Doc (downstream boundary) station on the Bassac River (black squares in Figure 2), observed water level by Cambodian Hydrographic Office (CHO) survey [65] was provided. Lateral river inflow from 18 tributary rivers to TSL (light green squares in Figure 2) by GBHM was specified along the nearest edge of MIKE11 river network. The input data for the present Mike 11 mainly consists of those generated by GBHM and a part of them have been complemented by a free software NAM. This treatment was necessary for preparing the hydrological data on ungauged catchment, which will become completely unnecessary by our filed observation planned in future. Note that this point does not affect the concept and structure of the present model.
The simulation results for the year 2002 at the confluence of the Mekong mainstream, Tonle Sap and Bassac Rivers (purple squares in Figure 2) are presented in Figure 4. A reasonable agreement between the observed and simulated discharges is confirmed at the Chrui Changvar, Koh Norea, the Monivong Bridge and the Phnom Penh Port. The computational results show that the model can represent the unique flow dynamics and its balance of the Chak Tomuk junction. Figure 5 shows the simulated and observed discharge at Prek Kdam and the Phnom Penh Port (see Figure 2), demonstrating the reasonable model accuracy again.
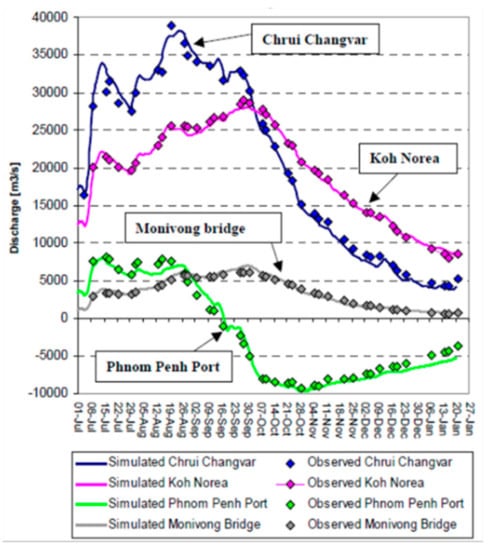
Figure 4.
Model Verification of the discharges in 2002.
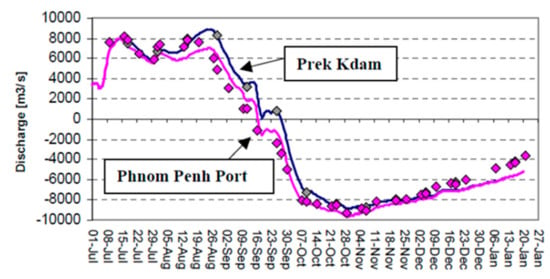
Figure 5.
Model Verification of the Tonle Sap River in 2002.
4.3.3. 2-D Local Inertial Equation
The 2D LIE was setup with the following initial and boundary conditions. On the initial condition, it is hard to obtain spatial distribution of water depth over the lake at particular time, hydrostatic condition with the constant water level of 2 m from the Ha Tien 1960 height was given over the domain, on which lake area corresponds to observed one at initial time of July 1st, 1998. The simulation was performed from July 1998 to December 2003 including spin-up period from July 1998 to December 1999.
On the boundary conditions, the upstream inflow discharge from tributary rivers to the lake was given by the simulated results of GBHM. The water level at the mouth of the Tonle Sap River (yellow points in Figure 2) simulated from MIKE 11 was set as the lower boundary condition, so that the backwater effect observed in the rainy season [41] is reasonably taken into account. This nesting system from hydrological modelling and 1-D hydraulic modelling to 2-D hydraulic modelling turns out to realize accurate lake flow simulation. Elevation data is provided from SRTM modified using bathymetry data on the Tonle Sap Lake and River. Source to the lake, that is, rainfall and evapotranspiration were provided in the same way as the GBHM.
4.4. Results and Discussion
To validate the connectivity between MIKE11 and 2-D LIE, the simulated hydrographs at the Prek Kdam station from the two were firstly compared (Figure 6). As indicated in the figure, the computational results from the both models compare well, indicating that Mike11 smoothly connects to the 2-D LIE without any technical difficulty. Our strategy to connect the two sub-models thus successfully worked for simulating the surface water dynamics.
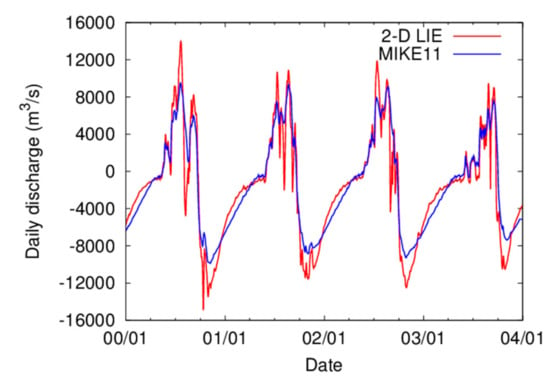
Figure 6.
River discharge at the Prek Kdam station simulated using 2-D LIE (red) and MIKE11 (blue).
Secondly, in Figure 7, the simulated water level with the 2-D LIE is compared with the observed water stage data available at the Kampong Luong and Kampong Chhnang stations, respectively (see also Figure 2). During the observation period, water stages at the both stations are quite accurately reproduced by the 2-D LIE driven by the boundary conditions from GBHM and Mike11. The error magnitude for the whole period is −1.12 m to 0.622 m and that of annual maximum water level is −0.223 m to 0.0288 m. These error magnitudes are considered to be acceptable since the water stages dynamically vary several meters at these stations.
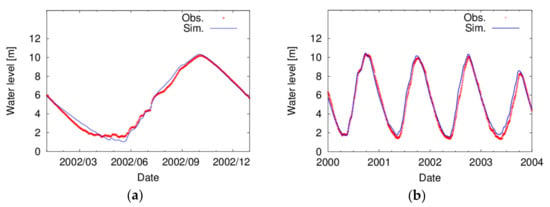
Figure 7.
Observed (red) and simulated (blue) water level at (a) the Kampong Chhnang and (b) Kampong Luong stations.
Finally, the computed overall flood area is validated with the corresponding satellite image data. The time series of the degree of agreement, which is here defined as the ratio of the total number of flooded cells in the simulation to that in the satellite image, is depicted in Figure 8. We see that the simulated flood area explains 80% to 90% of the observed flood area, implying satisfactory performance of the present integrated model. Similarly, the degree of overestimation, which is defined as the ratio of the number of flooded cells only in the simulation to that in both the simulation and satellite image is shown in Figure 9. The computational results demonstrate that the simulated flood area is twice as large as the observed flood area in the transition period from the dry season to rainy season (May to August). For example, spatial distribution of the degree of agreement on 20 August 2000 is plotted in Figure 10. In this figure, the yellow cells show the flood area in both the satellite image and simulation; the green cells show one only in the simulation; and the blue cells show one only in the satellite image. We find that the overestimation mainly occurs in the north-western parts of the TSL. This is the case for all the four years examined. As indicated in the Google image (Figure 11a), these areas are actually flooded forest and thus difficult to judge flooding occurring there with MODIS. As a compensation, a Landsat image, which is considered to provide clearer judgement flooding if not affected by cloud, was overlaid on the simulated result on the nearest day to 20 August 2000 (same as Figure 10) among ones when Landsat image is available for the west part of the lake (16 August 2000) in Figure 11b. As demonstrated in the figure, the Landsat image more clearly captures the flooding in and round the flooded forest, implying that the overestimation is caused by incomplete judgement of flooding in the flooded forest.
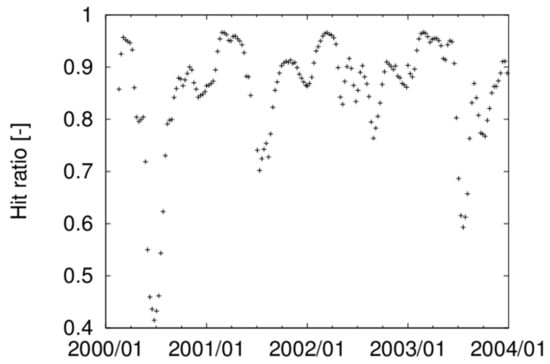
Figure 8.
Ratio of the number of flooded cells in both the simulation and satellite image and ones in satellite image.
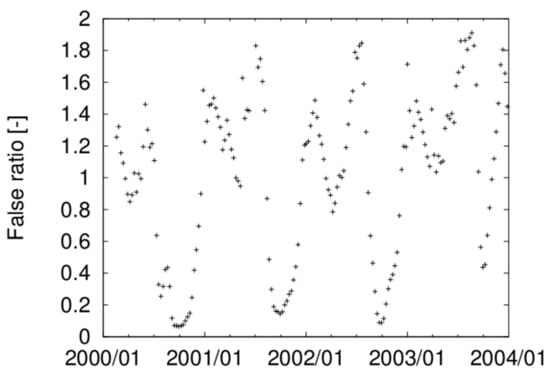
Figure 9.
Ratio of the number of flooded cells in only the simulation and ones in both the simulation and satellite image.
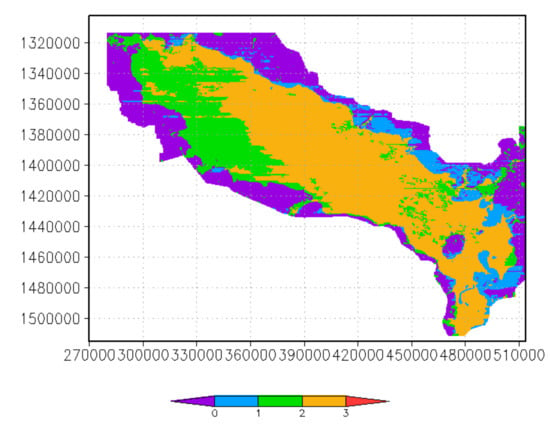
Figure 10.
Spatial distribution of the degree of agreement on 20 August 2000. The yellow cells show the flood area in both the satellite image and simulation; the green cells show one only in the simulation; and the blue cells show one only in the satellite image.
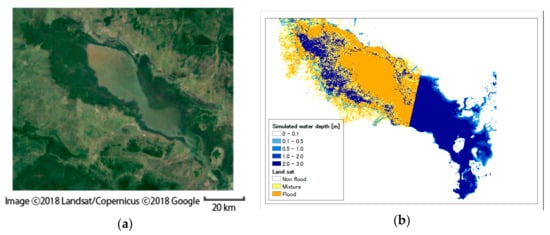
Figure 11.
(a) The Google image of TSL and its floodplain area, (b) simulated water depth overlaid with the flooded area from the Landsat image on 16 August 2000 (same period as Figure 9). The yellow and orange pixels were judged as “mixture” and “flood” (see definition in Section 4.2) in the Landsat image.
4.5. Sensitivity Analysis
Our cascade of the sub-models is possibly subject to high uncertainty due mainly to difficulty of finding a globally most accurate set of the parameter values. This point is analyzed focusing on the impacts of the inputs on the backwater flow at the outlet of the TSL. The input components examined here are the downstream water stage by MIKE11 and the Manning’s roughness coefficient, both of which are essential drivers of the surface water dynamics in and around TSL. The Manning’s roughness coefficient was set as 0.03 m−1/3s, 0.06 m−1/3s, or 0.10 m−1/3s. Although it should be dependent on land use, this analysis here sets spatially uniform value to see the magnitude of the impact over the whole TSL simulation. The bias of the water stage at the Prek Kdam station was introduced by modulating the water stage by 5%, 10%, 20%, 30% and 40%.
The simulated water stage at the Kampong Luong station (a) and flood area (b) with different magnitudes of the biases applied to the Manning’s roughness coefficient and the downstream boundary water stage are compared in Figure 12 and Figure 13, respectively. On the Manning’s roughness coefficient, Figure 12 shows that both the simulated water stage and flood area with different coefficients give similar computational results in the rainy season, while the larger values of the coefficient lead to the higher water stage and wider flood area expansion in the dry season. When the Manning’s roughness coefficient was set as 0.06 m−1/3s or 0.1 m−1/3s, the water stage at the Kampong Luong station was 1.69 times and 2.57 times larger and the flood area was 1.35 and 1.77 larger in maximum than those in the reference simulation, respectively. On the other hand, Figure 13 indicates that the bias of the water stage at the Prek Kdam station has the direct impacts on both water stage and flood area of TSL. The water stage at the Kampong Luong station and the flood area were 1.47 times and 1.37 times larger than those in the reference simulation, respectively.
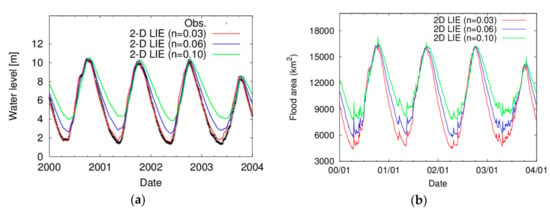
Figure 12.
Simulated (a) water stage at the Kampong Luong station and (b) flood area for Manning’s roughness coefficient of 0.03 (red), 0.06 (blue), 0.10 (green). Black dots in (a) shows the observed water stage.
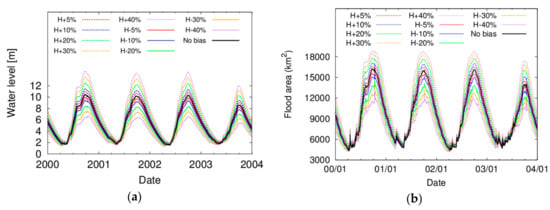
Figure 13.
(a) water stage at the Kampong Luong station and (b) flood area simulated with downstream boundary water stage at the Prek Kdam station increased (solid line) and decreased (dashed line) by 5% (red), 10% (blue), 20% (green), 30% (yellow) and 40% (purple). Black lines show simulated results with original tributary discharges.
The obtained computational results imply that, in the rainy season, the expansion of the flood flow is shaped by the backwater coming from the Mekong River through the Tonle Sap River and the impacts of the roughness are rather small. In other words, the uncertainty of the roughness coefficient, which is expected to be high in general, does not critically affect the accuracy of the present integrated model if the focus is on the flood area estimation in the rainy season. On the other hand, we need careful identification of the roughness coefficient when the focus is on environmental issues and/or sediment transportation, which depend on lake flow throughout the year.
5. Conclusions
We developed an integrated and numerically efficient hydrological-hydraulic model for practical simulation of surface water dynamics in a tropical lake and its floodplain. The model has been applied to TSL and its floodplain. The validity of applying smaller time step than the conventional CFL condition is examined for efficient and stable simulation of the core model 2-D LIE. Then, the resulting model accurately reproduced the observed results, implying that the cascade of the sub-models effectively worked successfully. The sensitivity analysis of the model focusing on the backwater effects indicated relatively high sensitivity of the model on the roughness coefficient. The results would be useful for operating the present integrated model under different land uses and covers around TSL.
The goal of our research is not simple establishment of the integrated model but its application to water environmental assessment in and around TSL. In this regard, modelling suspended sediment dynamics in TSL and its downstream Mekong delta is a crucial topic related to human lives in Cambodia and Vietnam [66,67,68,69,70]. This research topic will be addressed with the present integrated model coupled with a sediment transport model like an advection-dispersion equation that governs the sediment concentration dynamics. Application of the present model to assessment of fisheries in and around TSL is also an important issue, especially for the impacts assessment of hydrological and hydraulic changes on seasonal migrations of key freshwater fish species [71,72,73]. Our paper is a first attempt to operate the present model under a realistic condition. The framework of our model is flexible because of the versatility of each sub-model. For example, we will be able to apply the present model to simulating surface water dynamics occurring in other shallow and wide lakes if the outflow downstream condition is specified and the inflows into the lakes from their watersheds and tributaries are computed.
Author Contributions
Conceptualization, C.Y., S.L. and H.Y.; Methodology, H.F. (Mike 11), S.S. (GBHM), T.T. (LIE) and Remote Sensing (Y.F. and K.H.); Mathematical Analysis, H.Y. and T.T.; Validation, T.T.; Writing-Review & Editing, H.Y. and T.T; Supervision, H.Y.; Project Administration, C.Y.; Funding Acquisition, C.Y.
Funding
This research was funded by SATREPS project “Establishment of Environmental Conservation Platform of Tonle Sap Lake”.
Acknowledgments
The authors thank Yoneda at Yamagata University for kind help with running MIKE11.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This appendix presents proofs of the stability analysis results of the 1-D LIE. The semi-implicit scheme and the explicit scheme are examined for comparison, which demonstrate higher stability of the semi-implicit one. The procedure here follows that of the conventional linear stability analysis in the von Neumann’s sense. Namely, we firstly linearize the 1-D LIE based on a steady flow condition and then discretize the linearized equation. It turns out that the stability analysis here is not tractable but can be performed numerically using a simple algorithm.
The 1-D LIE
s considered in an infinitely long uniform open channel domain with the bed slope of and is linearized based on a uniform flow. The flow discharge of the uniform flow is calculated with the specified water depth and the slope as . By a straightforward calculation, the linearized 1-D LIE that governs spatio-temporal evolution of the perturbations and is derived as
Here, it is noted that combining (A3) and (A4) yields the telegraph equation having an advection term
implying that the 1-D LIE can be written as a simple
equation; however, what we use in what follows is the system (A3) and (A4) rather than (A5) since the former has a more convenient form for the stability analysis. The continuity equation of the linearized 1-D LIE has the same form with the original one, while the momentum equations seem to be remarkably different with each other. The origin of each term of the linearized momentum Equation (A4) is as follows. The first term is from the temporal partial differential term of the original LIE, the second one from the water surface gradient term and the last one from the friction term. The third term is an important term for stability analysis, which comes from the nonlinearity of the surface gradient term and the linearization of h−10/3 in the friction slope term.
Following the original semi-implicit scheme, the linearized 1-D LIE (A3) and (A4) is discretized as
The one-sided discretization of in the third term of (A7) comes from (9) where it results in
for the present uniform flow case. The last term (A7) is a consequence of the semi-implicit discretization of the friction term, which is replaced by for the explicit discretization. We eliminate from the system (A6) and (A7) and seek for the exact solution of of the form where is the non-zero complex amplification factor, is the wave number, and . Finally, we derive an algebraic equation that governs :
where
The scheme is judged to be stable in the Von Neumann’s sense if for all . Since the condition cannot be judged analytically, we numerically compute and then for discrete, but sufficiently densely chosen values of the wave number .
Appendix B
This appendix summarizes the equations used in GBHM for simulating surface water dynamics in the watershed of TSL. GBHM solves the continuity, momentum and energy equations using the two modules: the hillslope module and the river routing module. The details of equations used in each module are described below. The notations of the parameters and variables apply only to the equations in this appendix.
Appendix B.1. Hillslope Module
In this module, the hillslope length is calculated as:
where is the accumulative area at flow distance is the number of upstream rivers at the flow distance . The bed rock slope is assumed to be parallel to the surface.
The non-uniform vertical distribution is represented using an exponential assumption of the vertically decreasing hydraulic conductivity. that is, the hydraulic conductivity decreases with an increase in soil depth as
where is the saturated hydraulic conductivity at the depth taken positive in the downward direction, is the saturated hydraulic conductivity of surface soil, and is the fitting parameter.
The macrospore in top soil is represented using an anisotropy ratio, defined as:
where is the anisotropy ratio, and are the saturated hydraulic conductivities in the directions normal (n) and parallel (p) to the slope, respectively.
For different vegetation or crop species, or of different time periods, the canopy interception ability can be different. The interception capacity at time is given as
and the canopy storage as
where is the maximum interception ability of the vegetation in a year, is the vegetation coverage, is the leaf-area-index, is the maximum annual leaf-area-index of the vegetation, is the deficit of canopy water storage, is the canopy water storage. Assume the uniform rainfall intensity occurs within the time interval , the actual interception is determined as
The evapotranspiration (ET) from the canopy contains the evaporation from the canopy interception and the transpiration of the soil water extracted by the root system and lost from the dry fraction of canopy. Similarly, the bare soil evaporation consists of the loss from the soil surface interception and the evaporation of soil moisture . They are parameterized as follows.
and
Here, is the crop coefficient, is the potential evaporation rate, is the root distribution function, is the soil moisture function, and is the volumetric water content. and are piecewise linear functions of .
The unsaturated zone water flow is described using the vertically 1-D Richards’ equation
where represents the source or sink, i.e., evaporation and transpiration, is the soil moisture flux given by
where is hydraulic conductivity and is capillary suction.
The basic equations used for the saturated zone are mass balance and Darcy’s law. The mass balance is given by
where is the change rate of groundwater storage in unconfined aquifer, is the recharge rate from the upper unsaturated zone, is the plane area of the hillslope element, and is the discharge to the river per unit width given by the formula
Here, is the hydraulic conductivity of the unconfined aquifer, is the hill slope length, and are the hydraulic heads in the hill slope and the river, and and are the corresponding groundwater depths.
Appendix B.2. River Routing Module
This module is based on the kinematic wave equations closed by the Manning’s formula:
where is the wetted cross-sectional area, is discharge, is the lateral inflow, is the river bed slope, is the Manning’s roughness coefficient, and is the wetting perimeter.
References
- Alcrudo, F.; Benkhaldoun, F. Exact solutions to the Riemann problem of the shallow water equations with a bottom step. Comput. Fluids 2001, 30, 643–671. [Google Scholar] [CrossRef]
- Ancey, C.; Iverson, R.M.; Rentschler, M.; Denlinger, R.P. An exact solution for ideal dam-break floods on steep slopes. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Chesnokov, A.A. Symmetries and exact solutions of the rotating shallow-water equations. Eur. J. Appl. Math. 2009, 20, 461–477. [Google Scholar] [CrossRef]
- Thacker, W.C. Some exact solutions to the nonlinear shallow-water wave equations. J. Fluid Mech. 1981, 107, 499–508. [Google Scholar] [CrossRef]
- Miller, C.T.; Dawson, C.N.; Farthing, M.W.; Hou, T.Y.; Huang, J.; Kees, C.E.; Kelley, C.T.; Langtangen, H.P. Numerical simulation of water resources problems: Models, methods, and trends. Adv. Water Resour. 2013, 51, 405–437. [Google Scholar] [CrossRef]
- Zhang, W.; Cundy, T.W. Modeling of two-dimensional overland flow. Water Resour. Res. 1989, 25, 2019–2035. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; John Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Szymkiewicz, R. Numerical Modeling in Open Channel Hydraulics; Springer Science & Business Media: Dordrecht, The Netherlands, 2010; Volume 83. [Google Scholar]
- Li, Y.; Yuan, D.; Lin, B.; Teo, F.Y. A fully coupled depth-integrated model for surface water and groundwater flows. J. Hydrol. 2016, 542, 172–184. [Google Scholar] [CrossRef]
- Şen, O.; Kahya, E. Determination of flood risk: A case study in the rainiest city of Turkey. Environ. Model. Softw. 2017, 93, 296–309. [Google Scholar] [CrossRef]
- Singh, V.P.; Woolhiser, D.A. Mathematical modeling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef]
- Viero, D.P.; Peruzzo, P.; Carniello, L.; Defina, A. Integrated mathematical modeling of hydrological and hydrodynamic response to rainfall events in rural lowland catchments. Water Resour. Res. 2014, 50, 5941–5957. [Google Scholar] [CrossRef]
- Yang, X.; Chen, H.; Wang, Y.; Xu, C.Y. Evaluation of the effect of land use/cover change on flood characteristics using an integrated approach coupling land and flood analysis. Hydrol. Res. 2016, 47, 1161–1171. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; Wilson, M.D. Simple spatially-distributed models for predicting flood inundation: A review. Geomorphology 2007, 90, 208–225. [Google Scholar] [CrossRef]
- Tanaka, T.; Yoshioka, H. Applicability of the 2-D local inertial equations to long-term hydrodynamic simulation of the Tonle Sap Lake. In Proceedings of the 2nd International Symposium on Conservation and Management of Tropical Lakes, Siem Reap, Cambodia, 24–26 August 2017. [Google Scholar]
- Almeida, G.A.; Bates, P. Applicability of the local inertial approximation of the shallow water equations to flood modeling. Water Resour. Res. 2013, 49, 4833–4844. [Google Scholar] [CrossRef]
- Kazezyılmaz-Alhan, C.M.; Medina, M.A., Jr. Kinematic and diffusion waves: Analytical and numerical solutions to overland and channel flow. J. Hydraul. Eng. 2007, 133, 217–228. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Chen, L.; Li, J.C.; Singh, V.P. Two-dimensional kinematic wave model of overland-flow. J. Hydrol. 2004, 291, 28–41. [Google Scholar] [CrossRef]
- Ponce, V.M. Kinematic wave controversy. J. Hydraul. Eng. 1991, 117, 511–525. [Google Scholar] [CrossRef]
- Rudorff, C.M.; Melack, J.M.; Bates, P.D. Flooding dynamics on the lower Amazon floodplain: 1. Hydraulic controls on water elevation, inundation extent, and river-floodplain discharge. Water Resour. Res. 2014, 50, 619–634. [Google Scholar] [CrossRef]
- Ikeuchi, H.; Hirabayashi, Y.; Yamazaki, D.; Kiguchi, M.; Koirala, S.; Nagano, T.; Kotera, A.; Kanae, S. Modeling complex flow dynamics of fluvial floods exacerbated by sea level rise in the Ganges–Brahmaputra–Meghna Delta. Environ. Res. Lett. 2015, 10, 124011. [Google Scholar] [CrossRef]
- Apel, H.; Trepat, O.M.; Hung, N.N.; Chinh, D.T.; Merz, B.; Dung, N.V. Combined fluvial and pluvial urban flood hazard analysis: Concept development and application to Can Tho City, Mekong Delta, Vietnam. Nat. Hazards Earth Syst. 2016, 16, 941–961. [Google Scholar] [CrossRef]
- Yamazaki, D.; Sato, T.; Kanae, S.; Hirabayashi, Y.; Bates, P.D. Regional flood dynamics in a bifurcating mega delta simulated in a global river model. Geophys. Res. Lett. 2014, 41, 3127–3135. [Google Scholar] [CrossRef]
- Yamazaki, D.; Almeida, G.A.; Bates, P.D. Improving computational efficiency in global river models by implementing the local inertial flow equation and a vector-based river network map. Water Resour. Res. 2013, 49, 7221–7235. [Google Scholar] [CrossRef]
- Ikeuchi, H.; Hirabayashi, Y.; Yamazaki, D.; Muis, S.; Ward, P.J.; Winsemius, H.C.; Verlaan, M.; Kanae, S. Compound simulation of fluvial floods and storm surges in a global coupled river-coast flood model: Model development and its application to 2007 Cyclone Sidr in Bangladesh. J. Adv. Model. Earth Syst. 2017, 9, 1847–1862. [Google Scholar] [CrossRef]
- Coles, D.; Yu, D.; Wilby, R.L.; Green, D.; Herring, Z. Beyond ‘flood hotspots’: Modelling emergency service accessibility during flooding in York, UK. J. Hydrol. 2017, 546, 419–436. [Google Scholar] [CrossRef]
- Dottori, F.; Todini, E. Testing a simple 2D hydraulic model in an urban flood experiment. Hydrol. Process. 2013, 27, 1301–1320. [Google Scholar] [CrossRef]
- Falter, D.; Vorogushyn, S.; Lhomme, J.; Apel, H.; Gouldby, B.; Merz, B. Hydraulic model evaluation for large-scale flood risk assessments. Hydrol. Process. 2013, 27, 1331–1340. [Google Scholar] [CrossRef]
- Yin, J.; Yu, D.; Wilby, R. Modelling the impact of land subsidence on urban pluvial flooding: A case study of downtown Shanghai, China. Sci. Total Environ. 2016, 544, 744–753. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Yu, D.; Yin, Z.; Liu, M.; He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 2016, 537, 138–145. [Google Scholar] [CrossRef]
- Zellou, B.; Rahali, H. Assessment of reduced-complexity landscape evolution model suitability to adequately simulate flood events in complex flow conditions. Nat. Hazards 2017, 86, 1–29. [Google Scholar] [CrossRef]
- Pontes, P.R.M.; Fan, F.M.; Fleischmann, A.S.; de Paiva, R.C.D.; Buarque, D.C.; Siqueira, V.A.; Jardim, P.F.; Sorribas, M.V.; Collischonn, W. MGB-IPH model for hydrological and hydraulic simulation of large floodplain river systems coupled with open source GIS. Environ. Model. Softw. 2017, 94, 1–20. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Djordjević, S. A well balanced Roe scheme for the local inertial equations with an unstructured mesh. Adv. Water Resour. 2015, 83, 351–363. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Djordjević, S. Analytical and numerical solutions of the Local Inertial Equations. Int. J. Non-Linear Mech. 2016, 81, 222–229. [Google Scholar] [CrossRef]
- Martins, R.; Leandro, J.; Djordjević, S. Wetting and drying numerical treatments for the Roe Riemann scheme. J. Hydraul. Res. 2017, in press. [Google Scholar] [CrossRef]
- Carbonnel, J.P.; Guiscafre, J. Ministiere des Affaires Etrangeres. Gouvernement Royal du Cambodge Grand Lac du Cambodge; Muséum National D’histoire Naturelle de Paris: Paris, France, 1962; 63p. [Google Scholar]
- Lamberts, D. The Tonle Sap Lake as a productive ecosystem. Int. J. Water Resour. Dev. 2006, 22, 481–495. [Google Scholar] [CrossRef]
- Uk, S.; Yoshimura, C.; Siev, S.; Try, S.; Yang, H.; Oeurng, C.; Li, S.; Hul, S. Tonle Sap Lake: Current status and important research directions for environmental management. Lakes Reserv. Res. Manag. 2018, in press. [Google Scholar] [CrossRef]
- Ahamed, A.; Bolten, J.D. A MODIS-based automated flood monitoring system for southeast Asia. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 104–117. [Google Scholar] [CrossRef]
- Hai, P.T.; Masumoto, T.; Shimizu, K. Development of a two-dimensional finite element model for inundation processes in the Tonle Sap and its environs. Hydrol. Process. 2008, 22, 1329–1336. [Google Scholar] [CrossRef]
- Masumoto, T.; Hai, P.T.; Shimizu, K. Impact of paddy irrigation levels on floods and water use in the Mekong River basin. Hydrol. Process. 2008, 22, 1321–1328. [Google Scholar] [CrossRef]
- Tangdamrongsub, N.; Ditmar, P.G.; Steele-Dunne, S.C.; Gunter, B.C.; Sutanudjaja, E.H. Assessing total water storage and identifying flood events over Tonlé Sap basin in Cambodia using GRACE and MODIS satellite observations combined with hydrological models. Remote Sens. Environ. 2016, 181, 162–173. [Google Scholar] [CrossRef]
- Hung, N.N.; Delgado, J.M.; Güntner, A.; Merz, B.; Bárdossy, A.; Apel, H. Sedimentation in the floodplains of the Mekong Delta, Vietnam. Part I: Suspended sediment dynamics. Hydrol. Process. 2014, 28, 3132–3144. [Google Scholar] [CrossRef]
- Kabeya, N.; Kubota, T.; Shimizu, A.; Nobuhiro, T.; Tsuboyama, Y.; Chann, S.; Tith, N. Isotopic investigation of river water mixing around the confluence of the Tonle Sap and Mekong rivers. Hydrol. Process. 2008, 22, 1351–1358. [Google Scholar] [CrossRef]
- Västilä, K.; Kummu, M.; Sangmanee, C.; Chinvanno, S. Modelling climate change impacts on the flood pulse in the Lower Mekong floodplains. J. Water Clim. Chang. 2010, 1, 67–86. [Google Scholar] [CrossRef]
- Yang, D.; Oki, T.; Herath, S.; Musiake, K. A hillslope-based hydrological model using catchment area and width functions. Hydrol. Sci. J. 2002, 47, 49–65. [Google Scholar] [CrossRef]
- Fujii, H.; Garsdal, H.; Ward, P.; Ishii, M.; Morishita, K.; Boivin, T. Hydrological roles of the Cambodian floodplain of the Mekong River. Int. J. River Basin Manag. 2003, 1, 253–266. [Google Scholar] [CrossRef]
- Cong, Z.; Yang, D.; Gao, B.; Yang, H.; Hu, H. Hydrological trend analysis in the Yellow River basin using a distributed hydrological model. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Wang, W.; Lu, H.; Yang, D.; Sothea, K.; Jiao, Y.; Gao, B.; Peng, X.; Pang, Z. Modelling hydrologic processes in the Mekong River Basin using a distributed model driven by satellite precipitation and rain gauge observations. PLoS ONE 2016, 11, e0152229. [Google Scholar] [CrossRef] [PubMed]
- Verdin, K.L.; Verdin, J.P. A topological system for delineation and codification of the Earth’s river basins. J. Hydrol. 1999, 218, 1–12. [Google Scholar] [CrossRef]
- Rauch, W.; Bertrand-Krajewski, J.L.; Krebs, P.; Mark, O.; Schilling, W.; Schütze, M.; Vanrolleghem, P.A. Deterministic modelling of integrated urban drainage systems. Water Sci. Technol. 2002, 45, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Kourgialas, N.N.; Karatzas, G.P. A hydro-sedimentary modeling system for flash flood propagation and hazard estimation under different agricultural practices. Nat. Hazards Earth Syst. 2014, 14, 625–634. [Google Scholar] [CrossRef]
- Li, Q.; Wang, T.; Zhu, Z.; Meng, J.; Wang, P.; Suriyanarayanan, S.; Zang, Y.; Song, S.; Lu, Y.; Yvette, B. Using hydrodynamic model to predict PFOS and PFOA transport in the Daling River and its tributary, a heavily polluted river into the Bohai Sea, China. Chemosphere 2017, 167, 344–352. [Google Scholar] [CrossRef] [PubMed]
- Doulgeris, C.; Georgiou, P.; Papadimos, D.; Papamichail, D. Ecosystem approach to water resources management using the MIKE 11 modeling system in the Strymonas River and Lake Kerkini. J. Environ. Manag. 2012, 94, 132–143. [Google Scholar] [CrossRef] [PubMed]
- Abbot, M.B.; Ionescu, F. On the numerical computation of nearly-horizontal flows. J. Hydraul. Res. 1967, 5, 97–117. [Google Scholar] [CrossRef]
- Yoshioka, H.; Tanaka, T. On mathematics of the 2-D local inertial model for flood simulation. In Proceedings of the 2nd International Symposium on Conservation and Management of Tropical Lakes, Siem Reap, Cambodia, 24–26 August 2017. [Google Scholar]
- Yoshioka, H.; Tanaka, T. Numerical stability analysis of the local inertial equation with semi- and fully-implicit friction term treatments. J. Adv. Simul. Sci. Eng. 2018, 4, 162–175. [Google Scholar]
- Sakamoto, T.; Nguyen, N.V.; Kotera, A.; Ohno, H.; Ishitsuka, N.; Yokozawa, M. Detecting temporal change in the extent of annual flooding within the Cambodia and the Vietnamese Mekong Delta from MODIS time-series imagery. Remote Sens. Environ. 2007, 109, 295–313. [Google Scholar] [CrossRef]
- Sakamoto, T.; Van, P.C.; Kotera, A.; Duy, K.N.; Yokozawa, M. Detection of yearly change in farming systems in the Vietnamese Mekong Delta from MODIS time-series imagery. Jpn. Agric. Res. Q. 2009, 43, 173–185. [Google Scholar] [CrossRef]
- FAO. The Digital Soil Map of the World and Derived Soil Properties, version 3.6; FAO/UNESCO: Rome, Italy, 2003. [Google Scholar]
- MRC. Consolidation of Hydro-Meteorological Data and Multi-Functional Hydrologic Roles of Tonle Sap Lake and its Vicinity Project; Main Report Chapter 9; Mekong River Commission: Phnom Penh, Cambodia, 2003; pp. 1–18. [Google Scholar]
- MRC. The Study on Hydro-Meteorological Monitoring for Water Quantity Rules in the Mekong River Basin; Final Report; Mekong River Commission: Phnom Penh, Cambodia, 2004; Volume 1, Part III; pp. 1–68. [Google Scholar]
- Kummu, M.; Tes, S.; Yin, S.; Adamson, P.; Jozsa, J.; Koponen, J.; Richey, J.; Sarkkula, J. Water balance analysis for the Tonle Sap Lake–floodplain system. Hydrol. Process. 2014, 28, 1722–1733. [Google Scholar] [CrossRef]
- Ministry of Public Works and Transport, Cambodia. JICA Map of Cambodia. 1:100,000; Ministry of Public Works and Transport, Cambodia: Phnom Penh, Cambodia, 1997.
- Kummu, M.; Penny, D.; Sarkkula, J.; Koponen, J. Sediment: Curse or blessing for Tonle Sap Lake? Ambio J. Hum. Environ. 2008, 37, 158–163. [Google Scholar] [CrossRef]
- Lu, X.; Kummu, M.; Oeurng, C. Reappraisal of sediment dynamics in the Lower Mekong River, Cambodia. Earth Surf. Process. Landf. 2014, 39, 1855–1865. [Google Scholar] [CrossRef]
- Schmitt, R.J.P.; Rubin, Z.; Kondolf, G.M. Losing ground-scenarios of land loss as consequence of shifting sediment budgets in the Mekong Delta. Geomorphology 2017, 294, 58–69. [Google Scholar] [CrossRef]
- Siev, S.; Yang, H.; Sok, T.; Uk, S.; Song, L.; Kodikara, D.; Oeurng, C.; Hul, S.; Yoshimura, C. Sediment dynamics in a large shallow lake characterized by seasonal flood pulse in Southeast Asia. Sci. Total Environ. 2018, 631–632, 597–607. [Google Scholar] [CrossRef] [PubMed]
- Thanh, V.Q.; Reyns, J.; Wackerman, C.; Eidam, E.F.; Roelvink, D. Modelling suspended sediment dynamics on the subaqueous delta of the Mekong River. Cont. Shelf Res. 2017, 147, 213–230. [Google Scholar] [CrossRef]
- Kc, K.; Bond, N.; Fraser, E.D.G.; Elliott, V.; Farrell, T.; McCann, K.; Rooney, N.; Bieg, C. Exploring tropical fisheries through fishers’ perceptions: Fishing down the food web in the Tonlé Sap, Cambodia. Fish. Manag. Ecol. 2017, 24, 452–459. [Google Scholar] [CrossRef]
- Kong, H.; Chevalier, M.; Laffaille, P.; Lek, S. Spatio-temporal variation of fish taxonomic composition in a South-East Asian flood-pulse system. PLoS ONE 2017, 12, e0174582. [Google Scholar] [CrossRef] [PubMed]
- Sogreah. Mathematical Model of Mekong Delta. Comprehensive Report of the Different Determinations on the Grand Lac Capacity; Sogreah: Phnom Penh, Cambodia, 1999. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).