Abstract
The province of Macerata, Italy, is a topographically complex region which has been little studied in terms of its temperature and precipitation climatology. Temperature data from 81 weather stations and precipitation data from 55 rain gauges were obtained, and, following quality control procedures, were investigated on the basis of 3 standard periods: 1931–1960, 1961–1990 and 1991–2014. Spatial and temporal variations in precipitation and temperature were analysed on the basis of six topographic variable (altitude, distance from the sea, latitude, distance from the closest river, aspect, and distance from the crest line). Of these, the relationship with altitude showed the strongest correlation. Use of GIS software allowed investigation of the most accurate way to present interpolations of these data and assessment of the differences between the 3 investigated periods. The results of the analyses permit a thorough evaluation of climate change spatially over the last 60 years. Generally, the amount of precipitation is diminished while the temperature is increased across the whole study area, but with significant variations within it. Temperature increased by 2 to 3 °C in the central part of the study area, while near the coast and in the mountains the change is between about 0 and 1 °C, with small decreases focused in the Appennine and foothill belt (−1 to 0 °C). For precipitation, the decrease is fairly uniform across the study area (between about 0–200 mm), but with some isolated areas of strong increase (200–300 mm) and only few parts of territory in which there is an increase of 0–200 mm, mainly in the southern part of the coast, to the south-west and inland immediately behind the coast. The monthly temperature trend is characterized by a constant growth, while for precipitation there is a strong decrease in the amount measured in January, February and October (between 25 and 35 mm on average).
1. Introduction
Macerata is the largest of the provinces in the Marche Region of Italy, with an area of about 2800 km2 (Figure 1). Macerata is bordered by the province of Perugia (Umbria Region) to the west, by the Adriatic Sea, an arm of the Mediterranean Sea, to the east, and by three other provinces in the same Region, Ancona to the north, Fermo to the south and Ascoli Piceno to the southwest.
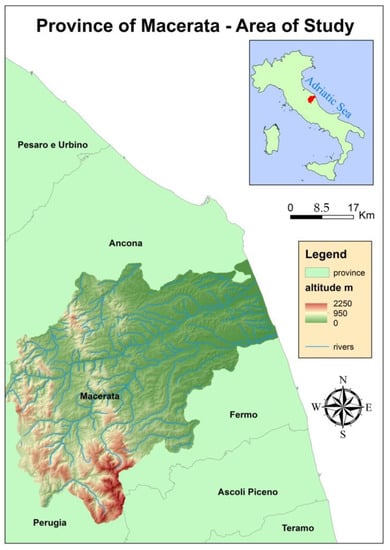
Figure 1.
Geography of the study area.
This part of Central Italy is a transition point between coastal areas with a Mediterranean climate, an inland Temperate climate and then to the west the Highland climates of the mountains (Cs, Cf and H respectively in the Kӧppen-Geiger classification [1]). In some years there is a dominance of one climate type over the other, even if this difference is only shown strongly in the coastal zone. The aim of the present study was to create a new way to analyze temperature and precipitation, through GIS software, in order to have a spatial analysis of climate variability across this topographically complex region. In the literature there are several climate reports for Italy, but not for the Marche Region. Indeed, there is only one published work, by the Experimental Geophysical Observatory of Macerata [2] which can be considered a climate report; however, the study cited has taken an arbitrary time interval from 1950 to 2000, which is not in line with the WMO (World Meteorological Organization) approach [3]. There are two different studies for the Marche Region focusing on climate change aspects. One considers the variations through projections until 2100 using climate modeling [4] and the other investigates the extreme indeces [5], to assess whether there are any trends in the observed data. The extreme indecesis a group of 27 indeces, defined by ETCCDI (Clivar Working Group on Climate Change Detection) [6,7,8] which allow quantitative assessment of temperatures and precipitation variations for each year starting from daily observations (ex. number of frost days, maximum number of consecutive days with less than 1 mm of rainfall, etc.).Finally there is another study for a larger area in Central Italy that analyses climatic variations in relation to land, sea, social reaction and adaptation [9], but this does not consider the Marche Region. Consequently, there is a lack of any detailed studies analyzing and mapping temperature and precipitation patterns in Macerata province which can highlight climate change. In this context the present research fills this scientific gap through an indepth analysis of precipitation and temperatures in the 3 standard periods considered (1931–1960, 1961–1990, 1991–2014). The strength of this research is the completeness, because there are many studies in the world that analyze interpolation methods [10,11,12] or investigate the topographic variables through polynomial regressions [13]; Other researches assess climate change over a long period of time [14,15] or through GIS software [16,17], or even climatic variations assessed through math between rasters [18]. However, no research mixes all these aspects to create a complete climate framework for the area of study. From an operational point of view, this project starts with a careful evaluation of the data quality, passing through the study of the geotopographic factors most correlated to temperature and precipitation, in order to obtain a spatialization of the data more in line with the reality. The spatialization of data through geostatistical methods led to the creation of several maps for each standard period, which then were compared to observed climate change in the area from 1931–1960 and 1991–2016. Finally, the averages of the differences between standard periods (1931–1960 and 1991–2016) were performed allowing a graphic and synthetic evaluation.
2. Materials and Methods
Temperature and precipitation data were collected from 5 institutions: the former National Hydrographic Service (SIMN), Multiple-Risk Functional Center of the Civil Protection, Italian Air Force, Service Agency for the Agrifood Sector of the Marche Region (ASSAM), Functional Center of Umbria. Temperature data from 81 weather stations and precipitation data from 55 rain gauges were obtained. For further analyses these were divided on the basis of 3 standard periods: 1931–1960, 1961–1990 and 1991–2014.
2.1. Quality Control Procedures
The data were validated with 5 quality controls on the basis of the WMO prescriptions [19] and through the procedures developed by Gentilucci et al. in 2018 [20]: logical and gross error check, internal consistency check, tolerance test, temporal consistency, and spatial consistency. For logical and gross error checking, temperatures outside the range (−40 °C; +50 °C) were removed [21] and precipitation measurements greater than 2000 mm were also excluded [20]. The internal consistency check verified the consistency of the data: for example, whether a maximum value was higher than a minimum one, for temperature, and if there were negative values for precipitation. Temporal consistency was useful to investigate errors between temporally contiguous values, for example if there is too much difference between one day and the next, by setting a limit of 3 times the standard deviation added (upper limit) or subtracted (lower limit) to the mean [22]. In the case of temporal consistency, the deletion of data is not immediate, but was subject to the spatial consistency. The spatial consistency was performed taking into consideration the neighbouring weather stations, grouped on the basis of their similarity [20]. After validation, climate data were homogenized through the creation of a reference time series for each candidate weather station. There are no reference weather stations of demonstrated reliability near the study area, so to assess the suitability of the data it is necessary to reconstruct some reference time series to compare the weather stations under investigation. The creation of the reference time series was performed daily on the basis of 10 neighbouring weather stations, for all investigated periods, with empirical Bayesian kriging (EBK), after a comparison with the inverse distance weighted (IDW) and the ordinary co-kriging based on altitude, which is the most correlated independent variable [23]. An interpolation was then prepared for each day by EBK and the climate value taken in the exact coordinates of the weather station under investigation. The creation of the reference time series for each weather station is indispensable for the analysis of breakpoints, which are points where there is a sudden difference (an error) between the reading before and after the current one in the climatic values time series of the same weather station. The breakpoints were analyzed through the SNHT (Standard Normal Homogeneity Test) [24], and the penalized t-test [25] was used to avoid an excess of false breakpoints near the extremes of the time series. Finally, again using the SNHT method, the time series was homogenized, multiplying it with the ratio between the mean before and after shifting, produced by the breakpoint. The aim was to homogenize the time series of the weather station with the most reliable part of it, which is mainly represented by the latest climate values (if there are no systematic errors detected in the most recent data of the time series).
2.2. Basic Cartography and Correlation of Independent Variables
A GIS database was prepared by editing a detailed Digital Elevation Model (DEM) with a cell size 5 × 5 m, obtained using CTR (Regional Technical Map, Regione Marche, 2000), topographical map and LIDAR relief [26]. The relationship of climatic variables with topographical parameters was assessed and the elevation has been found to be the most correlated factor [27]. Six topographic variables were assessed using the adjusted coefficient of determination (R2) [23], with an assessment of the goodness of correlation represented by the calculation of the standard error of the mean and the F-test. These 3 parameters can explain the relation between the topographic variables and temperature or precipitation; in fact the R2 adjusted (R2adj) shows the amount of variation explained by the estimated regression line [28]:
= sample size
= number of explanatory variables (independent), in this case 6
and = mean values of dependent and independent variables
and = values of dependent and independent variables
The standard error of the mean allows calculation of the dispersion of sample means around the population:
= standard deviation
= number of observations
Finally, the F-test was performed to estimate if there can be a significant difference (based on 5% of rejection probability) between the sample means of precipitation or temperature and those of the geographic variables. When the variances of the two populations are equal, the variable cannot be used as independent to obtain a correlation factor with the dependent one, because both of them would be estimators of an unknown quantity σ2. The variance is an index of variability and it is expressed by the formula:
whilst the F-test is obtained from the ratio between major and minor sampling variances.
This process described above has improved the results of interpolation through the use of geostatistical technique based on independent variables.
2.3. Geostatistical Analyses
- Geostatistics is the branch of statistics that is deals with the analysis and interpretation of geographical data. In this case the ordinary cokriging (with one or more independent variables) was chosen after a cross-validation assessment with simple cokriging, kriging (ordinary and simple), empirical Bayesian kriging and universal cokriging. Cokriging and in particular ordinary cokriging was the method that minimized the error (in terms of Mean Error, RMSE, Mean Standardized error, RMSSE, Mean standard error) more than all the others. The Ordinary co-kriging, [29] can be considered a particular case of the universal cokriging, in which the residuals mean is assumed constant and unknown.= weights of the data assigned to and varies between 0 and 100%.= regionalized data at a given location, primary and secondary data.
- Simple co-kriging, [30] is used when the mean is stationary and the residuals mean is considered a global constant and known in the whole study area, this method can be good only if there are a large number of sample points.= mean of the primary and secondary data
- Universal Co-Kriging, [31] a generalization of the ordinary cokriging, is used when the mean isn’t stationary, i.e., if there is a trend, and the residual isn’t correlated to the trend (stationarity of the residuals).= mean of the residuals in the primary and secondary variable.
The interpolation was prepared with altitude as independent variable and precipitation or temperature as the dependent one. The ordinary cokriging has been chosen by an iterative process through many tests of cross-validation performed within the ArcGis extension, Geostatistical Analyst. The interpolation maps obtained were compared between different periods (1931–1960, 1961–1990, 1991–2014) through GIS with the mathematics between rasters, in order to assess spatial climatic variations.
3. Results
3.1. Data Quality Control
The first important result achieved was to have reliable data after the accurate quality controls and homogeneity tests have been carried out. The validation process removed 0.02% of the data for temperature and 1.67% of the data for precipitation. Instead, the homogenization, performed with the SNHT and the Penalized t-test, after a long process of reference time series construction, involved only the data of 4 weather stations. The EBK [32] was compared with IDW and ordinary co-Kriging and was found that it improves the performance of IDW of about 5% (in terms of root mean square error) on the same dataset, while it is quicker and easier, even if less accurate than ordinary co-kriging (Table 1).

Table 1.
Comparison between 3 interpolation methods (Inverse Distance Weighting (IDW), empirical Bayesian kriging (EBK) and Ordinary Co-Kriging).
The reference time series obtained with EBK was related with the candidate time series, in order to investigate if this series (candidate) needs homogenization. The result of subsequent homogenization leads to 2 weather stations homogenized for temperature and 2 rain gauges for precipitation. In particular, the case of Civitanova Marche, a city on the Adriatic coast, is particularly evident with a growing mean, after the breakpoint, of about 300 mm (Figure 2) which is homogenized by the tests [24,25] (Figure 3).
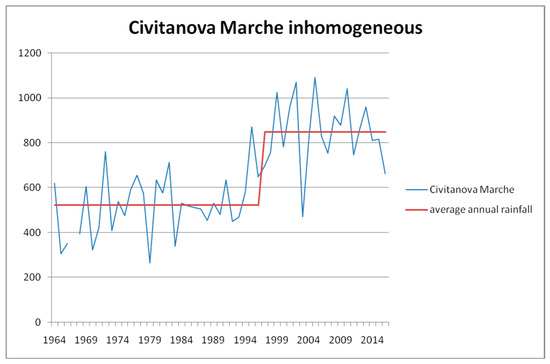
Figure 2.
Civitanova Marche rain gauge inhomogeneous.
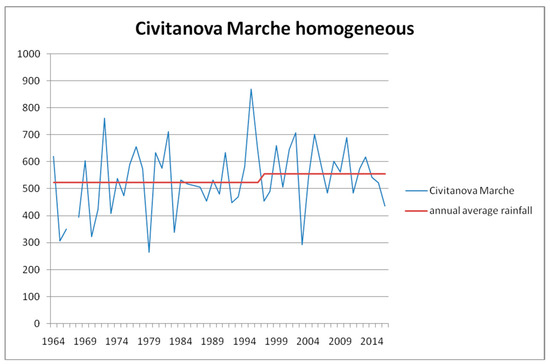
Figure 3.
Civitanova Marche rain gauge homogeneous.
3.2. Assessment of Correlation between Topographical and Climatic Variables
The adjusted data were used for the creation of detailed interpolation maps, passing through an assessment of the influence of topographic co-variables on precipitation and temperature in this area for all investigated periods (1931–1960/1961–1990/1991–2014) (Figure 4). Six different topographic variables were considered [23]: altitude, distance from the sea, latitude, distance from the closest river, aspect, and distance from the crest line. A graph has been prepared for each topographic variable and each month, assessing the various statistical indicators (R2adj; st. error and F-test).
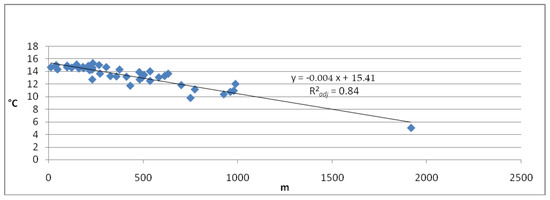
Figure 4.
Ratio between elevation and temperature annual mean in the period 1991–2014.
The results show that the altitude has the better value compared to the other topographic variables both for temperature (Table 2) and precipitation (Table 3). As demonstrated in Gentilucci et al., 2018 [23] for precipitation (Table 3), even for temperatures the most correlated variable for the whole period (1931–2014) is the altitude (Table 2).

Table 2.
Comparison between topographic variables and mean annual temperature 1931–2014.

Table 3.
Comparison between topographic variables and mean annual precipitation 1931–2014.
Thus, Table 2 and Table 3 highlight the goodness of the correlation between altitude and temperature or precipitation, in order to have a reliable independent variable for interpolation by cokriging methods. A good correlation for the distance from the sea, even if lower than with altitude, can also be observed for precipitation.
3.3. Interpolation and Climate Change Analysis
The geostatistical system used was ordinary cokriging, which showed the best results in terms of error reduction (Table 4).

Table 4.
Comparison between 3 interpolation methods ordinary cokriging (OCK), simple cokriging (SCK) and universal cokriging (UCK), for annual average precipitation 1991–2014.
The ordinary cokriging was used in interpolations with elevation as an independent variable (Table 4), whereas the dependent one was temperature or precipitation [32]. All interpolations were verified through 4 statistical indicators [33], which allowed selection of the correct parameters for the semivariogram setting:
- Root Mean Square Error (RMSE)—the standard deviation between observed and predicted values: this parameter allows an assessment of the prediction errors for different weather stations. The value of RMSE should be the smallest possible and similar to the average standard error (SEM):= measured value at position ;= predicted value at position ;= number of weather stations;= standard deviation of the population.
- Average Standard Error (SEM)—this statistical tool is known from the mean and it is used to estimate the standard deviation of a sampling distribution. A value close to zero and similar to RMSE represents a very low error in the estimation of the variability of the sampling distribution.
- Mean Standardized Error (MSE)—is similar to the mean error and calculates the difference between measured and predicted values; however, MSE values aren’t related to single variables, but it can be used to compare different variables.
- Root Mean Square Standardized Error (RMSSE)—allows assessment of the goodness of prediction models. It is desirable to have a value close to 1. If the value of RMSSE is lower than 1 the variability is overestimated, otherwise it is underestimated. This is a dimensionless statistical tool.
The results of this cross-validation were represented by a table (for example) for each investigated period (1931–1960/1961–1990/1991–2014), in which it is possible to assess the goodness of interpolations for temperatures (maximum, mean, minimum) [34] and precipitation, on a monthly and annual basis.
Table 5 highlights the quality of interpolation, with the statistical indicators always close to the optimum value of the 4 statistical indicators. In fact, the value of the root mean square error standardized is about 1 in all interpolations and the mean standardized error is close to 0. In this way 65 maps were created, in order to observe the distribution of temperature maximum, mean, minimum and of precipitation, in the area of study. The varied climate condition of Macerata Province is shown in Figure 5: there is a decrease of temperature and an increase of precipitation going from east (Adriatic Coast) to west (Appennine Mountains).

Table 5.
Period 1961–1990, statistical indicators for interpolations of maximum, mean and minimum temperatures.
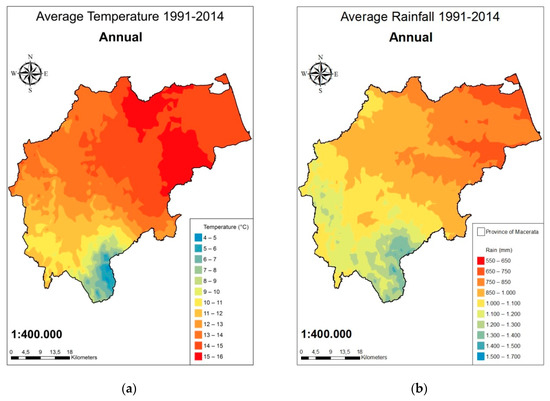
Figure 5.
Meanannual temperature (a) and meanannual precipitation (b) in the period 1991–2014 for Macerata province.
The interpolation maps were averaged with the raster math tool, in order to compare different periods of the same parameter. A positive trend from the past to the present is evident for temperature, and a negative one for precipitation (Figure 6).
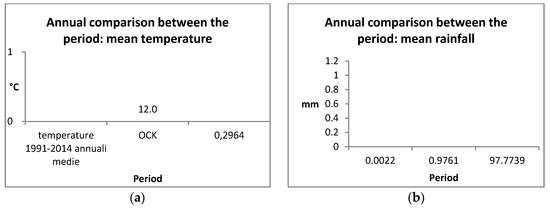
Figure 6.
Interpolation annual mean of the 3 periods (1931–1960/1961–1990/1991–2014) for temperature (a) and precipitation (b).
Finally, the most important part of this research is represented by the comparison between the interpolation maps of 1931–1960 and those of 1991–2014, to assess climate change in the last 60 years. These variation maps (Figure 7) were obtained through the raster math tool, by subtracting to the values of 1991–2014 from those of 1931–1960.
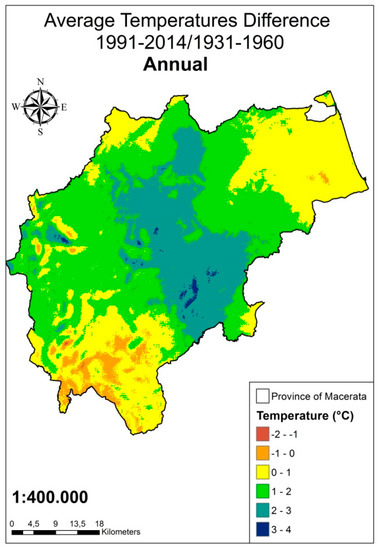
Figure 7.
Variations of mean annual temperature between 1991–2014 and 1931–1960.
The variation map of mean temperature (Figure 7) shows a strong increase in the hilly zone, the central part of the study area, while there is a slight decrease of temperature in the mountainous region (west). For mean annual rainfall, the variation map (Figure 8) highlights a decrease in precipitation over the whole province overall, but with small localized parts in which there is an increase.
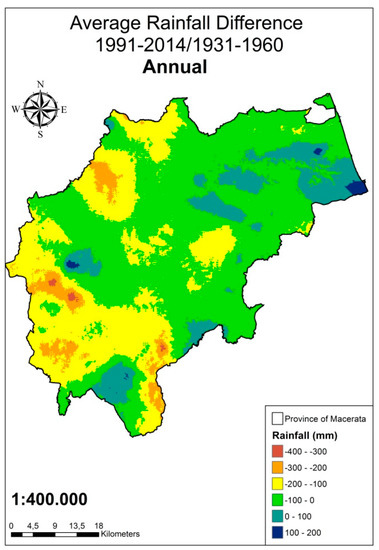
Figure 8.
Variations of mean annual rainfall between 1991–2014 and 1931–1960.
The graphs (Figure 9) records the differences on average in the whole territory between the periods 1991–2014 and 1931–1960; it highlights, for each parameter, a bell-shaped trend strongly increasing in spring and summer months, with a drop during winter and autumn. In February and September, minimum temperatures are in a counter trend because there is no strong temperature increase in these two months.
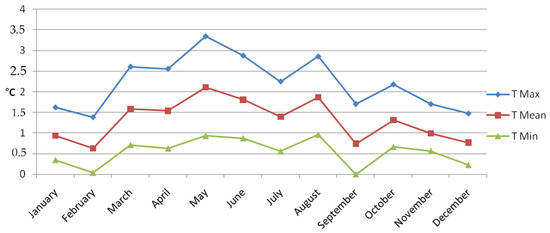
Figure 9.
Monthly temperature variations (maximum, mean and minimum) between the periods 1991–2014 and 1931–1960.
Precipitation has a reverse trend compared with temperatures (Figure 10) in that there is an absence or even an augmentation of precipitation in spring and summer, while the decreasing peak is focused on January, February and October, with significant amount between 25 mm and 35 mm. December is an exception, because it shows the highest augmentation of rainfall (about 15 mm).
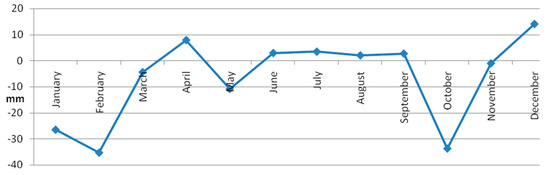
Figure 10.
Trend of monthly variations in precipitation between the periods 1991–2014 and 1931–1960 for precipitations.
4. Discussion
This analysis has achieved some important goals for understanding and mapping the climate of Macerata Province, Italy. Firstly, it has described the conditions of temperature and precipitation of Macerata province in 3 different standard periods 1931–1960, 1961–1990, 1991–2014. The GIS software allowed creation of maps, in order to comprehend the spatial distribution of temperature and precipitation. Furthermore, a strong relationship with altitude has been identified. In fact, there is a differentiation that follows the altitudinal trend quite well, from the coast with high temperature, even if the highest temperatures are located in the hilly belt behind the coast, to the lowest temperatures in the Appennine Mountains (west). For precipitation, the smallest amount occurs on the southern part of the coast, while the highest quantity is in the Appennine Mountains to the south-west.
The second and most important result is represented by the study of climate change, with GIS software in order to assess the variations through algebraic operations between rasters. The differences between the period 1991–2014 and 1931–1960 were investigated in order to assess the climatic change in the last 60 years. Generally, the amount of precipitation from 1931–1960 to 1991–2014 is diminished while the temperature is increased. However, spatially the situation is more complex. In fact, there is a central part of the study area in which temperature increased strongly by 2 to 3 °C, while near the coast and in the mountains the change is about 0–1 °C, with small decreases focused in the Appennine and foothill belt (−1 to 0 °C). For precipitation, the decrease is fairly uniform across the study area (between about 0–200 mm), but with some isolated areas of strong increase (200–300 mm) and only few parts of territory in which there is an increase of 0–200 mm, mainly in the southern part of the coast, to the south-west and inland immediately behind the coast. The monthly temperature trend is characterized by a constant growth, while for precipitation there is a strong decrease in the amount measured in January, February and October (between 25 and 35 mm on average).
This analysis, unlike previous studies, allows consideration of the spatial climate change, which is moderately strong and unequivocal, but with some important counter-trends. It is necessary to specify that the average results are in accordance with what has already been observed by previous scientific researches [35,36,37,38], with an increase of temperatures and a decrease of precipitation. There is also a clear trend towards higher temperatures in the summer season, which is reflected in Europe [39]. Atmospheric circulation seems to play a major role in climate change in this area. Studies have shown that there is an increase in anticyclones in this area and an increase in atmospheric pressures in winter [40,41]. Even if it is possible to detect areas in countertrend using the raster analysis, it would be interesting to study any correlation between the different areas within the province and atmospheric circulation, in order to evaluate the differences with the surrounding areas. Furthermore, to improve analysis, it would be desirable to install more reliable weather stations, especially in the Appennine area (as this region is under sampled).
5. Conclusions
The present research has obtained remarkable results for the area in question, which can be summarized as follows:
- Homogenization and validation of about 80 years of climatic data relating to precipitations and temperatures, applying a new method [8].
- Identification of altitude as the geotopographic variable most closely related to temperature and precipitation.
- Interpolation of temperature and precipitation data for the province of Macerata with geostatistical techniques.
- Assessment of space and the average climate change between the standard periods 1931–1960 and 1991–2014.
Author Contributions
M.G., M.B., P.B. analyzed data; M.G. software GIS; M.G., M.B., P.B. wrote the paper; M.G. Methodology, P.B. checked language.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Köppen, W.; Geiger, R. Klima der Erde (Climate of the Earth); Wall Map 1:16 Mill; Klett-Perthes: Gotha, Germany, 1954. [Google Scholar]
- Amici, M.; Spina, R. Campo medio dellaprecipitazioneannuale e stagionalesulle Marche per ilperiodo 1950–2000; Centro di Ecologia e Climatologia-Osservatorio Geofisico Sperimentale: Macerata, IT, USA, 2002. [Google Scholar]
- World Meteorological Organization (WMO). Handbook on Climat and Climat Temp Reporting; WMO/TD No. 1188; WHO: Geneva, Switzerland, 2009. [Google Scholar]
- Sangelantoni, L.; Coluccelli, A.; Russo, A. EGU General Assembly Conference Abstracts; Publons: Wien, Germany, 2014. [Google Scholar]
- Soldini, L.; Darvini, G. Extreme rainfall statistics in the Marche region, Italy. Hydrol. Res. 2017, 48, 686–700. [Google Scholar] [CrossRef]
- Karl, T.R.; Nicholls, N.; Ghazi, A. CLIVAR/GCOS/WMO workshop on indices and indicators for climate extremes: Workshop summary. Clim. Chang. 1999, 42, 3–7. [Google Scholar] [CrossRef]
- Peterson, T.C.; Folland, C.; Gruza, G.; Hogg, W.; Mokssit, A.; Plummer, N. Report on the Activities of the Working Group on Climate Change Detection and Related Rapporteurs 1998–2001; WMO: Geneve, Switzerland, 2001; 143p. [Google Scholar]
- Zhang, X.; Hegerl, G.; Zwiers, F.W.; Kenyon, J. Avoiding Inhomogeneity in Percentile-Based Indices of Temperature Extremes. J. Clim. 2005, 18, 1641–1651. [Google Scholar] [CrossRef]
- Appiotti, F.; Krželj, M.; Russo, A.; Ferretti, M.; Bastianini, M.; Marincioni, F.A. multidisciplinary study on the effects of climate change in the northern Adriatic Sea and the Marche region (Central Italy). Reg. Environ. Chang. 2014, 14, 2007–2024. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Saz-Sánchez, M.A.; Cuadrat, J.M. Comparative analysis of interpolation methods in the middle Ebro Valley (Spain): application to annual precipitation and temperature. Clim. Res. 2003, 24, 161–180. [Google Scholar] [CrossRef]
- Price, D.T.; McKenney, D.W.; Nalder, I.A.; Hutchinson, M.F.; Kesteven, J.L. A comparison of two statistical methods for spatial interpolation of Canadian monthly mean climate data. Agric. For. Meteorol. 2000, 101, 81–94. [Google Scholar] [CrossRef]
- Crespi, A.; Brunetti, M.; Lentini, G.; Maugeri, M. 1961–1990 high-resolution monthly precipitation climatologies for Italy. Int. J. Climatol. 2018, 38, 878–895. [Google Scholar] [CrossRef]
- Ninyerola, M.; Pons, X.; Roure, J.M. A methodological approach of climatological modelling of air temperature and precipitation through GIS techniques. Int. J. Climatol. 2000, 20, 1823–1841. [Google Scholar] [CrossRef]
- Brunetti, M.; Buffoni, L.; Mangianti, F.; Maugeri, M.; Nanni, T. Temperature, precipitation and extreme events during the last century in Italy. Glob. Planet. Chang. 2004, 40, 141–149. [Google Scholar] [CrossRef]
- Begert, M.; Schlegel, T.; Kirchhofer, W. Homogeneous temperature and precipitation series of Switzerland from 1864 to 2000. Int. J. Climatol. 2005, 25, 65–80. [Google Scholar] [CrossRef]
- Rahman, M.R.; Lateh, H. Climate change in Bangladesh: A spatio-temporal analysis and simulation of recent temperature and rainfall data using GIS and time series analysis model. Theor. Appl. Climatol. 2017, 128, 27–41. [Google Scholar] [CrossRef]
- Amin, A.; Nasim, W.; Mubeen, M.; Sarwar, S.; Urich, P.; Ahmad, A.; Rehmani, M.I.A. Regional climate assessment of precipitation and temperature in Southern Punjab (Pakistan) using SimCLIM climate model for different temporal scales. Theor. Appl. Climatol. 2018, 131, 121–131. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.; Ma, X. Spatio-temporal temperature variations in the Chinese Yellow River basin from 1981 to 2013. Weather 2018, 73, 27–33. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Guidelines on Quality Control Procedures for Data from Automatic Weather Stations; CBS/OPAG-IOS/ET AWS-3/Doc. 4, 2; WMO: Geneva, Switzerland, 2004. [Google Scholar]
- Gentilucci, M.; Barbieri, M.; Burt, P.; D’Aprile, F. Preliminary Data Validation and Reconstruction of Temperature and Precipitation in Central Italy. Geosciences 2018, 8, 202. [Google Scholar] [CrossRef]
- Grykałowska, A.; Kowal, A.; Szmyrka-Grzebyk, A. The basics of calibration procedure and estimation of uncertainty budget for meteorological temperature sensors. Meteorol. Appl. 2015, 22, 867–872. [Google Scholar] [CrossRef]
- Omar, M.H. Statistical Process Control Charts for Measuring and Monitoring Temporal Consistency of Ratings. J. Educ. Meas. 2010, 47, 18–35. [Google Scholar] [CrossRef]
- Gentilucci, M.; Bisci, C.; Burt, P.; Fazzini, M.; Vaccaro, C. Interpolation of Rainfall through Polynomial Regression in the Marche Region (Central Italy). In Lecture Notes in Geoinformation and Cartography; Mansourian, A., Pilesjö, P., Harrie, L., van Lammeren, R., Eds.; Springer: Cham, Switzerland, 2018; pp. 55–73. [Google Scholar]
- Alexanderson, H.A. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Wang, X.L.; Wen, Q.H.; Wu, Y. Penalized maximal t test for detecting undocumented mean change in climate data series. J. Appl. Meteorol. Climatol. 2007, 46, 916–931. [Google Scholar] [CrossRef]
- Liu, X.; Hu, H.; Hu, P. Accuracy assessment of lidar-derived digital elevation models based on approximation theory. Remote Sens. 2015, 7, 7062–7079. [Google Scholar] [CrossRef]
- Diodato, N. The influence of topographic variables on the spatial variability of precipitation over small regions of complex terrain. Int. J. Climatol. 2005, 25, 351–363. [Google Scholar] [CrossRef]
- Witt, G. Using Data from Climate Science to Teach Introductory Statistics. J. Stat. Educ. 2013, 21, 1. [Google Scholar] [CrossRef]
- Goovaerts, P. Ordinary Cokriging Revisited. Math. Geol. 1998, 30, 21–42. [Google Scholar] [CrossRef]
- Helterbrand, J.D.; Cressie, N. Universal cokriging under intrinsic coregionalization. Math. Geol. 1994, 26, 205. [Google Scholar] [CrossRef]
- Newlands, N.K.; Davidson, A.; Howard, A.; Hill, H. Validation and inter-comparison of three methodologies for interpolating daily precipitation and temperature across Canada. Environmetrics 2011, 22, 205–223. [Google Scholar] [CrossRef]
- Krivoruchko, K. Empirical Bayesian Kriging; Esri: Redlands, CA, USA, 2012. [Google Scholar]
- Johnston, K.; Ver Hoef, J.M.; Krivoruchko, K.; Lucas, N. Using ArcGIS Geostatistical Analyst, 380; Esri: Redlands, CA, USA, 2001. [Google Scholar]
- Ishida, T.; Kawashima, S. Use cokriging to estimate surface air temperature from elevation. Theor. Appl. Climatol. 1993, 47, 147–157. [Google Scholar] [CrossRef]
- Polemio, M.; Casarano, D. Climate change, drought and groundwater availability in southern Italy. Geol. Soc. Lond. Spec. Publ. 2008, 288, 39–51. [Google Scholar] [CrossRef]
- Coppola, E.; Giorgi, F. An assessment of temperature and precipitation change projections over Italy from recent global and regional climate model simulations. Int. J. Climatol. 2010, 30, 11–32. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Monti, F.; Nanni, T. Temperature and precipitation variability in Italy in the last two centuries from homogenised instrumental time series. Int. J. Climatol. 2006, 26, 345–381. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Können, G.P. Trends in indices of daily temperature and precipitation extremes in Europe, 1946–99. J. Clim. 2003, 16, 3665–3680. [Google Scholar] [CrossRef]
- Schär, C.; Vidale, P.L.; Lüthi, D.; Frei, C.; Häberli, C.; Liniger, M.A.; Appenzeller, C. The role of increasing temperature variability in European summer heatwaves. Nature 2004, 427, 332. [Google Scholar] [CrossRef] [PubMed]
- Brunetti, M.; Maugeri, M.; Nanni, T. Atmospheric circulation and precipitation in Italy for the last 50 years. Int. J. Climatol. 2002, 22, 1455–1471. [Google Scholar] [CrossRef]
- Ventura, F.; Pisa, P.R.; Ardizzoni, E. Temperature and precipitation trends in Bologna (Italy) from 1952 to 1999. Atmos. Res. 2002, 61, 203–214. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).