Abstract
Oxidation ditches are popularly used in rural areas and decentralized treatment facilities where energy deficiency is of concern. Aeration control technologies are well established for diffusion systems in order to improve energy efficiency, but there are still challenges in their application in oxidation ditches because surface aerators have unique characteristics with respect to oxygen transfer and energy consumption. In this paper, an integral energy model was proposed to include the energy, aeration, and fluidic effects of surface aerators, by which the energy for aeration of each aerator can be estimated using online data. Two types of rotating disks with different diameters (1800 mm and 1400 mm) were monitored in situ to estimate the model parameters. Furthermore, a feedforward–feedback loop control strategy was proposed using the concept of energy analysis and optimization. The simplified control system was implemented in a full-scale Orbal oxidation ditch, achieving an approximately 10% saving in full-process energy consumption. The cost–benefit analysis and carbon emission assessment confirmed the economic feasibility and environmental contribution of the control system. The energy model can help process designers and operators to better understand and optimally control the aeration process in oxidation ditches.
1. Introduction
The energy performance in wastewater treatment plants (WWTPs) is generally sub-optimal in most countries [1], although the optimal water–energy nexus has been intensively studied in sustainable development [2]. The energy intensity of wastewater facilities increases along with the aging infrastructures in conventional technologies, resulting in concerns with respect to energy deficiency and intensive carbon emissions [3]. For example, as one of the oldest wastewater treatment processes, the oxidation ditch is still used in about 30% of running wastewater facilities in China, especially in rural areas and decentralized stations [4]. The typical energy consumption of an oxidation ditch is close to 0.40 kWh·m−3, which is around 33% higher than for activated sludge processes [4,5]. High energy intensity and poor maintenance prevent such processes from application in energy neutral initiatives, e.g., next-generation urban water systems in China [6]. Thus, energy-saving techniques and processes are necessary to upgrade WWTPs for a sustainable society.
Aeration energy usually occupies half of the total energy consumption in WWTPs, for which optimization is important in order to reduce the carbon footprint of the process. The techniques of instrumentation, control, and automation have been developed for smart aeration control in WWTPs since the 1970s [7,8]. In diffusive aeration systems, the dissolved oxygen (DO) in bulk solution and the oxygen transfer coefficient (KLa) of diffusers are used to compile the DO-KLa feedback control loop for minimizing aeration energy [7]. Commercial process simulators are usually used to assist the design and optimization of aeration control, and accurate aeration models of diffusive aeration system are also available for engineers [9]. Diffusive aeration control can achieve energy savings ranging from 10% to 25% of total energy [10,11,12,13].
On using the DO control method from diffusion systems, much effort has been directed at optimizing the aeration of oxidation ditches [14,15,16,17,18]. However, the surface aeration is different from the diffusive aeration system. First, the aeration and fluidic motion are strongly coupled by the movement of bubbles [19]. The flow rate, KLa, and tank volume are together necessary to describe the aeration performance [20]. Second, aeration is only supplied at the position of the surface aerator, resulting in discrete DO transfer events along the process. For example, in Orbal oxidation ditches the presence of a number of DO probes right after the aerators is necessary to capture the spatial DO profile [21]. Thus, a proper control variable is necessary instead of DO for aeration control in such reactors.
The surface aerators supply aeration and fluidic motion. If the aeration energy can be calculated from the total energy consumption monitored by online electric meters, it can be used as a control variable instead of the DO to describe the aeration intensity in the control loop. Thus, the challenge of surface aeration control is transformed into the question of how to calculate the aeration energy online and how to establish the control system for it. In this study, we proposed an energy consumption model and demonstrated how to derive the aeration energy from the online process data. Moreover, we integrated the energy description into a feedforward–feedback control strategy. A case study was provided to simplify and implement the control system in a full-scale Orbal oxidation ditch, which achieved an energy saving of about 10%.
2. Materials and Methods
2.1. Description of the Orbal Oxidation Ditch
The Orbal oxidation ditch shown in Figure 1 was selected for the field study. The oxidation ditch has the capacity of 50,000 cubic meter per day (m3·d−1) and is located in Wuxi City in southern China. There are three concentric circling lanes in the oxidation ditch, including outer lane (OL), middle lane (ML), and inner lane (IL), as shown in Figure 1a. The wastewater flows into OL to mix with return sludge, and passes through the ML, IL, and clarifier in consequence (Figure 1b).
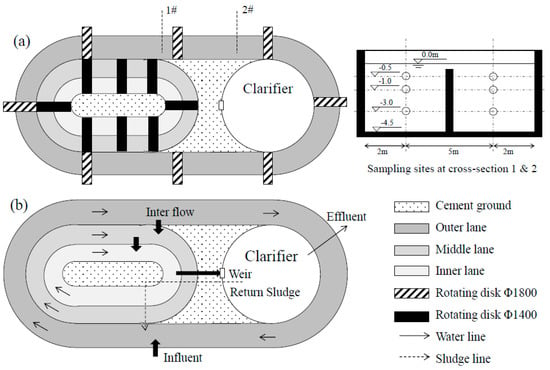
Figure 1.
Scheme of an Orbal oxidation ditch and sampling sites. (a) Rotating disks on the oxidation ditch and the sampling sites at the cross-section; (b) Fluidic directions between the reactors.
There are eight rotating disks in OL, with a diameter of 1800 mm (Φ1800). The ML and IL share other eight rotating disks with a smaller diameter of 1400 mm (Φ1400) in Figure 1a. The OL contains oxic and anoxic zones, while ML and IL are almost oxic due to the rapid mixing. Methanol is dosed in the outer lane before cross section #1 to assist in the microbial denitrification. Poly alumina ferrous salt is added at the effluent weir before the clarifier to enhance the chemical removal of phosphorous.
2.2. Energy Consumption Model of a Single Surface Aerator
The effective energy consumption (Ee) of surface aerators consists of aeration energy (Ea) and motion energy (Em). The aeration energy is consumed to disperse the air bubbles into the liquid, in order to drive oxygen molecules from the gas phase to the liquid [22]. The dissipation energy of air in the water thus can be assumed proportional to the total mass of oxygen transferred into the water. The motion energy is consumed to drive the water in continuous fluid, which stands alone from the gas dispersion. The motion energy can be assumed equal to the pressure loss of the fluid, which is proportional to the square of fluid velocity (v2). Thus, we have the energy model as follows:
where R is the oxygen transfer rate (OTR) in g·s−1, t is the time in s, ae is the constant energy for transferring 1 g of oxygen in J·g−1, v is the fluid velocity in m·s−1; and ξ is the gross coefficient of pressure loss in dimensionless unit.
Ea = ∫(ae·R)dt ≈ ae·R·Δt
Em = ∫(ξ·v2)dt ≈ ξ·v2·Δt
For a single aerator, such as a rotating disk, the operation variables include rotating frequency (ω) and wet depth of the rotators (h). The wet depth represents the height of the rotator beneath the water level. Usually, ω and h are continuously varied in operation [23]. In an actual reactor, the ascending ω or h of rotators will increase the fluidic velocity to a maximum until the equipment capacity reaches its limits, as qualitatively shown by the convex curve in Figure 2a. The trend can be explained by different models. For convenience, we used Monod equation to describe the saturation relationship as follows:
where vs is the fluidic velocity driven by the single aerator in m·s−1; ω is rotating frequency in s−1; h is wet depth in m; vm is the maximum fluidic velocity equal to the averaged linear velocity of the rotating aerator in m·s−1; Kh and Kω are constants.
vs = vm·h/(Kh + h)·ω/(Kω+ ω)
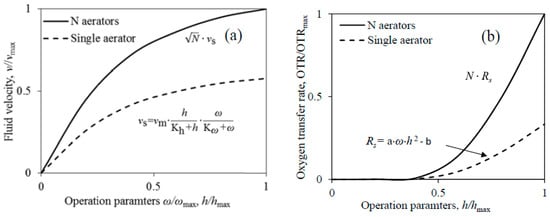
Figure 2.
The concept of the multiple surface aerators. (a) Model of fluid velocity; (b) Model of oxygen transfer rate (OTR). vmax and hmax are the observed maximal fluid velocity and wet depth for normalization, respectively. N is the number of rotators. vs and vm are the actual and maximal fluid velocity by a single aerator, respectively. Rs is the OTR of single aerator. ω is the rotating frequency and h is the wet depth of aerator. Kh, Kω, a and b are constants.
The OTR of a surface aerator depends on the wet area and its refreshing frequency. It is well known that the gas holdup greatly affects the surface aeration performance [24]. The wet area determines the quantity of air bubbles to be dragged into the water in each roll, which can be expressed by h2. The refreshing frequency of the wet area can be described as ω. Thus, we can correlate the OTR of single rotator (Rs) with operational variables as follows:
where Rs is the OTR of a single aerator in g·s−1, a is the coefficient in g·m−2, and b is the interception to represent the minimum of ω and h required for aeration, in g·s−1. When the linear speed of aerator is lower than the fluid velocity or the wet depth is too small, the OTR will drop to zero because the capacity of the rotators for carrying air bubbles into the water is destroyed under the extreme conditions.
Rs = a·ω·h2 − b
2.3. Energy Consumption Model of Multiple Surface Aerators
In multiple-running mode of surface aerators, all aerators share the total aeration energy and motion energy. If the N pieces of surface aerators in same type are under operation, their aeration and motion energy are N times the value for a single aerator. Because the motion energy is determined by v2, the fluidic velocity of N aerators is times of the fluidic velocity by a single aerator, as shown in Figure 2a. Considering that the aeration energy is proportional to the OTR, the OTR of N aerators is just N times the Rs of a single aerator (Figure 2b). We can describe the performance of a group of aerators as follows:
where N is the running number of multiple aerators; and v(N) and R(N) are the fluidic velocity and OTR by N pieces of aerators, respectively.
Ee(N) = N·Ee= N·(Ea + Em)
R(N) = N·Rs
2.4. Online Estimation of In Situ OTR
In order to estimate the actual OTR in the activated sludge process, we used a simple mass balance model modified from the literature [25]. Using the spatial DO distribution (Figure S1) and the monitored in situ oxygen uptake rate (OUR), we calculated the actual OTR (Rs) as follows:
where OUR is the oxygen uptake rate of activated sludge in g·m−3·s−1; DO1 and DO2 are the DO concentrations at two cross-sections in g·m−3; AV is the area of cross-section in m2; and L12 is the distance between the two cross-sections in m. As shown in Figure 1a, cross-section 1# was about 5 m away before the rotating disk to avoid the interference of the back fluid. Cross-section 2# was selected after the rotating disk ensuring that the DO2 did not drop to zero.
Rs = OUR·(AV·L12) + v·AV·(DO1 − DO2)
2.5. Process Monitoring of OUR, DO, Velocity, and Shaft Power
The OUR of activated sludge was measured by the standard method using a DO probe and magnetic stirrer [26]. Briefly, after intensive aeration to increase DO over 4 mg·L−1, the activated sludge was moved into a glass bottle and mixed by a magnetic stirrer. The DO concentrations along the time were recorded by a portable DO probe and the descendant slope of the DO by time was used to determine the OUR. The robustness of OUR monitoring to estimate KLa has been proved in lab reactors in previous studies [27]. Although the OUR can be calculated by the DO profile in the model case [28] or in a pilot plant [29], in practice the DO slope is sensitive to the uneven spatial distribution velocity in the reactor. Therefore, using standard tests to determine in situ OUR was recommended for OTR estimation instead of using DO profiles along the reactor.
In order to compensate the layered fluid in Orbal circulating reactor [30], six sampling points were set at each cross-section (Figure 1a) to average the values of DO detected by a portable DO meter, as well as the fluidic velocity monitored by a droplet flow meter (LSH10-1, Boyida Company, Xiamen, China). The horizontal values were firstly averaged algorithmically, and the vertical positions were then averaged geometrically to be the representative observation for the cross section.
The electric voltage and current of each aerator was recorded to calculate the shaft power p by p = U·I·cosφ, where U is equivalent electric voltage in unit V; I is the recorded current in unit A; and cosφ is the phase coefficient of electricity, which is usually higher than 93%. The electric voltage is usually constant and thus the power is proportional to the electric current.
2.6. Experiments for Model Marameter Estimation
The online observations of X and P, including OTR, velocity, and shaft power, are necessary to determine the coefficients. A matrix equation is used to describe the system state as A·X = P, where A is the coefficient matrix by combining vector (ae,i, ξi) for the ith experiment; X is the state variable vector (OTR; v2); and p is the vector of shaft power of surface aerators as (p1; p2; …; pi), with power:
p = Ee/Δt = (Ea + Em)/Δt
A series of aeration experiments are necessary to estimate the parameters in Equations (1)–(4). For example, the effluent weir openness is changed to acquire different wet depths [31], and the bulk DO, OTR, velocity, and electricity are monitored to determine the parameters. The wet depth was calculated by the axis position of the aerator and the water level from an ultrasonic water level meter (FMU30, Endress+Hauser Company, Lörrach, Germany).
2.7. Optimizing Algorithm for Process Control
The control algorithm for the oxidation ditch is to minimize the bias between the aeration energy and to ensure the aeration is enough to make effluent water quality fall below the discharge criteria. The objective function Z is as follows:
where Ea,d and Ea,t are demanded and actual aeration energy at time t respectively in unit J s−1; Q is flow rate in unit m3 s−1; Cin is the concentration of influent pollutant (usually ammonia) in unit g m−3; Cout is the effluent concentration that should be lower than discharge criteria (Cstd) in unit g m−3; f is the function of feedforward compensation by influent flowrate and ammonia, PI is the function of feedback control loop based on the effluent ammonia or carbon, and g is the function derived from the energy consumption model of N pieces of surface aerators.
Z = min{|Ea,d − Ea,t|}
In practice, the wet depth of surface aerator varies in a very limited range (h = 0.6–0.8 radium), and thus the energy consumption model can be simplified in linear form. With this convenience, the indirect expression in Equation (6) could be replaced by the linear increment of the influent loading rates and the operational parameters as follows.
where Ka and Kb are the correlation coefficient in J·g−1; ΔQ is the variation of influent flow rate in m3·s−1; Cin is the concentration of influent pollutant in g·m−3; Kc and Kd are the coefficients to correlate the manipulation variables of ω and h to the aeration energy of a single aerator; Ea,s is the aeration energy of a single aerator in J·m−3; Ea,d, Ea,t, and the other variables are same as in Equation (6).
ΔEa,d = Ka·Δ(Cin·Q) + Kb·Δ[(Cout − Cstd)·Q]
ΔEa,t = Σn(Kc·Δω + Kd·Δh) + ΔN·Ea,s
2.8. Feedforward Control Strategies and Implementation
The feedforward–feedback control system is proposed in Figure 3. The influent feedforward compensation function f, feedback control function PI, and energy model function g are same as in Equation (6). The manipulation variables, including h, ω, and N, are optimized by the linearized model, and are controlled by the effluent weir motor, varied frequency driver, and power switches, respectively.
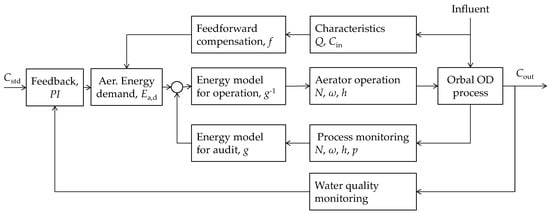
Figure 3.
The feedforward control strategy basing on aeration energy to manipulate surface aerators in the Orbal oxidation ditch (OD). The parameters are same as those in Equation (6). Cout is actual ammonia concentration in effluent and Cstd is the set point of ammonia as the discharged criteria. PI is proportional and integral algorithm. f and g are model functions. N, ω, h and p are model variables. Q is influent flow rate and Cin is influent ammonia concentration.
The control system was simplified and implemented in the full-scale Orbal oxidation ditch. Because the frequency of the rotating disks was not tunable and fixed at two levels of 60 and 45 rpm, the frequency ω was viewed as a constant in the model. Therefore, the energy consumption model was simplified to depend linearly on wet depth h and number N only. The dual manipulation variables follow a simple preset logic: firstly, the effluent weir was changed, and if the weir openness was operated at its high or low limit, the number N of aerators was adjusted to rapidly restore the aeration energy in the proper range.
In the real-time control system, the output of feedback PI in Equation (7) was ignored due to the much lower effluent ammonia (Cout < 1 mg L−1) than the discharge criteria (Cstd = 5 mg L−1). Thus, only feedforward compensation remains to determine the demanded aeration energy to deal with the fluctuated influent loading as Cin·Q, which might be affected by peak loading, storm event, and unit malfunction, etc. Under extreme conditions, manual setting the wet depth h and number N was available when instant operation was required. For example, the control system may result in the upper limit of effluent weir for high peak loading and lower limit for the storm water influent.
In late 2015, such a simplified control system was implemented in a full-scale oxidation ditch. The bulk ammonia concentrations along the reactor were monitored by lab analysis using a standard method (Figure S2). Electricity consumption of the full process was audited to evaluate the energy savings by the control system. Simple economic analysis was achieved by calculating the return period on investment for the scenario of process retrofitting on the control system. The prices of hardware, software, and system implementation were determined by suggestions from experienced engineers, as shown in Table S2. The commercial electricity rates usually depend on the time and locations. For convenience, we used 0.8 RMB Yuan·kWh−1 (1 US $ ≈ 6.5 RMB Yuan) as the typical average value [32]. The environmental impact of the process retrofitting was represented by the reduction of CO2 emissions due to the energy saving. The CO2 emission factors by power generation also vary in a large range from 0 to 1.3 kgCO2·kWh−1 [33]. The midpoint of the range, 0.65 kgCO2·kWh−1, was used for estimation in this study. The working duration was assumed as 350 days per year.
3. Results
3.1. Fluid Velocity Analysis
Figure 4 shows the monitored and modeled fluid velocity for the Φ1400 mm and Φ1800 mm aerators. The fluidic velocity by a single aerator was estimated by the performance model (solid line in Figure 4a,b). The maximum velocity of the Φ1400 mm aerator was 0.28 m·s−1, equal to 25% of the linear speed of rotating disks (1.1 m·s−1). That in the Φ1800 mm aerator was 0.63 m·s−1, about 45% of the linear speed of rotating disks (1.4 m·s−1). The geometrically averaged fluid velocity (diamond dots) showed good fitting with model predictions for the OL, ML, and IL. However, the fluid velocity appeared in strong variance (solid circle dots in Figure 4b), with relative standard deviation as about 20% in the OL. The large distribution of velocity was also found by computational fluidic dynamics (CFD) simulation in the literature [30].
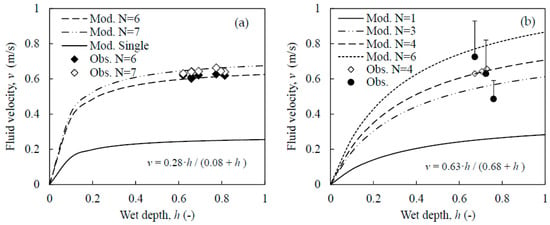
Figure 4.
The observation and modeling of fluid velocities. (a) Φ1400 mm disks in the ML and IL (the running numbers N are 7 and 6 in the ML and IL, respectively); (b) Φ1800 mm disks in the OL—N varies from 3 to 6, and the error bar represents the standard deviation (n = 6). Rotating frequency ω is 60 rpm. Dots are observation data, lines are modeling results. Mod and Obs refer to modeling and observation, respectively. IL, ML, and OL are abbreviations of the inner, middle and outer lane, respectively.
The multiple running model is helpful for process design. If the minimum fluid velocity is set to be 0.40 m·s−1 in ML, at least three aerators should be operated and the velocity is predicted to be 0.42 m·s−1. Two aerators were necessary in OL to achieve the similar fluid velocity.
3.2. Oxygen Transfer Rate Analysis
Figure 5 shows the correlation between OTR and wet depth for each type of aerators. At the same wet depth at 0.7, OTR values were about 60, 20, and 10 g·s−1 in the OL, ML, and IL, respectively. The different OTRs might be caused by three factors. The first is disk size. The wet area of the Φ1800 mm disk in OL is (0.9/0.7)2 ≈ 2 times the area of Φ1400 mm disk in the ML and IL, which contributed to the higher OTR. The second factor is the disk number in a single aerator. Aerators in ML are in the same size as that in the IL but the OTR in the ML is higher. The disk number was 40 pieces for a single aerator in ML but only 32 pieces in IL. The aeration capacity of the aerator is the sum of every single disk when ignoring the interaction between the disks. The third factor is bulk DO concentration. Higher bulk DO will decrease the OTR by reducing the driving forces across the gas–liquid dual film. The averaged bulk DO concentrations were 0.5, 1.0, and 2.0 mg·L−1 in the OL, ML, and IL, respectively. The higher bulk DO in ML and IL contributed to the lower OTR values.
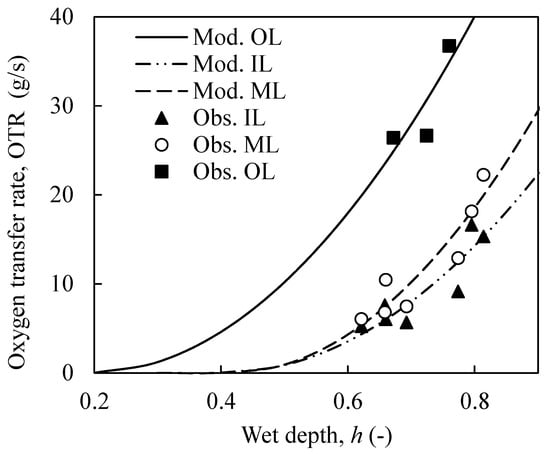
Figure 5.
The relationship between the OTR and wet depth of rotating disks. Dots are acquired by observation, and lines are modeling calculation. Mod and Obs refer to modeling and observation, respectively. IL, ML, and OL are abbreviations of inner, middle and outer lanes, respectively.
The zero point of OTR curves in horizontal coordinate axis indicates the scenario that only impelling effects existed by the aerators. OTR curves of aerators in ML and IL shared a common zero point because the size of their aerators was same at 1400 mm. The wet depth was approximately 0.19 for the zero OTR of aerators in OL, less than that in ML and IL (0.40–0.41), indicating higher aeration capacity in the larger sized aerators.
3.3. Energy Consumption Analysis
Figure 6a–c shows the dependence of aeration and motion energy on the wet depth of a single aerator in the OL, ML, and IL, respectively. Equation (5) was used to decompose the gross variables in the observation. The ratio of aeration energy over total energy was once assumed as a constant for certain surface aerators, which was actually determined by both aerator features (e.g., diameter) and the process operation (e.g., h). At the wet depth at 0.7, the aeration energy in OL was 41% of the total energy consumption, while those in the ML and IL were only 14% and 7.6%, respectively. The gas dissipation power by a Rushton turbine in a lab tank was estimated to be 35–44% by CFD calculation [22], which could be a reference to the analysis.
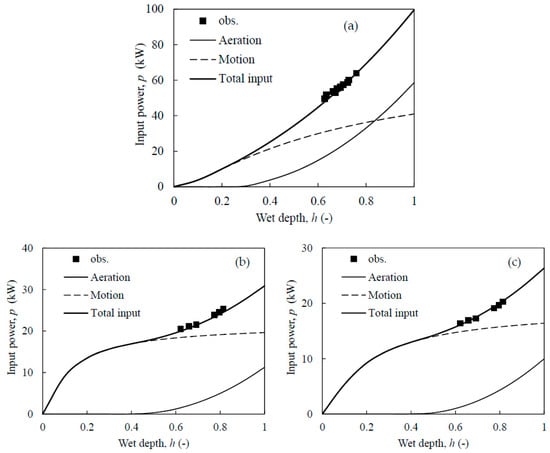
Figure 6.
The dependence of input total power p on wet depth h in highest rotating frequency ω at 60 rpm. (a) Φ1800 mm aerators in the OL; (b) Φ1400 mm aerators in the ML; and (c) Φ1400 mm aerators in the IL. Obs is observed data. Solid and dash lines represent aeration energy and motion energy. Bold solid line represents total input power.
The estimated parameters in the energy model are shown in Table S1. The aeration coefficients (ae) of aerators were 0.83, 0.35, and 0.27 in the OL, ML, and IL respectively, implying obvious geometric effects from the diameter of the aerators. The motion coefficients (ξ) were estimated to be 330, 320, and 240, and were affected by the geometric features of the tanks, e.g., length and width of the reactor. The widths of the cross sections in the OL and ML are 12.2 m and the width in the IL is 8.2 m.
3.4. Control System and Performance
The performance of the full-scale control system is shown in Figure 7. With the control system running, the group of running aerators was fixed and the water level varied timely to keep the total electric current at 160 A for the aerators in the OL (Figure 7a,b). The effluent ammonia was lower than 0.5 mg·L−1. In the case without control, the effluent weir was fixed and the group of aerators was modified manually (Figure 7c,d). The total electric current varied in a range from 400 to 600 A, with an average at about 500 A. The data reflected the experience and decisions from the different operators.
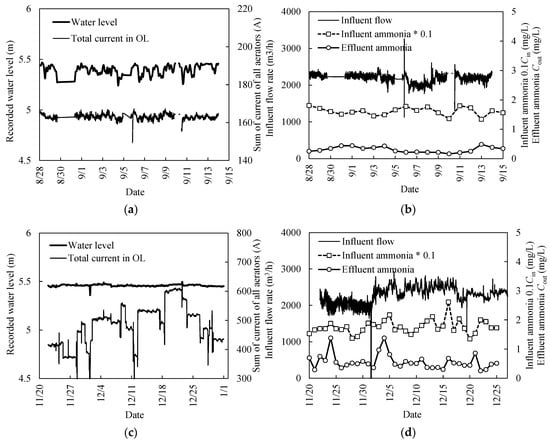
Figure 7.
Process performances and electricity consumption with and without aeration control in the Orbal oxidation ditch in 2015. (a) water level and electricity current with control, and over the period the running numbers of rotators are fixed at constant; (b) influent flowrates, influent and effluent ammonia concentrations with control; (c) water level and electricity current without control, and over the period the running numbers of rotators are modified manually; (d) influent flowrates, influent and effluent ammonia concentrations without control. Curves of influent ammonia concentrations are zoomed in ten times for better vision.
According to Figure 7, manipulating the running number N has larger effects on the total energy consumption than wet depth h, which could also be induced from the curve shapes in Figure 6. Moreover, in Figure 7b there is no adverse effect on effluent ammonia by the very low aeration in OL, where shaft power is only one-third of the uncontrolled state. The reason is partially due to the overaeration in the ML and OL, where aerators are operated in full number. As for the performance of the full process, the total energy consumption from July to December 2015 was audited to be 0.358 kWh·m−3, about 10% lower than without control (0.398 kWh·m−3).
The total investment of the control system and its operational cost are estimated in Tables S2 and S3, respectively, including the system component, construction, instruments, and maintenance. The total investment was 560,000 RMB Yuan and the cost-saving balance was 350,000 RMB Yuan per year for the process with capacity of 50,000 m3·d−1. Thus, the return period of investment was calculated to be 1.6 years. The CO2 emissions taking into account the energy savings were reduced by 455 tons CO2 yearly for this case. Considering both the economic efficiency and the environmental contribution, such a control system is worthy of implementation for better operation and sustainability.
4. Discussion
4.1. Application of the Energy Consumption Model
Theoretically, dissolving oxygen from gas into water is a spontaneous process due to the higher entropy of oxygen in the water. In the same environmental conditions, the OTR per surface area is constant and the absolute OTR is governed by the total surface area [25,34]. When more aeration intensity is demanded, more surface area is created by the aerators to meet the requirement of total OTR. These facts support the assumption that the aeration energy is directly correlated with OTR. According to the energy conservation law, the aeration energy is transferred to the surface tension potential of the air bubbles in water to sustain the dispersion state. Thus, the aeration energy can and should be separated from the total energy consumption.
Decoupling the aeration from the fluidic motion is still a challenge for the optimal aeration [35]. The balance between aeration demand and fluidic velocity often fails in practice, resulting in excessive demand of aeration or motion in oxidation ditches. As shown in Figure 4, only three aerators in the ML were necessary to maintain satisfactory mixing with the fluidic velocity higher than 0.4 m·s−1. However, more aerators were demanded for aeration because only 14% of the total energy input was used for aeration in the ML (Figure 6). A detailed understanding of the dynamic features of rotating disks is helpful for engineers to design aeration systems with balanced aeration and motion.
The model and analysis of rotating disks is provided as an example of surface aerators in this study. However, such a concept is also feasible to estimate other surface aerators, such as inverted umbrellas and rotating brushes. Taking the inverted umbrella as example, the wet area is the function of h3 and thus the dependence of aeration energy on wet depth can be derived by the same method, but the formulas will be different from those of the horizontal rotating disks which wet area is the function of h2. The model of rotating brushes is same as that of rotating disks due to their similar geometric properties. Moreover, the principle is also capable of describing the diffusion system, such as microbubble diffusers and membrane aerators. For example, in membrane aeration reactors, the membrane module was used for diffusing oxygen and carrying biofilm simultaneously [36,37]. The wet area in the reactor is equal to the surface areas of the static membrane modules. Thus, the aeration energy is minimized because no extra energy is necessary to maintain the dispersion of the air bubble into the water.
4.2. Benefits of Actual OTR Estimation
The oxygen transfer efficiency (OTE) was estimated by dividing the OTR over the shaft power, which represents the efficiency of the aeration. The OTE for the Φ1800 mm rotating disks varied in the range of 1.6–2.1 kgO2·kWh−1 along the wet depth, with an average of 1.83 kgO2·kWh−1. The average OTEs for the Φ1400 mm rotating disks in the ML and IL were 1.86 and 1.82 kgO2·kWh−1, respectively. However, according to the manufacturers, the OTE value of the rotating disks in clean water is 2.86 kgO2·kWh−1. That means the OTE in actual operation was only about 60% of that in clean water for the rotating disks. This ratio is close to the 66% OTE reduction for diffusion systems in the literature [38]. Due to such a reduction, the aeration design using OTE in clean water may fail to deal with the aeration demands in peak flows.
To deal with the uncertainty of the OTE selection, designers usually select large safety coefficients for surface aeration systems, at 1.5 to 2-fold higher than the average demand. The empirically over-designed aeration capability compensates the lower OTE of surface aerators in the actual process. By using the energy model in this study, it is possible to quantify the selection by reasonable and accurate analysis, which is helpful to control the redundancy and to revisit the design criteria.
4.3. Low DO Control via Energy Control Loop
Reducing the aeration intensity provide the benefits in oxidation ditches both of energy saving and better nitrogen removal. Extremely low DO (0.3 mg·L−1) was found favorable for nutrient removal [39] and could save 25% energy by advanced control strategies [34]. The nitrification activity was decreased when DO was reduced from 1.5 mg·L−1, but it did not cease even when DO dropped to 0.2 mg·L−1 [15]. However, controlling the DO in very low level is quite a challenge in practice. Firstly, the DO meter is unstable with extremely low DO (0.3 mg·L−1), as it is designed to operate in range of 0–20 mg·L−1. The system noises may cover the true signals. Second, the classic feedback control loop failed in low DO because the DO set point is too close to the boundary of zero. A very large proportion coefficient is necessary to compensate this limit, resulting in frequent oscillation of the actuators. This challenge in the diffusion aeration system has not yet been solved. However, the energy-based control system in this study provides a feasible choice for low DO control in oxidation ditches, which is not limited by the DO meters and algorithmic constrains.
With the support from the energy model and control strategy, the low DO control can be achieved to ensure the simultaneous nitrification and denitrification. In a full-scale Orbal oxidation ditch, the low DO scenario (0.25 mg·L−1) was realized with satisfactory nitrification [40]. Moreover, reducing aeration intensity also results in lower emissions of aerosol or hazardous gas from the reactors. The aerosol near the oxidation ditches was found to contain bacteria and antibiotic-resistant genes [41], which increased the health risks of surrounding dwellers. On the contrary, lower DO was suspected to cause 4-fold higher nitrous oxide emissions in biological aerated filters due to the selection of microbes by DO level [42]. Therefore, how to select optimal DO and how to practice the aeration control in oxidation ditches are still open questions in research and practice. The fusion of energy model-based control with a classic DO-KLa loop is possible for better performance, and should be considered in further studies.
5. Conclusions
In this paper, an energy consumption model with single and multiple surface aerators was developed which can be used as an energy-saving control system. According to the empirical model, the aeration energy out of the total energy consumption can be estimated online. Using the OTR, OUR, and fluidic velocity in the reactor, the model parameters were estimated. A feedforward–feedback control strategy was established by the audit and prediction of the aeration energy. After linearization and simplification, the control system was implemented in a full-scale Orbal oxidation ditch. Two types of rotating disks in different sizes (Φ1800 mm and Φ1400 mm) were characterized by the energy model. The actual oxygen transfer efficiency of the surface aerators in process was about 60% of that in clean water. The control system achieved an energy saving of about 10%. The return period on investment in control system retrofitting was estimated to be 1.6 years, and the CO2 emissions were reduced by 455 tons per year. The energy consumption model of surface aerators is helpful for process designers and operators to save energy and reduce emissions.
Supplementary Materials
The following are available online at http://www.mdpi.com/2073-4441/10/7/945/s1, Figure S1: Dissolved oxygen (DO) profiles along the outer-lane reactor, Figure S2: Profiles of OUR and ammonia along the reactor. OL, ML and IL mean the outer, middle and inner lane respectively. OL-1, OL-2 and OL-3 represent the three sampling sites evenly distributed along the OL, which is the same for ML and IL. Eff represents the sampling site at the effluent weir. Error bars shows the standard deviation of OUR (n = 10) and ammonia (n = 3), Table S1: Parameter estimation for energy model and surface aerator model, Table S2: The components of total investment on the control system retrofitting, Table S3: Estimated cost and benefits of the operation of control system.
Author Contributions
Y.Q. and P.L. conceived the idea; Y.Q., C.Z. and B.L. gathered and analyzed the data; Y.Q. developed the model and composed the draft; P.L., X.Z., and Y.L. gave expertise on wastewater treatment; J.L. and X.H. managed the projects for finencial support. All authors contibuted to the proofreading and revision.
Funding
National Natural Science Foundation of China (51778325), Major Science and Technology Program for Water Pollution Control and Treatment of China (2014ZX07305-001), Science and Technology Project in Jiangsu Province (BE2015622), and Special fund of State Key Joint Laboratory of Environment Simulation and Pollution Control (16K05ESPCT).
Acknowledgments
The authors thank the two referees and the editor for their supports to improve the quality of the manuscript. The authors want to thank Tian Yuxin, Xiong Tianyu, and Zhang Fengying for conducting the field surveys. The authors also thank the managers and operators in the WWTP for sampling and experimental assistance.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| CFD | computational fluidic dynamics | A | coefficient matrix of energy model |
| DO | dissolved oxygen | X | independent variable in energy model |
| IL | inner lane | P | dependent vector in energy model |
| ML | middle lane | Ea | aeration energy consumption |
| OL | outer lane | Em | motion energy consumption |
| Orbal | a type of oxidation ditch | Ee | total effective energy consumption |
| OTR | oxygen transfer rate | ae | energy to transfer 1 g of oxygen |
| OTE | oxygen transfer efficiency | ξ | pressure loss coefficient |
| OUR | oxygen uptake rate | v | fluidic velocity |
| WWTP | wastewater treatment plant | t | time |
| vm | maximum fluidic velocity | cosφ | phase coefficient of electricity |
| ω | rotating frequency of disks | Ea,t | aeration energy at time t |
| h | wet depth of disks | Ea,d | demanded aeration energy |
| N | number of running disks | Ea,s | aeration energy of single aerator |
| R | oxygen transfer rate | Ka | coefficient in linear form of model |
| a | slope to estimate R | Kb | coefficient in linear form of model |
| b | intercept to estimate R | Kc | coefficient in linear form of model |
| p | power | Kd | coefficient in linear form of model |
| AV | area of cross-section of the reactor | Q | influent flow rate |
| L12 | length between site 1 and 2 | Cin | influent substrate concentration |
| U | voltage to the aerator | Cout | effluent substrate concentration |
| I | current to the aerator | Cstd | concentration of discharge criteria |
References
- Lled, C.; Mara, M. Efficiency assessment of wastewater treatment plants: A data envelopment analysis approach integrating technical, economic, and environmental issues. J. Environ. Manag. 2016, 167, 160–166. [Google Scholar]
- Lee, M.; Keller, A.A.; Chiang, P.; Den, W.; Wang, H.; Hou, C.; Wu, J.; Wang, X.; Yan, J. Water-energy nexus for urban water systems: A comparative review on energy intensity and environmental impacts in relation to global water risks. Appl. Energy 2017, 205, 589–601. [Google Scholar] [CrossRef]
- Wakeel, M.; Chen, B.; Hayat, T.; Alsaedi, A.; Ahmad, B. Energy consumption for water use cycles in different countries: A review. Appl. Energy 2016, 178, 868–885. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Yang, W.N.; Ngo, H.H.; Guo, W.S.; Jin, P.K.; Dzakpasu, M.; Yang, S.J.; Wang, Q.; Wang, X.C.; Ao, D. Current status of urban wastewater treatment plants in China. Environ. Int. 2016, 92–93, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Jin, P.; Wang, X.; Wang, X.; Huu, H.N.; Jin, X. A new step aeration approach towards the improvement of nitrogen removal in a full scale Carrousel oxidation ditch. Bioresour. Technol. 2015, 198, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Ren, N.; Wang, Q.; Wang, Q.; Huang, H.; Wang, X. Upgrading to urban water system 3.0 through sponge city construction. Front. Environ. Sci. Eng. 2017, 11, 9. [Google Scholar] [CrossRef]
- Olsson, G. ICA and me—A subjective review. Water Res. 2012, 46, 1585–1624. [Google Scholar] [CrossRef] [PubMed]
- Ryder, R.A. Dissolved-oxygen control of activated-sludge aeration. Water Res. 1972, 6, 441–445. [Google Scholar] [CrossRef]
- Schraa, O.; Rieger, L.; Alex, J. Development of a model for activated sludge aeration systems: Linking air supply, distribution, and demand. Water Sci. Technol. 2017, 75, 552–560. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Liang, P.; Yan, X.; Zuo, K.; Xiao, K.; Xia, J.; Qiu, Y.; Wu, Q.; Wu, S.; Huang, X.; et al. Reducing aeration energy consumption in a large-scale membrane bioreactor: Process simulation and engineering application. Water Res. 2016, 93, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Fu, G.; Butler, D. Cost-Effective River Water Quality Management using Integrated Real-Time Control Technology. Environ. Sci. Technol. 2017, 51, 9876–9886. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Wang, R.; Li, Y. Evaluation of the control strategy for aeration energy reduction in a nutrient removing wastewater treatment plant based on the coupling of ASM1 to an aeration model. Biochem. Eng. J. 2017, 124, 44–53. [Google Scholar] [CrossRef]
- Foscoliano, C.; Del Vigo, S.; Mulas, M.; Tronci, S. Predictive control of an activated sludge process for long term operation. Chem. Eng. J. 2016, 304, 1031–1044. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, R.; Li, W.; Ni, B.; Fang, F.; Sheng, G.; Yu, H.; Song, J.; Le, D.; Bi, X.; et al. Simulation and optimization of a full-scale Carrousel oxidation ditch plant for municipal wastewater treatment. Biochem. Eng. J. 2011, 56, 9–16. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, X.; Han, Y.; Liu, J.; Ren, J.; Wang, Y.; Guo, Y. Enhancing nitrogen removal in an Orbal oxidation ditch by optimization of oxygen supply: Practice in a full-scale municipal wastewater treatment plant. Bioprocess Biosyst. Eng. 2012, 35, 1097–1105. [Google Scholar] [CrossRef] [PubMed]
- Yoshino, H.; Suenaga, T.; Fujii, T.; Hori, T.; Terada, A.; Hosomi, M. Efficacy of a high-pressure jet device for excess sludge reduction in a conventional activated sludge process: Pilot-scale demonstration. Chem. Eng. J. 2017, 326, 78–86. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, H.; Shi, H.; Xia, L.; Shen, T.; Wang, G.; Wang, Z.; Wang, Y. Study of operational conditions of simultaneous nitrification and denitrification in a Carrousel oxidation ditch for domestic wastewater treatment. Bioresour. Technol. 2010, 101, 901–906. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Shi, H.; Shi, H.; Wang, Z. Study on a discrete-time dynamic control model to enhance nitrogen removal with fluctuation of influent in oxidation ditches. Water Res. 2010, 44, 5150–5157. [Google Scholar] [CrossRef] [PubMed]
- Loubiere, K.; Castaignede, V.; Hebrard, G.; Roustan, M. Bubble formation at a flexible orifice with liquid cross-flow. Chem. Eng. Process. 2004, 43, 717–725. [Google Scholar] [CrossRef]
- Abusam, A.; Keesman, K.J.; Meinema, K.; Van Straten, G. Oxygen transfer rate estimation in oxidation ditches from clean water measurements. Water Res. 2001, 35, 2058–2064. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, H.; Wang, Z.; Fan, L.; Shi, H. Approach to enhancing nitrogen removal performance with fluctuation of influent in an oxidation ditch system. Chem. Eng. J. 2013, 219, 520–526. [Google Scholar] [CrossRef]
- Gimbun, J.; Rielly, C.D.; Nagy, Z.K. Modelling of mass transfer in gas–liquid stirred tanks agitated by Rushton turbine and CD-6 impeller: A scale-up study. Chem. Eng. Res. Des. 2009, 87, 437–451. [Google Scholar] [CrossRef]
- Thakre, S.B.; Bhuyar, L.B.; Deshmukh, S.J. Oxidation ditch process using curved blade rotor as aerator. Int. J. Environ. Sci. Technol. 2009, 6, 113–122. [Google Scholar] [CrossRef]
- Sun, H.; Mao, Z.; Yu, G. Experimental and numerical study of gas hold-up in surface aerated stirred tanks. Chem. Eng. Sci. 2006, 61, 4098–4110. [Google Scholar] [CrossRef]
- Ben Alaya, S.; Haouech, L.; Cherif, H.; Shayeb, H. Aeration management in an oxidation ditch. Desalination 2010, 252, 172–178. [Google Scholar] [CrossRef]
- Li, B.; Qiu, Y.; Zhang, C.; Chen, L.; Shi, H. Understanding biofilm diffusion profiles and microbial activities to optimize integrated fixed-film activated sludge process. Chem. Eng. J. 2016, 302, 269–277. [Google Scholar] [CrossRef]
- Mahendraker, V.; Mavinic, D.S.; Hall, K.J. Comparison of oxygen transfer parameters determined from the steady state oxygen uptake rate and the non-steady-state changing power level methods. J. Environ. Eng. ASCE 2005, 131, 692–701. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.; Zuo, J.; Li, Y.; He, S.; Yang, X.; Zhang, K. Study on two operating conditions of a full-scale oxidation ditch for optimization of energy consumption and effluent quality by using CFD model. Water Res. 2011, 45, 3439–3452. [Google Scholar] [CrossRef] [PubMed]
- Lesage, N.; Sperandio, M.; Lafforgue, C.; Cockx, A. Calibration and application of a 1-D model for oxidation ditches. Chem. Eng. Res. Des. 2003, 81, 1259–1264. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, X.; Chen, Q.; Liu, J. Flow field and dissolved oxygen distributions in the outer channel of the Orbal oxidation ditch by monitor and CFD simulation. J. Environ. Sci. 2013, 25, 645–651. [Google Scholar] [CrossRef]
- Csepai, L.; Kabelka, H. Practical testing of automatically controlled overflow weirs. Water Res. 1996, 30, 749–752. [Google Scholar] [CrossRef]
- Lu, B.; Du, X.; Huang, S. The economic and environmental implications of wastewater management policy in China: From the LCA perspective. J. Clean. Prod. 2017, 142, 3544–3557. [Google Scholar] [CrossRef]
- Kodra, E.; Sheldon, S.; Dolen, R.; Zik, O. The North American Electric Grid as an Exchange Network: An Approach for Evaluating Energy Resource Composition and Greenhouse Gas Mitigation. Environ. Sci. Technol. 2015, 49, 13692–13698. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Qi, L.; Liu, G.; Zhang, Y.; Fan, Q.; Wang, H. Aeration optimization through operation at low dissolved oxygen concentrations: Evaluation of oxygen mass transfer dynamics in different activated sludge systems. J. Environ. Sci. 2017, 55, 224–235. [Google Scholar] [CrossRef] [PubMed]
- Prades, L.; Dorado, A.D.; Climent, J.; Guimera, X.; Chiva, S.; Gamisans, X. CFD modeling of a fixed-bed biofilm reactor coupling hydrodynamics and biokinetics. Chem. Eng. J. 2017, 313, 680–692. [Google Scholar] [CrossRef]
- Nerenberg, R. The membrane-biofilm reactor (MBfR) as a counter-diffusional biofilm process. Curr. Opin. Biotechnol. 2016, 38, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ngo, H.H.; Guo, W.; Peng, L.; Pan, Y.; Guo, J.; Chen, X.; Ni, B. Autotrophic nitrogen removal in membrane-aerated biofilms: Archaeal ammonia oxidation versus bacterial ammonia oxidation. Chem. Eng. J. 2016, 302, 535–544. [Google Scholar] [CrossRef]
- Pittoors, E.; Guo, Y.; Van Hulle, S.W.H. Oxygen transfer model development based on activated sludge and clean water in diffused aerated cylindrical tanks. Chem. Eng. J. 2014, 243, 51–59. [Google Scholar] [CrossRef]
- Keene, N.A.; Reusser, S.R.; Scarborough, M.J.; Grooms, A.L.; Seib, M.; Domingo, J.S.; Noguera, D.R. Pilot plant demonstration of stable and efficient high rate biological nutrient removal with low dissolved oxygen conditions. Water Res. 2017, 121, 72–85. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Han, Y.; Guo, X. Identification and evaluation of SND in a full-scale multi-channel oxidation ditch system under different aeration modes. Chem. Eng. J. 2015, 259, 715–723. [Google Scholar] [CrossRef]
- Li, L.; Gao, M.; Liu, J.X. Distribution characterization of microbial aerosols emitted from a wastewater treatment plant using the Orbal oxidation ditch process. Process Biochem. 2011, 46, 910–915. [Google Scholar] [CrossRef]
- He, Q.; Zhu, Y.; Li, G.; Fan, L.; Ai, H.; Huangfu, X.; Li, H. Impact of dissolved oxygen on the production of nitrous oxide in biological aerated filters. Front. Environ. Sci. Eng. 2017, 11, 141–151. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).