Abstract
In the absence of long-series streamflow records in plain areas, design storm, which serves as the most important input in a hydrologic model, plays an important role in flood control and water resources management. For a large drainage basin, design storm may be estimated for sub-basins separately; thus the spatial distribution of design storm needs to be carefully treated. However, few studies have been carried out to evaluate the rationality of the spatial distribution in a design storm, which means the storm over space should be in accordance with actual needs or its distributing patterns. Taking the Tai Lake Basin (TLB), 3-d Copula-based models combining extreme rainfall of different sub-basins were built using long-term rainfall data, and conditional probabilities of sub-basins encountering certain amounts of rainfall were investigated to evaluate the rationality of the design storm. Results show that the spatial distribution of the design storm based on a typical year is hardly rational, in which rainfall of the northeastern part of the basin is suggested to be weakened while in the southwest to be strengthened; after the rainfall is redistributed based on long-term information, it shows a better rationality of spatial distribution. Such information provides valuable significance in guiding flood control of TLB, and the considered evaluating method can be used for similar basins in plain areas.
1. Introduction
Flood control planning is used strategically in dealing with flood events in a basin or river. In flood control planning, design flood, which is usually derived from long-series streamflow data, provides the basis for flood control standards (usually described as a return period). In a way, it serves as macro guidance of the construction and operation of hydraulic structures. However, this method is practically impossible for plain areas where it is ungauged or streamflow is difficult to measure because it can flow back and forth. Under this circumstance, an alternative method came into being with the rapid development of hydrologic models [1,2,3], through which design flood can be derived using design storm as a model input. Hence, in such areas design storm becomes important since it can have an indirect but far-reaching influence on flood control planning of the whole basin. There are basins all over the world using design storm as a model input (as long as the long-term rainfall data is available) to get design flood [4,5]. Researchers have been applying this idea to estimate design flood in different works [6,7,8,9] even though there exist some disputes concerning whether return periods of rainfall and discharge can be regarded as equal [10].
Since design storm can determine design flood, it is significant to offer a rational spatial distribution of the storm in accordance with our actual needs or its natural distribution patterns; otherwise, it can implement an influence on design flood far from our intention. Such actual needs include flood control purpose, such as strengthening the design rainfall in partial areas of the basin more worthy of protecting, so that the authorities can attach more importance or attention to flood control of these particular areas (we can name them “prioritized areas”).
When it comes to design storm of the rest of sub-basins (similarly, we can name them “non-prioritized areas”), one method which is commonly used in deriving design storm is called “typical year method”—To derive rainfall from a historical outstanding rainfall event/year [11]. This method tends to get a design storm which has a similar spatial distribution to historical rainfall events; the main interest consists in the fact that administrators might consider the ability of a hydraulic structure to cope with an extreme recorded event/year. However, a rational problem can arise because rainfall in these non-prioritized sub-basins is usually accompanied by being strengthened or being weakened during the designing process; rainfall disparity between these non-prioritized sub-basins can be amplified, let alone rainfall of a typical year in these areas may not be able to represent rational distribution. It is noteworthy that we can significantly overestimate or underestimate flood risks if we do not provide a rational rainfall variation over space. For one thing, a different design storm in a sub-basin will definitely result in a corresponding water level change in this sub-basin; for another, model experiments show that rainfall of one sub-basin can have a huge impact on the results of its surrounding sub-basins because it provides different boundary conditions to them [12,13,14,15]. In a word, it is crucial to evaluate the spatial distribution rationality of a storm in non-prioritized areas, and it’s better to come up with an alternative if the previous one is not rational.
If two sub-basins are far enough from each other, it can be assumed that their rainfall events are statistically independent. Therefore, the return periods of a design storm in these sub-basins can be estimated separately. However, if sub-basins are close to each other, it can be problematic to ignore the correlations between rainfall events of different sub-basins, especially when administrators try to maintain a certain amount of design rainfall in the whole basin and prioritized sub-basins simultaneously. That means there are “preconditions” to be taken into consideration when designing rainfall in non-prioritized sub-basins.
In recent years, the application of Copula functions have witnessed huge developments owing to their diverse forms, flexible usage and simple solutions [16,17,18], and these functions have shown a great advantage in dealing with “precondition” problems. Researchers have been utilizing them in all kinds of multivariate hydrological problems, for instance, (1) rainfall and flood analysis [19,20,21,22,23], where bivariate frequency analysis between peak volume, duration and rainfall amount are carried out instead of conventional univariate frequency analysis; (2) meteorological drought analysis [24,25], where joint behaviors of drought variables including duration, area and severity are identified and characterized spatio-temporally; (3) encountering between rainfall and storm tide [26,27], in which joint probability of extreme rainfall and storm tide are investigated in coastal areas. All these studies have indicated that Copula functions perform well in capturing joint behaviors of hydrological variables.
In order to provide an assessment of the distribution rationality of design storm in non-prioritized areas, this study takes the Tai Lake Basin (TLB) as an example, and proposes a 3-dimensional (3-d) Copula-based method for the joint distribution among extreme rainfall of different sub-basins, and investigates conditional probability equations of 3-d Copula models. Also, aiming at the potential problem caused by the “typical year method”, this study proposes a spatial distributing method which is based on the long-term average information of rainfall, and evaluates the spatial rationality of both rainfall distributing schemes in the non-prioritized sub-basins using the proposed method.
The study consists of three parts. Part 1 focuses on the methods, including the marginal and joint distributions, goodness of fit and derivation of conditional probability equations based on 3-d Copulas. Part 2 serves as an overview of the study domain and basic data. Part 3 establishes and selects the optimal marginal and joint distributions for the 3-d relationship, performs calculation on coincidence and conditional probabilities of rainfall combinations, and evaluates the distribution rationality of two distributing schemes based on the derived conditional probability equations.
2. Methods
In the flood control planning text of TLB, administrators are designing a storm in which rainfall values of the whole basin and the prioritized sub-basin are fixed (assume that return periods of both are 50/100 years), while, rainfall values over the non-prioritized sub-basins are spatially distributed based on a typical year. Since rainfall of the whole basin and prioritized area is settled, the problem lies in how the remaining rainfall is spatially distributed over the non-prioritized sub-basins.
3-d Copulas are utilized to establish joint distributions among three extreme rainfall variables. Figure 1 shows the flow chart of how to build joint distributions among the three variables. The first and the second variables are rainfall of the whole basin and prioritized sub-basin, respectively, and are regarded as conditional ones. Then, each one of the non-prioritized sub-basins is taken out as the third variable to build a 3-d joint distribution along with the two conditional variables. Afterwards, the probability of each non-prioritized sub-basin encountering a certain amount of rainfall is derived under the two conditional variables. Based on the results, analysis and evaluation is carried out accordingly. This method ensures that the potential correlations among rainfall of different sub-basins and the intentions of administrators are all taken into consideration.
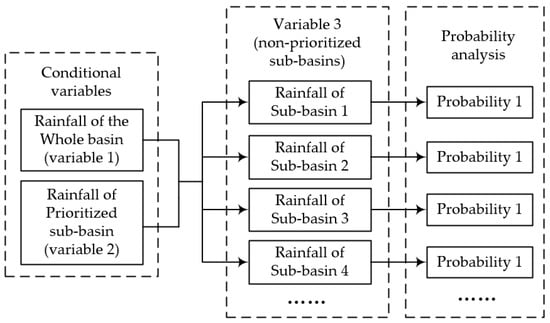
Figure 1.
Flow chart of how spatial distribution rationality is evaluated using conditional probability analysis.
2.1. Distributing Schemes
Two schemes of rainfall distribution in non-prioritized sub-basins need to be evaluated, one is the so-called “typical year scheme” which is currently used in the TLB flood control, and derives rainfall from an outstanding historical rainfall year. In consideration of the potential problem in the current scheme, an alternative which is based on the average rainfall information in the past decades is proposed (we may name it “average scheme”). Equation (1) shows how rainfall distribution in different non-prioritized sub-basins is derived.
where XD represents the design rainfall we try to derive, XB and XN are the design rainfall of the whole basin and northern part of the basin, respectively, F and FN are the area of the whole basin and northern part of the basin respectively, n is the number of non-prioritized sub-basins, i is the ordinal of the non-prioritized sub-basins, xi and fi are the typical rainfall and area of each non-prioritized sub-basins, XM represents the typical rainfall of the non-prioritized sub-basins.
It is noteworthy that the difference between the “typical year scheme” and “average scheme” lies in the value of XM, that is, if the formal scheme is chosen, XM is derived using the rainfall information of a typical outstanding year, if the latter, an average information of rainfall over the past decades is applied to XM.
2.2. Maginal and Joint Distribution
The first step involved in building Copulas is to decide the optimal marginal distribution. Researchers have pointed out that some certain distributions may not be proposed as general models [28], and one recent study [29] has presented a framework which attempts to propose a single approach for stochastic modelling of any hydroclimatic process. However, it is hardly our main goal here to discuss the best marginal distribution. In this study, four types of commonly used distributions in hydrology are adopted as candidates, namely Pearson III type distribution (P-III), Logistic distribution (LOG), Log-normal distribution (LOGN) and Weibull distribution (WEI). For the sake of achieving better accuracy, this study selects the optimal one for every rainfall variable.
Afterwards, the second step is the joint distribution in which Copula functions are utilized. The Copula function is a multi-variable joint distribution with a domain between 0 and 1, this offers us convenient access to combine two or more marginal distributions into a probabilistic model. Taking a 2-d combination, assume that FX(x) = u and FY(y) = v represent cumulative distribution functions of variable X and Y, respectively, their Copula function can be described as follows:
where F(x, y) serves as the joint distribution function of stochastic variable X and Y, θ and Cθ represent the parameter of the Copula function and the Copula function itself.
2-d Copulas are also involved when dealing with conditional probabilities of 3-d Copulas, thus relevant joint distribution calculation involves both 2-d and 3-d ones. The Archimedean Copula family, which is commonly used in hydrology [19,20,21,22,23,24,25,26,27], is adopted as candidates of joint distributions in this study. This Copula family includes three main members, namely Clayton, Gumbel and Frank; eventually, an optimal one will be selected for probability calculation for the sake of accuracy. All of these Copulas are single-parameter functions which are easy and flexible to build and solve. The expressions of these Copulas are shown in Table 1.

Table 1.
Cumulative distribution of the 2-dimensional and 3-dimensional Copulas.
2.3. Goodness of Fit
Criteria are necessary to assess the fit quality of marginal and joint distributions. In terms of marginal distributions, this study utilizes the Kolmogorov-Smimov (K-S) test and least Akaike information criterion (AIC) to select the optimal ones; when it comes to joint distributions, we use AIC and the criteria of ordinary least square (OLS) to assess the fitting quality between theoretical and empirical distributions of samples. The OLS and AIC are specifically the following equations:
where Femp(xi1 , xi2 , …, xim ), C( ui1 , ui2 , …, uim ) are empirical and theoretical cumulative probabilities respectively; m is the dimension of the function; n is the number of observations; k is the number of parameters; MSE is the root mean square error. The goodness of fit is believed to be better when a smaller AIC or OLS value is obtained.
For 3-d observations (pi, qj, zk), the empirical frequency can be calculated using the equation below:
where Femp(pi, qj, zk) is the empirical frequency, N is the number of observations, nijk represents the times when measured data is less than (pi, qj, zk) simultaneously.
2.4. Conditional Probability
A 3-d conditional probability of the joint distribution can be derived using expressions of 2-d and 3-d Copulas. According to the requirements of calculation, for a data group (X1, X2, X3), the probability of X1 ≤ x1 under condition of X2 = x2, X3 = x3 can be derived using Equation (7).
where is the conditional probability, , are 3-d joint distributions, while , are 2-d joint distributions.
On the basis of Equation (7), Equations (8)–(11) show the derivation process of probability U3 ≤ u3 under the condition of U1 = u1, U2 = u2. The following derivations are based on Clayton Copula because it was proven to outperform the other two types, Frank and Gumbel Copula in this study (see Section 4.2 for discussion).
First, the joint distribution of the 3-d Clayton Copula can be described as the following:
The partial derivative of C3 over u1, u2 is derived:
The partial derivative of C2 over u1, u2 is derived:
According to Equation (7), the conditional probability of Clayton Copula can be derived using the following:
3. Study Domain and Data
3.1. Study Domain
The TLB, located in the southern part of Yangtze River Delta, China (within 119°3′1″–121°54′26″ E, 30°7′19″–32°14′56″ N), has a typical humid sub-tropical monsoon climate, with the annual mean rainfall of about 1177 mm. The area of the basin is around 36,500 km2, which is definitely a rather large one. Figure 2 depicts the relative geographical location of TLB and its seven sub-basins which are divided according to terrain and flood control needs. The area of North, YCDM, SH, HJH, HQ and ZX is 11,510, 4314, 4466, 7480, 3192 and 5930 km2, respectively. As is revealed from the elevation, the TLB shows a high altitude in the West mountainous area while the rest is basically plain areas.
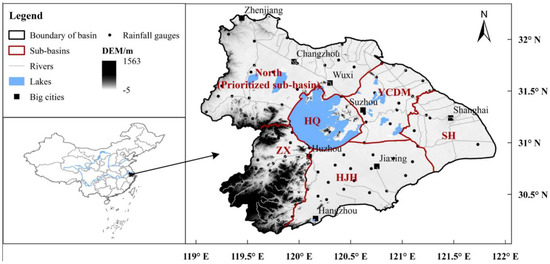
Figure 2.
Elevation of the Tai Lake Basin and its 7 sub-basins.
As one of the most developed regions of China, the TLB has witnessed impressive economic achievements in the past decades. With the degree of urbanization of 80% in 2015 [30], the basin supports 4.8% of the nation’s population (1.39 billion) and produces 11.6% of the gross domestic product (GDP), with 0.38% of the land area of China [31]. Also, flood disasters have been taking place frequently in the basin due to the long duration of rainfall in summer [32]. According to the most outstanding flood disasters of TLB in recent decades, the northern part of the basin (namely sub-basin HX and WCXY) has been suffering more rainfall compared with the rest of the sub-basins. With several big cities (such as the city of Wuxi and Changzhou) located within the North, this area is suffering heavy losses in the economy and has drawn attention from administrators. This explains why the northern part of the basin is considered to be the so called “prioritized area”; accordingly, the rest of the sub-basins (namely YCDM, SH, HQ, HJH, and ZX) are the non-prioritized ones.
According to the flood control planning of TLB, when a 50 years return period storm is designed for the whole basin, it is suggested that rainfall in the prioritized area remains a relatively high return period (50 years also), due to frequent disasters and heavy economic losses; meanwhile, rainfall of the non-prioritized sub-basins is spatially distributed based on the measurement of a typical year (namely 1991). Nevertheless, it turned out the real rainfall of year 1991 varies significantly in space over the rest of the sub-basins, that is to say, its spatial distribution needs to be evaluated and furtherly replaced with an alternative if necessary.
3.2. Data Collection
High-density rainfall gauges (see Figure 1) have been established in the basin, thus, the long-time series rainfall data is collected. According to hydrological yearbooks and the latest monitoring data from the administration, the Arithmetical Average Method is adopted to derive daily rainfall series between 1951~2014 as the research data; the Annual Maximum method is used to extract the maximum 30-day, 60-day and 90-day rainfall of the whole basin or different sub-basins, which will be used for building marginal and joint distribution models.
Figure 3 provides daily rainfall of TLB between 1951~2014, the grey dotted lines represent daily rainfall of all the years except 1991, the dotted blue one is the average of them, and the solid black one represents 1991. Compared with the average, the year 1991 saw a significantly outstanding rainfall during flood season in the historical records; especially, there were two tight rainfall periods in the middle of June and beginning of July, respectively, which were rather harsh for the flood control, it explains why rainfall of 1991 is widely used as a model input in previous studies of TLB [33], and of course, it is picked as “typical year” in this study.
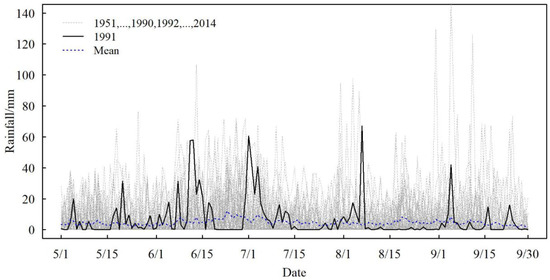
Figure 3.
Comparison of daily rainfall during flood season in 1991 and other years.
The rainfall data from stations have undergone quality control, including analytical processing to ensure their consistency, reliability and representativeness.
4. Results and Discussion
4.1. Marginal Distribution
Table 2 shows the test results for four marginal distributions of extreme rainfall of different sub-basins (including the whole basin and North part of the basin), the bold numbers, which are smallest among the four candidate distributions, represent the best fitting according to the AIC. Results indicate that all distributions have shown good linear fitting except for relatively poor fitting with Weibull distribution. All four distributions are all below the K-S threshold of 0.2098, which means the marginal distributions are all qualified for the fitting. According to the AIC criteria, extreme rainfall of the basin, HQ, SH, HJH and ZX follow the log-normal distribution best, while the North part of the basin and YCDM follow P-III distribution. Results seem consistent when analyzing for the maximum 30-day, 60-day, and 90-day rainfall data.

Table 2.
Marginal distribution fitting test results for extreme rainfall in different sub-basins.
4.2. Joint Distribution
With the 3-d Copulas, theoretical frequencies are derived with the equations in Table 1, while empirical frequencies are obtained using Equation (6). In order to select the optimal Copula type for fitting the joint distributions, AIC and OLS values are calculated and shown below as Figure 4 and Figure 5. The labels of horizontal axis represent the sub-basin names in “non-prioritized areas”. It is obvious that all three Copula functions show a good fitting accuracy but generally Clayton has the least errors. To be more detailed, Clayton Copula fits the joint distributions best in all types, except for the AIC value of Max 90-d HJH, where Frank Copula is slightly better. Frank Copula is the second best in terms of AIC values, while regarding OLS values, Frank and Gumbel are similar and both are worse than Clayton. Therefore, Clayton Copula should be selected as the optimal type in fitting the joint distributions, which consists of the generally accepted conclusion that Clayton may perform better than others when applied to positive dependence [34].
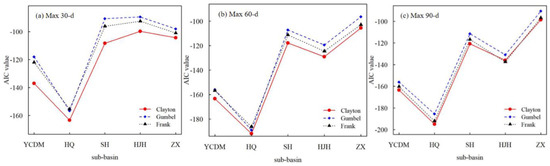
Figure 4.
AIC values of fitting for extreme rainfall by 3 types of 3-dimensional Copulas. (a) Maximum 30 day; (b) Maximum 60 day; (c) Maximum 90 day.
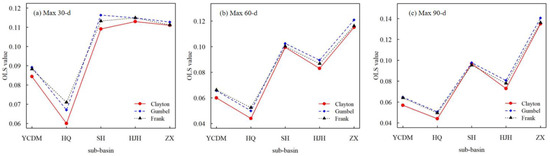
Figure 5.
OLS values of fitting for extreme rainfall by 3 types of 3-dimensional Copulas. (a) Maximum 30 day; (b) Maximum 60 day; (c) Maximum 90 day.
The scatterplots of theoretical and empirical frequency pairs of maximum 30-d, 60-d and 90-d extreme rainfall which are fitted using 3-d Clayton Copulas as shown in Figure 6. The fitted dots all locate beside “y = x”, and the Nash Sutcliffe Efficiency (NSE) coefficients are between 0.61 and 0.92, which indicates pretty good fits generally.
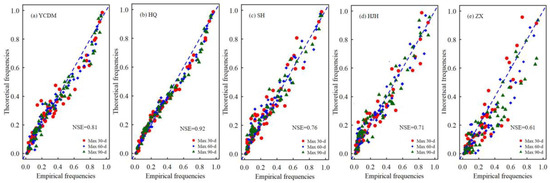
Figure 6.
Scatterplots of theoretical-empirical frequencies fitted by 3-dimensional Clayton Copulas. (a) Sub-basin YCDM; (b) Sub-basin HQ; (c) Sub-basin SH; (d) Sub-basin HJH; (e) Sub-basin ZX.
4.3. Conditional Probability
Two schemes of design storm (namely “typical year scheme” and “average scheme”) remain to be evaluated. Based on the selected 3-d joint distributions, conditional probabilities of the five non-prioritized sub-basins encountering a corresponding rainfall are calculated using Equation (11). Rationality of spatial distribution is evaluated and analyzed afterwards. Before analysis, there is one thing we should highlight: In previous studies (for instance [35]), researches usually get conditional probabilities of U2 ≤ u2 under the condition of U1 > u1, while in this study, we derived the conditional probability of U3 ≤ u3 under the condition of (U1 = u1, U2 = u2) instead. The equation has to be derived in this way because it needs to keep consistent with the rainfall we are studying.
In scheme 1, conditional probabilities of the five non-prioritized sub-basins are shown in Table 3. It is notable that only a max-90-day rainfall result with 100 years return period is provided, since administrators did not derive the other two durations with 100 years return period in the manual. Taking the 50-year return-period and max-30-day rainfall for the example, conditional probabilities for YCDM, SH and ZX encountering a rainfall which exceeds 601.0, 532.5, and 456.3 mm are 1.42%, 2.73%, and 44.32%, respectively. It means when a max-30-day rainfall of an exact 50 years return period takes place in the whole basin and in the North simultaneously, there exists huge differences among the probabilities of YCDM, SH and ZX encountering the corresponding rainfall. Obviously, if we take the rainfall of the whole basin and North as a premise, the spatial distribution of max-30-day rainfall over the non-prioritized sub-basins is considered to be quite uneven, which we believe is too big for YCDM and SH while too small for ZX (no problem with this expression because the total rainfall of the non-prioritized sub-basins is fixed). The analysis with max-60-day and max-90-day rainfall shows a similar situation but less remarkable, one possible reason is that max-30-day rainfall of 1991 is more unevenly distributed than the other two durations over the non-prioritized sub-basins, it illustrates the fact that deriving a storm from only one typical year is in a way arbitrary and can be problematic.

Table 3.
Conditional probabilities of the five non-prioritized sub-basins encountering corresponding rainfall in scheme 1 (“typical year scheme”).
For rainfall of a 100 years return period, there still exists pretty huge gaps among probabilities, the probabilities of HJH and ZX are 12.29% and 12.96%, while YCDM and HQ are 2.26% and 2.04%. Moreover, it is seen that the probabilities decrease in general from 50 years return period to 100 years return period, this is comprehensible since it always becomes less probable to encounter a larger quantity of rainfall. In order to make a comparison straightforwardly among the possibilities, radar plots are shown in Figure 7. It is clearly seen that the shapes of radar plots are quite irregular.
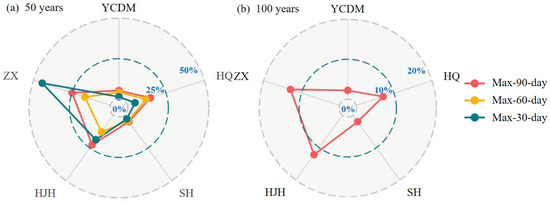
Figure 7.
Radar plots of conditional probabilities of the five non-prioritized sub-basins encountering a corresponding rainfall (scheme 1 ”typical year scheme”). (a) 50 years return period; (b) 100 years return period.
Hence, considering the five non-prioritized sub-basins, the spatial distribution of design storm in the flood control planning (scheme 1) is not quite reasonable. Extreme rainfall would be too large in YCDM and SH, but too small in ZX. It shows a different degree of reasonability when it comes to different durations or different return periods.
Similarly, conditional probabilities in non-prioritized sub-basins of scheme 2 are shown in Table 4, and accordingly, radar plots are also provided in Figure 8. For extreme rainfall of 50 years return period, conditional probabilities of the five sub-basins are between 9.0%~13.7%, 9.0%~16.3%, and 10.5%~17.7%, respectively, for max-30-day, max-60-day and max-90-day rainfall. For max-90-day rainfall of 100 years return period, probabilities are between 5.4%~9.5%. It is obvious that compared with scheme 1, the values of probabilities are all bounded to a much smaller range, also, radar plots also show a much more regular shape with different duration periods. In other words, conditional probabilities of the non-prioritized sub-basins become more uniform after the rainfall is redistributed over the space based on a long-term information of rainfall data. Thus, scheme 2 can show a more reasonable spatial distribution in terms of different durations and return periods.

Table 4.
Conditional probabilities of the five non-prioritized sub-basins encountering corresponding rainfall in scheme 2 (“average scheme”).
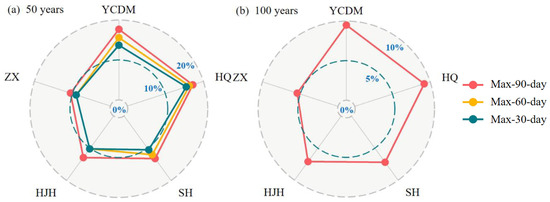
Figure 8.
Radar plots of conditional probabilities of the five non-prioritized sub-basins encountering a corresponding rainfall (scheme 2 ”average scheme”). (a) 50 years return period; (b) 100 years return period.
Based on the analysis and evaluation above, it is proven that the “typical year scheme” for distributing the storm over the non-prioritized sub-basins is hardly reasonable, and it can be problematic if applied to guiding flood control or construction of hydraulic structures in the TLB.
To be specific, if we adopt the “typical year scheme” as the default storm of the TLB, for sub-basin YCDM and SH, flood risk can be overestimated by hydrologic models, accordingly, this might lead to unnecessary public spending on flood control in these sub-basins. Moreover, higher water levels in these areas can further influence the water yield distribution in the whole basin. Meanwhile, for sub-basin ZX, it leads to a severe underestimation of flood risk which may expose the sub-basin itself to a higher flood risk than expected. With this sub-basin located in the mountainous area of TLB (see Figure 2), it can be problematic since ZX is frequently suffering from torrential flood hazards during the flood season. On the contrary, if the “average scheme” is adopted instead, flood risks taken by the non-prioritized sub-basins can be more uniform, which is better for the flood control of the TLB as a whole. Of course, this method can be applied to other similar basins if administrators have similar “requests” for the storm of the whole basin and “prioritized sub-basin”; moreover, flexibility is also a highlight since it provides a new perspective, for instance, a 2-d copula can be applied when we only consider the “prioritized sub-basin” as our “pre-condition”.
5. Conclusions
Aimed at tackling the spatial distribution problem of a design storm over non-prioritized sub-basins, this study takes the TLB as an example, it proposes 3-d Copula-based models which can build joint distributions among extreme rainfall of different sub-basins, and investigates and derives conditional probability solutions using mathematical methods. Afterwards, with the calculated conditional probabilities, the rationality of two distributing schemes is analyzed and evaluated. The following conclusions have been reached:
- For the “typical year scheme”, the probability analysis of extreme rainfall shows huge gaps among non-prioritized sub-basins, especially for the max-30-day rainfall of 50 years return period. If this scheme is applied to hydrologic modelling for TLB, sub-basin YCDM and SH are considered to take a higher flood risk than they should, which can lead to unnecessary public spending on hydraulic structures in these sub-basins. Meanwhile, sub-basin ZX is taking a lower flood risk than it should, and it can be dangerous since this sub-basin is suffering from torrential flood disasters in reality. Generally, the scheme shows a different degree of rationality when it comes to different durations or different return periods, thus it is in urgent need to be redistributed spatially over the five non-prioritized sub-basins.
- Conditional probabilities of the non-prioritized sub-basins can be more uniform after rainfall is redistributed based on long-term information of data. This new scheme shows a more rational spatial distribution, in which flood risks taken by different non-prioritized sub-basins are much more uniform and are better for the flood prevention of the TLB as a whole.
- The proposed 3-d Copula-based method is proven to be very useful to evaluate spatial distribution of design storm in a large-scale drainage basin where sub-basins need to be considered separately for design storm. Further studies are needed to propose a more reasonable scheme for design storm of sub-basins where rainfall events are not independent.
Author Contributions
Conceptualization, L.W., Q.H. and Z.Z.; Methodology, L.W., Q.H., and Y.W.; Software, L.W., and Q.H.; Validation, Y.W., and Z.Z.; Formal Analysis, L.W., and L.L.; Investigation, L.W.; Resources, Y.L., and T.C.; Data Curation, L.W., Q.H. and Z.Z.; Writing-Original Draft Preparation, L.W.; Writing-Review & Editing, L.W., and Z.Z.; Visualization, Z.Z.; Supervision, L.W., Z.Z., and Y.W.; Project Administration, Q.H. and Y.W.; Funding Acquisition, Q.H. and Y.W.
Funding
This research was funded by [National Key Research and Development Program of China] grant number [2016YFC0400902], [National Non-profit Research Program of China] grant number [201501014], [National Natural Science Foundation of China] grant number [51479118, 51509157, 51609140].
Acknowledgments
The authors appreciate the Nanjing Hydraulic Research Institute for the support of data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moradkhani, H.; Sorooshian, S. General Review of Rainfall-Runoff Modeling: Model Calibration, Data Assimilation, and Uncertainty Analysis. In Hydrological Modelling and the Water Cycle; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–24. [Google Scholar]
- Pumo, D.; Viola, F.; Noto, L.V. Generation of Natural Runoff Monthly Series at Ungauged Sites Using a Regional Regressive Model. Water 2016, 8, 209. [Google Scholar] [CrossRef]
- Bureau of the Tai Lake Basin, Water Resources Ministry of China. The Flood Control Planning of the Tai Lake Basin; Bureau of the Tai Lake Basin, Water Resources Ministry of China: Shanghai, China, 2008. [Google Scholar]
- Department of Irrigation and Drainage, Ministry of Natural Environment Malaysia. Hydrological Procedure NO. 1-Estimation of Design Storm in Peninsular Malaysia; Department of Irrigation and Drainage, Ministry of Natural Environment Malaysia: Kuala Lumpur, Malaysia, 2010.
- Bureau Veritas North America, Inc. Analysis of Results for the County of San Diego Rainfall Distribution Study Project; Bureau Veritas North America, Inc.: San Diego, CA, USA, 2013. [Google Scholar]
- Urbonas, B. Reliability of design storms in modeling. In Proceedings of the International Symposium on Urban Storm Runoff, Lexington, KY, USA, 23–26 July 1979. [Google Scholar]
- Cheng, Q.W. Analysis of the design storm time-intensity pattern for medium and small watersheds. J. Hydrol. 1987, 96, 305–317. [Google Scholar]
- Hromadka, T.V.; Whitley, R.J. The design storm concept in flood control design and planning. Stoch. Hydrol. Hydraul. 1988, 2, 213–239. [Google Scholar] [CrossRef]
- Kang, M.S.; Goo, J.H.; Song, I.; Chun, J.A.; Her, Y.G.; Hwang, S.W.; Park, S.W. Estimating design floods based on the critical storm duration for small watersheds. J. Hydrol. Environ. Res. 2013, 7, 209–218. [Google Scholar] [CrossRef]
- Rogger, M.; Kohl, B.; Pirkl, H.; Viglione, A.; Komma, J.; Kirnbauer, R.; Merz, R.; Blöschl, G. Runoff models and flood frequency statistics for design flood estimation in Austria—Do they tell a consistent story? J. Hydrol. 2012, 456, 30–43. [Google Scholar] [CrossRef]
- Carbone, M.; Turco, M.; Brunetti, G.; Piro, P. A cumulative rainfall function for subhourly design storm in Mediterranean urban areas. Adv. Meteorol. 2015, 2015. [Google Scholar] [CrossRef]
- Arnaud, P.; Bouvier, C.; Cisneros, L.; Dominguez, R. Influence of rainfall spatial variability on flood prediction. J. Hydrol. 2002, 260, 216–230. [Google Scholar] [CrossRef]
- Sangati, M.; Borga, M.; Rabuffetti, D.; Bechini, R. Influence of rainfall and soil properties spatial aggregation on extreme flash flood response modelling: An evaluation based on the Sesia River Basin, North Western Italy. Adv. Water Resour. 2009, 32, 1090–1106. [Google Scholar] [CrossRef]
- Cristiano, E.; Veldhuis, M.-C.T.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Zhang, J.; Han, D. Assessment of rainfall spatial variability and its influence on runoff modelling—A case study in the Brue catchment, UK. Hydrol. Process. 2017, 31, 2972–2981. [Google Scholar] [CrossRef]
- Favre, A.-C.; El Adlouni, S.; Perreault, L.; Thiémonge, N.; Bobée, B. Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Genest, C.; Favre, A.C. Everything You Always Wanted to Know about Copula Modeling but Were Afraid to Ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Dupuis, D.J. Using Copulas in Hydrology: Benefits, Cautions, and Issues. J. Hydrol. Eng. 2014, 12, 381–393. [Google Scholar] [CrossRef]
- Jeong, D.I.; Sushama, L.; Khaliq, M.N.; Roy, R. A copula-based multivariate analysis of Canadian RCM projected changes to flood characteristics for Northeastern Canada. Clim. Dyn. 2014, 42, 2045. [Google Scholar] [CrossRef]
- Kao, S.-C.; Govindaraju, R.S. Trivariate statistical analysis of extreme rainfall events via the Plackett family of copulas. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.D.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Chang. 2015, 5, 1093–1097. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Multivariate multiparameter extreme value models and return periods: A copula approach. Water Resour. Res. 2010, 46, 46. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Kao, S.-C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Xu, K.; Ma, C.; Lian, J.; Bin, L. Joint probability analysis of extreme precipitation and storm tide in a coastal city under changing environment. PLoS ONE 2014, 9, e109341. [Google Scholar] [CrossRef] [PubMed]
- Tu, X.; Du, Y.; Singh, V.P.; Chen, X. Joint distribution of design precipitation and tide and impact of sampling in a coastal area. Int. J. Climatol. 2018, 38, e290–e302. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2012, 45, 51–57. [Google Scholar] [CrossRef]
- Papalexiou, S.M. Unified theory for stochastic modelling of hydroclimatic processes: Preserving marginal distributions, correlation structures, and intermittency. Adv. Water Resour. 2018, 115, 234–252. [Google Scholar] [CrossRef]
- Cai, W.; Liu, K. Studies on planning and layout of water sources for urban agglomeration in the Taihu Basin. China Water Resour. 2017, 19, 53–56. [Google Scholar]
- Xu, X.; Yang, G.; Tan, Y.; Tang, X.; Jiang, H.; Sun, X.; Zhuang, Q.; Li, H. Impacts of land use changes on net ecosystem production in the Taihu Lake Basin of China from 1985 to 2010. J. Geophys. Res. Biogeosci. 2017, 122, 690–707. [Google Scholar] [CrossRef]
- Harvey, G.L.; Thorne, C.R.; Cheng, X.; Evans, E.P.; Simm, J.D.; Han, S.; Wang, Y. Qualitative analysis of future flood risk in the Taihu Basin, China. J. Flood Risk Manag. 2009, 2, 85–100. [Google Scholar] [CrossRef]
- Sun, S.; Mao, R. An Introduction to Lake Taihu. In Lake Taihu, China; Qin, B., Ed.; Springer: Dordrecht, The Netherlands, 2008; Volume 87, pp. 12–15. [Google Scholar]
- Vandenberghe, S.; Verhoest, N.E.C.; De Baets, B. Fitting bivariate copulas to the dependence structure between storm characteristics: A detailed analysis based on 105 year 10 min rainfall. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Ghosh, S. Modelling bivariate rainfall distribution and generating bivariate correlated rainfall data in neighbouring meteorological subdivisions using copula. Hydrol. Process. 2010, 24, 3558–3567. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).