Abstract
Six-hourly three-dimensional ensemble variational (3DEnVar) (6H-3DEnVar) data assimilation (DA) assumes constant background error covariance (BEC) during a six-hour DA window and is, therefore, unable to account for temporal evolution of the BEC. This study evaluates the one-hourly 3DEnVar (1H-3DEnVar) and six-hourly 4DEnVar (6H-4DEnVar) DA methods for the analyses and forecasts of hurricanes with rapidly evolving BEC. Both methods account for evolving BEC in a hybrid EnVar DA system. In order to compare these methods, experiments are conducted by assimilating inner core Tail Doppler Radar (TDR) wind for Hurricane Edouard (2014) and by running the Hurricane Weather Research and Forecasting (HWRF) model. In most metrics, 1H-3DEnVar and 6H-4DEnVar analyses and forecasts verify better than 6H-3DEnVar. 6H-4DEnVar produces better thermodynamic analyses than 1H-3DEnVar. Radar reflectivity shows that 1H-3DEnVar produces better structure forecasts. For the first 24–48 h of the intensity forecast, 6H-4DEnVar forecast performs better than 1H-3DEnVar verified against the best track. Degraded 1H-3DEnVar forecasts are found to be associated with background storm center location error as a result of underdispersive ensemble storm center spread. Removing location error in the background improves intensity forecasts of 1H-3DEnVar.
1. Introduction
Tropical Cyclones (TCs) can cause losses of life and billions of dollars in damage. For example, recent category 5 hurricanes Irma (2017), Maria (2017), Michael (2018), and Dorian (2019) each caused more than $5 billion in damage and several dozen direct deaths along with hundreds of injuries and indirect deaths. Despite being weaker on the Saffir-Simpson scale at landfall, Harvey (2017), and Florence (2018) produced additional significant impacts through widespread heavy rain and inland flooding after stalling near the coast. Summaries can be found at (https://www.nhc.noaa.gov/data/tcr, accessed on 12 April 2021). One way to reduce the significant risk to life and property is through improving numerical predictions of hurricanes. For example, if rapid intensification (RI) can be more confidently forecasted in advance, the decision to evacuate could be made sooner. While forecasts can be improved through several avenues, this study focuses on improving the forecasts of hurricanes by applying advanced data assimilation (DA) techniques.
Early studies used various bogusing vortex initialization methods to initialize hurricane forecasts when inner-core observations were limited or lacking [1,2,3,4,5,6]. Although these methods were shown to improve forecast skill, the initial storm produced may not be dynamically and thermodynamically consistent. Recent studies have shown promise using ensemble-based data assimilation (DA) to directly ingest inner core observations to initialize hurricane predictions. Such techniques allow more dynamic and thermodynamic consistency in the TC analysis through the use of flow dependent ensemble covariances. These studies include the use of pure Ensemble Kalman Filters (EnKF) [7,8,9,10,11,12,13,14,15].
Another ensemble-based approach for hurricane initialization uses the hybrid Ensemble-Variational (EnVar) approach. This approach typically incorporates the flow dependent ensemble error covariances into the variational framework [16,17,18,19,20,21]. EnVar has been implemented on both global or convection parameterizing numerical models with a focus on hurricane track prediction [20,22,23,24,25] and convection allowing or near convection allowing models with a focus on hurricane intensity and structure prediction [15,26,27,28,29]. These studies showed that hybrid EnVar can produce better track or intensity forecast than the pure variational method which uses flow-independent background covariance.
Although intensity forecasts have improved as a result of using more advanced data assimilation methods to ingest inner core observations, challenges still remain. One challenge is associated with the rapid evolution of TCs during the DA window. In such case, DA approaches which assume the background error statistics to be fixed during the DA window can introduce considerable errors in the analysis. For example, Wang and Lei (2014) [25] demonstrated using Hurricane Daniel (2010) that when the background is evolving rapidly, the 3DEnVar increment for a six-hourly assimilation window can be nearly the opposite of expected. Lu et al., (2017) [29] demonstrated with hurricane Edouard (2014) that 3DEnVar produces poor inner core structure when the background is evolving. Such errors can be significant if the storm were to undergo rapid intensification or rapid weakening.
One method to account for rapidly evolving TC background error is to use a four-dimensional (4D) data assimilation approach where the evolution of the error covariance within the finite DA window is accounted for. Such approach includes 4DEnVar, which accounts for the 4D error covariance through the use of ensemble covariance [25,29,30]. For example, Wang and Lei (2014) [25] found that in Hurricane Daniel (2010) 4DEnVar produced an increment at the end of the DA window similar to that produced by propagating the increment valid at the beginning of the window directly using the numerical model. Lu et al., (2017) [29] found 4DEnVar produced better inner-core structure and intensity forecasts compared to 3DEnVar when assimilating high-resolution inner-core observations such as Tail Doppler Radar (TDR) and High-Definition Sounding System (HDSS) dropsondes. Another approach is 4DVar where the background covariance is propagated through TL/AJ of the model. For example, Poterjoy et al., (2014) [31] and Poterjoy and Zhang (2016) [32] tested 4DVar in hurricane Karl (2010) and additionally demonstrated hybridizing the ensemble with 4DVar produced smaller errors and a more favorable moisture field in hurricane Karl (2010) compared to a pure 4DVar.
The second method to account for a rapidly evolving TC during DA is simply to reduce the length of the cycling interval for the 3D DA approach [11,12]. In the context of a linear system, the 4D with a long window and the 3D with multiple short windows should be equivalent [33]. However, the same cannot be claimed for the nonlinear system such as TC. While either 4D techniques or shorter 3D cycles can account for rapidly evolving TC background error covariances, it is unclear how the two methods compare in a case with non-linear error evolution such as a hurricane. Compared to a long window 4D approach, shorter 3D DA cycles can produce background error that is close to being under linear growth, which fits better to the most DA approaches with Gaussian assumption. However, frequent interruptions to the model can result in an increased imbalance in short window 3D compared to long window 4D approaches, which can result in degraded analyses and forecasts. In nonlinear scenario, the error growth captured by a short-term ensemble vs. a long-term ensemble may also behave differently.
This study aims to compare and understand the differences of one-hourly 3DEnVar with six-hourly 4DEnVar in hurricanes with rapidly evolving background error covariance (BEC) assimilating inner core observations. Furthermore, both methods are compared with six-hourly Hybrid-3DEnVar to quantify the improvements provided by accounting for the evolution of the background error covariance. To best of the authors’ knowledge, there is no published study comparing one-hourly 3DEnVar with 6-Hourly 4DEnVar for inner-core hurricane DA. The remainder of this paper is organized as follows: Section 2 describes the system configurations, Section 3 describes the model and experiment designs, Section 4 describes the results, Section 5 investigates the spindown problem in one-hourly 3DEnVar, and Section 6 is the discussion and conclusions.
2. Description of Cycled Hybrid Ensemble DA System
Following Lu et al., (2017) [29], this study utilizes a Gridpoint Statistical Interpolation (GSI) based hybrid EnKF-Var DA system for HWRF [28]. This DA system has both 3DEnVar and 4DEnVar capabilities with six-hourly frequency (Lu et al., 2017) [29] and is extended to include 3DEnVar with one-hourly frequency in this study. The system is briefly described here mirroring subsections 2(a)–2(d) in Lu et al., (2017) [29].
2.1. General Overview
This study uses a GSI based dual resolution EnKF-Variational (EnVar) DA system with a 40-member ensemble and a separate control member. The control member is updated using a variational framework where the ensemble covariance contributes to the BEC estimation as described in Section 2.2. The 40-member ensemble is updated by the ensemble square root filter (EnSRF) [34] as described in Section 2.3. Prior to the first DA cycle the ensemble and control member are initialized using the ensemble analysis from the National Centers for Environmental Predictions (NCEP) operational GFS hybrid DA system [20]. After a 6 h spinup, the system is continuously cycled. For each cycle, vortex relocation (VR) [5,35] is used. Take the 6-hourly 3DEnVar as an example. VR is used to update the 6 h ensemble forecast, and 3, 6, and 9 h control forecasts initialized from the previous analysis. The modified ensemble and control member are then used as the background for the first DA cycle.
The Hybrid DA process [20] consists of four steps:
- The relocated background for the control member is updated by the dual-resolution GSI augmented control vector (GSI-ACV) [21] using the BEC from the relocated ensemble.
- The relocated ensemble is updated using EnSRF.
- The ensemble is recentered such that the ensemble mean matches the control analysis.
- The outermost domain is replaced with the GFS Ensemble and control grids for all members.
A 120 h free forecast is initialized from the control analysis. To prepare for the next DA cycle, a forecast is initialized from the background and control analyses. Following Lu et al., (2017) [29], a directed moving nest strategy is employed for all ensemble forecasts to prevent non-overlapping domains for the next DA.
2.2. GSI-ACV
The Dual-resolution GSI-ACV updates the relocated control background and is further detailed here following Wang (2010) [21], Wang et al., (2013) [20], Wang and Lei (2014) [25], and Lu et al., (2017) [29]. For dual-resolution 4DEnVar, the analysis increment at time t is defined as
where D is an operator mapping coarse ensemble model fields to the finer control model grid, is the augmented control vectors for the k-th ensemble member, is the k-th ensemble perturbation that is normalized by at time t, with K being the ensemble size, and ◦ is the Schur product. The cost function is unchanged from single resolution 4DEnVar [25]:
where a is <a1, a2, …, ak> for k = 1, …, K; A is the matrix defining the localization to the ensemble covariance, the length of the DA window is defined by L, , and are the innovation vector, linearized observation operator and observation error covariance valid at time t, respectively. In other words, the ACV is formed by concatenating k unitless vectors, and are constrained by a block diagonal matrix, A, during the variational minimization (Equation (2)). Wang et al., (2007) [36] demonstrates the equivalence of this approach to using the localized ensemble covariance as the background error covariance. The localization matrix A is defined with E-folding distance of 1600 km for the horizontal localizations and 1.1 scale height (natural log of pressure) for the vertical localization using the Gaspari and Cohn (1999) [37] localization function following Wang et al., (2013) [20] and Lu et al., (2017) [28,29]. When only a single time is considered, Equations (1) and (2) describe 3DEnVar [20].
2.3. EnKF
Following Lu et al., (2017) [28,29] the ensemble members are updated by an EnKF, specifically the EnSRF [34]. EnSRF is a three-step process:
First, the ensemble mean is updated by
where is the analysis ensemble mean, is the prior ensemble mean, is the Kalman gain, y is the observation vector, and H is the observation operator. K is given by , where is the ensemble error variance, and R is the observation error variance.
Second, the ensemble perturbations are updated by:
where is the ensemble analysis perturbations, I is the identity matrix, is the reduced Kalman gain computed as , and is the prior ensemble perturbations.
Finally, Equations (3) and (4) are combined to produce the final analysis
where is the analysis ensemble.
The EnSRF code [34] is designed for use with HWRF and uses the observations preprocessing, forward operators and quality control provided by GSI. Horizontal and vertical localization implemented to treat sampling errors are similar to those used in the GSI-ACV. Further, the Relaxation to prior spread (RTPS) multiplicative inflation algorithm developed by Whitaker and Hamill (2002) [34] is adopted and the inflation parameter is set to 0.9 following Lu et al., (2017) [29].
2.4. Vortex Relocation and Modification
For 6 h forecasts the average storm location error is 15–40 km [38,39]. Location errors of this magnitude can degrade the analysis due to violation of the gaussian error assumption [28,29,40,41]. Therefore, following Lu et al., (2017) [28,29], we adopt the HWRF vortex relocation (VR) (Vortex Relocation (VR) and Vortex Modification (VM) are 2 steps that compose Vortex Initialization (VI) in the operational HWRF [42]). VR takes the simulated vortex and moves it to a new location, while VM adjusts the size and intensity of the vortex) procedure [5,35,42,43,44] for both the ensemble and control members. In addition, the vortex modification (VM) procedure is adopted for the control member when there are no inner core observations. The storm center locations are determined using the EnSRF method from Whitaker and Hamill (2002) [34] for a single-variable problem. The observation is the TCVitals storm center location with error estimated to be 10 km following Trahan and Sparling (2012) [37]. The TC vortex is removed from the model background and then placed in the desired location, where dynamical balancing is applied to ensure coherency of the model fields. Details can be found in Lu et al., (2017) [28].
Initial tests suggest that applying VR provides benefits in both intensity and track forecasts for experiments with both 1 and 6 h frequency when compared to the forecasts that did not use VR (not shown). As a result, VR procedures are applied prior to each DA cycle in all experiments. Because negative impacts resulting from the interaction between the assimilation of actual observations and VM have been seen [45], VM is not used when inner core data (e.g., TDR data) are available following Lu et al., (2017) [28,29].
3. Experiment Design
3.1. Hurricane Edouard and Observations Assimilated
This study uses Hurricane Edouard (2014) to evaluate the performance of one-hourly 3DEnVar and six-hourly 4DEnVar for hurricanes with rapidly evolving BEC for the period where abundant inner core data such as those from TDR are available. Hurricane Edouard developed 720 n mi west of the Cape Verde Islands on 1200 UTC 11 September 2014. Edouard peaked in intensity at 105 kts at 1200 UTC 16 September 2014 before immediately weakening due to an eyewall replacement cycle (https://www.nhc.noaa.gov/data/tcr/AL062014_Edouard.pdf, accessed on 14 February 2019). Edouard began a northward then northeastward motion during this weakening phase, accelerating ahead of a midlatitude trough. Finally, Edouard transitioned into a post-tropical cyclone on 19 September, before the remnant low was absorbed into a frontal system on 21 September.
Observations from HWRF operational data stream including conventional observations, clear-sky radiances from satellites (intermediate domain only), satellite derived winds [41], and radial velocities from TDR (Table 1) are assimilated. Except where indicated all data are assimilated on both the intermediate and innermost domains. Radial velocities are recorded by TDR mounted on the NOAA P-3 aircraft. Descriptions of the processing of TDR data can be found in Gamache et al., (2015) [46] and Lu et al., (2017) [28].

Table 1.
Data types assimilated.
DA experiments are performed and compared during cases in which inner-core TDR data are available (Figure 1; Table 2). Because data collection during TDR missions is independent of DA cycle windows, TDR data from a single TDR mission may not be homogeneously distributed in these DA windows when assimilated in the six-hourly DA configurations. For example, for the six-hourly DA, DA cycles will be performed at 1200 UTC 15 September (E1), 1800 UTC 15 September, 1800 UTC 16 September (E2), 1800 UTC 17 September (E3), 1200 UTC 17 September (E4), and 1800 UTC 17 September (E5), among which the 1200 UTC and 1800 UTC 15 September cycles share data from a single flight, as do the 1200 UTC and 1800 UTC 17 September cycles. Therefore, inner-core data may not be temporally symmetric in these DA windows when assimilated with six-hourly DA. The data that corresponds to a single 6 h DA window will be referred to as a batch.
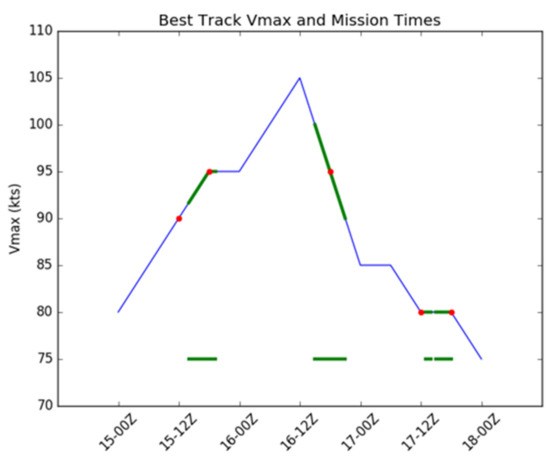
Figure 1.
Edouard (2014) Best track maximum wind speed (Vmax; blue) with Tail Doppler Radar (TDR) data availability overlaid (green). Center of six-hourly DA windows marked with red dot.

Table 2.
Table of Edouard (2014). Time provided is the center of the 6 h data assimilation (DA) window in the six-hourly DA experiments, and the center of the corresponding batch of data.
3.2. HWRF Configuration
The HWRF model is developed by the Environmental Modeling Center (EMC) with the Geophycisal Fluid Dynamics Laboratory (GFDL) and the University of Rhode Island (URI) since 2002 [41,42]. This study uses the 2014 HWRF configuration and codes (HWRF v3.6a) [41] with a two-way triple nested domain with horizontal grid spacing of 0.18°/0.06°/0.02° (approximately 27/9/3 km). There are 61 vertical levels with the model top at 2 hPa following Lu et al., (2017) [28,29]. The outermost, intermediate, and innermost domain use 216 × 432, 232 × 454, and 181 × 322 horizontal grid points, respectively. Table 3 shows the physics parameters follow the 2014 operational HWRF [41], except that ocean coupling is disabled.

Table 3.
Table of model physics used for Edouard (2014).
A dual resolution EnVar is used to update the control member as described in Section 2.2. Briefly, the 3 km grid and the 9 km grid both ingest the ensemble from the 9 km grid for their EnVar updates. The ensemble of the 9 km grid is updated using an EnSRF as described in Section 2.3 and recentered on the control member as described in Lu et al., (2017) [28,29].
3.3. Experiments
To test the hypothesis that six-hourly 4DEnVar and one-hourly 3DEnVar produce better analyses and forecasts than six-hourly 3DEnVar, three experiments are conducted. The first is 6H-3DEnVar, the second is 6H-4DEnVar and the third is 1H-3DEnVar. The results of the latter two experiments will be further compared to each other to determine what the difference is between the two systems.
The backgrounds for each experiment are generated from a continuously cycled six-hourly 3DEnVar system for HWRF from Lu et al., (2017) [29], initialized at 12 UTC 11 September for Edouard (2014). Given our goal is to compare six-hourly 3DEnVar, six-hourly 4DEnVar, and one-hourly 3DEnVar for inner core data, experiments are conducted when TDR data are available, corresponding to cycles 16, 17, 21, 24, and 25 of Lu et al., (2017) [29]. For homogeneous comparison each experiment will start with the same background from Lu et al., (2017) [29], and one free forecast will be initialized once all the data in a single batch has been assimilated. For batches E2 and E5 our experiments are continuously cycled using our E1 and E4 forecasts as backgrounds rather than using the Lu et al., (2017) [29] background. When comparing experiments, the discussion will focus on the data batches rather than individual cycles unless otherwise noted.
3.3.1. 6H-3DEnVar
As stated in Section 2.1 and Section 2.4, VR is performed on the control backgrounds at hours 3, 6, and 9, and on ensemble forecast at hour 6 in six-hourly3DEnVar prior to DA (Figure 2a). Such location updates on the additional control backgrounds at hours 3 and 9 are due to the requirement of the First Guess at Appropriate time (FGAT) [37] technique, which is used during the 3DEnVar GSI-ACV step of the DA to interpolate the background to the time of each observation. The 6H-3DEnVar analysis is valid at the center of the 6 h DA window with observations of ±3 h from analysis time being assimilated.
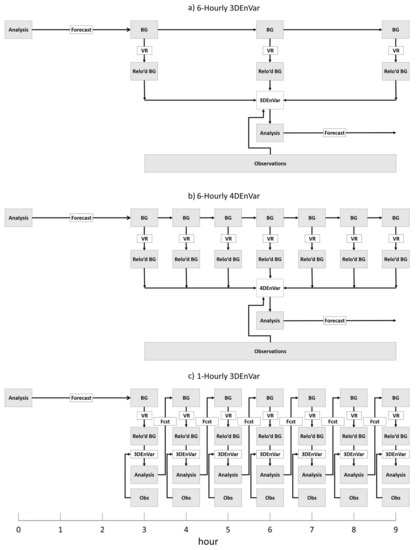
Figure 2.
Comparison of the (a) six-hourly 3DEnVar, (b) six-hourly 4DEnVar, and (c) one-hourly 3DEnVar systems.
3.3.2. 6H-4DEnVar
Like six-hourly 3DEnVar, a 9 h forecast is initialized from the previous control analysis for six-hourly 4DEnVar and a single analysis is output at the center of the 6 h DA window each cycle. Additionally, 9 h ensemble background forecasts are launched from each ensemble analysis (Figure 2b). VR is used to relocate the background each hour from 3 to 9 h for both control and ensemble members. Instead of 3DEnVar, the 4DEnVar DA algorithm [25] is used for the GSI-ACV step. As stated earlier, for homogeneous comparison, if no TDR data are available for the previous cycle, the forecast from the previous 6H-3DEnVar cycle from Lu et al., (2017) [29] is used. If TDR data are available for consecutive 6 h DA cycles 6H-4DEnVar uses the forecast from the previous 6H-4DEnVar cycle as the background.
3.3.3. 1H-3DEnVar
As stated earlier, each batch of data is assimilated through seven one-hourly DA cycles. An analysis is valid at each hour, including at the beginning and end of the mission (Figure 2c). Like 6H-4DEnVar, 1H-3DEnVar is only run when TDR data are available. When TDR data are available in consecutive batches, 1H-3DEnVar uses the final analysis from the previous 1H-3DEnVar batch as the background, effectively completing a full 1 h cycle. When no TDR data are available in the previous batch, the 3 h forecast initialized from the previous Lu et al., (2017) [29] six-hourly 3DEnVar analysis is used as the background. VR modifies the background before each hourly DA cycle. A 3DEnVar GSI-ACV update is performed on the control member as in the six-hourly 3DEnVar, except only using data that occurs during the 1 h window as described above. Similarly, the ensemble is updated by the EnKF using only the data in the 1 h window. The standard six-hourly GFS ensemble is interpolated in time to initialize the outermost domain. To ensure same observations are assimilated across experiments before launching forecasts, the 5-day free forecast for 1H-3DEnVar is launched from the final analysis of each 6 h period.
3.3.4. Experiments to Investigate Sensitivity to Relocated Storm Position
To investigate the impact of storm center location on the analysis and forecast two additional experiments are conducted. 6H-4DEnVar-sl and 1H-3DEnVar-sl are the same as 6H-4DEnVar and 1H-3DEnVar, respectively, except that during vortex relocation storm center locations are manually determined using satellite imagery. All members are relocated to this location instead of using TCVitals and EnSRF to determine the position of each member. All experiments are summarized in Table 4, and the flow charts are shown in Figure 2.

Table 4.
Table of experiments.
4. Results
4.1. Intensity Forecast
Maximum wind speed (Vmax) and minimum sea-level pressure (MSLP) forecasts are verified against the National Hurricane Center’s (NHC) best track data for the five data batches where TDR data are available. Two spuriously strong maximum wind speed analyses are seen in 6H-3DEnVar (Figure 3a) leading to large Vmax root mean square error (RMSE) for 0–6 h (not shown). As a result, 6H-3DEnVar remained too strong once Edouard began to weaken. Both 1H-3DEnVar and 6H-4DEnVar eliminate the spuriously strong wind analyses seen in 6H-3DEnVar. However, spindown occurs in three forecasts for 1H-3DEnVar. Spindown is defined as Vmax decreasing greater than 5 m s−1 (6 h)−1 during the first 6–12 h of model integrationwith no such weakening occurring in observations [47]. An investigation of the cause of this spindown is shown in Section 5. None of the 3 experiments were able to accurately predict the peak intensity of Edouard. However, forecasts of 6H-3DEnVar from E1 and E2 most accurately capture the maximum wind speed increasing trend. Analysis of 6H-4DEnVar valid at E3 best capture the high Vmax. Analyses of 1H-3DEnVar capture the Vmax more closely than 6H-4DEnVar for E1 and E2. Forecasts initialized during the weakening phase (E4 and E5) in both 6H-4DEnVar and 1H-3DEnVar verify better against the best track than 6H-3DEnVar. As is the case for Vmax, MSLP (Figure 3b) is spuriously strong in multiple forecast for 6H-3DEnVar at early lead times. 6H-4DEnVar and 1H-3DEnVar produce overall more accurate MSLP values in the analyses. While the tendency for spindown in 1H-3DEnVar Vmax does not produce a corresponding significant increase in MSLP, the 1H-3DEnVar forecast tends to produce a bias toward a weak storm during peak intensity.
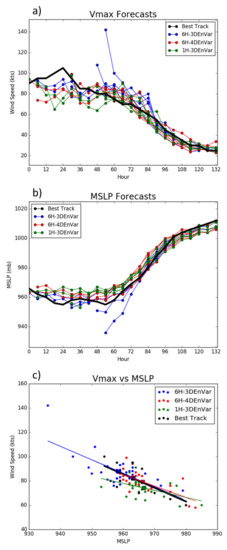
Figure 3.
(a) Vmax and (b) MSLP Forecasts plotted over Best track. Hour is hours from 1200 UTC 15 September. Scatter plot of (c) Vmax vs. MSLP plotted over Best track. Red is 6H-4DEnVar, blue is 6H-3DEnVar, green is 1H-3DEnVar, and black is best track. Squares represent the mean of each experiment and lines are the slope. p = 0.17 for difference of 1H-3DEnVar and Best track slopes.
Figure 3c shows the relationship between Vmax and MSLP. If the model is capturing the intensity evolution correctly the slope and the mean of each variable will be similar to best track. 6H-3DEnVar and 6H-4DEnVar have similar slopes to best track but 6H-3DEnVar shows an apparent strong intensity bias along the slope. 1H-3DEnVar has a smaller slope than best track (significant at 83% level), suggesting that for a given change in MSLP the change in Vmax is less than expected based on the best track. This relationship shown in 1H-3DEnVar is primarily seen in the 0–30 h analysis and forecast due to the spindown occurring in Vmax. Overall, 6H-4DEnVar produces the best Vmax and MSLP relationship.
Figure 3 shows that 1H-3DEnVar and 6H-4DEnVar overall produce better Vmax and MSLP analyses than 6H-3DEnVar. Further, once the spindown in 1H-3DEnVar has recovered, 1H-3DEnVar and 6H-3DEnVar produce better forecasts on average than 6H-3DEnVar. Specifically, 6H-3DEnVar produces spuriously strong analyses that result in poor early forecasts, while 6H-4DEnVar and 1H-3DEnVar forecasts correspond more closely to the best track values. This suggests that accounting for the evolution of the BEC is beneficial. However, 1H-3DEnVar experiences spindown, and therefore a less accurate evolution of Vmax and MSLP compared to 6H-4DEnVar. In summary, 6H-4DEnVar outperforms 6H-3DEnVar and 1H-3DEnVar for Vmax and MSLP verification. Further diagnostics are conducted in the following sections to verify the structure and thermodynamic fields, to further investigate the differences in analyses and forecasts, and to diagnose the causes of these differences.
4.2. Three-Dimensional Structure Correlation
In order to evaluate the three-dimensional structure of the TC produced by the models, the three-dimensional spatial correlation of the model wind field with the TDR wind composite (Available at: https://www.aoml.noaa.gov/hrd/Storm_pages/edouard2014/radar.html, accessed on 9 July 2018) is calculated. The TDR data are recentered for each experiment to match the center of the simulated storm. This three-dimensional spatial correlation (Figure 4) reveals that 6H-3DEnVar provides a worse wind analysis than other experiments. 6H-3DEnVar never produces the highest correlation and the mean of the correlation is about 4.7% smaller that of 1H-3DEnVar and 6H-4DEnVar. 6H-4DEnVar and 1H-3DEnVar produce similar wind analysis correlations on average. E3 and E4 show the largest difference between experiments, with 6H-4DEnVar having the highest correlation, 1H-3DEnVar the second highest, and 6H-3DEnVar is the lowest. To demonstrate the differences in structure correlation, Figure 4b–d show E4 analyses at 1000 m above ground level (AGL). 6H-3DEnVar has a spuriously strong wind maximum on the east side of the storm, consistent with the lower structure correlation and the strong Vmax seen in Figure 3. Further investigation into structure and thermodynamic variables are conducted in the next few sections to differentiate the experiments forecasts and to further understand the analyses.
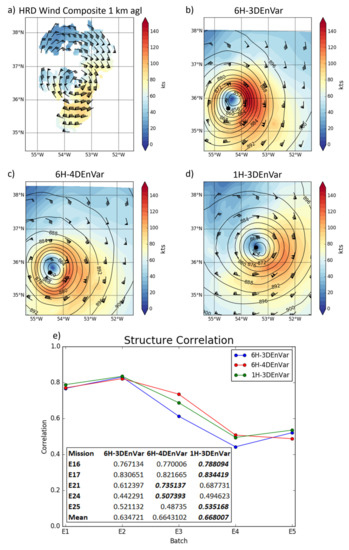
Figure 4.
(a) HRD wind composite at 15 UTC 17 September 2014 at 1000 m, 3 h after the valid time of E4. (b) E4 1000 m wind and pressure analysis for 6H-3DEnVar (c) E4 1000 m wind and pressure analysis for 6H-4DEnVar (d) E4 1000 m wind and pressure analysis for 1H-3DEnVar (e) three-dimensional spatial correlation coefficient of the model wind speed analysis with the TDR wind composite (the values with the highest correlation coefficient among experiments are bolded).
4.3. Simulated Reflectivity
In order to better understand the structure of the forecasts, model simulated reflectivity is compared to reflectivity from TDR. Given HWRF does not cycle hydrometeors during the DA, only forecasts are compared to reflectivity. Two TDR batches observe the inner core near two forecast valid times: valid at 1800 UTC 15 September and 1200 UTC 17 September in corresponding to the 6 h forecast from batch 1 (E1 + 6 h; not shown) and the 18 h forecast from batch 3 (E3 + 18 h; Figure 5), respectively. For the E2 + 6 h forecast, no experiments produced results with consistent distinguishable differences. Therefore, this analysis focuses on the E3 + 18 h case.
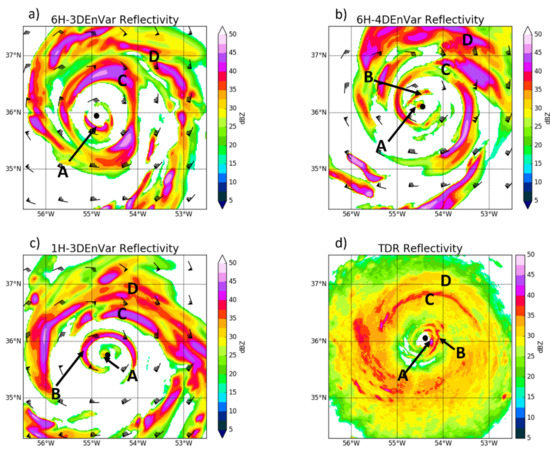
Figure 5.
Simulated radar reflectivity valid 1200 UTC 17 September for (a) 6H-3DEnVar, (b) 6H-4DEnVar from forecast launched 1800 UTC 16 September and, (c) 1H-3DEnVar from forecast launched at 2100 UTC 16 September (E3) (d) and observed TDR reflectivity valid at 1312 17 UTC September. A and B are structures within the inner eyewall, C marks the secondary eyewall, and the rainband marked with D.
Observations show a double eyewall structure at 1200 UTC 17 September (Figure 5d). Each experiment is able to produce the double eyewall structure with varying accuracy. The structure within the inner eyewall A/B is captured by both the 6H-4DEnVar (Figure 5b) and 1H-3DEnVar (Figure 5c), with each capturing 2 distinct maxima in the reflectivity. 6H-3DEnVar (Figure 5a) only displays one maximum with a small region of lower reflectivity extending to the south (A in Figure 5a). The outer eyewall C is well defined in both 6H-3DEnVar and 1H-3DEnVar, while in 6H-4DEnVar the outer eyewall is present but is not as coherent as the other experiments. Randband D is too strong in each experiment, with 6H-4DEnVar producing notably higher reflectivity values than the 3DEnVar experiments. Overall, 1H-3DEnVar is able to capture the structure of both the eyewalls and the rainband more accurately compared to the observations than either the 6H-3DEnVar or the 6H-4DEnVar.
4.4. Verification against Stepped Frequency Microwave Radiometer
Instruments onboard the NOAA WP-3D aircraft allow for some in situ and independent measurements to verify model analyses and forecasts. The Stepped Frequency Microwave Radiometer (SFMR) provides wind speed measurements with which the inner-core structure of the simulated TC is verified. RMSEs for analyses and model forecasts during each penetrating leg are calculated and the mean of the RMSEs for each leg of each flight mission are computed. Statistical significance for this and all further RMSEs in this paper are calculated using the F-Test for equal variances. Model output is recentered so the simulated TC center matches the observed TC location, allowing the direct comparison of the hurricane structure. The number of legs in each case is listed in Table 2. For each free forecast, only the first forecast lead time where SFMR and flight level data are available is verified. Specifically, these cases are: the 6 h forecast of batch 1 (E1 + 6 h), 24 h forecast from batch 2 (E2 + 24 h), 18 h forecast from batch 3 (E3 + 18 h) and 6 h forecast from batch 4 (E4 + 6 h). No forecast is verified for batch 5 as there is no data available after analysis time. SFMR wind speed verification of the analyses shows that 6H-3DEnVar has a mean RMSE 40% larger than those of both 6H-4DEnVar and 1H-3DEnVar (Figure 6a), and 6H-3DEnVar has a larger RMSE than both 1H-3DEnVar and 6H-4DEnVar for 4 of the 5 analyses. Figure 7 shows the increased error in 6H-3DEnVar can be attributed to a wider eye with stronger wind maxima than other experiments. No notable difference in RMSE occurs between 1H-3DEnVar and 6H-4DEnVar. 1H-3DEnVar produces a storm with a properly sized eye, but 6H-4DEnVar captures the wind speed better (smaller RMSE) except in the eyewall. For the forecast, 3 of 4 6H-4DEnVar and 1H-3DEnVar cases produce better forecasts than 6H-3DEnVar (Figure 6b). Similarly, the mean RMSE of all cases shows the largest RMSE for 6H-3DEnVar, although the difference is smaller than for the analyses. 6H-3DEnVar produced the largest wind speed forecast of any experiment in all legs (Figure 8). Because all experiments result in similarly sized eyes, the primary differences are caused by the strength of the eyewall. In summary, verification against SFMR data suggests that both 1H-3DEnVar and 6H-4DEnVar produce both better surface wind analyses and forecasts than 6H-3DEnVar. However, SFMR only samples small slices of the storm and may not be representative of the entire storm.
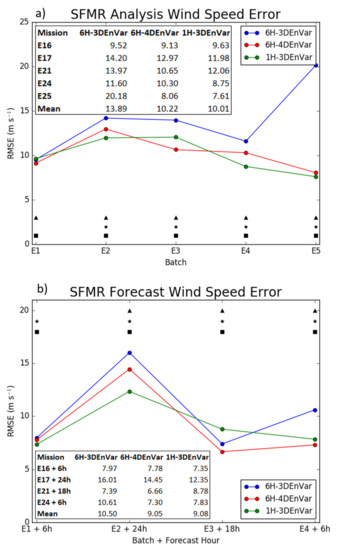
Figure 6.
Wind speed (a) Analysis error and (b) Forecast as verified using Stepped Frequency Microwave Radiometer (SFMR). The value for each experiment is combined RMSE of the penetrating legs for each case. Black triangles indicate statistically significant difference between 6H-3DEnVar and 6H-4DEnVar at 95% level, black stars indicate statistically significant differences between 6H-3DEnVar and 1H-3DEnVar at 95% level, and black squares indicate statistically significant differences between 6H-4DEnVar and 1H-3DEnVar at 95% level.
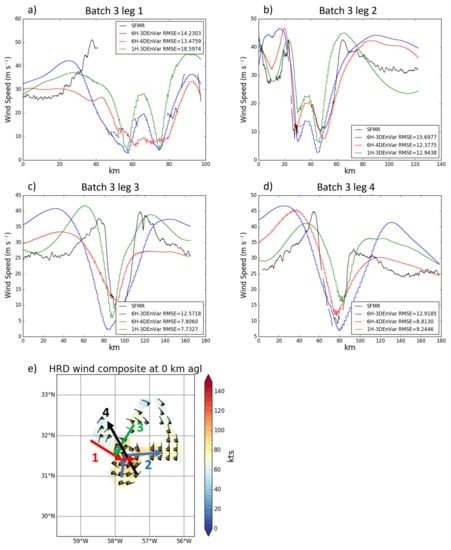
Figure 7.
(a–d) SFMR wind speed (black) and model surface wind speed along the SFMR flight track for each leg. (e) HRD 0 m wind speed composite with penetrating flight legs overlayed (Arrows). Numbers correspond to leg number, and color of number corresponds to the color of the arrow representing the leg. Analysis valid at 1800 UTC 16 September 2014.
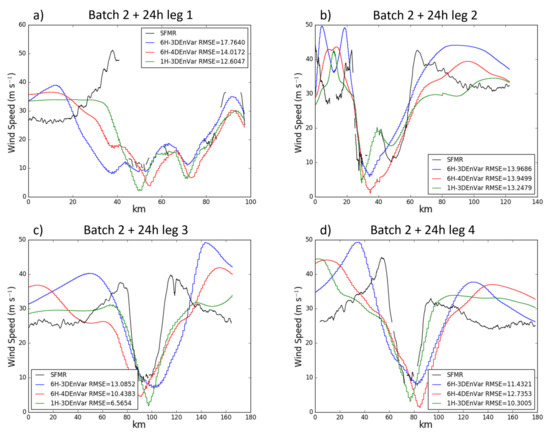
Figure 8.
(a–d) SFMR wind speed (black) and model surface wind speed along the SFMR flight track for each leg. Forecast valid at 1800 UTC 16 September 2014 from forecast launched 24 h prior. The flight path is the same as in Figure 7.
5. Diagnosis of Spindown Issue in 1H-3DEnVar
Frequent spindown is observed in 1H-3DEnVar (Figure 3c), causing a degradation of the Vmax forecast at early lead times. An investigation into the cause of the spindown is discussed in this section. First, the impact of imbalance due to frequent interruption by DA with shortened interval is investigated. To further investigate additional cause of the inferior performance of 1H-3DEnVar, in depth diagnostics is performed on a representative case on 1800 UTC 15 September 2014 case is chosen (Batch 2). The spindown in 1H-3DEnVar for this batch is typical of all cases.
5.1. Imbalance
Previous studies have shown that dynamical imbalance can be introduced during the DA process [20]. Mean absolute sea level pressure tendency (Mdpdt) is calculated following Equation (6) to evaluate the imbalance.
where p is pressure, t is time, m and n are the number of grid points along each axis in the subdomain being averaged over. Higher values of Mdpdt indicate that absolute value of mean pressure is changing more rapidly, which indicates that the model is less balanced and is an undesired artifact of the analysis. The imbalance introduced by DA may be seen in MSLP as wave propagating outward from the imbalance. Averaging over the outermost domain reveals that Mdpdt in 1H-3DEnVar increases steadily over time (Figure 9a), while the 6H-4DEnVar and 6H-3DEnVar do not show a similar increase. However, when averaging over the region corresponding to the innermost domain, the peak magnitude of dpdt is similar for all experiments. No growth is seen in 1H-3DEnVar and Mdpdt returns to similar baseline levels as 6H-3DEnVar and 6H-4DEnVar before each analysis. The wave propagates outside of the inner domain in 45 min (seen as a return to baseline values of Mdpdt in Figure 9b–d), within the 1 h window and before the start of next 1 h DA. Therefore, the instability is not impacting future DA in the innermost domain.
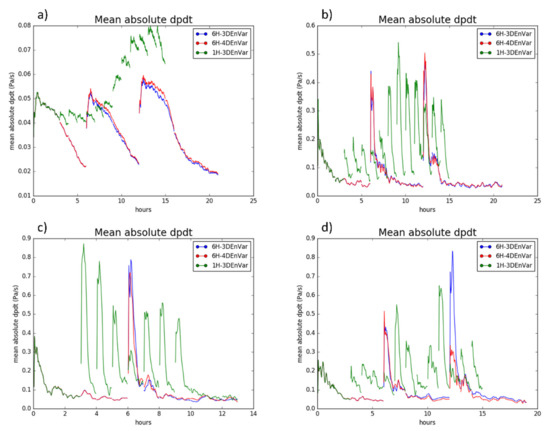
Figure 9.
Mean absolute pressure tendency averaged over (a) the full outermost domain for E1 and E2, and (b–d) over the innermost domain during (b) E1 and E2, (c) E3, and (d) E4 and E5.
5.2. Dry Air Intrusion
A region of anomalously dry air develops near the inner core in the 1H-3DEnVar analyses for batch 2 (E2). This region of dry air is advected into the inner core leading to spindown. This dry air results from a persistent region of spuriously strong negative moisture increments in the 1H-3DEnVar analysis. Figure 10 shows that negative moisture increments occur over several consecutive cycles at 2 km above ground level (AGL) to the north and northwest of Edouard. This region of drying is not seen in 6H-4DEnVar (not shown). Comparing simulated long wave infrared (LWIR) brightness temperature to GOES 13 LWIR (Band 4) satellite imagery suggests that these increments result in a 1H-3DEnVar analysis that is too dry. In contrast, the 6H-4DEnVar analysis is not nearly as dry (Figure 11). While there is another region to the northeast of Edouard with persistent drying (Figure 10), it does not impede on the inner core and does not have a strong impact on the intensity.
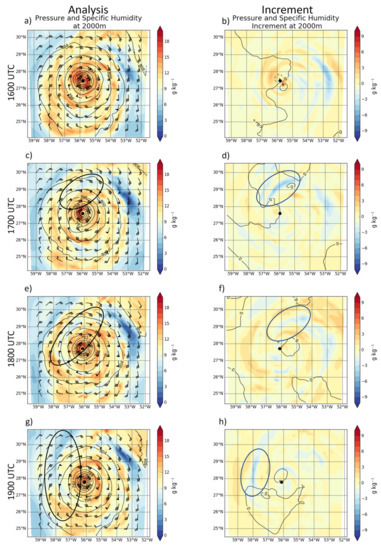
Figure 10.
Left column: Specific humidity analysis (colors) for E2 1H-3DEnVar at (a) 1600 UTC, (c) 1700 UTC, (e) 1800 UTC, and (g) 1900 UTC with pressure (contours) every 4 hPa and wind barbs overlaid. Regions of new dry air and dry air advected during forecasts are circled. Right column: Specific humidity (colors) and pressure (contours) increments for E2 1H-3DEnVar at (b) 1600 UTC, (d) 1700 UTC, (f) 1800 UTC, and (h) 1900 UTC. The main regions of negative Q increments are circled.
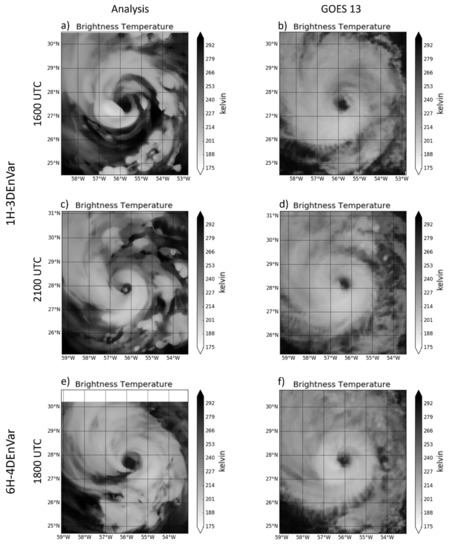
Figure 11.
Simulated brightness temperature from the E2 1H-3DEnVar analysis in (a,c) at 1600 UTC and 2100 UTC, respectively, and (e) 6H-4DEnVar analysis at 1800 UTC. Observed GOES 13 LWIR in (b,d,f) at 1600 UTC, 2100 UTC, and 1800 UTC 15 September 2014, respectively.
In addition to simulated satellite imagery, dropsonde data are used for in situ verification of the specific humidity. Figure 12 shows histograms of analysis specific humidity minus observation specific humidity for E2. 1H-3DEnVar (Figure 12c) analysis has a larger standard deviation (SD) of errors and a more negative (dry) mode than 6H-3DEnVar (Figure 12a) and 6H-4DEnVar (Figure 12b). In the cycle shown in this section, the anomalously dry regions contribute to weakening of the storm, which is consistent with the spindown seen in the forecast. The smaller SD in 6H-4DEnVar is similarly consistent with the improved performance during this cycle. This is consistent with the satellite imagery suggesting larger dry regions in the 1H-3DEnVar compared to the 6H-4DEnVar.
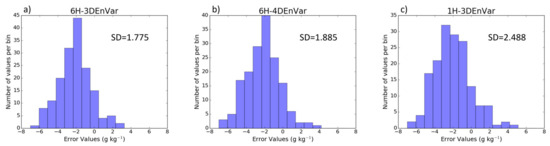
Figure 12.
Analysis specific humidity error for the 700–900 mb layer as calculated against dropsonde observations for batch E2 for (a) 6H-3DEnVar, (b) 6H-4DEnVar, (c) 1H-3DEnVar.
A small difference in storm location is observed between the model background and the satellite imagery and confirmed by wind speed innovations (Figure 13a,b). Due to a strong gradient in wind speed near the eyewall, a small location difference can lead to a large difference between the background and the observations. The TDR radial wind observations with absolute innovations > 10 m s−1 are shown in Figure 13 with the 1000 m background wind speed and pressure. In order to use the wind observations to update additional state variables, the cross-variable covariance is used. Because the dominant component of the wind increment is the meridional (U) component, ensemble cross-covariances between U and specific humidity is computed for a location representative of the large innovations shown in Figure 13b. Figure 13c shows that the largest positive cross-covariances for the sample observation are co-located with the largest specific humidity increments in Figure 10. As the U innovation is negative, the positive cross-covariance leads to drying, which is consistent with the sign of the increments in Figure 10. This result suggests that the difference in storm location between the relocated background and the observations is responsible for the drying through the innovations and cross-variable covariances. A similar cross-covariance pattern exists for 6H-4DEnVar, but the drying problem is not as severe. As suggested further in Section 5.3, the magnitude of the cross-covariances is larger in 1H-3DEnVar than in 6H-4DEnVar. The innovation in 1H-3DEnVar is also larger than in 6H-4DEnVar. Both are attributed to the under-dispersiveness of storm locations in the 1H-4DEnVar background ensemble.
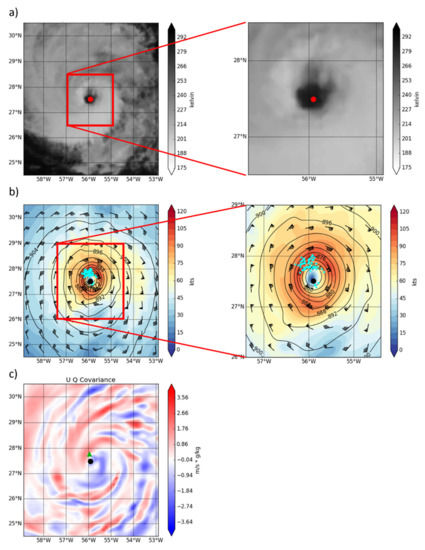
Figure 13.
(a) GOES 13 long wave infrared Satellite imagery with TCVital (red) overlaid. (b) 1H-3DEnVar E2 at 1700 UTC wind analysis (colors and barbs) overlaid with wind speed increments > 10 m/s (blue dots) and TCVital (black). (c) 1700 UTC 1H-3DEnVar Ensemble cross-covariance between U wind speed and specific humidity (Q) for a sample observation (green triangle) corresponding to the region of large innovations. TCVital overlaid (Black dot).
5.3. Underdispersive Ensemble of Storm Center Locations
Diagnostics show that the drying issue is likely associated with the underdispersive location spread of the ensemble, leading to insufficient correct of storm location and therefore poor storm location in the control background of 1H-3DEnVar. Such a poor location in the control leads to large innovation shown in Figure 13. Figure 14 shows that the 1H-3DEnVar background ensemble is consistently more under-dispersive compared to 6H-4DEnVar, although both use the same RTPS ensemble inflation. When the ensemble is underdispersive, the observation is under-utilized, leading to a smaller than optimal storm location update. Such a suboptimal update will lead to large innovation seen in Figure 13 for observations near large gradients in the observed variable. The 6H-4DEnVar ensemble is also underdispersive, however the spread to error ratio is larger than in 1H-3DEnVar. As a result, 6H-4DEnVar does not experience the same problems with poor location updates. The underspersiveness in the one-hourly ensemble appears to develop due to slow growth of the ensemble spread during the 1 h forecast. Hamill and Whitaker (2011) [48] similarly demonstrated that ensemble perturbation growth rate can be slow for EnKF initilaized forecasts espeically for short lead times.
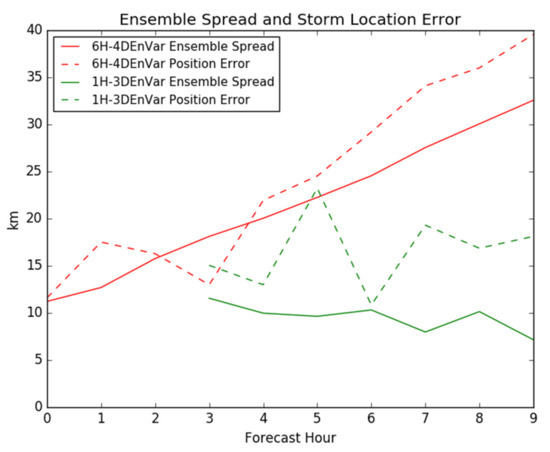
Figure 14.
Ensemble spread (solid lines) and mean background position error (dotted lines) for 6H-4DEnVar (red) and 1H-3DEnVar (green) by forecast hour.
To test the hypothesis that the suboptimal DA analysis resulting from poor background storm location due to underdispersive location spread is leading to spindown in the 1H-3DEnVar, additional experiments are conducted. Both 1H-3DEnVar and 6H-4DEnVar are rerun. To isolate the impact of location error, all backgrounds are relocated to the satellite derived storm centers. Using the satellite derived storm centers reduces the position error associated with the linear interpolation of TCVitals. As 6H-3DEnVar does not use hourly relocation, and the six-hourly tcvitals are in agreement with the satellite locations, 6H-3DEnVar is not rerun with the satellite data derived location. Figure 15 shows reduced spindown in 1H-3DEnVar-sl compared to 1H-3DEnVar. This is consistent with the hypothesis that position error plays a crtical role in the spindown of 1H-3DEnVar. However, the 1H-3DEnVar-sl continues to produce a weaker Vmax than other experiments during peak storm intensity, and no improvement is seen in 1H-3DEnVar-sl MSLP forecast compared to 1H-3DEnVar. Further, there was some improvement in 6H-4DEnVar-sl analysis compared to 6H-4DEnVar. This suggests that both the 1H-3DEnVar and 6H-4DEnVar systems could benefit from improved VR strategies.
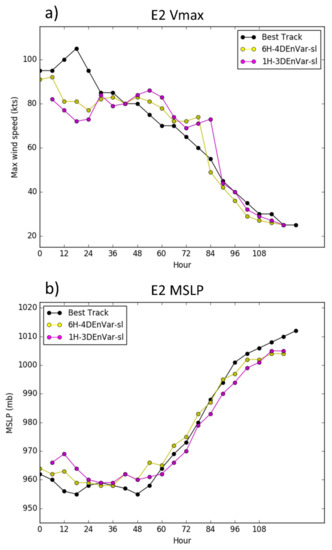
Figure 15.
Vmax (a) and MSLP (b) for E2 using satellite derived locations during VR.
6. Summary and Discussion
The six-hourly four-dimensional and one-hourly three-dimensional EnVar are compared with the six-hourly three-dimensional EnVar for the assimilation of the inner core TDR observations for hurricane prediction. Experiments are conducted using hurricane Edouard (2014) to evaluate the impact of accounting for the evolution of background error covariance in hurricanes with rapidly evolving BEC. Specifically, one-hourly 3DEnVar and six-hourly 4DEnVar are proposed as alternatives to the six-hourly Hybrid-3DEnVar system that uses stationary covariances over the 6 h DA window. Furthermore, the two approaches that both take into account of the rapid background error covariance evolution, one-hourly Hybrid-3DEnVar and six-hourly Hybrid-4DEnVar, are intercompared. 6H-3DEnVar is seen to produce the worst analyses, often with spuriously strong wind maxima and pressure minima. 6H-3DEnVar analyses have the largest RMSE when verified against independent SFMR and dropsonde observations. Structure correlation shows a similar result but with a small difference in magnitude. These results suggest that both 6H-4DEnVar and 1H-3DEnVar produce better analyses than 6H-3DEnVar, supporting the hypothesis that accounting for background evolution when the background is evolving rapidly improves the analysis. Comparing 6H-4DEnVar and 1H-3DEnVar analyses, the 6H-4DEnVar produced better moisture analyses than 1H-3DEnVar, particularly in cases where 1H-3DEnVar experienced spindown in the forecast. Further diagnostics showed that the degraded moisture analyses were responsible for the spindown that degraded the 1H-3DEnVar forecasts.
During the forecast, simulated reflectivity and SFMR wind speed suggest that 6H-3DEnVar in general does not perform as well as 1H-3DEnVar and 6H-4DEnVar. Vmax and MSLP forecast by 6H-3DEnVar is in general inferior to that of 1H-3DEnVar and 6H-4DEnVar. Additionally, although 6H-3DEnVar shows a similar slope of the Vmax and MLSP relationship to best track, 6H-3DEnVar shows a bias toward strong storms.
1H-3DEnVar has a larger weak bias than 6H-4DEnVar. These issues appear to be related to spindown seen in the 1H-3DEnVar forecast where Vmax weakens, and there is no notable corresponding increase in MSLP. This spindown was shown to be a result of poorly predicted storm locations in the relocated background that lead to a poor moisture analysis and subsequent spindown. A strong wind gradient exists in the transition from eye to eyewall, and a slight dislocation between the observations and the background can result in large innovations. This problem is further exacerbated by an underdispersive 1H-3DEnVar ensemble of storm center locations. As a result, little update to the background storm center occurs during VR. To prove this hypothesis, additional experiments were conducted to relocate all background members to the best possible TC locations. Given the temporal frequency limitation of the TCVitals, satellite derived storm centers were used in 1H-3DEnVar. Spindown of 1H-3DEnVar is largely alleviated with the improved VR.
Initial cost analysis including both CPU hours and IO shows that the cost of 1H-3DEnVar is about 5 times that of 6H-3DEnVar. Breakdown of the individual components of the cost analysis show that the 5 times increase is primarily due to increased utilization of vortex relocation on an hourly basis and the hourly IO associated with shorter cycles. Similar analysis shows that 6H-4DEnVar is around 2.5–3 times more expensive than 6H-3DEnVar. Analysis of the individual components of the cost suggests this is primarily due to the use of VR component on hourly backgrounds. Without considering VR, 4DEnVar is only about 1.5 times as expensive as 6H-3DEnVar. This 50% cost increase in 6H-4DEnVar is attributed to the increased IO associated with hourly backgrounds and the 9 h background ensemble forecasts.
In summary, both 6H-4DEnVar and 1H-3DEnVar perform better than 6H-3DEnVar by most verification metrics in both the analysis and early forecast but become similar after about 48 h. Most differences between 6H-4DEnVar and 1H-3DEnVar are small except for (1) Moisture analysis, (2) spindown. Diagnostics suggests that improved vortex relocation can further reduce the differences between 6H-4DEnVar and 1H-3DEnVar. As a first attempt to understand 6H-3DEnVar, 6H-4DEnVar and 1H-3DEnVar, a case study is performed. Systematic experimentation with more storms are needed for further studies.
Author Contributions
Conceptualization, B.D. and X.W.; methodology, B.D. and X.W.; software, B.D., X.L. and X.W.; validation, B.D.; formal analysis, B.D. and X.W.; investigation, B.D., X.W. and X.L.; resources, X.W.; data curation, B.D., X.L. and X.W.; writing—original draft preparation, B.D.; writing—review and editing, B.D., X.W. and X.L.; visualization, B.D.; supervision, X.W.; project administration, X.W.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NOAA grants NA14NWS4680021 and NA16NWS4680028.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data and codes produced during this study have been archived locally and are available upon request to the corresponding author.
Acknowledgments
The computing for this project was performed at the OU Supercomputing Center for Education & Research (OSCER) at the University of Oklahoma, GOES Satellite imagery was obtained via the NOAA Comprehensive Large Array-DATA Stewardship System (CLAss). Tail Doppler Radar (TDR) data produced by NOAA Hurricane Research Division of AOML.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Van Thu, T.; Krishnamurti, T.N. Vortex initialization for typhoon track prediction. Theor. Appl. Clim. 1992, 47, 117–126. [Google Scholar] [CrossRef]
- Bender, M.A.; Ross, R.J.; Tuleya, R.E.; Kurihara, Y. Improvements in Tropical Cyclone Track and Intensity Forecasts Using the GFDL Initialization System. Mon. Weather Rev. 1993, 121, 2046–2061. [Google Scholar] [CrossRef]
- Kurihara, Y.; Bender, M.A.; Ross, R.J. An Initialization Scheme of Hurricane Models by Vortex Specification. Mon. Weather Rev. 1993, 121, 2030–2045. [Google Scholar] [CrossRef]
- Zou, X.; Xiao, Q. Studies on the Initialization and Simulation of a Mature Hurricane Using A Variational Bogus Data Assimilation Scheme. J. Atmos. Sci. 1999, 57, 836–860. [Google Scholar] [CrossRef]
- Liu, Q.; Marchok, T.; Pan, H.-L.; Bender, M.; Lord, S. Improvements in Hurricane Initialization and Forecasting at NCEP with Global and Regional (GFDL) Models; NCEP Office Note: College Park, MD, USA, 2000; p. 472. [Google Scholar]
- Pu, Z.-X.; Braun, S.A. Evaluation of Bogus Vortex Techniques with Four-Dimensional Variational Data Assimilation. Mon. Weather Rev. 2001, 129, 2023–2039. [Google Scholar] [CrossRef]
- Torn, R.D.; Hakim, G.J. Ensemble Data Assimilation Applied to RAINEX Observations of Hurricane Katrina (2005). Mon. Weather Rev. 2009, 137, 2817–2829. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y.; Sippel, J.A.; Meng, Z.; Bishop, C. Cloud-Resolving Hurricane Initialization and Prediction through Assimilation of Doppler Radar Observations with an Ensemble Kalman Filter. Mon. Weather Rev. 2009, 137, 2105–2125. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Fiorino, M.; Benjamin, S. Global Ensemble Predictions of 2009′s Tropical Cyclones Initialized with an Ensemble Kalman Filter. Mon. Weather Rev. 2011, 139, 668–688. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y.; Gamache, J.; Marks, F. Performance of convection-permitting hurricane initialization and prediction during 2008–2010 with ensemble data assimilation of inner-core airborne Doppler radar observations. Geophys. Res. Lett. 2011, 38, 2–7. [Google Scholar] [CrossRef]
- Aksoy, A.; Aberson, S.D.; Vukićević, T.; Sellwood, K.J.; Lorsolo, S.; Zhang, X. Assimilation of High-Resolution Tropical Cyclone Observations with an Ensemble Kalman Filter Using NOAA/AOML/HRD’s HEDAS: Evaluation of the 2008–11 Vortex-Scale Analyses. Mon. Weather Rev. 2013, 141, 1842–1865. [Google Scholar] [CrossRef]
- Aksoy, A.; Lorsolo, S.; Vukićević, T.; Sellwood, K.J.; Aberson, S.D.; Zhang, F. The HWRF Hurricane Ensemble Data Assimilation System (HEDAS) for High-Resolution Data: The Impact of Airborne Doppler Radar Observations in an OSSE. Mon. Weather Rev. 2012, 140, 1843–1862. [Google Scholar] [CrossRef]
- Weng, Y.; Zhang, F. Assimilating Airborne Doppler Radar Observations with an Ensemble Kalman Filter for Convection-Permitting Hurricane Initialization and Prediction: Katrina (2005). Mon. Weather Rev. 2012, 140, 841–859. [Google Scholar] [CrossRef]
- Dong, J.; Xue, M. Assimilation of radial velocity and reflectivity data from coastal WSR-88D radars using an ensemble Kalman filter for the analysis and forecast of landfalling hurricaneIke (2008). Q. J. R. Meteorol. Soc. 2012, 139, 467–487. [Google Scholar] [CrossRef]
- Poterjoy, J.; Zhang, F. Intercomparison and Coupling of Ensemble and Four-Dimensional Variational Data Assimilation Methods for the Analysis and Forecasting of Hurricane Karl (2010). Mon. Weather Rev. 2014, 142, 3347–3364. [Google Scholar] [CrossRef]
- Hamill, T.M.; Snyder, C. A Hybrid Ensemble Kalman Filter—3D Variational Analysis Scheme. Mon. Weather Rev. 2000, 128, 2905–2919. [Google Scholar] [CrossRef]
- Lorenc, A.C. The potential of the ensemble Kalman filter for NWP—A comparison with 4D-Var. Q. J. R. Meteorol. Soc. 2003, 129, 3183–3203. [Google Scholar] [CrossRef]
- Wang, X.; Barker, D.M.; Snyder, C.; Hamill, T.M. A Hybrid ETKF-3DVAR Data Assimilation Scheme for the WRF Model. Part I: Observing System Simulation Experiment. Mon. Weather Rev. 2008, 136, 5116–5131. [Google Scholar] [CrossRef]
- Wang, X.; Barker, D.; Snyder, C.; Hamill, T.M. A Hybrid ETKF–3DVAR Data Assimilation Scheme for the WRF Model. Part II: Real Observation Experiments. Mon. Weather Rev. 2008, 136, 5132–5147. [Google Scholar] [CrossRef]
- Wang, X.; Parrish, D.; Kleist, D.T.; Whitaker, J.S. GSI 3DVar-Based Ensemble—Variational Hybrid Data Assimilation for NCEP Global Forecast System: Single-Resolution Experiments. Mon. Weather Rev. 2013, 141, 4098–4117. [Google Scholar] [CrossRef]
- Wang, X. Incorporating Ensemble Covariance in the Gridpoint Statistical Interpolation Variational Minimization: A Mathematical Framework. Mon. Weather Rev. 2010, 138, 2990–2995. [Google Scholar] [CrossRef]
- Wang, X. Application of the WRF Hybrid ETKF–3DVAR Data Assimilation System for Hurricane Track Forecasts. Weather Forecast. 2011, 26, 868–884. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Liu, Z.; Huang, X.-Y. Sensitivity of Limited-Area Hybrid Variational-Ensemble Analyses and Forecasts to Ensemble Perturbation Resolution. Mon. Weather Rev. 2015, 143, 3454–3477. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Liu, Z.; Huang, X.-Y.; Kuo, Y.-H.; Fong, C.-T. Comparing Limited-Area 3DVAR and Hybrid Variational-Ensemble Data Assimilation Methods for Typhoon Track Forecasts: Sensitivity to Outer Loops and Vortex Relocation. Mon. Weather Rev. 2013, 141, 4350–4372. [Google Scholar] [CrossRef]
- Wang, X.; Lei, T. GSI-Based Four-Dimensional Ensemble–Variational (4DEnsVar) Data Assimilation: Formulation and Single-Resolution Experiments with Real Data for NCEP Global Forecast System. Mon. Weather Rev. 2014, 142, 3303–3325. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Xue, M. Assimilation of Radar Radial Velocity Data with the WRF Hybrid Ensemble—3DVAR System for the Prediction of Hurricane Ike (2008). Mon. Weather Rev. 2012, 140, 3507–3524. [Google Scholar] [CrossRef]
- Li, X.; Ming, J.; Xue, M.; Wang, Y.; Zhao, K. Implementation of a dynamic equation constraint based on the steady state momentum equations within the WRF hybrid ensemble—3DVar data assimilation system and test with radar T-TREC wind assimilation for tropical Cyclone Chanthu (2010). J. Geophys. Res. Atmos. 2015, 120, 4017–4039. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Li, Y.; Tong, M.; Ma, X. GSI-based ensemble-variational hybrid data assimilation for HWRF for hurricane initialization and prediction: Impact of various error covariances for airborne radar observation assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 223–239. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Tong, M.; Tallapragada, V. GSI-Based, Continuously Cycled, Dual-Resolution Hybrid Ensemble—Variational Data Assimilation System for HWRF: System Description and Experiments with Edouard (2014). Mon. Weather Rev. 2017, 145, 4877–4898. [Google Scholar] [CrossRef]
- Zhang, S.; Pu, Z. Numerical Simulation of Rapid Weakening of Hurricane Joaquin with Assimilation of High-Definition Sounding System Dropsondes during the Tropical Cyclone Intensity Experiment: Comparison of Three- and Four-Dimensional Ensemble—Variational Data Assimilation. Weather Forecast. 2019, 34, 521–538. [Google Scholar] [CrossRef]
- Poterjoy, J.; Zhang, F.; Weng, Y. The Effects of Sampling Errors on the EnKF Assimilation of Inner-Core Hurricane Observations. Mon. Weather Rev. 2014, 142, 1609–1630. [Google Scholar] [CrossRef]
- Poterjoy, J.; Zhang, F. Comparison of Hybrid Four-Dimensional Data Assimilation Methods with and without the Tangent Linear and Adjoint Models for Predicting the Life Cycle of Hurricane Karl (2010). Mon. Weather Rev. 2016, 144, 1449–1468. [Google Scholar] [CrossRef]
- Evensen, G. Analysis of iterative ensemble smoothers for solving inverse problems. Comput. Geosci. 2018, 22, 885–908. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Ensemble Data Assimilation without Perturbed Observations. Mon. Weather Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Liu, Q.; Lord, S.; Surgi, N.; Zhu, Y.; Wobus, R.; Toth, Z.; Marchok, T. Hurricane Re-location in Global Ensemble Forecast System. In Proceedings of the 27th Conference on Hurricanes and Tropical Meteorology, Monterey, CA, USA, 23–28 April 2006; Available online: https://ams.confex.com/ams/pdfpapers/108503.pdf (accessed on 16 July 2019).
- Wang, X.; Snyder, C.; Hamill, T.M. On the Theoretical Equivalence of Differently Proposed Ensemble—3DVAR Hybrid Analysis Schemes. Mon. Weather Rev. 2007, 135, 222–227. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Trahan, S.; Sparling, L. An Analysis of NCEP Tropical Cyclone Vitals and Potential Effects on Forecasting Models. Weather Forecast. 2012, 27, 744–756. [Google Scholar] [CrossRef]
- Tong, M.; Sippel, J.A.; Tallapragada, V.; Liu, E.; Kieu, C.; Kwon, I.-H.; Wang, W.; Liu, Q.; Ling, Y.; Zhang, B. Impact of Assimilating Aircraft Reconnaissance Observations on Tropical Cyclone Initialization and Prediction Using Operational HWRF and GSI Ensemble—Variational Hybrid Data Assimilation. Mon. Weather Rev. 2018, 146, 4155–4177. [Google Scholar] [CrossRef]
- Chen, Y.; Snyder, C. Assimilating Vortex Position with an Ensemble Kalman Filter. Mon. Weather Rev. 2007, 135, 1828–1845. [Google Scholar] [CrossRef]
- Yang, S.-C.; Lin, K.-J.; Miyoshi, T.; Kalnay, E. Improving the spin-up of regional EnKF for typhoon assimilation and forecasting with Typhoon Sinlaku (2008). Tellus A Dyn. Meteorol. Oceanogr. 2013, 65, 20804. [Google Scholar] [CrossRef][Green Version]
- Tallapragada, V.; Gopalakrishnan, S.G.; Liu, Q.; Marchok, T.P. Hurricane Weather Research and Forecasting (HWRF) Model: 2014 Scientific Documentation; Technical Report; Developmental Testbed Center: Boulder, CO, USA, 2014; pp. 1–105. Available online: https://dtcenter.org/sites/default/files/community-code/hwrf/docs/scientific_documents/HWRFv3.6a_ScientificDoc.pdf (accessed on 7 March 2017).
- Tallapragara, V.; Bernardet, L.; Biswas, M.; Ginis, I.; Kwon, Y.; Liu, Q.; Marchok, T.; Sheinin, D.; Thomas, B.; Tong, M.; et al. Hurricane Weather Research and Forecasting (HWRF) Model: 2015 Scientific Documentation; UCAR/NCAR-Research Data Archive: Boulder, CO, USA, 2016; p. 105. [Google Scholar]
- Liu, Q.; Zhang, X.; Tong, M.; Zhang, Z.; Liu, B.; Wang, W.; Zhu, L.; Zhang, B.; Xu, X.; Trahan, S.; et al. Vortex Initialization in the NCEP Operational Hurricane Models. Atmosphere 2020, 11, 968. [Google Scholar] [CrossRef]
- Zhou, C.; Shao, H.; Ligia, B. Applications of the GSI-Hybrid Data Assimilation for High-Resolution Tropical Storm Forecasts: Tackling the intensity spindown issue in 2014 HWRF. In Proceedings of the 16th WRF Users Workshop, Boulder, CO, USA, 15–19 June 2015; Available online: https://dtcenter.org/eval/data_assim/publications/GSI-Hybridat2015WRFUsersWorkshop.v2poster.pdf (accessed on 10 July 2019).
- Gamache, J.F.; Franklin, J.; Surgi, N.; Liu, Q. Real-Time Dissemination of Hurricane Wind Fields Determined from Airborne Doppler Radar Data Real-Time Dissemination of Hurricane Wind Fields Determined; Technical Report; NOAA: Washington, DC, USA, 2005; 38p. Available online: http://www.nhc.noaa.gov/jht/2003-2005reports/DOPLRgamache_JHTfinalreport.pdf (accessed on 16 July 2019).
- Lu, X.; Wang, X. Improving Hurricane Analyses and Predictions with TCI, IFEX Field Campaign Observations, and CIMSS AMVs Using the Advanced Hybrid Data Assimilation System for HWRF. Part I: What is Missing to Capture the Rapid Intensification of Hurricane Patricia (2015) when HWRF is already Initialized with a More Realistic Analysis? Mon. Weather Rev. 2019, 147, 1351–1373. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S. What Constrains Spread Growth in Forecasts Initialized from Ensemble Kalman Filters? Mon. Weather Rev. 2011, 139, 117–131. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).