Multidirectional Dynamic Response and Swing Shedding of Grapes: An Experimental and Simulation Investigation under Vibration Excitation

Abstract

During mechanized table grape harvesting, berries are subjected to vibration and collision, which can cause shedding and damage to the fruit. Research on table grape berry shedding has primarily focused on macroscopic swing modes, which are reflected in the integrated grape cluster structure and idealized particle interactions, as well as static response treatments. However, these approaches are unable to accurately explain the characteristics of berry wobbling during picking, predict shedding-prone areas, or identify factors affecting shedding. In this paper, we study the dynamic response characteristics of grape berries in the X, Y, and Z directions by establishing a dynamic model and combining harmonic response and random vibration characteristics with finite element analysis. Our studies revealed that grape berries exhibit various forms (swinging and rebounding) under the same stimulus during harvesting. The grape berry amplitude in the X, Y, and Z directions were 14.71, 12.46, and 27.10 mm, respectively, with the most obvious response being in the Z direction and the flattest response in the Y direction. Berries in the lower cob system part were relatively stable, while those in the upper right side were more prone to swinging and falling, with areas most likely to fall off concentrated in the upper right side. This system accurately predicted the dynamic response characteristics of fruit during vibration harvesting and provided an ideal basis for mechanized grape harvesting. Optimization and research on fruit collection equipment may benefit from this theoretical basis.

1. Introduction

Non-destructive fruit picking is an important challenge in mechanical and automatic harvesting, particularly for thin-skinned, multigrain berry fruits such as grapes. As they are fresh fruits, it is crucial to study non-destructive harvesting methods for grapes. However, as a seasonal plant, grape growth is greatly influenced by environmental factors, which often overlap with the experimental and harvest cycles. The harvest cycle is usually determined by the season or year, and a shorter harvest cycle can increase labor costs [1]. Mechanized harvesting is the most effective method for stalk plants, but the shaking and falling of berries during the harvesting process can damage the integrity of grape bunches, which ultimately affects the economic value of table grapes [2,3]. Therefore, studying the dynamic responses of grapes during harvest is essential to achieving low-damage or non-damaging picking.

To date, research on automatic grape picking is mainly focused on grape fruit positioning and identification [4,5,6,7], fruit stem picking point positioning [8,9,10], and robot arm path planning anti-collision problems. There are few studies on the picking mechanism, vibration excitation after contact with the fruit stem, and a series of excitation responses caused by this process [11,12]. The location of the picking point is realized by three-dimensional positioning [13,14,15]. Through related stalk fruit picking harvests, Van Henten et al. [16] analyzed harvesting and found that the low positioning accuracy of the end effector on the fruit stem was the main factor affecting the low picking efficiency. Based on this research, an autonomous harvesting robot capable of picking a single cucumber from different harvesting positions was developed, greatly increasing the success rate. Li et al. [17] studied a manual apple robot by statistically analyzing the minimum gripping pressure and corresponding damage degree of the picked fruit; the researchers selected a reasonable mechanical harvesting method. Additionally, some statistical separation parameters were used to describe fruit separation and to finally realize effective robot picking using three-finger gripper recognition. To study efficient and harmless picking of apples and the fruit shedding mode, Bu et al. [18] analyzed the effects of four basic picking methods—horizontal stretching, vertical stretching, bending, and twisting—on fruit shedding. The results showed that tension parameters, such as horizontal tension and vertical tension during harvest, were the main factors affecting fruit separation, and fruits that experienced tangential force were more likely to fall off. Moreover, the optimization results showed that horizontal pulling with bending and twisting motions was a potentially optimal combination, and these results provided a theoretical basis for future research on robotic apple picking. Davidson et al. [19] evaluated the manual apple picking technology. In this study, apples grown in several environments were selected, and sensors including force sensors and inertial measurement units were used to obtain fruit swing information. The normal contact force and rotation angle during three-finger power grasping were obtained, providing a basis to select apple picking modes. Zhou et al. [20] analyzed the kinematic response of the ginkgo system during mechanized harvesting and the separation force obtained by fruit separation. First, finite element analysis was performed on the harvested ginkgo to obtain the mode shape and natural frequency range of the seed–stem system. Finally, the variability model of the dynamic responses of the ginkgo stem system under different vibration parameters was studied as a basis. The results showed that the main resonance frequency of the seed–stem system under horizontal excitation approached the natural frequency. Under vertical excitation, when the excitation acceleration exceeded the gravitational acceleration, the seed–stem system bounced violently, providing a theoretical guidance for the mechanical vibration harvesting of ginkgo seeds. To analyze the kinetic characteristics of Camellia oleifera during harvesting, Chen et al. [21] established a three-degree-of-freedom model of forced vibration under canopy shaking conditions; a camellia tree solid model was established in SolidWorks and ANSYS, and the multimodal harmonic response simulation of Camellia oleifera was simulated using a finite element model. The simulation results were compared with those of the dynamic model, and the validity of the three-degree-of-freedom forced vibration system model was verified. Zhou et al. [22] designed a vibration device to test the three excitation modes—horizontal, vertical, and rotation—to study the dynamic responses and shedding frequencies of jujube fruit. The researchers found that the response of fruit under horizontal excitation was mainly swinging; however, the frequency of fruit shedding was small. Under vertical excitation, the fruit response was more complex, mainly comprising swinging and twisting compound motions. With an increase in harvest incentives, the frequency of fruit shedding gradually decreased. The best excitation method for jujube was vertical excitation with an amplitude of 10 mm and a frequency of 6–10 Hz. Yan et al. [23] first deduced the theoretical angular velocity of fruit shedding by establishing a grape fruit–stem dynamic model. Then, ABAQUS software was used to conduct vibration finite element analysis on the simplified model of grapes and obtain critical shedding parameters such as the displacement, velocity, acceleration, and stress and strain of grape berries. The grape berries began to fall off when the swing amplitude was 49.88 mm, the peak velocity was 0.92 mm/s, and the peak acceleration was 39.08 mm/s². This research could provide a theoretical basis for the parameter design of the anti-falling picking mechanism. Peng used finite element method (FEM) explicit dynamics combined with experiments and modal analysis to study and simulate the dynamic response of the jujube fruit–stem system under harvest vibration conditions. The researchers found that the greater the vibration amplitude of the jujube fruit, the greater the maximum stress on the stem; and the location of the maximum stress depended on the vibration direction.

The above research shows that microscopic research on stalk fruits is of great significance in optimizing picking mechanisms, predicting shedding and damage, and constructing simulation experiment systems. Compared to non-berry or non-bunch fruits, such as apples, cucumbers, and ginkgos, research on the microvibration excitation model of thin-skinned, multigrain berry fruits represented by table grapes is more meaningful. However, the actual harvest of table grapes inevitably creates incentives that cause berry drop at maturity. Recent academic research mainly focuses on the macroscopic performance of the fruit. However, the swinging and jumping of string-shaped fruits are macroscopic manifestations of X-, Y-, and Z-axis excitation. To accurately analyze the response forms of fruits, it is necessary to study the dynamic responses of fruits in the X, Y, and Z directions under harvest excitation, which are lacking in existing research.

Grape swinging with many fruits is nonlinear and multidirectional, and the macroscopic performance of grape berry swinging alone cannot accurately describe fruit shedding under harvest incentives. By studying the dynamic responses of grape berries in the X, Y, and Z directions under the extrusion state, we can better predict the tendency of the berries to swing and fall off. In this paper, the swing and vibration models of grapes are established, and the swing equation of berries is theoretically deduced. Then, a finite element model is established based on grape berries under extrusion, and the random and harmonic response vibration characteristics of the berries are analyzed. Under the same stimulus, the expression forms and easy-shedding areas of berries in different directions are studied.

2. Material and Methods

2.1. Establishment of the Grape Swing Model

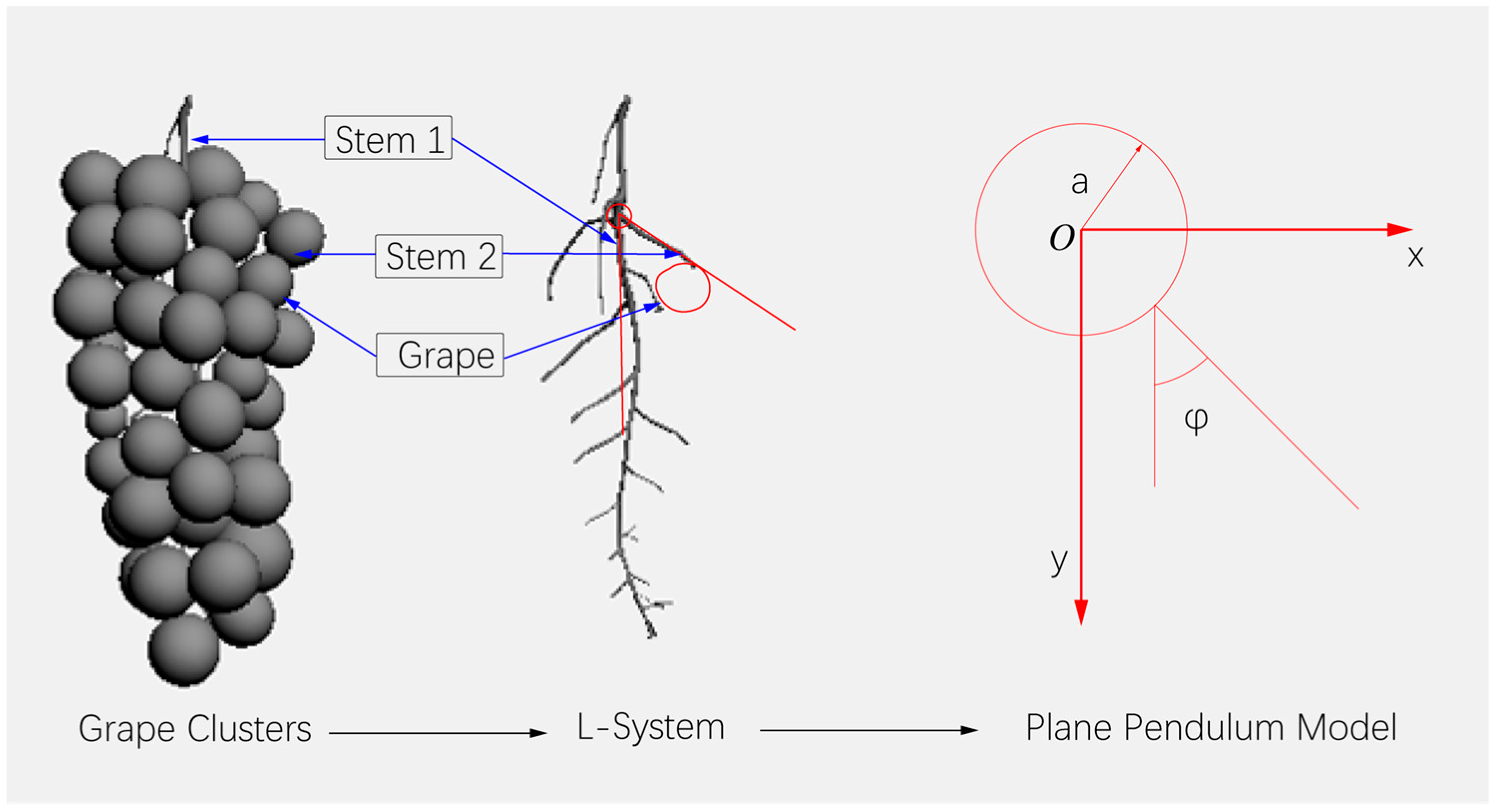
Grapes in the natural environment are multigrain, squeezed, and affected by climate, light and other factors, showing great differences in biomorphology [24]. This phenomenon results in various swing postures during harvesting; in general, the vibration responses of grapes have certain similarities. This vibration response is not strictly in the horizontal or vertical directions; however, the macroscopic effects of vibration are in the horizontal and vertical directions. Studying the vibration problem in grape harvesting involves studying the effects of horizontal and vertical vibration on grape fruits. In the actual harvest, the sudden cutting of the main cob of the grape inevitably produces cutting vibration; the original static state of the grape system composed of the fruit and the cob is broken. The grape system is composed of the fruit, fruit stem, main–substalk junction, and substalk end. The fixed connection point at the junction of the main stem and the substem is relatively hard; thus, the swing range is small. The substalks are soft, and the tip is more elastic. Under vibration, the swing range of the fruit is large, the trajectory is generally ellipse or quasiellipse, and the fruit often falls off at the tip. When the vibration generated by the harvest excitation is transmitted to each branch stem and fruit through the main cob, the grape fruit produces relative motion. Since both the substalks and the fruit swing relatively to the main stem, the grape swings in the vertical plane are under mostly plane single pendulum and plane double pendulum motions. The dynamic situation occurs in the vertical and horizontal direction. Therefore, we divided the fruit swing in the vertical plane into the swing in the vertical plane and in the horizontal plane for analysis.

The substalks in the plane pendulum model are long and often drive the junction of the main–substems to perform circular motions. The end of the second branch stem connects a mass ball with a certain quality $m_1$; this phenomenon is mainly reflected in the swinging and falling off of the fruit during swing, and the fruit stem is not pulled off, as shown in Figure 1. The plane pendulum system includes substem l and the fruit composition. The fruit particles in the model are all isotropic grape balls; the center of the main–substem junction is taken, and the horizontal direction and vertical direction are considered as x and y, O is the junction of the main stem and the sub-stem, and a is the maximum swing range of the junction, respectively.

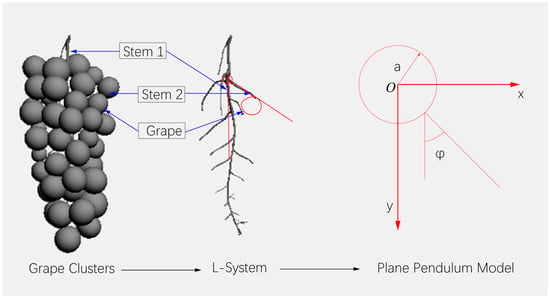
Figure 1. Grape plane pendulum model.

At time t, the fruit vibrates to a certain position, the angle between the fruit and the vertical direction is $\phi$, and the coordinates of the mass point m are as follows:

The Lagrangian function is obtained as follows:

$$x=a\cos \gamma t+l\sin \phi$$

(1)

$$y=-a\sin \gamma t+l\cos \phi$$

(2)

The Lagrangian function is obtained as follows:

$$L=\frac{m{l}^2}{2}{\dot{\phi }}^2+mla{\gamma }^2\sin (\phi -\gamma t)+mgl\cos \phi$$

(3)

The swing time in the picking process is extremely short. For the convenience of analysis, the items that only depend on time and that can be written as $mla\gamma \cos (\phi -\gamma t)$, which is the total derivative with respect to time, are omitted.

The swinging amplitude of the fruit is small, and the energy tends to attenuate; thus, the vibration of the fruit is a microvibration model, and the motion equation of the microvibration is $\phi <<1$:

$$\ddot{\phi }+{\omega }_0^2\left[1+4\frac{a}{l}\cos \left(2{\omega }_0+\epsilon \right)t\right]\phi =0$$

(4)

where ${\omega }_0^2=g/l$. According to $4a/l$, the size of the amplitude is determined.

The fruit–stalk swinging system is a non-closed vibrating system, and the cutting force that causes the system to vibrate varies with time. Parametric resonance occurs when the cob and fruit swing frequencies are near each other during the swing process:

$$s^2=\frac{1}{4}\left[{\left(\frac{h{\omega }_0}{2}\right)}^2-{\epsilon }^2\right]>0$$

(5)

Therefore, parametric resonance occurs in $2{\omega }_0$, which is the interval on both sides of the frequency:

$$-\frac{h{\omega }_0}{2}<\epsilon <\frac{h{\omega }_0}{2}$$

(6)

The width of this interval is proportional to the amplitude h, and the value of the vibration amplification factor s in this interval is the magnitude of the amplitude, taking the following form:

$$|\epsilon |<\frac{2a\sqrt{g}}{l^{3/2}}$$

(7)

The vibration of the grape fruit is decomposed into regular $a\cos \gamma t$ horizontal vibration and vertical vibration.

To analyze the vibration in the horizontal direction, the coordinates of the mass point m are as follows:

$$x=a\cos \gamma t+l\sin \phi$$

(8)

$$y=l\cos \phi$$

(9)

The Lagrange function after omitting the full derivative term is as follows:

$$L=\frac{m{l}^2}{2}{\dot{\phi }}^2+mla{\gamma }^2\cos \gamma t\sin \phi +mgl\cos \phi$$

(10)

where the variable force in the horizontal direction is as follows:

$$f=mla{\gamma }^2\cos \gamma t\cos \phi$$

(11)

Then, the following equation is obtained:

$$U_{\mathrm{eff}}=mgl\left[-\cos \phi +\frac{a^2{\gamma }^2}{4gl}{\cos }^2\phi \right]$$

(12)

If $a^2{\gamma }^2<2gl$, the equilibrium position of the $\phi =0$ grape fruit is considered stable. If $a^2{\gamma }^2>2gl$, the stable equilibrium position corresponds to the following equation:

$$\cos \phi =\frac{2gl}{a^2{\gamma }^2}$$

(13)

This equation is stable, and the vibration is continuous.

By analyzing the vibration in the vertical direction, the Lagrangian function of the vertical vibration is obtained:

$$L=\frac{m{l}^2}{2}{\dot{\phi }}^2+mla{\gamma }^2\cos \gamma t\cos \phi +mgl\cos \phi$$

(14)

The variables in this case are as follows:

$$f=-mla{\gamma }^2\cos \gamma t\sin \phi$$

(15)

Variable x is represented by angle $\phi$; thus, the effective potential energy of swinging in the vertical direction is as follows:

$$U_{\mathrm{eff}}=mgl\left(-\cos \phi +\frac{a^2{\gamma }^2}{4gl}{\sin }^2\phi \right)$$

(16)

The stable equilibrium position of the fruit swing corresponds to the minimum value of this function. The vertical downwards position ($\phi =0$) is always stable if the following condition is satisfied.

$$a^2{\gamma }^2>2gl$$

(17)

Then, the vertical upwards position ($\phi =\pi$) is stable.

The vibration of grape fruit under cutting excitation is divided into horizontal vibration and vertical vibration. When satisfying $a^2{\gamma }^2>2gl$, both the horizontal direction and the vertical direction reach a stable equilibrium position. According to Equation (17), the balance in vertical vibration shows that the position is easier to reach; that is, the vertical upwards vibration in the swing model is more stable than the vertical downwards vibration. Thus, the bouncing and falling off of the fruit are mainly vertical downwards in the macroscopic view.

In the actual picking operation, the corresponding shearing tool contacts with the main cobs of grapes after positioning, and the grapes start to vibrate.

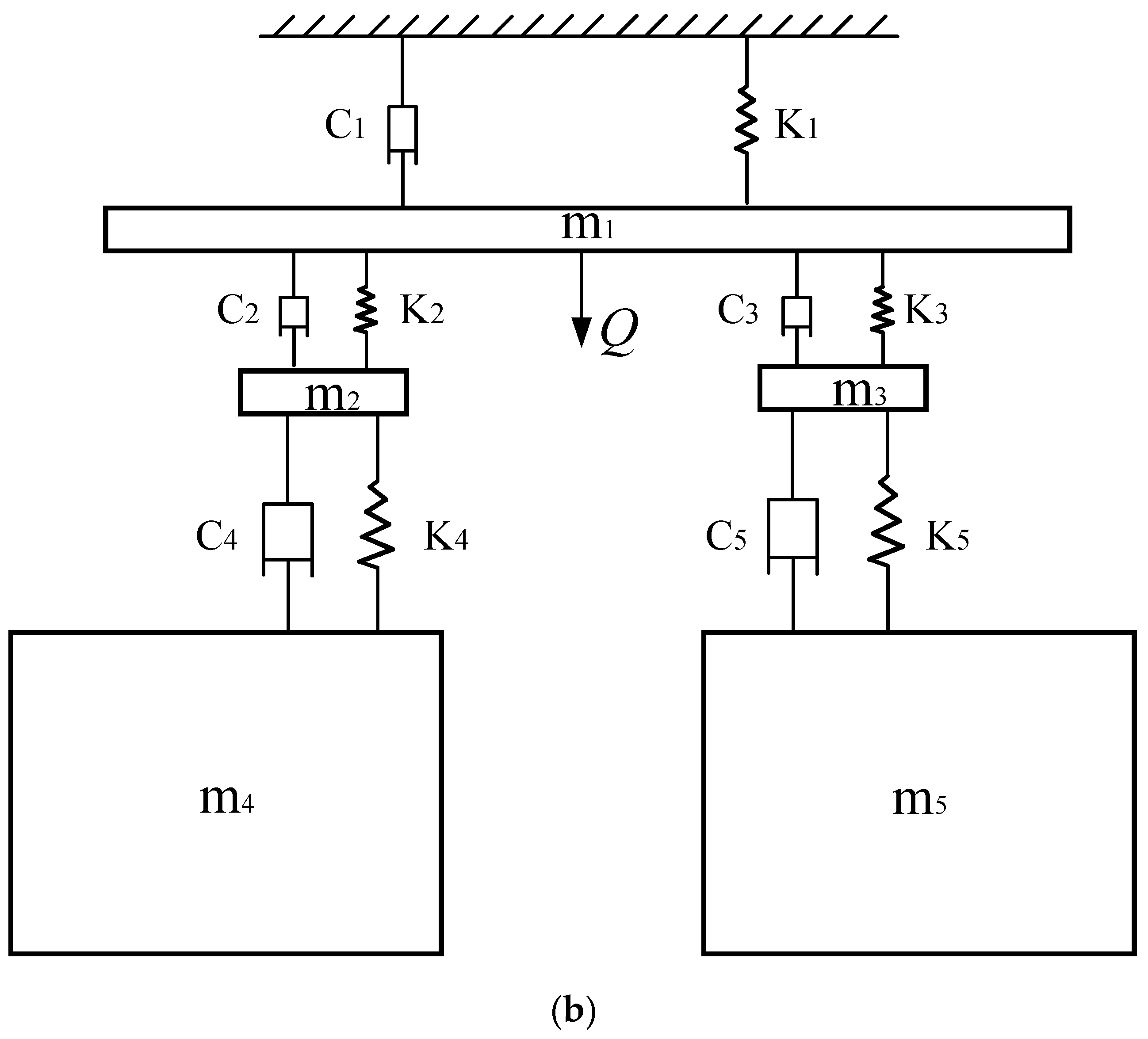
2.2. Establishment of the Grape Vibration Model

On the basis of a series of studies on the structure and hand of grapes, as shown in Figure 2a, the vibration model of grapes was derived and optimized [25].

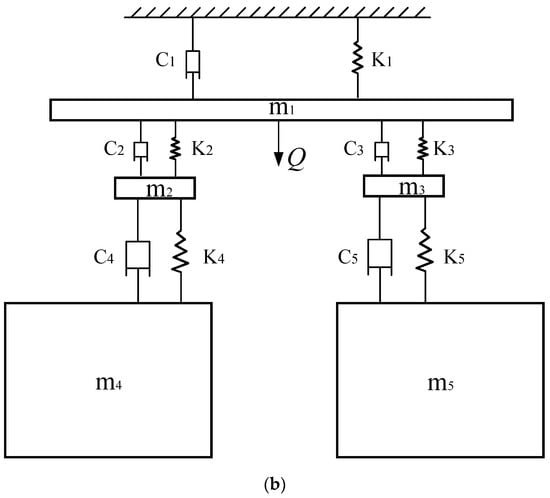
Figure 2. Development and dynamic model of the grape fruit–stem system oscillation. (a) The team studied the structure of the fruit. (b) Dynamic model of the grape fruit–stem system oscillation.

The main cob is connected to the vine through springs and dampers and to the subcobs on the left and right; the particles on the left and right sides are simplified into two mass blocks. Thus, a spring-five-mass-damping system is established, as shown Figure 2b, C stands for damping, K stands for stiffness, m stands for mass, and Q stands for vertical excitation.

The vibration differential equation of the fruit–stem system is as follows:

$$\left\{\begin{array}{l}{m}_1{\ddot{x}}_1=-c_1{\dot{x}}_1-k_1{x}_1+c_2\left({\dot{x}}_2-{\dot{x}}_1\right)+c_3\left({\dot{x}}_3-{\dot{x}}_1\right)+k_2\left(x_2-x_1\right)+k_3\left(x_3-x_1\right)\\ m_2{\ddot{x}}_2=-c_2\left({\dot{x}}_2-{\dot{x}}_1\right)-k_2\left(x_2-x_1\right)+c_4\left({\dot{x}}_4-{\dot{x}}_2\right)+k_4\left(x_4-x_2\right)\\ m_3{\ddot{x}}_3=-c_3\left({\dot{x}}_3-{\dot{x}}_1\right)-k_3\left(x_3-x_1\right)+c_5\left({\dot{x}}_5-{\dot{x}}_3\right)+k_5\left(x_5-x_3\right)\\ m_4{\ddot{x}}_4=-c_4\left({\dot{x}}_4-{\dot{x}}_2\right)-k_4\left(x_4-x_2\right)\\ m_5{\ddot{x}}_3=-c_5\left({\dot{x}}_5-{\dot{x}}_3\right)-k_5\left(x_5-x_3\right)\end{array}\right.$$

(18)

The deformations are as follows:

$$\left\{\begin{array}{l}{m}_1{\ddot{x}}_1+c_1{\dot{x}}_1+k_1{x}_1-c_2\left({\dot{x}}_2-{\dot{x}}_1\right)-c_3\left({\dot{x}}_3-{\dot{x}}_1\right)-k_2\left(x_2-x_1\right)-k_3\left(x_3-x_1\right)=Q\sin \omega t\\ m_2{\ddot{x}}_2+c_2\left({\dot{x}}_2-{\dot{x}}_1\right)+k_2\left(x_2-x_1\right)-c_4\left({\dot{x}}_4-{\dot{x}}_2\right)-k_4\left(x_4-x_2\right)=0\\ m_3{\ddot{x}}_3+c_3\left({\dot{x}}_3-{\dot{x}}_1\right)+k_3\left(x_3-x_1\right)-c_5\left({\dot{x}}_5-{\dot{x}}_3\right)-k_5\left(x_5-x_3\right)=0\\ m_4{\ddot{x}}_4+c_4\left({\dot{x}}_4-{\dot{x}}_2\right)+k_4\left(x_4-x_2\right)=0\\ m_5{\ddot{x}}_3+c_5\left({\dot{x}}_5-{\dot{x}}_3\right)+k_5\left(x_5-x_3\right)=0\end{array}\right.$$

(19)

where Q is the downwards component force along the vertical direction when cutting the fruit stem, which is transformed into a matrix form:

$$\begin{array}{l}\left[\begin{array}{ccccc}{m}_1& 0& 0& 0& 0\\ 0& m_2& 0& 0& 0\\ 0& 0& m_3& 0& 0\\ 0& 0& 0& m_4& 0\\ 0& 0& 0& 0& m_5\end{array}\right]\left[\begin{array}{l}{\ddot{x}}_1\hfill \\ {\ddot{x}}_2\hfill \\ {\ddot{x}}_3\hfill \\ {\ddot{x}}_4\hfill \\ {\ddot{x}}_5\hfill \end{array}\right]+\left[\begin{array}{ccccc}{c}_1+c_2+c_3& -c_2& -c_3& 0& 0\\ -c_2& c_2+c_4& 0& -c_4& 0\\ -c_3& 0& c_3+c_5& 0& -c_5\\ 0& -c_4& 0& c_4& 0\\ 0& 0& -c_5& 0& c_5\end{array}\right]\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ {\dot{x}}_4\\ {\dot{x}}_5\end{array}\right]+\left[\begin{array}{ccccc}{k}_1+k_2+k_3& -k_2& -k_3& 0& 0\\ -k_2& k_2+k_4& 0& -k_4& 0\\ -k_3& 0& k_3+k_5& 0& -k_5\\ 0& -k_4& 0& k_4& 0\\ 0& 0& -k_5& 0& k_5\end{array}\right]\\ \left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]=\left[\begin{array}{c}Q\\ 0\\ 0\\ 0\\ 0\end{array}\right]sin\omega t\end{array}$$

(20)

This equation is abbreviated as follows:

$$[M]\cdot \left\{\ddot{x}\right\}+[c]\left\{\dot{x}\right\}+[k]\left\{x\right\}=\left\{Q\right\}$$

(21)

According to the vibration system, $[M]$ is the mass matrix, $[c]$ is the damping matrix, and $[k]$ is the stiffness matrix, $\left\{x\right\}$, $\left\{\dot{x}\right\}$, and $\left\{\ddot{x}\right\}$ are the displacement vector, velocity vector, and acceleration vector, respectively, and $\left\{Q\right\}$ is the cutting force vector.

$$n=\frac{c}{2M}{\omega }_0=\sqrt{\frac{k}{M}}$$

(22)

Then, the following equation is obtained:

$$r_{1,2}=\frac{-2n\pm \sqrt{4n^2-4{\omega }_0^2}}{2}=-n\pm \sqrt{n^2-{\omega }_0^2}$$

(23)

where $\omega =\sqrt{{\omega }_0^2-n^2}$

$$X=c_1{e}^{-nt}\cos \omega t+c_2{e}^{-nt}\sin \omega t$$

(24)

Unpicked grapes are still in the state of multiparticle extrusion, and only the fruit particles that are close together eliminate the exciting force, thus showing a stable state to the outside. The whole fruit–stem system is near the undamped state. By considering the elasticity of the cob, the system is approximated as a small damping state; the grapes have not been sheared in the initial state. Thus, the initial velocity is 0. When t = 0, the system is in the initial unpicked state, and the speed is 0:

$${\left.X\right|}_{t=0}={\left.x_0\frac{dx}{dt}\right|}_{t=0}=v_0=0$$

(25)

where

$x_0$: Displacement when not picked.

$v_0$: Speed when not picked.

The vibration equation solution for the dynamic model is as follows:

$$x=e^{-nt}\left[x_0\cos \omega t+\frac{V_0+n{x}_0}{\omega }\sin \omega t\right]$$

(26)

$$X=A{e}^{-nt}\sin (\omega t+\phi )$$

(27)

where

$$A=2x_0\sqrt{\frac{kM}{4kM-c^2}}$$

$$\omega =\sqrt{\frac{4kM-c^2}{2M}}$$

$$\tan \phi =\frac{\omega }{n}=\frac{\sqrt{4kM-c^2}}{c}$$

In the actual picking operation, the corresponding cutting tool contacts the main cobs of the grapes after positioning; the grapes start to vibrate at this time. By simplifying the fruit–stem system into a spring–five mass–damper system, it is found from a theoretical point of view that the vibration of a grape fruit is affected by other fruits and shows a trend of attenuation.

2.3. Simulation and Test Materials

We selected large-scale grapes in South China for research, used ripe grape bunches in August as test samples, selected 100 grape bunches, and measured the geometric size and shape of the research object. The picking target was N: 23°09′ E: 113°, where there were four-year-old summer black grapes in the open air near 16′. The grape ripening process is accompanied by changes in stem diameter, length, and berry maturity [26,27,28]. The parameters are shown in Table 1. By considering the purpose of the ripe grape picking experiment, the mean data of the ninth week and the tenth week with the highest and second highest maturity were selected as the experimental modelling material object. The grape system was composed of cobs and berries, and the cobs were regarded as skeleton network structures with several branches and a main branch. Unlike normal fruits, bunches of grapes are multi-berry squeezed fruits. The junction of the berries with the tip of the stalk is extremely soft; the experiments were conducted immediately after the bunches were harvested to maintain the elasticity between them.

Table 1. Tracked and measured grape growth data.

Time (Week)	Stem Length (mm)	Fruit Transverse Diameter (mm)	Fruit Longitudinal Diameter (mm)	Fruit Shape Index	Single Fruit Weight (g)
1 Week	101.20 ± 0.16 a	4.15 ± 0.14 a	4.30 ± 0.13 a	1.036	0.22 ± 0.11 b
2 Week	131.27 ± 0.24 b	9.20 ± 0.35 a	10.10 ± 0.34 a	1.097	1.52 ± 0.13 c
3 Week	142.25 ± 0.12 c	11.48 ± 0.39 c	12.73 ± 0.48 b	1.108	2.87 ± 0.24 b
4 Week	151.02 ± 0.26 c	14.77 ± 0.21 c	14.93 ± 0.31 d	1.010	4.36 ± 0.12 d
5 Week	160.87 ± 0.36 d	15.57 ± 0.58 c	16.06 ± 0.49 c	1.031	4.90 ± 0.12 b
6 Week	169.03 ± 0.12 d	16.69 ± 0.26 d	17.08 ± 0.41 cd	1.023	5.92 ± 0.29 c
7 Week	176.48 ± 0.11 cd	19.97 ± 0.38 b	21.00 ± 0.60 c	1.051	7.70 ± 0.17 c
8 Week	183.62 ± 0.45 e	21.00 ± 0.44 d	22.91 ± 0.38 d	1.090	8.69 ± 0.24 e
9 Week	188.93 ± 0.25 e	22.45± 0.28 e	23.96± 0.05 d	1.062	9.13 ± 0.21 e
10 Week	191.24 ± 0.21 e	23.54 ± 0.24 e	24.75± 0.30 e	1.051	9.41 ± 0.29 e

Note: different lowercase letters in English indicate significant differences (p < 0.005).

2.4. Establishment of the Finite Element Model

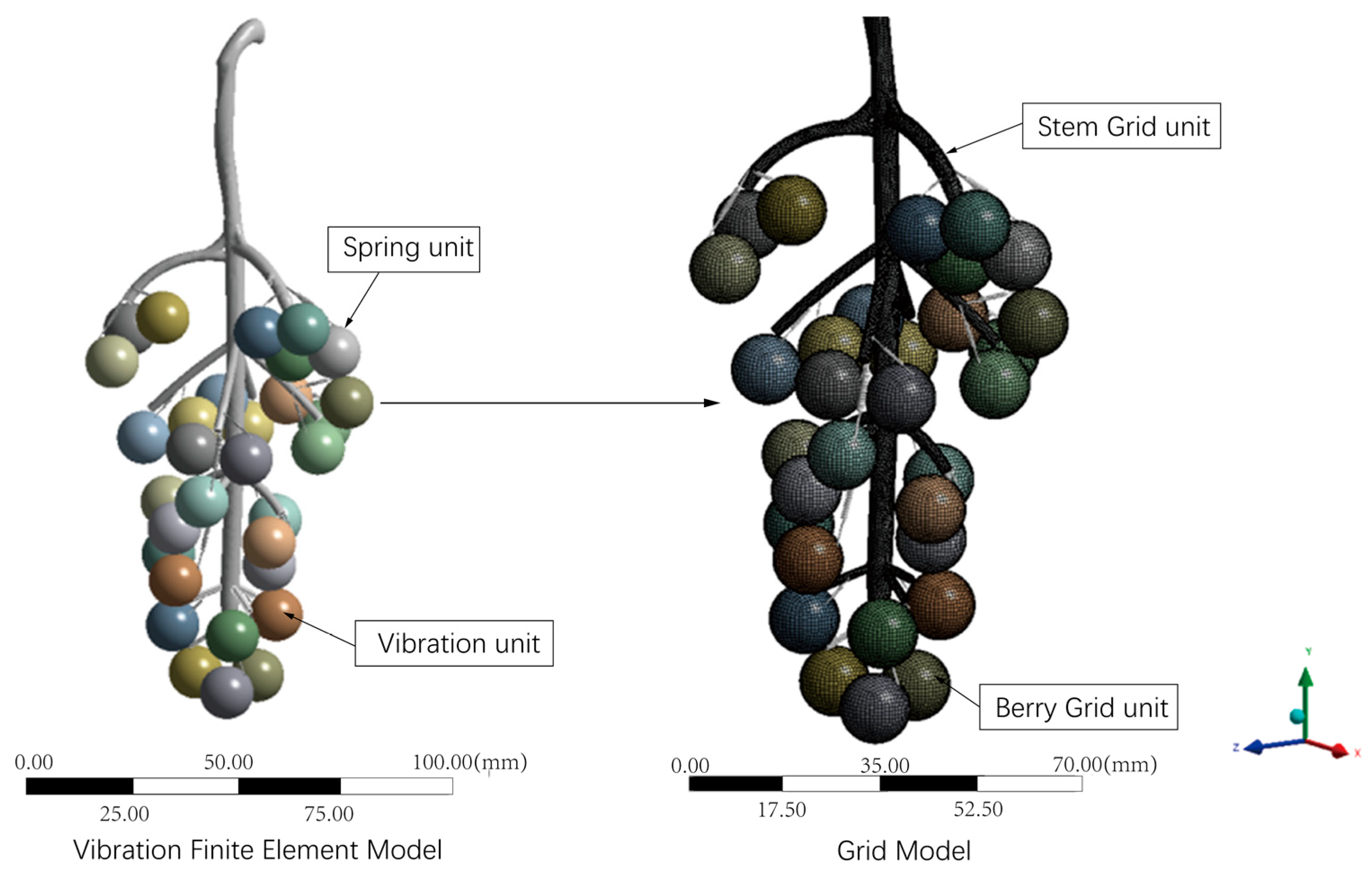
The fit between the simulation model and the actual picking determines the accuracy of the simulation results. In this paper, Dassault Systemes Solidworks 2019 sp5.1 was used to establish the three-dimensional model of the main stem–stem–berry of the grape fruit–cob system; the grape model was imported into Ansys Workbench for modal, frequency sweep, and random vibration processing. First, we set the material properties and physical properties of the fruit stem. Under forced vibration, the dynamic behavior of the grape fruit shows different swing patterns and shedding, and it occurs at the end of the stem; thus, a spring connection was set between the stem and the end of the berry. In this study, the stem and berries were set as near-rigid bodies, and the berries were set as linear elastic spheres. The grape fruit–cob system obtained in the simulation process was quite different from the real situation; thus, it was an indispensable step to continuously assign new material parameter values to continuously correct and modify the grape model [29,30]. The simulation model was divided into precise meshes by unit parts, and each part was connected by nodes. The weight of the whole bunch of grapes was near the experimental value; the quality of each component remained unchanged during the simulation process, making the grape model more accurate. Since it is difficult to observe the microscopic deformation of cobs and berries in the actual picking process, only the macroscopic swinging and shedding results are seen; thus, setting the stress in the dynamic simulation produced deformation.

The difference in berry maturity in the simulation process was small; thus, the elastic modulus and Poisson’s ratio values of all berries in the model were the same, as shown in Table 2. However, taking into account the characteristics of the plant itself, the cob was fixed, and the length of the fruit stem was constant for finite element analysis. The grape finite element model was an irregular CAD structure, and the main cob and vines were particularly complex. The cob was set as a mass spring model, as shown in Figure 3. Therefore, secondary vines were simulated by spring length and stiffness.

Table 2. Parameter settings, such as Poisson’s ratio.

Physical Components		Value
Trunk	Length (mm)	198.4
	Elastic modulus (MPa)	512
	Poisson’s ratio	0.32
Branches	Length (mm)	14.3
	Elastic modulus (MPa)	512
	Poisson’s ratio	0.32
Berry	Long diameter (mm)	18.6
	Short diameter (mm)	15.8
	Density (g·mm−3)	1.788 × 10−2
	Elastic modulus (MPa)	13.2
	Poisson’s ratio	0.33
	Mass (g)	16.5

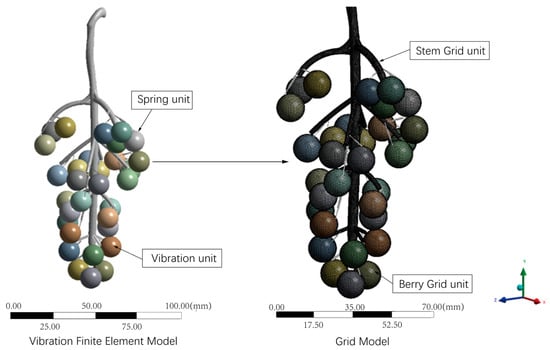
Figure 3. Grape finite element model.

3. Modal Simulation Experiment and Analysis

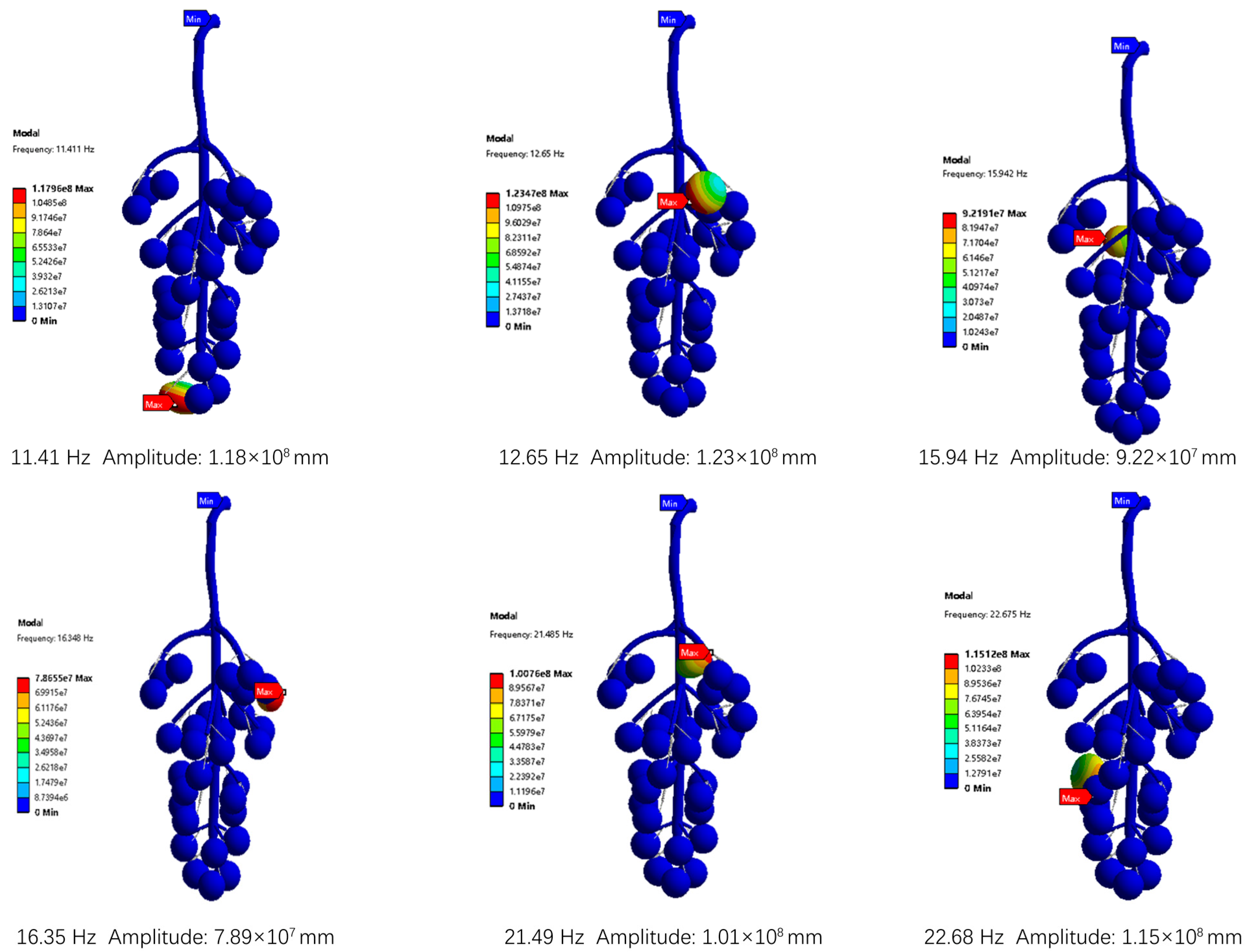
To observe the natural frequencies and mode shapes of the whole bunch of grapes, modal analysis was used to study the dynamic behavior and shaking shape characteristics of grape berries [31]. Due to the adhesion between the fruit stems, fruit branches do not swing easily. To ensure the random vibration sweep range, the residual mode was set [32]. Through modal analysis, the berries in the simulation process showed high similarities with the actual picked berries. The modal analysis shows that the first-order mode of the grape bunch was 0, and the mode shapes and natural frequencies of the second to seventh orders are shown in Figure 4.

Figure 4. Grape modal analysis and swing shape.

The response of grape berries during picking and harvesting is affected by various factors, such as the distance of the stimulus transmission and the strength of the stimulus shear source signal [33,34]. The vibration excitation transmitted from the fruit to the cob shows a decaying trend; however, the excitation force transmitted to each location has different effects on the jumping amplitude of the berries. The first-order frequency under the modal analysis was near 0, and the states of the grapes did not change significantly and still maintained the original static state. However, at the frequency of 12.65 Hz on the third order, 15.94 Hz on the fourth order, 16.35 Hz on the fifth order, and 21.49 Hz on the sixth order, the fruit on the upper part of the grape bunch was extremely active; there were various phenomena, such as single-berry shaking, shaking, and jumping. Due to the large elastic modulus at the joint between the fruit pedicle and the fruit, this phenomenon was accompanied by irregular rebounding in all directions. However, the middle and lower berries do not change much and remain in a stable state, which is caused by the relatively loose extrusion of the upper berries and tight extrusions of the middle and lower berries. However, at the second-order frequency of 11.41 Hz, the berries in the lower part of the grape bunches exhibited a violent swing phenomenon, and there was a wavelike diffusion phenomenon, greatly affecting berry shedding during picking [35]. At the seventh frequency of 22.68 Hz, the berries in the middle of the grape cluster were the most active and gradually began to shake, showing that the berries in the middle were the least likely to fall off.

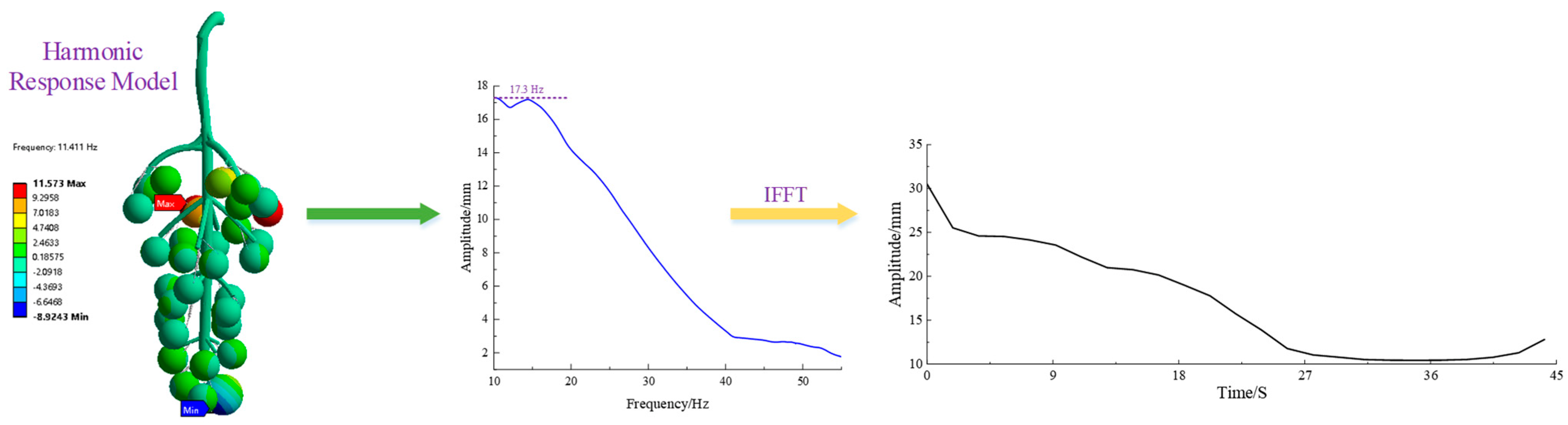
The harmonic response analysis showed that under the frequencies of cutting fruit stems, grape bunches showed different dynamic responses. The displacement change curve under the extracted dynamic response is shown in Figure 5. Approximately 11.41 Hz was the key mode of grape bunch berry swinging, greatly influencing the structure. The key mode of the fruit–stalk system was 11.41 Hz; the maximum deformation of the berry reached 11.57 mm, at which time the fruit–cob system reached resonance. The frequency domain curve shows that the amplitude of the vibrated berry gradually decreased as the response frequency gradually increased, reaching a maximum swing displacement of 17.3 mm at 10.49 Hz; the swing amplitude of the berry after 10.49 Hz was submerged. After 40 Hz, the amplitude in berries with the maximum vibration amplitude gradually decreased in a smooth manner, which is consistent with the law of amplitude changes studied by previous researchers; however, there were some differences in where and when the maximum amplitude occurred. This phenomenon was seen in the time domain curve, indicating the gradual completion of the picking cycle.

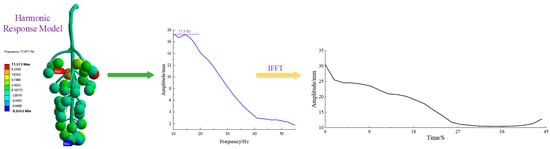
Figure 5. Grape harmonic response analysis.

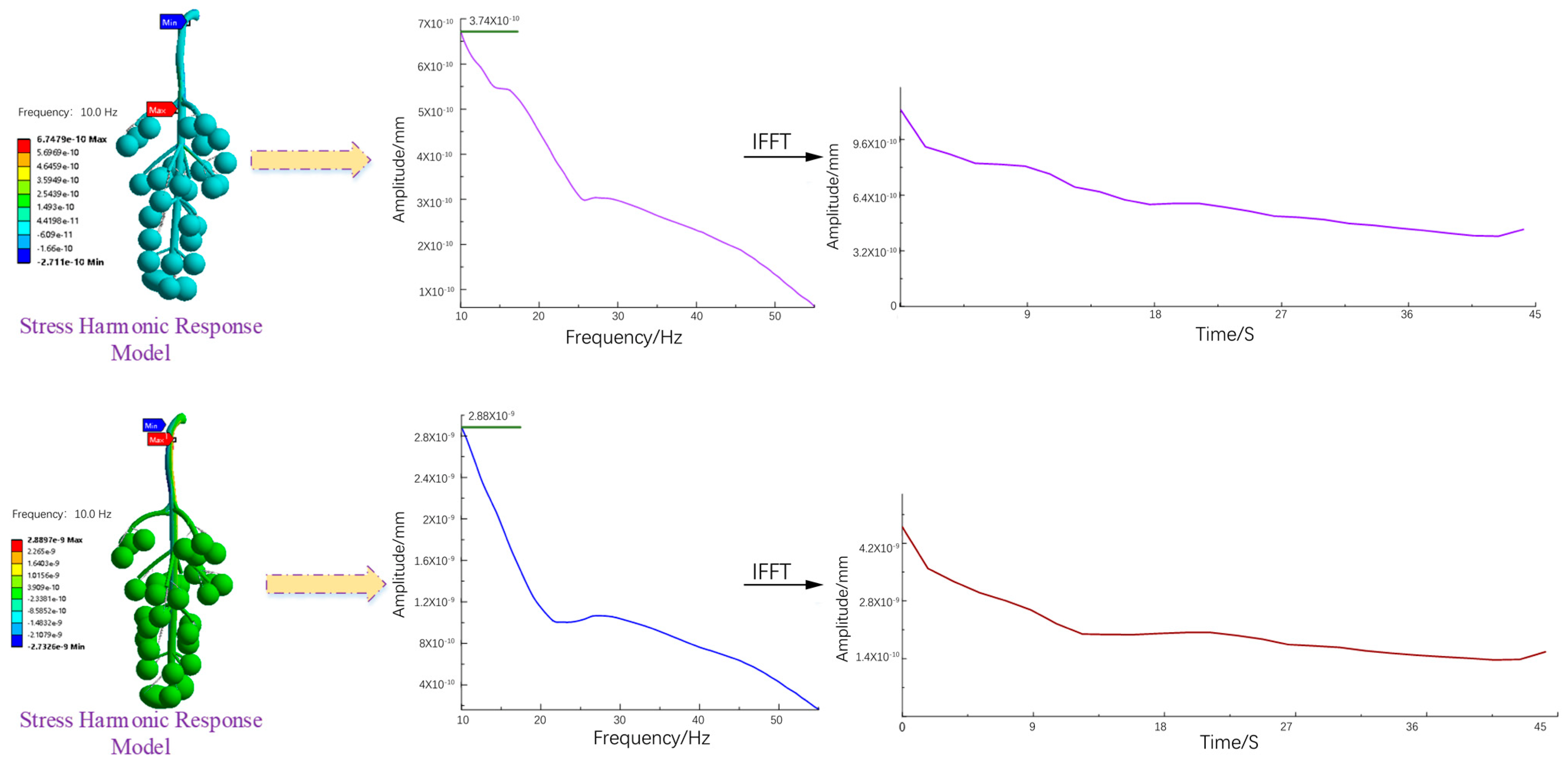
The dynamic response of the berry is the macroperformance of the grape bunch and the compound of the microvibration response in the X and Y directions. During the vibration process, the berries continued to show different amplitudes of shaking, jumping, and rebounding at different stages. This phenomenon was related to the excitation frequency, shear force, and other factors, such as the sizes and locations of grape berries. As shown in Figure 6, the frequency domain curve was extracted through the X-direction stress response model, and it was found that the maximum amplitude of the berries reached 3.74 × 10⁻¹⁰ mm when it approached 10 Hz and then decreased to 0 Hz. Collisions between the berries occurred in the X direction; when the binding force at the fruit pedicle did not sustain this collision force continuously, the berries broke away from the end of the stalk and dropped. If the collision force causes the generated stress to superimpose instantaneously, it causes the instantaneous stress loss of the fruit stem to exceed the maximum stress of its material; the fruit cob may suddenly break and fail. The time-domain curve extracted by the inverse fast Fourier transform (IFFT) showed that the amplitude gradually decreased with the progress of the picking cycle, which is in line with the actual picking situation. According to the frequency domain curve extracted by the stress response model in the Y direction, when the frequency was approximately 10 Hz, the vibrating berries produced a swing displacement of 2.88 × 10⁻⁹ mm that then gradually decreased to 0. The comparison showed that at the same frequency, the amplitudes of the berries in the Y direction were larger than those in the X direction, and the corresponding berry vibration response was more intense; thus, the jumping and rebounding phenomena were mostly the main phenomena. The response process may be accompanied by torsion and fracture of the cob, affecting the stress state of the grape bunch in the vertical direction; individual berries may jump and the whole bunch of grapes may fall. In the stage of theoretical analysis and modeling, spherical berries and linear elastic fruit stems were set as a unified complex with different elastic moduli. Vibration simulation experiments showed that berries had similar laws in the X and Y directions. The IFFT of the frequency domain curve of the vibrated fruit showed that after the excitation of the vibrated fruit reached its maximum value, it began to decrease until it stopped, which was consistent with the dynamic response of the berry in the X direction.

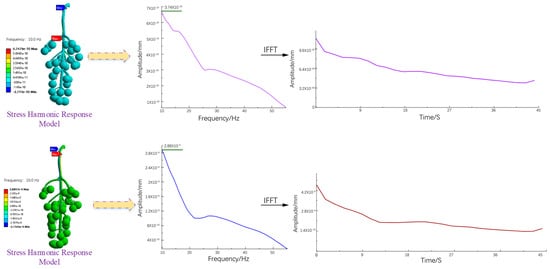
Figure 6. Stress curves in different directions.

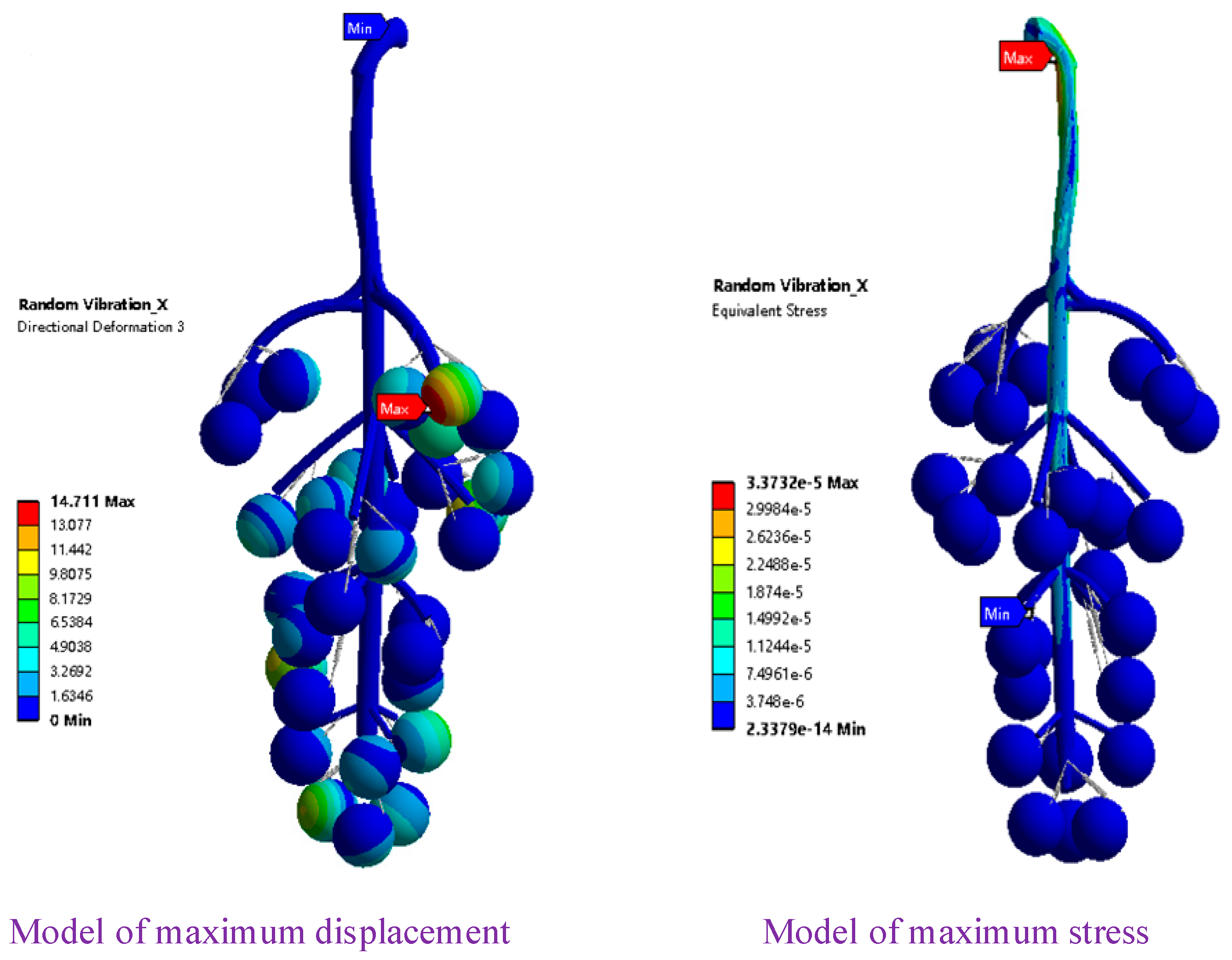
As shown in Figure 7, through the random vibration analysis of grapes in the X direction under excitation, both the cob axis and the berries vibrated randomly. The berries with the largest displacement appeared on the right side of the upper end of the grape bunch. The exciting force transmitted to the berries from top to bottom caused the berries to produce a detachment force in the horizontal direction that exceeded the fruit-pedicle connection force; the detachment force caused the berries to fall irregularly. In this process, the berry excitation caused by the cob excitation locally caused a sudden change in the berry stress, and the maximum stress reached 3.37 × 10⁻⁵ MPa, which appeared mostly at the upper end of the main cob. However, the strength of the main cob was relatively large, and the structure was not damaged.

Figure 7. Vibration response in the X direction.

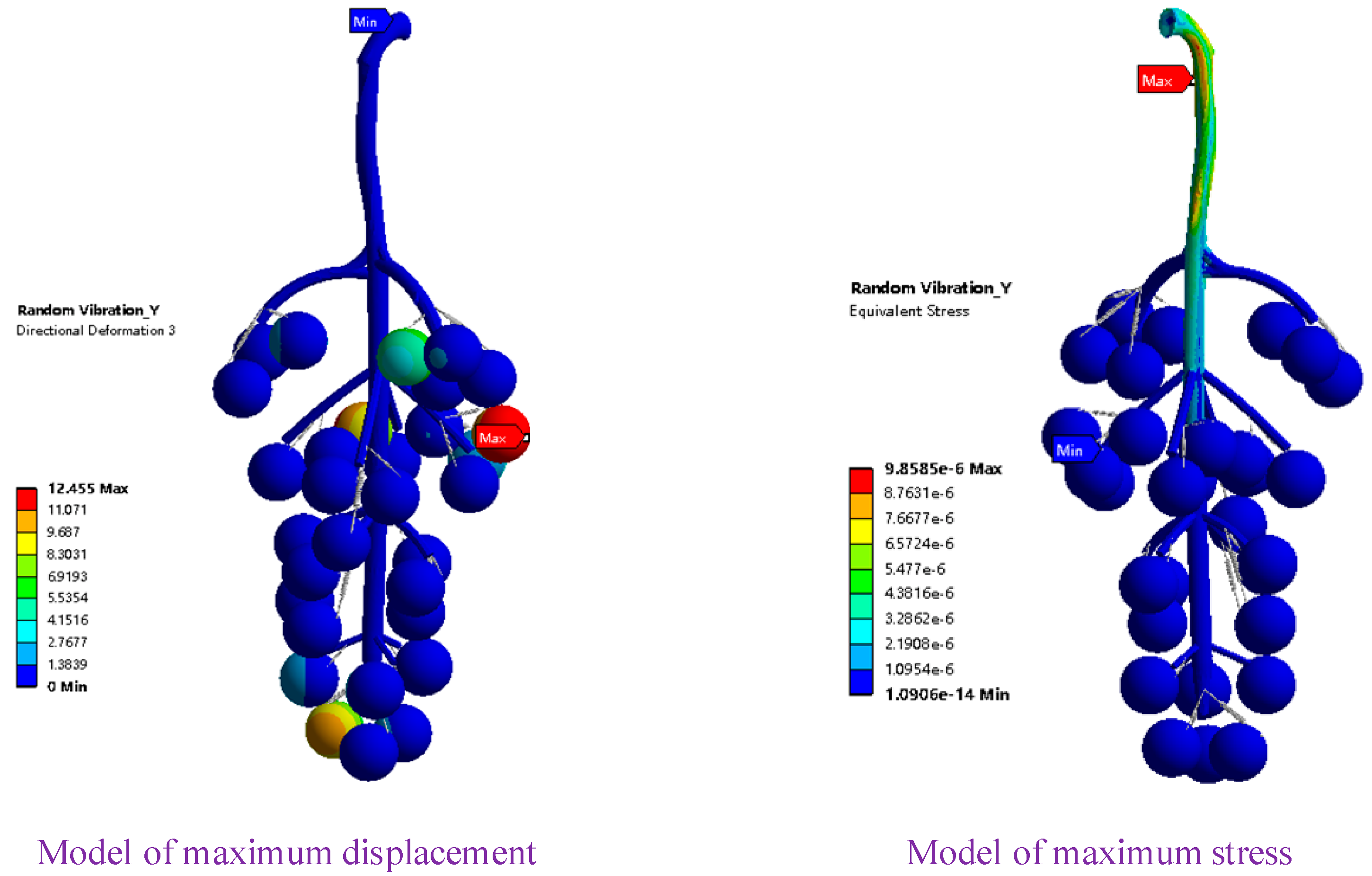
The exciting force caused the berries to oscillate randomly in the Y direction. As shown in Figure 8, the berries at the upper and lower parts of the grape bunch both vibrated significantly. The berries with the largest displacement (approximately 12.46 mm) appeared on the right side of the upper end. The exciting force in the Y direction caused the berries to swing and fall off in the vertical direction; in this process, the cobs were twisted and bent. When the cob material stress exceeded its material stress, the berry was displaced relative to the fruit-pedicle junction. In vertical shaking, vertical excitation induced a stress of 9.86 × 10⁻⁶ MPa on the main cob, which was accompanied by a large strain; however, the effect on the berries was not as great.

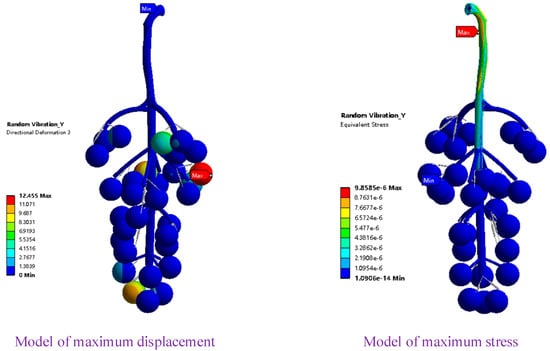
Figure 8. Vibration response in the Y direction.

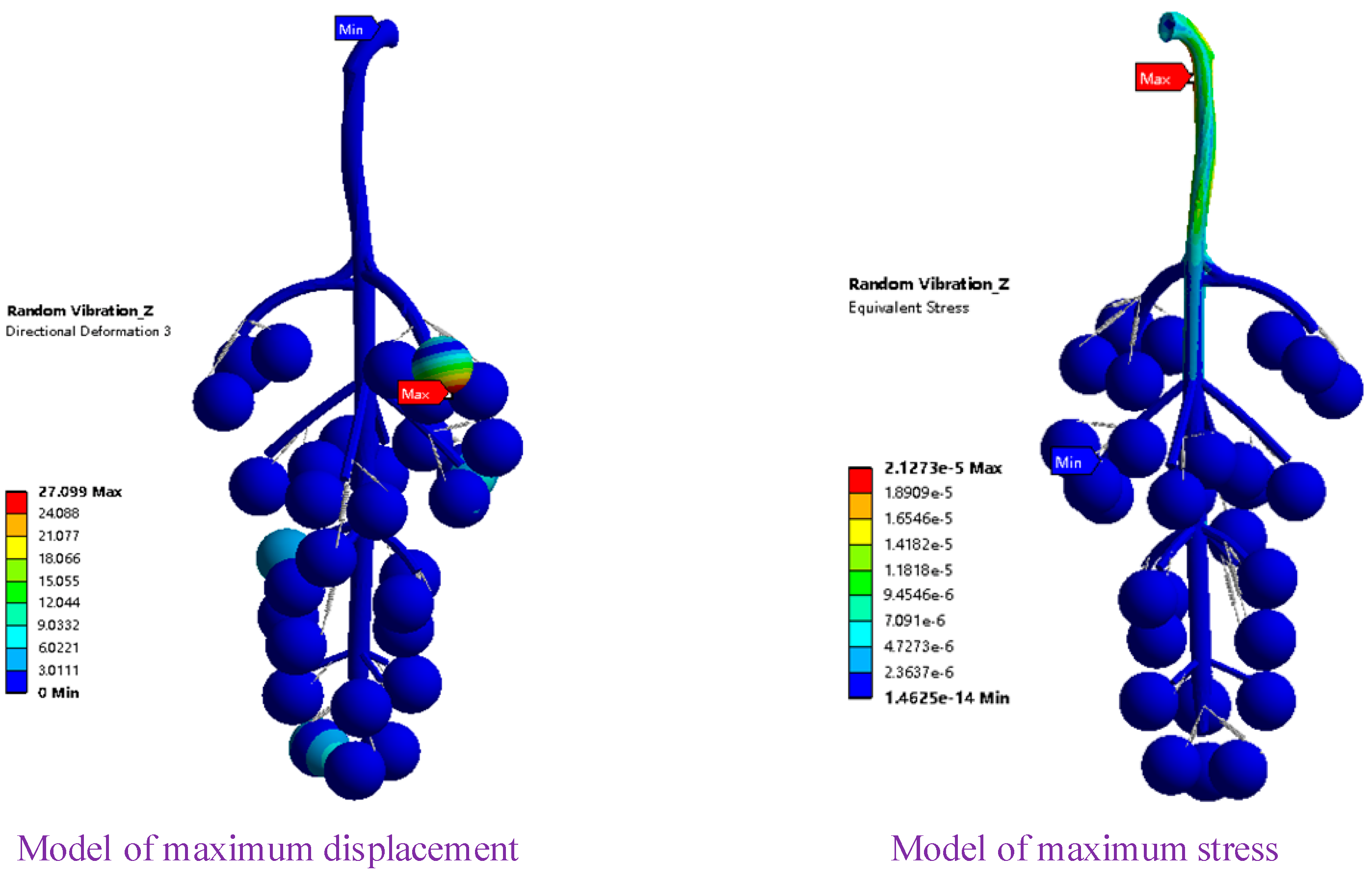
The forced vibration caused the fruit–cob system to produce torsion in the Z direction, which often manifested as fruit stem torsion and berry reverse rotation. The main cob and upper part of the grape bunch had the largest local deformation and stress, as shown in Figure 9. The berries with the largest swing displacement appeared on the right side of the upper end and produce a torsional swing of 27.10 mm in the Z direction, causing the berries to vibrate and fall off in the Z direction. The stress of the main cob changed abruptly during the transmission of vibration excitation, reaching 2.13 × 10⁻⁵ MPa locally, accompanying the process of excitation transmission of the main cob with stress transmission. The impacts on berries in the squeezed state were mostly swinging and jumping; however, this phenomenon may have eventually caused stress failure or fracture of the fruit stem [36].

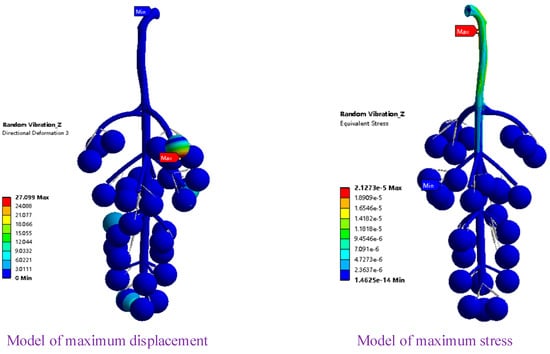
Figure 9. Vibration response in the Z direction.

The dynamic response of the fruit–cob system was jointly determined by the swings in the X, Y, and Z directions. In the random vibration analysis of grape bunches, the vibration amplitudes of berries in the Z direction were greater than those in the X direction; the vibration amplitude in the X direction was greater than that in the Y direction. Therefore, under the same excitation, the vibration amplitude of the berry was the largest in the XOZ plane. The Y direction of the grape bunch was in the vertical direction, which was the direction in which the berries fell off; the main cob had large rigidity and was not easily twisted and broken. Thus, this phenomenon showed that the berries fell off in the Y direction. The vibration excitation characteristics of berries in the Z direction affected torsional shedding in other directions. When the excitation in the three directions reached its maximum, the whole fruit–cob system resonated. At high vibration frequencies, the composite acceleration in the three directions reached its maximum value and exceeded the natural acceleration of the junction [37]. The berries were prone to falling. According to the vibration analysis of grapes in three directions, the most dangerous area for falling off was the upper right side of the grape bunch. The vibration response of the whole system was minimal when the excitations in the three directions canceled each other. Although the berries under low vibration and high frequency showed the phenomena of swaying and shaking, the jumping acceleration produced was less than the natural acceleration of the joint; the whole bunch of grapes hardly moved at this instant. The impact of the vibration on the berries in the squeezed state was multidirectional and irregular, and the shaking posture was one of the factors affecting berry drop, which is consistent with previous research conclusions [38].

4. Conclusions

In this paper, we established a spring-five-mass-damper system to study the motion behaviors of grape berries during harvesting, which provided a theoretical basis for studying their dynamic responses. Through modal analysis, we found that the swing of the berries at the second order of 11.41 Hz was very lively, possibly due to the A factor being tighter and the upper part being closer to the cut. In harmonic response analysis, we observed that when the frequencies of the X and Y directions were approximately 10 Hz, the fruit–cob system resonated around the Z direction, which was the high-frequency cycle of berry shedding. Further random analysis showed that the excitation in the Z direction was the largest and led to the largest swinging and stress. The berries in the upper right side of the grape bunch were the most prone to shedding, while the other berries were almost stationary.

Based on these findings, we make the following suggestions for related research. To avoid the system resonance phenomenon that causes many fruits to fall off, the vibration frequency of the picking mechanism should be approximately 10 Hz, and the random vibration direction should not simultaneously satisfy the resonance conditions in all three directions. When designing and updating the picking method and the collection of fallen fruits, asymmetric structure optimization of the upper right side of the grape cluster should be considered, as this is the area of the highest shedding concentration.

In future microsimulation and digital twin experiments, natural environments such as wind can be introduced to further optimize the pendulum-vibration dual model and achieve more realistic all-in-the-loop simulations of the environment, mechanism, and grape cluster.