Determining Farmers’ Willingness to Pay for Irrigation Water in the Alentejo Region (Southern Portugal) by the Residual Value Method

Abstract

This paper aims to determine farmers’ willingness to pay for irrigation water, using the residual value method, for the most representative crops at six Irrigation Communities from the Alentejo region, southern Portugal. The main objective of this assessment was to determine the value that farmers would be able to pay for the water to irrigate different crops at different locations, and to show that this approach can be used to provide information about farming economic sustainability and provide support on if crop prices need to be revised or if a national policy should be conceived to cover for farming costs. The results show that vegetables and fruit trees have the highest Residual Value of Water (RV_W), while Wheat, Sunflower, Fodder crops, Semi-intensive Olive Orchards and Rice tend to have an RV_W lower than the current variable irrigation water price. The results also show that, while, for Melon, Tomato, Onion, Super-high-density Olive Orchards, Peach and Almonds, both yields and price may decrease significantly, allowing one to save for faming inputs, Sunflower and Rice would require an increase in yields or prices to cover for the irrigation water price.

1. Introduction

Irrigation is fundamental for southern European agriculture due to its arid and semi-arid climate. Improving irrigation management is of relevant importance to ensure a sustainable use of resources in water-scarce areas. Among the actors involved in water management, Irrigation Communities (ICs) are key players [1]. The Directive 2000/60/EC ‘Water Framework Directive’ (WFD) declares the norm for managing water resources in Europe. The WFD is essentially an environmental law, which supports the use of economics as a key discipline. Among its instruments, the goal of full cost recovery for water services stands out as one of the key aspects to compensate for environmental and resource costs. According to [2], rational decisions supporting water resource development, allocation, and use require measuring the value of water in alternative uses. Those authors also state that the economic value of water would measure the contribution of that water to accomplishing the user decision’s aim and should be defined as the amount that a rational user of a publicly or privately supplied water resource is willing to pay for it. Based on the fact that this value should, on the one hand, cover for environmental and resource costs, and, on the other hand, establish a value that measures the benefit of using this resource (allowing one to control superfluous consumptions), ICs charge farmers with a water price that aims to cover for all these costs/benefits.

Ward and Michelsen [2] also state that the economic benefit of additional water used in irrigation may be measured as the change in value of agricultural products less changes in associated production costs. Based on this assumption, the valuation of irrigation water, for supporting sustainable water management, has been assessed by different authors using different approaches. Young and Loomis [3] provided a list of different types of economic water valuation methods, their characteristics and uses. From those methods, the contingent valuation method (CVM), the linear programming (LP) and the residual value method (RVM) stand out as being mostly used to determine the farmers’ willingness to pay for irrigation water.

The CVM is a flexible, non-market valuation method and has been widely used by many authors to estimate irrigation water prices [4,5,6,7,8,9]. However, and since the direct approach used in CVM has been to directly ask survey respondents to state the maximum price that they are willing to pay for water for a particular use or non-use value of the water. Thus, and since it is based on survey results, a CVM study should be properly and extremely carefully conducted, or the assessment may lead to misleading conclusions [10].

LP has also been used for the last four decades to determine the value of water. Previous studies [11,12,13,14,15,16,17] attempted to valuate this resource based on mathematical models. However, LP is normally based on the single criterion of maximizing the economic return, lacking to be capable to maximize the valuation based on farmer’s preferences and choices.

Contrarily, the RVM is a deductive approach, as an estimation of rents to water is derived from models of farm firm behavior, which forecasts revenue and then subtracts expected costs of purchased inputs and the estimated opportunity costs of owned inputs other than water [3]. However, few studies have been conducted based on this method. Berbel et al. [18] use the RVM to economically analyze irrigation water at the basin level for the Guadalquivir River, southern Spain. Kiprop et al. [19] determined the disaggregated economic value of irrigation water used across crops at the basin level in Kenya. In a similar study, Muchara et al. [20] aimed to estimate water values among smallholder farmers, focusing on the potato crop, in South Africa. However, Kiprop et al. [19] and Muchara et al. [20] estimated the consumptive water amounts using simulation models. Qureshi et al. [21] applied the RVM as a complement to other methods for determining the value of the water used over a wide range of irrigated crops in different seasons and regions in Australia; however, not as a standalone approach.

This study aims to determine the farmers’ willingness to pay for water based on the Residual Value Method. The area selected as a case study is the Alentejo region, southern Portugal. Due to its climate, farmers resort to irrigation; many studies tried to understand the impacts of irrigation on the cropping systems, but no relative study has taken place to determine farmers’ willingness to pay for such a fundamental resource.

2. Materials and Methods

2.1. Case study Description

This study was conducted in the Alentejo region, southern Portugal. The region has a surface area of 31,604 km², representing 33% of inland Portugal, and a population of more than 780,000 inhabitants (less than 8% of the total Portuguese population). The region is responsible for 46% of the total national agricultural production. The region, according to the Köppen–Geiger classification, has a Csa climate and is characterized by a semi-arid Mediterranean climate of hot and dry season in the summer and mild temperature associated to annual rainfall in winter. Due to these characteristics, farmers resort to irrigation in order to achieve farming sustainability and profitability. Water demand for agriculture is around 79%, totaling an average of 491 hm³ per year.

The Irrigation Communities (ICs) selected for this case study are among the most economically important ones in the Alentejo region—Campilhas e Alto Sado, Lucefecit, Odivelas, Roxo, Vale do Sado and Vigia. The total irrigated area and the area cropped by the main crops of each IC are presented in Table 1. Figure 1 shows the location of the six ICs. Campilhas e Alto Sado and Odivelas differ from the other ICs since they manage more than one Irrigation District (ID). Each ID consists of an individual irrigation network, managed independently of the others.

Table 1. Main crop areas of each Irrigation Community (IC).

IC	Irrigated Area (ha)										Commanded Area (ha)			Annual Average Irrigation Water Supply (m3 ha−1)
	A	C	Fr	V	M	S	O/V	F	R	Total	LP	HP	Total
Campilhas e Alto Sado	-	60	30	316	1402	-	1498	64	1258	4628	6244	-	6244	6660
Lucefecit	-	161	3	26	331	-	194	96	-	811	208	964.5	1172.5	5355
Odivelas	360	837	289	478	656	318	5033	829	278	9078	3798	8900	12698	3780
Roxo	515	469	252	96	275	273	3143	191	343	5557	4831	3595	8426	4430
Vale do Sado	-	-	3	16	12	-	31	363	4835	5260	6171	-	6171	7720
Vigia	32	219	-	26	240	120	1 325	20	-	1982	0	1982	1982	2410

A—Almond Orchards; C—Cereals (except maize); Fr—Fruit Orchards; V—Vegetables; M—Maize; S—sunflower; O/V—Olive Orchards and Vineyards; F—Fodder crops; R—Rice. Source: IC managers.

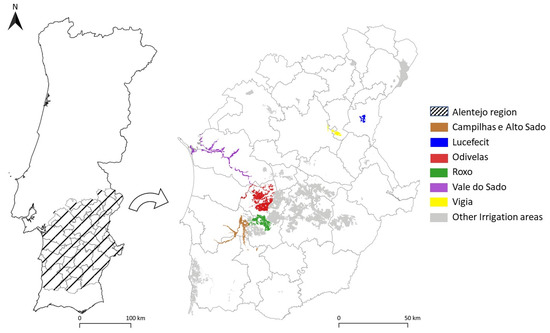
Figure 1. Study area.

Figure 2 shows the proportion of the cropped area per crop over the total cropped area and the water usage per crop over the total water consumption across all ICs. From all crops, the ones that stand out the most are Almond Orchards and Vegetables that use 3% of the area and 3% of the water usage, being the most balanced crops, Olive Orchards and Vineyards that occupy 41% of the area and use 27% of total water consumption, and rice that consumes 43% of the water usage while cropping 25% of the total. These data show that the cropped area/water usage relation is quite heterogeneous across the ICs.

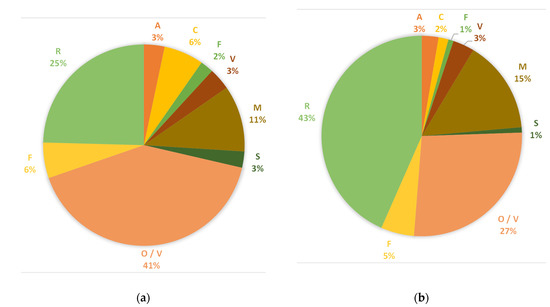
Figure 2. Proportion of the (a) cropped area per crop over the total cropped area and (b) the water usage per crop over the total water consumption across all ICs. A—Almond Orchards; C—Cereals (except maize); Fr—Fruit Orchards; V—Vegetables; M—Maize; S—sunflower; O/V—Olive Orchards and Vineyards; F—Fodder crops; R—Rice

Crop areas and water allocation within each IC is done according to farmers’ demand and registration of land use in the beginning of each irrigation season.

In terms of water prices, all IC charges farmers with two different components: a fixed and a variable amount. A fixed water price (EUR/ha) is charged to farmers according to the ID and water pressure regime and/or irrigated crop. The variable water price (EUR/m³) component aims to cover the energy and environmental cost of each cubic meter used for irrigation. For Vale do Sado IC, in the fields where rice is grown, the soils have limitations for the production of other crops due to saline intrusion. In order to avoid abandoning those agricultural fields, the IC chooses to apply a lower variable water price to try to make rice production economically viable. For farmers outside the ID, i.e., farms to which water is allocated despite of being outside the network infrastructure, only a variable water price is charged, higher than the one for farmers inside the ID in order to cover for real costs but also to reflect an opportunity cost for water availability. The values for both the fixed and variable water prices for each IC and ID, reported to 2019, are presented in Table 2.

Table 2. Fixed and variable water price for each IC.

IC	Irrigation Districts (IDs)/Crops	Fixed Water Price (EUR/ha)		Variable Water Price (EUR/m3)
		Farmers Inside ID (FI)		Farmers Inside ID (FI)		Farmers Outside ID (FO)
		Low Pressure (LP)	High Pressure (HP)	Low Pressure (LP)	High Pressure (HP)	Low Pressure (LP)	High Pressure (HP)
Campilhas e Alto Sado (CAS)	Alto Sado Irrigation District	35	-	0.0220	-	0.0350	-
	Other Irrigation Districts	31		0.0215
Lucefecit (L)	Row Crops	60	82.5	0.0130	0.0500	-	-
	Fodder crops	52.5	70
	Field crops	45	60
	Landscape	150	175
	Other uses	30	45
Odivelas	Irrigation District 4 (O4)	-	43.65		0.0559	-	0.0820
	Other Irrigation Districts (O)	-	48.5
	Low-pressure Irrigation District (OLP)	30.93	-	0.0264	-	0.0464	-
Roxo (R)	Total area	27	49	0.0307	0.0582	0.0496	0.0782
Vale do Sado (VS)	Rice	45	-	0.0223	-	-	-
	Other crops			0.0262
Vigia (V)	Total area	-	30	-	0.0500	-	0.0650

2.2. The Residual Value Method

The residual value method (RVM) was used in this study to evaluate the willingness to pay for irrigation water by farmers across the six ICs. The RVM assumes that: (a) producers maximize their yields/profits; and (b) the total value of the product is assigned to each input according to its marginal productivity. If appropriate prices can be assigned to all inputs but one, the remainder of the total value of product is attributed to the remaining or residual input, which in this specific case is water [22].

Young and Loomis [3] established that a single production process (Y) where it is desired to impute a value for the unpriced input, water (W), might be defined as a function:

Y = f(X_M, X_H, X_K, X_L, X_W)

(1)

where M is the purchased materials and equipment, H is the human input such as labour (from hired workers, supervisors, and managers), K is the equity capital, L is other natural resources, such as land, and W is water.

If all the inputs are paid according to their value marginal product (VMP), the total value of product (TVP) may be expressed by:

TVP = (Y × P_Y) = (VMP_M × X_M) + (VMP_H × X_H) + (VMP_K × X_K) + (VMP_L × X_L) + (VMP_W × X_W)

(2)

where Y × P_Y represents total value of product Y; VMP_i represents the VMP of resource i; and X_i is the quantity of the ith resource. Equation (2) follows the fundamental product exhaustion theorem with the amount of inputs weighted by their VMP sum to TVP. Assuming that agricultural input markets are competitive, the prices for these inputs may be treated as known constants, and, for each input i, the producer chooses the level of input such that VMP_i = P_i, Equation (2), may be rearranged as:

(P_W × X_W) = (Y × P_Y) − [(P_M × X_M) + (P_H × X_H) +(P_K × X_K) + (P_L × X_L)]

(3)

If all prices and quantities are on the right side of the equation, the contribution of (P_W × X_W) on TVP may be derived.

As the quantity of water consumed, X_W, per crop may be known for each location and the crop may be known, the expression can be solved to find P_W. If P_W is not yet assigned, the residual value of water, denoted RV_W (EUR/m³), is used as a substitute for the water price, resulting:

$${\mathrm{RV}}_{\mathrm{W}}= \frac{\left(\mathrm{Y} \times { \mathrm{P}}_{\mathrm{Y}}\right) - \left[\left({\mathrm{P}}_{\mathrm{M}} \times { \mathrm{X}}_{\mathrm{M}} \right) + \left({\mathrm{P}}_{\mathrm{H}} \times { \mathrm{X}}_{\mathrm{H}} \right) +\left({\mathrm{P}}_{\mathrm{K}} \times { \mathrm{X}}_{\mathrm{K}} \right) + \left({\mathrm{P}}_{\mathrm{L}} \times { \mathrm{X}}_{\mathrm{L}} \right)\right]}{{\mathrm{X}}_{\mathrm{W}}}$$

(4)

Therefore, RV_W should be considered the maximum value to be paid for water, in the break-even point.

Based on the fact that the TVP and the VMPs, except for water, are known, the model application is straightforward. The RV_W will be used not only to assess the willingness of farmers to pay for water but also to compare this value with the actual variable water price in order to better understand if the current Y or P_Y are enough to cover for all production costs (including water).

2.3. Economic Characterization of Each Crop in the ICs

For the application of the residual water value method, data were made available by IC managers for all case studies under assessment, which results from a consultation with farmers in each community. Standard crop budgets have been created for each crop, which result from these surveys. For each crop, the average input costs (labour, purchased materials, equipment, crop installation, energy for irrigation, land cost (EUR/ha), and other general expenses) and yield returns (yield and prices) were defined, assuming that each farm adopted standard production techniques. Both input costs and crop prices are mean values for the entire region and for the last decade [23]. In addition, for each crop, a mean amount of water applied was considered, based on the average amounts accounted at each IC. Table 3 presents the data used for the application of the RVM, including farming costs and yields, and water applied for each crop.

Table 3. Production cost for each crop in the Alentejo region (not including water costs).

Variable Crop	Labour (EUR/ha)	Purchased Materials 1 (EUR/ha)	Equipment (EUR/ha)		Crop Installation (EUR/ha)		Energy 2 (EUR/m3)	Other Costs (EUR/ha)	Land Cost (EUR/ha)	Water Amount (m3/ha)	Crop Yield (ton/ha)	Crop Prices (EUR/ton)
			High-Pressure Regime	Low-Pressure Regime	High-Pressure Regime	Low-Pressure Regime
Maize	110	1807	221	232	-	-	0.025	90	200	6500	15	190
Wheat	103	877	190	210	-	-	0.025	44	200	2500	5	265
Sunflower	89	730	200	200	-	-	0.025	37	200	4000	3	380
Melon	1873	2078	346	385	-	-	0.025	104	200	4500	37.5	220
Tomato	253	5173	377	377	-	-	0.025	259	200	4500	100	80
Onion	722	2695	305	320	-	-	0.025	135	200	4000	55	125
Fodder	85	900	195	195	-	-	0.025	45	200	6000	11	140
SHD 3 Olive orchards	532	1111	625	625	720	766	0.025	56	200	3000	12.5	300
SI 4 Olive orchards	398	590	250	250	200	246	0.025	30	200	2000	6	300
Peach	2212	1858	610	640	778	778	0.025	93	200	4500	22	320
Almond	1100	953	530	563	320	320	0.025	48	200	4000	2.5	2550
Vineyards	398	590	150	250	200	246	0.025	30	200	1500	6	300
Rice	230	1300	-	150	-	50	0.025	65	200	12,000	7	260

¹ except energy for irrigation; ² for irrigation on low-pressure regimes; ³ SHD—Super-high-density; ⁴ SI—Semi-intensive. Source: IC managers.

3. Results

3.1. Results of Residual Value of Water in the Alentejo Region

Using Equation (4), the RV_W was computed for each crop/IC combination, obtaining a range of results that is shown in Table 4. For each ID, the production cost for each crop (Table 3) and the fixed water price for each IC/ID (Table 2) were adopted. Table 4 also presents the differences of residual value versus the variable water prices (WPs) applied at each IC/ID. The red cells show the crop/ID combination where the RV_W is lower than the WP; the green cells highlight the cases where the RV_W is high enough to cover for the WP.

Table 4. Residual value of water (RV_W) for all crops and Irrigation Districts (ID)s.

	CAS				L		O		O4		OLP		R				VS	V
	Alto Sado		Others
	FI	FO	FI	FO	FI	FO	FI	FO	FI	FO	FI	FO	FI		FO		FI	FI	FO
	LP	LP	LP	LP	HP	LP	HP	HP	HP	HP	LP	LP	HP	LP	HP	LP	LP	HP	HP
Maize	0.033	0.038	0.033	0.038	0.056	0.031	0.057	0.065	0.058	0.065	0.033	0.038	0.058	0.034	0.065	0.038	0.031	0.060	0.065
Wheat	−0.083	−0.069	−0.081	−0.069	−0.060	−0.087	−0.055	−0.036	−0.053	−0.036	−0.081	−0.069	−0.055	−0.079	−0.036	−0.069	−0.087	−0.048	−0.036
Sunflower	−0.063	−0.054	−0.062	−0.054	−0.044	−0.065	−0.041	−0.029	−0.040	−0.029	−0.062	−0.054	−0.041	−0.061	−0.029	−0.054	−0.065	−0.036	−0.029
Melon	0.769	0.777	0.770	0.777	0.798	0.767	0.800	0.811	0.801	0.811	0.770	0.777	0.800	0.771	0.811	0.777	0.767	0.804	0.811
Tomato	0.407	0.415	0.408	0.415	0.426	0.405	0.429	0.440	0.430	0.440	0.408	0.415	0.429	0.409	0.440	0.415	0.405	0.433	0.440
Onion	0.667	0.676	0.668	0.676	0.663	0.665	0.666	0.678	0.667	0.678	0.668	0.676	0.666	0.669	0.678	0.676	0.665	0.671	0.678
Fodder	−0.012	−0.006	−0.011	−0.006	0.008	−0.015	0.011	0.019	0.012	0.019	−0.011	−0.006	0.011	−0.010	0.019	−0.006	−0.013	0.014	0.019
SHD Olive orchards	0.117	0.128	0.118	0.128	0.168	0.108	0.179	0.195	0.181	0.195	0.118	0.128	0.179	0.119	0.195	0.128	0.113	0.185	0.195
Semi-intensive Olive orchards	0.001	0.018	0.003	0.018	−0.001	−0.012	0.016	0.040	0.018	0.040	0.003	0.018	0.016	0.005	0.040	0.018	−0.004	0.025	0.040
Peach	0.247	0.255	0.248	0.255	0.268	0.241	0.276	0.286	0.277	0.286	0.248	0.255	0.276	0.249	0.286	0.255	0.245	0.280	0.286
Almond	0.764	0.773	0.765	0.773	0.812	0.758	0.820	0.832	0.821	0.832	0.765	0.773	0.820	0.766	0.832	0.773	0.762	0.825	0.832
Vineyards	0.008	0.031	0.010	0.031	0.195	−0.009	0.218	0.250	0.221	0.250	0.010	0.031	0.217	0.013	0.250	0.031	0.001	0.230	0.250
Rice	0.008	0.010	0.008	0.010	0.005	0.007	0.006	0.010	0.007	0.010	0.008	0.010	0.006	0.008	0.010	0.010	0.007	0.008	0.010
WP *	0.022	0.035	0.022	0.035	0.050	0.013	0.056	0.082	0.056	0.082	0.026	0.046	0.058	0.031	0.078	0.050	0.026	0.050	0.065

CAS—Campilhas e Alto Sado; L—Lucefecit; O—Odivelas’s Other Irrigation Districts; O4—Odivelas’s Irrigation District 4; OLP—Odivelas’s Low-Pressure Irrigation District; R—Roxo; VS—Vale do Sado; V—Vigia; FI—Farmers inside Irrigation District; FO—Farmers outside Irrigation District; LP—Low Pressure; HP—High Pressure. * variable water price for each IC/ID (reported to 2019). Red cells—RV_W is lower than the WP; Green cells—RV_W is higher than the WP.

Table 4 shows that Melon, Tomato, Onion, Super-high-density Olive Orchards, Peach and Almonds present RV_W values higher than the actual water price for all ICs. From those crops, Melon and Almond are the ones that present the higher values; this can be explained due to the high yields and crop price for the former, and due to the exceptional high crop price for the latter. The results show that most vegetables and fruits have great potential to be cropped in the Alentejo region.

Contrarily, Wheat, Sunflower, Fodder crops, Semi-intensive Olive Orchards and Rice led to an RV_W lower than the actual WP. For Wheat and Sunflower, the RV_W is negative for all ID, meaning that cropping those crops, for the current crop prices, leads to negative farming income. As for Maize, one of the most representative crops in the region, for farmers outside the irrigation district (FO) at Odivelas (O, O4 and OLP), Roxo, and Vale do Sado and Vigia, the RV_W is lower than the WP. This can be explained due to the fact that the WP for FO tries to cover for the additional water allocation expenses for areas outside the network infrastructure. The results also show that Vineyards are not suitable for low-pressurized IC/IDs for the actual crop yields and prices.

Due to current crop prices, the production costs (including the charged fixed water price) for some crops tend to be higher than the total revenue; one should argue: what should be the crop yields and prices thresholds for each crop/IC combination that lead to RV_W = WP? The answer to this question will allow to better understanding how yields and prices should be managed and trying to determine how fewer valuable crops may be valued.

3.2. Crop Yields and Prices Thresholds

Based on the assumption that some crops in some ICs may not be suitable since the RVW is lower than the WP, there the need to define crop yields and prices thresholds that would compensate for the actual water price, where RVW = WP. These thresholds were determined by: (a) how much can the crop yields may increase or decrease if the current crop price does not change; (b) how much can the crop prices may increase or decrease if the current crop yields remain the same.

Table 5 and Table 6 present, respectively, the crop yields and prices that lead to a residual water value equal to the actual water price. A color scale is used to ease the reading of the results: the greener the cell, the lower the yield/price can be; the redder, the higher the yield/price will have to be.

Table 5. Threshold crop yields, for each crop and IDs, to RV_W = WP.

	Current Yield (kg/ha) *	Crop Yield (kg/ha) for RVW = WP
		CAS				L		O		O4		OLP		R				VS	V
		Alto Sado		Others
		FI	FO	FI	FO	FI	FO	FI	FO	FI	FO	FI	FO	FI		FO		FI	FI	FO
		LP	LP	LP	LP	HP	LP	HP	HP	HP	HP	LP	LP	HP	LP	HP	LP	LP	HP	HP
Maize	15,000	14,631	14,891	14,593	14,891	14,807	14,376	14,948	15,586	14,923	15,586	14,760	15,281	15,030	14,886	15,456	15,391	14,826	14,649	15,004
Wheat	5000	5986	5977	5966	5977	6033	5939	6046	6109	6027	6109	6012	6084	6069	6038	6073	6115	6063	5920	5948
Sunflower	3000	3891	3936	3875	3936	3988	3822	4020	4167	4007	4167	3926	4056	4046	3961	4127	4089	3961	3909	3988
Melon	37,500	22,211	22,318	22,183	22,318	22,209	22,072	22,277	22,590	22,255	22,590	22,282	22,551	22,326	22,353	22,513	22,616	22,342	22,072	22,243
Tomato	100,000	81,352	81,646	81,274	81646	81833	80,971	82,021	82,883	81,961	82,883	81,549	82,287	82,157	81,741	82,669	82,467	81,711	81,458	81,927
Onion	55,000	34,358	34,494	34,310	34,494	35,374	34,150	35,471	35,918	35,432	35,918	34,466	34,859	35,548	34,572	35,796	34,961	34,571	35,134	35,374
Fodder	11,000	12,443	12,750	12,393	12,750	12,821	12,182	12,921	13,693	12,886	13,693	12,602	13,239	13,023	12,759	13,530	13,376	12,693	12,536	12,964
SHD Olive orchards	12,500	11,552	11,565	11,534	11,565	11,324	11,545	11,270	11,369	11,254	11,369	11,582	11,679	11,295	11,612	11,331	11,711	11,627	11,149	11,199
Semi-intensive Olive orchards	6000	6142	6112	6125	6112	6342	6165	6268	6280	6252	6280	6157	6188	6285	6173	6255	6209	6203	6167	6167
Peach	22,000	18,836	18,909	18,816	18,909	18,933	18,787	18,909	19,125	18,894	19,125	18,885	19,069	18,943	18,933	19,071	19,114	18,926	18,768	18,886
Almond	2500	1336	1343	1334	1343	1305	1332	1301	1323	1299	1323	1341	1360	1305	1346	1317	1366	1346	1285	1296
Vineyards	6000	6072	6020	6056	6020	5275	6110	5191	5160	5175	5160	6080	6077	5204	6089	5141	6093	6126	5100	5075
Rice	7000	8823	9288	8785	9288	10,212	8446	10,440	11,458	10,421	11,458	9011	9815	10,548	9194	11,282	9962	8877	10,096	10,673

SHD—Super-high-density; CAS—Campilhas e Alto Sado; L—Lucefecit; O—Odivelas’s Other Irrigation Districts; O4—Odivelas’s Irrigation District 4; OLP—Odivelas’s Low-Pressure Irrigation District; R—Roxo; VS—Vale do Sado; V—Vigia; FI—Farmers inside Irrigation District; FO—Farmers outside Irrigation District; LP—Low Pressure; HP—High Pressure. * Source: IC managers. The greener the cell, the lower the yield can be; the redder the cell, the higher the yield will have to be.

Table 6. Threshold crop prices, for each crop and IC, to RV_W = WP.

	Current Crop Price (Euro/ton) *	Crop Price (Euro/ton) for RVW = WP
		CAS				L		O		O4		OLP		R				VS	V
		Alto Sado		Others
		FI	FO	FI	FO	FI	FO	FI	FO	FI	FO	FI	FO	FI		FO		FI	FI	FO
		LP	LP	LP	LP	HP	LP	HP	HP	HP	HP	LP	LP	HP	LP	HP	LP	LP	HP	HP
Maize	190	185	189	185	189	188	182	189	197	189	197	187	194	190	189	196	195	188	186	190
Wheat	265	317	317	316	317	320	315	320	324	319	324	319	322	322	320	322	324	321	314	315
Sunflower	380	493	499	491	499	505	484	509	528	508	528	497	514	512	502	523	518	502	495	505
Melon	220	130	131	130	131	130	129	131	133	131	133	131	132	131	131	132	133	131	129	130
Tomato	80	65	65	65	65	65	65	66	66	66	66	65	66	66	65	66	66	65	65	66
Onion	125	78	78	78	78	80	78	81	82	81	82	78	79	81	79	81	79	79	80	80
Fodder	140	158	162	158	162	163	155	164	174	164	174	160	168	166	162	172	170	162	160	165
SHD Olive orchards	300	277	278	277	278	272	277	270	273	270	273	278	280	271	279	272	281	279	268	269
Semi-intensive Olive orchards	300	307	306	306	306	317	308	313	314	313	314	308	309	314	309	313	310	310	308	308
Peach	320	274	275	274	275	275	273	275	278	275	278	275	277	276	275	277	278	275	273	275
Almond	2550	1363	1369	1360	1369	1331	1358	1327	1349	1325	1349	1368	1388	1331	1373	1343	1393	1373	1310	1322
Vineyards	300	304	301	303	301	264	306	260	258	259	258	304	304	260	304	257	305	306	255	254
Rice	260	328	345	326	345	379	314	388	426	387	426	335	365	392	341	419	370	330	375	396

SHD—Super-high-density; CAS—Campilhas e Alto Sado; L—Lucefecit; O—Odivelas’s Other Irrigation Districts; O4—Odivelas’s Irrigation District 4; OLP—Odivelas’s Low-Pressure Irrigation District; R—Roxo; VS—Vale do Sado; V—Vigia; FI—Farmers inside Irrigation District; FO—Farmers outside Irrigation District; LP—Low Pressure; HP—High Pressure. * Source: IC managers. The greener the cell, the lower the yield can be; the redder the cell, the higher the yield will have to be.

Results show for the most suitable crops to be adopted (Melon, Tomato, Onion, Super-high-density Olive Orchards, Peach and Almonds) both yields and price may decrease significantly. For the vegetable crops, this decrease averages 40.4%, 18.1% and 36.3%, for Melon, Tomato and Onion, respectively; the decrease can be as high as 41.1% for Melon cropped by farmers outside Lucefecit ID and by farmers inside Vigia ID. For Super-high-density Olive Orchards, Peach and Almonds the decrease is also considerable. While for Super-high-density Olive Orchards, Peach the yield/price decrease averages 8.4% and 13.9%, respectively, for Almonds the decrease can be higher that 45.4%. it can be concluded that all of these crops are suitable to be cropped in all ICs since they show resistance, both to lower prices and to significant yield losses.

For farmers outside the irrigation district at Odivelas (O, O4 and OLP), Roxo, Vale do Sado and Vigia that crop Maize, yields/prices would require an average increase of 2.2%. Vineyards, for the low-pressurized IC/IDs, would need an average yield/price increase of 1.2%.

On the contrary, Wheat, Sunflower, Fodder crops, Semi-intensive Olive Orchards and Rice, in order to be suitable, would need to improve their yields or their prices. While Semi-intensive Olive Orchards are more prone to become economically suitable, since an average increase of 3.4% in yields/prices would be required to reach the threshold, the remaining crops behave differently. Fodder crops would require an average increase of 17.3%, and Wheat an increase averaging 20.5%. Sunflower would require an even higher increase (averaging 33.1%), while Rice yields or prices would need to be 41.4% higher than the current values. However, these required levels of productivity are not easily achievable. The current farming practices aim to improve yields while optimizing the use of farming inputs. To reach these levels of productivity would require some farming practices to become, eventually, unsustainable. A different approach could go through the assurance of higher crop prices; however, since most of these crops are traded as commodities, a national policy would be required to help farmers improving their farming economic returns.

The residual value is the remaining value after all farming inputs are paid, representing a long-term mean value that farmers are willing to pay for an unpriced input. In the short-term, farmers may opt to not fully pay for some factors, such as their own labor or the owned capital in order to maintain a positive gross margin. However, in the long-term, all production costs need be paid for and, if the residual value of water is negative, there are three alternatives:

(1)

Farmers opt for non-irrigated crops, leading to less irrigated area and, consequently, higher water prices to cover for the resource allocation;

(2)

Farmers choose to crop higher value crops (such as Melon, Tomato, Onion, Super-high-density Olive Orchards, Peach and Almonds) in order to improve their farming economic returns;

(3)

A national policy would be required to cover for the farming inputs.

As shown in Table 4, the highest residual value of water is for Almond and for Melon. Both these crops are highly remunerated due to market demand. However, since those crops are highly dependent on the global production, future RV_W may differ from the current study. Contrarily, both Sunflower and Rice, due to current prices, are not advisable unless a national policy is created.

The creation and implementation of a national policy to support certain crops can also be seen as defensible, or desirable, according to two objectives: that of maintaining the most diversified systems and, therefore, those that are more resilient and sustainable; that of limiting the excessive expansion of permanent crops, whose demand for water is practically fixed, enabling annual crops, whose demand for water is variable. In fact, in the context of climate change in which we already live, the annual crops can function as a kind of fuse, which allows one to balance availability with the demand for the water resource.

4. Conclusions

This study aimed to apply the Residual Value Method (RVM) approach for irrigation water to be applied at different crops in six Irrigation Communities (ICs) in the Alentejo region, southern Portugal, to evaluate the willingness to pay for irrigation water by farmers across the ICs. The main objective of this assessment was to answer a question: what is the value that farmers would be able to pay for the water to irrigate different crops at different locations? The aim of this study was to show that this approach can be used to provide information about farming economic sustainability and to provide support on if crop prices need to be revised or if a national policy should be conceived to cover for farming costs.

The results show that vegetables and fruit trees have the highest Residual Value of Water (RV_W), while Wheat, Sunflower, Fodder crops, Semi-intensive Olive Orchards and Rice tend to have an RV_W lower than the current variable irrigation water price. The results also show that, while, for Melon, Tomato, Onion, Super-high-density Olive Orchards, Peach and Almonds, both yields and price may decrease significantly, allowing one to save for farming inputs, Sunflower and Rice would require an increase in yields or prices to cover for the irrigation water price.

The results of this research may serve as a tool for IC managers and decision-makers on how irrigation water should be priced in order for some crops to be suitable. Also, it provides standard values for the most representative crops in the region, thereby offering support for new farmers on which crop should be cropped on those ICs.