Abstract
This work introduces a novel numerical method designed to address three-dimensional unsteady free surface flows incorporating integral viscoelastic constitutive equations, specifically the K–BKZ–PSM (Kaye–Bernstein, Kearsley, Zapas–Papanastasiou, Scriven, Macosko) model. The new proposed methodology employs a second-order finite difference approach along with the deformation fields method to solve the integral constitutive equation and the marker particle method (known as marker-and-cell) to accurately capture the evolution of the fluid’s free surface. The newly developed numerical method has proven its effectiveness in handling complex fluid flow scenarios, including confined flows and extrudate swell simulations of Boger fluids. Furthermore, a new semi-analytical solution for velocity and stress fields is derived, considering fully developed flows of a K–BKZ–PSM fluid in a pipe.
1. Introduction
Discovered and developed in the late twentieth century, viscoelastic materials have been used in a number of different applications (polymer industry, biomedicine, automotive industry, food, paints, etc.). Their use is often based on trial and error procedures, resulting in wasting raw material and time before a good end product is achieved. To mitigate this problem, numerical simulations are often used to predict the best material processing conditions. Usually, the simulations are based on the finite element, finite volume and finite difference methods, and the constitutive equations are, in most cases, defined by rheological differential models, such as Oldroyd-B [], UCM (Upper-convected Maxwell) [,], PTT (Phan–Thien–Tanner) [,], FENE-P (Finite Extensible Nonlinear Elastic Peterlin) [,] and Giesekus models []. Simulations of three-dimensional real-world applications require a great deal of computational effort, making the convergence of the algorithms in a reasonable amount of time a difficult task []. However, recent technological advances in scientific computing and the development of faster computers have led researchers to perform simulations in more complex geometries and use more sophisticated rheological models (that use integral equations instead of partial differential equations).
It is known that integral constitutive equations can better model various viscoelastic fluids, such as high-density polyethylene (HDPE) [,] and low-density polyethylene (LDPE) [] (used in the injection molding industry), and one of the most successful integral models is the K–BKZ–PSM [,,] (see also [,]). Therefore, there is significant interest among research groups worldwide in developing numerical methods to deal with the K–BKZ model, particularly with an emphasis on its application to polymer flows. Many studies have focused on simulating data and phenomena associated with polymer melt flows in rheology and polymer processing; however, there is still a need for further efforts to tackle numerical solutions of the K–BKZ–PSM for three-dimensional, time-dependent, free surface flows.
The vast majority of problems studied in the literature (considering integral models) are about confined flows, such as entry flows [,,] and flows in abrupt contractions [,,,,]. Regarding free surface flows, Mitsoulis and Malamataris [] extended the implementation of the free boundary condition (FBC) method to viscoelastic fluids governed by integral constitutive equations. Specifically, they focused on the K–BKZ–PSM model. To validate their numerical approach, they used the finite element method (FEM) to obtain results in simple test cases, including planar flow at an angle and Poiseuille flow in a tube, where analytical solutions are available for comparison. Furthermore, they have applied the FBC method to the K–BKZ–PSM model using data from a benchmark polymer melt, specifically the IUPAC-LDPE melt. Some other researchers have also considered flows with free surfaces [,,,,,,]. Ganvir et al. [] developed a novel approach for simulating extrudate swell using an Arbitrary Lagrangian Eulerian (ALE) technique in conjunction with a finite element formulation. The constitutive behavior of the melt was modeled using a differential exponential Phan–Thien–Tanner (PTT) viscoelastic model. With the proposed method, they have conducted simulations of extrudate swell in both planar and axisymmetric extrusion scenarios, which involve an abrupt contraction ahead of the die exit. Regarding three-dimensional (3D) flows, Rasmussen [] developed a Galerkin finite element method for simulating three-dimensional transient viscoelastic flows. The method used a Lagrangian kinematic description and integral constitutive models. The numerical implementation was validated with the calculation of various transient and steady drag correction factors for the motion of a sphere in a cylinder containing an upper convected Maxwell fluid. Later, Marín and Rasmussen [] extended the Galerkin finite element method for simulating three-dimensional transient and non-isothermal flows of K–BKZ type fluids. Tomé et al. [] proposed a novel numerical approach to tackle the simulation of 3D viscoelastic unsteady free surface flows governed by the Oldroyd-B differential constitutive equation. The numerical method involves solving the governing equations using a finite difference approach on a 3D-staggered grid. To validate the accuracy and reliability of the proposed technique, an exact solution of the flow of an Oldroyd-B fluid inside a 3D-pipe was employed. The results obtained through numerical simulations included the analysis of transient extrudate swell and jet buckling.
Summarizing, previous studies in the field of free surface flows have predominantly centered around two-dimensional (2D) scenarios and used the finite element method. These investigations primarily revolve around the extrudate swell problem, considering both steady and unsteady flows; however, it is worth noting that these studies relied on differential viscoelastic constitutive equations. Therefore, this work introduces a novel numerical method specifically designed to address 3D unsteady free surface flows incorporating integral viscoelastic constitutive equations, specifically, the K–BKZ–PSM model. The key innovation lies in the development of a robust numerical method for integral models using the finite difference method on a staggered grid, which enables accurate predictions of extrudate swell phenomena. We also derive a new semi-analytical solution for the fully developed flow of a K–BKZ–PSM viscoelastic fluid, which can serve for other authors to verify their own numerical implementations of the K–BKZ–PSM integral viscoelastic model.
It is worth noting that the FEM prominently features in the limited body of work concerning this subject. Nevertheless, both FEM and FDM stand as extensively used numerical approaches for tackling partial differential equations (PDEs). When properly employed within suitable conditions, both techniques exhibit stability. Within our research group, a longstanding tradition exists regarding leveraging the finite difference method [,,,,,], resulting in a profound mastery of its implementation. Furthermore, the group has made innovative strides in enhancing the fundamental finite difference methodology. This progression equips us to adeptly handle different grid structures and a range of discretization choices. Consequently, this method takes precedence in our current work.
The paper is structured as follows. In Section 2, we introduce the governing equations for isothermal and incompressible viscoelastic flows modelled by the K–BKZ–PSM constitutive equation. Section 3 is devoted to the numerical method, where the variant of the marker particle method that employs the finite difference method on a staggered grid is described for 3D flows using the K–BKZ–PSM viscoelastic integral model. In Section 4, we derive a new semi-analytical solution for the fully developed flow of a K–BKZ–PSM viscoelastic fluid. For validation of the newly developed numerical method, two case studies are analyzed in Section 5, the confined pipe flow and the extrudate swell free surface flow of a Boger fluid. The paper ends with the conclusions in Section 6.
2. Governing Equations
The isothermal and incompressible fluid flow considered in this work is governed by the dimensionless continuity and linear momentum equations [],
together with a constitutive equation for the stress. is a stress tensor given by
where is a non-Newtonian stress tensor, is the velocity field, p is the kinematic pressure, is the gravity acceleration vector and t is the time. In these equations, is the Froude number, is the Reynolds number, is the zero-shear-rate viscosity, is the fluid density, g the magnitude of the gravity acceleration vector and U and L are the characteristic velocity and length scales, respectively. Note that all variables are dimensionless, with: , , , and .
The constitutive equation for the non-Newtonian stress tensor is given by the K–BKZ–PSM model [],
where
is the memory function, is the relaxation time of the fluid, is a model parameter and is the number of modes. is the Papanastasiou–Scriven–Macosko decay function, being given by
is the Finger tensor, and , are the first and second invariants of , respectively. The parameters and are obtained from a fit to rheological data. is the Weissenberg number, the viscosity is given by and is the mean relaxation time [].
In this work, the method of deformation fields [] is used to update the Finger tensor as the fluid flows. In this methodology, -deformation instants () are defined in the interval where the history of deformation is stored. This deformation is updated by solving the transport equation for ,
The governing equations are solved in a Cartesian 3D system where
This results in the following system of equations that need to be solved for the pressure, velocity and stress:
- continuity equation:
- linear momentum equations:
- stress tensor :
3. Numerical Method
The governing equations are solved by a variant of the marker particle method [,], which employs the finite difference method on a staggered grid. This methodology is implemented in the FREEFLOW-3D code developed by researchers from the Institute of Mathematical and Computing Sciences (ICMC) at the University of São Paulo (USP) in Brazil. Code details can be found in [,,,] considering 2D, 3D and radial symmetry flows. The precision of the numerical technique and its validation for three-dimensional viscoelastic flows with a free surface is presented in the works of Tomé et al. [,] (which only uses differential constitutive equations). The use of integral models in three-dimensional flows (considering free surface problems) has not yet been tested on this system (see Tomé et al. [,,,]). The novelty of this work is to incorporate equations for viscoelastic fluids using integral models (more complex than the differential type models) in the FREEFLOW-3D system.
In this methodology, the velocity field is approximated in the face of the cells, and the other variables, denoted by , are evaluated in the center of the computational cells (see Figure 1a). The technique adopted here is presented by Tomé et al. [,] for differential models, where the free surface is defined by marker particles that move with the local fluid velocity. In addition, the computational cells are defined as (see also Figure 1b):
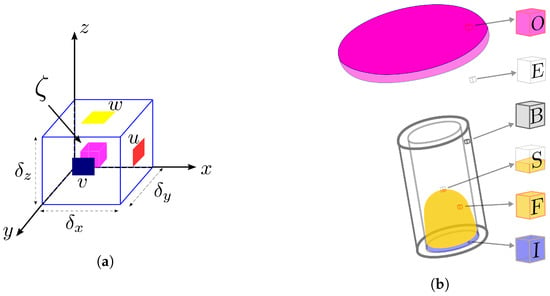
Figure 1.
(a) Typical three-dimensional staggered cell and (b) illustration of cell type classification used.
- ■
- Fluid entrance: Inflow — I,
- ■
- Fluid exit: Outflow — O,
- ■
- Rigid boundaries: Boundary — B,
- ■
- Empty cells: Empty — E,
- ■
- Free surface cells: Surface — S,
- ■
- Full cells: Full — F.
To solve Equations (1) and (2), one must specify boundary conditions for the velocity field. A velocity field () is prescribed in the fluid inlet cells (inflows), and a fully developed flow is assumed in the outflow (a homogeneous Neumann boundary condition is assumed, where n is the normal direction to the contour). In the fluid inlet cells (inflows), we assume that and the Finger tensor is the identity matrix. In outflow regions, we assume Neumann conditions for Finger tensor , and we assume . We also take in rigid boundaries. Details of the boundary conditions adopted in this work can be found in Tomé et al. [] or Castelo et al. [].
The solutions and at time step are obtained in the following way: first, using the values of , the velocity and pressure fields at time are calculated. Then, is used to calculate the tensor by the method of deformation fields, and, lastly, the free surface is updated. Specifically, the following steps are performed:
- Step 1 — Calculation of and
It is assumed that, at time t, the variables and the marker’s positions are known. Then, and are obtained as follows:
1. Calculate , and, from the EVSS [] transformation, obtain ;
2. Calculate an intermediate velocity field using the ideas of the projection method [,] to uncouple the conservation of mass and momentum equations. An intermediate velocity field is obtained from Equation (2) using explicit Euler Methods, where is an approximation to . The boundary conditions for are the same as those for the final velocity . Details of boundary conditions for full cells (F), outflow cells (O) and free surface cells (S) are provided in detail in Tomé et al. [,] and will not be presented here for the sake of conciseness. It can be shown that possesses the correct vorticity at time , but it does not conserve mass in general. Therefore, there is a potential function so that,
3. Solve the Poisson equation for the potential function for every F-cell in the domain,
The boundary conditions required for solving this Poisson equation are the homogeneous Neumann conditions for rigid walls and inflows, while homogeneous Dirichlet conditions are used at outflows.
4. Compute the final velocity field from Equation (13);
5. Compute the final pressure field (see []) by
Details of the discretization of the equations (temporal and spatial) considering all types of cells (see Figure 1b) are given in [,,].
- Step 2 — Calculation of the extra stress tensor and free surface update
To calculate the extra stress tensor , initially, the Finger tensor is updated at for every full cell (F) and surface cell (S) for every intermediate time using Equation (7). Details of the calculation of the Finger B tensor (in two dimensions) can be found in [] and will not be presented here because the extension to three dimensions is straightforward. Note that, for each computational cell (F and S), Equation (7) is solved N times (for each ), considering each of the components of the Finger tensor. Thus, considering three-dimensional flows, the computational cost to obtain the deformation history in each cell is high, demanding a great deal of memory and simulation time (since, for each cell, it is necessary to calculate the Finger tensor N times for each component of the deformation matrix). For inflow cells (I), boundary cells (B) and empty cells (E), the Finger tensor is the identity tensor. In the outflow, the Neumann condition is assumed.
The definition of the points for the calculation of the components of the Finger tensor and the tensor are given as follows. Let , be -points in the interval . Then, the constitutive equation can be written in the form
where an even N is assumed. For , and, therefore, the first integral becomes
and can be solved exactly.
Each integral under the summation operator is approximated by the 3-points quadrature formula
The coefficients are obtained by solving the linear system
and are found to be
One of the key issues of the deformation fields method is how the integration nodes are distributed over the interval because such distribution can affect the accuracy of the results when solving complex flows. In this work, we used an ad hoc methodology for the discretization of the interval , where a geometric progression is employed to calculate the integration nodes. Note that we consider time-dependent flows, and, therefore, the integration nodes are calculated at time as follows:
- (a)
- Set and ;
- (b)
- , where .
The last step in the calculation is to update the position of the moving free surface (the S-cell in Figure 1b). The fluid surface is represented by a piecewise linear surface composed of triangles and quadrilaterals having marker particles on their vertices (see []). The particle coordinates, stored at each time step, are updated, solving the equation
by Euler’s method. With the new coordinates of each marker particle, a reclassification of the free surface cells is performed. A free surface cell can become an empty cell (E-cell in Figure 1b) or a full cell (F-cell in Figure 1b) or remain an S-type cell. Details on the marker particles that define the free surface and the steps for inserting and removing particles will not be shown here, but the reader can consult Tomé et al. [] or Castelo et al. [].
4. Semi-Analytical Solution
We will now derive a semi-analytical solution for a fully developed three-dimensional tube flow of a K–BKZ–PSM fluid to validate the numerical implementation. Due to the complexity of the integral model, some simplifications need to be assumed to develop the analytical solution, which is only possible for some types of domains. We consider cylindrical coordinates (see Figure 2) for simplicity and assume pure shear flow. After finding the semi-analytical solution, we present the change in variables to obtain the solution in Cartesian coordinates.
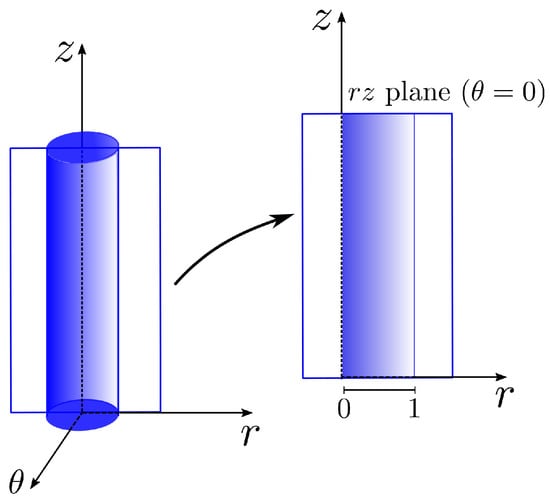
Figure 2.
Representation of the pipe and a section in the plane.
We assume that and
The invariants and that are required in the Papanastasiou function take the form
and the tensor components are given by
Taking the change in variables , these equations are rewritten as
Thus, the equations of continuity and balance of momentum become
Integrating Equation (26), we obtain
Thus,
and Equation (27) is rewritten as
The left hand side of Equation (30) is just a function of r, so must be constant, let us say C, and therefore . In this way, it follows that
where should be finite and therefore , leading to
The second equation in Equation (25) can then be rewritten as
The inlet boundary condition allows one to determine the constant C. The inflow velocity is given by
thus,
By mass conservation,
and integrating by parts leads to
with
Thus, to determine C, we must obtain from Equation (33) and verify that
The steps to calculate semi-analytical solutions are as follows:
- Step 1:
- Set an interval such that .
- Step 2:
- Determine the zero for taking , where is a small value ( is the tolerance for the error). We carefully selected the value of to ensure the attainment of a semi-analytical solution accurate to six significant digits. Using Gauss–Laguerre quadrature in Equation (33), obtain . Using Equation (39), obtain the value of using Simpson 1/3 quadrature.
- Step 3:
The solution in three dimensions is obtained by making the change in coordinates as follows:
where
Thus, in three-dimensional Cartesian coordinates, we have that
5. Results
The numerical code will now be used to solve confined (see Section 5.1) and free surface flows (see Section 5.2).
5.1. Confined Pipe Flows
In this confined pipe flow, the fluid is assumed to have only one relaxation mode. Therefore, it is possible to compare the simulation results with the semi-analytical solution presented before. The parameters used in this simulation are (see Tomé et al. [] and Quinzani et al. []):
- Diameter ;
- ;
- Number of deformation fields ;
- ;
- Geometry: × × ;
- Meshes (number of cells in the x, y and z directions): (), (), (), () and ().
Figure 3a,b show the velocity profiles w and u, respectively, with corresponding cross-section velocity distributions in the plane (obtained mesh ). The velocity profiles are fully developed at , suggesting that they have reached a steady-state condition. The velocity profile w shows a parabolic shape in the cross-section represented in Figure 3a, while the influence of the inflow can be observed in the cross-section depicted in Figure 3b, but the solution for u exhibits the expected physical behavior outside this region. Notice that, in all full cells, the initial velocity vector is defined as .
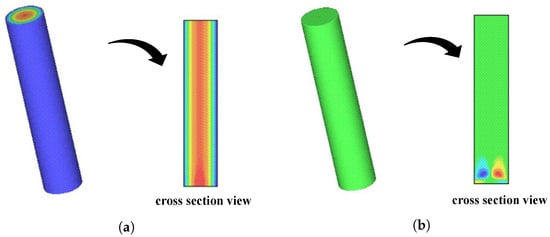
Figure 3.
Velocity components u and w of along the plane () at . (a) Visualization of the velocity profile w. (b) Visualization of the velocity profile u.
Similar to the velocity vector, initial conditions for pressure and tensors are set to zero in full cells. As shown in Figure 4a,b, the pressure and tensor profiles are in agreement with the physically expected profiles, i.e., linear profiles across the longitudinal direction (flow direction) and transverse direction (perpendicular to the flow), respectively. In addition, the values obtained for are comparable with the behavior of the analytical solution (see Figure 5b). In the cross-section represented in Figure 4b, there is an influence of the inflow (tensors are defined as zero in the inflow, and the Finger tensor is defined as the identity matrix), but, outside this region, the expected linear profile is obtained as previously stated (for further details, refer to Figure 5b).
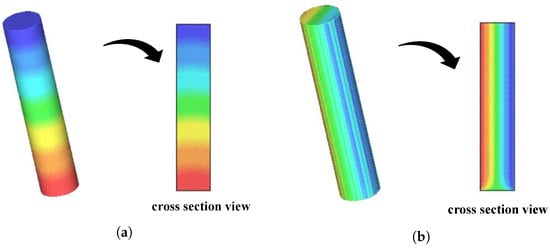
Figure 4.
Pressure and distribution along the plane (). (a) Visualization of the pressure p. (b) Visualization of the tensor component.
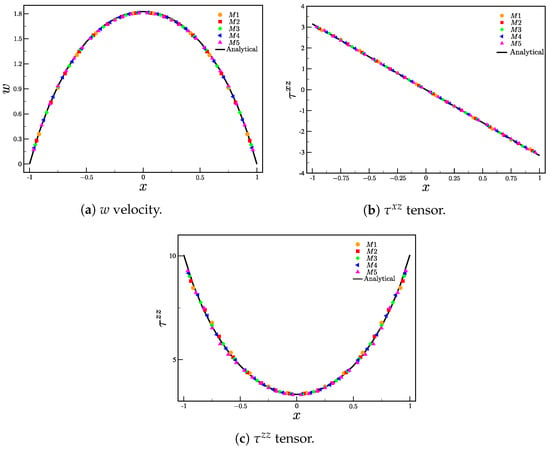
Figure 5.
Comparison between the analytical and numerical solutions for (a) w velocity component and tensors components (b) and (c) .
Figure 5a–c show, respectively, the solution for the velocity w and stress components and using meshes –. The profiles were obtained at and were taken in the center of the pipe, for (or ). The results were compared with the semi-analytical solution, with good agreement between the numerical results (M1–M5) and the semi-analytical results. The instant () was chosen because the velocity and stresses already show a steady state behavior (the velocity residual is small (see Equation (42)). The residual (for the velocities) is calculated as
where t is the simulation time, is the time step and is the number of computational cells. The slight variances between the analytical and numerical solutions can be attributed to approximations made in the numerical simulations, which differ from the precise analytical solution. Although the tube’s length appears adequate for the complete development of velocity and shear stress profiles, this completeness is not reflected in the tensor. Consequently, these disparities remain minor. It is worth noting that, across all meshes, the average relative error remains below .
Figure 6 shows the calculation of the residuals in meshes M1–M5 up to time (or, equivalently, ). It can be observed that the residuals in the five meshes M1–M5 decrease and show convergence towards a steady-state solution, thus proving the robustness of the numerical method. As expected, we also observe a smaller residual for the most refined meshes.
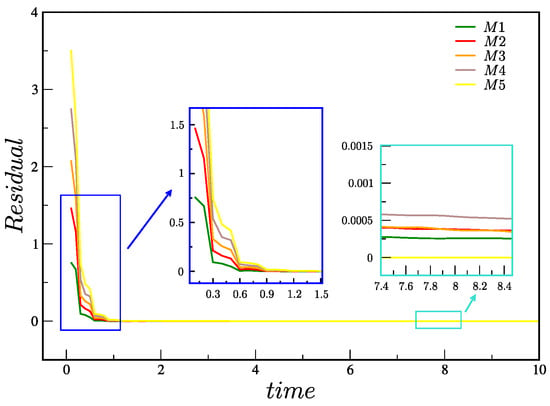
Figure 6.
Total residual in meshes , , , and up to (or ).
5.2. Free Surface Flows
In this subsection, we test the numerical method’s robustness by simulating the extrudate swell phenomenon of Boger fluids. Please note that our aim is not to conduct an in-depth study of this type of flow in Boger fluids; instead, we focus on assessing the reliability of the numerical approach.
The phenomenon known as extrudate swell is very present in various industrial processes. In this phenomenon, the fluid flows over a pipe/die and swells outside the free surface region (the cross-sectional area of the extrudate—the material being extruded—is larger after exiting the die compared to the die orifice). This behavior is mainly due to the elastic recovery of the polymer chains after being subjected to high pressures and shear forces during the extrusion process. Figure 7a shows the domain used in the simulation, and Figure 7b illustrates the phenomenon of extrudate swell (with the contour lines representing the trajectory of the fluid’s free surface).
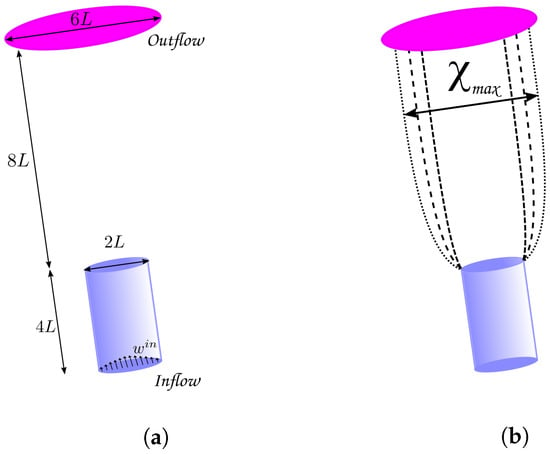
Figure 7.
Schematic of a free surface simulation in the FREEFLOW-3D software. (a) Schematic representation of the domain; (b) illustration of the extrudate swell. The fluid exits the tube and starts to swell.
It should be remarked that simulating extrudate swell can be challenging due to several numerical difficulties, which are now outlined: the extrusion process involves highly non-uniform and complex flow patterns, especially near the die exit. These flows experience rapid changes in pressure and velocity, making it difficult to model accurately; simulating extrusion processes requires discretizing the computational domain into smaller elements or cells, and the geometry of the die can be quite intricate. Moreover, the simulation must maintain numerical stability, which can be problematic in high-pressure and high-shear regions; simulating extrudate swell is computationally intensive, especially for large-scale industrial extrusion processes and using integral models; extrudate swell is a time-dependent phenomenon as the material continuously deforms and recovers during extrusion. Capturing this transient behavior accurately in numerical simulations requires precise time-stepping algorithms and may increase computational complexity. To address these challenges, researchers often resort to simplifications and assumptions to reduce computational complexity. However, in the context of this work, we take a different approach by considering the complete system of equations and accounting for the full 3D geometry.
To test the robustness of the new numerical procedure, two different Weissenberg numbers were considered (case C1 − and case C2 − ), both using non-shear-thinning highly elastic polymer solutions (Boger fluids — see Table 1). Boger fluids are a type of dilute polymer solution known for their remarkable elasticity, particularly at low apparent shear rates, and this unique characteristic gives rise to a significant extrudate swell during the extrusion process [,,,]. This makes Boger fluids ideal to test the numerical implementation. Numerical simulation of extruded swelling in two dimensions using the data used here (see Table 1) is presented in Mitsoulis [].

Table 1.
Parameters of the fluid used in the extrudate swell problem (see Mitsoulis []).
The following parameters were used in the simulations (see Mitsoulis [] and Tomé et al. []):
- Pipe dimension: ; (see Figure 7a);
- Pipe diameter ;
- Number of deformation fields ;
- C1 − , , ;
- C2 − , , .
Figure 8 shows the flow development of a Boger fluid for two different Weissenberg number values (cases and ). We conducted flow measurements at six different time points to analyze the behavior of the fluid in the system. The first four time instants were identical for both and cases, while the last two time points differed. Specifically, for the lower inlet velocity case, we considered time points and 6 s, and, for the other case, the time points were and s. During the initial stages of both cases, the fluid exhibited a smooth flow with a parabolic profile as it exited the tube. However, as the process continued, swell occurred, causing the cross-sectional area of the extrudate to increase after leaving the die. This swelling behavior significantly affects the flow dynamics and needs to be carefully considered in the analysis. The simulation results show the development of the fluid front as it reaches the wall. Notably, there are distinct differences in swelling between two specific time instances: () and ().
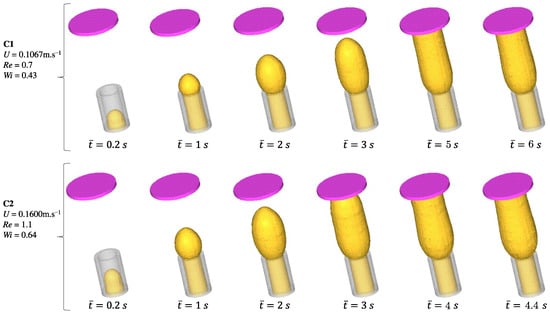
Figure 8.
Flow development of a Boger fluid for two different inlet velocities (cases and ).
To characterize the extrudate swell phenomenon, an important parameter is the dimensionless swelling rate , where is the maximum swelling value and r is the pipe radius. For case , the maximum swelling value is found to be , while, for case , the swelling rate increases to . This was expected since the Weissenberg number represents the ratio of the characteristic time scale of the elastic forces acting on a fluid to the characteristic time scale of viscous forces, and, when a polymer melt is subjected to shear flow (for example, in an extruder), the long polymer chains experience deformation due to the flow-induced stretching and alignment. A higher Weissenberg number indicates a more elastic behavior of the polymer melt, leading to more significant elastic recovery and increased extrudate swell.
We may therefore conclude that the numerical method employed in the simulations demonstrates its capability to capture the transient physics of the extrudate swell problem in detail, even for a small difference in the Weissenberg number (cases and ). It accurately predicts the swelling behavior and allows for a better understanding of the process dynamics. By accounting for the material properties and flow conditions, the simulation provides valuable insights into the extrusion process and contributes to the optimization of extrusion operations.
6. Conclusions
In this work, a novel numerical method was developed to address three-dimensional unsteady free surface flows incorporating integral viscoelastic constitutive equations, specifically the K–BKZ–PSM (Kaye–Bernstein, Kearsley, Zapas–Papanastasiou, Scriven, Macosko) model. To implement this new approach, we integrated it into the FREEFLOW-3D code [], enhancing its capabilities for handling viscoelastic fluid behavior.
To validate the numerical methodology, we conducted simulations of K–BKZ–PSM fluids in a pipe. The results were compared with a newly derived semi-analytical solution, and we found that the simulations performed on five different meshes yielded excellent agreement with the analytical solution. Furthermore, we applied our methodology to tackle flows with free surfaces. One notable example was the simulation of the classic extrudate swell problem, which involved a highly elastic polymeric solution known as the Boger fluid.
The significance of this work lies in the scarcity of literature concerning the simulation of unsteady three-dimensional flows of K–BKZ–PSM fluids (and integral viscoelastic models in general) using finite differences, especially when considering problems with moving free surfaces. Therefore, we hope that our contributions will inspire and encourage other researchers to further develop and explore the numerical methods we have presented here.
In conclusion, our newly developed numerical method has proven its effectiveness in handling complex fluid flow scenarios, including free surface flows such as extrudate swell simulations. The successful validation against analytical solutions reinforces the reliability of our approach and opens up opportunities for broader applications in the field of viscoelastic fluid dynamics.
Author Contributions
Conceptualization, J.B., A.C., L.L.F. and C.F.; Methodology, J.B., A.C., L.L.F. and C.F.; Software, J.B. and A.C.; Validation, A.C., L.L.F. and C.F.; Supervision, A.C., L.L.F. and C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by São Paulo Research Foundation (FAPESP) grants 2013/07375-0, 2019/07316-0; the National Council for Scientific and Technological Development (CNPq) grant 307483/2017-7; FCT (Fundação para a Ciência e a Tecnologia) and CMAT (Centre of Mathematics of the University of Minho) projects UIDB/00013/2020 and UIDP/00013/2020 and FCT funding, project 2022.06672.PTDC and contract 2022.00753.CEECIND.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
J. Bertoco acknowledges the support by CMCC — Center for Mathematics, Computing and Cognition, UFABC. A. Castelo thanks the financial support from the São Paulo Research Foundation (FAPESP) grants 2013/07375-0, 2019/07316-0 and the National Council for Scientific and Technological Development (CNPq) grant 307483/2017-7. A. Castelo and J. Bertoco acknowledge the support by ICMC — Institute of Mathematics and Computational Sciences — University of Sao Paulo (USP). L.L. Ferrás would like to thank FCT (Fundação para a Ciência e a Tecnologia) for financial support through CMAT (Centre of Mathematics of the University of Minho) projects UIDB/00013/2020 and UIDP/00013/2020 and would also like to thank FCT for the funding of project 2022.06672.PTDC. C. Fernandes acknowledges the support by FEDER funds through the COMPETE 2020 Programme and National Funds through FCT (Portuguese Foundation for Science and Technology) under the contract FCT/2022.00753.CEECIND. Research carried out using the computational resources of the Center for Mathematical Sciences Applied to Industry (CeMEAI) funded by FAPESP grant 2013/07375-0.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| K–BKZ | Kaye–Bernstein, Kearsley, Zapas |
| PSM | Papanastasiou, Scriven, Macosko |
| EVSS | Elastic–Viscous Split Stress |
| UCM | Upper-convected Maxwell |
| PTT | Phan–Thien–Tanner |
| FENE-P | Finite Extensible Nonlinear Elastic Peterlin |
| HDPE | High-Density Polyethylene |
| LDPE | Low-Density Polyethylene |
| FEM | Finite element Method |
| FDM | Finite Difference Method |
| PDE | Partial Differential Equation |
| ALE | Arbitrary Lagrangian Eulerian |
| FBC | Free Boundary Condition |
References
- Clermont, J.-R.; Normandin, M. Numerical simulation of extrudate swell for Oldroyd-B fluids using the stream-tube analysis and a streamline approximation. J. Non-Newton. Fluid Mech. 1993, 50, 193–215. [Google Scholar] [CrossRef]
- Tomé, M.F.; Castelo, A.; Afonso, A.M.; Alves, M.A.; Pinho, F.T. Application of the log-conformation tensor to three-dimensional time-dependent free surface flows. J. Non-Newton. Fluid Mech. 2012, 175–176, 44–54. [Google Scholar] [CrossRef]
- Mompean, G.; Thais, L.; Tomé, M.F.; Castelo, A. Numerical prediction of three-dimensional time-dependent viscoelastic extrudate swell using differential and algebraic models. Comput. Fluids 2011, 44, 68–78. [Google Scholar] [CrossRef]
- Tomé, M.F.; Paulo, G.S.; Pinho, F.T.; Alves, M.A. Numerical solution of the PTT constitutive equation for unsteady three-dimensional free surface flows. J. Non-Newton. Fluid Mech. 2010, 165, 247–262. [Google Scholar] [CrossRef]
- Béraudo, C.; Fortin, A.; Coupez, T.; Demay, Y.; Vergnes, B.; Agassant, J.F. A finite element method for computing the flow of multi-mode viscoelastic fluids: Comparison with experiments. J. Non-Newton. Fluid Mech. 1998, 75, 1–23. [Google Scholar] [CrossRef]
- Mu, Y.; Zhao, G.; Wu, X.; Zhai, J. Modeling and simulation of three-dimensional planar contraction flow of viscoelastic fluids with PTT, Giesekus and FENE-P constitutive models. Appl. Math. Comput. 2012, 218, 8429–8443. [Google Scholar] [CrossRef]
- Hulsen, M.A.; van der Zanden, J. Numerical simulation of contraction flows using a multi-mode Giesekus model. J. Non-Newton. Fluid Mech. 1991, 38, 183–221. [Google Scholar] [CrossRef]
- Goublomme, A.; Crochet, M.J. Numerical prediction of extrudate swell of a high-density polyethylene: Further results. J. Non-Newton. Fluid Mech. 1993, 47, 281–287. [Google Scholar] [CrossRef]
- Park, H.J.; Mitsoulis, E. Numerical simulation of circular entry flows of fluid M1 using an integral constitutive equation. J. Non-Newton. Fluid Mech. 1992, 42, 301–314. [Google Scholar] [CrossRef]
- Dupont, S.; Crochet, M.J. The vortex growth of a K.B.K.Z. fluid in an abrupt contraction. J. Non-Newton. Fluid Mech. 1988, 29, 81–91. [Google Scholar] [CrossRef]
- Papanastasiou, A.C.; Scriven, L.E.; Macosko, C.W. An Integral Constitutive Equation for Mixed Flows: Viscoelastic Characterization. J. Rheol. 1983, 27, 387–410. [Google Scholar] [CrossRef]
- Bernstein, B.; Kearsley, E.A.; Zapas, L.J. A Study of Stress Relaxation with Finite Strain. Trans. Soc. Rheol. 1963, 7, 391–410. [Google Scholar] [CrossRef]
- Kaye, A. Non-Newtonian Flow in Incompressible Fluids. Aerosp. Eng. Rep. 1963, 134. [Google Scholar]
- Mitsoulis, E. Extrudate swell of Boger fluids. J. Non-Newton. Fluid Mech. 2010, 165, 812–824. [Google Scholar] [CrossRef]
- Mitsoulis, E. 50 Years of the K-BKZ Constitutive Relation for Polymers. ISRN Polym. Sci. 2013, 2013, 1–22. [Google Scholar] [CrossRef]
- Luo, X.-L.; Mitsoulis, E. An efficient algorithm for strain history tracking in finite element computations of non-Newtonian fluids with integral constitutive equations. Int. J. Numer. Methods Fluids 1990, 11, 1015–1031. [Google Scholar] [CrossRef]
- Ansari, M.; Alabbas, A.; Hatzikiriakos, S.G.; Mitsoulis, E. Entry Flow of Polyethylene Melts in Tapered Dies. Int. Polym. Process. 2010, 25, 287–296. [Google Scholar] [CrossRef]
- Chai, M.S.; Yeow, Y.L. Modelling of fluid M1 using multiple-relaxation-time constitutive equations. J. Non-Newton. Fluid Mech. 1990, 35, 459–470. [Google Scholar] [CrossRef]
- Luo, X.-L.; Mitsoulis, E. A numerical study of the effect of elongational viscosity on vortex growth in contraction flows of polyethylene melts. J. Rheol. 1990, 34, 309–342. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Malamataris, N.A. The free (open) boundary condition with integral constitutive equations. J. Non-Newton. Fluid Mech. 2012, 177–178, 97–108. [Google Scholar] [CrossRef]
- Olley, P.; Spares, R.; Coates, P.D. A method for implementing time-integral constitutive equations in commercial CFD packages. J. Non-Newton. Fluid Mech. 1999, 86, 337–357. [Google Scholar] [CrossRef]
- Araújo, M.S.B.; Fernandes, C.; Ferrás, L.L.; Tuković, Ž.; Jasak, H.; Nóbrega, J.M. A stable numerical implementation of integral viscoelastic models in the OpenFOAM® computational library. Comput. Fluids 2018, 172, 728–740. [Google Scholar] [CrossRef]
- Luo, X.-L.; Mitsoulis, E. Memory Phenomena in Extrudate Swell Simulations for Annular Dies. J. Rheol. 1989, 33, 1307–1327. [Google Scholar] [CrossRef]
- Goublomme, A.; Draily, B.; Crochet, M.J. Numerical prediction of extrudate swell of a high-density polyethylene. J. Non-Newton. Fluid Mech. 1992, 44, 171–195. [Google Scholar] [CrossRef]
- Ganvir, V.; Lele, A.; Thaokar, R.; Gautham, B.P. Prediction of extrudate swell in polymer melt extrusion using an Arbitrary Lagrangian Eulerian (ALE) based finite element method. J. Non-Newton. Fluid Mech. 2009, 156, 21–28. [Google Scholar] [CrossRef]
- Ahmed, R.; Liang, R.F.; Mackley, M.R. The experimental observation and numerical prediction of planar entry flow and die swell for molten polyethylenes. J. Non-Newton. Fluid Mech. 1995, 59, 129–153. [Google Scholar] [CrossRef]
- Tomé, M.F.; Castelo, A.; Ferreira, V.G.; McKee, S. A finite difference technique for solving the Oldroyd-B model for 3D-unsteady free surface flows. J. Non-Newton. Fluid Mech. 2008, 154, 179–206. [Google Scholar] [CrossRef]
- Rasmussen, H.K. Time-dependent finite-element method for the simulation of three-dimensional viscoelastic flow with integral models. J. Non-Newton. Fluid Mech. 1999, 84, 217–232. [Google Scholar] [CrossRef]
- Marín, J.M.R.; Rasmussen, H.K. Lagrangian finite element method for 3D time-dependent non-isothermal flow of K-BKZ fluids. J. Non-Newton. Fluid Mech. 2009, 162, 45–53. [Google Scholar] [CrossRef]
- Tomé, M.F.; Filho, A.C.; Cuminato, J.A.; Mangiavacchi, N.; Mckee, S. GENSMAC3D: A numerical method for solving unsteady three-dimensional free surface flows. Int. J. Numer. Methods Fluids 2001, 37, 747–796. [Google Scholar] [CrossRef]
- Castello, F.; Tomé, M.F.; César, C.N.L.; McKee, S.; Cuminato, J.A. Freeflow: An integrated simulation system for three-dimensional free surface flows. Comput. Vis. Sci. 2000, 2, 199–210. [Google Scholar] [CrossRef]
- Tomé, M.F.; Bertoco, J.; Oishi, C.M.; Araujo, M.S.B.; Cruz, D.; Pinho, F.T.; Vynnycky, M. A finite difference technique for solving a time strain separable K-BKZ constitutive equation for two-dimensional moving free surface flows. J. Comput. Phys. 2016, 311, 114–141. [Google Scholar] [CrossRef]
- Hulsen, M.A.; Peters, E.A.J.F.; van den Brule, B.H.A.A. A new approach to the deformation fields method for solving complex flows using integral constitutive equations. J. Non-Newton. Fluid Mech. 2001, 98, 201–221. [Google Scholar] [CrossRef]
- Rajagopalan, D.; Armstrong, R.C.; Brown, R.A. Finite element methods for calculation of steady, viscoelastic flow using constitutive equations with a Newtonian viscosity. J. Non-Newton. Fluid Mech. 1990, 36, 159–192. [Google Scholar] [CrossRef]
- Quinzani, L.M.; McKinley, G.H.; Brown, R.A.; Armstrong, R.C. Modeling the rheology of polyisobutylene solutions. J. Rheol. 1990, 34, 705–748. [Google Scholar] [CrossRef]
- Mitsoulis, E. The numerical simulation of Boger fluids: A viscometric approximation approach. Polym. Eng. Sci. 1986, 26, 1552–1562. [Google Scholar] [CrossRef]
- López-Aguilar, J.E.; Tamaddon-Jahromi, H.R. Computational Predictions for Boger Fluids and Circular Contraction Flow under Various Aspect Ratios. Fluids 2020, 5, 85. [Google Scholar] [CrossRef]
- Satrape, J.V.; Crochet, M.J. Numerical simulation of the motion of a sphere in a Boger fluid. J. Non-Newton. Fluid Mech. 1994, 55, 91–111. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).