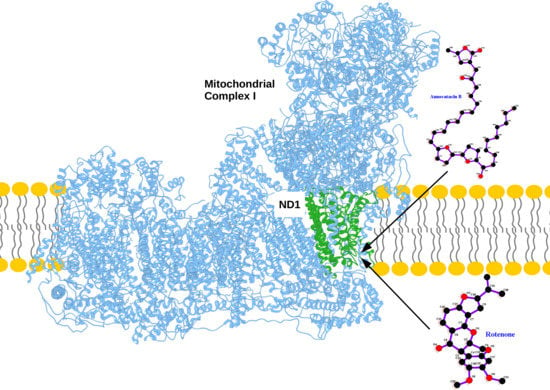
Structural and Energetic Affinity of Annocatacin B with ND1 Subunit of the Human Mitochondrial Respiratory Complex I as a Potential Inhibitor: An In Silico Comparison Study with the Known Inhibitor Rotenone
Abstract
1. Introduction
2. Computational Details
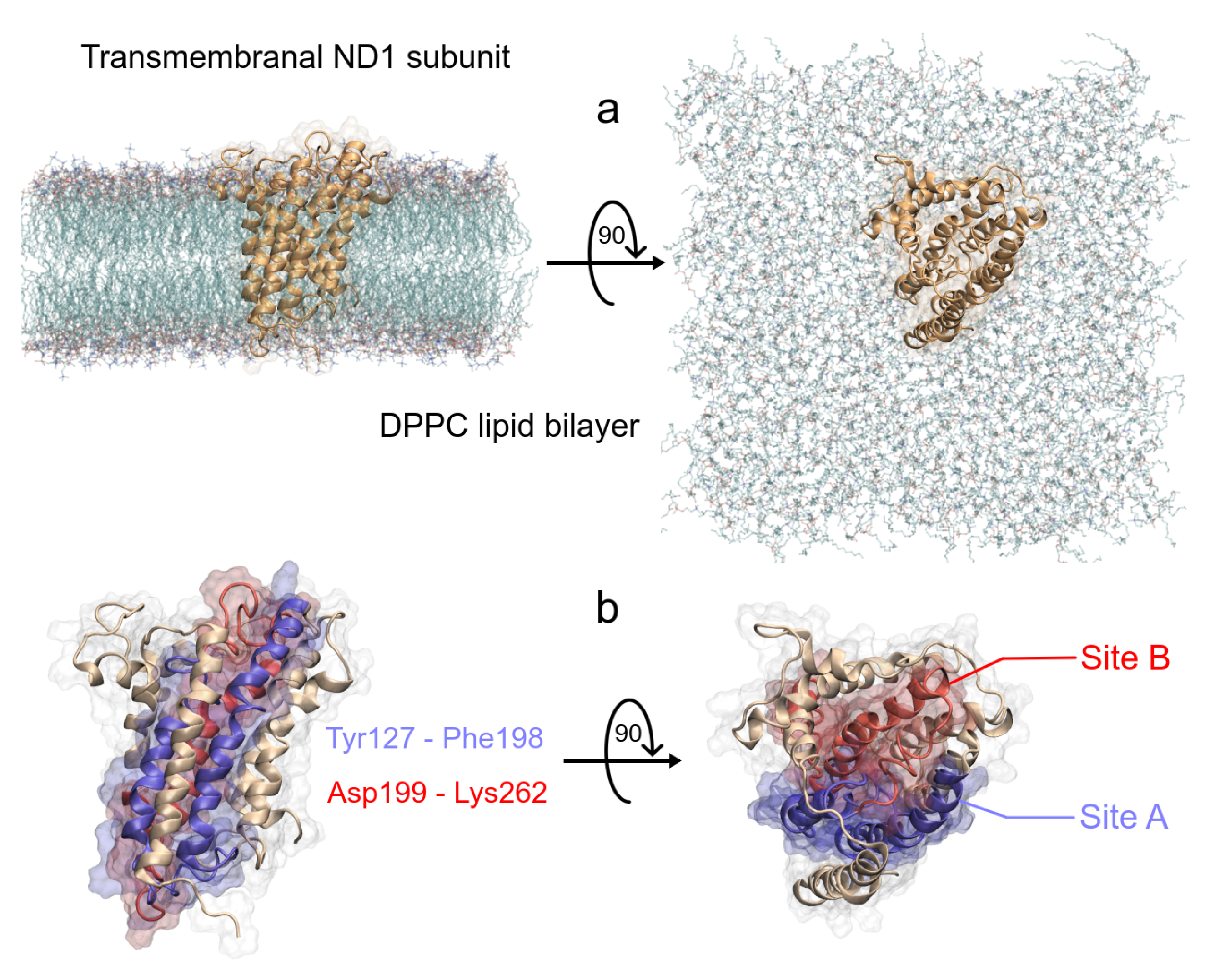
2.1. Structural Preparation
2.2. MD Simulations
2.3. Molecular Docking Calculations
2.4. MM/PBSA Calculations
2.5. Structure and Data Analysis
3. Results and Discussion
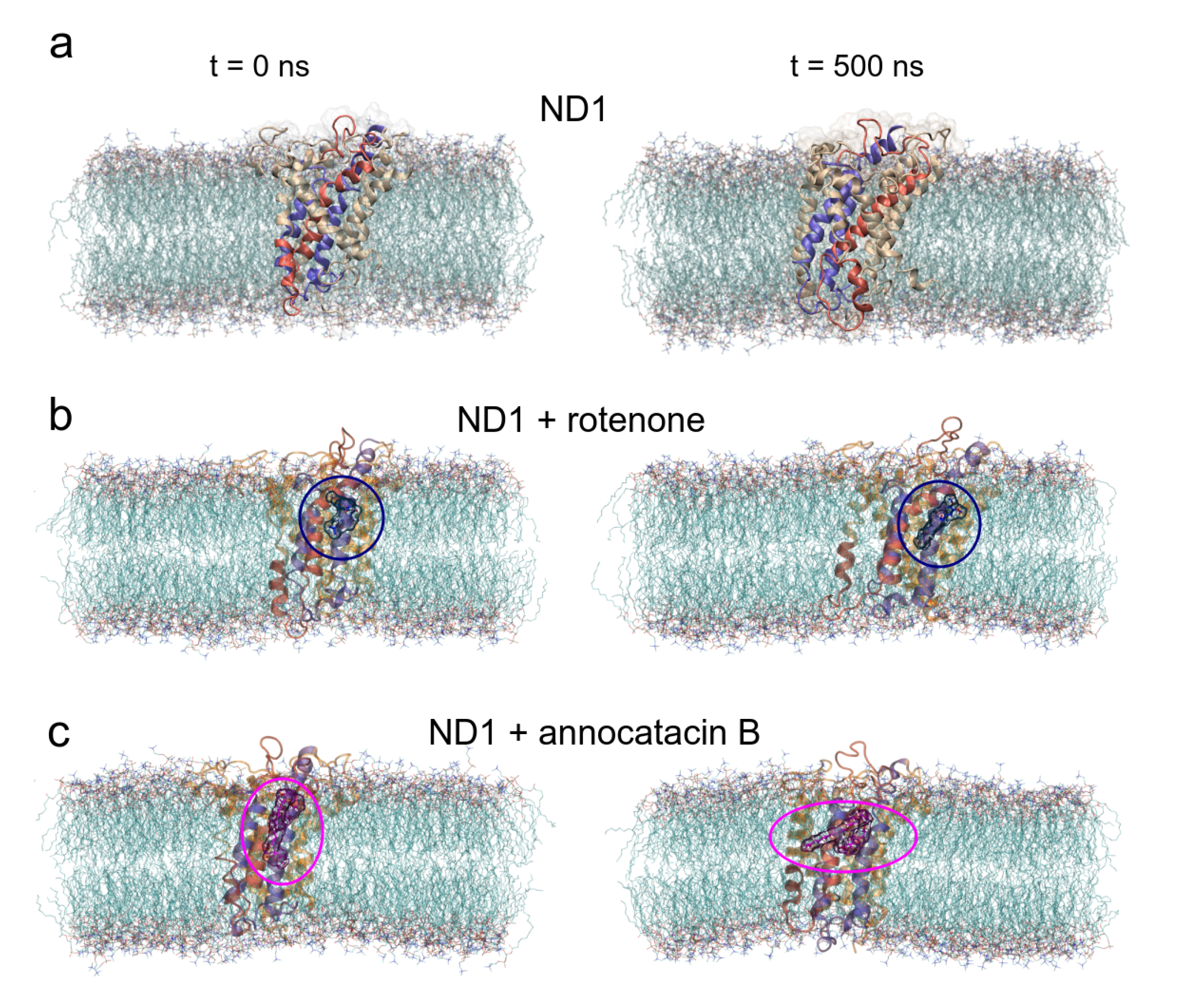
3.1. Structural Analysis
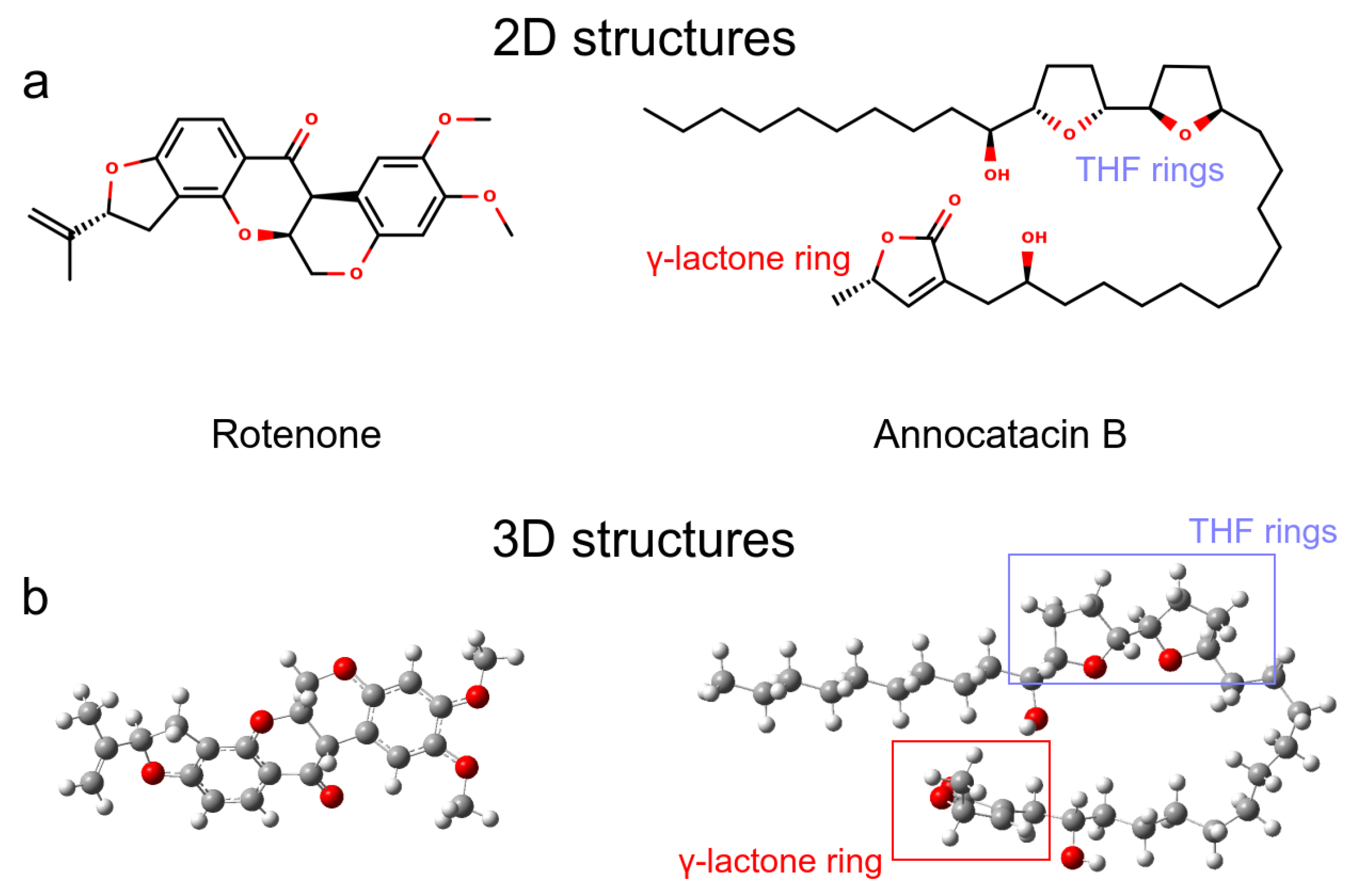
3.1.1. Rotenone and Annocatacin B
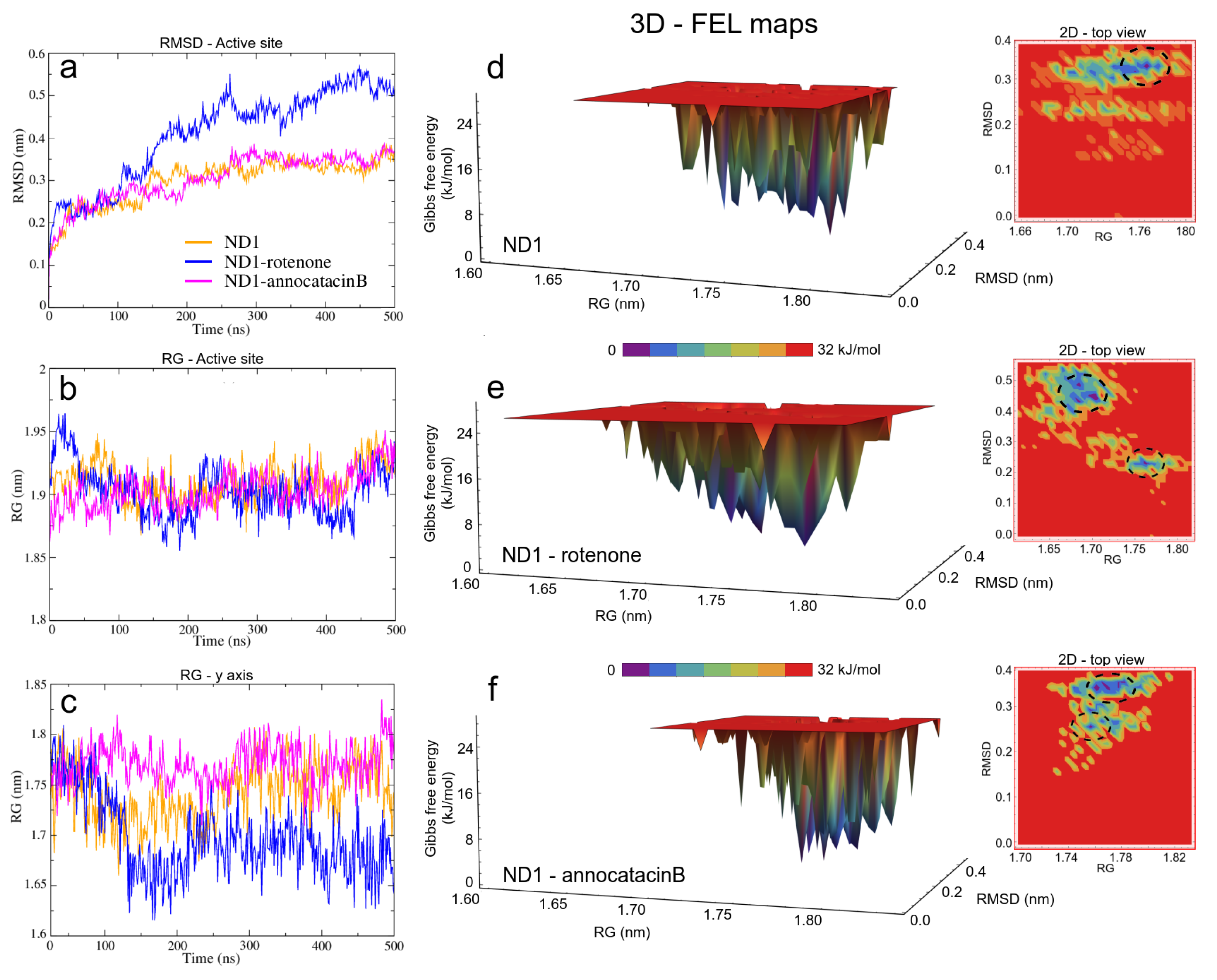
3.1.2. ND1—Ligand Complexes and Stability Descriptors
3.1.3. Hydrogen Bond Analysis
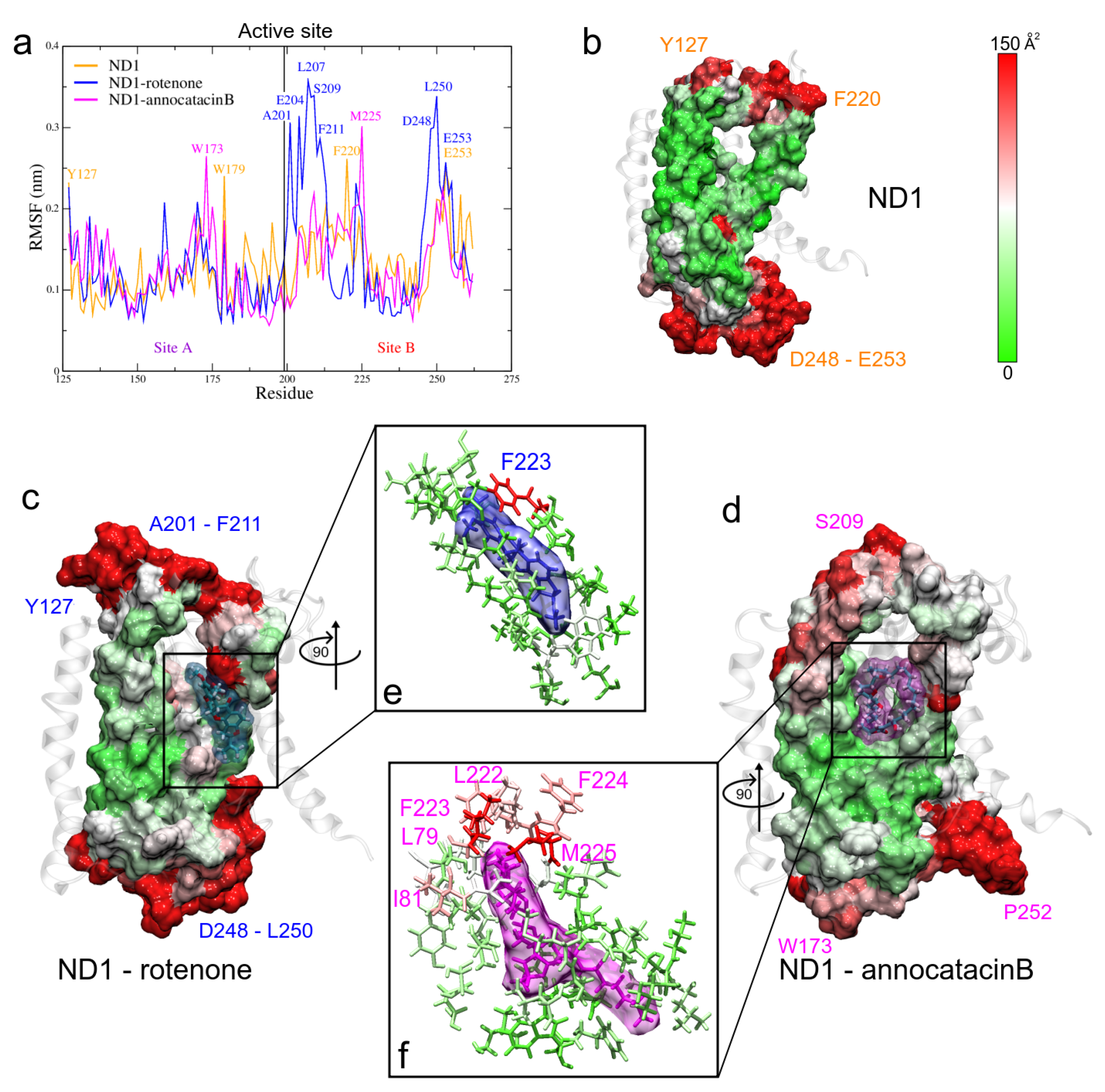
3.1.4. RMSF and B-Factor Analysis
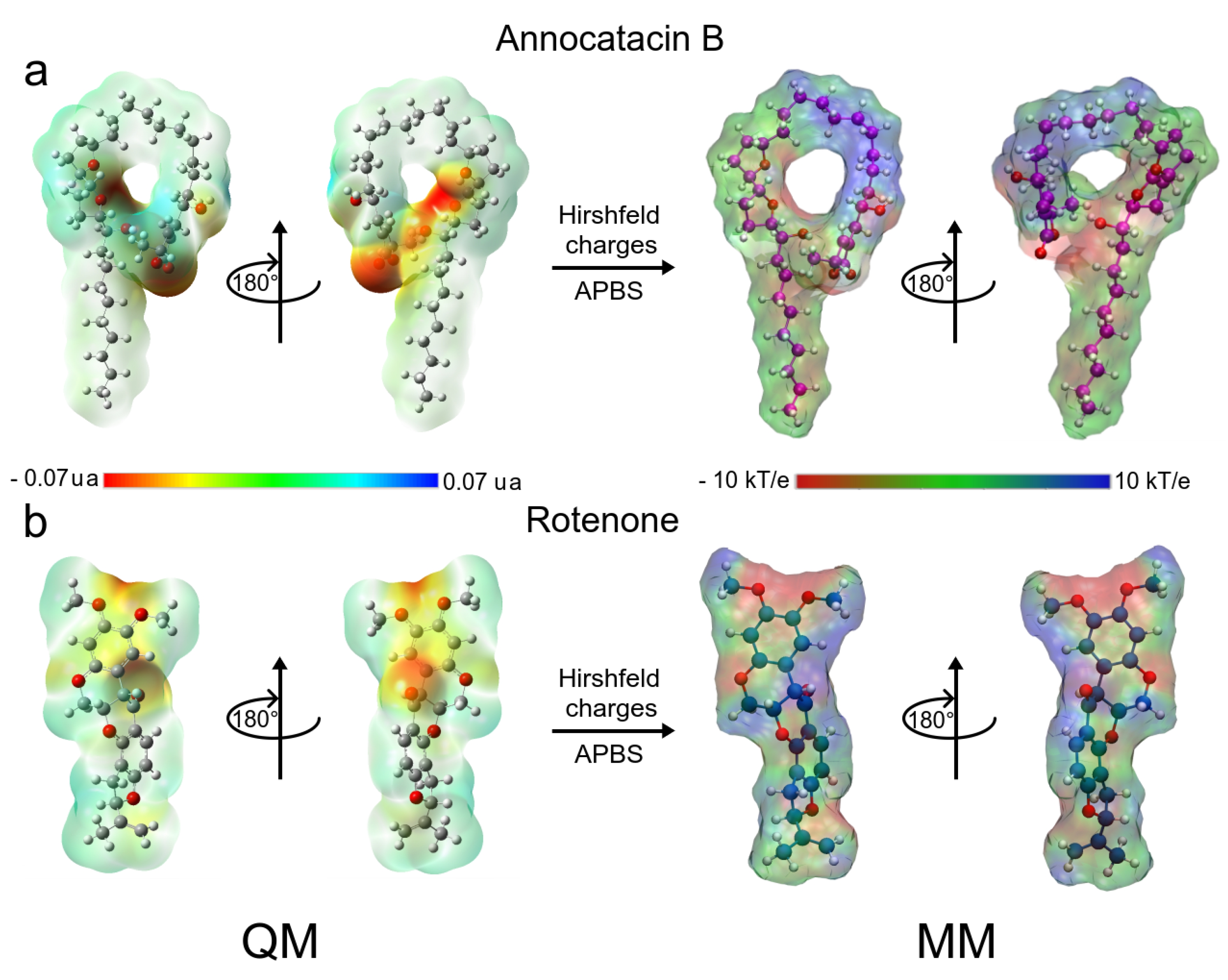
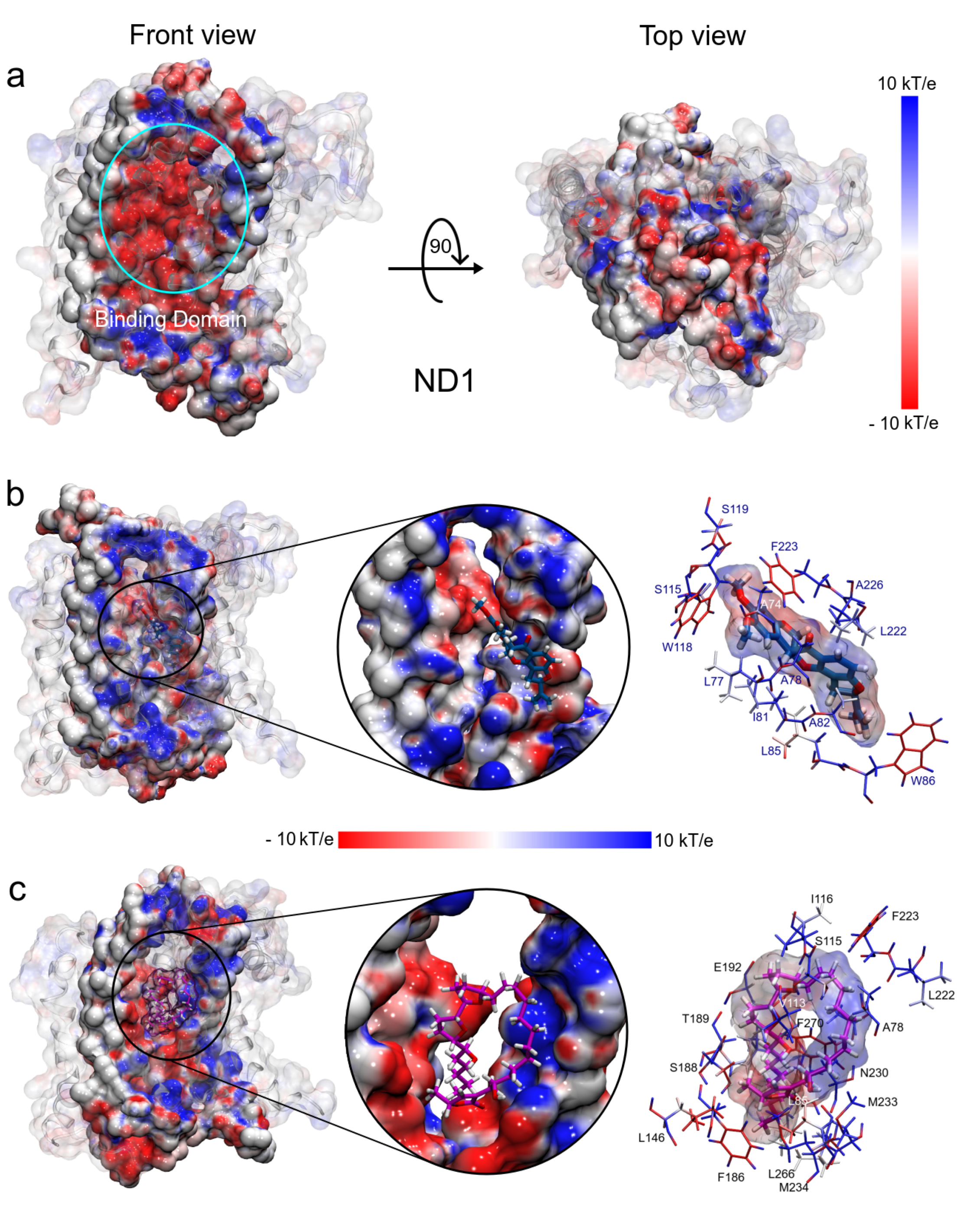
3.1.5. MM Electrostatic Potential Surfaces
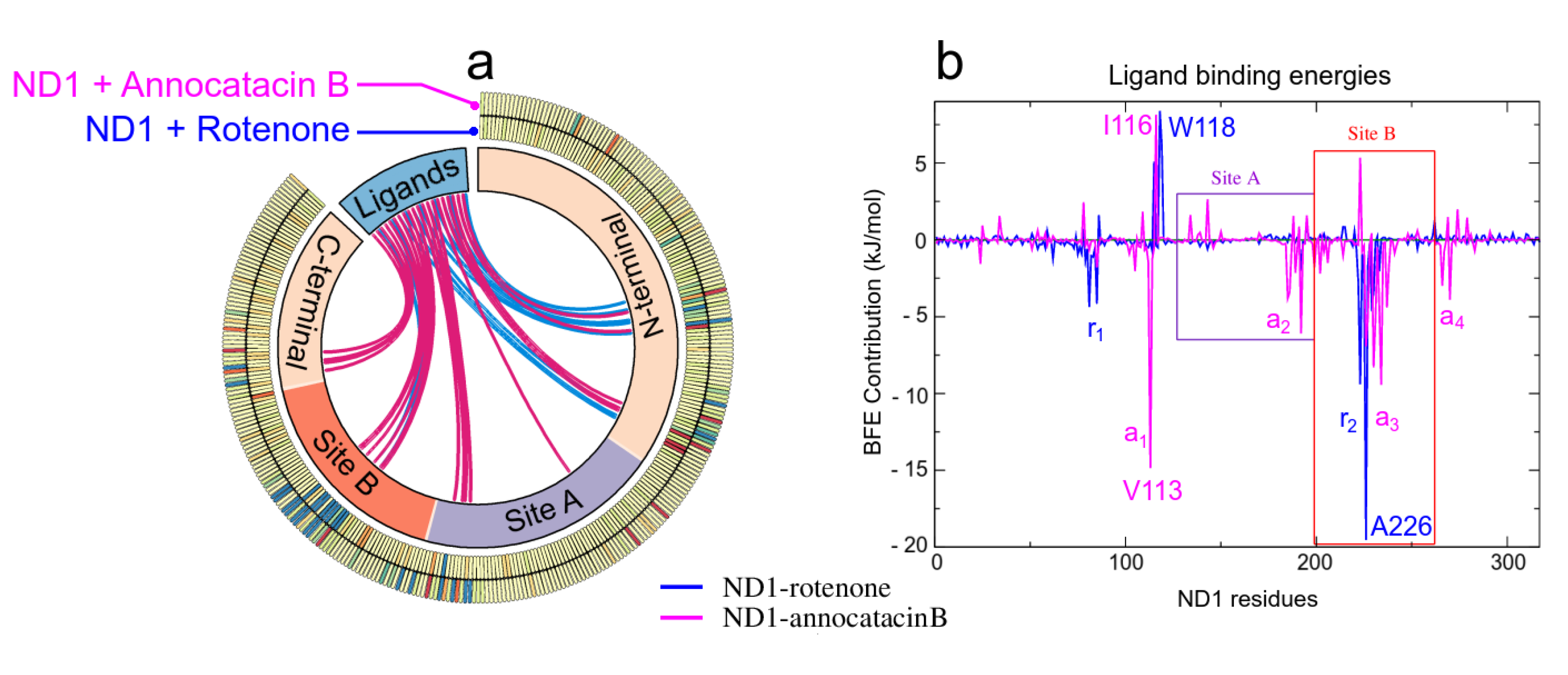
3.2. Binding Free Energy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Warburg, O.H.; Dickens, F. Metabolism of Tumours; Constable & Co. Ltd.: London, UK, 1930. [Google Scholar]
- Ganapathy-Kanniappan, S.; Geschwind, J.F.H. Tumor glycolysis as a target for cancer therapy: Progress and prospects. Mol. Cancer 2013, 12, 152. [Google Scholar] [CrossRef]
- Vander Heiden, M.G.; Cantley, L.C.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033. [Google Scholar] [CrossRef]
- Wallace, D.C. Mitochondria and cancer. Nat. Rev. Cancer 2012, 12, 685. [Google Scholar] [CrossRef]
- Koppenol, W.H.; Bounds, P.L.; Dang, C.V. Otto Warburg’s contributions to current concepts of cancer metabolism. Nat. Rev. Cancer 2011, 11, 325. [Google Scholar] [CrossRef]
- Jose, C.; Bellance, N.; Rossignol, R. Choosing between glycolysis and oxidative phosphorylation: A tumor’s dilemma? Biochim. Biophys. Acta (BBA) Bioenergy 2011, 1807, 552–561. [Google Scholar] [CrossRef] [PubMed]
- Smolková, K.; Plecitá-Hlavatá, L.; Bellance, N.; Benard, G.; Rossignol, R.; Ježek, P. Waves of gene regulation suppress and then restore oxidative phosphorylation in cancer cells. Int. J. Biochem. Cell Biol. 2011, 43, 950–968. [Google Scholar] [CrossRef]
- Moreno-Sánchez, R.; Rodríguez-Enríquez, S.; Marín-Hernández, A.; Saavedra, E. Energy Substrate Modulates in tumor cells. FEBS J. 2007, 274, 1393–1418. [Google Scholar] [CrossRef] [PubMed]
- Burlaka, A.; Ganusevich, I.; Vovk, A.; Burlaka, A.; Gafurov, M.; Lukin, S. Colorectal Cancer and Mitochondrial Dysfunctions of the Adjunct Adipose Tissues: A Case Study. BioMed Res. Int. 2018, 2018, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Philley, J.V.; Kannan, A.; Qin, W.; Sauter, E.R.; Ikebe, M.; Hertweck, K.L.; Troyer, D.A.; Semmes, O.J.; Dasgupta, S. Complex-I alteration and enhanced mitochondrial fusion are associated with prostate cancer progression. J. Cell. Physiol. 2016, 231, 1364–1374. [Google Scholar] [CrossRef]
- Cormio, A.; Musicco, C.; Gasparre, G.; Cormio, G.; Pesce, V.; Sardanelli, A.M.; Gadaleta, M.N. Increase in proteins involved in mitochondrial fission, mitophagy, proteolysis and antioxidant response in type I endometrial cancer as an adaptive response to respiratory complex I deficiency. Biochem. Biophys. Res. Commun. 2017, 491, 85–90. [Google Scholar] [CrossRef] [PubMed]
- Santidrian, A.F.; Matsuno-Yagi, A.; Ritland, M.; Seo, B.B.; LeBoeuf, S.E.; Gay, L.J.; Yagi, T.; Felding-Habermann, B. Mitochondrial complex I activity and NAD+/NADH balance regulate breast cancer progression. J. Clin. Investig. 2013, 123, 1068–1081. [Google Scholar] [CrossRef]
- Basit, F.; Van Oppen, L.M.; Schöckel, L.; Bossenbroek, H.M.; Van Emst-de Vries, S.E.; Hermeling, J.C.; Grefte, S.; Kopitz, C.; Heroult, M.; Willems, P.H. Mitochondrial complex I inhibition triggers a mitophagy-dependent ROS increase leading to necroptosis and ferroptosis in melanoma cells. Cell Death Dis. 2017, 8, e2716. [Google Scholar] [CrossRef]
- Pamies, D.; Block, K.; Lau, P.; Gribaldo, L.; Pardo, C.A.; Barreras, P.; Smirnova, L.; Wiersma, D.; Zhao, L.; Harris, G. Rotenone exerts developmental neurotoxicity in a human brain spheroid model. Toxicol. Appl. Pharmacol. 2018, 354, 101–114. [Google Scholar] [CrossRef] [PubMed]
- Chadderton, L.; Kelleher, S.; Brow, A.; Shaw, T.; Studholme, B.; Barrier, R. Testing the efficacy of rotenone as a piscicide for New Zealand pest fish species. In Managing Invasive Freshwater Fish in New Zealand, Proceedings of the Workshop Hosted by Department of Conservation, Hamilton, New Zeland, 10–12 May 2001; Department of Conservation: Wellington, New Zealand, 2001; pp. 10–12. [Google Scholar]
- Biñas, E.E., Jr. A Review on Tubli Plant used as Organic Pesticide: Input toward Sustainable Agriculture. Int. J. Res. Appl. Sci. Biotechnol. 2021, 8, 107–115. [Google Scholar]
- Betarbet, R.; Sherer, T.B.; MacKenzie, G.; Garcia-Osuna, M.; Panov, A.V.; Greenamyre, J.T. Chronic systemic pesticide exposure reproduces features of Parkinson’s disease. Nat. Neurosci. 2000, 3, 1301. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Ragheb, K.; Lawler, G.; Sturgis, J.; Rajwa, B.; Melendez, J.A.; Robinson, J.P. Mitochondrial complex I inhibitor rotenone induces apoptosis through enhancing mitochondrial reactive oxygen species production. J. Biol. Chem. 2003, 278, 8516–8525. [Google Scholar] [CrossRef] [PubMed]
- Cunningham, M.L.; Soliman, M.S.; Badr, M.Z.; Matthews, H. Rotenone, an anticarcinogen, inhibits cellular proliferation but not peroxisome proliferation in mouse liver. Cancer Lett. 1995, 95, 93–97. [Google Scholar] [CrossRef]
- Bhurtel, S.; Katila, N.; Srivastav, S.; Neupane, S.; Choi, D.Y. Mechanistic comparison between MPTP and rotenone neurotoxicity in mice. Neurotoxicology 2019, 71, 113–121. [Google Scholar] [CrossRef]
- Nopparat, C.; Porter, J.E.; Ebadi, M.; Govitrapong, P. 1-Methyl-4-phenylpyridinium-induced cell death via autophagy through a Bcl-2/Beclin 1 complex-dependent pathway. Neurochem. Res. 2014, 39, 225–232. [Google Scholar] [CrossRef]
- Murai, M.; Ishihara, A.; Nishioka, T.; Yagi, T.; Miyoshi, H. The ND1 subunit constructs the inhibitor binding domain in bovine heart mitochondrial complex I. Biochemistry 2007, 46, 6409–6416. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, J.W.; Zhai, J.H.; Wang, Y.; Wang, S.L.; Li, X. Antitumor activity and toxicity relationship of annonaceous acetogenins. Food Chem. Toxicol. 2013, 58, 394–400. [Google Scholar] [CrossRef]
- Patel, M.S.; Patel, J.K. A review on a miracle fruits of Annona muricata. J. Pharmacogn. Phytochem. 2016, 5, 137. [Google Scholar]
- Moghadamtousi, S.; Fadaeinasab, M.; Nikzad, S.; Mohan, G.; Ali, H.; Kadir, H. Annona muricata (Annonaceae): A review of its traditional uses, isolated acetogenins and biological activities. Int. J. Mol. Sci. 2015, 16, 15625–15658. [Google Scholar] [CrossRef]
- Prasad, S.K.; Varsha, V.; Devananda, D. Anti-cancer properties of Annona muricata (L.): A Review. Med. Plants Int. J. Phytomed. Relat. Ind. 2019, 11, 123–134. [Google Scholar] [CrossRef]
- Gavamukulya, Y.; Wamunyokoli, F.; El-Shemy, H.A. Annona muricata: Is the natural therapy to most disease conditions including cancer growing in our backyard? A systematic review of its research history and future prospects. Asian Pac. J. Trop. Med. 2017, 10, 835–848. [Google Scholar] [CrossRef]
- Zafra-Polo, M.C.; González, M.C.; Estornell, E.; Sahpaz, S.; Cortes, D. Acetogenins from Annonaceae, inhibitors of mitochondrial complex I. Phytochemistry 1996, 42, 253–271. [Google Scholar] [CrossRef]
- Mangal, M.; Imran Khan, M.; Mohan Agarwal, S. Acetogenins as potential anticancer agents. Anti-Cancer Agents Med. Chem. Formerly Curr. Med. Chem. Anti-Cancer Agents 2016, 16, 138–159. [Google Scholar] [CrossRef]
- Chang, F.R.; Liaw, C.C.; Lin, C.Y.; Chou, C.J.; Chiu, H.F.; Wu, Y.C. New adjacent bis-tetrahydrofuran annonaceous acetogenins from Annona muricata. Planta Med. 2003, 69, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView 6.0. 16; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Ritchie, J.P. Electron density distribution analysis for nitromethane, nitromethide, and nitramide. J. Am. Chem. Soc. 1985, 107, 1829–1837. [Google Scholar] [CrossRef]
- Ritchie, J.P.; Bachrach, S.M. Some methods and applications of electron density distribution analysis. J. Comput. Chem. 1987, 8, 499–509. [Google Scholar] [CrossRef]
- Mikhailovich, K.P. ERG Research Group. 2008. Available online: http://erg.biophys.msu.ru/tpp/ (accessed on 28 April 2021).
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Kandt, C.; Ash, W.L.; Tieleman, D.P. Setting up and running molecular dynamics simulations of membrane proteins. Methods 2007, 41, 475–488. [Google Scholar] [CrossRef]
- Guo, R.; Zong, S.; Wu, M.; Gu, J.; Yang, M. Architecture of human mitochondrial respiratory megacomplex I2III2IV2. Cell 2017, 170, 1247–1257. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Tieleman, D.P.; Berendsen, H. Molecular dynamics simulations of a fully hydrated dipalmitoylphosphatidylcholine bilayer with different macroscopic boundary conditions and parameters. J. Chem. Phys. 1996, 105, 4871–4880. [Google Scholar] [CrossRef]
- Duhovny, D.; Nussinov, R.; Wolfson, H.J. Efficient unbound docking of rigid molecules. In Proceedings of the International Workshop on Algorithms in Bioinformatics, Rome, Italy, 17–21 September 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 185–200. [Google Scholar]
- Schneidman-Duhovny, D.; Inbar, Y.; Nussinov, R.; Wolfson, H.J. PatchDock and SymmDock: Servers for rigid and symmetric docking. Nucleic Acids Res. 2005, 33, W363–W367. [Google Scholar] [CrossRef]
- Kakutani, N.; Murai, M.; Sakiyama, N.; Miyoshi, H. Exploring the Binding Site of Δlac-Acetogenin in Bovine Heart Mitochondrial NADH- Ubiquinone Oxidoreductase. Biochemistry 2010, 49, 4794–4803. [Google Scholar] [CrossRef]
- Homeyer, N.; Gohlke, H. Free energy calculations by the molecular mechanics Poisson- Boltzmann surface area method. Mol. Inform. 2012, 31, 114–122. [Google Scholar] [CrossRef]
- Kumari, R.; Kumar, R.; Consortium, O.S.D.D.; Lynn, A. g_mmpbsa A GROMACS tool for high-throughput MM-PBSA calculations. J. Chem. Inf. Model. 2014, 54, 1951–1962. [Google Scholar] [CrossRef]
- Brown, S.P.; Muchmore, S.W. Large-scale application of high-throughput molecular mechanics with Poisson- Boltzmann surface area for routine physics-based scoring of protein- ligand complexes. J. Med. Chem. 2009, 52, 3159–3165. [Google Scholar] [CrossRef]
- Rastelli, G.; Rio, A.D.; Degliesposti, G.; Sgobba, M. Fast and accurate predictions of binding free energies using MM-PBSA and MM-GBSA. J. Comput. Chem. 2010, 31, 797–810. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Turner, P.; Grace, X. Version 5.1. 19. Center for Coastal and Land-Margin Research; Oregon Graduate Institute of Science and Technology: Beaverton, OR, USA, 2005. [Google Scholar]
- Wallace, A.C.; Laskowski, R.A.; Thornton, J.M. LIGPLOT: A program to generate schematic diagrams of protein-ligand interactions. Protein Eng. Des. Sel. 1995, 8, 127–134. [Google Scholar] [CrossRef]
- Baker, N.A.; Sept, D.; Joseph, S.; Holst, M.J.; McCammon, J.A. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA 2001, 98, 10037–10041. [Google Scholar] [CrossRef]
- Dolinsky, T.J.; Nielsen, J.E.; McCammon, J.A.; Baker, N.A. PDB2PQR: An automated pipeline for the setup of Poisson–Boltzmann electrostatics calculations. Nucleic Acids Res. 2004, 32, W665–W667. [Google Scholar] [CrossRef]
- WR Inc. Mathematica, Version 12.1; WR Inc.: Champaign, IL, USA, 2020. [Google Scholar]
- Lobo-Jarne, T.; Ugalde, C. Respiratory chain supercomplexes: Structures, function and biogenesis. In Seminars in Cell & Developmental Biology; Elsevier: Amsterdam, The Netherlands, 2018; Volume 76, pp. 179–190. [Google Scholar]
- Fedor, J.G.; Hirst, J. Mitochondrial supercomplexes do not enhance catalysis by quinone channeling. Cell Metab. 2018, 28, 525–531. [Google Scholar] [CrossRef]
- Fiedorczuk, K.; Letts, J.A.; Degliesposti, G.; Kaszuba, K.; Skehel, M.; Sazanov, L.A. Atomic structure of the entire mammalian mitochondrial complex I. Nature 2016, 538, 406. [Google Scholar] [CrossRef]
- Nakanishi, S.; Abe, M.; Yamamoto, S.; Murai, M.; Miyoshi, H. Bis-THF motif of acetogenin binds to the third matrix-side loop of ND1 subunit in mitochondrial NADH-ubiquinone oxidoreductase. Biochim. Biophys. Acta (BBA) Bioenergy 2011, 1807, 1170–1176. [Google Scholar] [CrossRef]
- Pérez de la Luz, A.; Aguilar-Pineda, J.A.; Méndez-Bermúdez, J.G.; Alejandre, J. Force field parametrization from the Hirshfeld molecular electronic density. J. Chem. Theory Comput. 2018, 14, 5949–5958. [Google Scholar] [CrossRef]
- Riquelme, M.; Lara, A.; Mobley, D.L.; Verstraelen, T.; Matamala, A.R.; Vohringer-Martinez, E. Hydration free energies in the FreeSolv database calculated with polarized iterative Hirshfeld charges. J. Chem. Inf. Model. 2018, 58, 1779–1797. [Google Scholar] [CrossRef]
- Ishizuka, R.; Matubayasi, N. Effective charges of ionic liquid determined self-consistently through combination of molecular dynamics simulation and density-functional theory. J. Comput. Chem. 2017, 38, 2559–2569. [Google Scholar] [CrossRef]
- Gastegger, M.; Marquetand, P. Molecular dynamics with neural network potentials. In Machine Learning Meets Quantum Physics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 233–252. [Google Scholar]
- Llanos, A.G.; Vöhringer-Martinez, E. pKa Calculations of Asp26 in Thioredoxin with Alchemical Free Energy Simulations and Hirshfeld-I Atomic Charges. ChemRxiv 2018. [Google Scholar] [CrossRef]
- Pires, D.E.; Blundell, T.L.; Ascher, D.B. pkCSM: Predicting small-molecule pharmacokinetic and toxicity properties using graph-based signatures. J. Med. Chem. 2015, 58, 4066–4072. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.P. Use of multiple picosecond high-mass molecular dynamics simulations to predict crystallographic B-factors of folded globular proteins. Heliyon 2016, 2, e00161. [Google Scholar] [CrossRef]

| System | Strand | Alpha Helix | 3–10 Helix | Other | Total Res. |
|---|---|---|---|---|---|
| ND1 | 0 (0.00%) | 154 (48.40%) | 9 (2.80%) | 155 (48.70%) | 318 |
| ND1—Annocatacin B | 0 (0.00%) | 129 (39%) | 28 (8.80%) | 166 (52.20%) | 318 |
| ND1—Rotenone | 0 (0.00%) | 148 (46.50%) | 11 (3.50%) | 159 (50.00%) | 318 |
| ADMET | |||
|---|---|---|---|
| Property | Model Name | Predicted Value | |
| Annocatacin B | Rotenone | ||
| Absorption | Water solubility | −5.85 | −5.05 |
| Absorption | Caco2 permeability | 0.40 | 1.31 |
| Absorption | Intestinal absorption | 86.98 | 99.63 |
| Absorption | Skin Permeability | −2.70 | −2.75 |
| Absorption | P-glycoprotein substrate | Yes | No |
| Absorption | P-glycoprotein I inhibitor | Yes | Yes |
| Absorption | P-glycoprotein II inhibitor | Yes | Yes |
| Distribution | VDss (human) e | −0.29 | −0.04 |
| Distribution | Fraction unbound (human) | 0.05 | 0 |
| Distribution | BBB permeability | −0.95 | −0.87 |
| Distribution | CNS permeability | −2.90 | −2.82 |
| Metabolism | CYP2D6 substrate | No | No |
| Metabolism | CYP3A4 substrate | Yes | Yes |
| Metabolism | CYP1A2 inhibitior | No | Yes |
| Metabolism | CYP2C19 inhibitior | No | Yes |
| Metabolism | CYP2C9 inhibitior | No | Yes |
| Metabolism | CYP2D6 inhibitior | No | No |
| Metabolism | CYP3A4 inhibitior | No | Yes |
| Excretion | Total Clearance | 1.601 | 0.195 |
| Excretion | Renal OCT2 substrate | No | No |
| Toxicity | AMES toxicity | No | No |
| Toxicity | Max. tolerated dose (human) | −0.64 | 0.16 |
| Toxicity | hERG I inhibitor | No | No |
| Toxicity | hERG II inhibitor | No | No |
| Toxicity | Oral Rat Acute Toxicity (LD50) | 3.03 | 2.87 |
| Toxicity | Oral Rat Chronic Toxicity (LOAEL) | 0.79 | 1.43 |
| Toxicity | Hepatotoxicity | No | No |
| Toxicity | Skin Sensitisation | No | No |
| Toxicity | T.Pyriformis toxicity | 0.31 | 0.35 |
| Toxicity | Minnow toxicity | −1.89 | −0.33 |
| System | Region | RMSD | RMSF | RG | H B | ||
|---|---|---|---|---|---|---|---|
| Intra | Inter/Solv | Inter/Mem | |||||
| ND1 | whole prot | 0.40 ± 0.02 | 0.19 ± 0.09 | 2.12 ± 0.01 | 209 ± 9 (200) | 338 ± 15 (336) | 33 ± 5 (39) |
| Active site | 0.30 ± 0.05 | 0.13 ± 0.04 | 1.91 ± 0.01 | 89 ± 6 (77) | 166 ± 10 (165) | 6 ± 2 (6) | |
| y-axis | 1.74 ± 0.03 | ||||||
| ND1 + rotenone | whole prot | 0.48 ± 0.02 | 0.20 ± 0.10 | 2.13 ± 0.01 | 203 ± 8 (202) | 356 ± 13 (356) | 31 ± 5 (38) |
| Active site | 0.41 ± 0.11 | 0.14 ± 0.07 | 1.90 ± 0.02 | 84 ± 6 (88) | 176 ± 10 (174) | 8 ± 3 (10) | |
| y-axis | 1.70 ± 0.04 | ||||||
| ND1 + annocatacin B | whole prot | 0.44 ± 0.01 | 0.20 ± 0.09 | 2.13 ± 0.01 | 213 ± 11 (207) | 341 ± 14 (330) | 26 ± 5 (23) |
| Active site | 0.30 ± 0.03 | 0.13 ± 0.05 | 1.90 ± 0.01 | 89 ± 6 (81) | 167 ± 10 (161) | 5 ± 3 (2) | |
| y-axis | 1.77 ± 0.02 | ||||||
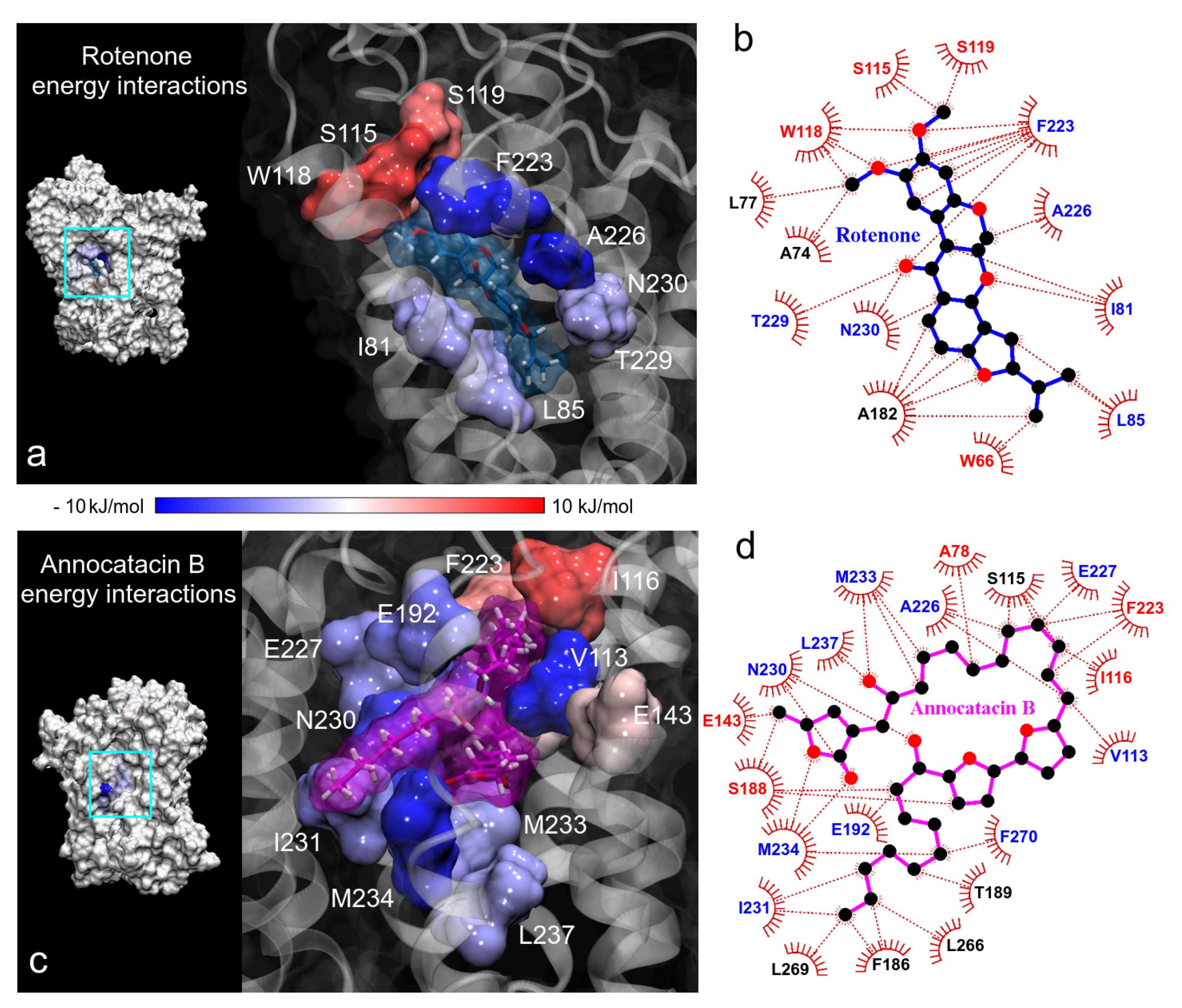
| System | Active Site | Other Sites | |||||
|---|---|---|---|---|---|---|---|
| Site A | Site B | ||||||
| ND1 + rot + mem | T73(21) | A74(19) | L77(37) | ||||
| L22(23) | F223(144) | A78(15) | L79(45) | I81(20) | |||
| A226(14) | T229(17) | A82(18) | L83(37) | L85(19) | |||
| N230(36) | I232(10) | W86(68) | L89(30) | M91(23) | |||
| M233(20) | S115(23) | I116(38) | W118(41) | ||||
| S119(37) | |||||||
| ND1 + ann + mem | L222(94) | F223(103) | A78(102) | L79(179) | I81(101) | ||
| E143(39) | L146(27) | F224(106) | M225(232) | A82(76) | L85(43) | S109(48) | |
| W185(14) | F186(41) | A226(70) | E227(48) | A112(40) | V113(53) | Y114(52) | |
| S188(13) | T189(14) | T229(27) | N230(25) | S115(39) | I116(70) | L117(74) | |
| A191(14) | E192(15) | I231(37) | M233(49) | L266(28) | T267(19) | L269(46) | |
| M234(36) | L237(50) | F270(26) | I273(49) | ||||
| System | |||||
|---|---|---|---|---|---|
| ND1-Annocatacin B | −358.76 ± 1.26 | −23.04 ± 0.69 | 85.00 ± 0.92 | −36.38 ± 0.10 | −333.18 ± 2.14 |
| ND1-Rotenone | −219.81 ± 0.89 | −21.14 ± 0.39 | 45.01 ± 0.34 | −22.21 ± 0.06 | −218.15 ± 1.78 |
| ND1—Rotetone | ||||
|---|---|---|---|---|
| A226 | −8.18 ± 0.12 | 0.92 ± 0.06 | −12.27 ± 0.19 | −19.53 ± 0.24 |
| F223 | −14.37 ± 0.20 | 3.94 ± 0.08 | 1.06 ± 0.63 | −9.41 ± 0.60 |
| I81 | −9.21 ± 0.11 | 0.66 ± 0.02 | 4.19 ± 0.14 | −4.36 ± 0.19 |
| T229 | −4.32 ± 0.11 | 5.20 ± 0.13 | −5.06 ± 0.32 | −4.17 ± 0.35 |
| L85 | −5.97 ± 0.11 | 0.72 ± 0.07 | 1.10 ± 0.13 | −4.15 ± 0.16 |
| N230 | −1.35 ± 0.06 | 0.72 ± 0.06 | −2.86 ± 0.14 | −3.49 ± 0.16 |
| L222 | −9.03 ± 0.10 | 2.46 ± 0.07 | 3.79 ± 0.18 | −2.77 ± 0.22 |
| M225 | −3.74 ± 0.13 | 1.19 ± 0.07 | 0.24 ± 0.12 | −2.31 ± 0.13 |
| M233 | −2.77 ± 0.07 | 2.23 ± 0.07 | −1.51 ± 0.11 | −2.05 ± 0.13 |
| E192 | −1.61 ± 0.08 | −0.17 ± 0.15 | −0.22 ± 0.01 | −2.00 ± 0.16 |
| ND1—Annocatacin B | ||||
| V113 | −12.39 ± 0.22 | 2.74 ± 0.12 | −5.20 ± 0.34 | −14.84 ± 0.54 |
| M234 | −10.30 ± 0.16 | 3.67 ± 0.08 | −2.80 ± 0.16 | −9.43 ± 0.24 |
| N230 | −10.59 ± 0.19 | 6.10 ± 0.13 | −3.82 ± 0.17 | −8.30 ± 0.25 |
| A226 | −4.94 ± 0.22 | 0.60 ± 0.08 | −2.59 ± 0.46 | −6.92 ± 0.61 |
| E192 | −8.48 ± 0.20 | 1.29 ± 0.35 | 1.11 ± 0.22 | −6.09 ± 0.33 |
| I231 | −4.26 ± 0.10 | −0.19 ± 0.02 | −0.74 ± 0.09 | −5.19 ± 0.13 |
| E227 | −0.98 ± 0.26 | −3.77 ± 0.29 | −0.35 ± 0.10 | −5.09 ± 0.30 |
| M233 | 9.20 ± 0.16 | 4.13 ± 0.08 | 0.61 ± 0.09 | −4.46 ± 0.18 |
| L237 | −6.74 ± 0.20 | 1.18 ± 0.03 | 1.15 ± 0.07 | −4.40 ± 0.19 |
| F270 | −7.34 ± 0.16 | 1.39 ± 0.06 | 2.06 ± 0.10 | −3.90 ± 0.15 |
| ND1—Rotetone | ||||
|---|---|---|---|---|
| W118 | −7.31 ± 0.12 | 2.65 ± 0.07 | 13.05 ± 0.30 | 8.39 ± 0.30 |
| S119 | −1.11 ± 0.04 | 1.12 ± 0.07 | 6.11 ± 0.23 | 6.12 ± 0.22 |
| S115 | −4.37 ± 0.11 | 1.67 ± 0.06 | 7.78 ± 0.20 | 5.09 ± 0.20 |
| W86 | −4.52 ± 0.10 | 0.93 ± 0.05 | 5.21 ± 0.25 | 1.61 ± 0.25 |
| K262 | 1.14 ± 0.01 | −0.13 ± 0.01 | 0.22 ± 0.00 | 1.23 ± 0.01 |
| R195 | 1.61 ± 0.03 | −0.58 ± 0.04 | 0.00 ± 0.00 | 1.03 ± 0.05 |
| E214 | 1.53 ± 0.03 | −0.75 ± 0.02 | 0.07 ± 0.00 | 0.85 ± 0.02 |
| Y215 | −0.47 ± 0.02 | 0.41 ± 0.03 | 0.91 ± 0.12 | 0.84 ± 0.13 |
| A78 | −9.30 ± 0.11 | 2.64 ± 0.06 | 7.37 ± 0.23 | 0.71 ± 0.29 |
| E59 | 1.05 ± 0.02 | −0.30 ± 0.01 | −0.17 ± 0.00 | 0.58 ± 0.01 |
| ND1—Annocatacin B | ||||
| I116 | −3.78 ± 0.09 | 0.51 ± 0.03 | 11.40 ± 0.24 | 8.14 ± 0.23 |
| F223 | −4.83 ± 0.13 | 2.67 ± 0.15 | 7.50 ± 0.25 | 5.35 ± 0.30 |
| E143 | −7.08 ± 0.23 | 8.98 ± 0.56 | 0.70 ± 0.10 | 2.65 ± 0.52 |
| A78 | −3.20 ± 0.08 | 2.23 ± 0.09 | 3.42 ± 0.15 | 2.44 ± 0.16 |
| R274 | −1.97 ± 0.13 | 4.04 ± 0.10 | −0.08 ± 0.01 | 1.98 ± 0.13 |
| S109 | −5.27 ± 0.17 | 5.55 ± 0.15 | 1.55 ± 0.10 | 1.82 ± 0.21 |
| R134 | 1.12 ± 0.02 | 0.65 ± 0.03 | −0.16 ± 0.00 | 1.61 ± 0.04 |
| R195 | 0.83 ± 0.04 | 0.74 ± 0.03 | 0.01 ± 0.00 | 1.59 ± 0.04 |
| R34 | −0.24 ± 0.06 | 1.88 ± 0.06 | −0.08 ± 0.00 | 1.55 ± 0.08 |
| S188 | −6.55 ± 0.12 | 6.38 ± 0.14 | 1.72 ± 0.09 | 1.55 ± 0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Febres-Molina, C.; Aguilar-Pineda, J.A.; Gamero-Begazo, P.L.; Barazorda-Ccahuana, H.L.; Valencia, D.E.; Vera-López, K.J.; Davila-Del-Carpio, G.; Gómez, B. Structural and Energetic Affinity of Annocatacin B with ND1 Subunit of the Human Mitochondrial Respiratory Complex I as a Potential Inhibitor: An In Silico Comparison Study with the Known Inhibitor Rotenone. Polymers 2021, 13, 1840. https://doi.org/10.3390/polym13111840
Febres-Molina C, Aguilar-Pineda JA, Gamero-Begazo PL, Barazorda-Ccahuana HL, Valencia DE, Vera-López KJ, Davila-Del-Carpio G, Gómez B. Structural and Energetic Affinity of Annocatacin B with ND1 Subunit of the Human Mitochondrial Respiratory Complex I as a Potential Inhibitor: An In Silico Comparison Study with the Known Inhibitor Rotenone. Polymers. 2021; 13(11):1840. https://doi.org/10.3390/polym13111840
Chicago/Turabian StyleFebres-Molina, Camilo, Jorge A. Aguilar-Pineda, Pamela L. Gamero-Begazo, Haruna L. Barazorda-Ccahuana, Diego E. Valencia, Karin J. Vera-López, Gonzalo Davila-Del-Carpio, and Badhin Gómez. 2021. "Structural and Energetic Affinity of Annocatacin B with ND1 Subunit of the Human Mitochondrial Respiratory Complex I as a Potential Inhibitor: An In Silico Comparison Study with the Known Inhibitor Rotenone" Polymers 13, no. 11: 1840. https://doi.org/10.3390/polym13111840
APA StyleFebres-Molina, C., Aguilar-Pineda, J. A., Gamero-Begazo, P. L., Barazorda-Ccahuana, H. L., Valencia, D. E., Vera-López, K. J., Davila-Del-Carpio, G., & Gómez, B. (2021). Structural and Energetic Affinity of Annocatacin B with ND1 Subunit of the Human Mitochondrial Respiratory Complex I as a Potential Inhibitor: An In Silico Comparison Study with the Known Inhibitor Rotenone. Polymers, 13(11), 1840. https://doi.org/10.3390/polym13111840