Cocrystals of 2-Aminopyrimidine with Boric Acid—Crystal Engineering of a Novel Nonlinear Optically (NLO) Active Crystal

Abstract

Crystal engineering of novel materials for nonlinear optics (NLO) based on 2-aminopyrimidine yielded two molecular cocrystals with boric acid—trigonal (P3₂21 space group) 2-aminopyrimidine—boric acid (3/2) and monoclinic (C2/c space group) 2-aminopyrimidine—boric acid (1/2). In addition to crystal structure determination by single crystal X-ray diffraction, the cocrystals were characterized by powder X-ray diffraction and vibrational spectroscopy (FTIR and FT Raman). Large single crystals of the non-centrosymmetric cocrystal 2-aminopyrimidine—boric acid (3/2) were grown to study the optical properties and determine the second harmonic generation (SHG) efficiency (using 800 nm fundamental laser line) of powder samples.

1. Introduction

One of the most promising directions in current research trends focused on nonlinear optical (NLO) materials is crystal engineering of novel materials based on organic molecules. Organic molecules in general, but especially their salts and cocrystals, exhibit a favorable combination of sufficient hyperpolarizability and optical transparency with adequate thermal stability and outstanding resistance to optical damage.

Within a very diverse family of studied organic molecules, 2-aminopyrimidine and its monocation represent simple heteroaromatic systems with highly delocalized π-electrons, which can act as promising carriers of NLO properties. In this context, we have previously demonstrated that the χ⁽²⁾ NLO properties of these moieties are closely related to their protonation—the neutral 2-aminopyrimidine molecule has a 1.6 times higher total hyperpolarizability (β_tot) than its protonated monocation [1]. Considering these properties, crystal engineering has two main objectives—to incorporate the 2-aminopyrimidine moiety into molecular crystals with proper symmetry and to preserve it preferably as a neutral molecule. Moreover, several organic molecular crystals and “semi-organic” materials are promising as stimulated Raman scattering (SRS)-active materials, which could also exhibit various χ⁽²⁾ and χ⁽³⁾ NLO effects including third harmonic generation and cascaded self-frequency doubling and tripling [2,3].

In addition to inorganic borates, which are undoubtedly one of the most successful groups of NLO materials [4], boric acid itself has a considerable potential in crystal engineering of organic/inorganic hybrid compounds. The presence of this weak inorganic acid in molecular form has been reported in several cocrystals (adducts) (see e.g., [5,6,7,8,9,10]) and coordination compounds (see e.g., [9,10,11]), which were mainly studied with respect to their linear and nonlinear optical [9,10,11] or ferroelastic properties [5,6]. Moreover, several crystalline materials derived from boric acid esters formed by reactions with hydroxy carboxylic acids have also been prepared and characterized (including their basic NLO properties) (see e.g., [12,13,14]).

In this paper, we report the preparation, crystal structure determination, and spectroscopic and optical properties of two molecular cocrystals of 2-aminopyrimidine with boric acid, i.e., trigonal 2-aminopyrimidine—boric acid (3/2), (2-AMP)₃(H₃BO₃)₂, and monoclinic 2-aminopyrimidine—boric acid (1/2), 2-AMP(H₃BO₃)₂. These hydrogen-bonded materials were isolated within a crystal engineering study employing promising inorganic and organic molecular carriers of NLO properties.

2. Experimental Setup

2.1. Materials and Methods

All chemicals were purchased from Fluka (2-aminopyrimidine, 97%, Seelze, Germany) and Lachema (boric acid, p.a., Brno, Czech Republic) companies.

Infrared spectra of powder samples were recorded by nujol and fluorolube mull transmission techniques on a Thermo Scientific Nicolet 6700 FTIR spectrometer (Madison, WI, USA) in the 400–4000 cm⁻¹ region (2 cm⁻¹ resolution, KBr beamsplitter, Happ–Genzel apodization). Raman spectra of powder samples were recorded on a Nicolet 6700 FTIR spectrometer (equipped with a Thermo Scientific Nicolet Nexus (Madison, WI, USA) FT Raman module (2 cm⁻¹ resolution, Happ–Genzel apodization, 1064 nm Nd:YVO₄ laser excitation, 250 mW power at the sample) in the 100–3700 cm⁻¹ region. Raman spectra of microcrystalline samples were also collected on a dispersive confocal Raman microscope MonoVista CRS+ (Spectroscopy & Imaging GmbH, Germany) interfaced to an Olympus microscope (objectives 20× and 50×) using a 785 nm diode excitation laser (10 mW laser power, 40–3800 cm⁻¹ spectral range, 300 lines/mm grating). The spectrometer was wavelength- and intensity-calibrated using a software-controlled autoalignment and calibration procedure with mercury and Ne–Ar lamps.

Second harmonic generation (SHG) measurements of (2-AMP)₃(H₃BO₃)₂ were performed using the modified Kurtz–Perry powder method [15]. The samples were irradiated with 160 fs laser pulses generated at an 82 MHz repetition rate by a Ti:sapphire laser (MaiTai, Spectra Physics, Santa Clara, CA, USA) at 800 nm. For quantitative determination of SHG efficiency, the intensity of the back-scattered laser light generated in the sample at 400 nm was measured on a grating spectrograph with a diode array (InstaSpect II, Oriel Newport Corporation Irvine, CA, USA), and the signal was compared with that produced by a potassium dihydrogen phosphate (KDP) standard. The initial experiments were performed on a powdered sample (100–150 μm particle size) loaded into a 5 mm glass cell using a mechanical vibrator. The measurements were repeated on different areas of the same sample, and the results were averaged. This experimental procedure minimized signal fluctuations induced by sample packing. Lastly, the measurements were performed also with size-fractioned samples (particle size: 25–45, 45–63, 63–75, 75–100, 100–125, and 125–150 μm).

The UV–Vis spectra of the powder samples were recorded using an Agilent Technologies Cary Series 4000 UV–Vis spectrometer (Santa Clara, CA, USA) equipped with internal DRA-900 accessory (diffuse reflectance with integrating sphere) in the 175–850 nm spectral region with a 0.5 nm spectral resolution.

Powder X-ray diffraction patterns were collected at room temperature using a Philips/PANalytical X’pert PRO MPD diffractometer (Royston, UK) (Bragg–Brentano geometry, ultrafast X’Celerator detector and Cu Kα radiation, λ = 1.5418 Å). The data were analyzed using the FullProf software [16]. Theoretical diffraction patterns for confirmation of phase purity were calculated from single-crystal X-ray diffraction data using the PLATON program [17].

2.2. Syntheses

(2-AMP)₃(H₃BO₃)₂ cocrystals were prepared by slow evaporation at room temperature of the aqueous solution of 2-aminopyrimidine and boric acid mixed in a 1:1 molar ratio. The resulting colorless crystals were filtered off and dried in air. The second studied compound, 2-AMP(H₃BO₃)₂, was similarly prepared from an aqueous solution containing an excess of boric acid (1:2 molar ratio). Unfortunately, the crystalline product always contained some amount of pure boric acid, thus requiring washing it with ethanol. After drying in air, the product was mechanically separated (based on differences in crystal morphology) from the remaining traces of boric acid. The purity of the final products was confirmed by Raman microspectroscopy and powder X-ray diffraction (see Figures S1 and S2, Tables S1 and S2, Supplementary Materials). The solubility of 2-(AMP)₃(H₃BO₃)₂ crystals in water is highly temperature-dependent and increased from 123.6 g/L (293 K), 130.8 g/L (303 K), and 157.6 g/L (313 K) to 214.0 g/L (318 K).

2.3. Crystal Structure Determination

X-ray structural data were collected on a Kappa CCD (Bruker Nonius, Billerica, MA, USA) diffractometer equipped with an Apex II CCD detector (Bruker, Billerica, MA, USA) and with a Cryostream Cooler (Oxford Cryosystems, Oxford, UK) using graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) and were corrected for absorption by the methods incorporated in the software of the diffractometer (multiscan routine [18]). The phase problem was solved using direct methods (SHELXT [19]), and the structure was refined using the full-matrix least-squares routine based on F² (SHELXL2017 [20]). Nonhydrogen atoms were refined with anisotropic displacement parameters. The hydrogen atoms attached to carbon atoms were included in their calculated positions and refined as riding atoms, while hydrogen atoms residing on nitrogen and oxygen atoms were identified on the difference electron density maps and refined similarly with U_iso(H) set to 1.2 U_eq (pivot atom). The basic crystallographic data, measurement, and refinement details are summarized in Table 1. The crystallographic data of (2-AMP)₃(H₃BO₃)₂ and 2-AMP(H₃BO₃)₂ were deposited at the Cambridge Crystallographic Data Centre as supplementary publications CCDC 1586908 and CCDC 1586909, respectively. A copy of the data is available free of charge from CCDC, 12 Union Road, Cambridge CG21, EZ, UK (fax: +44 1223 336033; e-mail: deposit@ccdc.cam.ac.uk).

Table 1. Crystal data and structure refinement details of the studied cocrystals.

Identification code	(2-AMP)3(H3BO3)2	2-AMP(H3BO3)2
Empirical formula	C12H21B2N9O6	C4H11B2N3O6
Formula weight	409.00	218.78
Temperature (K)	150(2)	150(2)
a (Å)	13.1632(4)	3.7634(2)
b (Å)	13.1632(4)	13.8978(7)
c (Å)	9.9288(3)	18.2041(8)
α (°)	90	90
β (°)	90	91.757(2)
γ (°)	120	90
Volume (Å3)	1489.88(10)	951.68(8)
Z	3	4
Calculated density (Mg/m3)	1.368	1.527
Crystal system	Trigonal	Monoclinic
Space group	P3221	C2/c
Absoption coefficient (mm-1)	0.108 mm−1	0.134 mm−1
F(000)	642	456
Crystal size (mm)	0.60 × 0.57 × 0.31	0.58 × 0.17 × 0.16
Diffractometer and radiation	Nonius Kappa CCD, Mo λ = 0.71073 Å
Scan technique	ω and ψ scans to fill the Ewald sphere
Completeness to θ	99.9%	99.9%
Range of h, k and l	−17→17, −17→17, −12→12	−4→3, −18→18, −20→23
θ Range for data collection (°)	1.79–27.47°	2.24–27.48°
Refl. collected/unique (Rint)	26047/2287 (0.022)	7829/1097 (0.019)
No. of observed reflections	2216	997
Criterion for observed reflections	I > 2σ(I)
Absorption correction	multi-scan	multi-scan
Function minimized	Σ w(Fo2 - Fc2)2
Parameters refined	134	70
R; wR(F2) (I>2σ(I))	0.0267; 0.0752	0.0293; 0.0769
R; wR(F2) (all data)	0.0280; 0.0764	0.0326; 0.0791
Value of S	1.074	1.080
Absolut struct. param. (Flack)	-0.1(2)
Δρmax and Δρmin (eÅ−3)	0.17 and −0.16	0.18 and –0.19
Weighting scheme	W = [σ2(Fo2) + aP2 + bP]−1
	P = (Fo2 + 2Fc2)/3
	a = 0.0491	a = 0.0418
	b = 0.1274	b = 0.4767

2.4. Crystal Growth

The congruent and high (see Section 2.2) solubility of (2-AMP)₃(H₃BO₃)₂ in H₂O allows crystal growth from aqueous solution with stoichiometric ratio of the crystal constituents, (i.e., (2-AMP):H₃BO₃ at 3:2). Best results of crystal growth experiments were obtained using the method of controlled slow evaporation of the solvent at constant temperature of 311 K. During a growth period of 5 months, crystals of dimensions up to approximately 15 × 15 × 5 mm³ resulted. However, the crystal quality suffered greatly from the perfect cleavage of the crystals parallel to (001) and very easy plastic deformation. This softness of the crystals readily affected the quality of obtainable seed crystals, and crystal defects propagated during growth in the crystals, thus leading to cloudy regions and cleavage cracks inside the crystals (see Figure 1). The morphology of the crystals is dominated by the pinacoid {001} (leading to a platy habit) and prisms {100} and {110}, see Figure 1.

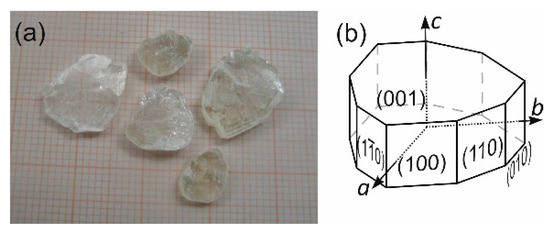
Figure 1. (a) Example of cleaved plates of grown crystals of (2-AMP)₃(H₃BO₃)₂. (b) Typical, idealized morphology of the trigonal crystals of (2-AMP)₃(H₃BO₃)₂, shown in (a).

2.5. Quantum Chemical Computations

Quantum chemical computations (Gaussian 09W program package [21]) were performed using the closed-shell restricted density functional theory (B3LYP) method with a 6-311G+(d,p) basis set, applying tight convergence criteria and an ultrafine integration grid. Geometry optimization of the isolated 2-aminopyrimidine molecule was followed by vibrational frequency calculations using the same method and a basis set. Theoretical Raman intensities of computed normal modes were calculated (RAINT program [22]) for a 1064 nm excitation wavelength taking Raman scattering activities from Gaussian output. The assignment of computed normal vibrational modes of 2-aminopyrimidine molecule was based on visualization of atom motions in the GaussView program [23]. The comparison of recorded vibrational spectra of 2-aminopyrimidine with computed normal modes, which were scaled using dual scaling [24] and WLS (wavenumber-linear scale) [25] procedures, is presented in Table S3, Supplementary Materials.

Solid-state DFT studies of (2-AMP)₃(H₃BO₃)₂ were conducted using the CRYSTAL17 program (version 1.0.2.) [26]. Computations employed the B3LYP functional, applying the 8-411d11G basis set [27] for oxygen atoms, and the 6-31G(d) basis set for all other atoms. DFT integration utilized an extra-large integration grid default in the program. Both the Pack–Monkhorstand and Gilat nets for sampling the Brillouin zone consisted of 8 points. Derivatives required for IR and Raman spectra were computed using the coupled perturbed Kohn–Sham [28,29] analytical approach. Fractional coordinates of individual atoms were taken from the diffraction experiment and optimized using tightened convergence criteria before computing the spectral properties. The theoretical Raman spectrum was corrected for an experimental wavelength of 1064 nm and for a temperature of 293 K. All vibrational frequencies obtained by computations were scaled using an empirical factor of 0.96.

2.6. Optical Properties

For the trigonal crystals of (2-AMP)₃(H₃BO₃)₂, the two principal refractive indices, n_o with wave polarization in the plane perpendicular to the 3-fold axis and n_e with wave polarization along the 3-fold axis (which is parallel to the optic axis of the optical indicatrix), were determined by the prism method with normal incidence on a prism with incidence face (hk0). Using a clear region of a grown crystal, a small prism with approximately 5 × 7 mm² incidence face dimensions was prepared by cutting and careful lapping of the prism surface. However, the prism quality was affected by the high plastic deformability and unavoidable cleavage cracks of (2-AMP)₃(H₃BO₃)₂ crystals. Refractive indices were measured with a precision goniometer/spectrometer system (Möller–Wedel, for experimental details see, e.g., [30]) at nine discrete wavelengths in the range between 435.8 and 1083.0 nm for n_o (with wave polarization parallel to the cleavage planes of the crystal). Measurement of refractive indices n_e (with wave polarization perpendicular to the cleavage planes) was only possible for the wavelengths 546.07 and 852.11 nm.

3. Results and Discussion

3.1. Crystal Structure Description

The cocrystal (2-AMP)₃(H₃BO₃)₂ belongs to the trigonal system with a non-centrosymmetric P3₂21 (resp. P3₁21) space group. The asymmetric unit with atom numbering is presented in Figure 2. The crystal structure is based on parallel layers formed by the motifs containing the boric acid molecule surrounded by three molecules of 2-aminopyrimidine, which are interconnected by N–H...O and O–H...N hydrogen bonds with donor…acceptor distances ranging from 2.923(2) to 3.000(2) Å and from 2.746(2) to 2.822(2) Å, respectively. The hydrogen bonding pattern of these motifs (see Figure 3) can be described by the graph set descriptor $R_2^2\left(8\right)$. The arrangement of parallel layers in the crystal structure of (2-AMP)₃(H₃BO₃)₂ is depicted in Figure 6a. Bond lengths, angles, and hydrogen bond characteristics are outlined in Table S4, Supplementary Materials.

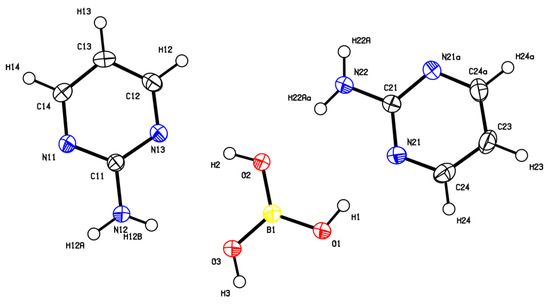
Figure 2. ORTEP plot of the asymmetric unit of (2-AMP)₃(H₃BO₃)₂ with atom numbering. The displacement parameters are shown at the 50% probability level.

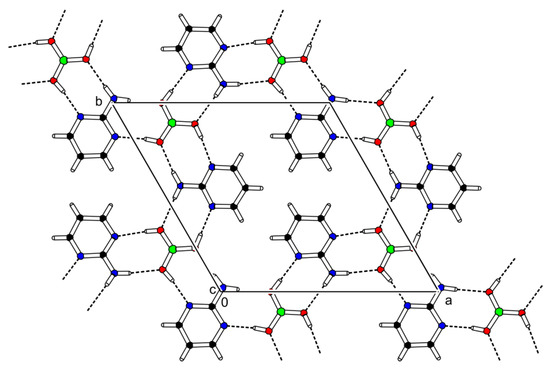
Figure 3. Packing scheme of (2-AMP)₃(H₃BO₃)₂—simplified projection of the ab plane displaying only one layer of the crystal structure. Dashed lines indicate hydrogen bonds.

2-AMP(H₃BO₃)₂ crystallizes in the monoclinic system with space group C2/c. The asymmetric unit with atom numbering is depicted in Figure 4. The crystal structure consists of ribbons formed by boric acid molecules connected by O–H…O hydrogen bonds with donor…acceptor distances 2.798(1) and 2.721(1) Å (graph set descriptors $R_2^2\left(8\right)$). These ribbons are interconnected via 2-aminopyrimidine molecules by O–H...N and N–H...O hydrogen bonds (graph set descriptors $R_2^2\left(8\right)$) with donor…acceptor distances 2.688(1) and 3.335(1) Å, respectively (see Figure 5). The mutual arrangement of flat 2-aminopyrimidine molecules oriented in parallel and ribbons formed by boric acid molecules is depicted in Figure 6b. Bond lengths, angles, and hydrogen bonds characteristics of 2-AMP(H₃BO₃)₂ are outlined in Table S5, Supplementary Materials.

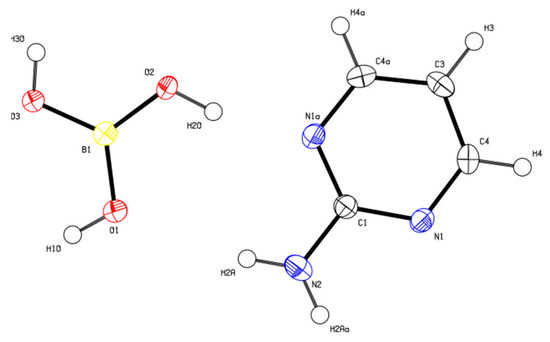
Figure 4. ORTEP plot of the asymmetric unit of 2-AMP(H₃BO₃)₂ with atom numbering. The displacement parameters are shown at the 50% probability level.

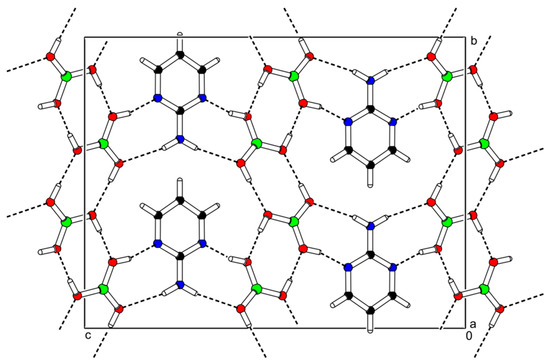
Figure 5. Packing scheme of the 2-AMP(H₃BO₃)₂—projection is on the bc plane. Dashed lines indicate hydrogen bonds.

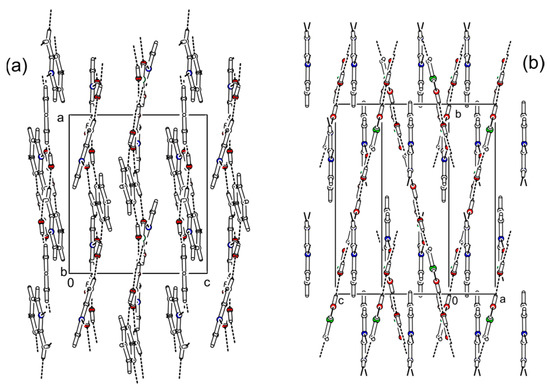
Figure 6. Comparison of crystal packing between (2-AMP)₃(H₃BO₃)₂ (a) and 2-AMP(H₃BO₃)₂ (b). Dashed lines indicate hydrogen bonds.

3.2. Vibrational and UV-Vis Spectra

The number of expected normal modes of the studied crystals was determined by nuclear site group analysis [31]. The crystals of (2-AMP)₃(H₃BO₃)₂ and 2-AMP(H₃BO₃)₂ belong to the space groups P3₂21 ($D_3^6$) and C2/c ($C_{2h}^6$) with 27 atoms (Z = 3) and 15 atoms (Z = 4) per asymmetric unit, respectively. In contrast to atoms N22, C21, C23, and H23 (see Figure 2), which occupy three-fold Wyckoff positions b(C₂), all remaining atoms of the asymmetric unit of (2-AMP)₃(H₃BO₃)₂ occupy the general six-fold Wyckoff positions c(C₁). Most atoms of the asymmetric unit of 2-AMP(H₃BO₃)₂ occupy general eight-fold Wyckoff positions f(C₁). Only atoms C1, N2, C3, and H3 (see Figure 4) occupy four-fold Wyckoff positions e(C₂).

Symmetry analysis of the optical vibrational modes (see Table 2) gave 14A₁(Ra) + 15A₂(IR) + 29E(IR,Ra) representations for the external modes, 59A₁(Ra) + 61A₂(IR) + 120E(IR,Ra) representations for the internal modes of (2-AMP)₃(H₃BO₃)₂, and 8A_g(Ra) + 7A_u(IR) + 10B_g(Ra) + 8B_u(IR) representations for the external modes and 29A_g(Ra) + 29A_u(IR) + 31B_g(Ra) + 31B_u(IR) representations for the internal modes of 2-AMP(H₃BO₃)₂.

Table 2. Results of the nuclear site group analysis of (2-AMP)₃(H₃BO₃)₂ and 2-AMP(H₃BO₃)₂ crystals.

Compound		(2-AMP)3(H3BO3)2			2-AMP(H3BO3)2
		$\mathit{P}{3}_{2}21\left({\mathit{D}}_3^6\right)$			$\mathit{C}2/\mathbf{c}\left({\mathit{C}}_{2\mathit{h}}^6\right)$
Representations		A1	A2	E	Ag	Au	Bg	Bu
	Acoustic		1	1		1		2
External modes	Translational	7	7	14	4	3	5	3
	Librational	7	8	15	4	4	5	5
Internal modes		59	61	120	29	29	31	31
	Total	73	77	150	37	37	41	41
Activity	IR		z	x, y		x		y, z
	Raman	αxx+αyy, αzz		(αxxx-αyyx,αxyy), (αxzy,αyzx)	αxx,αyy,αzz, αxy		αxz,αyz

IR and Raman spectra (see Figure 7 and Figure 8 and Table 3 and Table 4) were assigned according to results from our quantum chemical calculations and recently published study on boric acid [32]. The assignment of the bands of stretching and out-of-plane bending vibrations of the N–H and O–H groups involved in hydrogen bonding is based on correlation curves [33,34] concerning the position of the vibrational bands and appropriate hydrogen bond lengths.

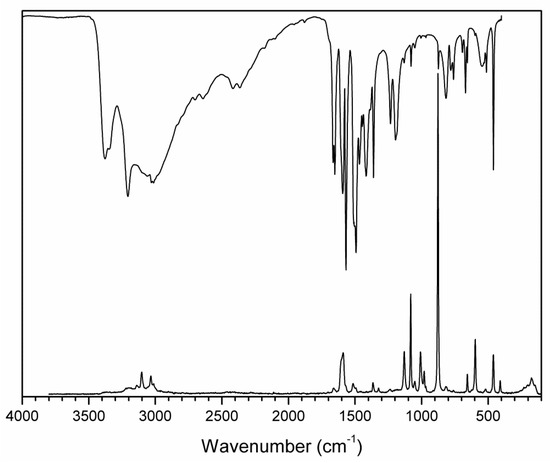
Figure 7. FTIR (compiled from nujol and fluorolube mulls) and FT Raman spectra of (2-AMP)₃(H₃BO₃)₂.

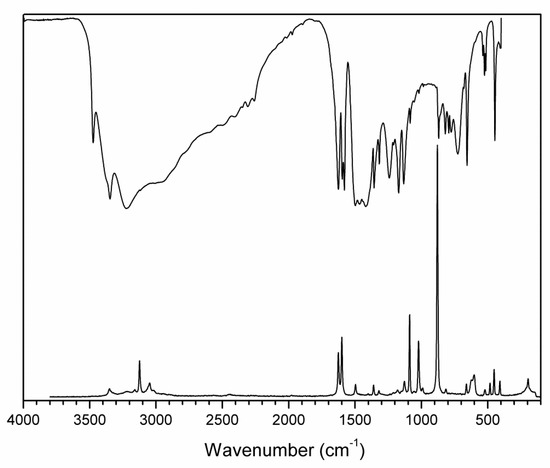
Figure 8. FTIR (compiled from nujol and fluorolube mulls) and FT Raman spectra of 2-AMP(H₃BO₃)₂.

Table 3. Recorded FTIR and FT Raman maxima (cm⁻¹) of (2-AMP)₃(H₃BO₃)₂ and their assignment.

IR	Raman	Assignment	IR	Raman	Assignment
	174w	γrg, γC-NH2	1416m		νBO, δBOH
	409w	δNCN	1446w		δCH, νrg, δNCN
460m	460w	γrg	1467m		νC-NH2, δNH2, δNCN, νBO,
513w	518w	τNH2, δOBO, δBOH	1493s		δBOH
546w		γCH, γrg, δOBO, δBOH	1510sh
	597w	δrg, δNCN	1568s		νrg, δrg, δNCN, ρNH2, δCH
657w	657w		1592m	1589w	δNH2, νC-NH2, νrg
670w		γBO3	1652m
693w		?	1664m	1660w
760w		γBO3, γXH(…X)	2364w		?
779w		γCH, γBO3, γXH(…X)	2418w
817w	818w	γrg, γCN3, γBO3	2641w
874w	877vs	δBO3, γBO3, νsrg, δsrg	2700w
	981w	γCH	3012s	3012w	νOH(…N), νCH
	1008w	νrg, δrg	3030s	3033w
1050w	1050w	ρNH2, δCH	3060sb		νOH(…N)
1080w	1081s	δCH, νrg	3100sh	3102w	νOH(…N), νCH
1131w	1131w	δCH, ρNH2		3140w
1185sh		?	3205s	3200wb	νNH(…O)
1196m		νBO, δBOH	3345s
1233m		νrg, δrg, ρNH2	3378m
1362m	1365w	δCH, νC-NH2

Table 4. Recorded FTIR and FT Raman maxima (cm⁻¹) of 2-AMP(H₃BO₃)₂ and their assignment.

IR	Raman	Assignment	IR	Raman	Assignment
	195w	external mode	1212m		νrg, δrg, ρNH2
406w	408w	δNCN	1244m		νrg, δrg, ρNH2, νBO, δBOH
446m	451w	γrg	1319m	1319w	δCH, ρNH2
	482w	δOBO, δBOH	1359m	1360w	δCH, νC-NH2
515w		τNH2, δOBO, δBOH	1421s		νBO, δBOH
524w	520w		1468s		νC-NH2, δNH2, δNCN, νBO,
537w		γCH, γrg, δOBO, δBOH	1501s	1496w	δBOH
	601w	δrg, δNCN	1582s		νrg, δrg, δNCN, ρNH2, δCH
	623w		1599m	1600m	δNH2, νC-NH2, νrg
658m	661w	δrg, δNCN, γBO3	1629s	1626m
726m		γBO3, γXH(…X)	2263m		?
777m		γCH, γBO3	2313m
794m			2410m
821m	816w	γrg, γCN3, γBO3	3000sb	3020w	νOH(…N), νCH
870m	879vs	δBO3, γBO3, νsrg, δsrg		3047w	νCH
	990w	γCH	3124sh	3124m
	1022m	νrg, δrg		3159w	νOH(…O)
1087m	1089m	δCH, νrg	3230sb	3220w
1135m	1128w	δCH, ρNH2	3350s		νOH(…N), νNH(…O)
1174s	1180w	δCH, ρNH2, νBO, δBOH	3480m

Abbreviations and Greek symbols used for vibrational modes: rg, ring; _s, symmetric; ν, stretching; δ, deformation or in-plane bending; γ, out-of-plane bending; ρ, rocking; ω, wagging; τ, twisting; and X = N, O.

The overall character of the recorded spectra is fully consistent with the results from the crystal structure determination (i.e., with molecular crystals consisting of hydrogen-bonded uncharged molecules of 2-aminopyrimidine and boric acid). Differences in crystal packing and in hydrogen bonding patterns are mainly reflected in the shape and positions of the bands corresponding to stretching vibrations of N–H and O–H groups involved in O–H…O, O–H…N. and N–H…O hydrogen bonds (3500–2500 cm⁻¹ region in the IR spectra). The presence of boric acid molecules in the crystal structure is clearly evident as strong to medium intensity bands (partly overlapping with 2-aminopyrimidine modes) at 1550–1370 cm⁻¹ and 1250–1150 cm⁻¹ (νBO and δBOH modes), 850–650 cm⁻¹ (γBO₃ modes), and 550–510 cm⁻¹ (δOBO and δBOH modes). The shape of these bands, especially in the IR spectrum of AMP(H₃BO₃)₂ (see Figure 8), is very similar to that of crystalline boric acid [32] (see Figure S3, Supplementary Materials).

Characteristic broadening and intensity increase of the IR-active bands of νBO and δBOH modes (1550–1370 cm⁻¹ region) and γBO₃ modes (850–650 cm⁻¹ region) is likely related to the existence of O–H…O hydrogen bonds interconnecting boric acid molecules in AMP(H₃BO₃)₂. This interaction is not present in the crystal structure of (2-AMP)₃(H₃BO₃)₂ where such bands are much less pronounced (see Figure 7 and Figure S3, Supplementary Materials). Differences in crystal packing and particularly in hydrogen bonding are also reflected in vibrational manifestations of 2-aminopyrimidine molecules in all spectra, especially in the 1680–1560 cm⁻¹ region where highly mixed modes of heteroaromatic ring and amino group are located. The most intense bands in the Raman spectra, corresponding to the mixed modes of δBO₃, γBO₃, and symmetric stretching/deformation vibrations of the heteroaromatic ring, were recorded at 877 and 879 cm⁻¹ for (2-AMP)₃(H₃BO₃)₂ and AMP(H₃BO₃)₂, respectively. The complete assignment of IR and Raman spectra is outlined in Table 3 and Table 4.

The assignment of (2-AMP)₃(H₃BO₃)₂ vibrational spectra was also confirmed by solid state quantum-chemical computations using the CRYSTAL17 program. The comparison between recorded spectra and computed vibrational modes is shown in Figures S4 and S5, Supplementary Materials. The predicted positions and intensities of the modes fit to the recorded spectra very well. Some discrepancies can be observed in the computed positions of the IR active modes in the 1260–1150 cm⁻¹ region (representing νrg, δrg, ρNH₂ and νBO, δBOH modes) and in intensities of computed modes at 827 and 541 cm⁻¹. In addition, the computed positions of the Raman active modes in the 1620–1580 cm⁻¹ region are slightly shifted to higher wavenumbers.

The UV–Vis spectrum of a polycrystalline sample (see Figure S6, Supplementary Materials) reveals that (2-AMP)₃(H₃BO₃)₂ is optically transparent at least down to 375 nm.

3.3. Optical Properties of (2-AMP)₃(H₃BO₃)₂

Crystals of (2-AMP)₃(H₃BO₃)₂ show pronounced optical activity, which can be observed in the direction of the optical axis. The rotation of the plane of the linearly polarized light in this direction amounts approximately 22.5°/mm at 546.7 nm wavelength, as measured using three (001) crystal plates of different thicknesses and a polarizing microscope with rotatable polarizer. Since the crystal structure of (2-AMP)₃(H₃BO₃)₂ possesses no chiral constituents, the compound can crystallize with equal probability with either of the enantiomorphic space groups P3₁21 or P3₂21. In consequence, both levo- and dextro-rotatory optically active crystals of (2-AMP)₃(H₃BO₃)₂ can occur with equal probability. In Figure 9a, an interference figure in conoscopic illumination of a (001) plate of about 2 mm thickness, taken with a polarizing microscope and crossed polarizers using monochromatic light of 546.7 nm wavelength and a quarter-wave plate between the crystal and the analyzer of the microscope, is given. The observed spirals indicate levo-rotatory optical activity of the used crystal. The occurrence of optical activity of (2-AMP)₃(H₃BO₃)₂ corroborates its chiral symmetry.

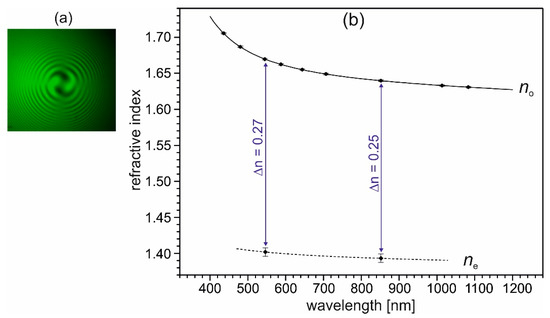
Figure 9. (a) Interference figure of a (001) plate of (2-AMP)₃(H₃BO₃)₂, taken with a polarizing microscope in conoscopic illumination with crossed polarizers, using monochromatic (546.7 nm) light and a quarter-wave plate between the crystal and the analyzer. The spirals in the interference figure indicate a levo-rotatory optical activity of the used crystal of (2-AMP)₃(H₃BO₃)₂. Note, that dextro-rotatory crystals occur with equal probability during crystal growth. (b) Principal refractive indices n_o and n_e of trigonal (2-AMP)₃(H₃BO₃)₂ and their wavelength dispersion. Measured data are indicated by dots (with given error bars), the line for n_o indicates the fitting curve with a Sellmeier-type equation (see text). The dashed line connecting the two data points of n_e is a guide to the eye.

The measured refractive indices n_o and their wavelength dispersion, given in Figure 9b, were fitted with a Sellmeier-type equation (Equation (1)).

$$n^2(\lambda )=D_1+\frac{D_2}{({\lambda }^2-D_3)}-D_4{\lambda }^2\left(\mathrm{with}\mathsf{\lambda }\mathrm{in}\mathsf{\mu }\mathrm{m}\right)$$

(1)

The Sellmeier coefficients for n_o are D₁ = 2.654(1), D₂ = 0.0327(5), D₃ = 0.063(1), and D₄ = 0.021(1) (sum of the squares of residuals ξ² = 7 × 10⁻⁹). For n_e, no fit was calculated; the dashed line in Figure 9b is a guide to the eye. As can be seen in Figure 9b, crystals of (2-AMP)₃(H₃BO₃)₂ possess an exceptionally high birefringence Δn of about 0.25 in the visible range. In comparison, the birefringence Δn of calcite amounts to 0.173 at 560.0 nm [35]. Crystals of (2-AMP)₃(H₃BO₃)₂ are uniaxially negative, which corresponds to the layered crystal structure. As a consequence of the large birefringence, phase matching for collinear second harmonic generation (SHG) of type I cannot be realized within the transparency range of the crystal. Also, for the collinear SHG type II process, the possibility for phase matching within the transparency range is improbable. Here, however, a definitive statement is not possible due to the lacking knowledge of the dispersion of the refractive index n_e in the shorter wavelength range.

3.4. Second Harmonic Generation (SHG) Measurements of (2-AMP)₃(H₃BO₃)₂

SHG measurements of the non-centrosymmetric crystalline compound (2-AMP)₃(H₃BO₃)₂ using powder samples revealed marked SHG activity. To quantify this activity, the measurements were compared to the SHG activity of potassium dihydrogen phosphate (KDP). The intensity I^2ω of the generated second harmonic with frequency 2ω was I^(2ω)((2-AMP)₃(H₃BO₃)₂) = 0.43 I^(2ω)(KDP). Using particle size dependent measurements, a qualitative check for phase matchability of the compound was performed (see Figure 10). However, these measurements did not yield a clear result because the perfect cleavage of the crystal impeded the preparation of a powder with isometric particles and, therefore, the precise control of the effective particle size.

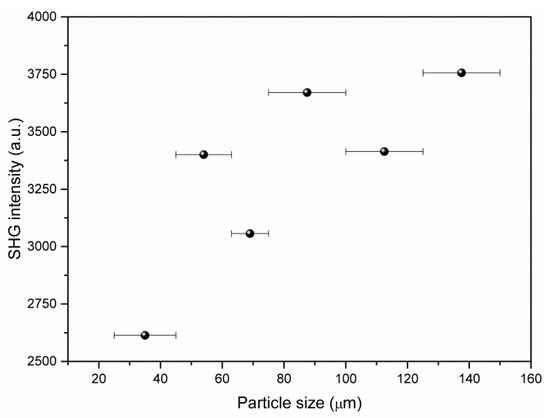
Figure 10. Observed dependence of second harmonic generation (SHG) intensity (using 800 nm fundamental laser line) on particle size for (2-AMP)₃(H₃BO₃)₂.

4. Conclusions

Two cocrystals based on hydrogen-bonded molecules of 2-aminopyrimidine and boric acid, non-centrosymmetric (2-AMP)₃(H₃BO₃)₂ and centrosymmetric 2-AMP(H₃BO₃)₂, were prepared and characterized. The formation of these products as cocrystals containing neutral molecules of 2-aminopyrimidine (pKa = 3.54 [36]) and boric acid (pKa(1) = 9.24 [37]) is consistent with the “pKa rule” previously presented for extensive sets of acid–base crystalline complexes [38]. The obtained cocrystals belong to “zone 1”, fulfilling ΔpKa < –1 condition.

The crystal structure of (2-AMP)₃(H₃BO₃)₂ consists of twisted 2D layers formed by isolated 2-aminopyrimidine and boric acid molecules interconnected by the system of O–H…N and N–H…O hydrogen bonds. The ribbons of boric acid molecules, formed via O–H…O hydrogen bonds, are present in the crystal structure of 2-AMP(H₃BO₃)₂. These ribbons are interconnected by isolated 2-aminopyrimidine molecules (via O–H…N and N–H…O hydrogen bonds) and form a complex 3D crystal structure.

The overall character of the recorded vibrational spectra is consistent with the results from the crystal structure determination, and they were assigned according to quantum-chemical computations. The IR spectrum of 2-AMP(H₃BO₃)₂ contains characteristic strong- to medium-intensity bands resulting from the vibrational modes of boric acid molecules interconnected by O–H…O hydrogen bonds. Both Raman spectra exhibit a very strong sharp band associated with manifestations of mixed modes of boric acid and aminopyrimidine ring at approximately 880 cm⁻¹.

Although for crystals of (2-AMP)₃(H₃BO₃)₂ the refractive indices and the considerable birefringence could perhaps allow collinear SHG phase matching of type II close to the UV absorption edge, the mechanical softness and the perfect cleavage spoils the quality of the crystals obtained from crystal growth and rules out the preparation of high-quality samples. This discourages the use of (2-AMP)₃(H₃BO₃)₂ crystals for technical applications. However, this newly discovered cocrystal of 2-aminopyrimidine with boric acid investigated in the present work provides a good example of the effectiveness of the crystal engineering approach that aimed to preserve the neutral 2-aminopyrimidine molecule (because of the amount of its total hyperpolarizability [1]) in a crystal structure with suitable (non-centrosymmetric) symmetry.