Abstract
We combine theoretical and experimental tools to study elastic properties of Fe-Al-Ti superalloys. Focusing on samples with chemical composition Fe71Al22Ti7, we use transmission electron microscopy (TEM) to detect their two-phase superalloy nano-structure (consisting of cuboids embedded into a matrix). The chemical composition of both phases, Fe66.2Al23.3Ti10.5 for cuboids and Fe81Al19 (with about 1% or less of Ti) for the matrix, was determined from an Energy-Dispersive X-ray Spectroscopy (EDS) analysis. The phase of cuboids is found to be a rather strongly off-stoichiometric (Fe-rich and Ti-poor) variant of Heusler Fe2TiAl intermetallic compound with the L21 structure. The phase of the matrix is a solid solution of Al atoms in a ferromagnetic body-centered cubic (bcc) Fe. Quantum-mechanical calculations were employed to obtain an insight into elastic properties of the two phases. Three distributions of chemical species were simulated for the phase of cuboids (A2, B2 and L21) in order to determine a sublattice preference of the excess Fe atoms. The lowest formation energy was obtained when the excess Fe atoms form a solid solution with the Ti atoms at the Ti-sublattice within the Heusler L21 phase (L21 variant). Similarly, three configurations of Al atoms in the phase of the matrix with different level of order (A2, B2 and D03) were simulated. The computed formation energy is the lowest when all the 1st and 2nd nearest-neighbor Al-Al pairs are eliminated (the D03 variant). Next, the elastic tensors of all phases were calculated. The maximum Young’s modulus is found to increase with increasing chemical order. Further we simulated an anti-phase boundary (APB) in the L21 phase of cuboids and observed an elastic softening (as another effect of the APB, we also predict a significant increase of the total magnetic moment by 140% when compared with the APB-free material). Finally, to validate these predicted trends, a nano-scale dynamical mechanical analysis (nanoDMA) was used to probe elasticity of phases. Consistent with the prediction, the cuboids were found stiffer.
Keywords:
superalloys; Fe-Al; Heusler; ab initio; stability; elasticity; disorder; off-stoichiometry; nano-scale; nanoDMA; anti-phase boundaries 1. Introduction
Fe-Al-based alloys possess great potential for high-temperature applications [1,2,3,4,5,6] as well as for other functional and structural use [7,8,9,10,11,12,13,14,15]. A detailed review can be found, e.g., in Ref. [16]. A subset of these materials is represented by two-phase Fe-Al-Ti superalloys in which sub-micron cuboids of an Fe-Al-Ti intermetallic phase are coherently embedded into an Fe-Al matrix (see, e.g., Refs. [2,17,18,19,20,21]).
The phase of cuboids is a variant of Fe2TiAl which crystallizes in the Heusler L21-structure. Material properties of stoichiometric Fe2TiAl were intensively studied by quantum-mechanical calculations including thermodynamic and magnetic properties [22,23], electronic properties [24,25], and elastic properties under ambient conditions [26] or under hydrostatic pressures [23]. The theoretical predictions related to the level of spin-polarization were confirmed by experiments by Kourov and co-workers [27]. Interestingly, there is a long-lasting discrepancy related to the low-temperature magnetic moment of Fe2TiAl which was theoretically predicted nearly an order of magnitude higher than the experimental value. Density functional theory (DFT) calculations resulted in 0.9 μB per 4-atom formula unit (abbreviated as f.u.) in Refs. [24,28] in contrast to experimental values, 0.1 μB/f.u. reported in Ref. [25] or 0.11 μB/f.u. in Ref. [29] for T = 4.2 K. Our recent study [30], which was focused on this discrepancy, indicates that off-stoichiometric Fe-rich and Ti-poor states of Fe2TiAl, which were not considered in previous theoretical studies, play a very important role. Our calculations of the off-stoichiometric Fe2TiAl predicted low magnetic moments comparable with the experimental values.
The phase of the matrix appearing in Fe-Al-Ti superalloys is a disordered Fe-Al solid solution of about 19 at.% Al in a body-centered cubic (bcc) ferromagnetic (FM) iron, -Fe. This phase was also intensively studied both experimentally (e.g., in Refs. [21,31]) and theoretically. Regarding theoretical calculations, the electronic structure and energetics of the dissolution of Al in bcc Fe and the interaction between Al atoms and vacancies were investigated by ab initio calculations in Ref. [32]. The stability of complexes containing Al and vacancies was found to be driven by strong Al-vacancy attractions and an Al-Al repulsion. The vibrational entropy of chemically disordered and ordered Fe-Al compounds were calculated in Ref. [33]. Further, the electronic structure of disordered bcc FexAl1−x (0.4 < x < 0.75) alloys around the equiatomic stoichiometry was computed in Ref. [34]. In particular, the disordered phases were studied by the coherent potential approximation (CPA) and the intermetallic compounds by the tight-binding linear muffin-tin orbital (TB-LMTO) method. Large local magnetic moments were found in the case of transition metal antisite defect in FeAl when studying magnetism in Fe-Al (in agreement with the experimental findings). In another theoretical study [35], a series of quantum-mechanical calculations for a large set of different Fe-Al compositions and local atomic arrangements was performed to explain the anomalous volume-composition dependence in Fe-Al alloys. It was found that the spin-polarized calculations of Fe-rich compounds resulted in an anomalous lattice-constant behavior in qualitative agreement with experiments. However, the nonmagnetic and fixed-spin-moment calculations of Fe-Al states provided only linear trends without any anomaly. These studies clearly identified the change in magnetism of iron atoms caused by an increasing number of Al atoms in the first coordination sphere of the Fe atoms as the decisive driving force for the anomalous behavior. In a further study, Fähnle et al. [36] applied a cluster-expansion method to predict the phase diagram for the system Ni-Fe-Al including binary Fe-Al states.
The present study focuses on elastic properties of nano-phases appearing in Fe-Al-Ti superalloys. A particular attention was paid to the impact of atomic order on elasticity, which has been commonly neglected in previous studies. We employ quantum-mechanical calculations in order to examine the elasticity of both phases. As a complement to our calculations, we also probe the elastic properties experimentally by nano-scale dynamical mechanical analysis.
2. Materials and Methods
Fe-Al-Ti samples were prepared from high-purity elements Fe (99.95%), Ti (99.8%), and Al (99.95%) and button-type ingots were produced by arc melting using a MAM-1 furnace (Edmund Bühler GmbH, Bodelshausen, Germany). In order to achieve a good chemical homogeneity each ingot was melted four times. Then the ingots were cut using spark erosion in deionized water into discs of about 500 µm thick and 18 mm in diameter. The surface of these disc-samples was firstly grinded and polished to remove oxides. Subsequently the samples were polished by Vibromet for 24 h using colloidal silica suspension (grain size 0.05 µm) from LECO Corporation to guarantee the best possible surface smoothness. The samples were treated at 1273 K for 168 h in Ar atmosphere, then the heating was switched off and the samples were furnace-cooled under Ar to room temperature (approx. 2–3 h).
A TESCAN LYRA 3XMU FEG/SEM scanning electron microscope with an accelerating voltage of 20 kV equipped with an XMax80 Oxford Instruments detector for energy dispersive X-ray analysis (EDS) and focused ion beam (FIB) column was used to follow the chemical composition. Prior to these SEM observations, sample cross sections were shortly chemically etched in Nital. A transmission electron microscope (TEM) Jeol JEM 2100F HRTEM with a Schottky cathode operating at 200 kV was used to study microstructural details. The TEM lamella was taken using a FIB milling method from appropriately oriented grain (i.e., approximately perpendicular to the supposed [001] orientation).
For the phases identified by electron microscopy we also performed quantum-mechanical calculations. They were based on density functional theory [37,38] as implemented in the Vienna Ab initio Simulation Package (VASP) [39,40] using projector augmented wave pseudopotentials [41,42]. The generalized gradient approximation (GGA) was used for the exchange and correlation energy according to the parametrization by Perdew and Wang [43] employing the Vosko-Wilk-Nusair correction [44]. The used plane-wave energy cut-off was equal to 350 eV and the reciprocal space was sampled by a 10 × 10 × 6 Monkhorst-Pack k-point mesh. The two studied phases were modeled by 32-atom supercells which were multiples of cubic-shape 16-atom supercells based on 2 × 2 × 2 elementary bcc cells (see Figure 1). To illustrate relations between the 16-atom and 32-atom supercells, Figure 1 visualizes them in the case of the stoichiometric Fe2TiAl with the Heusler L21 structure. The stoichiometric Fe2TiAl is chosen as an example so as to show crystallographic relations without considering any disorder (which is important for the studied phases). All atomic positions and supercell shape and volume were relaxed. Atomic positions were relaxed so as to reduce the residual forces acting upon atoms under 0.001 eV/Å. All magnetic states were initially ferromagnetic but the magnetic degrees of freedom were also allowed to change when searching for minimum-energy states (but limited to either collinear or anti-collinear arrangement of local magnetic moments of atoms).
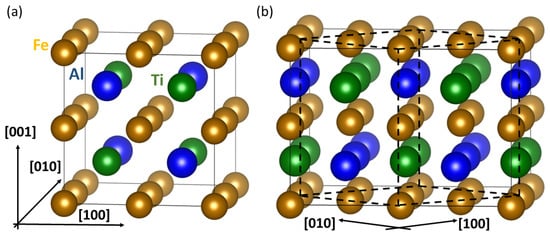
Figure 1.
A schematics showing relations between a 16-atom cubic-shape supercell of stoichiometric Fe2TiAl with the Heusler L21 structure (a) and a 32-atom supercell (b) of the type which we used for our study. The dashed lines in the part (b) show the 45°-rotated 16-atom cell exhibited in part (a).
To complement our theoretical analysis, hardness and elastic modulus were measured and evaluated by depth sensing nanoindentation technique performed on a Hysitron TI950 Triboindenter equipped with a cube corner tip. The tip diameter was approximately 40 nm. The nanoscale measuring head with resolution of 1 nN and load noise floor less than 30 nN was used for this study. The samples were tested in the range of indentation loads from 0.01 to 10 mN. The quasistatic indentation tests were carried out in a load controlled regime using a constant loading rate of 0.2 mN/s. Moreover, the dynamic modulus mapping method was used to study the response of the sample to dynamic loading in the range from 200 to 300 Hz. During this measurement, the nanoindentation tip scanned the sample surface in a raster mode in order to image the sample topography. Simultaneously, the tip oscillated during the surface scanning. Because the tip oscillation was much faster than the feedback response of the piezoscanner, the in-situ image was not affected by the oscillations. The phase and amplitude signals were analysed in order to get the stiffness and damping data. In order to calculate the storage and loss moduli from these data, the projected contact area between the tip and the sample was measured at the same indentation depths which were used for the modulus mapping tests. In order to determine the correct contact area a special area function was applied using tip calibration with low indentation loads [45]. The dynamic load amplitude was in the range from 0.5 to 3 µN, whereas the static contact load was in the range from 2 to 6 µN. The lateral resolution of the modulus mapping method depends on mechanical properties of the measured material, the nanoindenter tip shape and the settings of the lock-in amplifier which is used to process the displacement signal [45]. The lateral resolution of modulus mapping can be approximated by the size of the contact radius calculated on the basis of Hertz’s contact theory [45,46]. In the case of the presented results the estimated lateral resolution was around 5 nm.
3. Results and Discussion
3.1. Transmission Electron Microscopy of Fe-Al-Ti Phases
Our TEM analysis of the samples with the overall composition Fe71Al22Ti7 revealed a two-phase superalloy microstructure (see Figure 2a). The subsequent EDS study (Figure 2b–d) and line-scans (Figure 2e,f) provided the chemical composition of both phases. The chemical composition agreed on average with the published thermodymanical assessment of the Fe-Al-Ti system [16]. In this assessment the composition Fe71Al22Ti7 is located in a two-phase region within the ternary Fe-Al-Ti phase diagram. The phase Fe66.2Al23.3Ti10.5 of cuboid precipitates is Fe-rich and the Ti-poor variant of the Fe2TiAl Heusler L21-structure. The composition of the matrix was estimated to be Fe80Al19Ti1.
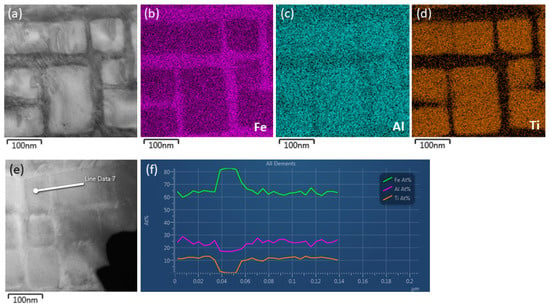
Figure 2.
A transmission electron microscope (TEM) micrograph (a) showing the superalloy nano-structure in our Fe71Al22Ti7 sample. The corresponding chemical composition (b–d) as detected by the Energy-Dispersive X-ray (EDS) spectroscopy in the same spot of our TEM lamellae. The analysis is accompanied by one of our line-scans (e) together with the corresponding chemical profile (f).
3.2. Theoretical Calculations of Thermodynamic and Elastic Properties
In order to determine the nano-scale elastic properties of the two phases identified by electron microscopy (see Figure 2), we have employed quantum-mechanical calculations. Starting with the phase of cuboids, we used three 32-atom periodically repeated supercells with composition Fe62.5Al25Ti12.5 (20 atoms of Fe, 8 atoms of Al and 4 atoms of Ti) as an approximant of the above-discussed chemical composition (Fe66.2Al23.3Ti10.5). While we know the overall composition, which is different from the stoichiometric Fe2TiAl Heusler compound, we do not know where the additional Fe atoms are located. Therefore, we have considered three different supercells which differ in the distribution of atoms. As the first polymorph we consider a completely disordered solid solution (A2). It is modeled using the general special quasi-random structure (SQS) concept [47] and generated by the USPEX code [48,49,50] (see Figure 3a). The second variant consists of an ordered sublattice of regular Fe atoms in the Heusler L21 structure (see yellow dashed lines in Figure 3b). However, Al, Ti as well as excess Fe atoms form a solid-solution (modeled by another SQS) on the Al and Ti sublattices of the L21 structure (the B2 case). The third polymorph consists of regular Fe atoms and Al atoms that occupy their corresponding sublattices within the L21 structure (see yellow and blue dashed lines in Figure 3c). The excess Fe atoms and Ti atoms form a random solid solution (an SQS) at the Ti sublattice (the L21 variant). Let us remind that the three above-described variants (which we call A2, B2 and L21) have the same composition Fe62.5Al25Ti12.5 and, for example, the L21 case is thus an off-stoichiometric variant of the stoichiometric Heusler compound with the L21 structure.
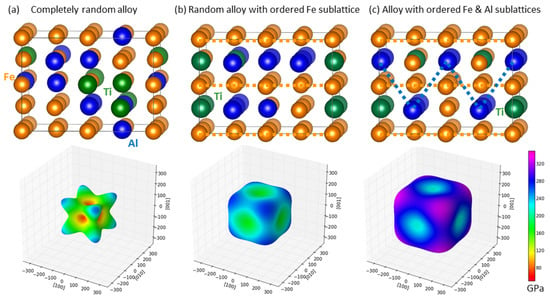
Figure 3.
(Upper row) Schematic visualization of the employed 32-atom computational supercells with the chemical composition Fe62.5Al25Ti12.5 (20 atoms of Fe, 8 atoms of Al and 4 atoms of Ti). These structures are used for modeling the phase of cuboids for which the equilibrium composition was determined to be Fe66.2Al23.3Ti10.5. The supercells differ in the distribution of atoms (see text). Yellow and blue dashed lines indicate ordered sublattices as in stoichiometric Heusler structure. (Lower row) Visualization of the anisotropic elastic properties for each atomic distribution in the form of directional dependences of the Young’s modulus (using the SC-EMA software [51,52], scema.mpie.de).
The thermodynamic stability of the polymorphs was assessed from their computed energies E by evaluating the formation energy (FexAlyTiz) = (E(FexAlyTiz) −)/() where are the numbers of Fe, Al and Ti atoms in the supercells and μ’s are their chemical potentials, i.e., energies of elemental bcc ferromagnetic Fe, non-magnetic fcc Al and non-magnetic hcp Ti. The formation energies are −0.183 eV/atom (Figure 3a, A2), −0.272 eV/atom (Figure 3b, B2) and −0.318 eV/atom (Figure 3c, L21). The L21 polymorph (Figure 3c) is thus thermodynamically the most stable one. The other two, A2 and B2, can be considered as models for non-equilibrium or high-temperature states. Considering our computational supercells as models for materials with different levels of disorder, we also evaluate the ideal configurational entropy . As different polymorphs have different numbers of ordered and disordered sublattices (with different number of lattice sites), we use a generalized formula (see, e.g., Ref. [53]) derived for the sublattice model [54] where R is the universal gas constant, i runs over different chemical species, over different sublattices, is the ratio of lattice sites of a sublattice with respect to the total number of all lattice sites and is the concentration of a chemical species i on a sublattice . In our case all studied variants have only one disordered “sublattice” which contains either all atomic sites (the A2 variant), a half of them (the B2 variant) or one quarter of all lattice sites (the L21 variant). The ideal configurational entropy is therefore with the a coefficient equal to 1, 1/2 and 1/4 for the A2, B2 and L21 variant, respectively, and being the concentrations of chemical species on the disordered (sub-)lattice. The configurational entropy of the three studied variants is (in units of R) equal to 0.90026, 0.51986 and 0.17329 for the A2, B2 and L21 variant, respectively. The more ordered variants are predicted to have lower formation energies but they have lower configurational entropies. Consequently, depending on the actual values, order-to-disorder transitions are possible at elevated temperatures. In order to address them we approximately evaluate the free energies of formation for each variant using the formula , where we put the entropy term S equal to discussed above. A L21-to-B2 transition is predicted at 1267 °C while the other transition temperatures (L21-to-A2 and B2-to-A2) are much higher than the considered temperature range, and thus the ordered phase is certainly stable here. A direct comparison of the predicted and experimental L21-to-B2 transition temperature is, unfortunately, not possible because (i) the Fe-Al-Ti phase diagram [16] for 1200 °C has no two-phase region for compositions close to the overall composition of our samples (Fe71Al22Ti7) and (ii) it is uncertain whether phases with off-stoichiometric L21 structure exist at these temperatures for compositions close to that which we simulate for the cuboids (the competing orderings are, in fact, the simulated ones, i.e., the B2 and A2, see Ref. [16]). Regarding magnetic and structural properties of the studied variants, their magnetic moments (in μB per 32 atoms) are 37.35 (A2), 14.88 (B2) and 9.94 (L21) and their volumes (in Å3 per atom) are 12.59 (A2), 11.84 (B2) and 11.78 (L21). The lower volumes roughly correspond to lower magnetic moments.
For all three polymorphs (Figure 3a–c) we computed a complete set of elastic constants using the stress-strain method [55]. The calculated matrices of elastic constants were determined in the coordinate system of these supercells. These are formed by multiples of a cubic-shape 16-atom supercell with the standard Cartesian coordination system of a cubic cell. Due to this construction, the axes of the 32-atom supercells (Figure 3a–c) are pointing in the [110] and [10] directions of the standard system (along the cube-cell edges of an elementary 2-atom bcc cell). Therefore, we first rotate the computed elasticity matrices using our recently developed software tool MELASA (to be published, freely available at https://melasa.cerit-sc.cz/). Next, due to the SQS distribution of atoms, the computed systems do not have a full cubic symmetry while a large-enough crystal of the studied material has cubic-symmetry properties due to averaging over different spatial distributions of atoms in different parts (and along different directions) of the crystal. Therefore, the calculated elastic constants were projected onto a set of elastic constants possessing a cubic symmetry according to the rigorous mathematical theory by Moakher and Norris [56]. Similar concepts are often used in the case of systems with any form of disorder (see, e.g., Refs. [57,58,59,60,61]). The Appendix A contains an example of this procedure in the case of the L21 polymorph of the phase of cuboids (Figure 3c).
The resulting cubic-symmetry elastic constants equal to = 177 GPa, = 125 GPa, = 105 GPa for the SQS where all atoms form a general solid solution (see Figure 3a, A2). Next, = 226 GPa, = 91 GPa and = 116 GPa for the SQS with the sublattice of regular Fe atoms ordered in the Heusler L21 phase but the other atoms are randomly distributed over the remaining sublattices (see Figure 3b, B2). Finally, = 303 GPa, = 135 GPa and = 136 GPa for the SQS where the sublattices of regular Fe and Al atoms are ordered and defect-free while the excess Fe atoms and Ti atoms form a solid solution on the original Ti sublattice of the stoichiometric Heusler structure (see Figure 3c, the L21 case). The elastic properties were then visualized in the form of directional dependences of the Young’s modulus in the lower row of Figure 3. As can be seen, the overall stiffness grows with increasing chemical ordering (from Figure 3a to Figure 3c) while the elastic anisotropy (expressed by the Zener anistropy ratio 2/(–)) is 4.04 (the A2 case), 1.72 (B2) and 1.62 (L21), respectively.
When studying the Fe-Al phase of the matrix, we have re-evaluated the Al-Al repulsion reported in Ref. [32] using our own computational set-up. In particular, two Al atoms in 32-atom supercells with the Fe atoms were located as 1st, 2nd, 3rd and 4th nearest neighbors (NN) pairs (see Figure 4). Indeed, the energy decreases with Al atoms further apart. Locally, also non-equilibrium atomic configurations can occur. We have therefore simulated three additional distributions representing different internal distributions of atoms employing 32-atom supercells (see Figure 5a–c). Their composition was Fe81.25Al18.75 (26 atoms of Fe and 6 atoms of Al) as approximants for the above-discussed chemical composition (Fe80Al19Ti1, the minor amount, 1%, of Ti is neglected). The first polymorph corresponds to a distribution where all atoms form a complete disordered solid solution (A2) modeled by a general special quasi-random structure, SQS (Figure 5a). The second variant is a B2-type SQS with the Al atoms on one of the two sublattices only, i.e., there are no 1st Al-Al NN pairs, Figure 5b, B2). The third polymorph is a D03-type SQS with Al atoms on only one of the three sublattices, i.e., there are no 1st and 2nd Al-Al nearest-neighbor pairs, Figure 5c, D03). We note that all the three variants of the phase of the matrix have the same concentration of Al (18.75 at.%) and the B2 and D03 cases are thus off-stoichiometric.
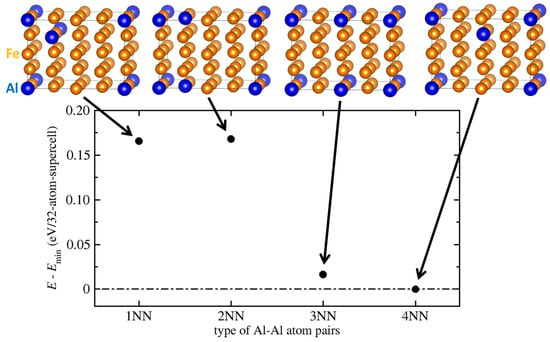
Figure 4.
Results of quantum-mechanical calculations of interactions of Al atoms in a ferromagnetic body- centered-cubic (bcc) Fe. The calculated energies are shown as energy differences relative to the lowest obtained energy (when the Al atoms are located mutually as the 4th nearest neighbors (NN) pairs) which is set to be the energy zero (dash-dotted horizontal line).
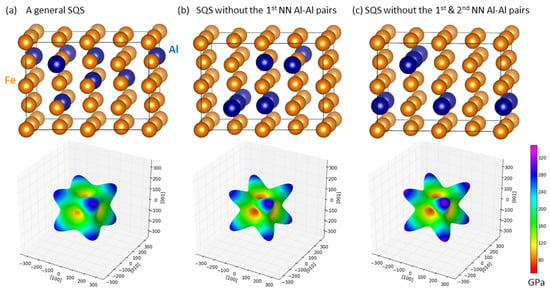
Figure 5.
Upper row: Schematic visualization of the 32-atom computational supercells with chemical composition Fe82.25Al18.75 (26 atoms of Fe and 6 atoms of Al) used for modeling of the Fe-Al phase of the matrix. The supercells differ in the distribution of atoms (see the text for details). The left variant is a distribution when all atoms form a complete disordered solid solution modeled by a general special quasi-random structure, the A2 case (a). The middle variant is a B2-type SQS with all the Al atoms on only one of the two sublattices, i.e., there are no 1st NN Al-Al pairs (b). The right figure shows a D03-type SQS with the Al atoms on only one of the three sublattices—there are no 1st and 2nd Al-Al NN pairs (c). Lower row: Visualization of anisotropic elastic properties for each atomic distribution in the form of directional dependences of the Young’s modulus (visualized by the SC-EMA software [51,52]).
The corresponding formation energies are −0.119 eV/atom (Figure 5a, A2), −0.121 eV/atom (Figure 5b, B2) and −0.144 eV/atom (Figure 5c, D03). The polymorph with the least disordered distribution (Figure 5c) and Al atoms further apart is thus thermodynamically the most stable in line with the discussed Al-Al repulsion as well as with experimental data obtained for the Fe-Al binary system (this tendency is behind the formation of the Fe3Al intermetallics with the D03 structure). The other two structures (A2 and B2) can be considered as models for non-equilibrium or high-temperature states. Similarly as in the case of the cuboid phase, we can evaluate the ideal configurational entropy for the three variants of the matrix phase. Their configurational entropies (in units of R) are equal to 0.48258, 0.33078 and 0.14058 for the A2, B2 and D03 variant, respectively.
The higher configurational entropy of the A2 and B2 variants may (among other factors) prevent the matrix from crystallizing in the D03 variant (which has the lowest formation energy) at non-zero temperatures. The lowest formation energy obtained for the D03 variant is understandable as it reflects the nature of the Fe-Al system where the Fe3Al intermetallics with the D03 structure exists for 25 at.% of Al. The reasons for this behavior include the Al-Al repulsion (see above). Regarding magnetic and structural properties of the studied variants, their magnetic moments (in μB per 32 atoms) are 56.57 (A2), 56.31 (B2) and 55.49 (D03) and their volumes (in Å3 per atom) are 11.84 (A2), 11.57 (B2) and 11.76 (D03). The changes due to different atomic configurations are smaller than those in the variants of the phase of cuboids.
Following just the same procedure as described above in the case of the three variants of the phase of cuboids, we have determined elastic constants with a cubic symmetry. Their values are = 205 GPa, = 135 GPa and = 122 GPa for the A2 SQS when the Fe and Al atoms form an ideal solid solution (Figure 5a), = 195 GPa, = 146 GPa and = 124 GPa for the B2 SQS without the 1st Al-Al NN pairs (Figure 5b) and = 195 GPa, = 149 GPa and = 130 GPa for the D03 SQS without the 1st and 2nd Al-Al NN pairs (see Figure 5c). These results agree quite well with (close to T = 0 K) experimental data [62]: = 188 GPa, = 126 GPa and = 130 GPa. The elastic properties were then again visualized by the directional dependences of the Young’s modulus in the lower row of Figure 5. The maximum value of the Young’s modulus (in the ⟨111⟩ family of directions) grows with increasing ordering (from the A2, Figure 5a, to D03, Figure 5c) while the elastic anisotropy (the Zener anistropy ratio) increases from 3.49 to 5.06 and eventually to 5.65.
When comparing the elasticity of the thermodynamically most stable cuboid polymorph (Figure 3c) with that of the phase of the matrix (Figure 5c), we find the phase of cuboids to be elastically stiffer. The elasticity difference reaches its maximum for the ⟨001⟩ family of directions when the phase of cuboids has the Young’s modulus equal to 220 GPa while the matrix exhibits only 98 GPa. These values are obtained applying the ELATE software [63] on our computed elastic constants. The difference in the Young’s modulus of both phases becomes gradually smaller when changing the direction from the ⟨001⟩ family towards the ⟨111⟩ family. Here, the difference is smallest with the Young’s modulus equal to 330 GPa in the case of the phase of cuboids and 290 GPa in the case of the Fe-Al matrix. The overall elasticity of the phase of cuboids is thus predicted to be stiffer than that of the phase of the matrix.
3.3. Nano-Scale Dynamical Mechanical Analysis of Fe-Al-Ti Phases
To complement the quantum-mechanical predictions, a nano-scale dynamical mechanical analysis (nanoDMA) was employed to determine elastic properties of both phases, see Figure 6. A characteristic surface pattern, shown in Figure 6, allows to distinguish two elastically different phases—one (brighter in Figure 6) surrounded by another darker one. The size of these features is very comparable with that of our TEM analysis, see Figure 2, which we assigned to cuboids within the matrix. The nanoDMA results suggest that the phase of cuboids is elastically stiffer than the matrix confirming our computed trends.
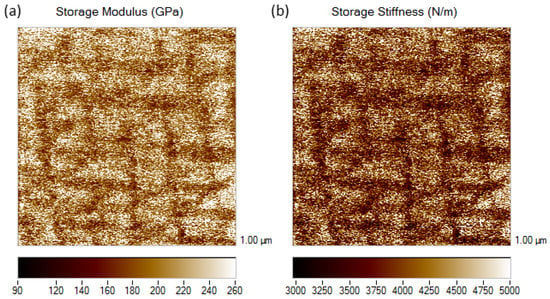
Figure 6.
Nano-scale elastic properties of the studied Fe-Al-Ti superalloy detected by Hysitron nanoDMA (nano-scale dynamical mechanical analysis) detector.
Based on the above analysis we can conclude that (i) the elasticity of the phase of cuboids is much more sensitive to the actual arrangement of atoms (i.e., the level of chemical order in the different sublattices, see Figure 3) while (ii) the elastic properties of the Fe-Al matrix are less sensitive (see Figure 5) and (iii) the variant of the phase of cuboids with the lowest formation energy is stiffer in most crystallographic directions than the phase of the matrix. These theoretical conclusions can be obtained directly from the results. However, interlinking them with the experimental nanoDMA results (see Figure 6) is less straightforward since the calculations are based on certain approximations. The calculations were performed for defect-free crystals with atoms in their equilibrium positions, i.e., corresponding to very low temperature (close to T = 0 K), while the nanoDMA measurements were performed at room temperature. Since the melting temperature of Fe-Al-Ti alloys is much higher than room temperature, the impact of temperature is probably not crucial.
The defect-free nature of the computed crystals is more serious. In experimental samples, due to cooling of the samples from the annealing temperature of 1000 °C down to room temperature, a microstructure with a complex internal structure of co-existing phases formed. The details of the structure of phases is known to depend sensitively on the thermo-mechanical sample history, see, e.g., Refs. [64,65,66,67]. Considering the equilibrium phase diagrams for different temperatures published in Refs. [16,18], it is likely that the single-phase A2-type Fe71Al22Ti7 solid solution partly orders upon cooling into the B2 phase (900–950 °C). It may then (below 800 °C) further decompose into a two-phase A2 + L21 composite material. Unfortunately, our experimental sample characterization techniques do not allow to determine the actual level of order in the two co-existing phases. Our quantum-mechanical calculations, which simulated different atomic arrangements with various levels of ordering in each of the constituting phase, were, in fact, performed to compensate (at least partly) for this lack of experimental data.
While the existence of differently ordered phases can be covered by our theoretical analysis discussed above, there is another issue related to internal phase transformations: they lead to the formation of anti-phase domains which crucially affect the mechanical properties. In order to estimate the impact of anti-phase domains and, in particular, anti-phase boundaries (APBs) separating them, on the elastic properties, we have determined the elasticity of an APB-containing phase of cuboids (see Figure 7a). The variant of the phase of cuboids with the lowest formation energy, see Figure 3c, was chosen because it has the most ordered sublattices and, therefore, it may be assumed that an impact of antiphase boundaries will be the most significant. As detailed information related to the atomic-scale structure of APBs in Fe-Al-Ti system is lacking, we simulate an APB by using the approach proposed by Marcinkowski and Brown [68] in the case of ordered Fe3Al with the D03 lattice. This choice is motivated by the fact that the D03 lattice is a binary variant of the ternary L21 lattice, i.e., it has nearly identical atomic configurations as that shown in Figure 3c except for the off-stoichiometry.
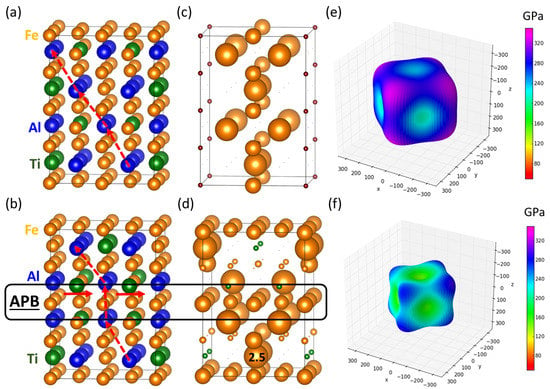
Figure 7.
Schematic visualization of the Fe-Al-Ti phase of cuboids modeled by a double 64-atom supercell without any anti-phase boundaries (a) and with an anti-phase boundary (APB) (b) together with the corresponding ab initio calculated local magnetic moments (c,d) and elastic properties (e,f) visualized in the form of a directional dependence of the Young’s modulus for both the APB-free and the APB-containing case, respectively. The magnitude of the local magnetic moments is visualized by the diameter of spheres representing the atoms (the scaling can be deduced from an example of one of the Fe atoms for which its local atomic magnetic moment of 2.5 μB is listed). The change of the overall magnetic moment is very significant: the APB-containing state (see part (b)) has the total magnetic moment higher by 140% than the APB-free one (see a similar effect in, e.g., Ref. [69]). Red dashed arrows in (a,b) indicate layering of Al atoms, which is altered due to the APB shift (full red arrow).
Further, regarding our choice of the type of APB, we are aware that this type may have a lower impact on the properties but we expect also a lower energy of the interface for this type of APB and thus a higher density of these defects (and, consequently, their higher importance). To model the APB, we double the supercell shown in Figure 3c along the [001] crystallographic direction so that the supercell contains 64 atoms (see Figure 7a). Then, we alter the layering of atoms in the upper half of this doubled supercell with respect to the lower part (see Figure 7b). Using this approach we find the minimum energy state by relaxing atomic positions, the volume as well as the shape of this supercell. The corresponding local atomic moments of atoms are visualized in Figure 7c,d for both the APB-free and the APB-containing case, respectively, and a significant impact of the studied APB on magnetism is seen. Having optimized the studied APB, we employ the stress-strain method to determine the elastic constants of the corresponding supercell (Figure 7b).
The calculated elastic properties of the APB-containing material are visualized in Figure 7f. We can compare this directional dependence of the Young’s modulus (Figure 7f) with that of the APB-free cuboid material, see Figure 3c—the elastic properties are visualized here again (see Figure 7e) without the 45° rotation and higher-symmetry mapping. It becomes clear that the simulated APB makes the phase of cuboids softer. In particular, the elastic constants of the APB-containing material, = 227 GPa, = 117 GPa and = 126 GPa, are lower than those obtained for the APB-free crystal ( = 303 GPa, = 135 GPa and = 136 GPa discussed above). The simulated APB in the phase of cuboids, as defects affecting the elastic properties, would thus make the elasticity of the phase of cuboids more similar to that of the Fe-Al phase of the matrix. Nevertheless, it should be stated that this softening is determined for our APB-containing supercell (Figure 7b) which has an unrealistically high density of APBs (two per supercell). Therefore, the above-discussed softening is predicted for an infinite stack of periodically repeated and ideally flat APBs of the simulated type. In reality, the density of APBs would very likely be lower and the structure and the type of APBs would be much more complex. Regarding the former aspects, i.e., the lower density of APBs, the impact of APBs in reality is assumed to be smaller than the calculated one.
As another microstructural feature which can significantly impact the properties, we consider the possibility of a finer sub-structure of individual cuboids, i.e., the other phases coherently co-existing inside the larger cuboids. This has been observed for ferritic Fe-Al-Cr-Ni-Ti alloys [70]. Again, our characterization techniques do not allow to test the existence of these phases. Considering the fact that cuboids contain Fe, Al and Ti as constituting elements and assuming that the finer phases would be binaries with close-to-equiatomic compositions (which are typically the same or thermodynamically close to the most stable compounds), we examined FeAl, FeTi and TiAl with the B2-structure. In particular, we have determined the lattice parameters of all these three binary phases and compared them with the lattice parameter of the variant of the phase of cuboids with the lowest formation energy (L21 parameter is equal to 2.866 Å). Our calculations show that the B2-TiAl and B2-FeTi have lattice parameters that are way too large to form coherent particles, 3.181 and 2.944 Å, respectively. In contrast, B2-FeAl matches nearly perfectly the cuboid matrix with a lattice parameter theoretically predicted to be 2.872 Å. Moreover, elemental iron with computed lattice parameter of 2.829 Å would also structurally match the cuboid matrix very well. It should be noted that the equilibrium higher-temperature Fe-Al-Ti phase diagrams do not contain any of the additional coherently-coexisting phases which we considered in our analysis. However, the studied phases can be off their equilibrium and, therefore, the sub-nanometer internal phases can exist due to a sluggish diffusion as frozen-in metastable phases (or even unstable ones stabilized by surrounding material).
4. Conclusions
We have combined theoretical and experimental techniques to study nano-scale elastic properties of Fe-Al-Ti superalloys with the composition Fe71Al22Ti7. After confirming a two-phase sub-micron superalloy nano-structure (cuboids of one phase coherently embedded into a matrix of another phase) by TEM, we have determined the chemical composition of both phases by EDS data as well as those from a previous thermodynamic assessment (see, e.g., Ref. [16]). The phase of cuboids is observed to be a strongly off-stoichiometric (Fe-rich and Ti-poor) Fe66.2Al23.3Ti10.5 variant of the Heusler Fe2TiAl intermetallic compound with the L21 structure. The phase of the matrix is a solid solution of Al atoms in a ferromagnetic body-centered cubic (bcc) Fe with composition Fe81Al19. Not having detailed information about the atomic distributions in the studied nano-phases from experiments, we have computed and compared properties of three different types of distributions of Al atoms in the phase of the matrix and three different distributions of atoms in the phase of cuboids employing the special quasi-random structure (SQS) concept. In particular, three different distributions of chemical species (A2, B2 and L21) were simulated for the phase of cuboids in order to determine the preference of the excess Fe atoms for the various sublattices. Our calculations predict the lowest formation energy (and so the highest termodynamic stability) for a solid solution of excess Fe atoms and Ti atoms at the Ti-sublattice within the Heusler L21 phase (the L21 phase). Similarly, the studied polymorphs of the phase of the matrix include a general randomly distributed variant (A2) as well as B2 and D03 cases when the 1st or the 1st and 2nd nearest-neighbor (NN) Al-Al pairs are eliminated (the B2 and D03 variants, respectively). In agreement with the reported repulsion of Al atoms and the experimental data for the Fe-Al binary system, the SQS without the 1st and 2nd NN Al-Al pairs (the D03 variant) turned out to have the lowest formation energy. It should be noted that our assessment of the thermodynamic stability of different atomic configurations was based only on the evaluation of formation energies of static lattices and partly also of the configurational entropy (an analysis of other effects/terms, such as those related to phonons or magnons, we suggest as a topic for future studies).
After computing complete tensors of elastic constants of all studied phases, we observe clear trends: First, an increasing order in the sublattices typically leads to a higher stiffness and a lower (higher) elastic anisotropy in the case of the cuboid (matrix) phase. Second, the cuboid L21 phase is found to be elastically stiffer than the phase of the matrix. Notably, the Young’s modulus of 220 GPa is more than twice higher than that of 98 GPa in the case of the ⟨001⟩ family of directions. On the other hand, the stiffness of both phases is nearly equal along the ⟨111⟩ family of directions.
To complement the ab initio calculations, a nano-scale dynamical mechanical analysis (nanoDMA) was used to determine elastic properties of both phases. The phase of cuboids was found elastically stiffer than the phase of the matrix. While the nanoDMA data qualitatively agree with the theoretical results, a direct quantitative comparison is difficult due to the structural complexity of the experimental samples (compositional variations, structural defects, anti-phase boundaries, nano-scale coherently co-existing phases, etc.). In order to qualitatively estimate the impact of structural defects, we have simulated an APB in the L21 phase of cuboids. The studied APB is shown to soften the phase of cuboids. A quantitative estimate would, however, require more information related to the APB-affected material. As another impact of APBs, we predict a significant increase of the magnetic moment.
Finally, considering the fact that anisotropic elastic properties of both the matrix and cuboids have a significant impact on the morphology of superalloy microstructure (see, e.g., Ref. [71]), which in turn is crucial for their high-temperature strength and creep resistance, we hope that our study will provide input values for these coarse-grained approaches (as in Ref. [71]) that can shed a new light on intricate structure-property relations in these materials.
Author Contributions
Conceptualization, M.F., V.B., Y.J.; Methodology, D.H., N.K. and J.F.; Validation, A.S., V.H., D.J. and I.M.; Thermodynamic Analysis, J.P.; Resources, M.F. and M.Š.; Writing—Original Draft Preparation, M.F., J.P., V.B., Y.J. and N.P.; Writing—Review & Editing, A.S., I.M., D.H., N.P., M.V., J.F., J.N. and M.Š.; Visualization, M.F., M.V., N.P., V.B., A.S. and I.M.; Supervision, M.Š., J.N. and M.F.; Project Administration, M.F.; Funding Acquisition, M.F.
Funding
The authors acknowledge the Czech Science Foundation for the financial support received under the Project No. 17-22139S (M.F., V.B., N.P., J.P., V.H., Y.J., A.S, I.M. and J.F.). Additional resources were provided by the Ministry of Education, Youth and Sports of the Czech Republic under the Project CEITEC 2020, LQ1601 (M.Š, M.V.). D.J. acknowledges financial support from the Slovak Research and Development Agency—Projects Nos. VEGA 2/0082/17 and APVV-15-0049.
Acknowledgments
M.F., A.S., I.M., M.V., Y.J., J.F., N.P. and M.Š. also acknowledge supports from the Academy of Sciences of the Czech Republic (Institutional Project No. RVO:68081723) and from the Ministry of Education, Youth and Sports of the Czech Republic via the research infrastructure IPMINFRA (Project. No. LM2015069). Computational resources were made available by the Ministry of Education, Youth and Sports of the Czech Republic under the Projects CESNET (Project No. LM2015042), CERIT-Scientific Cloud (Project No. LM2015085) and IT4Innovations National Supercomputer Center (Project No. LM2015070) within the program Projects of Large Research, Development and Innovations Infrastructures. Figure 1, the upper rows of Figure 3, Figure 4 and Figure 5 as well as parts (a,b) of Figure 7 were visualized using the VESTA [72]. The authors gratefully acknowledge discussions with Martin Palm and Frank Stein from the Max-Planck-Institut für Eisenforschung in Düsseldorf, Germany.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
As an example of our computational procedure related to elastic constants we consider the case of the L21 phase of cuboids (Figure 3c). The ab initio calculated elastic constants are
When rotating the coordinate system by 45° around the z-axis by the MELASA tool, we obtain:
Finally, after neglecting all values with absolute value smaller than 1 GPa, i.e., clearly smaller than our computational errors, and projecting the elastic constants onto a set of elastic constants possessing a cubic symmetry [56], we have the above-listed values = 303 GPa, = 135 GPa, = 136 GPa.
References
- Gorzel, A.; Palm, M.; Sauthoff, G. Constitution-based alloy selection for the screening of intermetallic Ti-Al-Fe alloys. Z. Metallkd. 1999, 90, 64–70. [Google Scholar]
- Palm, M. Concepts derived from phase diagram studies for the strengthening of Fe-Al-based alloys. Intermetallics 2005, 13, 1286–1295. [Google Scholar] [CrossRef]
- Brady, M.P.; Smialek, J.L.; Brindley, W.J. Oxidation-resistant Ti-Al-Fe alloy for diffusion barrier coatings. U.S. Patent No. 5,776,617, 7 July 1998. [Google Scholar]
- Dew-Hughes, D.; Kaufman, L. Ternary phase diagrams of the manganese-titanium-iron and the aluminum-titanium-iron systems: A comparison of computer calculations with experiment. Calphad 1979, 3, 175–203. [Google Scholar] [CrossRef]
- Raghavan, V. Al-Fe-Ti (aluminum-iron-titanium). J. Phase Equilib. 1993, 14, 617–618. [Google Scholar] [CrossRef]
- Raghavan, V. Al-Fe-Ti (Aluminum-Iron-Titanium). J. Phase Equilib. 2002, 23, 367–374. [Google Scholar] [CrossRef]
- Krein, R.; Palm, M.; Heilmaier, M. Characterization of microstructures, mechanical properties, and oxidation behavior of coherent A2+L21 Fe-Al-Ti. J. Mater. Res. 2009, 24, 3412–3421. [Google Scholar] [CrossRef]
- Capdevila, C.; Aranda, M.M.; Rementeria, R.; Chao, J.; Urones-Garrote, E.; Aldazabal, J.; Miller, M.K. Strengthening by intermetallic nanoprecipitation in Fe-Cr-Al-Ti alloy. Acta Mater. 2016, 107, 27–37. [Google Scholar] [CrossRef]
- Nakata, J.; Terada, Y.; Takizawa, S.; Ohkubo, K.; Mohri, T.; Suzuki, T. Thermal conductivity in X2YZ Heusler type intermetallic compounds. Mater. Trans. JIM 1996, 37, 442–447. [Google Scholar] [CrossRef]
- Kainuma, R.; Urushiyama, K.; Ishikawa, K.; Jia, C.; Ohnuma, I.; Ishida, K. Ordering and phase separation in bcc aluminides of the Ni-Fe-Al-Ti system. Mater. Sci. Eng. Struct. Mater. Prop. Microstruct. Process. 1997, 240, 235–244. [Google Scholar] [CrossRef]
- Fomina, K.A.; Marchenkov, V.V.; Shreder, E.I.; Weber, H.W. Electrical and optical properties of X2YZ (X = Co, Fe; Y = Cr, Mn, Ti; Z = Ga, Al, Si) Heusler alloys. Solid State Phenom. 2011, 168–169, 545–548. [Google Scholar] [CrossRef]
- Brzakalik, K. Nearest-neighbor configurations of Fe atoms in Fe3−xTixAl ordered alloys. Intermetallics 2008, 16, 1053–1060. [Google Scholar] [CrossRef]
- Suzuki, R.; Kyono, T. Thermoelectric properties of Fe2TiAl Heusler alloys. J. Alloys Compd. 2004, 377, 38–42. [Google Scholar] [CrossRef]
- Friák, M.; Deges, J.; Krein, R.; Frommeyer, G.; Neugebauer, J. Combined ab initio and experimental study of structural and elastic properties of Fe3Al-based ternaries. Intermetallics 2010, 18, 1310–1315. [Google Scholar] [CrossRef]
- Palm, M. Fe–Al materials for structural applications at high temperatures: Current research at MPIE. Int. J. Mater. Res. 2009, 100, 277–287. [Google Scholar] [CrossRef]
- Palm, M.; Lacaze, J. Assessment of the Al-Fe-Ti system. Intermetallics 2006, 14, 1291–1303. [Google Scholar] [CrossRef]
- Krein, R.; Friák, M.; Neugebauer, J.; Palm, M.; Heilmaier, M. L21-ordered Fe-Al-Ti alloys. Intermetallics 2010, 18, 1360–1364. [Google Scholar] [CrossRef]
- Palm, M.; Inden, G.; Thomas, N. The Fe-Al-Ti system. J. Phase Equilib. 1995, 16, 209–222. [Google Scholar] [CrossRef]
- Palm, M.; Sauthoff, G. Deformation behaviour and oxidation resistance of single-phase and two-phase L21-ordered Fe-Al-Ti alloys. Intermetallics 2004, 12, 1345–1359. [Google Scholar] [CrossRef]
- Michalcová, A.; Senčekova, L.; Rolink, G.; Weisheit, A.; Pešička, J.; Stobik, M.; Palm, M. Laser additive manufacturing of iron aluminides strengthened by ordering, borides or coherent Heusler phase. Mater. Des. 2017, 116, 481–494. [Google Scholar] [CrossRef]
- Jirásková, Y.; Pizúrová, N.; Titov, A.; Janickovic, D.; Friák, M. Phase separation in Fe-Ti-Al alloy—Structural, magnetic, and Mössbauer study. J. Magn. Magn. Mater. 2018, 468, 91–99. [Google Scholar] [CrossRef]
- Gilleßen, M.; Dronskowski, R. A combinatorial study of full Heusler alloys by first-principles computational methods. J. Comput. Chem. 2009, 30, 1290–1299. [Google Scholar] [CrossRef] [PubMed]
- Xian-Kun, L.; Cong, L.; Zhou, Z.; Xiao-Hua, L. First-principles investigation on the structural and elastic properties of cubic-Fe2TiAl under high pressures. Chin. Phys. B 2013, 22, 087102. [Google Scholar] [CrossRef]
- Shreder, E.; Streltsov, S.V.; Svyazhin, A.; Lukoyanov, A.; Anisimov, V. Electronic structure and physical properties of Fe2MAl (M = Ti, V, Cr) Heusler alloys. In Proceedings of the Third International Symposium on Magnetism, Moscow, Russia, 26–30 June 2005; p. 220. [Google Scholar]
- Shreder, E.; Streltsov, S.V.; Svyazhin, A.; Makhnev, A.; Marchenkov, V.V.; Lukoyanov, A.; Weber, H.W. Evolution of the electronic structure and physical properties of Fe(2)MeAl (Me = Ti, V, Cr) Heusler alloys. J. Phys. Condens. Matter 2008, 20, 045212. [Google Scholar] [CrossRef]
- Adebambo, P.O.; Adetunji, B.I.; Olowofela, J.A.; Oguntuase, J.A.; Adebayo, G.A. Prediction of metallic and half-metallic structure and elastic properties of Fe2Ti1−xMnxAl Heusler alloys. Phys. B Condens. Matter 2016, 485, 103–109. [Google Scholar] [CrossRef]
- Kourov, N.I.; Marchenkov, V.V.; Belozerova, K.A.; Weber, H.W. Specific features of the electrical resistivity of half-metallic ferromagnets Fe2MeAl (Me = Ti, V, Cr, Mn, Fe, Ni). J. Exp. Theor. Phys. 2014, 118, 426–431. [Google Scholar] [CrossRef]
- Slebarski, A.; Goraus, J.; Deniszczyk, J.; Skoczen, L. Electronic structure, magnetic properties and electrical resistivity of the Fe2V1−xTixAl Heusler alloys: Experiment and calculation. J. Phys. Condens. Matter 2006, 18, 10319–10334. [Google Scholar] [CrossRef]
- Buschow, K.H.J.; van Engen, P.G. Magnetic and magneto-optical properties of Heusler alloys based on aluminum and gallium. J. Magn. Magn. Mat. 1981, 25, 90–96. [Google Scholar] [CrossRef]
- Friák, M.; Slávik, A.; Miháliková, I.; Holec, D.; Všianská, M.; Šob, M.; Palm, M.; Neugebauer, J. Origin of the low magnetic moment in Fe2TiAl: An ab initio study. Materials 2018, 11, 1732. [Google Scholar] [CrossRef]
- Stein, F.; Palm, M. Re-determination of transition temperatures in the Fe–Al system by differential thermal analysis. Int. J. Mater. Res. 2007, 98, 580–588. [Google Scholar] [CrossRef]
- Amara, H.; Fu, C.C.; Soisson, F.; Maugis, P. Aluminum and vacancies in α-iron: Dissolution, diffusion, and clustering. Phys. Rev. B 2010, 81, 174101. [Google Scholar] [CrossRef]
- Liu, S.; Duan, S.; Ma, B. First-principles calculation of vibrational entropy for Fe-Al compounds. Phys. Rev. B 1998, 58, 9705–9709. [Google Scholar]
- Kulikov, N.I.; Postnikov, A.V.; Borstel, G.; Braun, J. Onset of magnetism in B2 transition-metal aluminides. Phys. Rev. B 1999, 59, 6824–6833. [Google Scholar] [CrossRef]
- Friák, M.; Neugebauer, J. Ab initio study of the anomalous volume-composition dependence in Fe-Al alloys. Intermetallics 2010, 18, 1316–1321. [Google Scholar] [CrossRef]
- Fähnle, M.; Drautz, R.; Lechermann, F.; Singer, R.; Diaz-Ortiz, A.; Dosch, H. Thermodynamic properties from ab-initio calculations: New theoretical developments, and applications to various materials systems. Phys. Status Solidi B Basic Solid State Phys. 2005, 242, 1159–1173. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 1980, 58, 1200. [Google Scholar] [CrossRef]
- Zlotnikov, I.; Zolotoyabko, E.; Fratzl, P. Nano-scale modulus mapping of biological composite materials: Theory and practice. Prog. Mater. Sci. 2017, 87, 292–320. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Zunger, A.; Wei, S.; Ferreira, L.; Bernard, J. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Oganov, A.R.; Lyakhov, A.O.; Valle, M. How evolutionary crystal structure prediction works and why. Acc. Chem. Res. 2011, 44, 227–237. [Google Scholar] [CrossRef]
- Friák, M.; Counts, W.; Ma, D.; Sander, B.; Holec, D.; Raabe, D.; Neugebauer, J. Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties. Materials 2012, 5, 1853–1872. [Google Scholar] [CrossRef]
- Zhu, L.-F.; Friák, M.; Lymperakis, L.; Titrian, H.; Aydin, U.; Janus, A.M.; Fabritius, H.-O.; Ziegler, A.; Nikolov, S.; Hemzalová, P.; et al. Ab initio study of single-crystalline and polycrystalline elastic properties of Mg-substituted calcite crystals. J. Mech. Behav. Biomed. Mat. 2013, 20, 296–304. [Google Scholar] [CrossRef]
- Miracle, D.; Senkov, O. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Hillert, M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Zhou, L.; Holec, D.; Mayrhofer, P.H. First-principles study of elastic properties of cubic Cr1−xAlxN alloys. J. Appl. Phys. 2013, 113, 043511. [Google Scholar] [CrossRef]
- Moakher, M.; Norris, A.N. The closest elastic tensor of arbitrary symmetry to an elasticity tensor of lower symmetry. J. Elast. 2006, 85, 215–263. [Google Scholar] [CrossRef]
- Tasnádi, F.; Abrikosov, I.A.; Rogström, L.; Almer, J.; Johansson, M.P.; Oden, M. Significant elastic anisotropy in Ti1−xAlxN alloys. Appl. Phys. Lett. 2010, 97, 3524502. [Google Scholar] [CrossRef]
- Tasnádi, F.; Odén, M.; Abrikosov, I.A. Ab initio elastic tensor of cubic Ti0.5Al0.5N alloys: Dependence of elastic constants on size and shape of the supercell model and their convergence. Phys. Rev. B 2012, 85, 144112. [Google Scholar] [CrossRef]
- Von Pezold, J.; Dick, A.; Friák, M.; Neugebauer, J. Generation and performance of special quasirandom structures for studying the elastic properties of random alloys: Application to Al-Ti. Phys. Rev. B 2010, 81, 094203. [Google Scholar] [CrossRef]
- Holec, D.; Tasnádi, F.; Wagner, P.; Friák, M.; Neugebauer, J.; Mayrhofer, P.H.; Keckes, J. Macroscopic elastic properties of textured ZrN-AlN polycrystalline aggregates: From ab initio calculations to grainscale interactions. Phys. Rev. B 2014, 90, 184106. [Google Scholar] [CrossRef]
- Šesták, P.; Friák, M.; Holec, D.; Všianská, M.; Šob, M. Strength and brittleness of interfaces in Fe-Al superalloy nanocomposites under multiaxial loading: An ab initio and atomistic study. Nanomaterials 2018, 8, 873. [Google Scholar] [CrossRef]
- Leamy, H.; Gibson, E.; Kayser, F. Elastic stiffness coefficients of iron-aluminum alloys. i. experimental results and thermodynamic analysis. Acta Metal. 1967, 15, 1827. [Google Scholar] [CrossRef]
- Gaillac, R.; Pullumbi, P.; Coudert, F.X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef]
- Mendiratta, M.; Ehlers, S.; Lipsitt, H. D03-B2-α phase-relations in Fe-Al-Ti alloys. Metal. Trans. A Phys. Metal. Mater. Sci. 1987, 18, 509–518. [Google Scholar] [CrossRef]
- Su, C.W.; Chao, C.G.; Liu, T.F. Formation of (B2+D03)phases at a/2⟨100⟩ anti-phase boundary in an Fe-23 at.%Al-8.5 at.%Ti alloy. Scr. Mater. 2007, 57, 917–920. [Google Scholar] [CrossRef]
- Su, C.W.; Jeng, S.C.; Chao, C.G.; Liu, T.F. Orientation relationship between C14 precipitate and (A2+D03) matrix in an Fe-20at.%Al-8at.%Ti alloy. Scr. Mater. 2007, 57, 125–128. [Google Scholar] [CrossRef]
- Su, C.W.; Chao, C.G.; Liu, T.F. Formation of (B2+D0(3)) two-phase microstructure in a Fe-23Al-7Ti alloy. Mater. Trans. 2007, 48, 2993–2996. [Google Scholar] [CrossRef]
- Marcinkowski, M.J.; Brown, N. Direct observation of antiphase boundaries in the Fe3Al superlattice. J. Appl. Phys. 1962, 33, 537–552. [Google Scholar] [CrossRef]
- Murakami, Y.; Niitsu, K.; Tanigaki, T.; Kainuma, R.; Park, H.S.; Shindo, D. Magnetization amplified by structural disorder within nanometre-scale interface region. Nat. Commun. 2014, 5, 4133. [Google Scholar] [CrossRef]
- Liebscher, C.H.; Radmilovic, V.R.; Dahmen, U.; Vo, N.Q.; Dunand, D.C.; Asta, M.; Ghosh, G. A hierarchical microstructure due to chemical ordering in the bcc lattice: Early stages of formation in a ferritic Fe-Al-Cr-Ni-Ti alloy. Acta Mater. 2015, 92, 220–232. [Google Scholar] [CrossRef]
- Fratzl, P.; Penrose, O.; Lebowitz, J.L. Modeling of phase separation in alloys with coherent elastic misfit. J. Stat. Phys. 1999, 95, 1429. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).