Abstract
Crystal structures of simple metals and binary alloy phases based on the face-centered cubic (fcc) structure are analyzed within the model of Fermi sphere–Brillouin zone interactions to understand the stability of the original cubic structure and derivative structures with distortions, superlattices and vacancies. Examination of the Brillouin–Jones configuration in relation to the nearly-free electron Fermi sphere for several representative phases reveals significance of the electron energy contribution to the phase stability. Representation of complex structures in the reciprocal space clarifies their relationship to the basic cubic cell.
1. Introduction
Crystal structures of metals have three principal lattices: face-centered cubic (fcc), close-packed hexagonal (hcp) and body-centered cubic (bcc) with high symmetry and a close packing atomic arrangement. The prevalence of these structures is determined by high symmetry and high coordination numbers with the resulting high values of the Madelung constant and low electrostatic term of the crystal energy, called Ewald energy, EEwald. Another significant crystal energy term is the band structure energy, EBS, defined by ion–electron interactions for a given structure.
Intermetallic compounds are mostly based on these types of structures with deformations, superlattices and vacancies, caused by differences in atomic sizes and electronegativities of components. One of the key factors for phase stability is “electron concentration”—a number of valence electrons per atom [1,2,3]. Crystal energy is reduced due to the level of the valence electron energy (Fermi level) approaching the Brillouin zone plane and causing a formation of an energy gap.
The binary alloy system Cu–Zn represents a classical example of Hume–Rothery phases that include the key metallic close-packed structures: fcc, hcp and bcc. The sequence of the phases as a function of the average number of valence electrons per atom fcc → bcc → complex γ-phase → hcp is defined by the following values of the valence electron concentration 1.35 → 1.5 → 1.62 → 1.75 (electron/atom). Similar phase sequences have been observed in many other binary alloy systems containing a noble metal from the group IB and a neighboring element from groups IIB–VB. The Cu–Zn alloy system is a relatively simple system with only five intermediate phases that exhibit quite simple structures with the ground high-symmetry metallic phases like fcc, bcc and hcp. Along with these basic metallic structures, there are phases Cu5Zn8-cI52 and CuZn3-hP3 that are related to bcc through superlattices, distortions and vacancies. In our previous papers, we have considered metallic phases based on the bcc and hcp structures [4,5].
Recently, we have considered intermediate phases in the Au–Cd alloy system that is isoelectronic to the Cu–Zn alloy system [6]. The Au–Cd phase diagram is more complicated containing about 12 intermediate phases that are related to the basic high-symmetry structures as well as the structurally complex phases defined by Hume–Rothery rules. Formation of the larger number of the structures with many-faced BZ polyhedrons in the Au–Cd phases comparing to the Cu–Zn phases is stimulated by the higher atomic numbers and higher difference in atomic numbers of constituent elements.
In the present work, we analyze necessary conditions for stability of the fcc structure and consider derivative complex structures. The subjects of analysis are the sp metals and binary alloys for which it is possible to assign a definite number of valence electrons.
2. Theoretical Background and Method of Analysis
Formation of binary compounds at a certain alloy composition is defined by some important factors such as the difference in atomic sizes, electronegativity, etc. Beyond these factors, formation of metallic structures is defined by effects of the Fermi sphere–Brillouin zone (FS–BZ) interaction. The Hume–Rothery mechanism has been identified to play a role in the stability of structurally complex alloy phases, quasicrystals and their approximants [7,8,9,10,11]. The Jones model can be used to account for the phase stability in tetrahedral cluster structures, icosahedral and trigonal-prismatic clusters as building blocks. Formation of the complex structures of elemental metals under pressure can also be related to the Hume–Rothery mechanism [12,13,14,15,16,17].
The band structure contribution to the crystal structure energy can be estimated by analyzing configurations of Brillouin–Jones zone planes in the nearly free-electron model. A special program BRIZ has been developed [18] to construct FS–BZ configurations and to estimate some parameters such as the Fermi sphere radius (kF), values of reciprocal wave vectors of BZ planes (qhkl) and volumes of BZ and FS. The BZ planes are selected to match the condition qhkl ≈ 2kF that have a significant structure factor. In this case, an energy gap is opened on the BZ plane leading to the lowering of the electron band energy. The ratio of ½qhkl to kF is usually less than 1 and equals ~0.95; it is called a “truncation” factor. In the FS–BZ presentations by the BRIZ program, the BZ planes cross the FS, whereas in the real system, the Fermi sphere is deformed and accommodated inside BZ. The “truncation” factor has a characteristic value of ~0.95 and corresponds to a decrease in the electron energy on the BZ plane.
The crystal structure of a phase chosen for the analysis by the BRIZ program is characterized by the lattice parameters and the number of atoms in the unit cell, which define the average atomic volume (Vat). The valence electron concentration (z) is the average number of valence electrons per atom that gives the value of the Fermi sphere radius kF = (3π2z/Vat)1/3. Further structure characterization parameters are the number of BZ planes that are in contact with the FS, the degree of “truncation” factor and the value of BZ filling by electronic states, defined as a ratio of the volumes of FS and BZ.
Presentations of the FS–BZ configurations are given with the orthogonal axes with the following directions in the common view: a* is looking forward, b*—to the right and c*—upward. For the hexagonal lattice in the reciprocal space, a* = a1h*cos30°, b = a2h* and c* = ch*. Structural data for binary phases considered in this paper have been found in the Pauling File [19] and in recent papers cited in the corresponding sections of this paper.
3. Results and Discussion
In this work, we selected two groups of fcc based phases: elemental simple sp metals (Table 1) and binary alloy phases (Table 2). Diffraction patterns and constructed Brillouin–Jones zones for these structures are presented in Figure 1 and Figure 2, respectively. Crystal structure description and element groups in the Periodic table are given following Pearson [20].

Table 1.
Structure parameters of several metal phases with the fcc and fcc-based structures. Fermi sphere radius kF, ratios of kF to distances of Brillouin zone planes ½qhkl and the filling degree of Brillouin zones (BZ) by electron states VFS/VBZ are calculated using the program BRIZ [18].

Table 2.
Structure parameters of several binary fcc-based phases from the literature data. Fermi sphere radius kF, ratios of kF to distances of Brillouin zone planes ½qhkl and the filling degree of Brillouin zones by electron states VFS/VBZ are calculated using the program BRIZ [18].
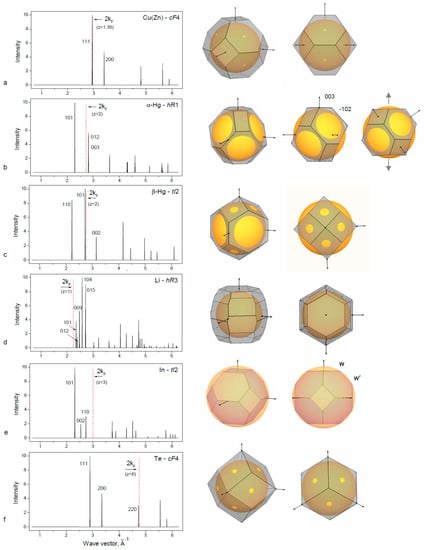
Figure 1.
Calculated diffraction patterns for selected phases from Table 1 (left panel) and corresponding Brillouin–Jones (BZ) zones with the Fermi spheres (FS) (right panel). The position of 2kF and the hkl indices of the planes used for the BZ construction are indicated on the diffraction patterns. Constructions of BZ–FS are given in common projection (first column) and in special projection (second column) (see text).
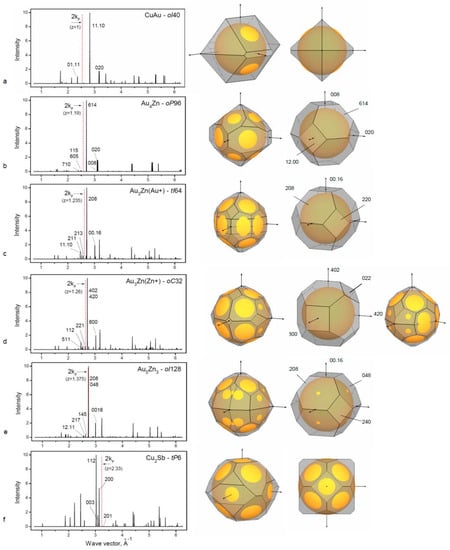
Figure 2.
Calculated diffraction patterns for selected phases from Table 2 (left panel) and corresponding Brillouin–Jones zones with the inscribed Fermi spheres (right panel). The position of 2kF and the hkl indices of the planes used for the BZ construction (first column) are indicated on the diffraction patterns. Constructions of BZ planes corresponding to the strong reflections (second column) show structural relationship to the basic cells (see text). For BZ of oC32 (d, third column) the projection is given along b* to show relation to oP128 (e). (See text for description of (a–f) sub-figures).
3.1. Simple sp Elements with the fcc-Based Structures
The fcc structure is one of the fundamental structures for metals along with hcp and bcc structures. These three atomic arrangements are characterized by high symmetry and close packing of atoms. It is interesting to consider chemical and physical factors that lead to the formation of complex and distorted phases—derivatives from these structures. Previously, we have considered simple metal structures based on bcc and hcp [4,5] demonstrating the valence electron concentration as a defining factor of structural stability.
3.1.1. fcc in the Simple sp Elements
The group IB elements Cu, Ag and Au crystallize in the fcc structure and do not change by variation of temperature or pressure, adhering to their name: “noble” metals. It should be noted that only for Au was the fcc–hcp transition experimentally observed above 250 GPa [22].
The group IA elements Li and others adopt at ambient pressure the bcc structure and transform to fcc with the pressure increase [23]. The difference in the ambient pressure structure for univalent elements from IA and IB group can be explained by the balance of the electrostatic (Madelung) and the valence electron (band structure) terms in the crystal structure energy. Alkali IA elements adopt bcc predominantly due to the electrostatic energy because the Madelung constant is higher for bcc structure than for fcc or hcp. Under pressure, the band structure term increases leading to the formation of fcc for alkali metals.
The group IB elements follow the transition metals in the periodic table, and they have a filled d-electron band. Therefore, there is some screening of EEwald and gaining of EBS. The common view of the Fermi surface for Cu, Ag and Au is a sphere with necks extending to the Brillouin planes of the (111) type.
The fcc structure remains stable for elements IB in the solid solution with the neighboring elements IIB and others. The limit of solubility is defined by the Hume–Rothery rule: at the valence electron concentration ~1.36, there is a contact of the Fermi sphere and the Brillouin Zone and the loss of stability for fcc. This case is shown for the Cu(Zn) alloy in Figure 1a.
3.1.2. Distorted fcc Structures of the IIB Element Hg
The light group IIB elements Zn and Cd crystallize in the hcp structures with the elongated c/a ratio analyzed in [5]. The heavy IIB element Hg adopts distortive fcc structures: hR1 for α-Hg and tI2 for β-Hg (Table 1). The rhombohedral α-Hg structure is closely related to fcc, as can be seen in Figure 1b from the construction of Brillouin zones for Hg-hR1 and for the hypothetical fcc with the same volume. BZ planes of the (111) type for fcc are divided into two sets of hR1 of (101) and (003) types in such a way that the latter is placed outside FS at the same distance as (012) planes, which are the former (200)-fcc planes. Rhombohedral distortion degree is defined by the condition q003 = q012 resulting in c/a = 1.936 for the rhombohedral cell in the hexagonal setting. This value is much lower than the ideal c/a = 2.45 for fcc. Hg-hR1 is obtained from fcc through contraction along one of the [111] axes as shown on Figure 2b (right panel). Rhombohedral cell of the Hg-hR1 structure has α = 70.52° in comparison to 60° of the fcc. At low temperature and high pressure, the β-Hg phase is stable.
The β-Hg structure can be described as a strong compression of fcc along the c-axis to c/a ~0.5. Standard description of β-Hg is as a body-centered tetragonal structure, bct, with c/a ~0.707 (close to ). For this structure, (101) planes are in contact with the FS as shown in Figure 2c. The coordination number for Hg-bct is close to N = 10.
The alloying of Hg with Sn under pressure was studied in [24]. The solubility of Sn in α-Hg was found to increase under pressure up to ~10 at. % Sn. The qualitative estimation from the condition kF ~ ½q012 gives the value z ~ 2.17, which corresponds to ~8–9 at. % of a tetravalent metal and to ~17 at. % of a trivalent metal. The latter case is realized in the Hg–In system, where the α-Hg(In) solution has been experimentally observed to extend to ~19 at. % In. Stability of the α-Hg(Sn) phase was observed to 30 GPa.
For pure Hg, transformation α–β occurs under pressure of ~3.4 GPa at room temperature with further transitions at 12 GPa to monoclinic structure (γ) and at 37 GPa to the close-packed hexagonal (hcp) structure [25,26]. Theoretical calculation [27] has shown that the fcc structure is extremely close to β-and γ-Hg. It should be noted that, for IIB elements, Zn, Cd and Hg, the common hcp phase exists under high pressure. The β-Hg phase is stabilized at ambient pressure in the Hg–Cd alloys at 4 to 70 at. % Cd [19]. This occurrence may be accounted for by the chemical pressure because the atomic volume of Cd is less than that for Hg (21.6 and 23.2 Å3, respectively).
3.1.3. Rhombohedral Distortions of fcc in Group IA Element Li
Rhombohedral structure of α-Hg-hR1 type occurs in alkali element Li under pressure above 39 GPa after the transition fcc → hR1 [28]. Lattice parameter of Li-hR1 at 39.8 GPa are a = 2.4023 Å, c = 5.516 Å, c/a = 2.296 for the hexagonal cell and the rhombohedral angle is 62.87°. The degree of rhombohedral distortion of fcc is less than for α-Hg. With this deformation, one set of the (111) planes of BZ for fcc is placed closer to the FS corresponding to z = 1, and there is some gain for the band structure energy term at the fcc → hR1 transition.
Another rhombohedral structure is known for Li and Na at low temperature at ambient pressure below 77 K and 25 K, respectively. This structure, usually defined as 9R or Sm-type, is close-packed structure with the sequence of hexagonal layers ABABCBCACA in contrast to the ABAB sequence for hcp and ABCABC for fcc. The physical source for energetic stability of the 9R phase was analyzed by Ashcroft using a Hume–Rothery argument [29]. The Brillouin–Jones zone of the 9R phase contains 26 planes that are close to the FS so that the overall electronic energy is reduced (see Table 1 and Figure 1d). The BZ for Li-hR3 is filled by electronic states up to 0.59 that is slightly more than 0.5 for Li-bcc.
3.1.4. Distortion of fcc in Group IIIB Elements
The lightest trivalent element Al has fcc structure and is found to be stable with the variation of temperature and pressure. This indicates the importance of the electrostatic (Madelung) contribution into the crystal energy for this light element. Recently at very high pressure of 217 GPa, the transformation fcc → hcp was observed for Al. For the heaviest IIIB metal thallium, the valence electron contribution is significant and the resulting ambient pressure structure is hcp. Under pressure 3.7 GPa, Tl transforms to fcc [30] and remains fcc up to 125 GPa [31].
The intermediate group IIIB metal In crystallizes at ambient pressure in a tetragonal structure that is a slight distortion of fcc with an elongation of c-axis to c/a = 1.076. Standard description of In structure is the body centered tetragonal, bct or tI2, as given in Table 1.
Physical reasons of the distorted In structure were considered within the model of Fermi sphere–Brillouin zone interactions [32]. The BZ polyhedron of fcc is deformed due to the attraction to the FS, in particular at the one set of corners of W′ type. Dependence of fcc distortion is defined by the valence electron concentration and the ideal fcc is realized when the Fermi sphere contacts the BZ at the corners of W type: this case occurs for z = 2.94 electron/atom and is realized in the In alloys with Cd or Hg at about ~6 at. %. The structural distortion of fcc in In increases with the addition of 4-valent metals Sn or Pb up to 12–15 at. %. At higher electron concentration, there is a phase transition to the fct with c/a < 1. The origin of existence of these two types of fct with c/a > 1 and c/a < 1 is related to different FS–BZ configurations where the FS is touched by the corners of BZ of W′ or W type, as discussed in [13,32].
Similar tetragonal phase is formed in Ga—the lighter neighbor of In in IIIB group—under high pressure above 14 GPa with c/a ~ 1.12 (for fct). The Ga-fct phase has graduate transition to fcc, observed near 70 GPa [23,33]. Thus, for group III elements, the most abundant structure under compression is fcc or slightly distorted fcc structure.
3.1.5. High Pressure fcc Phase in Polyvalent sp Elements
The group VIB elements contain six sp electrons, and their metallic phases obtained under pressure should be considered with respect not only to the first Brillouin zone but taking into account the planes of the larger Brillouin zones. An interesting case of the fcc structure was found recently for the group VIB element Te [34]. At normal pressure, Te is non-metallic and its structure consists of a spiral chain (trigonal hR1), which transforms under pressure to some complex structures including an incommensurately modulated structure [23] with metallic properties. Above 27 GPa, Te adopts the bcc structure. Above 100 GPa, it transforms to fcc with a superlattice and above 200 GPa to the fcc structure [34]. Consideration of Te-fcc phase with z = 6 shows the satisfaction with the FS–BZ interaction model (Table 1, Figure 1f). The FS contact with the BZ planes of the (220) type occurs for z = 5.92, and, with z = 6, there is a slight overlap with the FS near the ½q220, which is usual for the Hume–Rothery phases.
Iodine an element from group VIIB—and a neighbor to TE—is a typical diatomic molecular solid under ambient conditions. Transition to the metallic state has been found for Iodine above 16 GPa and several phases have been identified on the way from molecular to monatomic states including incommensurately modulated structure [35]. At pressures above 55 GPa, Iodine was found to crystallize in the fcc structure [36], which is stable to at least 273 GPa [37].
Appearance and stability of the fcc structure in the elements of groups VIB and VIIB at high pressures is supported by the model of the FS–BZ interaction with consideration of the extended Brillouin–Jones zones for polyvalent metals. In particular, for z = 6 and z = 7, the energetic gain is obtained due to the accommodation of the FS electrons into the BZ formed by (220) planes.
It should be noted that, for group IVB elements, the fcc appears only in the heaviest element Pb at normal pressure and transforms under compression to hcp and then to bcc. For group VB elements, the common high pressure phase is bcc (see reviews [13,23]).
3.2. Binary Alloy Phases with the fcc Based Structures
For the binary alloys, important factors of the phase formation are atomic size ratio and electronegativity. For our consideration, we select group IB elements with the neighboring group elements with the minimal differences of these two factors that are, however, sufficient for site-ordered phase formation. In all cases, it should be noted that the decisive factor for the structural stability is also the Hume–Rothery mechanism as is demonstrated for several representatives of binary phases (Table 2, Figure 2).
3.2.1. Long-Period Superlattice in the CuAu Alloy
Cu and Au are both univalent group IB metals with the atomic size difference ~12%. The CuAu alloy forms the tetragonally distorted fcc lattice where alternate (00h) planes contain either Cu or Au atoms and cause a contraction in c direction. Resulting tetragonal face-centered structure has c/a ratio of 0.92 [19]. In the temperature range ~380 °C to 410 °C, the superlattice CuAuII is formed which consist of CuAu-bct unit cells with the antiphase domains along the b-direction. There is a lattice shift of ½(a+c) at each five unit-cell length [38,39]. The superlattice CuAu II is described as orthorhombic cell with 10 cells along one of a direction, oI40.
The stabilization of long-period superlattices in CuAu and other alloys has been understood by considering that the Fermi surface touches the newly formed superlattice Brillouin zone boundaries {110} that are adjusted due to the formation of an extra period. Figure 2a is showing the touching of the Fermi sphere to the planes (01.11). The degree of overlapping (½qhkl)/kF for ideal FS is usually ~0.95 as was considered by Sato and Toth [38] and is called a “truncation” factor. In our paper, we use the reciprocal value to characterize the FS–BZ interaction in all considered cases.
3.2.2. Binary Alloy Au–Zn Phases Based on the fcc Structure
The Cu(Zn) fcc solid solution (considered above in the Section 3.1.1) exists up to the electron concentration z = 1.36 without any ordered phases at low temperatures. For alloys with Au(Zn), the fcc structure exists at high temperature (403–683 °C) within the same region of the electron concentration (up to 33% Zn). However, a number of ordered phases with long-period superlattices were found at low temperature [19]. Single crystal studies of 19, 23.5 and 26 at. % Zn by X-ray diffraction [40,41] allow structure characterization of these phases. We consider possible mechanism of structural stability due to formation of additional Brillouin zone plane causing lattice modulations (Table 2, Figure 2b–e).
For the Au4Zn-oP96 structure, the superlattice cell is related to the basic fcc cell (with af parameter) with a model: a = 6af, b = af and c = 4af [32]. Atomic positions are varied corresponding to the lattice modulation. In Figure 2b, the new BZ boundaries of the (115) and (710) types are shown crossing the FS, whereas for the basic BZ (shown right), there is no contact with FS. The phase stabilization is considered to be due to the formation of the new BZ planes in contact with the FS, which is reducing the crystal energy.
Au3+Zn-tI64 phase is related to fcc in the following way: , . Atomic shifts produce extra diffraction reflections [42], resulting in the BZ boundaries enveloping the FS (Figure 2c).
Au3Zu+-oC34 phase occurs through a phase transition from fcc in a similar way with b and c ~ and a = 4af (standardized data are used). FS–BZ construction is given in Figure 2d showing relation of two Au3Zn phases with slight difference in composition.
Au5Zn3-oI128 phase has also a relation to fcc and occurs at the alloy concentration boundary for the fcc stability. Cell parameters are produced from fcc cell in the following way: , and c = 8af, resulting in 32 fcc cells with 128 atoms (Figure 2e). Thus, in the Au – Zn alloy system in the composition range up to ~40 at. % Zn, there are several complex phases that are superlattices based on fcc. Formation of these superstructures is related to the Hume–Rothery mechanism.
3.2.3. Defect Structures Based on fcc
In this section, we consider another way of the structure adjustment to the Hume–Rothery rules via formation of defect structures with vacancies. For γ-brass in Cu–Ga and β-(NiAl), it was found that with increasing the average number of valence electrons z, these structures can be stabilized by skipping atoms out of the unit cell. Thus, for stability of the phase, it is fundamental to keep the constant number of electrons per unit cell zN (N is the atom number in the unit cell). In the Cu–Ga alloy systems, the γ-brass exists in the wide range of compositions 30–43 at. % Ga, and the number of atoms in the unit cell was found to decreased from 52 to 47 atoms [43].
A special case of defect superstructure is vacancies at certain atomic positions in the cell. The structure Cu2Sb-tP6 is related to the tetragonal distortion of the fcc with the double cell along the c-axis and with the absence of Cu atoms in the middle of c. The resulting number of atoms in the cell is N = 6 and the constructed FS–BZ configuration satisfies the Hume–Rothery mechanism (Figure 2f). Similar tI6 structure is found in Cu2As.
It is remarkable that the Cu2Sb-tP6 type structure is formed in the Cu–Te alloy at the composition of 41.7 at. % Te [19]. Because Te is an element from the next group (VIB) after the group of Sb (V B), there are more vacancies of Cu atoms for basic Cu positions 2c and 2a with occupation 0.7, which gives the resulting number of atoms N = 4.8 in the unit cell instead of N = 6 for Cu2Sb. This is the response of the crystal structure to FS–BZ interactions for the phase Cu1.4Te.
Another example of defect supercell formation based on bcc is CuGa2-tP3 with two bcc cells along the c-axis and with missing Cu atoms in the middle of c. This is a way to adjust structure to the number of valence electrons in the cell.
3.3. Miscibility Gap of Two fcc Phases in the Al–Zn Alloys
For polyvalent metals, the volume of the valence electrons, defined by the volume of the Fermi sphere, is always larger than the volume of the BZ. Therefore, the Fermi surface cuts many zone planes, and contributions to the crystal energy from regions near the plane intersections may lead to important effects for phase stability [44].
An interesting case of the fcc phase decomposition is observed in the Al–Zn alloy system, where Al(Zn) fcc solid solution is stable at high temperatures, and, below 352 °C, there is a miscibility gap of two fcc phases with 16.5 and 59 at. % Zn. The atomic radii of Al and Zn are very close (1.43 Å and 1.37 Å, respectively) and electronegativities are nearly equal (1.61 and 1.65), so there must be some other factor that defines the decomposition [20]. In this case, it is the electronic structure factor (see Figure 3). Theoretical consideration of the electronic topology in the fcc Al–Zn alloys has been performed in [45].
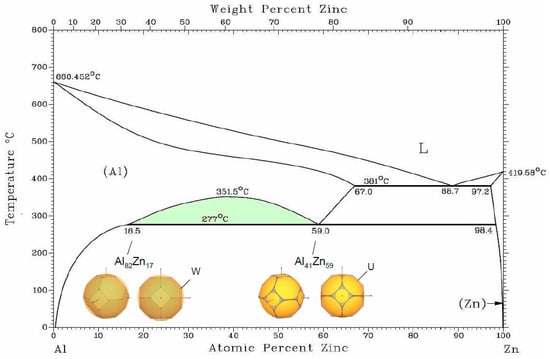
Figure 3.
The phase diagram Al–Zn [19]. The Al(Zn) solid solution region with the fcc structure contains a miscibility gap with two-phase region (colored). The boundary phases with 17 and 59 at. % Zn constructions of FS–BZ are given with a common view and a view along a* (see text).
We consider coexistence of two fcc Al(Zn) phases with the configuration of FS and BZ. It was discussed for In-fcc phase that the important factor for the structure stability is BZ accommodation within the Fermi sphere. The contact of FS with W-type corners occurs for z = 2.94, which corresponds to addition of ~7% Zn, and, due to the “truncation” factor, can be extended to z = 2.83, which corresponds to ~17 at. %Zn as observed in one of the fcc Al-Zn phase. Another factor for gaining in energy for fcc is a contact to the edges of (111) planes in the points K and U of BZ that occurs at z = 2.5 for ~50 at. % Zn. This results in the “truncation” factor 1.036—very acceptable for the Hume–Rothery conditions. It should be noted that the region of miscibility gap of the two Al(Zn) fcc extends under pressure along the temperature [46] in accordance with the common trend that an energy gap increases under pressure.
4. Conclusions
The phase sequence in the Cu–Zn alloy system consists of simple high-symmetry metallic structures fcc, bcc and hcp (α, β and ε) with an addition of two phases (γ-cI52 and δ-hP3) that are derivatives of the bcc structure. Phases α, β and ε are completely site-disordered because Cu and Zn, the constituent elements of the alloy, are close neighbors in the periodic table and have minimal differences in the atomic size and electronegativity. In the Au–Zn alloy system in the composition range up to ~40 at. % Zn, there are several complex phases that are superlattices based on fcc. Formation of these superstructures is related to the Hume–Rothery mechanism. Additional complexity of the Au–Zn alloys in comparison to the Cu–Zn alloys is related to the larger difference in atomic numbers of the alloy components that provides relatively strong diffraction peaks for site-ordered compounds. Remarkable example is a long-period superlattice of the CuAu with the size of domains defined by formation of superstructure reflections in contact to the Fermi sphere [38].
In the pure simple sp elements, the fcc phase is stable in group IB metals (Cu, Ag, Au) and their solid solutions up to ~1.35 electron/atom. In this case, the FS is inside the first BZ and touched the (111) planes. For the group IIIB element In, the fcc structure shows a tetragonal distortion that can be understood through the BZ deformation: FS accommodates the BZ by touching one type of the W corners. Similar tetragonal face-centered structure is observed for compressed Ga. The contact of the FS with the special points of BZ such as W-type corners or the edges of (111) planes of BZ in the points K and U can lead to a miscibility gap between two fcc phases as in the case of Al–Zn alloys.
In conclusion of this discussion, it should be noted that the fcc phase appears under pressure for group IA (alkali metals) and is followed by complex structures that show a decrease in coordination number and packing density (for Li and Na after cI16, for Rb and Cs after oC52 and oC84, respectively) [13,23]. The reason for this unexpected structural complexity in alkali elements under strong compression can be understood if one accepts the change in the valence electron number due to the overlap of the valence band and upper core electron levels [14,15]. Thus, the application of the FS–BZ interaction model allows us to estimate the effective number of valence electrons in the case of a change of the valence electron state, and also for complex spd valence states.
Acknowledgments
The authors gratefully acknowledge Olga Degtyareva for her valuable discussion and comments. This work is supported by the Program “The Matter under High Pressure” of the Russian Academy of Sciences.
Author Contributions
Valentina Degtyareva conceived the project and wrote the paper; Nataliya Afonikova analyzed the results, prepared figures and tables.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hume-Rothery, W. Researches on the nature, properties, and condition of formation of intermetallic compounds. J. Inst. Met. 1926, 35, 319–335. [Google Scholar]
- Mott, N.F.; Jones, H. The Theory of the Properties of Metals and Alloys; Oxford University Press: London, UK, 1936. [Google Scholar]
- Jones, H. The Theory of Brillouin Zones and Electron States in Crystals; North Holland Publ.: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Degtyareva, V.F.; Afonikova, N.S. Simple metal binary phases based on the body centered cubic structure: Electronic origin of distortions and superlattices. J. Phys. Chem. Solids 2013, 74, 18–24. [Google Scholar] [CrossRef]
- Degtyareva, V.F.; Afonikova, N.S. Simple metal and binary alloy phases based on the hcp structure: Electronic origin of distortions and superlattices. Solid State Sci. 2014, 37, 47–54. [Google Scholar] [CrossRef]
- Degtyareva, V.F.; Afonikova, N.S. Complex structures in the Au-Cd alloy system: Hume–Rothery mechanism as origin. Solid State Sci. 2015, 49, 61–67. [Google Scholar] [CrossRef]
- Lee, S.; Henderson, R.; Kaminsky, C.; Nelson, Z.; Nguyen, J.; Settje, N.F.; Schmidt, J.T.; Feng, J. Pseudo-fivefold diffraction symmetries in tetrahedral packing. Chem. Eur. J. 2013, 19, 10244–10270. [Google Scholar] [CrossRef] [PubMed]
- Mizutani, U. Hume–Rothery Rules for Structurally Complex Alloy Phases; Taylor& Francis: London, UK, 2010. [Google Scholar]
- Berger, R.F.; Walters, P.L.; Lee, S.; Hoffmann, R. Connecting the chemical and physical viewpoints of what determines structure: From 1-D chains to gamma-brasses. Chem. Rev. 2011, 111, 4522–4545. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Leighton, C.; Bates, F.S. Sphericity and symmetry breaking in the formation of Frank–Kasper phases from one component materials. Proc. Natl. Acad. Sci. USA 2014, 111, 17723–17731. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Hoffmann, N.W. Ashcroft, Double-diamond NaAl via pressure: Understanding structure through Jones zone activation. J. Chem. Phys. 2010, 132, 114106. [Google Scholar] [CrossRef] [PubMed]
- Degtyareva, V.F. Brillouin zone concept and crystal structures of sp metals under high pressure. High Press Res. 2003, 23, 253–257. [Google Scholar] [CrossRef]
- Degtyareva, V.F. Simple metals at high pressures: The Fermi sphere–Brillouin zone interaction model. Physics-Uspekhi 2006, 49, 369–388. [Google Scholar] [CrossRef]
- Degtyareva, V.F.; Degtyareva, O. Structure stability in the simple element sodium under pressure. New J. Phys. 2009, 11, 063037. [Google Scholar] [CrossRef]
- Degtyareva, V.F. Potassium under pressure: Electronic origin of complex structures. Solid State Sci. 2014, 36, 62–72. [Google Scholar] [CrossRef]
- Degtyareva, V.F. Structural simplicity and complexity of compressed calcium: Electronic origin. Acta Crystallogr. B 2014, 70, 423–428. [Google Scholar] [CrossRef] [PubMed]
- Degtyareva, V.F. Electronic Origin of the Orthorhombic Cmca Structure in Compressed Elements and Binary Alloys. Crystals 2013, 3, 419–430. [Google Scholar] [CrossRef]
- Degtyareva, V.F.; Smirnova, I.S. BRIZ: A visualization program for Brillouin zone–Fermi sphere configuration. Z. Kristallogr. 2007, 222, 718–721. [Google Scholar] [CrossRef]
- Villars, P.; Cenzual, K. (Eds.) Pauling File Binaries Edition; ASM International: Metal Park, OH, USA, 2002.
- Pearson, W.B. The Crystal Chemistry and Physics of Metals and Alloys; Wileyl: New York, NY, USA, 1972. [Google Scholar]
- Pearson, W.B. A Handbook of Lattice Spacings and Structures of Metals; Pergamon Press: New York, NY, USA, 1967; Volume 2. [Google Scholar]
- Dubrovinsky, L.; Dubrovinskaia, N.; Crichton, W.A.; Mikhaylushkin, A.S.; Simak, S.I.; Abrikosov, I.A.; de Almeida, J.S.; Ahuja, R.; Luo, W.; Johansson, B. Noblest of All Metals Is Structurally Unstable at High Pressure. Phys. Rev. Lett. 2007, 98, 045503. [Google Scholar] [CrossRef] [PubMed]
- McMahon, M.I.; Nelmes, R.J. High-pressure structures and phase transformations in elemental metals. Chem. Soc. Rev. 2006, 35, 943–963. [Google Scholar] [CrossRef] [PubMed]
- Degtyareva, V.F.; Bdikin, I.K.; Porsch, F.; Novokhatskaya, N.I. The stability of the rhombohedral α-Hg phase alloyed with Sn under high pressure up to 30 GPa. J. Phys. Condens. Matter 2003, 15, 7489–7500. [Google Scholar] [CrossRef]
- Takemura, K.; Fujihisa, H.; Nakamoto, Y.; Nakano, S.; Ohishi, Y. Crystal Structure of the High-Pressure Phase of Mercury: A Novel Monoclinic Distortion of the Close-Packed Structure. J. Phys. Soc. Jpn. 2007, 76, 023601. [Google Scholar] [CrossRef]
- Takemura, K.; Nakano, S.; Ohishi, Y.; Nakamotoand, Y.; Fujihisa, H. High-pressure structural study of solid mercury up to 200GPa. Mater. Res. Express 2015, 2, 016502. [Google Scholar] [CrossRef]
- Biering, S.; Schwerdtfeger, P. High-pressure transitions in bulk mercury: A density functional study. Theor. Chem. Acc. 2011, 130, 455–462. [Google Scholar] [CrossRef]
- Hanfland, M.; Syassen, K.; Christensen, N.E.; Novikov, D.L. New high-pressure phases of lithium. Nature 2000, 408, 174–178. [Google Scholar] [PubMed]
- Ashcroft, N.W. Quantum-solid behavior and the electronic structure of the light alkali metals. Phys. Rev. B 1989, 39, 10552–10559. [Google Scholar] [CrossRef]
- Schulte, O.; Nikolaenko, A.; Holzapfel, W.B. Pressure-Volume Relations For Zn, Cd, Ga, In and Tl at Room Temperature To 30 GPa and Above. High Press. Res. 1991, 6, 169–182. [Google Scholar] [CrossRef]
- Cazorla, C.; MacLeod, S.G.; Errandonea, D.; Munro, K.A.; McMahon, M.I.; Popescu, C. Thallium under extreme compression. J. Phys. Condens. Matter 2016, 28, 445401. [Google Scholar] [CrossRef] [PubMed]
- Degtyareva, O.; Degtyareva, V.F.; Porsch, F.; Holzapfel, W.B. Face-centred cubic to tetragonal transitions in In alloys under high pressure. J. Phys. Condens. Matter 2001, 13, 7295–7303. [Google Scholar] [CrossRef]
- Degtyareva, O.; McMahon, M.I.; Allan, D.R.; Nelmes, R.J. Structural Complexity in Gallium under High Pressure: Relation to Alkali Elements. Phys. Rev. Lett. 2004, 93, 205502. [Google Scholar] [CrossRef] [PubMed]
- Sugimoto, T.; Akahama, Y.; Ichikawa, T.; Fujihisa, H.; Hirao, N.; Ohishi, Y. Bcc-fcc structure transition of Te. J. Phy. Conf. Ser. 2014, 500, 192018. [Google Scholar] [CrossRef]
- Takemura, K.; Sato, K.; Fujihisa, H.; Onoda, M. Modulated structure of solid iodine during its molecular dissociation under high pressure. Nature 2003, 423, 971–974. [Google Scholar]
- Fujii, Y.; Hase, K.; Hamaya, N.; Ohishi, Y.; Onodera, A.; Shimomura, O.; Takemura, K. Pressure-induced face-centered-cubic phase of monatomic metallic iodine. Phys. Rev. Lett. 1987, 58, 796–799. [Google Scholar] [CrossRef] [PubMed]
- Reichlin, R.; McMahan, A.; Ross, M.; Martin, S.; Hu, J.; Hemley, R.; Mao, H.; Wu, Y. Optical, X-ray, and band-structure studies of iodine at pressures of several megabars. Phys. Rev. B 1994, 49, 3725–3731. [Google Scholar] [CrossRef]
- Sato, H.; Toth, R.S. Fermi surface of Alloys. Phys. Rev. Lett. 1962, 8, 239–241. [Google Scholar] [CrossRef]
- Sato, H.; Toth, R.S. Long-Period Superlattices in Alloys. II. Phys. Rev. 1962, 127, 469–484. [Google Scholar] [CrossRef]
- Iwasaki, H.; Hirabayashi, M.; Fujiwara, K.; Watanabe, D.; Ogawa, S. Study on the Ordered Phases with Long Period in the Gold-Zinc Alloy System I. Survey of Crystal Structures and Calorimetric Measurement. J. Phys. Soc. Jpn. 1960, 15, 1771–1783. [Google Scholar] [CrossRef]
- Terasaki, O. Study of the Incommensurate Two-Dimensional Antiphase Structure of Au3+Zn by High Voltage, High Resolution Electron Microscopy. J. Phys. Soc. Jpn. 1982, 51, 2159–2167. [Google Scholar] [CrossRef]
- Iwasaki, H. Study on the Ordered Phases with Long Period in the Gold-Zinc Alloy System II. Structure Analysis of Au3Zn[R1], Au3Zn[R2] and Au3+Zn. J. Phys. Soc. Jpn. 1962, 17, 1620–1633. [Google Scholar] [CrossRef]
- Betterton, J.O.; Hume Rothery, W. The Equilibrium diagram of the system copper—Gallium in the region 30–100 at. % gallium. J. Inst. Met. 1952, 80, 459–468. [Google Scholar]
- Heine, V.; Weaire, D. Pseudopotential Theory of Cohesion and Structure. Solid State Phys. 1970, 24, 249–463. [Google Scholar]
- Smirnova, E.A.; Korzhavyi, P.A.; Vekilov, Y.K.; Johansson, B.; Abrikosov, I.A. Electronic topological transitions and phase stability in the fcc Al-Zn alloys. Eur. Phys. J. B 2002, 30, 57–66. [Google Scholar] [CrossRef]
- Fujinaga, Y.; Tasaku, S. The aluminum-zinc phase diagram under high pressure. J. Alloys Compd. 1994, 209, 311–317. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).