Abstract
In this contribution, we present the first crystal structure of iron(III) salicylate without additional counterions. The octahedral complex contains two salicylate and two water molecules as ligands. One salicylate is mono-anionic while the other is di-anionic. Because of the centrosymmetry of the complex, the acidic hydrogen atom is disordered on the midpoint between two salicylate oxygens. The structure determination of the tiny crystal indicates the presence of reticular twinning. The structure solution of the twin is shown and an explanation based on the crystal packing is provided.
1. Introduction
Iron salicylates [1] and catecholates [2] play an important role in the study of non-heme iron enzymes. In these biological systems, the oxidation state of iron can be easily changed, which makes them catalytically interesting. In pharmaceutical sciences, salicylic acid has been proposed as a chelator for iron [3]. Another important application of the salicylate ligand is in analytical chemistry. Fe(III) salicylate is a colored complex that can be used for spectrophotometry [4,5]. Spectrophotometric procedures have also been used to establish the stability constants of Fe(III) salicylates [6]. Alternatively, the stability constants can be determined using potentiometric titrations [7,8,9,10]. In the course of such experiments, different complex structures and compositions have been proposed, but, to our knowledge, none of them have been characterized by a crystal structure analysis. We therefore set out to crystallize Fe(III) salicylate and succeeded using the gel crystallization technique. The starting salt was Fe(II) nitrate which slowly oxidized during the reaction with salicylic acid.
2. Results and Discussion
2.1. Intramolecular Interactions
Compound 1 (Scheme 1) crystallizes in the monoclinic space group with the Fe atom on an exact, crystallographic inversion center (Wyckoff position c). It is hexacoordinated by oxygen atoms originating from two salicylato and two aquo ligands, respectively. The geometry of the FeO polyhedron is octahedral with only a very slight deviation from perfect symmetry. This deviation can be expressed by a quadratic elongation of 1.003 and an angular variance of 1.42 deg [11]. Considering the complete complex, we find an approximate symmetry with an r.m.s. deviation of 0.0276 Å [12]. In the octahedron, the equatorial plane is formed by two symmetry equivalent salicylato ligands that coordinate as chelate in bidentate fashion. The salicylate molecule is essentially planar with a maximum torsion angle of 2.7(7) in the six-membered chelate ring. The axial positions of the octahedron are occupied by water molecules. The plane of the water molecule forms an angle of 30 with the water-Fe bond. This is halfway between a trigonal and a tetrahedral coordination mode. A molecular plot of the structure is shown in Figure 1.
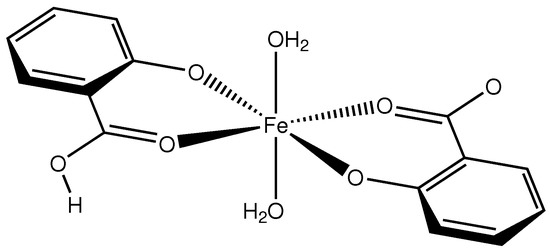
Scheme 1.
Molecular structure of compound 1.
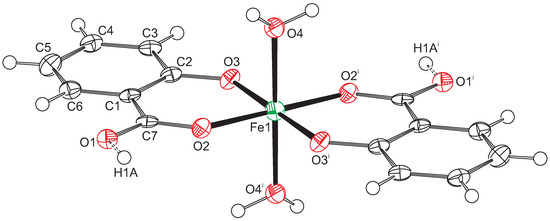
Figure 1.
Displacement ellipsoid plot of compound 1. Ellipsoids are drawn at the 50% probability level. Hydrogen atoms are drawn as small spheres with arbitrary radii. Atoms Fe1 and H1A are located on special positions. Consequently, only half of the O1 atoms are protonated. Symmetry code i: .
The Fe-O distances to the salicylate ligand are 1.925(6) and 1.973(6) Å and to the water molecule 2.092(6) Å. A comparison of these values with the literature [13,14] indicates that the iron must be in oxidation state +3. Bond–valence calculations [15] result in a bond–valence sum of 3.206 [16], confirming this oxidation state. With an oxidation state +3 for the iron, one of the two salicylate ligands must be protonated for charge balance. From steric considerations, protonation should take place at O1, which is the only oxygen not coordinated to the iron. Inspection of the intermolecular contacts indeed shows a short distance of 2.476(8) Å that can only be explained by the presence of a hydrogen bond (symmetry code ). We therefore introduced a hydrogen atom on the midpoint between O1 and O1, which is a special position (Wyckoff position d). With both Fe1 and H1A on special positions, the charge balance is achieved for a Fe(III) complex with the formula . With this description, the O1-H1A distance becomes rather long (1.24 Å). More likely is an alternative explanation such as a double-well hydrogen bond. Such double-well potentials preferably occur in very strong and stabilized hydrogen bonds [17,18]. A difference Fourier map at the position of H1A gives some indication for a double-well situation (Figure 2), but, due to the weak diffraction of the crystal and the twinned reflection data, this is not a full proof. For convenience, we left the hydrogen atom unrefined on the special position.
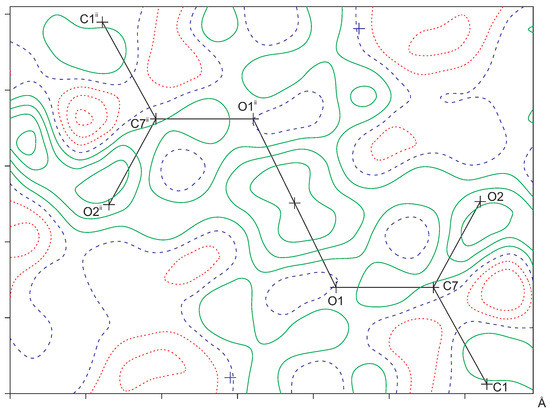
Figure 2.
Difference Fourier map in the C7-O1-O1 plane as calculated with the PLATON software [16]. The observed structure factors were de-twinned with SHELXL (instruction LIST 8) [19]. Hydrogen atom H1A was omitted in the calculation of . Contour level 0.1 e/Å. Positive contours are drawn in green, negative contours in red, and the zero contour in blue. Symmetry code : .
Salicylic acid (2-hydroxybenzoic acid, ) is a di-basic acid with values of 2.853(9) and 12.897(7) [20,21]. Metal complexes of the mono-anionic ligand are well known from the literature. For recent examples of transition metal complexes, see [22,23,24,25]. In the majority of cases, the hydroxyl group is protonated and the carboxylate group deprotonated. The carboxylate group can then act as monodentate, bidentate or bridging moiety. In total, 339 metal complexes of this kind are known in the Cambridge Structural Database [26]. It is very rare that the carboxylate group is protonated and the hydroxyl group deprotonated (Scheme 2). Coordination mode (I) is found in a Cu complex [27] and mode (II) in Ag compounds [28]. Coordination mode (III) of the present study has been first described for a MoO complex [29] and more recently in a Cu complex [30]. In total, five crystal structures with coordination mode (III) are known in the Cambridge Structural Database (update November 2016) [26] with determined atomic coordinates. Interestingly, all five complexes show a non-symmetric pattern with both and in the coordination environment. In all five structures, the metal complex is located on a general position with symmetry. Compound 1 of the present study also has both and in the coordination environment, but, as a consequence of the crystallographic symmetry, the ligands are non-distinguishable. While the Cu complex [30] is also described with a symmetric O–H⋯O hydrogen bond, compound 1 of the present study is the first molecule with the metal center and H1A on special positions.
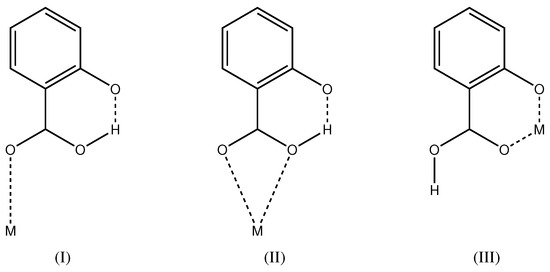
Scheme 2.
Coordination modes of mono-anionic where the carboxyl group is protonated and the hydroxyl group deprotonated.
From the statistical analysis of the crystal structures with the ligand, it is clear that the carboxylate group is much more easily deprotonated (339 cases) than the hydroxyl group (seven cases in modes I, II and III). Why do the structures with deprotonated hydroxyl group exist at all? The answer might be in the very strong intermolecular hydrogen bond in the crystal [31]. Indeed, the hydrogen bonded distance in compound 1 is very short (2.476(8) Å). This is generally the case in the structures with deprotonated hydroxyl group. This intermolecular effect might thus be the reason for the increased thermodynamic stability.
2.2. Intermolecular Interactions
The molecules of compound 1 are connected by hydrogen bonds with the protonated carboxylate group and the coordinated water molecules as hydrogen bond donors. The non-coordinated carboxylate oxygen O1 and the deprotonated hydroxyl group act as acceptors (Table 1). This hydrogen bonding pattern results in a two-dimensional network parallel to the -plane (Figure 3). No strong intermolecular interactions could be detected in c-direction, which leaves as the only possibility weak dispersive effects in this direction.

Table 1.
Hydrogen bonding interactions in compound 1. Symmetry codes i: : : .
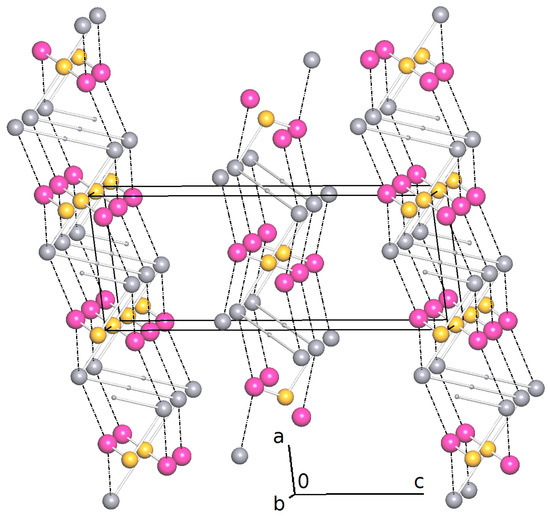
Figure 3.
Simplified net calculated with ToposPro [32]. Large gray spheres represent the nodes of , pink spheres HO and yellow spheres Fe. The O-H hydrogen atoms on special positions are drawn as small gray spheres. Coordinative Fe-O bonds are drawn as sticks and hydrogen bonds are drawn as dashed lines.
2.3. Reticular Twinning
The reflection data can be indexed with a C-centered orthorhombic symmetry (a = 7.24 Å, b = 74.79 Å, c = 4.85 Å). Concerning the X-ray intensities, the merging R values for this symmetry are reasonably low. Investigation of the systematic absences indicates space group , but there is an additional pseudo B-centering present. A closer inspection of the reflection data shows that this pseudo B-centering is caused by the presence of additional (non space group compatible) systematic absences: in the layers of , only reflections with are present. The structure solution in space group failed.
Because systematic absences incompatible with space group symmetry are a clear warning sign for twinning [33], we decided to select a primitive subgroup with monoclinic symmetry and a = 7.34 Å, b = 4.85 Å, c = 37.57 Å, (Scheme 3). Based on the metric orthorhombic symmetry, a twofold rotation about the a-axis was chosen as a potential twin operation. Systematic absences indicated space group . However, also in this setting, there are absences incompatible with the space group: in the layers of all reflections with l = odd are absent (Figure 4). Structure solution as a twin in space group was successful (see Experimental Section). There are two independent molecules in the asymmetric unit that are both located on general positions with symmetry.
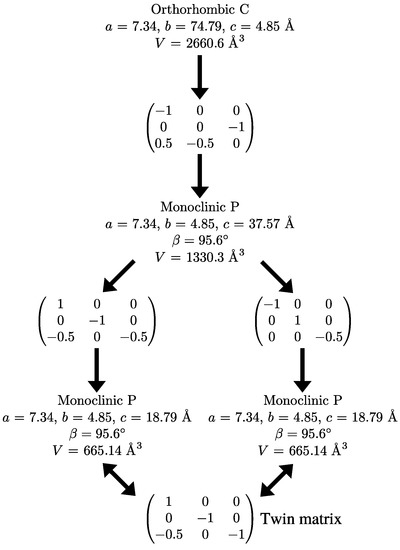
Scheme 3.
Supercell decomposition.
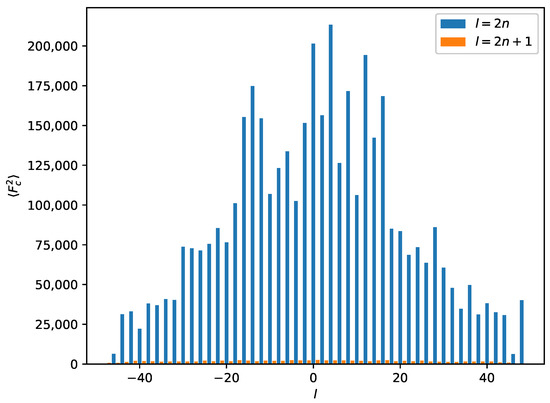
Figure 4.
Average for a perfect twin in the supercell for reflections with . The l-index is shown on the x-axis. Reflections with are absent (small orange bars). Systematic absences for a combination of and are incompatible with the space group.
Importing the structure into the PLATON routine ADDSYM [16] finds additional translational symmetry in c direction. Halving the c-axis results in the true unit cell (a = 7.34 Å, b = 4.85 Å, c = 18.79 Å and ) with space group . The relation between the supercell and the subcell can be seen in Figure 5, which also shows the stacking of the hydrogen bonded planes. Stacking faults in c-direction result in the twinned structure of the current analysis. This alternative stacking is shown in Figure 6. The stacking with true translational symmetry (Figure 5) as well as the alternative stacking with twinned symmetry (Figure 6) show no conflicting short contacts between the layers. We assume that both arrangements are energetically similar. The overlapping twin boundary is depicted in Figure 7 and shows an additional, approximate symmetry operation (, , ), which is a combination of the n-glide plane of the space group and the twin rotation about a. Twin generation by stacking faults have previously been discussed by Dornberger-Schiff in the context of the OD theory [34].
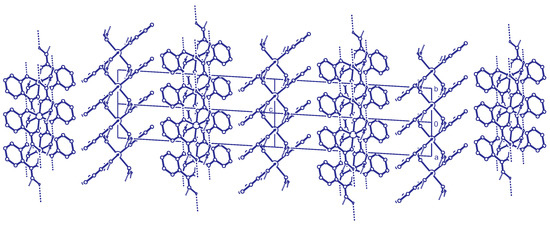
Figure 5.
Stacking of the hydrogen bonded layers. Projection along the direction. Two unit cells of the structure are shown. This doubled cell corresponds to the supercell described in the text. C-H hydrogen atoms are omitted for clarity.
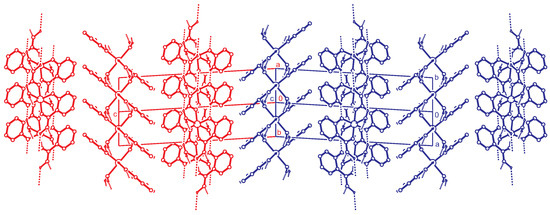
Figure 6.
Alternative stacking of the hydrogen bonded layers. Projection along the direction. The red and blue unit cells ( setting) are related by the twin operation about .C-H hydrogen atoms are omitted for clarity.
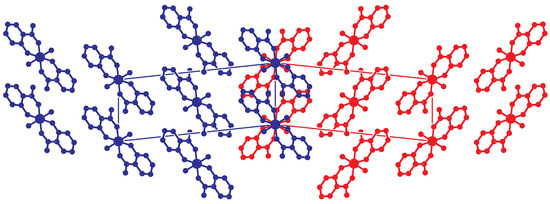
Figure 7.
View on the twinned structure along the direction ( setting). The second unit cell is generated by the twin operation about a. At the twin boundary, both components are drawn. The blue molecules are related to the red molecules by an approximate operation , , . This operation is not part of the space group but is obtained by a combination of the n-glide and the twin operation (rotation) about a: . Hydrogen atoms are omitted for clarity.
Figure 8 and Figure 9 show the direct and reciprocal lattice for this reticular twin. Figure 9 clearly shows that the twinning is the reason for space group incompatible absences. With the knowledge of the true unit cell size and true twin relation, it is possible to freely refine the cell parameters. Based on the non-overlapping reflections of the first twin component, this results in a = 7.3392(11) Å, b = 4.8493(6) Å, c = 18.794(3) Å and . With these values, the twin obliquity is as calculated with PLATON using the LEPAGE-twin algorithm [35].
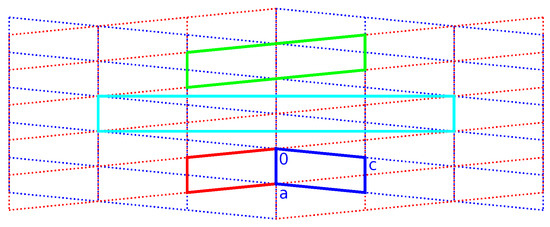
Figure 8.
Direct lattice of the unit cell as described in Table 2, viewed in the plane. Blue and red indicate the individual unit cells ( setting). Green and cyan, respectively, indicate monoclinic-P and orthorhombic-C twin supercells. The blue and red lattices are derived from the monoclinic superlattice (see Scheme 3).
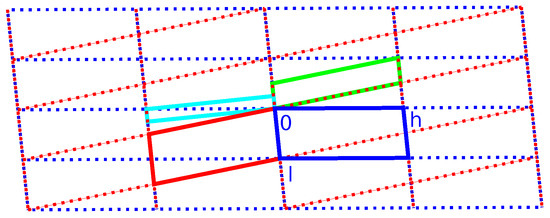
Figure 9.
Reciprocal lattice of the unit cell as described in Table 2, viewed in the plane. Blue and red indicate the individual unit cells ( setting). Green and cyan respectively indicate monoclinic-P and orthorhombic-C twin supercells. The blue and red lattices are derived from the monoclinic superlattice (see Scheme 3).
3. Materials and Methods
3.1. Synthesis and Crystallization
For the crystallization of the title compound, we used the gel technique of Arend and Connelly [36]. In addition, 6.26 g of FeSO·7HO was dissolved in 40.5 mL HO, which resulted in an orange solution. The solution was filtered, leaving a green-blue filtrate. Furthermore, 4.5 mL of tetramethoxysilane was added to the solution under stirring. Stirring was continued for fifteen minutes. The mixture was poured into a test tube and left to solidify for four days. The top layer had turned yellow and was subsequently removed. In addition, 0.9 g of sodium salicylate was dissolved in 10 mL of HO (pH ≈ 5.5). The solution was brought onto the gel. After five days, microcrystalline material had formed at the surface of the gel. One crystal (25 × 25 × 125 μm3) was selected for the single crystal diffraction experiment.
3.2. X-ray Crystal Structure Determination
X-ray intensities were measured on a Bruker Proteum diffractometer (Bruker AXS GmbH, Karlsruhe, Germany) with a rotating anode generator, Helios optics, and PLATINUM-135 CCD detector. A total of 1633 images was collected with a detector distance of 60 mm, a rotation increment of 0.5/frame, an exposure time of 120 s/frame, and a generator setting of 45 kV/60 mA. First attempts to index the reflections with the DIRAX software [37] suggested an orthorhombic C-centered unit cell (see Section 2.3). A single orientation matrix is sufficient to integrate all reflections. Space group determination and structure solution using this symmetry failed.
Therefore, the intensity integration was repeated using the monoclinic subgroup with a P lattice (c = 37.57 Å). Again, only one orientation matrix was used for the integration. A twin matrix of (−1 0 0/0 −1 0/1 0 1) was included for the structure solution with the program SHELXD [38] in space group . With this matrix, all reflections are overlapping (pseudo-merohedral twin). This gave a suitable starting model that could be completed by difference Fourier maps in the SHELXL software [19] based on the same twin matrix and space group.
The ADDSYM routine of the PLATON software [16] found additional translation symmetry resulting in a subcell with space group (c = 18.79 Å). This prompted us to re-integrate the reflection data in this subcell with two orientation matrices using the Eval15 software [39]. The two orientation matrices can be related by a twofold rotation about which corresponds to the matrix (1 0 0/0 −1 0/−0.5 0 −1) (Scheme 3). By a twofold rotation about the monoclinic b-axis, this is equivalent with a twofold twin rotation about in reciprocal space and the twin matrix (−1 0 0/0 −1 0/0.5 0 1). The latter relation was used for the intensity integration. Scaling, absorption correction and merging of symmetry equivalent reflections were performed with Twinabs [40]. Because of the tiny size, the crystal did not diffract further than Å. This cut-off is based on the merging R-value in the outer resolution shell. The non-overlapping reflections of the major twin component and the overlapping reflections of both twin components were stored in HKLF5 format [41] for the structure refinement.
Non-hydrogen atoms were refined freely with anisotropic displacement parameters. The rather low resolution of the data leads to a quite poor data/parameter ratio of 6.7. Consequently, all displacement parameters were restrained using the RIGU instruction [42]. C-H hydrogen atoms were introduced in calculated positions and refined with a riding model. The O-H hydrogen atom was located on position and kept fixed during the refinement. Further experimental details are given in Table 2.

Table 2.
Measurement details.
CCDC 1587792 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.
4. Conclusions
The octahedral complex molecules of are connected by intermolecular hydrogen bonds to form layers in the -plane. Stacking faults in the c-direction lead to the reticular, pseudo-orthorhombic twinning. The twin matrix was obtained by decomposition of the C-centered orthorhombic twin cell as (1 0 0/0 −1 0/−0.5 0 −1). This corresponds to a twofold rotation about the monoclinic a-axis. Two orientation matrices were used for the determination of the X-ray intensities. In every second layer in h-direction, the reflections of both twin domains fully overlap, while in the odd layers the reflections are separated. This situation is characteristic for reticular twinning. Taking this twinning situation into account, the chemistry of the complex can be consistently explained. The oxidation state of the Fe was determined as +3, and the O-H hydrogen atom is on the intermolecular midpoint between two carboxylate oxygens.
Acknowledgments
The X-ray diffractometer has been financed by the Netherlands Organisation for Scientific Research (NWO).
Author Contributions
Jitschaq Anne van der Horn and Martin Lutz designed and performed the synthesis, diffraction experiment and crystal structure determination. Bernd Souvignier contributed to the discussion of the reticular twinning. Jitschaq Anne van der Horn and Martin Lutz wrote the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| OD | Order–disorder |
| r.m.s. | root mean square |
| Salicylate di-anion () | |
| Salicylate mono-anion () | |
| Salicylic acid () |
References
- Roy, S.; Kästner, J. Synergistic Substrate and Oxygen Activation in Salicylate Dioxygenase Revealed by QM/MM Simulations. Angew. Chem. Int. Ed. 2015, 55, 1168–1172. [Google Scholar] [CrossRef] [PubMed]
- Bruijnincx, P.C.A.; Lutz, M.; Spek, A.L.; Hagen, W.R.; Weckhuysen, B.M.; van Koten, G.; Gebbink, R.J.M.K. Modeling the 2-His-1-Carboxylate Facial Triad: Ironcatecholato Complexes as Structural and Functional Models of the Extradiol Cleaving Dioxygenases. J. Am. Chem. Soc. 2007, 129, 2275–2286. [Google Scholar] [CrossRef] [PubMed]
- Hider, R.C.; Zhou, T. The Design of Orally Active Iron Chelators. Ann. N. Y. Acad. Sci. 2005, 1054, 141–154. [Google Scholar] [CrossRef] [PubMed]
- Reid, K.R.; Meyerhoff, M.E.; Mitchell-Koch, J.T. Salicylate Detection by Complexation with Iron(III) and Optical Absorbance Spectroscopy. An Undergraduate Quantitative Analysis Experiment. J. Chem. Educ. 2008, 85, 1658–1659. [Google Scholar] [CrossRef]
- Pozdnyakov, I.P.; Plyusnin, V.F.; Grivin, V.P.; Oliveros, E. Photochemistry of Fe(III) complexes with salicylic acid derivatives in aqueous solutions. J. Photochem. Photobiol. A Chem. 2015, 307–308, 9–15. [Google Scholar] [CrossRef]
- McBryde, W.A.E.; Rohr, J.L.; Penciner, J.S.; Page, J.A. Stability constants of three iron(III) salicylates. Can. J. Chem. 1970, 48, 2574–2586. [Google Scholar] [CrossRef]
- Park, M.V. Complex formation between iron(III) and some substituted salicylic acids. J. Chem. Soc. A 1966, 0, 816–820. [Google Scholar] [CrossRef]
- Chattopadhyaya, M. Effect of Substituents on the Relative Stabilities of Fe(III) Complexes of Substituted Salicylic Acids. J. Indian Chem. Soc. 1982, 59, 1416–1418. [Google Scholar]
- Furia, E.; Sindona, G. Interaction of Iron(III) with 2-Hydroxybenzoic Acid in Aqueous Solutions. J. Chem. Eng. Data 2012, 57, 195–199. [Google Scholar] [CrossRef]
- Porwal, S.K.; Furia, E.; Harris, M.E.; Viswanathan, R.; Devireddy, L. Synthetic, potentiometric and spectroscopic studies of chelation between Fe(III) and 2,5-DHBA supports salicylate-mode of siderophore binding interactions. J. Inorg. Biochem. 2015, 145, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Robinson, K.; Gibbs, G.V.; Ribbe, P.H. Quadratic Elongation: A Quantitative Measure of Distortion in Coordination Polyhedra. Science 1971, 172, 567–570. [Google Scholar] [CrossRef] [PubMed]
- Pilati, T.; Forni, A. SYMMOL: A program to find the maximum symmetry group in an atom cluster, given a prefixed tolerance. J. Appl. Crystallogr. 1998, 31, 503–504. [Google Scholar] [CrossRef]
- Nurchi, V.M.; Crespo-Alonso, M.; Toso, L.; Lachowicz, J.I.; Crisponi, G.; Alberti, G.; Biesuz, R.; Domínguez-Martín, A.; Niclós-Gutíerrez, J.; González-Pérez, J.M.; et al. Iron(III) and aluminium(III) complexes with substituted salicyl-aldehydes and salicylic acids. J. Inorg. Biochem. 2013, 128, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Zarembowitch, J.; Kahn, O.; Jaud, J.; Galy, J. Versatility of iron(III) upon coordination with the binucleating ligand N, N′-bis-(2-hydroxy, 3-carboxybenzilidene)1,2-diaminoethane. Inorg. Chim. Acta 1982, 65, L35–L36. [Google Scholar] [CrossRef]
- Brown, I.D. The Chemical Bond in Inorganic Chemistry; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. Sect. D 2009, 65, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Gilli, P.; Bertolasi, V.; Pretto, L.; Ferretti, V.; Gilli, G. Covalent versus Electrostatic Nature of the Strong Hydrogen Bond: Discrimination among Single, Double, and Asymmetric Single-Well Hydrogen Bonds by Variable-Temperature X-ray Crystallographic Methods in β-Diketone Enol RAHB Systems. J. Am. Chem. Soc. 2004, 126, 3845–3855. [Google Scholar] [CrossRef] [PubMed]
- Li, X.Z.; Walker, B.; Michaelides, A. Quantum nature of the hydrogen bond. Proc. Natl. Acad. Sci. USA 2011, 108, 6369–6373. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Farajtabar, A.; Gharib, F. Solvent effect on protonation constants of salicylic acid in mixed aqueous organic solutions of DMSO. Monatsheft Chem.-Chem. Mon. 2010, 141, 381–386. [Google Scholar] [CrossRef]
- García, M.; Ramis, G.; Mongay, C. Spectrophotometric determination of protonation constants of monoprotic systems in strong acid and strong basic media. Spectrochim. Acta Part A Mol. Spectrosc. 1982, 38, 1005–1009. [Google Scholar] [CrossRef]
- Ma, Z.; Lu, W.; Liang, B.; Pombeiro, A.J.L. Synthesis, characterization, photoluminescent and thermal properties of zinc(II) 4′-phenyl-terpyridine compounds. New J. Chem. 2013, 37, 1529–1537. [Google Scholar] [CrossRef]
- Seth, P.; Ghosh, S.; Figuerola, A.; Ghosh, A. Trinuclear heterometallic CuII-MnII complexes of a salen type Schiff base ligand: Anion dependent variation of phenoxido bridging angles and magnetic coupling. Dalton Trans. 2014, 43, 990–998. [Google Scholar] [CrossRef] [PubMed]
- Palanisami, N.; Rajakannu, P.; Murugavel, R. Non-covalently aggregated zinc and cadmium complexes derived from substituted aromatic carboxylic acids: Synthesis, spectroscopy, and structural studies. Inorg. Chim. Acta 2013, 405, 522–531. [Google Scholar] [CrossRef]
- Terada, T.; Hirabayashi, K.; Liu, D.; Nakamura, T.; Wakimoto, T.; Matsumoto, T.; Tatsumi, K. [3:1] Site-Differentiated [4Fe-4S] Clusters Having One Carboxylate and Three Thiolates. Inorg. Chem. 2013, 52, 11997–12004. [Google Scholar] [CrossRef] [PubMed]
- Groom, C.R.; Allen, F.H. The Cambridge Structural Database in retrospect and prospect. Angew. Chem. Int. Ed. 2014, 53, 662–671. [Google Scholar] [CrossRef] [PubMed]
- Lemoine, P.; Tomas, A.; Nguyen-Huy, D.; Viossat, B. Crystal structure of aquachloro (salicylato)(1,10-phenanthroline)-copper(II), C19H15CICuN2O4. Z. Kristallogr. New Cryst. Struct. 2000, 215, 521–522. [Google Scholar] [CrossRef]
- Banti, C.; Giannoulis, A.; Kourkoumelis, N.; Owczarzak, A.; Kubicki, M.; Hadjikakou, S. Silver(I) compounds of the anti-inflammatory agents salicylic acid and p-hydroxyl-benzoic acid which modulate cell function. J. Inorg. Biochem. 2015, 142, 132–144. [Google Scholar] [CrossRef] [PubMed]
- Edwards, C.F.; Griffith, W.P.; White, A.J.; Williams, D.J. A new bonding mode for salicylate: The X-ray crystal structure of (pyH)[MoO2(Hsal)(sal)]. Polyhedron 1992, 11, 2711–2712. [Google Scholar] [CrossRef]
- Palanisami, N.; Prabusankar, G.; Murugavel, R. A novel dimeric copper salicylate with an undissociated COOH group: Synthesis and crystal structure of [Cu2(HSal)(Sal)(2,2′-bpy)2](ClO4). Inorg. Chem. Commun. 2006, 9, 1002–1006. [Google Scholar] [CrossRef]
- Baroni, T.E.; Bembenek, S.; Heppert, J.A.; Hodel, R.R.; Laird, B.B.; Morton, M.D.; Barnes, D.L.; Takusagawa, F. Hydrogen bonding in tungsten (VI) salicylate free acids. Coord. Chem. Rev. 1998, 174, 255–282. [Google Scholar] [CrossRef]
- Blatov, V.A.; Shevchenko, A.P.; Proserpio, D.M. Applied topological analysis of crystal structures with the program package ToposPro. Cryst. Growth Des. 2014, 14, 3576–3586. [Google Scholar] [CrossRef]
- Herbst-Irmer, R. Crystal Structure Refinement: A Crystallographer’s Guide to SHELXL; Chapter 7: Twinning; Oxford University Press: Oxford, UK, 2006; pp. 106–149. [Google Scholar]
- Dornberger-Schiff, K. Reinterpretation of pseudo-orthorhombic diffraction patterns. Acta Crystallogr. 1966, 21, 311–322. [Google Scholar] [CrossRef]
- Le Page, Y. Mallard’s law recast as a Diophantine system: fast and complete enumeration of possible twin laws by [reticular][pseudo] merohedry. J. Appl. Crystallogr. 2002, 35, 175–181. [Google Scholar] [CrossRef]
- Arend, H.; Connelly, J. Tetramethoxysilane as gel forming agent in crystal growth. J. Cryst. Growth 1982, 56, 642–644. [Google Scholar] [CrossRef]
- Duisenberg, A.J.M. Indexing in single-crystal diffractometry with an obstinate list of reflections. J. Appl. Crystallogr. 1992, 25, 92–96. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Experimental phasing with SHELXC/D/E: Combining chain tracing with density modification. Acta Crystallogr. Sect. D 2010, 66, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Schreurs, A.M.M.; Xian, X.; Kroon-Batenburg, L.M.J. EVAL15: A diffraction data integration method based on ab initio predicted profiles. J. Appl. Crystallogr. 2010, 43, 70–82. [Google Scholar] [CrossRef]
- Sheldrick, G. TWINABS, Version 2012/1; University of Göttingen: Göttingen, Germany, 2012. [Google Scholar]
- Herbst-Irmer, R.; Sheldrick, G.M. Refinement of Twinned Structures with SHELXL97. Acta Crystallogr. Sect. B 1998, 54, 443–449. [Google Scholar] [CrossRef]
- Thorn, A.; Dittrich, B.; Sheldrick, G.M. Enhanced rigid-bond restraints. Acta Crystallogr. Sect. A 2012, 68, 448–451. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).