Abstract
We propose a high-Q photonic crystal cavity formed by introducing random disorder to the central region of an otherwise defect-free photonic crystal slab (PhC). Three-dimensional finite-difference time-domain simulations determine the frequency, quality factor, Q, and modal volume, V, of the localized modes formed by the disorder. Relatively large Purcell factors of 500–800 are calculated for these cavities, which can be achieved for a large range of degrees of disorders.
1. Introduction
Photonic crystals (PhCs) have been widely investigated because they can exhibit a photonic bandgap, i.e., a frequency region in which electromagnetic waves cannot propagate within the structure. This is achieved through the periodic variation of the dielectric constant of the structure, usually implemented through the fabrication of a periodic array of holes in a thin slab of high-index material [1]. In such 2D PhCs the periodic array holes leads to Bragg reflection in the plane of the slab, which, upon appropriate design, leads to the formation of a photonic bandgap. Meanwhile, the light is confined vertically in the slab by the total internal reflection. The presence of a photonic bandgap in PhCs gives rise to a variety of potential applications, for example they can act as filters [2], optical switches, as promising components for photonic integrated circuits [3], and as defect laser cavities [4]. PhC-based cavities offer compact and efficient optical confinement with high quality factors (Q) [5] and small modal volumes (V), which is advantageous for cavity QED experiments, for example using 2D geometries which can be coupled to quantum emitters [6,7]. In particular, the high-Q and small V offers the enhancement of the spontaneous emission rate of a coupled emitter-cavity system [8]. Various emitters that have been successfully coupled to PhC cavities include quantum dots [9,10,11,12] and colour centres [13,14,15]. PhC cavities and the associated modal confinement can be achieved by introducing a defect in the periodic lattice such as removing a hole from a 2D lattice of airholes, which leads to a localized state in the photonic bandgap. An alternative is a defect-free PhC cavity, i.e., a cavity in which none of the air holes is removed from the periodic lattice [16,17,18,19]. Rather, such cavities result in PhCs made of photosensitive chalcogenide glass [20], by the introduction of nanodiamonds into airholes [21], and in PhCs with airholes with graded radii [16,22]. The effect of fabrication-related positional disorder on defect-free PhC cavities has been reported [17,18,19], however these studies all consider position disorder of the airholes in the entire PhC.
The fabrication of 2D PhC cavities for optical wavelength generally requires high-precision lithography techniques such as electron beam or X-ray lithography [23,24], since the geometrical features of PhCs designed are on the sub-wavelength scale. Inevitably, the inability to accurately fabricate features with a size which is on the order of a visible wavelength leads to imperfection. Structural characteristics which are affected during fabrication include surface roughness, sidewall angle, and the size and position of holes [25]. This has attracted much research to determine the tolerance of structures to variation of physical parameters which perturb the photonic bandgap [19,26,27,28]. For PhC cavities, the parameters of interest are the resonant frequency, the quality factor, and modal volume.
In this paper, we show that high-Q cavities can be achieved by introducing local random disorder of the position of the airholes in the region around the centre of the 2D PhC. In addition to high-Q and small V, we show that such cavities can exhibit a large Purcell enhancement, which is associated with strong coupling between matter-photon interactions. The randomness of the cavity formation leads to a resonant wavelength and field distribution which cannot be predicted, which may be alleviated by the use of fluorescent molecules with slightly different resonant frequencies distributed throughout the proximity of the cavity. Section 2 outlines the theory and method, Section 3 contains the results and associated discussion.
2. Theory and Method
We consider a 2D silicon (nSi = 3.4) PhC slab with a hexagonal array of cylindrical air holes which extends for 36 periods both in the x- and y-directions (in-plane). The structure has a periodicity of a = 0.449 μm, slab thickness of h = 0.6a, and the radius of the cylindrical airholes is R = 0.25a. The plane positions of the 19 innermost airholes are all randomly perturbed. A schematic of the structure is shown in Figure 1a.
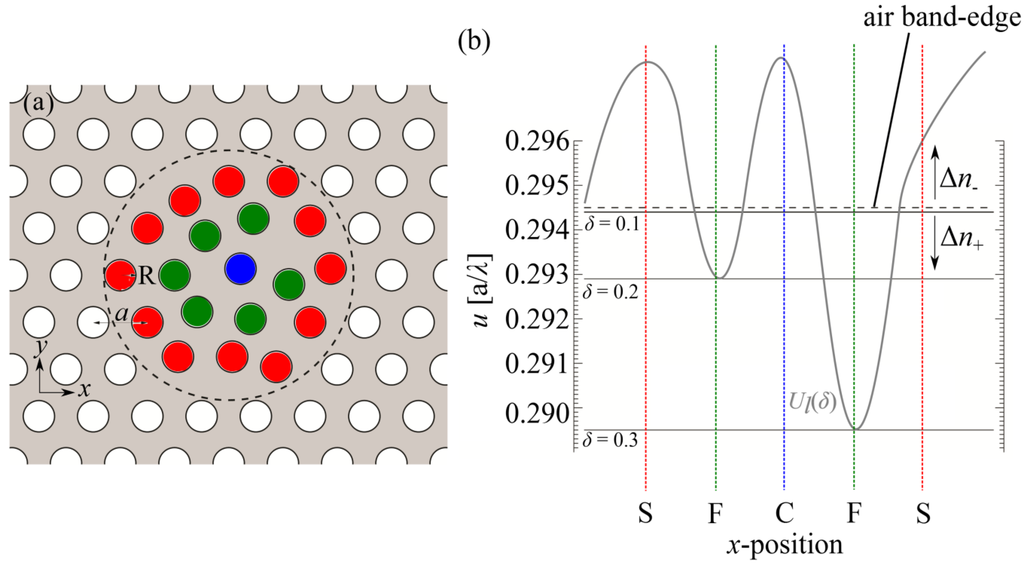
Figure 1.
(a) Schematic of the hexagonal array 2D silicon (grey) photonic crystal (PhC) slab with the dashed circle showing the boundary inside which the position of the cylindrical airholes are randomly perturbed. The origin, i.e., (x,y) = (0,0), is measured from the centre of the unperturbed blue airhole. Note: the centre airhole is perturbed in the figure; (b) Normalised frequency u of high-Q modes found for various disorder amplitudes, δ, (solid lines) relative to the air-band edge of the cavity. An arbitrarily shaped local potential well Ul(δ) created from the local refractive index distribution governed by its dependence on δ and a random function (see Equation (1)). The positions of the airholes are indicated by the colours blue (C—centre), green (F—first ring) and red (S—second ring) as a function of the x-position of the airholes. In some regions of the 2D PhC slab, the local refractive index either increases (below the band gap), Δn+, or decreases (above the band gap), Δn−, depending on the random positions of the airholes. In cases where the refractive index is increased, it is possible to obtain localised states inside the bandgap as indicated by the modes with disorder amplitudes of δ = 0.1, 0.2 and 0.3.
The perturbed positions of the airholes is defined by:
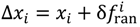 where xi is the unperturbed position of the ith airhole in either of the in-plane coordinates (see Figure 1a) of the random region, δ is the amplitude of randomness which controls the minimum and maximum value of the shift, and fran returns a random uniformly distributed number that lies within the range [−0.5,0.5]. Note, results shown below refer to a single realisation of fran only. We have also considered different fran functions, i.e., ensemble behaviour, and the same trends in frequencies, total Qs, modal volume and mode profiles were also observed for each instance fran.
where xi is the unperturbed position of the ith airhole in either of the in-plane coordinates (see Figure 1a) of the random region, δ is the amplitude of randomness which controls the minimum and maximum value of the shift, and fran returns a random uniformly distributed number that lies within the range [−0.5,0.5]. Note, results shown below refer to a single realisation of fran only. We have also considered different fran functions, i.e., ensemble behaviour, and the same trends in frequencies, total Qs, modal volume and mode profiles were also observed for each instance fran.
The randomness generates regions of higher and lower refractive index with respect to the unperturbed PhC which manifests in a variation of the global minimum of Ul(δ) for Figure 1b, where Ul is the local potential well induced that traps the cavity mode induced by the disorder. The variation is not uniform; it is dependent on the position of the airholes which can be either negative or positive. The modes shown in Figure 1b exist in regions with the overall increased refractive index, which redistributes modes locally deeper into the bandgap.
3D finite-difference time-domain (using RSoft’s FDTD implementation called FullWAVE, version 6.2) is used to simulate the modes of the disordered PhC. The computational domain window is halved by imposing field symmetry properties in the out-of-plane direction about the centre of the slab. Satisfactory convergence is obtained by using 28 points per period. At the computational domain boundaries, perfectly matched layers (PMLs) for width and height are 2a and 4h, respectively.
Cavity modes can be coupled to emitters enhancing their spontaneous emission rate. The degree of enhancement is given by the Purcell factor F, is given by [29].
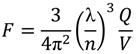 where Q is the total quality factor, λ is the resonant wavelength, and n is the refractive index. Q depends on the partial Qs that occur in-plane Q|| and out-of-plane Q⊥ with respect to the structure’s orientation (in-plane coordinates: xy-plane; out-of-plane direction: z-axis) and are related via 1/Q = 1/Q|| + 1/Q⊥. The in-plane term is further related to the partial Qs in each respective Cartesian direction: 1/Q|| = 1/Qx + 1/Qy [30].
where Q is the total quality factor, λ is the resonant wavelength, and n is the refractive index. Q depends on the partial Qs that occur in-plane Q|| and out-of-plane Q⊥ with respect to the structure’s orientation (in-plane coordinates: xy-plane; out-of-plane direction: z-axis) and are related via 1/Q = 1/Q|| + 1/Q⊥. The in-plane term is further related to the partial Qs in each respective Cartesian direction: 1/Q|| = 1/Qx + 1/Qy [30].
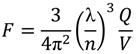
3. Results and Discussion
The random positions of the holes causes backscattering which yield non-propagating Bloch waves which localises the electric field [12]. Figure 1b shows that by introducing positional disorder to the cavity, a resonant mode can enter the photonic band gap (PBG). The normalised frequencies of the cavity modes with high-Q are uδ=0.1 = 0.295, uδ=0.2 = 0.293 and uδ=0.3 = 0.290. Increasing δ causes the modes to shift down in frequency away from the air band-edge and towards the centre of the PBG, which in turn corresponds to a mode which is more strongly confined in-plane. These modes are localised due to a local potential well being created and its functional form depends on δ and on the realization of the random process. Our calculations recover the frequency, the total and partial Qs and V of the disordered cavity modes. These results are given in the next section.
3.1. Total, Partial Qs and Purcell Effect
The total and partial Qs calculated for the cavity modes for increasing δ are shown in Table 1.
From Table 1, we note that the in-plane Qs increase with δ and whereas the out-of-plane Qsdecrease. This can be understood as follows: When the deviation from perfect periodicity increases more k-components enter the light cone leading to an increase in out-of-plane radiation losses. In contrast, as δ increases, the defect state goes deeper into the bandgap, thus improving the in-plane confinement and hence leading to an increase in Q||.
In Figure 2, we show the calculated partial in-plane Q|| (crosses) and out-of-plane Q⊥ (squares) as a function of δ. It can be seen that both partial Qs behave very differently, Q|| increases with random disorder, and conversely, Q⊥ decreases. The modal volumes were also calculated for the range of δ = 0.1 and 0.3 cavities, where they were found to vary between 2.03(λ/n)3 and 0.93(λ/n)3 respectively (see Table 1). As mentioned in Section 2 the same trends in total and partial Qs were also obtained for different fran. We have tested four different random functions.

Table 1.
Total, partial Qs (Q⊥,Q||), V and F of the cavity modes as a function of disorder amplitude δ. The modal volume for δ = 0.05 could not be determined because the computational domain was too large.
| δ | Q⊥ (×104) | Q|| (×104) | Q (×104) | V (λ/n)3 | F |
|---|---|---|---|---|---|
| 0.05 | 20.2 | 0.45 | 0.44 | – | – |
| 0.1 | 12 | 1.9 | 1.65 | 2.03 | 618 |
| 0.15 | 3.77 | 2.5 | 1.5 | 1.6 | 712 |
| 0.2 | 1.5 | 10.3 | 1.21 | 1.20 | 766 |
| 0.25 | 1.1 | 23.8 | 1.1 | 1.02 | 820 |
| 0.3 | 0.66 | 38.2 | 0.65 | 0.93 | 531 |
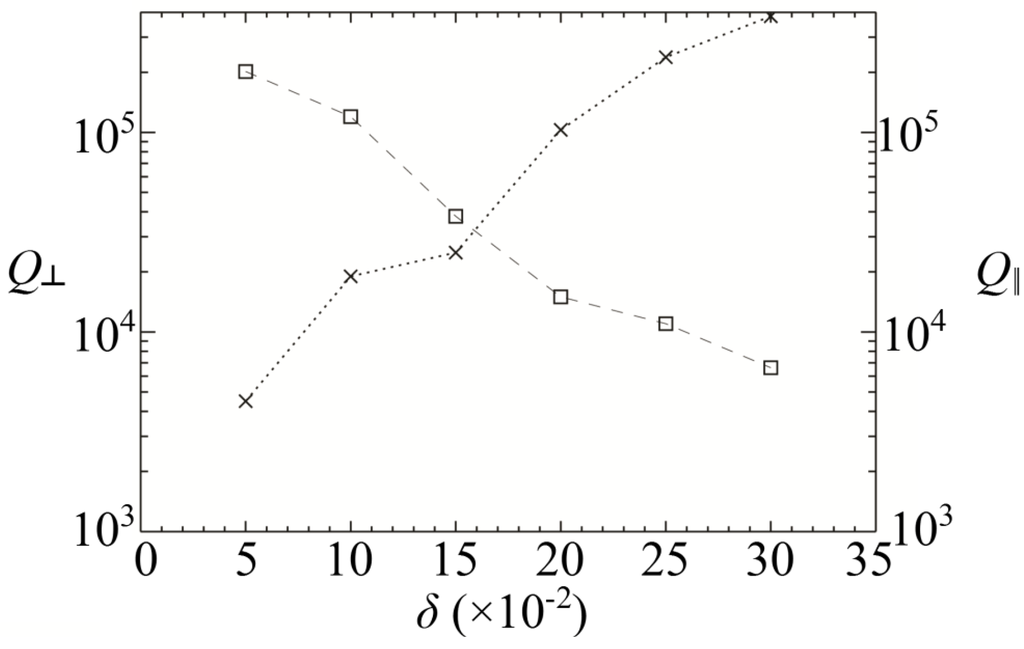
Figure 2.
In-plane (crosses) and out-of-plane (square) partial Qs of the cavity as a function of disorder amplitude δ.
3.2. Mode Profiles
The major electric field components Ex and Ey, and their Fourier transforms, of the in-plane coordinates for the disorder amplitudes δ = 0.1, 0.2 and 0.3 are shown in Figure 3. Figure 3a,c show the changes in-plane confinement for each respective mode given their associated disorder amplitude and it can be seen that the confinement around the central region of cavity improves as the disorder increases, subsequently V decreases. This is confirmed quantitatively since Q|| from Figure 2 varies from 1.90 × 104 to 3.82 × 105 for increasing disorder. Another indicator is the k-space distribution of Figure 3b,d which shows that the fraction of the field that falls within the leaky light-cone is higher for larger δ, confirming the behaviour seen in Figure 2 [30].
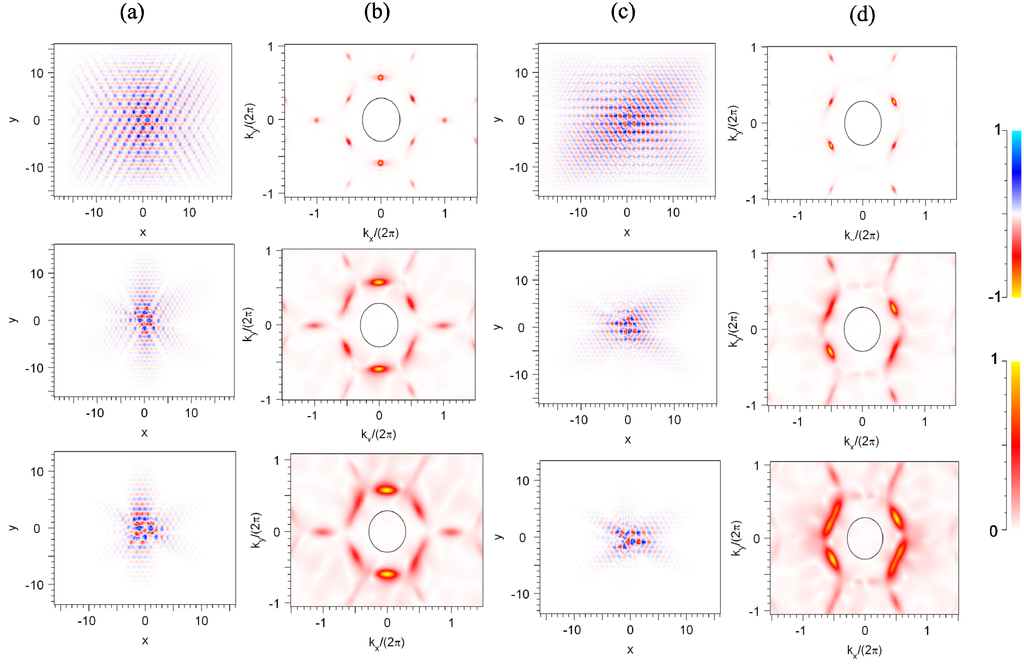
Figure 3.
The major electric field components in the middle of the slab for (a) Ex and its associated; (b) Fourier transform. Similarly; the (c) Ey major field component; and its (d) Fourier transform (circle represents the light). The top, middle and bottom rows correspond to disorder amplitudes δ = 0.1, 0.2 and 0.3 respectively.
4. Conclusions
We have shown through random local positional disorder that high-Q 2D PhC cavities can be achieved with significantly high Purcell enhancement up to F = 820 with a random disorder amplitude of δ = 0.25. This enhancement is approximately 55 times greater compared to Anderson-localized modes in a photonic crystal waveguide [31]. We have shown that a defect-free locally disordered 2D PhC slab is a promising geometry for large Purcell factors. This random disorder represents a fabrication disadvantage that can be directly addressed since cavity modes always exist below the air-band edge. Exploring this parameter space allows this seemingly fabrication disadvantage to become an advantage because modes will always be pulled into the bandgap and a high-Q can be achieved.
Acknowledgments
K.C. would like to acknowledge the receipt of the Melbourne Research Scholarship awarded by The University of Melbourne. R.R. acknowledges McKenzie Fellowship Scheme awarded by The University of Melbourne. S.T.-H. is supported by the ARC Australian Research Fellowship (project number DP1096288). This research was also undertaken with the assistance of resources provided at the NCI National Facility systems at The Australian National University through the National Computational Merit Allocation Scheme supported by the Australian Government.
Author Contributions
The conceptual idea was developed by S.T.-H., further discussion and clarification with C.M.dS. Simulations were conducted by K.C., T.J.K., S.T.-H. and R.R. The writing, editing and discussion of the paper was conducted by all authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krauss, T.F.; Rue, R.M.D.L.; Brand, S. Two-dimensional photonic-bandgap structures operating at near-infrared wavelengths. Nature 1996, 383, 699–702. [Google Scholar] [CrossRef]
- Noda, S.; Chutinan, A.; Imada, M. Trapping and emission of photons by a single defect in a photonic bandgap structure. Nature 2000, 407, 608–610. [Google Scholar] [CrossRef]
- Intonti, F.; Vignolini, S.; Turck, V.; Colocci, M.; Bettotti, P.; Pavesi, L.; Schweizer, S.L.; Wehrspohn, R.; Wiersma, D. Rewritable photonic circuits. Appl. Phys. Lett. 2006, 89, 211117:1–211117:3. [Google Scholar]
- Painter, O.; Lee, R.; Scherer, A.; Yariv, A.; O’Brien, J.; Dapkus, P.; Kim, I. Two-dimensional photonic band-gap defect mode laser. Science 1999, 284, 1819–1821. [Google Scholar] [CrossRef]
- Akahane, Y.; Asano, T.; Song, B.-S.; Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 2003, 425, 944–947. [Google Scholar] [CrossRef]
- Vučković, J.; Lončar, M.; Mabuchi, H.; Scherer, A. Design of photonic crystal microcavities for cavity QED. Phys. Rev. E 2001, 65, 016608:1–016608:11. [Google Scholar]
- Kiraz, A.; Reese, C.; Gayral, B.; Zhang, L.; Schoenfeld, W.; Gerardot, B.; Petroff, P.; Hu, E.; Imamoglu, A. Cavity-quantum electrodynamics with quantum dots. J. Opt. B Quantum Semiclass. Opt. 2003, 5. [Google Scholar] [CrossRef]
- Aharonovich, I.; Greentree, A.D.; Prawer, S. Diamond photonics. Nat. Photon. 2011, 5, 397–405. [Google Scholar] [CrossRef]
- Yoshie, T.; Scherer, A.; Hendrickson, J.; Khitrova, G.; Gibbs, H.; Rupper, G.; Ell, C.; Shchekin, O.; Deppe, D. Vacuum rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004, 432, 200–203. [Google Scholar] [CrossRef]
- Englund, D.; Faraon, A.; Fushman, I.; Stoltz, N.; Petroff, P.; Vučković, J. Controlling cavity reflectivity with a single quantum dot. Nature 2007, 450, 857–861. [Google Scholar] [CrossRef]
- Hennessy, K.; Badolato, A.; Winger, M.; Gerace, D.; Atatüre, M.; Gulde, S.; Fält, S.; Hu, E.L.; Imamoğlu, A. Quantum nature of a strongly coupled single quantum dot-cavity system. Nature 2007, 445, 896–899. [Google Scholar] [CrossRef]
- Yang, J.; Heo, J.; Zhu, T.; Xu, J.; Topolancik, J.; Vollmer, F.; Ilic, R.; Bhattacharya, P. Enhanced photoluminescence from embedded pbse colloidal quantum dots in silicon-based random photonic crystal microcavities. Appl. Phys. Lett. 2008, 92, 261110:1–261110:3. [Google Scholar]
- Faraon, A.; Santori, C.; Huang, Z.; Acosta, V.M.; Beausoleil, R.G. Coupling of nitrogen-vacancy centers to photonic crystal cavities in monocrystalline diamond. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
- Englund, D.; Shields, B.; Rivoire, K.; Hatami, F.; Vučković, J.; Park, H.; Lukin, M.D. Deterministic coupling of a single nitrogen vacancy center to a photonic crystal cavity. Nano Lett. 2010, 10, 3922–3926. [Google Scholar] [CrossRef]
- Wolters, J.; Schell, A.W.; Kewes, G.; Nüsse, N.; Schoengen, M.; Döscher, H.; Hannappel, T.; Löchel, B.; Barth, M.; Benson, O. Enhancement of the zero phonon line emission from a single nitrogen vacancy center in a nanodiamond via coupling to a photonic crystal cavity. Appl. Phys. Lett. 2010, 97, 141108:1–141108:3. [Google Scholar]
- Srinivasan, K.; Barclay, P.; Painter, O. Fabrication-tolerant high quality factor photonic crystal microcavities. Opt. Express 2004, 12, 1458–1463. [Google Scholar] [CrossRef]
- Moon, S.-K.; Yang, J.-K. Numerical study of the photonic-bandgap effect in two-dimensional slab photonic structures with long-range order. J. Opt. 2013, 15, 075704:1–075704:7. [Google Scholar]
- Molinari, D.; Fratalocchi, A. Route to strong localization of light: The role of disorder. Opt. Express 2012, 20, 18156–18164. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Zhang, X.; Zhang, Z.-Q. Disordered photonic crystals understood by a perturbation formalism. Phys. Rev. B 2000, 61. [Google Scholar] [CrossRef]
- Tomljenovic-Hanic, S.; de Sterke, C.M. Design of ultrahigh-Q photoinduced cavities in defect-free photonic crystal slabs. Opt. Express 2010, 18, 21397–21403. [Google Scholar] [CrossRef]
- Tomljenovic-Hanic, S.; Greentree, A.D.; Gibson, B.C.; Karle, T.J.; Prawer, S. Nanodiamond induced high-Q resonances in defect-free photonic crystal slabs. Opt. Express 2011, 19, 22219–22226. [Google Scholar]
- Srinivasan, K.; Barclay, P.E.; Painter, O.; Chen, J.; Cho, A.Y.; Gmachl, C. Experimental demonstration of a high quality factor photonic crystal microcavity. Appl. Phys. Lett. 2003, 83, 1915–1917. [Google Scholar] [CrossRef]
- Feiertag, G.; Ehrfeld, W.; Freimuth, H.; Kolle, H.; Lehr, H.; Schmidt, M.; Sigalas, M.; Soukoulis, C.; Kiriakidis, G.; Pedersen, T. Fabrication of photonic crystals by deep X-ray lithography. Appl. Phys. Lett. 1997, 71, 1441–1443. [Google Scholar] [CrossRef]
- Awazu, K.; Wang, X.; Fujimaki, M.; Kuriyama, T.; Sai, A.; Ohki, Y.; Imai, H. Fabrication of two- and three-dimensional photonic crystals of titania with submicrometer resolution by deep X-ray lithography. J. Vac. Sci. Technol. B 2005, 23, 934–939. [Google Scholar] [CrossRef]
- Khankhoje, U.; Kim, S.-H.; Richards, B.; Hendrickson, J.; Sweet, J.; Olitzky, J.; Khitrova, G.; Gibbs, H.; Scherer, A. Modelling and fabrication of GaAs photonic-crystal cavities for cavity quantum electrodynamics. Nanotechnology 2010, 21, 065202:1–065202:7. [Google Scholar]
- Fan, S.; Villeneuve, P.R.; Joannopoulos, J. Theoretical investigation of fabrication—Related disorder on the properties of photonic crystals. J. Appl. Phys. 1995, 78, 1415–1418. [Google Scholar] [CrossRef]
- Chutinan, A.; Noda, S. Effects of structural fluctuations on the photonic bandgap during fabrication of a photonic crystal. J. Opt. Soc. Am. B 1999, 16, 240–244. [Google Scholar] [CrossRef]
- Zhu, Z.; Ye, W.; Ji, J.; Yuan, X.; Zen, C. Influence of random errors on the characteristics of typical 2D photonic crystal microcavity. Appl. Phys. B 2007, 88, 231–236. [Google Scholar]
- Vahala, K. Optical Microcavities; World Scientific: Hackensack, NJ, USA, 2004. [Google Scholar]
- Englund, D.; Fushman, I.; Vučković, J. General recipe for designing photonic crystal cavities. Opt. Express 2005, 13, 5961–5975. [Google Scholar] [CrossRef]
- Sapienza, L.; Thyrrestrup, H.; Stobbe, S.; Garcia, P.D.; Smolka, S.; Lodahl, P. Cavity quantum electrodynamics with Anderson-localized modes. Science 2010, 327, 1352–1355. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).