Abstract
A review is given for recent theoretical studies on phase transitions in quasi-one-dimensional molecular conductors with a quarter-filled band. By lowering temperature, charge transfer salts exhibit a variety of transitions accompanying symmetry breaking, such as charge ordering, lattice dimerization, antiferromagnetic transition, spin-Peierls distortion, and so on. Analyses on microscopic quasi-one-dimensional models provide their systematic understandings, by the complementary use of different analytical and numerical techniques; they can reproduce finite-temperature phase transitions, whose results can be directly compared with experiments and give feedbacks to material design.
1. Introduction
Low-dimensional molecular conductors exhibit interplay between electron correlation highlighted by enhanced fluctuation and coupling to the lattice degree of freedom. In the last three decades or so, charge transfer-type salts which are represented as A2B with different molecular constituents have increasingly attracted considerable interests. Since the B unit is a closed-shell monovalent ion, therefore providing one electron or hole to the π orbital of A molecule, a quarter-filled band structure is realized as a stage to show such interplay [1,2]. Especially in quasi-one-dimensional (Q1D) systems, various types of phase transitions have been found experimentally, triggering numerous theoretical works [3]. Among the typical examples are families of TM2X [4,5] and DCNQI2X [6], whose electronic structures are Q1D because of the stacking nature of the planar TM/DCNQI molecules and anisotropic shape of molecular orbital (MO). TM representing TMTSF (tetramethyltetraselenafulvalene) or TMTTF (tetramethyltetrathiafulvalene) molecules form crystals with different monovalent anions X−, then a three quarter-filled HOMO band of TM molecule is realized, i.e., quarter-filled in terms of holes; on the other hand in the DCNQI (N,N′-dicyanoquinonediimine) salts, when their counterparts are monovalent cations X+ such as Ag and Li, a quarter-filled LUMO band of DCNQI is realized.
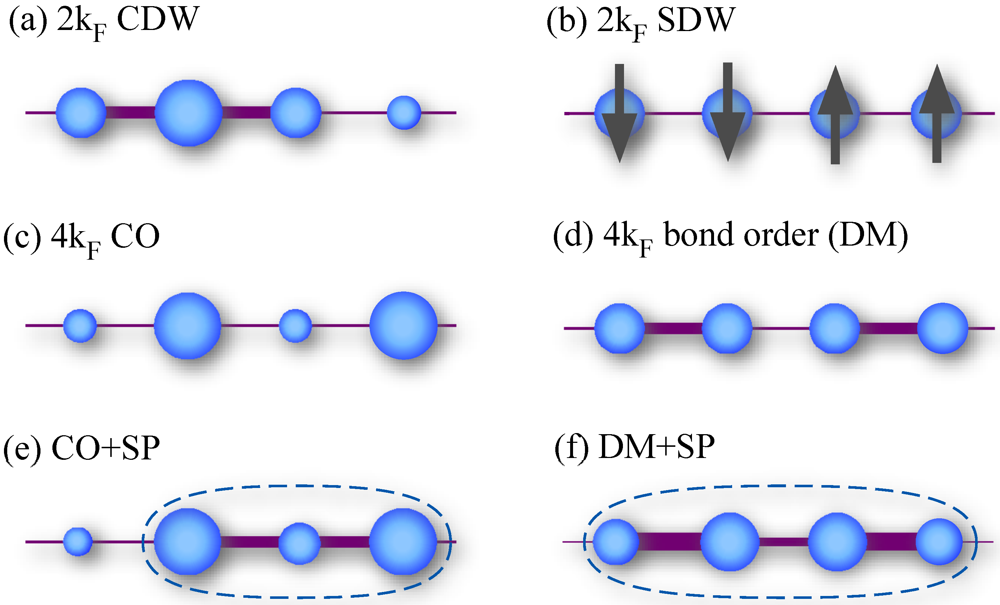
Figure 1.
Typical symmetry broken states seen in quarter-filled quasi-one-dimensional molecular conductors. The size of circles and the thickness of bonds represent charge density and the absolute value of transfer integrals, while arrows and broken line ellipses represent ordered spin moments and spin singlet formation, respectively. κF is the Fermi momentum, which is a measure for the periodicity for each state. CDW, SDW, CO, DM, and SP stand for charge-density-wave, spin-density-wave, charge ordered, dimer-Mott insulating, and spin-Peierls states, respectively. CO+SP and DM+SP are coexisting states of two orders.
In purely one-dimensional (1D) electronic systems, it is known that any phase transition does not occur at finite temperature (T) owing to the enhanced fluctuations. The metallic state in 1D called the Tomonaga–Luttinger liquid (TLL) has only collective excitations. Nevertheless, many-body effect is pronounced so that correlations toward ordered states, i.e., short-range order, can be enhanced at sufficiently low T. Symmetry breaking in the actual crystalline materials takes place by dimensionality effect added to such a situation, e.g., the coupling to the lattice and/or the interchain interaction, which bring about finite-T phase transitions to long-range ordered states. Below, we list typical broken symmetry states observed in the Q1D molecular conductors at quarter filling, which are schematically shown in Figure 1. The Fermi momentum κF is measured for a regular 1D chain with lattice constant α having a quarter-filled band, namely, one carrier per two lattice sites;  .
.
 .
.- 2κF charge density wave (CDW) state: This is a coexistence of modulation of charge density and lattice distortion (bond order) with the period of 4α. The origin is usually the Peierls instability, i.e., the nesting of the Fermi surface, when the electrons are coupled with the lattice degree of freedom (electron-phonon coupling); the modulation opens a gap at the Fermi energy εF in the case of a 1D band. Sometimes the term CDW is used just to represent a charge density modulation, regardless of its physical origin, such as the 4α modulation induced by the spin-Peierls (SP) states mentioned below.
- 2κF spin density wave (SDW) state: This indicates a Peierls instability-induced state as well, mostly, but with magnetic moments which are modulated with the period of 4α, instead of the charge and lattice in the case of CDW. However, for 1D electronic systems, the antiferromagnetic (AF) state in an insulating state due to strong electron correlation, which shows staggered pattern of the localized spin moments, has the same period; therefore they are often mixed up in terminology. These should be distinguished as they have distinct origins.
- 4κF charge order (CO): The intersite Coulomb interaction leads to CO with charge localized on every other site. This is essentially a strongly correlated insulator, where localized spins show up on the “charge rich” sites. We simply call this as the CO state in this review.
- 4κF bond order: 2α modulation of the bonds, namely, dimerization in the transfer integrals makes the system effectively half-filled, then the on-site Coulomb interaction can drive the system to a Mott insulating state. This is called as the dimer-Mott (DM) insulating state. As in the CO state, localized spins appear on the bonding orbitals (anti-bonding orbitals in the case of three quarter-filled band) of the dimerized sites.
- SP state: In the CO and DM insulators, the localized spin degree of freedom is described by the Heisenberg model. 1D Heisenberg chains are susceptible to SP states where spin singlets are aligned periodically. In the quarter-filling case their period is 4α (tetramerization); in other words, 2κF bond order emerges, while 2κF charge modulation is induced as well.
In this review, we will introduce theoretical results for such broken symmetry states in quarter-filled Q1D materials. First, in Section 2, we briefly summarize results for 1D models mainly focusing on the different ground states found there. Then in Section 3 and Section 4, we show recent progresses, theoretically reproducing finite-T phase transitions in such Q1D compounds, by using analytical and numerical methods, respectively: By considering the interchain Coulomb repulsion within the mean-field approximation, one can treat the effective 1D model with substantial accuracy, taking into account of the quantum and thermal fluctuation of the interacting electrons. The CO phase transition is analyzed by the use of standard 1D theories, namely, the bosonization and renormalization group (RG) scheme, while adopting numerical data when necessary (Section 3). The phase diagrams including different competing and co-existing states, which sometimes can be complex, are numerically investigated using quantum Monte Carlo simulations (Section 4). Section 5 and Section 6 are devoted to discussions and summary.
2. Extended Hubbard Model and Ground States
In most of the charge transfer salts, low energy properties can be well described by effective models based on one MO of the molecule consisting the valence band: for the A2B systems, a frontier MO of A. The anisotropic transfer integrals between the packed A molecules lead to the tight-binding model directly derived from the crystal structure, where each molecule is represented by a lattice site [7]. When interaction effects are added, one can discuss the physical properties of the material whose comparison between theory and experiment is straightforward [1]. In most typical cases, among different interactions, the on-site (= on-molecule) Coulomb repulsion is the largest energy scale: This is the Hubbard model. In recent years, the importance of including the nearest neighbor Coulomb repulsions as well, namely, considering the extended Hubbard model (EHM), has been recognized. In this section, we introduce main results of previous theoretical studies on 1D models, focusing on their ground state properties where the different broken symmetry states discussed in Section 1 are found. There, interplay between such strong Coulomb interaction and the coupling to the lattice (electron-phonon interaction) results in a variety of ordered states; they show rich phase diagrams with coexistences and competitions. For more details, see reviews [3,8] and references therein.
2.1. One-Dimensional Electronic Model
Let us start with a very basic model for the quarter-filled Q1D molecular conductors, the 1D EHM. It consists of an array of lattice sites with nearest-neighbor transfer integral t, on-site Coulomb repulsion U, and nearest-neighbor Coulomb repulsion V, whose Hamiltonian is written as:
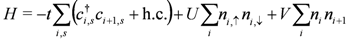
where the operator  creates an electron with spin
creates an electron with spin  or
or  at the i-th site along the chain. The density operators are defined as
at the i-th site along the chain. The density operators are defined as 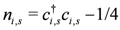 and
and 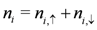 . The interchain coupling is completely neglected in this model. Its ground state consists of two phases for positive U and V: the TLL and the CO insulating states. The latter is stabilized as a long-range order only at T = 0 when both parameters (
. The interchain coupling is completely neglected in this model. Its ground state consists of two phases for positive U and V: the TLL and the CO insulating states. The latter is stabilized as a long-range order only at T = 0 when both parameters (  ,
,  ) are large (see Section 3). In the limit of
) are large (see Section 3). In the limit of  , for example, the TLL (CO insulator) is realized for
, for example, the TLL (CO insulator) is realized for  (
(  ).
).
 creates an electron with spin
creates an electron with spin  or
or  at the i-th site along the chain. The density operators are defined as
at the i-th site along the chain. The density operators are defined as 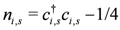 and
and 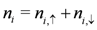 . The interchain coupling is completely neglected in this model. Its ground state consists of two phases for positive U and V: the TLL and the CO insulating states. The latter is stabilized as a long-range order only at T = 0 when both parameters (
. The interchain coupling is completely neglected in this model. Its ground state consists of two phases for positive U and V: the TLL and the CO insulating states. The latter is stabilized as a long-range order only at T = 0 when both parameters (  ,
,  ) are large (see Section 3). In the limit of
) are large (see Section 3). In the limit of  , for example, the TLL (CO insulator) is realized for
, for example, the TLL (CO insulator) is realized for  (
(  ).
).On the other hand, in many A2B salts, molecular stacking shows dimerization. This results in the alternating transfer integrals, and modifies the first term in Equation (1) as
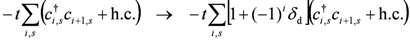
For example, in the TM2X family,  is estimated to be around 0.1–0.2, depending on the anion X. Finite dimerization leads to the folding of the Brillouin zone with a gap at the boundary
is estimated to be around 0.1–0.2, depending on the anion X. Finite dimerization leads to the folding of the Brillouin zone with a gap at the boundary  : A half-filled lower band is realized. Then, in the 1D dimerized EHM, the TLL is no longer stable once
: A half-filled lower band is realized. Then, in the 1D dimerized EHM, the TLL is no longer stable once  for positive U and V, and replaced by a Mott insulating state (the DM insulator). The CO region (where intrinsic DM “co-exists” [9]) is shifted toward larger (
for positive U and V, and replaced by a Mott insulating state (the DM insulator). The CO region (where intrinsic DM “co-exists” [9]) is shifted toward larger (  ,
,  ), whose critical line depends on
), whose critical line depends on  . Note that in the CO state with
. Note that in the CO state with  , the system loses the inversion symmetry: Ferrroelectricity arises [10,11,12].
, the system loses the inversion symmetry: Ferrroelectricity arises [10,11,12].
 is estimated to be around 0.1–0.2, depending on the anion X. Finite dimerization leads to the folding of the Brillouin zone with a gap at the boundary
is estimated to be around 0.1–0.2, depending on the anion X. Finite dimerization leads to the folding of the Brillouin zone with a gap at the boundary  : A half-filled lower band is realized. Then, in the 1D dimerized EHM, the TLL is no longer stable once
: A half-filled lower band is realized. Then, in the 1D dimerized EHM, the TLL is no longer stable once  for positive U and V, and replaced by a Mott insulating state (the DM insulator). The CO region (where intrinsic DM “co-exists” [9]) is shifted toward larger (
for positive U and V, and replaced by a Mott insulating state (the DM insulator). The CO region (where intrinsic DM “co-exists” [9]) is shifted toward larger (  ,
,  ), whose critical line depends on
), whose critical line depends on  . Note that in the CO state with
. Note that in the CO state with  , the system loses the inversion symmetry: Ferrroelectricity arises [10,11,12].
, the system loses the inversion symmetry: Ferrroelectricity arises [10,11,12].We note that the mutual interaction between the next nearest-neighbor site, 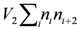 , is neglected in the present review though the EHM with V2-term shows several coexistent states [13,14,15,16].
, is neglected in the present review though the EHM with V2-term shows several coexistent states [13,14,15,16].
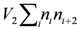 , is neglected in the present review though the EHM with V2-term shows several coexistent states [13,14,15,16].
, is neglected in the present review though the EHM with V2-term shows several coexistent states [13,14,15,16].2.2. Electron-Lattice Coupling
There are also many studies on 1D interacting electronic systems coupled to the lattice degree of freedom. Such situations implicitly include the dimensionality effect, since crystal, then the lattice structure, is a three-dimensional object. Therefore, as seen in the following sections, finite-T transitions should be expected.
At quarter-filling, the electron-lattice couplings give rise to various kinds of symmetry breaking. For instance, instabilities in the charge degree of freedom include the 2κF CDW state by the Peierls mechanism, and the DM insulator which can be generated spontaneously out of a uniform system. Besides this, the spin degree of freedom in the insulating states is also susceptible to a lattice-coupled instability: the SP transition. Such electron-lattice coupled states are stabilized, e.g., in 1D EHM coupled to translational and/or rotational displacement of the molecules described by the modulation in the transfer integrals: the so-called Su–Schrieffer–Heeger or Peierls-type electron-phonon interaction. The model is sometimes called as the (extended) Peierls–Hubbard model. Another important coupling is that with molecular deformations, i.e., intra-molecular vibration, which couples to the charge density on each MO: This is called e-mv coupling or the Holstein type electron-phonon interaction (Holstein-Hubbard model). In some situation, this coupling can considerably enhance the CO region.
Here we just show one typical example in Figure 2 [17], a phase diagram obtained numerically for the 1D EHM [Equation (1)] with the Peierls-type coupling treated within the adiabatic limit. The Hamiltonian is written as:

where the modulation in the transfer integral  increases the lattice energy whose renormalized spring constant is K. The 2κF CDW [Figure 1 (a)] appears in the small Coulomb repulsion region, reflecting its weak-coupling character. In the other diagonal of the phase diagram with large (
increases the lattice energy whose renormalized spring constant is K. The 2κF CDW [Figure 1 (a)] appears in the small Coulomb repulsion region, reflecting its weak-coupling character. In the other diagonal of the phase diagram with large (  ,
,  ), the CO state is realized, as in purely electronic models, while it shows lattice tetramerization due to the SP instability [CO+SP state, Figure 1 (e)]. In between these two, we find the co-existence of dimerization and tetramerization (mixture of bond and charge modulations) [18,19]; This can be interpreted as the spontaneous formation of the DM state, leading to charge localization, then the SP singlet formation [DM+SP state, Figure 1 (f)]. The Holstein coupling added to such a situation enhances the CO+SP region [19].
), the CO state is realized, as in purely electronic models, while it shows lattice tetramerization due to the SP instability [CO+SP state, Figure 1 (e)]. In between these two, we find the co-existence of dimerization and tetramerization (mixture of bond and charge modulations) [18,19]; This can be interpreted as the spontaneous formation of the DM state, leading to charge localization, then the SP singlet formation [DM+SP state, Figure 1 (f)]. The Holstein coupling added to such a situation enhances the CO+SP region [19].
 increases the lattice energy whose renormalized spring constant is K. The 2κF CDW [Figure 1 (a)] appears in the small Coulomb repulsion region, reflecting its weak-coupling character. In the other diagonal of the phase diagram with large (
increases the lattice energy whose renormalized spring constant is K. The 2κF CDW [Figure 1 (a)] appears in the small Coulomb repulsion region, reflecting its weak-coupling character. In the other diagonal of the phase diagram with large (  ,
,  ), the CO state is realized, as in purely electronic models, while it shows lattice tetramerization due to the SP instability [CO+SP state, Figure 1 (e)]. In between these two, we find the co-existence of dimerization and tetramerization (mixture of bond and charge modulations) [18,19]; This can be interpreted as the spontaneous formation of the DM state, leading to charge localization, then the SP singlet formation [DM+SP state, Figure 1 (f)]. The Holstein coupling added to such a situation enhances the CO+SP region [19].
), the CO state is realized, as in purely electronic models, while it shows lattice tetramerization due to the SP instability [CO+SP state, Figure 1 (e)]. In between these two, we find the co-existence of dimerization and tetramerization (mixture of bond and charge modulations) [18,19]; This can be interpreted as the spontaneous formation of the DM state, leading to charge localization, then the SP singlet formation [DM+SP state, Figure 1 (f)]. The Holstein coupling added to such a situation enhances the CO+SP region [19]. 3. Bosonization and Renormalization Group Study
The bosonization is one of the most powerful method to investigate 1D electronic systems, by which the quantum fluctuation can be fully taken into account [20]. In this section, we review recent developments and applications of such method to quarter-filled charge transfer salts, especially on the CO phenomena. We are now able to construct a theory for finite-T phase transition, based on the combination of bosonization and renormalization group (RG), while adopting numerical results as “inputs” when needed [21]. Let us introduce our results to some detail, since this is achieved based on a newly developed methodology.
3.1. One Dimensional Model
First, as a basis, we briefly introduce the bosonization approach to the quarter filled 1D EHM [Equation (1)]. The low energy Hamiltonian is separated into the charge part  and the spin part
and the spin part  ; this is called charge spin separation. They are written in terms of bosonic phase variables as,
; this is called charge spin separation. They are written in terms of bosonic phase variables as,
 and the spin part
and the spin part  ; this is called charge spin separation. They are written in terms of bosonic phase variables as,
; this is called charge spin separation. They are written in terms of bosonic phase variables as, 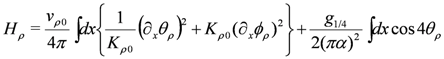
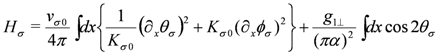
where  is a short distance cutoff of the order of the lattice spacing, α. The phase variables satisfy
is a short distance cutoff of the order of the lattice spacing, α. The phase variables satisfy 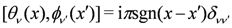 . The quantities,
. The quantities,  ,
,  ,
,  ,
,  ,
,  , and
, and  are bare parameters whose values are non-universal functions of the interaction and the Fermi velocity
are bare parameters whose values are non-universal functions of the interaction and the Fermi velocity  . The non-linear term in the charge sector,
. The non-linear term in the charge sector,  , originates from the 8κF-Umklapp scattering and leads to the insulating ground state with CO. On the other hand, the spin sector is essentially the same as the effective Hamiltonian of a Heisenberg chain. Therefore, the parameters
, originates from the 8κF-Umklapp scattering and leads to the insulating ground state with CO. On the other hand, the spin sector is essentially the same as the effective Hamiltonian of a Heisenberg chain. Therefore, the parameters  and
and  are not independent of each other due to the spin SU(2) symmetry and satisfy the following relation,
are not independent of each other due to the spin SU(2) symmetry and satisfy the following relation,
 is a short distance cutoff of the order of the lattice spacing, α. The phase variables satisfy
is a short distance cutoff of the order of the lattice spacing, α. The phase variables satisfy 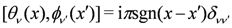 . The quantities,
. The quantities,  ,
,  ,
,  ,
,  ,
,  , and
, and  are bare parameters whose values are non-universal functions of the interaction and the Fermi velocity
are bare parameters whose values are non-universal functions of the interaction and the Fermi velocity  . The non-linear term in the charge sector,
. The non-linear term in the charge sector,  , originates from the 8κF-Umklapp scattering and leads to the insulating ground state with CO. On the other hand, the spin sector is essentially the same as the effective Hamiltonian of a Heisenberg chain. Therefore, the parameters
, originates from the 8κF-Umklapp scattering and leads to the insulating ground state with CO. On the other hand, the spin sector is essentially the same as the effective Hamiltonian of a Heisenberg chain. Therefore, the parameters  and
and  are not independent of each other due to the spin SU(2) symmetry and satisfy the following relation,
are not independent of each other due to the spin SU(2) symmetry and satisfy the following relation, 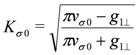
The low-energy properties of the bosonized Hamiltonians Equations (4,5) can be systematically investigated by the RG approach, where the long length scale properties are analyzed by solving the derived RG equations. Those for the charge part are written as
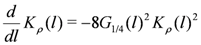
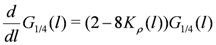
and for the spin part,
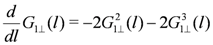
where 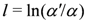 with the new length scale
with the new length scale  . The initial conditions for the above RG equations are given from the bare parameters as
. The initial conditions for the above RG equations are given from the bare parameters as 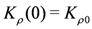 ,
, 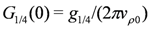 and
and 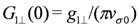 . Note that the relation Equation (6) still holds even under the renormalization procedure; the quantity
. Note that the relation Equation (6) still holds even under the renormalization procedure; the quantity  is written by using the solution of Equation (9) as
is written by using the solution of Equation (9) as
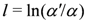 with the new length scale
with the new length scale  . The initial conditions for the above RG equations are given from the bare parameters as
. The initial conditions for the above RG equations are given from the bare parameters as 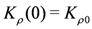 ,
, 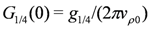 and
and 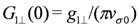 . Note that the relation Equation (6) still holds even under the renormalization procedure; the quantity
. Note that the relation Equation (6) still holds even under the renormalization procedure; the quantity  is written by using the solution of Equation (9) as
is written by using the solution of Equation (9) as 
Whether the ground state is the metallic TLL or the CO insulating state is judged by the solution of the RG equations for the charge part, Equations (7,8). The metallic TLL state is indicated by 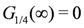 with
with 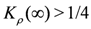 , whereas the CO insulating state is by
, whereas the CO insulating state is by 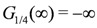 . The metal-insulator boundary is characterized by
. The metal-insulator boundary is characterized by 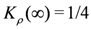 . On the other hand, the spin degree of freedom, as long as we consider repulsive interactions, has gapless excitations with
. On the other hand, the spin degree of freedom, as long as we consider repulsive interactions, has gapless excitations with 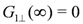 and
and 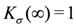 .
.
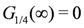 with
with 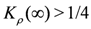 , whereas the CO insulating state is by
, whereas the CO insulating state is by 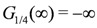 . The metal-insulator boundary is characterized by
. The metal-insulator boundary is characterized by 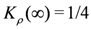 . On the other hand, the spin degree of freedom, as long as we consider repulsive interactions, has gapless excitations with
. On the other hand, the spin degree of freedom, as long as we consider repulsive interactions, has gapless excitations with 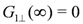 and
and 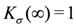 .
.The bare parameters in the bosonized Hamiltonian, Equations (4,5), can be analytically obtained from the standard bosonization procedure, where only the matrix elements of the mutual interaction between the one-particle states close to the Fermi level are taken into account. It should be remarked that careful treatment is necessary for the 8κF-Umklapp scattering, namely the  -term in Equation (4). This is because it originates from the interaction processes where four right-going electrons are scattered into four left-going states and vice versa, which include the one-particle states far from Fermi energy as intermediate states. The systematic way to obtain analytical expression for the coupling constant
-term in Equation (4). This is because it originates from the interaction processes where four right-going electrons are scattered into four left-going states and vice versa, which include the one-particle states far from Fermi energy as intermediate states. The systematic way to obtain analytical expression for the coupling constant  is as follows [22,23,24]. The one-particle states are divided into two parts: the states close to
is as follows [22,23,24]. The one-particle states are divided into two parts: the states close to  and those around
and those around  . The effective Hamiltonian for the former states are obtained by integrating out the latter states and treating the interaction processes including both kinds of states in perturbation expansion. The lowest order contribution to the 8κF-Umklapp scattering comes from the third order processes, which are shown in Figure 3. When the bare parameters obtained by the above treatment are used as the initial conditions for the RG equations, one can obtain the ground state phase diagram on the plane of
. The effective Hamiltonian for the former states are obtained by integrating out the latter states and treating the interaction processes including both kinds of states in perturbation expansion. The lowest order contribution to the 8κF-Umklapp scattering comes from the third order processes, which are shown in Figure 3. When the bare parameters obtained by the above treatment are used as the initial conditions for the RG equations, one can obtain the ground state phase diagram on the plane of  and
and  . The CO insulating state is realized for the large
. The CO insulating state is realized for the large  and
and  region, whereas the TLL state with both charge and spin excitation without a gap appears in the other region. The phase diagram is qualitatively the same as that derived from numerical methods [3,8]. We note that, as discussed in the previous section, the alternating transfer integrals change the TLL to the DM insulating state because the
region, whereas the TLL state with both charge and spin excitation without a gap appears in the other region. The phase diagram is qualitatively the same as that derived from numerical methods [3,8]. We note that, as discussed in the previous section, the alternating transfer integrals change the TLL to the DM insulating state because the  -Umklapp scattering is generated by the dimerization gap at
-Umklapp scattering is generated by the dimerization gap at  . In addition, the CO region on the U-V plane is reduced because the CO and the dimerization compete with each other [24]. However, CO is still stabilized even in the presence of the dimerization.
. In addition, the CO region on the U-V plane is reduced because the CO and the dimerization compete with each other [24]. However, CO is still stabilized even in the presence of the dimerization.
 -term in Equation (4). This is because it originates from the interaction processes where four right-going electrons are scattered into four left-going states and vice versa, which include the one-particle states far from Fermi energy as intermediate states. The systematic way to obtain analytical expression for the coupling constant
-term in Equation (4). This is because it originates from the interaction processes where four right-going electrons are scattered into four left-going states and vice versa, which include the one-particle states far from Fermi energy as intermediate states. The systematic way to obtain analytical expression for the coupling constant  is as follows [22,23,24]. The one-particle states are divided into two parts: the states close to
is as follows [22,23,24]. The one-particle states are divided into two parts: the states close to  and those around
and those around  . The effective Hamiltonian for the former states are obtained by integrating out the latter states and treating the interaction processes including both kinds of states in perturbation expansion. The lowest order contribution to the 8κF-Umklapp scattering comes from the third order processes, which are shown in Figure 3. When the bare parameters obtained by the above treatment are used as the initial conditions for the RG equations, one can obtain the ground state phase diagram on the plane of
. The effective Hamiltonian for the former states are obtained by integrating out the latter states and treating the interaction processes including both kinds of states in perturbation expansion. The lowest order contribution to the 8κF-Umklapp scattering comes from the third order processes, which are shown in Figure 3. When the bare parameters obtained by the above treatment are used as the initial conditions for the RG equations, one can obtain the ground state phase diagram on the plane of  and
and  . The CO insulating state is realized for the large
. The CO insulating state is realized for the large  and
and  region, whereas the TLL state with both charge and spin excitation without a gap appears in the other region. The phase diagram is qualitatively the same as that derived from numerical methods [3,8]. We note that, as discussed in the previous section, the alternating transfer integrals change the TLL to the DM insulating state because the
region, whereas the TLL state with both charge and spin excitation without a gap appears in the other region. The phase diagram is qualitatively the same as that derived from numerical methods [3,8]. We note that, as discussed in the previous section, the alternating transfer integrals change the TLL to the DM insulating state because the  -Umklapp scattering is generated by the dimerization gap at
-Umklapp scattering is generated by the dimerization gap at  . In addition, the CO region on the U-V plane is reduced because the CO and the dimerization compete with each other [24]. However, CO is still stabilized even in the presence of the dimerization.
. In addition, the CO region on the U-V plane is reduced because the CO and the dimerization compete with each other [24]. However, CO is still stabilized even in the presence of the dimerization.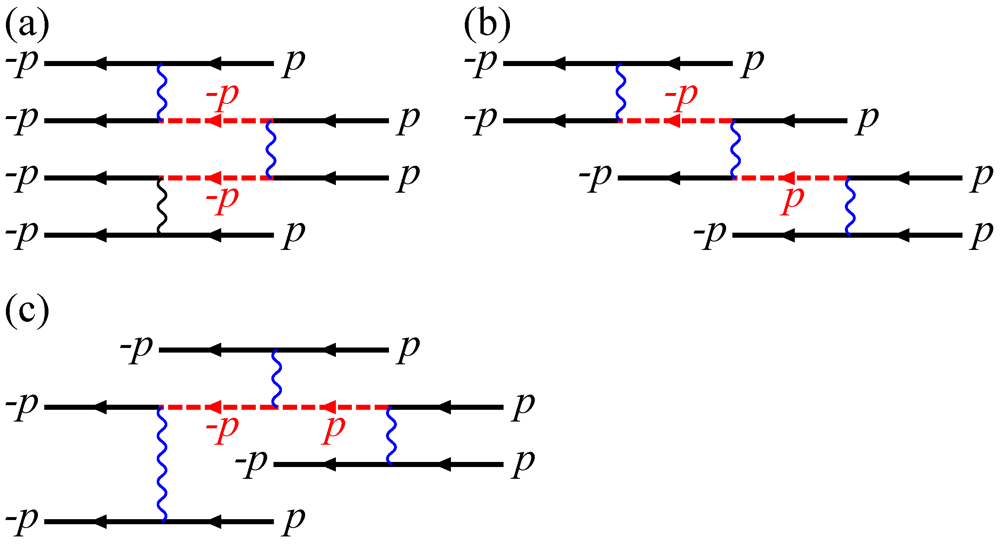
Figure 3.
Lowest order diagrams expressing the 8κF-Umklapp scattering [22,23]. Here,  indicates the right/left going state, and the solid and the dotted lines express the electrons close to
indicates the right/left going state, and the solid and the dotted lines express the electrons close to  and to
and to  , respectively.
, respectively.
 indicates the right/left going state, and the solid and the dotted lines express the electrons close to
indicates the right/left going state, and the solid and the dotted lines express the electrons close to  and to
and to  , respectively.
, respectively.
The quantitative discrepancy between the phase diagrams derived by the analytical bosonization procedure and the numerical method is ascribable, not to the procedure of using the bosonized Hamiltonian together with the RG equations, but to the choice of the initial conditions of the RG equations. As is already noted, the one-particle states around  are taken into account in the analytical bosonization procedure. When the mutual interaction becomes stronger, such a treatment does not endorse quantitatively correct results, because the interaction processes far from the Fermi energy play important roles. One of the most evident example is the 8κF-Umklapp scattering leading to the CO state noted above. However, it is difficult to obtain the accurate values of the initial conditions by such analytical procedures. Instead, the exact diagonalization method for finite size clusters can be used, as demonstrated for the 1D EHM [25]. Here, the size L is related to the variable l, as
are taken into account in the analytical bosonization procedure. When the mutual interaction becomes stronger, such a treatment does not endorse quantitatively correct results, because the interaction processes far from the Fermi energy play important roles. One of the most evident example is the 8κF-Umklapp scattering leading to the CO state noted above. However, it is difficult to obtain the accurate values of the initial conditions by such analytical procedures. Instead, the exact diagonalization method for finite size clusters can be used, as demonstrated for the 1D EHM [25]. Here, the size L is related to the variable l, as  . The initial conditions obtained by such a method lead to the phase diagram which shows good agreement with that by the “purely” numerical methods.
. The initial conditions obtained by such a method lead to the phase diagram which shows good agreement with that by the “purely” numerical methods.
 are taken into account in the analytical bosonization procedure. When the mutual interaction becomes stronger, such a treatment does not endorse quantitatively correct results, because the interaction processes far from the Fermi energy play important roles. One of the most evident example is the 8κF-Umklapp scattering leading to the CO state noted above. However, it is difficult to obtain the accurate values of the initial conditions by such analytical procedures. Instead, the exact diagonalization method for finite size clusters can be used, as demonstrated for the 1D EHM [25]. Here, the size L is related to the variable l, as
are taken into account in the analytical bosonization procedure. When the mutual interaction becomes stronger, such a treatment does not endorse quantitatively correct results, because the interaction processes far from the Fermi energy play important roles. One of the most evident example is the 8κF-Umklapp scattering leading to the CO state noted above. However, it is difficult to obtain the accurate values of the initial conditions by such analytical procedures. Instead, the exact diagonalization method for finite size clusters can be used, as demonstrated for the 1D EHM [25]. Here, the size L is related to the variable l, as  . The initial conditions obtained by such a method lead to the phase diagram which shows good agreement with that by the “purely” numerical methods.
. The initial conditions obtained by such a method lead to the phase diagram which shows good agreement with that by the “purely” numerical methods.3.2. Quasi One Dimension
Strictly 1D models do not show any phase transition at finite T as is noted in Section 1; The CO in the 1D EHM appears only at T = 0. In order to investigate the phase transition observed in the actual crystalline materials, one has to take into account the high-dimensionality. Let us discuss the Q1D model where the 1D chains described by the EHM are coupled via the interchain interaction,
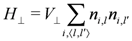
where  is the electron number of the i-th site in the l-th chain,
is the electron number of the i-th site in the l-th chain,  denotes a pair of adjacent chains, and the strength of the interchain repulsive interaction is expressed by
denotes a pair of adjacent chains, and the strength of the interchain repulsive interaction is expressed by  . In the following, we apply the mean-field approximation to the interchain interaction (interchain mean-field approximation),
. In the following, we apply the mean-field approximation to the interchain interaction (interchain mean-field approximation),
 is the electron number of the i-th site in the l-th chain,
is the electron number of the i-th site in the l-th chain,  denotes a pair of adjacent chains, and the strength of the interchain repulsive interaction is expressed by
denotes a pair of adjacent chains, and the strength of the interchain repulsive interaction is expressed by  . In the following, we apply the mean-field approximation to the interchain interaction (interchain mean-field approximation),
. In the following, we apply the mean-field approximation to the interchain interaction (interchain mean-field approximation), 
which enables us to investigate the finite transition temperature  [26,27] as well as the T-dependences of several quantities across
[26,27] as well as the T-dependences of several quantities across  [21] by the bosonization method. Such an interchain mean-field treatment has been applied to different Q1D systems and is known to be accurate as long as we have small interchain couplings [28,29].
[21] by the bosonization method. Such an interchain mean-field treatment has been applied to different Q1D systems and is known to be accurate as long as we have small interchain couplings [28,29].
 [26,27] as well as the T-dependences of several quantities across
[26,27] as well as the T-dependences of several quantities across  [21] by the bosonization method. Such an interchain mean-field treatment has been applied to different Q1D systems and is known to be accurate as long as we have small interchain couplings [28,29].
[21] by the bosonization method. Such an interchain mean-field treatment has been applied to different Q1D systems and is known to be accurate as long as we have small interchain couplings [28,29].3.2.1. Transition Temperature
We assume the CO pattern to be anti-phase between the adjacent chains,  , which is naturally expected to gain the energy for the positive
, which is naturally expected to gain the energy for the positive  . This leads our model to the effective 1D Hamiltonian given by,
. This leads our model to the effective 1D Hamiltonian given by,
 , which is naturally expected to gain the energy for the positive
, which is naturally expected to gain the energy for the positive  . This leads our model to the effective 1D Hamiltonian given by,
. This leads our model to the effective 1D Hamiltonian given by, 
where N and z are the total number of the sites in the chain and the number of the adjacent chains, respectively. The quantity n denotes the order parameter of CO. Notice that effects of n in the adjacent chains act as an alternating potential and thus induce a gap at 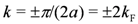 . As a result, the system effectively becomes half-filling, in which the
. As a result, the system effectively becomes half-filling, in which the  -Umklapp scattering appears. In the bosonized form, the Hamiltonian for the charge part (except the quadratic term of n) is written as follows,
-Umklapp scattering appears. In the bosonized form, the Hamiltonian for the charge part (except the quadratic term of n) is written as follows,
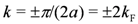 . As a result, the system effectively becomes half-filling, in which the
. As a result, the system effectively becomes half-filling, in which the  -Umklapp scattering appears. In the bosonized form, the Hamiltonian for the charge part (except the quadratic term of n) is written as follows,
-Umklapp scattering appears. In the bosonized form, the Hamiltonian for the charge part (except the quadratic term of n) is written as follows, 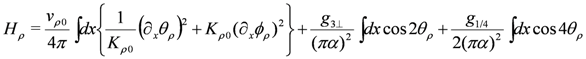
Here the second term expresses the  -Umklapp scattering. Naturally, the bare parameters are functions of the CO order parameter n. Up to the first order of n,
-Umklapp scattering. Naturally, the bare parameters are functions of the CO order parameter n. Up to the first order of n,  is proportional to n, whereas the other parameters are the same as those in the absence of n. Therefore, the transition temperature
is proportional to n, whereas the other parameters are the same as those in the absence of n. Therefore, the transition temperature  is determined by the following equation,
is determined by the following equation,
 -Umklapp scattering. Naturally, the bare parameters are functions of the CO order parameter n. Up to the first order of n,
-Umklapp scattering. Naturally, the bare parameters are functions of the CO order parameter n. Up to the first order of n,  is proportional to n, whereas the other parameters are the same as those in the absence of n. Therefore, the transition temperature
is proportional to n, whereas the other parameters are the same as those in the absence of n. Therefore, the transition temperature  is determined by the following equation,
is determined by the following equation, 
where 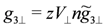 ,
, 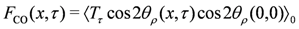 with
with  denoting the thermal average in terms of Equation (4), namely the Hamiltonian of the charge part in the absence of CO. The quantity
denoting the thermal average in terms of Equation (4), namely the Hamiltonian of the charge part in the absence of CO. The quantity  is written by the solution of RG Equation as
is written by the solution of RG Equation as
 ,
, 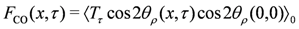 with
with  denoting the thermal average in terms of Equation (4), namely the Hamiltonian of the charge part in the absence of CO. The quantity
denoting the thermal average in terms of Equation (4), namely the Hamiltonian of the charge part in the absence of CO. The quantity  is written by the solution of RG Equation as
is written by the solution of RG Equation as 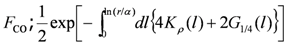
where  . With regard to the appearance of CO, the
. With regard to the appearance of CO, the 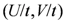 -plane can be separated into the three distinct regions, which is summarized in Figure 4 [26]. In the region (iii) where CO is found even in the absence of
-plane can be separated into the three distinct regions, which is summarized in Figure 4 [26]. In the region (iii) where CO is found even in the absence of  at T = 0, the infinitesimal
at T = 0, the infinitesimal  makes
makes  finite, as is naturally expected. There is another region in which
finite, as is naturally expected. There is another region in which  becomes finite under the infinitesimal
becomes finite under the infinitesimal  ; the region (ii) is specified by
; the region (ii) is specified by 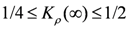 and the metallic TLL state is realized in the strictly 1D case. In contrast, a finite amount of
and the metallic TLL state is realized in the strictly 1D case. In contrast, a finite amount of  is necessary for appearance of CO insulating state at finite T for the region (i) with
is necessary for appearance of CO insulating state at finite T for the region (i) with 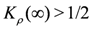 . Thus, the parameter region where the finite
. Thus, the parameter region where the finite  appears under the infinitesimal interchain coupling in the Q1D system is different from that where the CO is realized in the 1D system.
appears under the infinitesimal interchain coupling in the Q1D system is different from that where the CO is realized in the 1D system.
 . With regard to the appearance of CO, the
. With regard to the appearance of CO, the 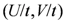 -plane can be separated into the three distinct regions, which is summarized in Figure 4 [26]. In the region (iii) where CO is found even in the absence of
-plane can be separated into the three distinct regions, which is summarized in Figure 4 [26]. In the region (iii) where CO is found even in the absence of  at T = 0, the infinitesimal
at T = 0, the infinitesimal  makes
makes  finite, as is naturally expected. There is another region in which
finite, as is naturally expected. There is another region in which  becomes finite under the infinitesimal
becomes finite under the infinitesimal  ; the region (ii) is specified by
; the region (ii) is specified by 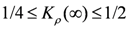 and the metallic TLL state is realized in the strictly 1D case. In contrast, a finite amount of
and the metallic TLL state is realized in the strictly 1D case. In contrast, a finite amount of  is necessary for appearance of CO insulating state at finite T for the region (i) with
is necessary for appearance of CO insulating state at finite T for the region (i) with 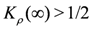 . Thus, the parameter region where the finite
. Thus, the parameter region where the finite  appears under the infinitesimal interchain coupling in the Q1D system is different from that where the CO is realized in the 1D system.
appears under the infinitesimal interchain coupling in the Q1D system is different from that where the CO is realized in the 1D system. 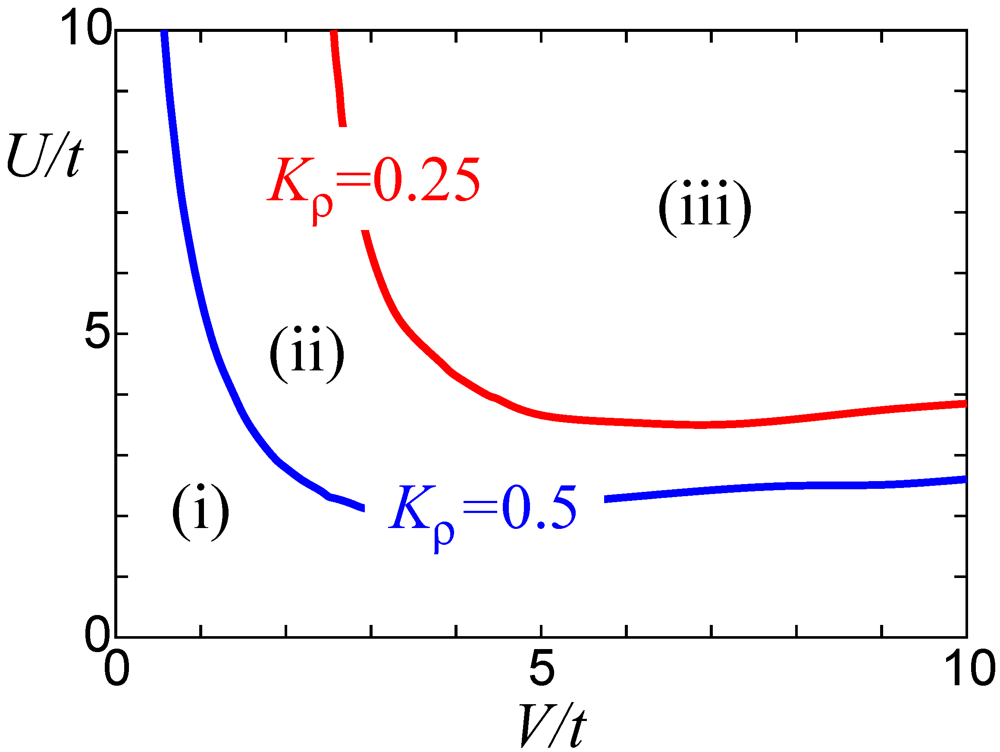
Figure 4.
Three distinct regions classified by the appearance of CO insulating states at the finite T [26]. Here,  in the figure corresponds to the solution
in the figure corresponds to the solution  of the RG equation, Equations (7,8).
of the RG equation, Equations (7,8).
 in the figure corresponds to the solution
in the figure corresponds to the solution  of the RG equation, Equations (7,8).
of the RG equation, Equations (7,8).
3.2.2. Quantities Across 
The bosonization and RG technique as discussed tells us how to incorporate the correlation effects into the non-interacting system in a controllable way. However, it is not straightforward to extend it to calculate quantitatively physical observables, particularly for the strong-coupling region. Here, we introduce a newly developed scheme combined with numerical methods, by which we can calculate quantities not only above but also below  . This is similar to the 1D case as discussed in Section 3.1; we adopt numerical results as “inputs”.
. This is similar to the 1D case as discussed in Section 3.1; we adopt numerical results as “inputs”.
 . This is similar to the 1D case as discussed in Section 3.1; we adopt numerical results as “inputs”.
. This is similar to the 1D case as discussed in Section 3.1; we adopt numerical results as “inputs”.In the presence of CO, the charge part of the effective Hamiltonian is written by Equation (14 ). The RG equations are given as
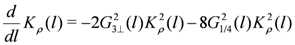
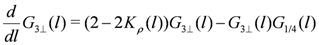
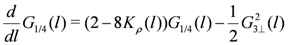
The initial condition for  is given by
is given by 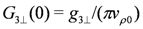 . On the other hand, the spin part of the bosonized Hamiltonian is unchanged (the parameters will be affected). Namely, the Hamiltonian is given by Equation (5) and the RG equation corresponding to it is written by Equation (9) together with the constraint Equation (6) from the SU(2) symmetry.
. On the other hand, the spin part of the bosonized Hamiltonian is unchanged (the parameters will be affected). Namely, the Hamiltonian is given by Equation (5) and the RG equation corresponding to it is written by Equation (9) together with the constraint Equation (6) from the SU(2) symmetry.
 is given by
is given by 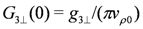 . On the other hand, the spin part of the bosonized Hamiltonian is unchanged (the parameters will be affected). Namely, the Hamiltonian is given by Equation (5) and the RG equation corresponding to it is written by Equation (9) together with the constraint Equation (6) from the SU(2) symmetry.
. On the other hand, the spin part of the bosonized Hamiltonian is unchanged (the parameters will be affected). Namely, the Hamiltonian is given by Equation (5) and the RG equation corresponding to it is written by Equation (9) together with the constraint Equation (6) from the SU(2) symmetry. 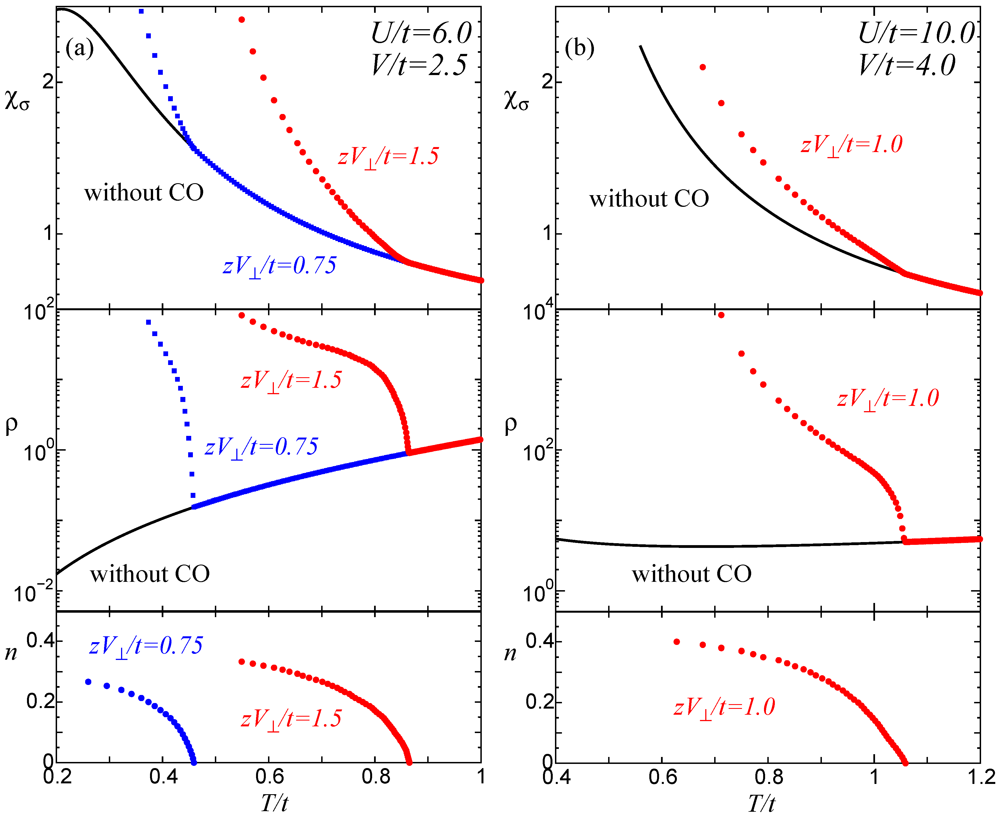
Figure 5.
Temperature dependences of the spin susceptibility  and the resistivity
and the resistivity  together with the CO order parameter
together with the CO order parameter  , (a) for the region (ii) in Figure 4[
, (a) for the region (ii) in Figure 4[  ] and (b) for the region (iii) [
] and (b) for the region (iii) [  ] [21]. The solid curve shows the data for
] [21]. The solid curve shows the data for  , without charge order at finite T.
, without charge order at finite T.
 and the resistivity
and the resistivity  together with the CO order parameter
together with the CO order parameter  , (a) for the region (ii) in Figure 4[
, (a) for the region (ii) in Figure 4[  ] and (b) for the region (iii) [
] and (b) for the region (iii) [  ] [21]. The solid curve shows the data for
] [21]. The solid curve shows the data for  , without charge order at finite T.
, without charge order at finite T.
In order to discuss the finite T properties, the RG scaling is cut off at the scale corresponding to T : 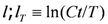 with C being an
with C being an  numerical constant. The initial conditions are obtained by the exact diagonalization method for small size clusters as is introduced above. It should be noted that the T-dependence of the CO order parameter
numerical constant. The initial conditions are obtained by the exact diagonalization method for small size clusters as is introduced above. It should be noted that the T-dependence of the CO order parameter  cannot be obtained within the bosonization and RG procedure because of the ambiguity in the relationship between n and the phase variables. Therefore we determine
cannot be obtained within the bosonization and RG procedure because of the ambiguity in the relationship between n and the phase variables. Therefore we determine  by the quantum Monte Carlo (QMC) method independently. The present procedure is explained in detail in [21]. The spin susceptibility
by the quantum Monte Carlo (QMC) method independently. The present procedure is explained in detail in [21]. The spin susceptibility  [30,31] and the resistivity
[30,31] and the resistivity  [32,33] are respectively written by the T dependent parameters as
[32,33] are respectively written by the T dependent parameters as
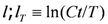 with C being an
with C being an  numerical constant. The initial conditions are obtained by the exact diagonalization method for small size clusters as is introduced above. It should be noted that the T-dependence of the CO order parameter
numerical constant. The initial conditions are obtained by the exact diagonalization method for small size clusters as is introduced above. It should be noted that the T-dependence of the CO order parameter  cannot be obtained within the bosonization and RG procedure because of the ambiguity in the relationship between n and the phase variables. Therefore we determine
cannot be obtained within the bosonization and RG procedure because of the ambiguity in the relationship between n and the phase variables. Therefore we determine  by the quantum Monte Carlo (QMC) method independently. The present procedure is explained in detail in [21]. The spin susceptibility
by the quantum Monte Carlo (QMC) method independently. The present procedure is explained in detail in [21]. The spin susceptibility  [30,31] and the resistivity
[30,31] and the resistivity  [32,33] are respectively written by the T dependent parameters as
[32,33] are respectively written by the T dependent parameters as 
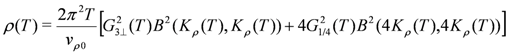
where  is the spin susceptibility in the noninteracting case normalized as
is the spin susceptibility in the noninteracting case normalized as  and
and 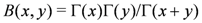 . It should be noted that
. It should be noted that  is not obtained by the RG scheme; we use usual finite size scaling procedure. The spin susceptibility and the resistivity are shown as a function of T for the region (ii) [
is not obtained by the RG scheme; we use usual finite size scaling procedure. The spin susceptibility and the resistivity are shown as a function of T for the region (ii) [  ] and for the region (iii) [
] and for the region (iii) [  ] in Figure 5. The spin susceptibility is enhanced below
] in Figure 5. The spin susceptibility is enhanced below  without any steep singularity at
without any steep singularity at  . The enhancement originates from the suppression of spin velocity due to the gap formation at
. The enhancement originates from the suppression of spin velocity due to the gap formation at  . On the other hand, the resistivity shows a clear cusp at
. On the other hand, the resistivity shows a clear cusp at  . The abrupt change originates from the emergence of 4κF-Umklapp scattering due to the gap in the energy dispersion at
. The abrupt change originates from the emergence of 4κF-Umklapp scattering due to the gap in the energy dispersion at  . Just below
. Just below  , the resistivity shows a curve which is convex upward in the semi-log plot. The behavior reflects the rapid increase of the CO order parameter n for
, the resistivity shows a curve which is convex upward in the semi-log plot. The behavior reflects the rapid increase of the CO order parameter n for 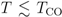 . At lower T, the curve turns convex downward showing an activation type behavior
. At lower T, the curve turns convex downward showing an activation type behavior 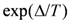 with the weak T-dependence of
with the weak T-dependence of  . We comment that the resistivity is difficult to calculate exactly by solely numerical simulations.
. We comment that the resistivity is difficult to calculate exactly by solely numerical simulations.
 is the spin susceptibility in the noninteracting case normalized as
is the spin susceptibility in the noninteracting case normalized as  and
and 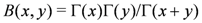 . It should be noted that
. It should be noted that  is not obtained by the RG scheme; we use usual finite size scaling procedure. The spin susceptibility and the resistivity are shown as a function of T for the region (ii) [
is not obtained by the RG scheme; we use usual finite size scaling procedure. The spin susceptibility and the resistivity are shown as a function of T for the region (ii) [  ] and for the region (iii) [
] and for the region (iii) [  ] in Figure 5. The spin susceptibility is enhanced below
] in Figure 5. The spin susceptibility is enhanced below  without any steep singularity at
without any steep singularity at  . The enhancement originates from the suppression of spin velocity due to the gap formation at
. The enhancement originates from the suppression of spin velocity due to the gap formation at  . On the other hand, the resistivity shows a clear cusp at
. On the other hand, the resistivity shows a clear cusp at  . The abrupt change originates from the emergence of 4κF-Umklapp scattering due to the gap in the energy dispersion at
. The abrupt change originates from the emergence of 4κF-Umklapp scattering due to the gap in the energy dispersion at  . Just below
. Just below  , the resistivity shows a curve which is convex upward in the semi-log plot. The behavior reflects the rapid increase of the CO order parameter n for
, the resistivity shows a curve which is convex upward in the semi-log plot. The behavior reflects the rapid increase of the CO order parameter n for 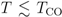 . At lower T, the curve turns convex downward showing an activation type behavior
. At lower T, the curve turns convex downward showing an activation type behavior 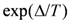 with the weak T-dependence of
with the weak T-dependence of  . We comment that the resistivity is difficult to calculate exactly by solely numerical simulations.
. We comment that the resistivity is difficult to calculate exactly by solely numerical simulations.Overall T dependence of the magnetic susceptibility of 1D electron systems is well fitted by the so-called Bonner–Fisher behavior, namely  decreases (increases) as a function of T for
decreases (increases) as a function of T for 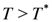 (
( 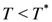 ), where
), where  is of the order of the effective spin-exchange coupling. The present results shown in Figure 5 express the case for
is of the order of the effective spin-exchange coupling. The present results shown in Figure 5 express the case for  . If smaller values of
. If smaller values of  are used, the other case of
are used, the other case of  would be possible. The former case may be observed in DI-DCNQI2Ag [34], whereas
would be possible. The former case may be observed in DI-DCNQI2Ag [34], whereas  of TMTTF2AsF6 seems to be lower than
of TMTTF2AsF6 seems to be lower than  [35].
[35].
 decreases (increases) as a function of T for
decreases (increases) as a function of T for 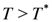 (
( 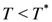 ), where
), where  is of the order of the effective spin-exchange coupling. The present results shown in Figure 5 express the case for
is of the order of the effective spin-exchange coupling. The present results shown in Figure 5 express the case for  . If smaller values of
. If smaller values of  are used, the other case of
are used, the other case of  would be possible. The former case may be observed in DI-DCNQI2Ag [34], whereas
would be possible. The former case may be observed in DI-DCNQI2Ag [34], whereas  of TMTTF2AsF6 seems to be lower than
of TMTTF2AsF6 seems to be lower than  [35].
[35].4. Numerical Study
Recent experimental progresses showing intricate phase competitions and coexistences have prompted us to explore issues beyond the quarter-filled 1D EHM, where additional terms including the dimensionality effects and electron-lattice couplings give rise to rich phase diagrams. Numerical methods are powerful in investigating and have been applied to reveal the finite-T properties of such models [36,37,38]. This is in contrast and complementary to the analytical approaches which provide insights to the phenomena, for example, described by means of the TLL parameters in the bosonization scheme.
Although there are a few approximation-free results in higher dimensions, numerical approaches such as exact diagonalization [39,40], QMC simulation [41,42,43,44], and density-matrix renormalization group method [45] have demonstrated their effectiveness in the quarter-filled 1D electronic models. Many of the studies along this line have been devoted to the ground-state (T = 0) properties, partly because no phase transition occurs there at finite T as discussed in the previous sections. We can apply the numerical methods to Q1D models as well, by considering the lattice degrees of freedom and/or using the inter-chain mean-field approximation as in the previous section. By fully taking into account of the 1D fluctuations by solving effective 1D models while determining the mean-fields self-consistently, we can draw finite-T phase diagrams for Q1D quarter-filled charge transfer salts, with sufficient accuracy [36,38].
We here discuss finite-T properties of the quarter-filled EHM coupled to the Peierls-type electron-lattice coupling in Q1D. The Hamiltonian consists of two parts,  . The first term represents the intra-chain part along the stacking direction of molecules,
. The first term represents the intra-chain part along the stacking direction of molecules,
 . The first term represents the intra-chain part along the stacking direction of molecules,
. The first term represents the intra-chain part along the stacking direction of molecules, 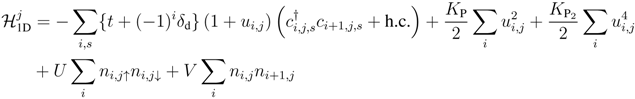
where  denotes the intrinsic lattice dimerization (alternation in the transfer integrals),
denotes the intrinsic lattice dimerization (alternation in the transfer integrals),  the renormalized lattice displacement, and,
the renormalized lattice displacement, and,  and
and  the coupling constants of the elastic energy up to the fourth order. The second term in H is the inter-chain Coulomb repulsion,
the coupling constants of the elastic energy up to the fourth order. The second term in H is the inter-chain Coulomb repulsion,
 denotes the intrinsic lattice dimerization (alternation in the transfer integrals),
denotes the intrinsic lattice dimerization (alternation in the transfer integrals),  the renormalized lattice displacement, and,
the renormalized lattice displacement, and,  and
and  the coupling constants of the elastic energy up to the fourth order. The second term in H is the inter-chain Coulomb repulsion,
the coupling constants of the elastic energy up to the fourth order. The second term in H is the inter-chain Coulomb repulsion, 
We apply two approximations to the model. The lattice displacements  , treated as classical variables, are taken into account by the adiabatic approximations, being optimized so as to minimize the free energy. The mean-field approximation is imposed to the inter-chain part,
, treated as classical variables, are taken into account by the adiabatic approximations, being optimized so as to minimize the free energy. The mean-field approximation is imposed to the inter-chain part, 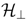 as discussed in Section 3.2. We consider periodicities up to four sites, as seen from Figure 1. The model is then reduced to the effective 1D model, which we can treat with full quantum and thermal fluctuations by numerical methods. We have used quantum transfer matrix method to seek for the rather high-T region [36], while the QMC method can be applied to the whole T range even including low-T phases [38]. For the QMC simulation, we employ the stochastic-series-expansion (SSE) method [46,47,48], which is high-precision and less expensive in computational time so that we can use it in iterative calculations of self-consistent loop needed for the adiabatic and mean-field approximations.
as discussed in Section 3.2. We consider periodicities up to four sites, as seen from Figure 1. The model is then reduced to the effective 1D model, which we can treat with full quantum and thermal fluctuations by numerical methods. We have used quantum transfer matrix method to seek for the rather high-T region [36], while the QMC method can be applied to the whole T range even including low-T phases [38]. For the QMC simulation, we employ the stochastic-series-expansion (SSE) method [46,47,48], which is high-precision and less expensive in computational time so that we can use it in iterative calculations of self-consistent loop needed for the adiabatic and mean-field approximations.
 , treated as classical variables, are taken into account by the adiabatic approximations, being optimized so as to minimize the free energy. The mean-field approximation is imposed to the inter-chain part,
, treated as classical variables, are taken into account by the adiabatic approximations, being optimized so as to minimize the free energy. The mean-field approximation is imposed to the inter-chain part, 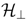 as discussed in Section 3.2. We consider periodicities up to four sites, as seen from Figure 1. The model is then reduced to the effective 1D model, which we can treat with full quantum and thermal fluctuations by numerical methods. We have used quantum transfer matrix method to seek for the rather high-T region [36], while the QMC method can be applied to the whole T range even including low-T phases [38]. For the QMC simulation, we employ the stochastic-series-expansion (SSE) method [46,47,48], which is high-precision and less expensive in computational time so that we can use it in iterative calculations of self-consistent loop needed for the adiabatic and mean-field approximations.
as discussed in Section 3.2. We consider periodicities up to four sites, as seen from Figure 1. The model is then reduced to the effective 1D model, which we can treat with full quantum and thermal fluctuations by numerical methods. We have used quantum transfer matrix method to seek for the rather high-T region [36], while the QMC method can be applied to the whole T range even including low-T phases [38]. For the QMC simulation, we employ the stochastic-series-expansion (SSE) method [46,47,48], which is high-precision and less expensive in computational time so that we can use it in iterative calculations of self-consistent loop needed for the adiabatic and mean-field approximations.
Figure 6.
Phase diagrams in the plane of  -T for
-T for  ,
,  ,
,  , and
, and  ; (a)
; (a)  and
and  ; (b)
; (b)  and
and  ; (c)
; (c)  and
and  [38].
[38].
 -T for
-T for  ,
,  ,
,  , and
, and  ; (a)
; (a)  and
and  ; (b)
; (b)  and
and  ; (c)
; (c)  and
and  [38].
[38].
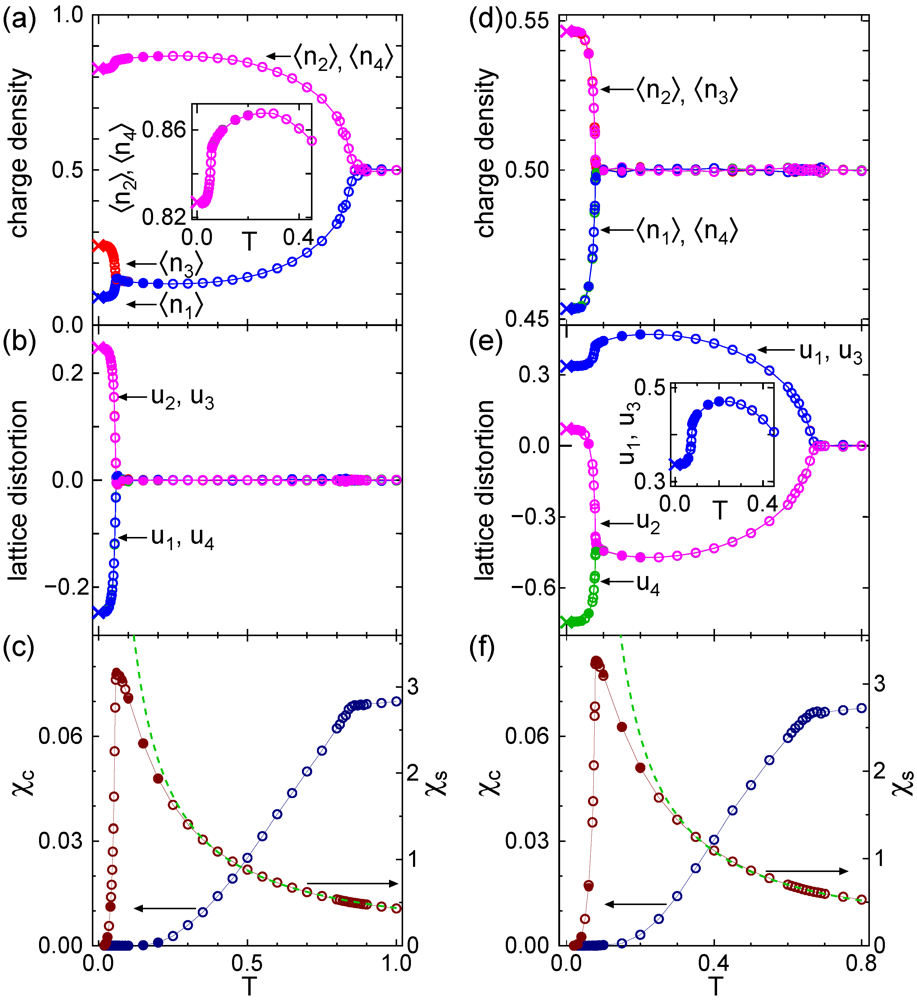
Figure 7.
Temperature dependences of charge densities, lattice distortions, and charge and magnetic susceptibilities for  ,
,  ,
,  ,
,  , and
, and  ; (a)–(c)
; (a)–(c)  ; (d)–(f)
; (d)–(f)  [38]. Open and closed circles represent results for N = 32 and 64, respectively. Statistical errors are smaller than the symbol sizes. Data shown by cross symbols at T=0 are obtained by the exact diagonalization (Lanczos) method for N = 12. The dashed line in (c) (f) shows a Curie–Weiss fit for
[38]. Open and closed circles represent results for N = 32 and 64, respectively. Statistical errors are smaller than the symbol sizes. Data shown by cross symbols at T=0 are obtained by the exact diagonalization (Lanczos) method for N = 12. The dashed line in (c) (f) shows a Curie–Weiss fit for  .
.
 ,
,  ,
,  ,
,  , and
, and  ; (a)–(c)
; (a)–(c)  ; (d)–(f)
; (d)–(f)  [38]. Open and closed circles represent results for N = 32 and 64, respectively. Statistical errors are smaller than the symbol sizes. Data shown by cross symbols at T=0 are obtained by the exact diagonalization (Lanczos) method for N = 12. The dashed line in (c) (f) shows a Curie–Weiss fit for
[38]. Open and closed circles represent results for N = 32 and 64, respectively. Statistical errors are smaller than the symbol sizes. Data shown by cross symbols at T=0 are obtained by the exact diagonalization (Lanczos) method for N = 12. The dashed line in (c) (f) shows a Curie–Weiss fit for  .
.
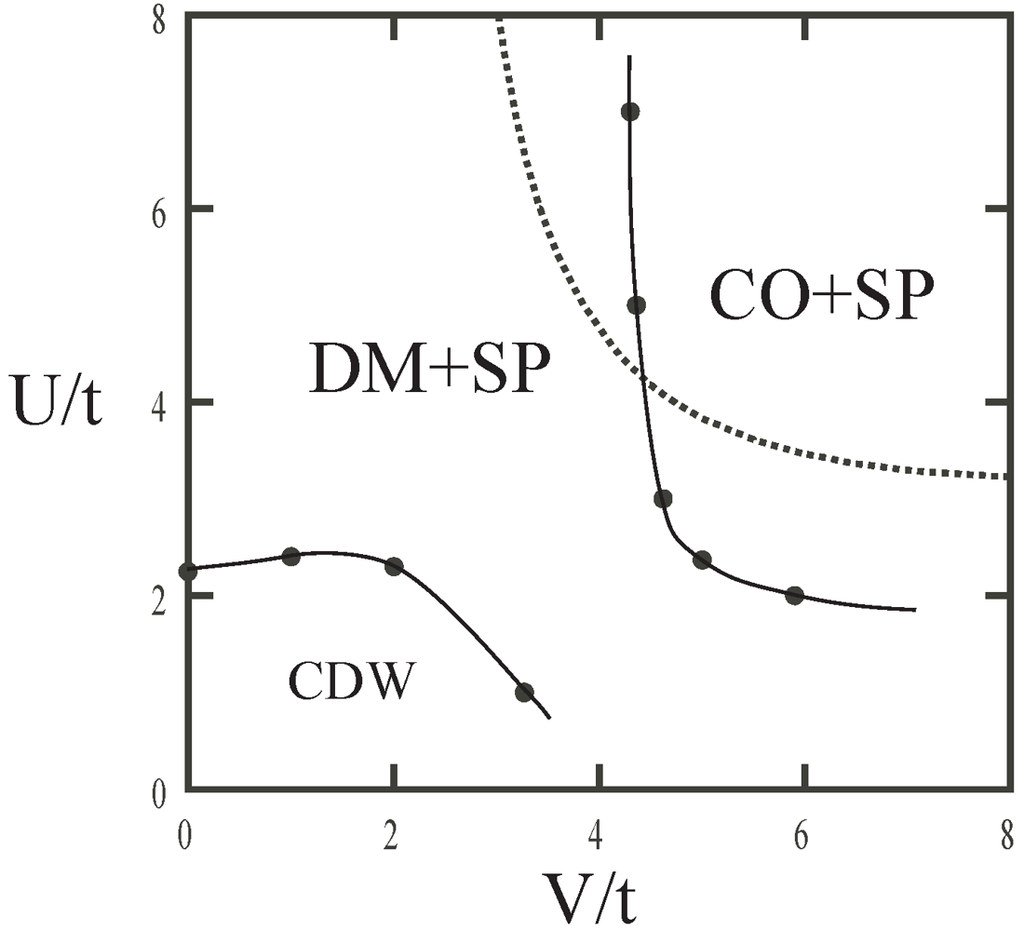
The results are summarized in the T-  phase diagrams shown in Figure 6, which are based on direct calculations of T dependences of the order parameters as shown in Figure 7. The global feature is that the uniform, i.e., paramagnetic metallic phase is driven to the insulating state which is DM or CO depending on the strength of
phase diagrams shown in Figure 6, which are based on direct calculations of T dependences of the order parameters as shown in Figure 7. The global feature is that the uniform, i.e., paramagnetic metallic phase is driven to the insulating state which is DM or CO depending on the strength of  when T is lowered. The boundary between DM and CO is very steep and likely of first order for
when T is lowered. The boundary between DM and CO is very steep and likely of first order for  ,
,  [Figure 6(a)]. On the other hand, when the anharmonic term in the elastic energy is finite (
[Figure 6(a)]. On the other hand, when the anharmonic term in the elastic energy is finite (  ), the coexistence phase of DM and CO emerges. This is analogous to the CO phase in the dimerized 1D EHM with electronic ferroelectricity, but different in the sense that the system is uniform at high-T, namely, the ferroelectricity is spontaneously generated [36]. In the case of the intrinsically dimerized lattice (
), the coexistence phase of DM and CO emerges. This is analogous to the CO phase in the dimerized 1D EHM with electronic ferroelectricity, but different in the sense that the system is uniform at high-T, namely, the ferroelectricity is spontaneously generated [36]. In the case of the intrinsically dimerized lattice (  ), the system always has finite dimerization and the transition at intermediate T occurs only to the CO state, which is continuous. Below these insulating phases, with further decreasing T, the system undergoes the SP transition showing tetramerization. The SP phases under DM and CO states are distinguishable [see Figure 1(e,f)] by the eight order parameters, though their T dependences of the charge and spin susceptibilities look alike as shown in Figure 7. We note that the paramagnetic insulating phases at intermediate region can not be obtained by simple one-body approximations such as the Hartree–Fock analysis, which usually needs magnetic ordering to open a charge gap.
), the system always has finite dimerization and the transition at intermediate T occurs only to the CO state, which is continuous. Below these insulating phases, with further decreasing T, the system undergoes the SP transition showing tetramerization. The SP phases under DM and CO states are distinguishable [see Figure 1(e,f)] by the eight order parameters, though their T dependences of the charge and spin susceptibilities look alike as shown in Figure 7. We note that the paramagnetic insulating phases at intermediate region can not be obtained by simple one-body approximations such as the Hartree–Fock analysis, which usually needs magnetic ordering to open a charge gap.
 phase diagrams shown in Figure 6, which are based on direct calculations of T dependences of the order parameters as shown in Figure 7. The global feature is that the uniform, i.e., paramagnetic metallic phase is driven to the insulating state which is DM or CO depending on the strength of
phase diagrams shown in Figure 6, which are based on direct calculations of T dependences of the order parameters as shown in Figure 7. The global feature is that the uniform, i.e., paramagnetic metallic phase is driven to the insulating state which is DM or CO depending on the strength of  when T is lowered. The boundary between DM and CO is very steep and likely of first order for
when T is lowered. The boundary between DM and CO is very steep and likely of first order for  ,
,  [Figure 6(a)]. On the other hand, when the anharmonic term in the elastic energy is finite (
[Figure 6(a)]. On the other hand, when the anharmonic term in the elastic energy is finite (  ), the coexistence phase of DM and CO emerges. This is analogous to the CO phase in the dimerized 1D EHM with electronic ferroelectricity, but different in the sense that the system is uniform at high-T, namely, the ferroelectricity is spontaneously generated [36]. In the case of the intrinsically dimerized lattice (
), the coexistence phase of DM and CO emerges. This is analogous to the CO phase in the dimerized 1D EHM with electronic ferroelectricity, but different in the sense that the system is uniform at high-T, namely, the ferroelectricity is spontaneously generated [36]. In the case of the intrinsically dimerized lattice (  ), the system always has finite dimerization and the transition at intermediate T occurs only to the CO state, which is continuous. Below these insulating phases, with further decreasing T, the system undergoes the SP transition showing tetramerization. The SP phases under DM and CO states are distinguishable [see Figure 1(e,f)] by the eight order parameters, though their T dependences of the charge and spin susceptibilities look alike as shown in Figure 7. We note that the paramagnetic insulating phases at intermediate region can not be obtained by simple one-body approximations such as the Hartree–Fock analysis, which usually needs magnetic ordering to open a charge gap.
), the system always has finite dimerization and the transition at intermediate T occurs only to the CO state, which is continuous. Below these insulating phases, with further decreasing T, the system undergoes the SP transition showing tetramerization. The SP phases under DM and CO states are distinguishable [see Figure 1(e,f)] by the eight order parameters, though their T dependences of the charge and spin susceptibilities look alike as shown in Figure 7. We note that the paramagnetic insulating phases at intermediate region can not be obtained by simple one-body approximations such as the Hartree–Fock analysis, which usually needs magnetic ordering to open a charge gap.In some molecular conductors showing SP transition, such as in MEM-(TCNQ)2, it is insisted that the lattice displacements are not adiabatic [49]. Effect of quantum nature of the lattice displacements on the finite-T phase diagrams is an interesting problem which remains to be investigated.
5. Discussion
Since we have developed well-organized ways of theoretically describing finite-T phase transitions in quarter-filled Q1D systems, essentially we can now make a direct comparison to experimental results for each compound. The canonical situation would be the CO phase transition in the EHM, without dimerization, as illustrated in the previous sections. However, it is rather rare to have such an example in the existing compounds; Many have intrinsic dimerization and/or complex interchain coupling. DI-DCNQI2Ag [34,50] was formally considered to be the typical system, while recently it has been proposed that the ordered phase below  220 K might be a complex CO, DM mixed state [Kakiuchi ~al.(2007)Kakiuchi, Wakabayashi, Sawa, Itou, and Kanoda, Seo and Motome(2009)].
220 K might be a complex CO, DM mixed state [Kakiuchi ~al.(2007)Kakiuchi, Wakabayashi, Sawa, Itou, and Kanoda, Seo and Motome(2009)].
 220 K might be a complex CO, DM mixed state [Kakiuchi ~al.(2007)Kakiuchi, Wakabayashi, Sawa, Itou, and Kanoda, Seo and Motome(2009)].
220 K might be a complex CO, DM mixed state [Kakiuchi ~al.(2007)Kakiuchi, Wakabayashi, Sawa, Itou, and Kanoda, Seo and Motome(2009)].TMTTF2X [35,53,54] family have been providing an ideal stage for such comparison, for systems with dimerization from the outset. As has been discussed in [38], the delicate competition and cooperation of DM, CO, and SP states under applied pressure are reproduced: The phase diagram in Figure 6 (c) shows a good agreement with the P-T phase diagram of X = AsF6 compound drawn based on NMR measurements [35]. Here,  correspond to the inverse of P; the effect of P acts strongly on transfer integrals, therefore the “effective” Coulomb interaction becomes smaller.
correspond to the inverse of P; the effect of P acts strongly on transfer integrals, therefore the “effective” Coulomb interaction becomes smaller.
 correspond to the inverse of P; the effect of P acts strongly on transfer integrals, therefore the “effective” Coulomb interaction becomes smaller.
correspond to the inverse of P; the effect of P acts strongly on transfer integrals, therefore the “effective” Coulomb interaction becomes smaller.Now, several Q1D compounds without dimerization have been synthesized where a CO transition is suggested, such as (o-DMTTF)2Br [55] and (EDT-TTF-CONMe2)2X [  AsF6 and Br] [56,57]. On the other hand, materials known from early days such as the compounds showing SP transition, MEM-(TCNQ)2 and (BCPTTF)2X (X = PF6, AsF6) [58,59,60], might be interesting to revisit with renewed understandings. In (EDO-TTF)2PF6 [61], a strong first-order phase transition is observed which is not reproduced in theory. More systematic comparisons are required.
AsF6 and Br] [56,57]. On the other hand, materials known from early days such as the compounds showing SP transition, MEM-(TCNQ)2 and (BCPTTF)2X (X = PF6, AsF6) [58,59,60], might be interesting to revisit with renewed understandings. In (EDO-TTF)2PF6 [61], a strong first-order phase transition is observed which is not reproduced in theory. More systematic comparisons are required.
 AsF6 and Br] [56,57]. On the other hand, materials known from early days such as the compounds showing SP transition, MEM-(TCNQ)2 and (BCPTTF)2X (X = PF6, AsF6) [58,59,60], might be interesting to revisit with renewed understandings. In (EDO-TTF)2PF6 [61], a strong first-order phase transition is observed which is not reproduced in theory. More systematic comparisons are required.
AsF6 and Br] [56,57]. On the other hand, materials known from early days such as the compounds showing SP transition, MEM-(TCNQ)2 and (BCPTTF)2X (X = PF6, AsF6) [58,59,60], might be interesting to revisit with renewed understandings. In (EDO-TTF)2PF6 [61], a strong first-order phase transition is observed which is not reproduced in theory. More systematic comparisons are required.From the theoretical point of view, several future directions can be listed. For example, the bosonization method introduced in Section 3.1 has been applied to the 1D electron-lattice coupled model [62,63,64]. In the presence of the lattice distortion with four-fold periodicity (  lattice distortion), the transition from SP state without CO to that with CO occurs at the ground state with increasing V [62]. For
lattice distortion), the transition from SP state without CO to that with CO occurs at the ground state with increasing V [62]. For  with
with  indicating the phase boundary, the lattice distortion has a maximum value, whereas it is suppressed for
indicating the phase boundary, the lattice distortion has a maximum value, whereas it is suppressed for 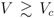 . The transition temperature of the SP state shows similar behavior [Sugiura ~al.(2005)Sugiura, Tsuchiizu, and Suzumura], consistent with the QMC results [38]. On the other hand, the alternating lattice modulation leads to the insulating state with spontaneous lattice dimerization, and appears between the metallic state and the CO insulating state [63]. A unified framework including such lattice degree of freedom, on top of the Q1D theory in Section 3, would provide a complementary understanding of the numerical works on the equivalent model in Section 4.
. The transition temperature of the SP state shows similar behavior [Sugiura ~al.(2005)Sugiura, Tsuchiizu, and Suzumura], consistent with the QMC results [38]. On the other hand, the alternating lattice modulation leads to the insulating state with spontaneous lattice dimerization, and appears between the metallic state and the CO insulating state [63]. A unified framework including such lattice degree of freedom, on top of the Q1D theory in Section 3, would provide a complementary understanding of the numerical works on the equivalent model in Section 4.
 lattice distortion), the transition from SP state without CO to that with CO occurs at the ground state with increasing V [62]. For
lattice distortion), the transition from SP state without CO to that with CO occurs at the ground state with increasing V [62]. For 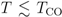 with
with  indicating the phase boundary, the lattice distortion has a maximum value, whereas it is suppressed for
indicating the phase boundary, the lattice distortion has a maximum value, whereas it is suppressed for 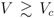 . The transition temperature of the SP state shows similar behavior [Sugiura ~al.(2005)Sugiura, Tsuchiizu, and Suzumura], consistent with the QMC results [38]. On the other hand, the alternating lattice modulation leads to the insulating state with spontaneous lattice dimerization, and appears between the metallic state and the CO insulating state [63]. A unified framework including such lattice degree of freedom, on top of the Q1D theory in Section 3, would provide a complementary understanding of the numerical works on the equivalent model in Section 4.
. The transition temperature of the SP state shows similar behavior [Sugiura ~al.(2005)Sugiura, Tsuchiizu, and Suzumura], consistent with the QMC results [38]. On the other hand, the alternating lattice modulation leads to the insulating state with spontaneous lattice dimerization, and appears between the metallic state and the CO insulating state [63]. A unified framework including such lattice degree of freedom, on top of the Q1D theory in Section 3, would provide a complementary understanding of the numerical works on the equivalent model in Section 4.Another direction is the coupling between charge and spin degrees of freedom. In Section 3 and Section 4, they are essentially decoupled: the spin-charge separation can be applied. Even in the same class of quarter-filled Q1D systems, the spin ordering, such as the AF state, is often observed; This indicates that not only the Coulomb but also the spin-exchange interactions between the 1D chains are non-negligible. The latter interactions stem from the interchain transfer integrals, which we neglected in the previous sections. Actually, recent works, experimental and theoretical, revealed that the interplay between such interchain couplings and the CO, together with the electron-lattice coupling, brings about the intricate phase competitions seen in TMTTF2X [54,65,66]. It is a challenging and desirable topic to incorporate the interchain spin-exchange interaction in the elaborated methodologies in Section 3 and Section 4.
The spin-charge coupling also appears more directly in some Q1D molecular systems, where the constituent molecule itself contains both the localized spin and itinerant carriers. A typical example is found in phthalocyanine (Pc) compounds such as TPP[Fe(Pc)(CN)2]2 [67], where observations of a giant magnetoresistance [68] has attracted much interest. In the latter material, π-electrons in the HOMO of Pc forms a 1D conduction band, whereas d-electrons in the center Fe atom are considered to be localized spins with strong anisotropy, namely Ising spins [68]. Since these two types of electron exist in one molecule, we expect strong π-d interaction between them. Then, we can model the system as 1D EHM coupled to local spins [69,70,71], as
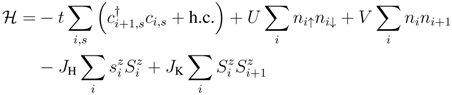
where the first three terms represent the 1D EHM for π-electron at quarter-filling and last two terms are for d spins.  denotes the π-d interaction. We also include the AF super-exchange interaction,
denotes the π-d interaction. We also include the AF super-exchange interaction,  , between d spins, whose short-range correlation is experimentally indicated by the analysis of the magnetic susceptibilities [72]. We have elucidated that, at low-T range compared to
, between d spins, whose short-range correlation is experimentally indicated by the analysis of the magnetic susceptibilities [72]. We have elucidated that, at low-T range compared to  , corresponding to a situation where the Ising spins are frozen antiferromagnetically, the π-d coupling,
, corresponding to a situation where the Ising spins are frozen antiferromagnetically, the π-d coupling,  , considerably enhances the correlation of CO [71], consistent with the insulating character seen in the compound. Calculations at finite-T including the magnetic field effect might elucidate the spin-charge coupled behavior in this new type of molecular system [73]. Another interesting example might be (Per)2M(mnt)2 (M = Ni, Pd, Pt, Fe) [74] where localized spins on M(mnt)2 and itinerant carriers on quarter-filled perylene chains interact with each other; in fact, the magnetic response suggests strong coupling of the SP and CDW states [75].
, considerably enhances the correlation of CO [71], consistent with the insulating character seen in the compound. Calculations at finite-T including the magnetic field effect might elucidate the spin-charge coupled behavior in this new type of molecular system [73]. Another interesting example might be (Per)2M(mnt)2 (M = Ni, Pd, Pt, Fe) [74] where localized spins on M(mnt)2 and itinerant carriers on quarter-filled perylene chains interact with each other; in fact, the magnetic response suggests strong coupling of the SP and CDW states [75].
 denotes the π-d interaction. We also include the AF super-exchange interaction,
denotes the π-d interaction. We also include the AF super-exchange interaction,  , between d spins, whose short-range correlation is experimentally indicated by the analysis of the magnetic susceptibilities [72]. We have elucidated that, at low-T range compared to
, between d spins, whose short-range correlation is experimentally indicated by the analysis of the magnetic susceptibilities [72]. We have elucidated that, at low-T range compared to  , corresponding to a situation where the Ising spins are frozen antiferromagnetically, the π-d coupling,
, corresponding to a situation where the Ising spins are frozen antiferromagnetically, the π-d coupling,  , considerably enhances the correlation of CO [71], consistent with the insulating character seen in the compound. Calculations at finite-T including the magnetic field effect might elucidate the spin-charge coupled behavior in this new type of molecular system [73]. Another interesting example might be (Per)2M(mnt)2 (M = Ni, Pd, Pt, Fe) [74] where localized spins on M(mnt)2 and itinerant carriers on quarter-filled perylene chains interact with each other; in fact, the magnetic response suggests strong coupling of the SP and CDW states [75].
, considerably enhances the correlation of CO [71], consistent with the insulating character seen in the compound. Calculations at finite-T including the magnetic field effect might elucidate the spin-charge coupled behavior in this new type of molecular system [73]. Another interesting example might be (Per)2M(mnt)2 (M = Ni, Pd, Pt, Fe) [74] where localized spins on M(mnt)2 and itinerant carriers on quarter-filled perylene chains interact with each other; in fact, the magnetic response suggests strong coupling of the SP and CDW states [75].6. Summary
In summary, we have reviewed recent progresses in theoretical works on the quasi-one-dimensional molecular conductors. The studies on CO as an origin of insulating behavior in the 2:1 charge transfer salts pointed to the importance of the strong-correlation effects, not only U but also V. The bosonization together with the renormalization group technique has made progress so that the finite-T phase transitions in Q1D systems can be discussed analytically. The scheme has also been combined with numerical methods to calculate physical observables such as the spin susceptibility and resistivity, whose results can be directly compared with experiments. The numerical simulations have also been applied to the model beyond the Q1D EHM, i.e., with coupling to the lattice, at finite-T. The obtained phase diagrams show a variety of the broken-symmetry states with coexistence and competition and well reproduce the  phase diagrams observed experimentally.
phase diagrams observed experimentally.
 phase diagrams observed experimentally.
phase diagrams observed experimentally.Acknowledgments
We are deeply grateful to Yukitoshi Motome and Masahisa Tsuchiizu for continued collaborations.
References
- Seo, H.; Hotta, C.; Fukuyama, H. Toward systematic understanding of diversity of electronic properties in low-dimensional molecular solids. Chem. Rev. 2004, 104, 5005–5036. [Google Scholar] [CrossRef]
- Lebed, A.G. The Physics of Organic Superconductors and Conductors; Springer-Verlag: Heidelberg, Germany, 2008. [Google Scholar]
- Seo, H.; Merino, J.; Hideo, Y.; Masao, O. Theoretical Aspects of Charge Ordering in Molecular Conductors. J. Phys. Soc. Jpn. 2006, 75, 051009:1–051009:20. [Google Scholar]
- Brown, S.E.; Chaikin, P.M.; Naughton, M.J. La Tour des Sels de Bechgaard. In The Physics of Organic Superconductors and Conductors; Lebed, A.G., Ed.; Springer-Verlag: Berlin, Germany, 2008; pp. 357–512. [Google Scholar]
- Bourbonnais, C.; Jérome, D. Interacting electrons in quasi-one-dimensional organic superconductors. In The Physics of Organic Superconductors and Conductors; Lebed, A.G., Ed.; Springer-Verlag: Berlin, Germany, 2008. [Google Scholar]
- Hünig, S.; Herberth, E. N,N′-dicyanoquinonediimines (DCNQIs): versatile acceptors for organic conductors. Chem. Rev. 2004, 104, 5535–5563. [Google Scholar]
- Mori, T.; Kobayashi, A.; Sasaki, Y.; Kobayashi, H.; Saito, G.; Inokuchi, H. The Intermolecular Interaction of Tetrathiafulvalene and Bis(ethylenedithio)tetrathiafulvalene in Organic Metals. Calculation of Orbital Overlaps and Models of Energy-band Structures. Bull. Chem. Soc. Jpn. 1984, 57, 627–633. [Google Scholar] [CrossRef]
- Mila, F.; Penc, K. Model calculations for 1D correlated systems. J. Electron. Spectrosc. 2001, 117–118, 451–467. [Google Scholar] [CrossRef]
- Seo, H.; Fukuyama, H. Antiferromagnetic Phases of One-Dimensional Quarter-Filled Organic Conductors. J. Phys. Soc. Jpn. 1997, 66, 1249–1252. [Google Scholar] [CrossRef]
- Monceau, P.; Nad, F.; Brazovskii, S. Ferroelectric Mott-Hubbard Phase of Organic (TMTTF)2X Conductors. Phys. Rev. Lett. 2001, 86, 4080–4083. [Google Scholar] [CrossRef]
- Tsuchiizu, M.; Orignac, E. Ising transition in a one-dimensional quarter-filled electron system with dimerization. J. Phys. Chem. Solids. 2002, 63, 1459–1463. [Google Scholar] [CrossRef]
- Ishihara, S. Electronic Ferroelectricity and Frustration. J. Phys. Soc. Jpn. 2010, 79, 011010:1–011010:11. [Google Scholar]
- Emery, V.J.; Noguera, C. Critical properties of a spin-1/2 chain with competing interactions. Phys. Rev. Lett. 1988, 60, 631–634. [Google Scholar] [CrossRef]
- Kobayashi, N.; Ogata, M.; Yonemitsu, K. Coexistence of SDW and Purely-Electronic CDW in Quarter-Filled Organic Conductors. J. Phys. Soc. Jpn. 1998, 67, 1098–1101. [Google Scholar] [CrossRef]
- Kishigi, K.; Hasegawa, Y. Two Kinds of the Coexistent States in One-Dimensional Quarter-Filled Systems under Magnetic Fields and Temperatures. J. Phys. Soc. Jpn. 2000, 69, 3621–3628. [Google Scholar] [CrossRef]
- Tomio, Y.; Suzumura, Y. Quarter-filled spin density wave states with long-range Coulomb interaction. J. Phys. Chem. Solids 2001, 62, 431–434. [Google Scholar] [CrossRef]
- Kuwabara, M.; Seo, H.; Ogata, M. Coexistence of Charge Order and Spin-Peierls Lattice Distortion in One-Dimensional Organic Conductors. J. Phys. Soc. Jpn. 2003, 72, 225–228. [Google Scholar]
- Ung, K.C.; Mazumdar, S.; Toussaint, D. Metal-Insulator and Insulator-Insulator Transitions in the Quarter-Filled Band Organic Conductors. Phys. Rev. Lett. 1994, 73, 2603–2606. [Google Scholar] [CrossRef]
- Clay, R.; Mazumdar, S.; Campbell, D. Pattern of charge ordering in quasi-one-dimensional organic charge-transfer solids. Phys. Rev. B 2003, 67, 115121:1–115121:9. [Google Scholar]
- Fukuyama, H.; Takayama, H. Dynamical Properties of Quasi-One-Dimensional Conductors–Phase Hamiltonian Approach. In Electronic Properties of Inorganic Quasi-One-Dimensional Compounds; Monceau, P., Ed.; Reidel Publishing: Dordrecht, The Nertherlands, 1985; p. 41. [Google Scholar]
- Yoshioka, H.; Tsuchiizu, M.; Otsuka, Y.; Seo, H. Finite-Temperature Properties across the Charge Ordering Transition–Combined Bosonization, Renormalization Group, and Numerical Methods. J. Phys. Soc. Jpn. 2010, 79, 094714:1–094714:9. [Google Scholar]
- Yoshioka, H.; Tsuchiizu, M.; Suzumura, Y. Correlation Effects in a One-Dimensional Quarter-Filled Electron System with Repulsive Interactions. J. Phys. Soc. Jpn. 2000, 69, 651–654. [Google Scholar] [CrossRef]
- Yoshioka, H.; Tsuchiizu, M.; Suzumura, Y. Effects of Next-Nearest-Neighbor Repulsion on One-Dimensional Quarter-Filled Electron Systems. J. Phys. Soc. Jpn. 2001, 70, 762–773. [Google Scholar] [CrossRef]
- Tsuchiizu, M.; Yoshioka, H.; Suzumura, Y. Crossover from Quarter-Filling to Half-Filling in a One-Dimensional Electron System with a Dimerized and Quarter-Filled Band. J. Phys. Soc. Jpn. 2001, 70, 1460–1463. [Google Scholar] [CrossRef]
- Sano, K.; Ōno, Y. Critical behavior near the metal-insulator transition in the one-dimensional extended Hubbard model at quarter filling. Phys. Rev. B 2004, 70, 155102:1–155102:7. [Google Scholar]
- Yoshioka, H.; Tsuchiizu, M.; Seo, H. Finite-Temperature Charge-Ordering Transition and Fluctuation Effects in Quasi One-Dimensional Electron Systems at Quarter Filling. J. Phys. Soc. Jpn. 2006, 75, 063706:1–063706:5. [Google Scholar]
- Yoshioka, H.; Tsuchiizu, M.; Seo, H. Charge-Ordered State versus Dimer-Mott Insulator at Finite Temperatures. J. Phys. Soc. Jpn. 2007, 76, 103701:1–103701:4. [Google Scholar]
- Scalapino, D.; Imry, Y.; Pincus, P. Generalized Ginzburg-Landau theory of pseudo-one-dimensional systems. Phys. Rev. B 1975, 11, 2042–2048. [Google Scholar]
- Schulz, H.J. Dynamics of Coupled Quantum Spin Chains. Phys. Rev. Lett. 1996, 77, 2790–2793. [Google Scholar] [CrossRef]
- Nélisse, H.; Bourbonnais, C.; Touchette, H.; Vilk, Y.; Tremblay, A.M. Spin susceptibility of interacting electrons in one dimension: Luttinger liquid and lattice effects. Eur. Phys. J. B 1999, 12, 351–365. [Google Scholar] [CrossRef]
- Fuseya, Y.; Tsuchiizu, M.; Suzumura, Y.; Bourbonnais, C. Effect of Intersite Repulsions on Magnetic Susceptibility of One-Dimensional Electron Systems at Quarter Filling. J. Phys. Soc. Jpn. 2005, 74, 3159–3162. [Google Scholar] [CrossRef]
- Giamarchi, T. Umklapp process and resistivity in one-dimensional fermion systems. Phys. Rev. B 1991, 44, 2905–2913. [Google Scholar] [CrossRef]
- Giamarchi, T. Resistivity of a one-dimensional interacting quantum fluid. Phys. Rev. B 1992, 46, 342–349. [Google Scholar]
- Hiraki, K.; Kanoda, K. Electronic state of the organic salt (DI-DCNQI)2Ag, where DI-DCNQI is 2,5-diiodo- N,N′-dicyanoquinonediimine. Phys. Rev. B 1996, 54, R17276–R17279. [Google Scholar] [CrossRef]
- Zamborszky, F.; Yu, W.; Raas, W.; Brown, S.; Alavi, B.; Merlic, C.; Baur, A. Competition and coexistence of bond and charge orders in (TMTTF)2AsF6. Phys. Rev. B 2002, 66, 081103:1–081103:4. [Google Scholar]
- Seo, H.; Motome, Y.; Kato, T. Finite-Temperature Phase Transitions in Quasi-One-Dimensional Molecular Conductors. J. Phys. Soc. Jpn. 2007, 76, 013707:1–013707:4. [Google Scholar]
- Clay, R.; Hardikar, R.; Mazumdar, S. Temperature-driven transition from the Wigner crystal to the bond-charge-density wave in the quasi-one-dimensional quarter-filled band. Phys. Rev. B 2007, 76, 205118:1–205118:12. [Google Scholar]
- Otsuka, Y.; Seo, H.; Motome, Y.; Kato, T. Finite-Temperature Phase Diagram of Quasi-One-Dimensional Molecular Conductors: Quantum Monte Carlo Study. J. Phys. Soc. Jpn. 2008, 77, 113705:1–113705:4. [Google Scholar]
- Mila, F.; Zotos, X. Phase Diagram of the One-Dimensional Extended Hubbard Model at Quarter-Filling. Eur. Phys. Lett. 1993, 24, 133–138. [Google Scholar] [CrossRef]
- Penc, K.; Mila, F. Phase diagram of the one-dimensional extended Hubbard model with attractive and/or repulsive interactions at quarter filling. Phys. Rev. B 1994, 49, 9670–9678. [Google Scholar] [CrossRef]
- Hirsch, J.; Scalapino, D. 2pF and 4pF Instabilities in the One-Dimensional Electron Gas. Phys. Rev. Lett. 1983, 50, 1168–1171. [Google Scholar] [CrossRef]
- Hirsch, J.; Scalapino, D. 2pF and 4pF instabilities in a one-quarter-filled-band Hubbard model. Phys. Rev. B 1983, 27, 7169–7185. [Google Scholar] [CrossRef]
- Hirsch, J.; Scalapino, D. 2pF and 4pF instabilities in the one-dimensional Hubbard model. Phys. Rev. B 1984, 29, 5554–5561. [Google Scholar] [CrossRef]
- Hirsch, J. Charge-Density-Wave to Spin-Density-Wave Transition in the Extended Hubbard Model. Phys. Rev. Lett. 1984, 53, 2327–2330. [Google Scholar] [CrossRef]
- Ejima, S.; Gebhard, F.; Nishimoto, S. Tomonaga-Luttinger parameters for doped Mott insulators. Euro. Phys. Lett. 2005, 70, 492–498. [Google Scholar] [CrossRef]
- Sandvik, A.W.; Kurkijärvi, J. Quantum Monte Carlo simulation method for spin systems. Phys. Rev. B 1991, 43, 5950–5961. [Google Scholar]
- Sandvik, A.W. A generalization of Handscomb’s quantum Monte Carlo scheme-application to the 1D Hubbard model. J. Phys. A 1992, 25, 3667–3682. [Google Scholar] [CrossRef]
- Sandvik, A.W. Stochastic series expansion method with operator-loop update. Phys. Rev. B 1999, 59, R14157–R14160. [Google Scholar] [CrossRef]
- Pouget, J.P. Bond and charge ordering in low-dimensional organic conductors. Physica B 2012, 407, 1762–1770. [Google Scholar] [CrossRef]
- Hiraki, K.; Kanoda, K. Wigner Crystal Type of Charge Ordering in an Organic Conductor with a Quarter-Filled Band: (DI-DCNQI)2Ag. Phys. Rev. Lett. 1998, 80, 4737–4740. [Google Scholar] [CrossRef]
- Wigner Crystallization in (DI-DCNQI)2AgDetected by Synchrotron Radiation X-Ray Diffraction. Phys. Rev. Lett. 2007, 98, 066402:1–066402:4.
- Seo, H.; Motome, Y. Spiral Charge Frustration in the Molecular Conductor (DI-DCNQI)2Ag. Phys. Rev. Lett. 2009, 102, 196403:1–196403:4. [Google Scholar]
- Chow, D.; Zamborszky, F.; Alavi, B.; Tantillo, D.; Baur, A.; Merlic, C.; Brown, S. Charge Ordering in the TMTTF Family of Molecular Conductors. Phys. Rev. Lett. 2000, 85, 1698–1701. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, F.; Zamborszky, F.; Alavi, B.; Baur, A.; Merlic, C.; Brown, S. Electron-lattice coupling and broken symmetries of the molecular salt (TMTTF)2SbF6. Phys. Rev. B 2004, 70, 121101:1–121101:4. [Google Scholar]
- Foury-Leylekian, P.; Auban-Senzier, P.; Coulon, C.; Jeannin, O.; Fourmigué, M.; Pasquier, C.; Pouget, J.P. Phase diagram of the correlated quarter-filled-band organic salt series (O-DMTTF)2X (X = Cl, Br, I). Phys. Rev. B 2011, 84, 195134:1–195134:17. [Google Scholar]
- Auban-Senzier, P.; Pasquier, C.; Jérome, D.; Suh, S.; Brown, S.; Mézière, C.; Batail, P. Phase Diagram of Quarter-Filled Band Organic Salts [EDT-TTF-CONMe2]2X, X = AsF2 and Br. Phys. Rev. Lett. 2009, 102, 257001:1–257001:4. [Google Scholar]
- Zorina, L.; Simonov, S.; Mézière, C.; Canadel, E.; Suh, S.; Brown, S.E.; Foury-Leylekian, P.; Fertey, P.; Pouget, J.P.; Batail, P. Charge ordering, symmetry and electronic structure issues and Wigner crystal structure of the quarter-filled band Mott insulators and high pressure metals
 -(EDT-TTF-CONMe2)2X, X = Br and AsF6. J. Mater. Chem. 2009, 19, 6980–6994. [Google Scholar]
-(EDT-TTF-CONMe2)2X, X = Br and AsF6. J. Mater. Chem. 2009, 19, 6980–6994. [Google Scholar] - Huizinga, S.; Kommandeur, J.; Sawatzky, G.A.; Thole, B.T.; Kopinga, K.; de Jonge, W.J.M.; Roos, J. Spin-Peierls transition in N-methyl-N-ethyl-morpholinium-ditetracyanoquinodimethanide [MEM-(TCNQ)2]. Phys. Rev. B 1979, 19, 4723–4732. [Google Scholar] [CrossRef]
- Liu, Q.; Ravy, S.; Pouget, J.P. Structural fluctuations and spin-peierls transitions revisited. Synth. Met. 1993, 56, 1840–1845. [Google Scholar] [CrossRef]
- Dumoulin, B.; Bourbonnais, C.; Ravy, S.; Pouget, J.P.; Coulon, C. Fluctuation Effects in Low-Dimensional Spin-Peierls Systems: Theory and Experiment. Phys. Rev. Lett. 1996, 76, 1360–1363. [Google Scholar] [CrossRef]
- Ota, A.; Yamochi, H.; Saito, G. A novel metal-insulator phase transition observed in (EDO-TTF)2PF6. J. Mater. Chem. 2002, 12, 2600–2602. [Google Scholar] [CrossRef]
- Sugiura, M.; Suzumura, Y. Competition of Dimerization and Charge Ordering in the Spin-Peierls State of Organic Conductors. J. Phys. Soc. Jpn. 2003, 72, 1458–1468. [Google Scholar] [CrossRef]
- Sugiura, M.; Tsuchiizu, M.; Suzumura, Y. Interplay of Lattice Dimerization and Charge Ordering in One-Dimensional Quarter-Filled Electron Systems. J. Phys. Soc. Jpn. 2004, 73, 2487–2493. [Google Scholar] [CrossRef]
- Sugiura, M.; Tsuchiizu, M.; Suzumura, Y. Spin-Peierls Transition Temperature in Quarter-Filled Organic Conductors. J. Phys. Soc. Jpn. 2005, 74, 983–987. [Google Scholar] [CrossRef]
- Yoshimi, K.; Seo, H.; Ishibashi, S.; Brown, S. Tuning the Magnetic Dimensionality by Charge Ordering in the Molecular TMTTF Salts. Phys. Rev. Lett. 2012, 108, 096402:1–096402:5. [Google Scholar]
- Yoshimi, K.; Seo, H.; Ishibashi, S.; Brown, S.E. Spin frustration, charge ordering, and enhanced antiferromagnetism in TMTTF2SbF6. Physica B 2012, 407, 1783–1786. [Google Scholar]
- Matsuda, M.; Naito, T.; Inabe, T.; Hanasaki, N.; Tajima, H.; Otsuka, T.; Awaga, K.; Narymbetov, B.; Kobayashi, H. A one-dimensional macrocyclic π-ligand conductor carrying a magnetic center.Structure and electrical, optical and magnetic properties of TPP[Fe(Pc)(CN)2]2 {TPP = tetraphenylphosphonium and [Fe(Pc)(CN)2] = dicyano(phthalocyaninato)iron(iii)}. J. Mater. Chem. 2000, 10, 631–636. [Google Scholar] [CrossRef]
- Hanasaki, N.; Matsuda, M.; Tajima, H.; Ohmichi, E.; Osada, T.; Naito, T.; Inabe, T. Giant Negative Magnetoresistance Reflecting Molecular Symmetry in Dicyano(phthalocyaninato)iron Compounds. J. Phys. Soc. Jpn. 2006, 75, 033703:1–033703:4. [Google Scholar]
- Hotta, C.; Ogata, M.; Fukuyama, H. Interaction of the Ground State of Quarter-Filled One-Dimensional Strongly Correlated Electronic System with Localized Spins. Phys. Rev. Lett. 2005, 95, 216402:1–216402:4. [Google Scholar]
- Hotta, C. Interplay of strongly correlated electrons and localized Ising moments in one dimension. Phys. Rev. B 2010, 81, 245104:1–245104:9. [Google Scholar]
- Otsuka, Y.; Seo, H.; Motome, Y. Charge ordering due to π-d coupling in one-dimensional system. Physica B 2010, 405, S317–S320. [Google Scholar]
- Tajima, H.; Yoshida, G.; Matsuda, M.; Hanasaki, N.; Naito, T.; Inabe, T. Magnetic torque and heat capacity measurements on TPP[Fe(Pc)(CN)2]2. Phys. Rev. B 2008, 78, 064424:1–064424:8. [Google Scholar]
- Otsuka, Y.; Seo, H.; Motome, Y. Magnetic field effect on one-dimensional quarter-filled extended Hubbard model. 2012. in preparation. [Google Scholar]
- Gama, V.; Henriques, R.T.; Bonfait, G.; Almeida, M.; Ravy, S.; Pouget, J.P.; Alcácer, L. The Interplay Between Conduction Electrons and Chains of Localised Spins in The Molecular Metals (Per)2M(mnt)2, M = Au, Pt, Pd, Ni, Cu, Co and Fe. Mol. Cryst. Liq. Cryst. 1993, 234, 171–178. [Google Scholar] [CrossRef]
- Green, E.; Brooks, J.; Kuhns, P.; Reyes, A.; Lumata, L.; Almeida, M.; Matos, M.; Henriques, R.; Wright, J.; Brown, S. Interaction of magnetic field-dependent Peierls and spin-Peierls ground states in (Per)2[Pt(mnt)2]. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).