Abstract
The recovery of radiation damage induced by 231-MeV xenon ions with varying fluence (from 5 × 1011 to 2 × 1014 cm−2) in α-Al2O3 (corundum) single crystals has been studied by means of isochronal thermal annealing of radiation-induced optical absorption (RIOA). The integral of elementary Gaussians (product of RIOA spectrum decomposition) OK has been considered as a concentration measure of relevant oxygen-related Frenkel defects (neutral and charged interstitial-vacancy pairs, F-H, F+-H−). The annealing kinetics of these four ion-induced point lattice defects has been modelled in terms of diffusion-controlled bimolecular recombination reactions and compared with those carried out earlier for the case of corundum irradiation by fast neutrons. The changes in the parameters of interstitial (mobile component in the recombination process) annealing kinetics—activation energy E and pre-exponential factor X—in ion-irradiated crystals are considered.
1. Introduction
Several metal oxides (binary ones, perovskites, spinel-structed, garnets) reveal fascinating physical–chemical properties, high melting temperature, and wide optical transparency region (energy gap, Eg exceeds 7 eV), and, therefore, these single crystals and polycrystalline ceramics are widely used for different scientific and technological application. In particular, aluminum oxide (corundum, sapphire, α-Al2O3 with lattice structure of space group [1]) is exploited as a host for ruby, titanium–sapphire, and color-center lasers [2,3,4,5]; material for optical windows and light guides, the medical and jewelry industry, and substrates for electronics [6]; scintillation detectors and luminescent dosimeters of radiation [7,8,9,10,11,12]; etc. Because of its high radiation tolerance, corundum is used in fission-based energetics and is considered a promising material for projected advanced and fusion reactors [13,14,15,16].
Radiation processes in α-Al2O3 crystals induced by incident energetic particles (neutrons, electrons, light and heavy ions) have been thoroughly investigated over many decades using different experimental methods [13,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]. To a large extent, the degradation of functional materials exploited under a radiation environment is determined by increasing radiation damage via the creation, accumulation, and aggregation of primary lattice defects, interstitial-vacancy (i-v) Frenkel pairs. In corundum, as well as in other radiation-resistant metal oxides, the formation energy of a Frenkel pair (displacement threshold energy) exceeds the Eg value by several times (see, e.g., Ref. [25] and references therein), and i-v pairs are predominantly formed due to elastic collisions of incident particles with material nuclei. It is generally accepted that such an impact (displacement) mechanism is solely responsible for the damage induced by fast fission neutrons [13,21,25,40,41]. However, some contribution of ionization losses could also be considered in case of material irradiation by swift heavy ions, which provide extremely high density of electronic excitations along ion tracks [32,34,42,43,44,45]. Irradiation with swift heavy ions causes intense local lattice disorder and efficient formation of extended defects.
Nowadays, oxygen vacancy-related defects have been studied more completely in α-Al2O3 single crystals. The optical characteristics (absorption/excitation and relevant emission bands) of a single oxygen vacancy with two or one trapped electron (the classical F and F+ center, respectively), as well as the simplest F2 dimer centers in different charge states (from two to four electrons localized in two adjacent oxygen vacancies), have been revealed in crystals either exposed to radiation [19,20,22,24,26,31,32,37,38] or grown under reducing atmosphere conditions (anion-deficient or thermochemically reduced crystals [24,26,46,47,48]). In addition, the EPR signal of the F+ center was revealed in neutron-irradiated corundum long ago [18], and the signal of the paramagnetic dimer of two adjacent F+ centers (total spin S = 1) was recently detected as well [38].
The processes of thermal annealing of the radiation-induced F- and F2-type defects in corundum crystals have also been studied [13,22,24,28,30,35,36,37,38,46,47]. It has been established that just oxygen interstitials act as a mobile component in a temperature-stimulated recombination of complementary defects from i-v Frenkel pairs. This conclusion is based on a very high thermal stability of the F centers (up to at least 1000 °C) in thermochemically reduced α-Al2O3 crystals (as well as in MgO [49]), which do not contain oxygen interstitials, while the F center annealing in the irradiated crystals takes place at significantly lower temperatures [24,46,47].
The thermal annealing kinetics of the F-type centers in corundum crystals has been theoretically analyzed [35,50], and lately also with the involvement of two types of mobile oxygen interstitials [37,51,52]. It is notable that isolated oxygen interstitials have been revealed only recently in neutron-irradiated α-Al2O3 crystals [36,51]. Such single interstitials have been detected via the EPR method in the form of a superoxide ion. Until then, only the ERP signals of oxygen interstitials associated with additional imperfections (in particular, with a cation vacancy) were detected in binary metal oxides (see, e.g., Refs. [36,53]).
The present study is a logical continuation of our previous paper [39], where the accumulation of different anion Frenkel defects with fluence of 231-MeV xenon ions was studied in α-Al2O3 single crystals. The isochronal annealing of oxygen-related Frenkel defects (the defect concentration is taken as an integral of a relevant elementary optical absorption band) has been measured in corundum crystals preliminary irradiated by energetic xenon ions with fluence varying from 5 × 1011 to 2 × 1014 cm−2. The experimentally obtained annealing kinetics have been theoretically analyzed in terms of the diffusion-controlled reactions between two pairs of oxygen Frenkel defects.
2. Experimental
Nominally pure α-Al2O3 single crystals were supplied by Alineason Materials Technology GmbH. The crystal plates with dimensions of 5 × 5 × 0.5 mm3 were cut off with a base orientation perpendicular to the c crystal axis and polished from both sides. Using the EPR method, the concentration of Cr3+ impurity centers was determined as ≈3.2 × 1015 cm−3, while commonly present Fe3+ ions were not detected at all (if present, significantly below 1014 cm−3).
The samples were irradiated by 231-MeV 132Xe ions (flux along the c axis) with nine different fluences Φ between 5 × 1011 and 2 × 1014 cm−2 at room temperature (RT) using the DC-60 accelerator in Astana, Kazakhstan. Based on SRIM-2013 calculations [54], the penetration depth (range) of ions into the crystals was estimated approximately as R = 13.5 μm.
The optical absorption spectra were measured at RT in a wide range of 1.5–8.5 eV using two setups: a JASCO V-660 spectrometer (till 6.5 eV) and a vacuum monochromator VMR-2 with a hydrogen discharge in a flow capillary tube as a light source. In the latter case, the number of incident photons was normalized via sodium salicylate luminescence. The absorption of a pristine crystal was subtracted from the spectrum for the same sample after irradiation. This difference spectrum of the so-called radiation-induced optical absorption (RIOA) was decomposed into Gaussians, which characterized the concentration of different point lattice defects.
The isochronal thermal annealing of the irradiated crystals was performed in an argon atmosphere as follows: a sample was heated to a predetermined temperature Tpr and stayed at this temperature for five minutes; finally, a quartz reactor tube with the sample was removed from a furnace and passively cooled down to RT. Such cycles were performed under the same conditions with an increase in Tpr by 20–40 K to up to 1250 K. After each preheating, the RIOA spectrum was measured at RT and decomposed into elementary components.
The concentration of paramagnetic centers (both impurities and radiation defects) in corundum crystals was determined by means of a tailored Bruker software and a 9.8 GHz spectrometer Bruker ELEXSYS-II E500. The estimation accuracy of the paramagnetic center concentration (impurity ions or radiation defects) was about 15% (see also Ref. [39]).
3. Results and Discussion
3.1. Thermal Annealing of RIOA Bands Related to Radiation-Induced Frenkel Defects
In the present paper, we focus on the thermal annealing kinetics of oxygen-related Frenkel pairs (both charged and neutral i-v pairs) in corundum single crystals irradiated by different fluences of energetic xenon ions. According to the literature data [19,23,24,46], two optical absorption bands that peaked at 4.8 and 5.3 eV are related to the F+ center, the structure of which ( in Kröger–Vink notation) is strictly confirmed by the EPR method (see, e.g., Refs. [18,38]. The absorption band, detected in thermochemically reduced and irradiated crystals and peaking around 6.1 eV, is attributed to the F centers (a neutral defect with respect to a regular lattice, ) [19,23,24,46].
The characteristics of oxygen interstitials, with defects being complementary to vacancy-containing F and F+ centers, have been revealed only recently. A single charged oxygen interstitial (labelled H− or in Kröger–Vink notation) stabilized by a trapped hole was detected in the form of superoxide ion in a neutron-irradiated corundum by the EPR method [36,51]. The analysis of isochronal annealing of the EPR signal and RIOA spectra allowed the 5.6 eV absorption band to be attributed to the H− centers [36,37,51,52]) and for the ≈6.6 eV RIOA band to be suggested as being connected with neutral oxygen interstitials (labelled as H0 or ) [37,51,52].
In the previous paper, we studied the evolution of optical absorption spectra with Xe-ion fluence and confirmed/proved the radiation-induced origin of the defects responsible for a RIOA above 4 eV (F+, F, H− and H0 centers) [39]. Note that the analysis of RIOA in neutron- or ion-irradiated corundum single crystals was always performed via spectra decomposition into Gaussian components related to different types of radiation defects [36,37,39,51,52]. Figure 1 presents the examples of the RIOA spectra decomposition into Gaussians in the crystals exposed to different Xe-ion fluences (Figure 1a,c) or after additional preheating of the irradiated crystals to prescribed temperatures Tpr (Figure 1b,d). The same parameters of Gaussian components (maximum position and bandwidth) were used in Ref. [39] and in the present study. The Gaussians marked by dashed lines belong to still-unidentified defects and are not the subject of this article. The F2-type dimer centers in different charge states possess characteristic absorption bands at 2.3–4.0 eV [22,24,32,36,37,47,51], their concentration in Xe-irradiated crystals is low, and these dimers are not considered in the present study.
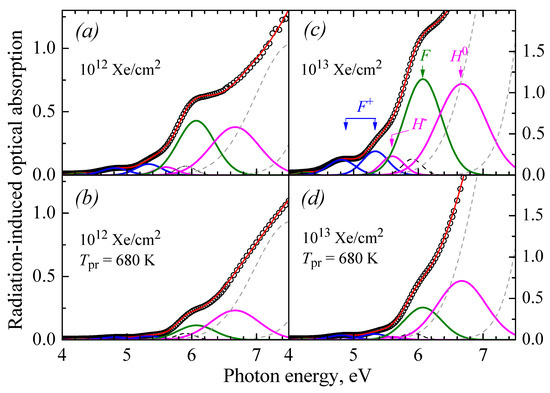
Figure 1.
The RIOA spectra and their decomposition into elementary components for α-Al2O3 single crystals irradiated with two fluences, Φ = 1012 Xe/cm2 and Φ = 1013 Xe/cm2. The symbols demonstrate experimental points, and the red solid line is the sum of all Gaussian components. The spectra are measured at RT after irradiation (a,c) and additional preheating of the irradiated crystal to Tpr = 680 K (b,d).
Figure 2 demonstrates the concentration dependences of four oxygen-related Frenkel defects on the fluence of corundum crystal irradiation with 231-MeV Xe ions (compared to Ref. [39], irradiations with three more fluences were performed). The continuous increase in defect concentration with fluence up to Φ = 2 × 1014 cm−2 proves that, similar to the classic F and F+ centers, the defects connected with the absorption Gaussians at ≈5.6 and ≈6.6 eV are the irradiation-induced lattice defects.
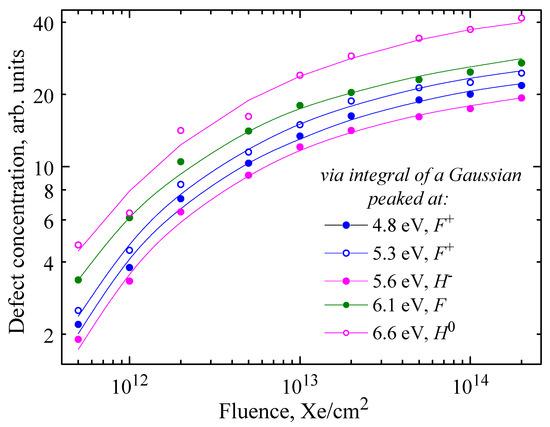
Figure 2.
Dependences of the defect concentration on the Xe-ion fluence in α-Al2O3 single crystals. The integral of a relevant Gaussian is used as a measure (concentration in arb. units) of different Frenkel defects. Solid lines serve as guides for the eye.
In Figure 2, the integral of a certain Gaussian (in arbitrary units) is taken as a concentration measure of the relevant Frenkel defects. At the same time, the concentration of paramagnetic defects—in particular, the F+ and H− centers—can directly be determined by the EPR method. Note that ion irradiation created defects only within a thin crystal layer and their absolute number in the crystal (number of unpaired spins) was significantly lower than in the case of neutron irradiation. Because of the features or relevant EPR spectra, only the signal of superoxide ions (an H− stabilized by a trapped hole) was clearly registered in our samples. At Φ = 1013 Xe cm−2, the concentration of H− interstitials was estimated as N = 1.5 × 1018 cm−3, the value approximately doubled for Φ = 1014 cm−2 (N = 3.2 × 1018 cm−3), and the concentration of reached N = 3.55 × 1018 cm−3 in the case of the highest Φ = 2 × 1014 cm−2. The accuracy of concentration estimation was about 15% (for details, see Ref. [39]). Note that in a neutron-irradiated corundum, the EPR signals of both the F+ and centers were clearly detectable and the concentration of these paramagnetic defects was practically equal [36,51].
Based on the above-described decomposition procedure, the thermal annealing of four Frenkel defects was studied in α-Al2O3 single crystals preliminary irradiated with different fluences of energetic xenon ions. The decomposition of RIOA spectra measured at RT after each preheating to a predetermined temperature Tpr (see examples in Figure 1b,d) allowed for the construction of concentration dependences on preheating temperatures for different defects (the defect concentration is proportional to the integral of a relevant Gaussian) induced by different ion fluences.
Figure 3 presents the examples of such isochronal annealing kinetics, which describe the thermal stability of a certain defect type, constructed for the corundum crystals ion-irradiated with Φ = 5 × 1012 cm−2 and Φ = 1013 cm−2. The normalization of annealing curves simplifies the separation of temperature-stability regions typical of different defects. It is clearly seen that only the annealing of charged interstitials H− could be roughly considered a one-stage process, while the decay of other Frenkel defects took place in several stages. The stability of the F+ centers was estimated via two RIOA Gaussians peaked around 4.8 and 5.3 eV, the annealing kinetics of which practically coincide (deviations in the region with rather low values of optical density illustrate the experimental accuracy).
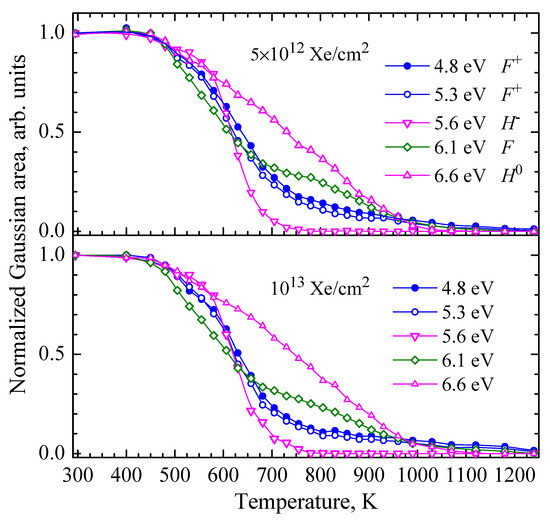
Figure 3.
Normalized thermal annealing curves of RIOA Gaussians (maxima at indicated photon energy) connected with oxygen-related Frenkel defects for corundum crystals irradiated by 231-MeV Xe ions with different fluences. The integral of an elementary Gaussian serves as a measure of relevant defect concentration. Solid lines serve as guides for the eye.
Of particular interest is the influence of irradiation fluence that should lead to different space topologies of radiation-induced defects on the kinetics of recombination processes between the complementary Frenkel defect. The experimentally obtained annealing curves of the F, F+, H−, and H0 defects induced by four different Xe-irradiation fluences are presented in Figure 4, Figure 5 and Figure 6. In comparison, the experimental annealing curves for the same Frenkel defects constructed on the basis of the relevant RIOA Gaussians in neutron-irradiated corundum (see our previous publications [36,37,51]) are shown in Figure 4, Figure 5 and Figure 6 as well.
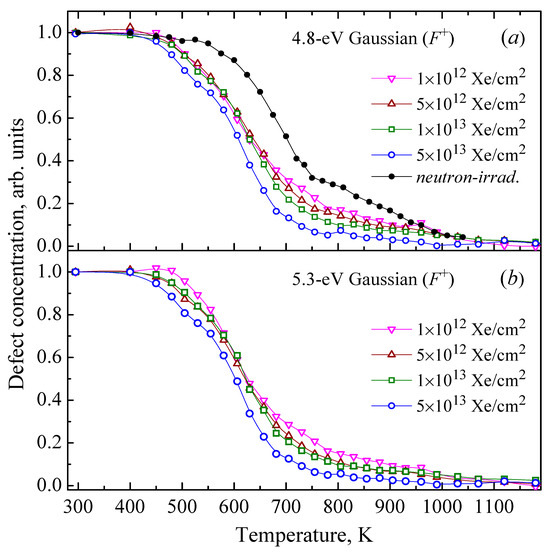
Figure 4.
Normalized annealing curves for the F+ centers induced by 231-MeV Xe ions or fast neutrons in α-Al2O3 single crystals. The integral of a RIOA Gaussian at Imax = 4.81 eV (a) and Imax = 5.33 eV (b) serves as a measure of defect concentration. Solid lines serve as guides for the eye.
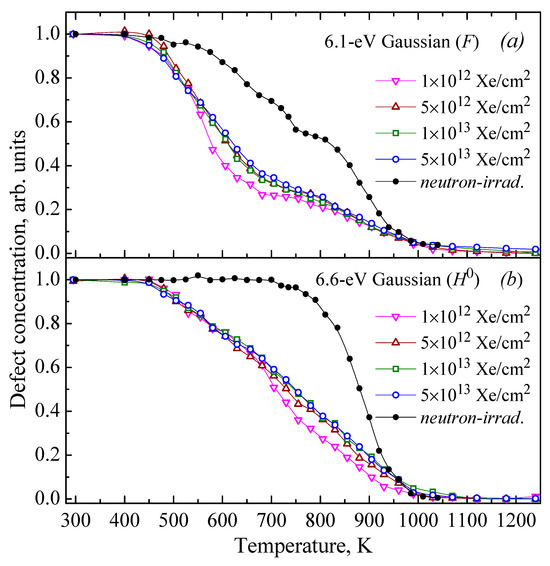
Figure 5.
Normalized annealing curves for the F and H0 centers induced by 231-MeV Xe ions or fast neutrons in α-Al2O3 single crystals. The integral of a RIOA Gaussian at Imax = 6.07 eV (a) and Imax = 6.67 eV (b) serves as a measure of a relevant defect concentration. Solid lines serve as guides for the eye.
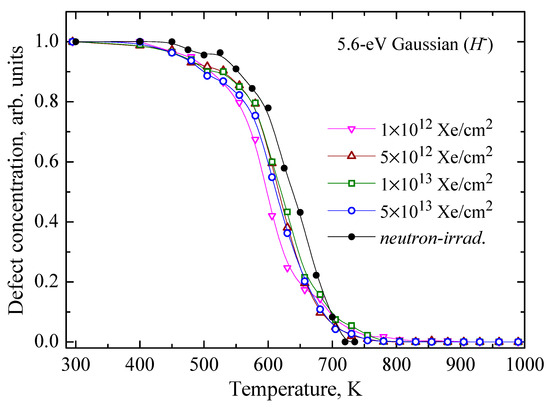
Figure 6.
Normalized annealing curves for the H− centers induced by 231-MeV Xe ions or fast neutrons in α-Al2O3 single crystals. The integral of a RIOA Gaussian (Imax = 5.6 eV) serves as a measure of defect concentration. Solid lines serve as guides for the eye.
It is notable that in neutron-irradiated corundum crystals, intense EPR signals related to the F+ and H− () defects allowed for precise registration of the defect concentration dependence on the preheating temperature. It has been clearly demonstrated that such dependences for paramagnetic F+ and H− centers practically coincide with those constructed on the basis of relevant RIOA Gaussians [36,37,51]. Unfortunately, the EPR method was not applicable for thermal annealing in the case of Xe irradiation. Due to the small range of energetic Xe ions (around 13.5 μm), the absolute number of ion-induced defects was too low, up to two orders of magnitude lower with respect to the crystals homogeneously colored in a whole volume by fast neutrons. As a result, in the present study, the annealing of Frenkel defects was studied only via the defect-related RIOA Gaussians (with the band integral proportional to the defect concentration).
It is clearly seen that only the annealing kinetics of the H− centers (RIOA at 5.6 eV) were very similar for both cases of irradiation (see Figure 6), while in general, the annealing of other Frenkel defects in ion-irradiated crystals started at lower temperatures than in neutron-irradiated crystals (see Figure 4 and Figure 5). Note that the thermal annealing kinetics of neutron-induced Frenkel defect pairs (F+-H− and F-H0) have already been modelled in terms of diffusion-controlled biomolecular reactions and the involvement of differently charged mobile oxygen interstitials [37,51,52]. The present study is a logical continuation of such theoretical analysis for the case of oxygen-related defect creation by energetic ions with different fluences.
3.2. Method and Kinetics Modelling
In this section, we discuss the main theoretical results by comparing two sets of defect annealing kinetics in the same material (α-Al2O3), subjected to different types of irradiation: neutrons and swift heavy ions. The case of neutron irradiation has been thoroughly investigated in our previous studies [37,51,52], where we developed a model describing the underlying processes and introduced an appropriate mathematical framework for defect recombination kinetics. The details of this model and the associated solution methods are extensively covered in the cited references; therefore, only key definitions and concepts will be summarized here.
We treat the neutron irradiation case as a reference or benchmark and seek to understand why the kinetics change qualitatively—sometimes appearing anomalous—under energetic ion irradiation. The model introduced in our studies [37,51,52] assumes that irradiation generates both neutral and charged Frenkel defects, while maintaining overall electrical neutrality. Specifically, two types of anion Frenkel defect pairs are created: charged defect pairs (F+-H−) and neutral defect pairs (F-H0).
Initially, the concentrations of each electron-type vacancy-containing centers and their complementary interstitials—either neutral (H0) or charged (H−)—are equal. These concentrations evolve through recombination processes, which, in turn, affect the relative proportions of neutral and charged radiation defects. Both neutral and charged interstitials can recombine not only with their respective counterparts but also with other types of vacancy-containing centers. The recombination rates vary, depending on the defect charges, with Coulomb attraction accelerating recombination between oppositely charged defects (see, e.g., Ref. [52]).
The annealing process in this model is formally a complex one due to the interaction of four defect species. However, the analysis is simplified by the fact that all recombination events are bimolecular and diffusion-controlled. The fundamental expression governing these processes is the Smoluchowski relation for the reaction rate [52,55]: , where D is the relative diffusion coefficient of the reacting species, and R is the recombination radius.
In oxide materials like α-Al2O3, it is well-established that vacancies exhibit significantly lower mobility than interstitials in the temperature range relevant to annealing. As a result, the mobility of vacancies can be neglected, and , and only the interstitials (H0 and H−) are mobile and govern the kinetics. These interstitials migrate via thermally activated jumps characterized by activation energies and , leading to diffusion coefficients of the form:
where and are the respective pre-exponential factors.
When solving the system of kinetic equations describing bimolecular recombination among the four defect types [52], the diffusion pre-factors appear as a part of effective process pre-exponentials:
These expressions combine several physical and experimental parameters, including the diffusion coefficients ( and ), recombination radius R, total concentration of vacancy-containing centers (equal to that of interstitials), and the effective heating rate β. Here, β is defined as a constant rate of temperature increase during annealing, . Overall, this kinetic analysis provides a pathway to infer the mobility of interstitial atoms—information that is otherwise challenging to obtain directly.
Figure 7 presents a comparison of the annealing kinetics for four types of Frenkel defects, whose recombination involves a complex interplay of cross-reactions, under two irradiation conditions: fast neutron irradiation (Figure 7a) and swift heavy ion irradiation (Figure 7b). Since the annealing kinetics are largely governed by mobile interstitials, particular attention should be paid to the RIOA bands corresponding to two differently charged interstitials: the band that peaked at 5.6 eV is related to the H− centers, while the maximum of the tentative H0 center absorption is around 6.6 eV.
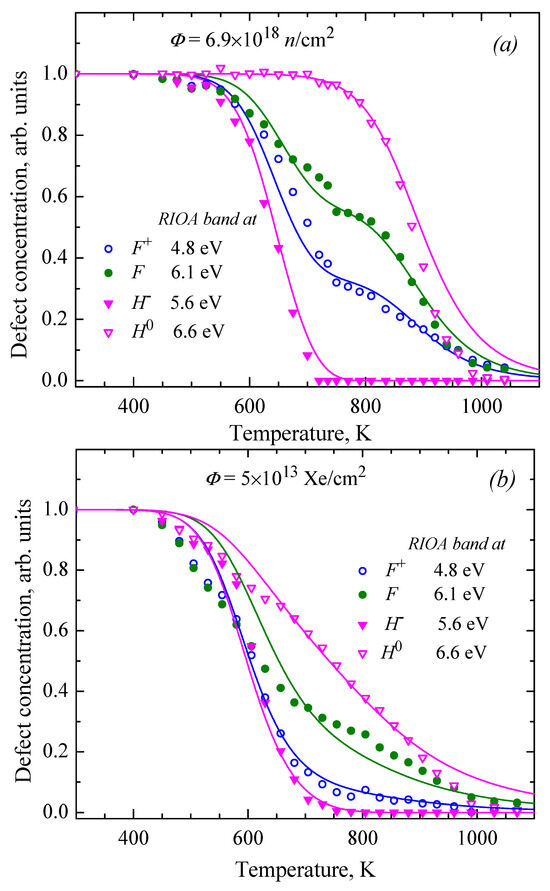
Figure 7.
The normalized experimental annealing kinetics for four types of radiation-induced Frenkel defects (symbols—on the basis of relevant RIOA Gaussians) and their theoretical analysis (full lines) for α-Al2O3 single crystals exposed to fast fission neutrons (part (a), see also Refs. [51,52]) and 231-MeV xenon ions (part (b)).
For both irradiation types, the experimental kinetics of the H− centers appear to be robust. This reliability stems from the fact that in the relevant energy range, spectral decomposition into Gaussian components is straightforward. As a result, the experimental data points align smoothly with the theoretical curves, and the associated errors are minimal. Consequently, the agreement between theory and experiment for the H− centers in Figure 7 can be considered very good.
In contrast, the two kinetics of neutral H0 centers present significant challenges. At higher energies (above a certain threshold), experimental measurements of RIOA are not feasible. In the case of ion-irradiation, the influence (overlapping) of the Gaussians of unknown origin peaking above 7 eV (labelled by dashed lines in Figure 1) on the bands of the H0 and even F centers is significant. In a neutron-irradiated corundum, the isolated maximum of the F-absorption is clearly registered at 6.07 eV, and this RIOA band intensity decreases till 7 eV by more than two times [36,37,51,52]. On the other hand, there is no isolated F-band in the RIOA spectra of Xe-irradiated crystals (see Figure 1a,c); a relative contribution of high-energy Gaussians (tentatively connected with more complex structural defects) increases with Tpr (see Figure 1b,d). According to Figure 8, these intense Gaussians are clearly detectable even after Tpr = 1240 K, i.e., total annealing of the Frenkel defects under consideration.
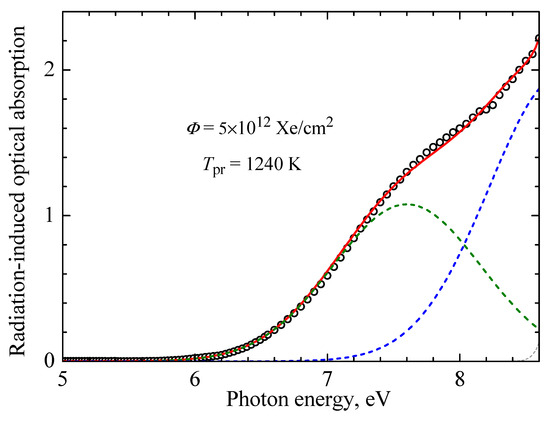
Figure 8.
The RIOA spectrum and its decomposition into elementary components for α-Al2O3 single crystals irradiated with Φ = 5 × 1012 Xe/cm2 and additionally preheated to Tpr = 1240 K. Symbols demonstrate experimental points, and the red solid line is the sum of Gaussian components. The spectrum was measured at RT.
As seen in Figure 7, the theoretical and experimental curves for the H0 centers diverged at high temperatures. Specifically, the amplitudes of bands reconstructed from these problematic spectral regions decayed too rapidly, in contradiction with the expected behavior dictated by chemical kinetics. Despite these difficulties, the diffusion-controlled model used in this study demonstrated high stability. In Figure 7, we compare experimental results with theoretical predictions based on the RIOA band, which peaked at 4.8 eV and was ascribed to the F+ center. Note that almost the same arrangement of modelled curves was obtained, taking the 5.3 eV RIOA band as a measure of the F+ centers (both bands were related to the same defect).
Our less obvious finding is concerned with the role of radiation fluence. Previous studies (see, e.g., Refs. [35,50]) have shown that fluence can significantly impact the annealing kinetics under electron, proton, and neutron irradiation, particularly altering diffusion activation energies. However, for heavy ion irradiation, our analysis indicates that annealing kinetics are largely fluence-independent. This is consistent with the level of agreement observed in Figure 7b. Notably, the reducing fluence increased experimental uncertainty and limited the scope for theoretical analysis. Consequently, it was impossible to reach the fluence regime when neutron and ion irradiation data hypothetically might have converge. So far, the results suggest that switching to ion irradiation qualitatively alters the annealing behavior. This weak or even negligible kinetics dependence on fluence during ion irradiation has also been previously observed [56], though a definitive explanation remains elusive.
As a result of fitting the theory to the experimental kinetics using the least squares method, we obtained the characteristics of the interstitials, which are summarized in Table 1. Before discussing the obtained numerical values, a necessary comment should be made. It is easy to see that in the case of neutron irradiation, both kinetics for interstitials showed a step, sharply falling in the temperature range of 100–200 K from the maximum to the minimum values. Meanwhile, to determine the activation energy with high accuracy, it is desirable to analyze the kinetic curves in a wide temperature range. Here, there is an analogue of the uncertainty relation between the temperature range and the error in determining the energy. This uncertainty was eliminated in Refs. [37,51,52] by equating the values of the diffusion activation energies to independent theoretical estimates, = 0.80 eV and eV, found for corundum by quantum chemistry methods (see Refs. [51,52] and references therein). The accuracy of these values can be estimated as 20%. The reason is trivial: the minimum of the optimized function is poorly expressed due to the noted uncertainty relation between energy and temperature.

Table 1.
The obtained migration energies of interstitials E and corresponding pre-exponential factors X.
As a result, for the case of neutron irradiation, it can be concluded that the inequality < is a reliably established fact (charged interstitials are more mobile than neutral ones), but the values of the activation energies in Table 1 are only rough estimates. Therefore, for charged interstitials, other results are also quite acceptable.
A comparison of Figure 7a,b demonstrates that the transition from neutron to ion irradiation qualitatively changed the kinetics of the radiation defect annealing: the characteristic step of annealing of the H0 interstitials disappeared and, instead, an unusual form of defect concentration decline, along a straight line with a certain slope, took place in a large temperature range (about 500 K). Nevertheless, Table 1 shows that the experimental kinetics can be approximated by theoretical ones within the framework of the same model involving four defect types, although the parameter values are different. It remains to be clarified which parameter changes are responsible for the noted visual changes.
For ion irradiation, the migration energy of charged interstitials = 0.65 eV was obtained by fitting to the experiment via the least squares method, without using estimates found by other methods. It can be seen that the found value falls within the uncertainty interval (20%) that we discussed in the case of neutron irradiation. There is every reason to conclude that the H− interstitials had the same nature for both irradiation types. Moreover, a comparison of the corresponding values of the kinetic pre-factors, = 2 × 103 K−1 for fast neutrons and = 3 × 102 K−1 for energetic Xe ions, showed a small difference. Let us pay also attention to Equation (3): When changing the radiation source from neutrons to ions, there is no guarantee that the same values of the initial concentration of the vacancy-containing centers (F and F+) are preserved. Therefore, a small discrepancy between the numerical values of the parameters is quite explainable.
For neutral interstitials H0, the data in Table 1 reveal not only a substantial reduction in the activation energy from = 1.20 eV to = 0.50 eV, but also a dramatic change in the pre-exponential factor by several orders of magnitude. Given the rough nature of these estimates, we cannot definitively claim that the previously assumed inequality < was reversed under ion irradiation. However, it is evident that the activation energies for the two types of interstitials under ion irradiation became comparable, which is a highly unusual conclusion.
It is important that within this scenario, the four-orders-of-magnitude drop in the pre-factor can no longer be attributed solely to the changes in the F-type center concentration. This kind of simultaneous decrease in both the activation energy and the pre-exponential factor is analyzed in detail in Ref. [50] and is considered a manifestation of a well-known phenomenon in disordered systems physics—the Meyer–Neldel rule [57,58]. According to this rule, a diminishing in activation energy E due to increasing material disorder is compensated by a corresponding drop in the diffusion pre-factor X.
A plausible interpretation of the presented findings is that irradiation induces structural disordering, possibly progressing from a nearly perfect crystalline state toward an almost amorphous structure [50]. Under heavy ion irradiation, such disordering is likely to be especially pronounced—detailed mechanisms may include the formation of collision cascades, defect clusters, extended defects, local lattice disordering (see, e.g., Refs. [25,34,44,45]). Our analysis suggests that the key difference in the annealing kinetics between neutron and ion irradiation arises from the higher degree of local lattice disordering introduced by ions. This disorder primarily affects neutral interstitials, significantly altering their kinetic behavior.
Of particular interest are the features of two kinetics for the F and F+ centers. In Figure 7a, the stepwise structure of these kinetics with a very unusual behavior is clearly visible: the decay began at approximately the same temperature, and the curves initially diverged (forked) but then converged again at higher temperatures. As is shown in detail in Refs. [37,52], such behavior is due to the Coulomb interaction of charged defects. As a result, the annealing curve of charged F+ centers always passes below the analogous curve for the neutral centers. In Figure 7b, the stepwise structure of the kinetics and the anomalous behavior (divergence or convergence of the curves) are expressed as significantly weaker. Such a discrepancy between the kinetics for neutron and ion irradiation has a simple explanation. So far in the discussion, we have not paid attention to a trivial fact: radiation creates pairs of charged and neutral defects, but in different proportions. A parameter was introduced in Refs. [37,51,52] as the fraction of charged defects when the annealing begins. The kinetics shown in Figure 7a,b correspond to different values of this parameter, namely, for neutron irradiation and for ion irradiation. In other words, in case (Figure 7a), the initial concentration of charged and neutral defects practically coincides, but in case (Figure 7b), these same concentrations are related as three to one. Meanwhile, Ref. [52] shows that such asymmetry in the initial concentrations leads to a systematic shift in the kinetics of the F and F+ centers, bringing them close to the annealing curve for the H− charged interstitials. Just such a shift effect can be seen in Figure 7b.
4. Conclusions
The thermal stability of oxygen-related Frenkel defects created in α-Al2O3 single crystals at room temperature by 231-MeV 132Xe (fluence from 5 × 1011 to 2 × 1014 cm−2) has been evaluated. Taking the integral of an elementary absorption band (obtained via decomposition of RIOA spectra into Gaussians) as a measure of the relevant defect concentration, the dependences of defect concentration on preheating temperature (isochronal annealing regime up to 1250 K) were constructed.
Such annealing curves for the classical vacancy-containing F and F+ centers (with RIOA bands that peaked at 6.1 eV and 4.8 eV, respectively), as well as complementary Frenkel defects —charged and neutral oxygen interstitials—for H− and H centers (bands at 5.6 eV and ≈6.6 eV), have been theoretically analyzed in terms of diffusion-controlled bimolecular recombination reactions. In addition, annealing kinetics of the F+-H− and F-H0 Frenkel pairs in Xe-irradiated crystals have been compared with those studied earlier in fast neutron-irradiated corundum (see our previous studies, Refs. [37,51,52]).
A comparison of the diffusion parameters extracted for neutron and Xe irradiation reveals that the migration energies for both charged and neutral interstitials are reduced in the latter case, very likely due to stronger structural disordering upon irradiation (according to the Meyer–Neldel rule discussed above).
Author Contributions
Conceptualization, K.A.E. and A.L.; formal analysis, V.N.K., V.S., I.K. and E.S.; investigation, G.B., I.K., A.P. and V.S.; methodology, K.A.E., V.N.K., A.L., E.S. and V.S.; resources, R.A. and G.B.; visualization, R.A. and A.P.; writing—original draft, A.L. and V.N.K.; writing—review and editing, K.A.E., V.S. and E.S. All authors have read and agreed to the published version of the manuscript.
Funding
The study was carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (grant agreement No. 101052200—EUROfusion). Views and opinions expressed are those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. This work was partially supported by the Estonian Research Council grant (PRG 2031), the Latvian Council for Science (LZP grant LZP-2024/1-0159), and the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan (grant No. AP19574768).
Data Availability Statement
The processed data are available on demand from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interests.
References
- Lee, W.E.; Lagerlof, K.P.D. Structural and electron diffraction data for sapphire (α-Al2O3). J. Electron Microsc. Tech. 1985, 2, 247–258. [Google Scholar] [CrossRef]
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Galtier, S.; Pivard, C.; Morville, J.; Rairoux, P. High-resolution dual comb spectroscopy using a free-running, bidirectional ring titanium sapphire laser. Opt. Express 2022, 30, 21148–21158. [Google Scholar] [CrossRef] [PubMed]
- Xuan, L.; Duffar, T. The growth of titanium doped sapphire for laser application. Prog. Cryst. Growth Charact. Mater. 2025, 71, 100666. [Google Scholar] [CrossRef]
- Basiev, T.T.; Mirov, S.B.; Osiko, V.V. Room-temperature color center lasers. IEEE J. Quantum Electron. 1988, 24, 1052–1069. [Google Scholar] [CrossRef]
- Dobrovinskaya, E.R.; Lytvynov, L.A.; Pishchik, V. Application of Sapphire. In Sapphire; Springer: Boston, MA, USA, 2009; pp. 1–54, Chapter 1. [Google Scholar]
- Luca, S.M.; Coron, N.; Dujardin, C.; Kraus, H.; Mikhailik, V.B.; Verdier, M.-A.; Di Stefano, P.C.F. Scintillating and optical spectroscopy of Al2O3:Ti for dark matter searches. Nucl. Instrum. Methods Phys. Res. Sect. A 2009, 606, 545–551. [Google Scholar] [CrossRef]
- Akselrod, M.S.; Kortov, V.S.; Kravetsky, D.J.; Gotlib, V.I. Highly sensitive thermoluminescent anion-defective α-Al2O3:C single crystal detectors. Radiat. Prot. Dosim. 1990, 32, 15–20. [Google Scholar]
- McKeever, S.W.S.; Akselrod, M.S.; Colyott, L.E.; Larsen, N.A.; Polf, J.C.; Whitley, V.H. Characterisation of Al2O3 for use in thermally and optically stimulated luminescence dosimetry. Radiat. Prot. Dosim. 1999, 84, 163–168. [Google Scholar] [CrossRef]
- Kortov, V.S.; Zvonarev, S.V.; Kiryakov, A.N.; Ananchenko, D.V. Dosimetric phosphor based on oxygen-deficient alumina ceramics. Radiat. Meas. 2016, 90, 196–200. [Google Scholar] [CrossRef]
- Kusumoto, T.; Akselrod, M.S.; Harrison, J.; Kodaira, S. Correction method of the coloration in fluorescent nuclear track detector. Radiat. Meas. 2023, 161, 106898. [Google Scholar] [CrossRef]
- Hu, J.; Kusumoto, T.; Kodaira, S. Coloration-dependent correction for heavy ion measurements in an Al2O3:C,Mg-based fluorescent nuclear track detector. Radiat. Meas. 2025, 181, 107384. [Google Scholar] [CrossRef]
- Pells, G.P. Radiation damage effects in alumina. J. Am. Ceram. Soc. 1994, 77, 368–377. [Google Scholar] [CrossRef]
- De Vicente, S.M.G.; Hodgson, E.R.; Shikama, T. Functional materials for tokamak in-vessel systems—Status and applications. Nucl. Fusion 2017, 57, 092009. [Google Scholar] [CrossRef]
- Blokhin, D.A.; Chernov, V.M.; Blokhin, A.I. Nuclear and physical properties of dielectrics under neutron irradiation in fast (BN-600) and fusion (DEMO-S) reactors. Phys. At. Nucl. 2017, 80, 1279–1284. [Google Scholar] [CrossRef]
- Was, G.S.; Petti, D.; Ukai, S.; Zinkle, S. Materials for future nuclear energy systems. J. Nucl. Mater. 2019, 527, 151837. [Google Scholar] [CrossRef]
- Gamble, F.T.; Bartram, R.H.; Young, C.G.; Gilliam, O.R.; Levy, P.W. Electron-spin resonances in reactor-irradiated aluminum oxide. Phys. Rev. 1965, 138, A577–A583. [Google Scholar] [CrossRef]
- La, S.Y.; Bartram, R.H.; Cox, R.T. The F+ center in reactor-irradiated aluminum oxide. J. Phys. Chem. Solids 1973, 34, 1079–1086. [Google Scholar] [CrossRef]
- Lee, K.H.; Crawford, J.H. Electron centers in single-crystal Al2O3. Phys. Rev. B 1977, 15, 4065–4070. [Google Scholar] [CrossRef]
- Evans, B.D.; Stapelbroek, M. Optical properties of the F+ center in crystalline Al2O3. Phys. Rev. B 1978, 18, 7089–7098. [Google Scholar] [CrossRef]
- Crawford, J.H. A review of neutron radiation damage on corundum crystals. J. Nucl. Mater. 1982, 108–109, 644–654. [Google Scholar] [CrossRef]
- Atobe, K.; Nishimoto, N.; Nakagawa, M. Irradiation-induced aggregate centers in single crystal Al2O3. Phys. Stat. Solidi A 1985, 89, 155–162. [Google Scholar] [CrossRef]
- Chen, Y.; Abraham, M.M.; Pedraza, D.F. Radiation damage in Al2O3 crystals implanted with 3.8 MeV Fe2+ ions. Nucl. Instrum. Methods Phys. Res. Sect. B 1991, 59–60, 1163–1166. [Google Scholar] [CrossRef]
- Evans, B.D. A review of the optical properties of anion lattice vacancies, and electrical conduction in α-Al2O3: Their relation to radiation-induced electrical degradation. J. Nucl. Mater. 1995, 219, 202–223. [Google Scholar] [CrossRef]
- Zinkle, S.J.; Kinoshita, C. Defect production in ceramics. J. Nucl. Mater. 1997, 251, 200–217. [Google Scholar] [CrossRef]
- Surdo, A.I.; Kortov, V.S.; Pustovarov, V.A. Luminescence of F and F+ centers in corundum upon excitation in the interval from 4 to 40 eV. Radiat. Meas. 2001, 33, 587–591. [Google Scholar] [CrossRef]
- Skuratov, V.A.; Gun, K.J.; Stano, J.; Zagorski, D.L. In situ luminescence as monitor of radiation damage under swift heavy ion irradiation. Nucl. Instrum. Methods Phys. Res. Sect. B 2006, 245, 194–200. [Google Scholar] [CrossRef]
- Izerrouken, M.; Benyahia, T. Absorption and photoluminescence study of Al2O3 single crystal irradiated with fast neutrons. Nucl. Instrum. Methods Phys. Res. Sect. B 2010, 468, 2987–2990. [Google Scholar] [CrossRef]
- Petrie, C.M.; Windl, W.; Blue, T.E. In-situ reactor radiation-induced attenuation in sapphire optical fibers. J. Am. Ceram. Soc. 2014, 97, 3383–3389. [Google Scholar] [CrossRef]
- Izerrouken, M.; Djouadi, Y.; Zirour, H. Annealing process of F- and F+-centers in Al2O3 single crystal induced by fast neutrons irradiation. Nucl. Instrum. Methods Phys. Res. Sect. B 2014, 319, 29–33. [Google Scholar] [CrossRef]
- Malo, M.; Moroño, A.; Hodgson, E.R. In situ luminescence qualification of radiation damage in aluminas: F-aggregation and Al colloids. Fusion Eng. Des. 2014, 89, 2179–2183. [Google Scholar] [CrossRef]
- Crespillo, M.L.; Graham, J.T.; Zhang, Y.; Weber, W.J. In-situ luminescence monitoring of ion-induced damage evolution in SiO2 and Al2O3. J. Lumin. 2016, 172, 208–218. [Google Scholar] [CrossRef]
- Costantini, J.M.; Watanabe, Y.; Yasuda, K.; Fasoli, M. Cathodo-luminescence of color centers induced in sapphire and yttria-stabilized zirconia by high-energy electrons. J. Appl. Phys. 2017, 121, 153101. [Google Scholar] [CrossRef]
- Grygiel, C.; Moisy, F.; Sall, M.; Lebius, H.; Balanzat, E.; Madi, T.; Been, T.; Marie, D.; Monnet, I. In-situ kinetics of modifications induced by swift heavy ions in Al2O3: Colour centre formation, structural modification and amorphization. Acta Mater. 2017, 140, 157–167. [Google Scholar] [CrossRef]
- Popov, A.I.; Lushchik, A.; Shablonin, E.; Vasil’Chenko, E.; Kotomin, E.A.; Moskina, A.M.; Kuzovkov, V.N. Comparison of the F-type center thermal annealing in heavy-ion and neutron irradiated Al2O3 single crystals. Nucl. Instrum. Methods Phys. Res. Sect. B 2018, 433, 93–97. [Google Scholar] [CrossRef]
- Seeman, V.; Lushchik, A.; Shablonin, E.; Prieditis, G.; Gryaznov, D.; Platonenko, A.; Kotomin, E.A.; Popov, A.I. Atomic, electronic and magnetic structure of an oxygen interstitial in neutron-irradiated Al2O3 single crystals. Sci. Rep. 2020, 10, 15852. [Google Scholar] [CrossRef]
- Lushchik, A.; Kuzovkov, V.N.; Popov, A.I.; Prieditis, G.; Seeman, V.; Shablonin, E.; Vasil’Chenko, E.; Kotomin, E.A. Evidence for the formation of two types of oxygen interstitials in neutron-irradiated α-Al2O3 single crystals. Sci. Rep. 2021, 11, 20909. [Google Scholar] [CrossRef]
- Seeman, V.; Popov, A.I.; Shablonin, E.; Vasil’Chenko, E.; Lushchik, A. EPR-active dimer centers with S = 1 in α-Al2O3 single crystals irradiated by fast neutrons. J. Nucl. Mater. 2022, 569, 153933. [Google Scholar] [CrossRef]
- Baubekova, G.; Assylbayev, R.; Feldbach, E.; Krasnikov, A.; Kudryavtseva, I.; Podelinska, A.; Seeman, V.; Shablonin, E.; Vasil’Chenko, E.; Lushchik, A. Accumulation of oxygen interstitial-vacancy pairs under irradiation of corundum single crystals with energetic xenon ions. Radiat. Meas. 2024, 179, 107324. [Google Scholar] [CrossRef]
- Clinard, F.W., Jr.; Hobbs, L.W. Physics of Radiation Effects in Crystals; Johnson, R.A., Orlov, A.N., Eds.; Elsevier: Amsterdam, The Netherland, 1986; Chapter 7. [Google Scholar]
- Nordlund, K.; Zinkle, S.J.; Sand, A.E.; Granberg, F.; Averback, R.S.; Stoller, R.E.; Suzudo, T.; Malerba, L.; Banhart, F.; Weber, W.J.; et al. Primary radiation damage: A review of current understanding and models. J. Nucl. Mater. 2018, 512, 450–479. [Google Scholar] [CrossRef]
- Itoh, N.; Duffy, D.M.; Khakshouri, S.; Stoneham, A.M. Making tracks: Electronic excitation roles in forming swift heavy ion tracks. J. Phys. Condens. Matter 2009, 21, 474205. [Google Scholar] [CrossRef]
- Lushchik, A.; Kärner, T.; Lushchik, C.; Schwartz, K.; Savikhin, F.; Shablonin, E.; Shugai, A.; Vasil’Chenko, E. Electronic excitations and defect creation in wide-gap MgO and Lu3Al5O12 crystals irradiated with swift heavy ions. Nucl. Instrum. Methods Phys. Res. Sect. B 2012, 286, 200–208. [Google Scholar] [CrossRef]
- Wesch, W.; Wendler, E.E. Ion Beam Modification of Solids; Springer Series in Surface Sciences; Springer Nature: Berlin, Germany, 2016; Volume 61. [Google Scholar]
- Crespillo, M.L.; Agulló-López, F.; Zucchiatti, A. Cumulative approaches to track formation under swift heavy ion (SHI) irradiation: Phenomenological correlation with formation energies of Frenkel pairs. Nucl. Instrum. Methods Phys. Res. Sect. B 2017, 394, 20–27. [Google Scholar] [CrossRef]
- Lee, K.H.; Crawford, J.H. Additive coloration of sapphire. Appl. Phys. Lett. 1978, 33, 273–275. [Google Scholar] [CrossRef]
- Ramírez, R.; Tardío, M.; Gonzalez, R.; Santiuste, J.E.M.; Kokta, M.R. Optical properties of vacancies in thermochemically reduced Mg-doped sapphire single crystals. J. Appl. Phys. 2007, 101, 123520. [Google Scholar] [CrossRef]
- Zorenko, Y.; Fabisiak, K.; Zorenko, T.; Mandowski, A.; Xia, Q.; Batentschuk, M.; Fri, J.; Zhusupkalieva, G. Comparative study of the luminescence of Al2O3:C and Al2O3 crystals under synchrotron radiation excitation. J. Lumin. 2013, 144, 41–44. [Google Scholar] [CrossRef]
- Chen, Y.; Kolopus, J.L.; Sibley, W.A. Luminescence of the F+ center in MgO. Phys. Rev. 1969, 186, 865–870. [Google Scholar] [CrossRef]
- Kotomin, E.; Kuzovkov, V.; Popov, A.I.; Maier, J.; Vila, R. Anomalous kinetics of diffusion-controlled defect annealing in irradiated ionic solids. J. Phys. Chem. A 2018, 122, 28–32. [Google Scholar] [CrossRef] [PubMed]
- Lushchik, A.; Seeman, V.; Shablonin, E.; Vasil’Chenko, E.; Kuzovkov, V.N.; Kotomin, E.A.; Popov, A.I. Detection of hidden oxygen interstitials in neutron-irradiated corundum crystals. Opt. Mater. X 2022, 14, 100151. [Google Scholar] [CrossRef]
- Lushchik, A.; Kuzovkov, V.N.; Kudryavtseva, I.; Popov, A.I.; Seeman, V.; Shablonin, E.; Vasil, E.; Kotomin, E.A. The two types of oxygen interstitials in neutron-irradiated corundum single crystals: Joint experimental and theoretical study. Phys. Stat. Solidi B 2022, 259, 2100317. [Google Scholar] [CrossRef]
- Halliburton, L.E.; Kappers, L.A. Radiation-induced oxygen interstitials in MgO. Solid State Commun. 1978, 26, 111–114. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter (2010). Nucl. Instrum. Methods Phys. Res. Sect. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Smoluchowski, M.V. Versuch Einer Mathematischen Theorie der Koagulationskinetik kolloider Losungen. Z. Phys. Chem. B 1917, 92, 129–168. [Google Scholar] [CrossRef]
- Kuzovkov, V.N.; Kotomin, E.A.; Lushchik, A.; Popov, A.I.; Shablonin, E. The annealing kinetics of the F-type defects in MgAl2O4 spinel single crystals irradiated by swift heavy ions. Opt. Mater. 2024, 147, 114733. [Google Scholar] [CrossRef]
- Meyer, W.; Neldel, H. Concerning the relationship between the energy constant epsilon and the quantum constant alpha in the conduction-temperature formula in oxydising semi conductors. Phys. Z. 1937, 38, 1014–1019. [Google Scholar]
- Jones, A.G. Compensation of the Meyer-Neldel Compensation Law for H diffusion in minerals. Geochem. Geophys. Geosyst. 2014, 15, 2616–2631. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).