Line Defects in Quasicrystals

Abstract

The six-dimensional framework of the integral formalism for line defects (straight dislocations and line forces) in anisotropic elasticity has been extended to a $2n$-dimensional integral formalism for line defects in quasicrystals ($n=4,5,6$ for one-, two-, and three-dimensional quasicrystals) including phonon and phason fields. The elastic fields of a line defect in a quasicrystal have a surprisingly simple and compact form in the integral formalism of quasicrystals.

1. Introduction

Quasicrystals represent an important class of novel materials discovered by Shechtman et al. [1]. In 2011, Shechtman received the Nobel Prize in Chemistry for this discovery. Quasicrystals belong to aperiodic crystals and possess a long-range orientational order but no translational symmetry in the quasiperiodic directions. Quasicrystals possess particular physical properties like high hardness, low conductivity, resistivity decreases with temperature, very low conductivity, small specific heat, low friction coefficients, and wear and oxidation resistance [2]. Quasicrystalline substances have many promising technological applications (see [3]). The basis of the continuum theory of solid quasicrystals consists of two elementary excitations: the phonons and the phasons [4,5,6]. Phonons are related to the translation of atoms, and phasons lead to the local rearrangements of atoms in a cell. The generalized elasticity theory of quasicrystals including phonon and phason fields was developed by Ding et al. [7].

Dislocations are important line defects in quasicrystals causing plasticity in quasicrystals (see [5,6,8,9,10,11,12,13]). The fields of dislocations in quasicrystals consist of phonon and phason parts. A dislocation in a quasicrystal can be considered as a “hyperdislocation” in the hyperlattice by means of a generalized Volterra process. Because the hyperlattice is periodic, the generalized Volterra process can be understood as the insertion or removal of a hyper-half plane (e.g., [14]). The Burgers vector of the “hyperdislocation” consists of phonon and phason components. A “hyperdislocation” is a line defect in a quasicrystal characterized by the Burgers vector and the direction of the dislocation line. For a perfect dislocation in a quasicrystal, both phonon and phason components are non-zero, and the Burgers vector is a lattice vector in the hyperspace. If the phason component is zero, then there exists a stacking fault along the cutting surface of the generalized Volterra process, and such a dislocation represents a partial dislocation since the phonon component alone is not a lattice vector in hyperspace (see [9,11,14]). Important defects in the approximants of quasicrystals are so-called metadislocations. Metadislocations are highly complex defects, including about 1000 atoms in the dislocation core [15,16]. In particular, metadislocations are specific partial dislocations characterized by Burgers vectors that correspond to certain short interatomic distances inside the crystallographic motif of the structure [17].

Using generalized elasticity theory of quasicrystals, the basic key equations of dislocations were given by Ding et al. [18,19] and Lazar and Agiasofitou [20]. The dislocation fields of dislocation loops in quasicrystals were given by Lazar and Agiasofitou [20]. The general expressions for the displacement fields induced by straight dislocations in quasicrystals in terms of the elastic Green tensor were given by Ding et al. [18,19]. Ding et al. [21] extended the Stroh formalism [22,23] and the integral formalism [24,25] for the displacement field of a dislocation in a quasicrystal (see also [11,26]). Ding et al. [21] derived the integral formalism from the Stroh formalism for quasicrystals using the eigenvectors and eigenvalues of the Stroh formalism. The Stroh formalism [22,23] is a complex variable formulation originally developed for solving the problems of two-dimensional linear anisotropic elasticity. The extended Stroh formalism was used by Li and Liu [27] to study a dislocation in an icosahedral quasicrystal. Radi and Mariano [28] investigated the steady-state propagation of dislocations in quasicrystals based on the extended Stroh formalism. Line defects in crystals and in quasicrystals are straight dislocations and line forces (see [29,30,31]). The detailed structure of the extended Stroh formalism including line defects for quasicrystals was given by Wang and Schiavone [31]. In the Stroh formalism, the fields of line defects are given as complex form solutions of an eigenvalue problem and in the integral formalism, and the fields of line defects are given as real form solutions of a matrix partial differential equation of the first order (see [30]). The integral formalism provides suitable expressions for the modeling of line defects. In approaches like the Stroh formalism and the integral formalism, which are based on anisotropic elasticity theory, a dislocation is considered as a Dirac $\delta$-dislocation, leading to singularities in the elastic fields at the dislocation line. In particular, the elastic distortion and stress fields of line defects possess the typical $1/r$-behavior. In the framework of the linear generalized elasticity of quasicrystals, we work in the limit of the vanishing phason self-action. However, a phason self-action can become important in the core region of dislocations in quasicrystals (see [16]).

The purpose of this work is to develop the extended integral formalism of line defects (straight dislocations and line forces) for quasicrystals in a straightforward manner without an unnecessary detour via the Stroh formalism. For the generalized plane strain of quasicrystals, we derive the appropriate two-dimensional matrix partial differential equation of the first order and their solution. The solution for the displacement fields and stress functions of line defects is logarithmic in the distance between field and source points plus an angular term. For quasicrystals, the solution gives the $2n$-dimensional vector of the n-dimensional displacement vector $\mathit{U}$ and the n-dimensional stress function vector $\mathbf{\Phi }$ of a straight dislocation with the Burgers vector $\mathit{b}$ and a line force of strength $\mathit{F}$. In order to complete the integral formalism for quasicrystals, we compute the extended elastic distortion tensor, the extended stress tensor, and the self-energy for straight dislocations and line forces in quasicrystals. Using the integral formalism, the Peach–Koehler force for straight dislocations and the Cherepanov force for line forces present in quasicrystals are given. Moreover, the two-dimensional Green tensor of quasicrystals is derived in the framework of the integral formalism.

2. Basic Equations for Quasicrystals

An $(n-3)$-dimensional quasicrystal can be generated by the projection of an n-dimensional periodic structure to the three-dimensional physical space ($n=4,5,6$). The n-dimensional hyperspace $E^n$ can be decomposed into the direct sum of two orthogonal subspaces,

$$\begin{array}{c}\hfill E^n=E_{\parallel }^3\oplus E_{\perp }^{(n-3)},\end{array}$$

(1)

where $E_{\parallel }^3$ is the three-dimensional physical or parallel space of the phonon fields, and $E_{\perp }^{(n-3)}$ is the $(n-3)$-dimensional perpendicular space of the phason fields. The symbol ⊕ denotes the direct sum. For $n=4,5,6$, we speak of one-dimensional, two-dimensional, and three-dimensional quasicrystals with the dimension of the corresponding hyperspace 4D, 5D, 6D, respectively. Here, indices in the parallel space are denoted by small Latin letters $i,j,k$ with $i,j,k=1,2,3$, and indices in the perpendicular space are denoted by Greek letters $\alpha ,\gamma$ with $\alpha ,\gamma =3$ for one-dimensional quasicrystals (with quasiperiodicity in $x_3$-direction), $\alpha ,\gamma =1,2$ for two-dimensional quasicrystals (with quasiperiodicity in $x_1{x}_2$-plane), and $\alpha ,\gamma =1,2,3$ for three-dimensional quasicrystals. Throughout the text, phonon fields are denoted by ${(·)}^{\parallel }$, and phason fields by ${(·)}^{\perp }$. All field quantities (phonon and phason fields) depend on the so-called material space coordinates (or spatial coordinates) $\mathit{x}\in {\mathbb{R}}^3$. Note that in the linear theory of quasicrystals, the material space coincides with the parallel space.

In the theory of the generalized elasticity of quasicrystals, the (elastic) phonon and phason distortion tensors ${\beta }_{kl}^{\parallel }$ and ${\beta }_{\gamma l}^{\perp }$ are defined as the gradient of the phonon displacement vector ($u_k^{\parallel }\in E_{\parallel }^3$) and of the phason displacement vector ($u_{\gamma }^{\perp }\in E_{\perp }^{(n-3)}$), respectively,

$$\begin{array}{cc}\hfill {\beta }_{kl}^{\parallel }& ={\partial }_l{u}_k^{\parallel },\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\beta }_{\gamma l}^{\perp }& ={\partial }_l{u}_{\gamma }^{\perp }.\hfill \end{array}$$

(3)

Here ${\partial }_l=\partial /\partial x_l$ denotes the partial differentiation with respect to the spatial coordinates $x_l$. The constitutive relations for quasicrystals are given by

$$\begin{array}{cc}\hfill {\sigma }_{ij}^{\parallel }& =C_{ijkl}{\beta }_{kl}^{\parallel }+D_{ij\gamma l}{\beta }_{\gamma l}^{\perp },\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\sigma }_{\alpha j}^{\perp }& =D_{kl\alpha j}{\beta }_{kl}^{\parallel }+E_{\alpha j\gamma l}{\beta }_{\gamma l}^{\perp },\hfill \end{array}$$

(5)

where ${\sigma }_{ij}^{\parallel }$ and ${\sigma }_{\alpha j}^{\perp }$ are the phonon and phason stress tensors, respectively. Note that the phonon stress tensor is symmetric, ${\sigma }_{ij}^{\parallel }={\sigma }_{ji}^{\parallel }$, whereas the phason stress tensor ${\sigma }_{\alpha j}^{\perp }$ is an asymmetric two-point tensor, ${\sigma }_{\alpha j}^{\perp }\ne {\sigma }_{j\alpha }^{\perp }$ (see [20,32]). $C_{ijkl}$ is the tensor of the elastic moduli of phonons,$E_{\alpha j\gamma l}$ is the tensor of the elastic moduli of phasons, and $D_{ij\gamma l}$ is the tensor of the elastic moduli of the phonon–phason coupling. The constitutive tensors possess the symmetries [7,20]

$$\begin{array}{c}\hfill C_{ijkl}=C_{klij}=C_{ijlk}=C_{jikl},D_{ij\gamma l}=D_{ji\gamma l},E_{\alpha j\gamma l}=E_{\gamma l\alpha j}.\end{array}$$

(6)

Using the hyperspace notation of quasicrystals introduced by Lazar and Agiasofitou [20], the phonon and phason fields can be unified in the corresponding extended fields in the hyperspace. The components of the extended fields will be denoted by capital letters, e.g., $I,K=1,\cdots ,n$. In the hyperspace notation, we have the extended displacement vector $U_K\in E_{\parallel }^3\oplus E_{\perp }^{(n-3)}$:

$$\begin{array}{c}\hfill U_K=\left\{\begin{array}{cc}{\displaystyle u_k^{\parallel },}\hfill & {\displaystyle K=1,2,3,}\hfill \\ {\displaystyle u_{\gamma }^{\perp },}\hfill & {\displaystyle K=4,\cdots ,n,}\hfill \end{array}\right.\end{array}$$

(7)

the extended elastic distortion tensor $B_{Kl}\in \left(E_{\parallel }^3\oplus E_{\perp }^{(n-3)}\right)\otimes E_{\parallel }^3$:

$$\begin{array}{c}\hfill B_{Kl}=\left\{\begin{array}{cc}{\displaystyle {\beta }_{kl}^{\parallel },}\hfill & {\displaystyle K=1,2,3,}\hfill \\ {\displaystyle {\beta }_{\gamma l}^{\perp },}\hfill & {\displaystyle K=4,\cdots ,n,}\hfill \end{array}\right.\end{array}$$

(8)

the extended stress tensor ${\mathsf{\Sigma }}_{Ij}\in \left(E_{\parallel }^3\oplus E_{\perp }^{(n-3)}\right)\otimes E_{\parallel }^3$:

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{Ij}=\left\{\begin{array}{cc}{\displaystyle {\sigma }_{ij}^{\parallel },}\hfill & {\displaystyle I=1,2,3,}\hfill \\ {\displaystyle {\sigma }_{\alpha j}^{\perp },}\hfill & {\displaystyle I=4,\cdots ,n,}\hfill \end{array}\right.\end{array}$$

(9)

and the tensor of the extended elastic moduli $C_{IjKl}\in \left(E_{\parallel }^3\oplus E_{\perp }^{(n-3)}\right)\otimes E_{\parallel }^3\otimes \left(E_{\parallel }^3\oplus E_{\perp }^{(n-3)}\right)\otimes E_{\parallel }^3$:

$$\begin{array}{c}\hfill C_{IjKl}=\left\{\begin{array}{ccc}{\displaystyle C_{ijkl},}\hfill & {\displaystyle I=1,2,3;}\hfill & {\displaystyle K=1,2,3,}\hfill \\ {\displaystyle D_{ij\gamma l},}\hfill & {\displaystyle I=1,2,3;}\hfill & {\displaystyle K=4,\cdots ,n,}\hfill \\ {\displaystyle D_{kl\alpha j},}\hfill & {\displaystyle I=4,\cdots ,n;}\hfill & {\displaystyle K=1,2,3,}\hfill \\ {\displaystyle E_{\alpha j\gamma l},}\hfill & {\displaystyle I=4,\cdots ,n;}\hfill & {\displaystyle K=4,\cdots ,n.}\hfill \end{array}\right.\end{array}$$

(10)

Here, ⊗ denotes the tensor (or dyadic) product. The tensor $C_{IjKl}$ retains the major symmetry

$$\begin{array}{c}\hfill C_{IjKl}=C_{KlIj}\end{array}$$

(11)

and must be positive definite to ensure a positive elastic energy density:

$$\begin{array}{c}\hfill W={\displaystyle \frac{1}{2}}{B}_{Ij}{C}_{IjKl}{B}_{Kl}>0.\end{array}$$

(12)

Using the hyperspace notation, Equations (2) and (3) reduce to

$$\begin{array}{c}\hfill B_{Kl}={\partial }_l{U}_K\end{array}$$

(13)

and the constitutive relations (4) and (5) become

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{Ij}=C_{IjKl}{B}_{Kl}=C_{IjKl}{\partial }_l{U}_K,\end{array}$$

(14)

which is the extended Hooke law for quasicrystals.

In absence of external forces, the extended stress tensor (9) can be written in terms of an extended stress function tensor ${\mathsf{\Phi }}_{Im}\in \left(E_{\parallel }^3\oplus E_{\perp }^{(n-3)}\right)\otimes E_{\parallel }^3$:

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{Ij}={ϵ}_{jkm}{\partial }_k{\mathsf{\Phi }}_{Im}\end{array}$$

(15)

with

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_{Im}=\left\{\begin{array}{cc}{\displaystyle {\mathsf{\Phi }}_{im}^{\parallel },}\hfill & {\displaystyle I=1,2,3,}\hfill \\ {\displaystyle {\mathsf{\Phi }}_{\alpha m}^{\perp },}\hfill & {\displaystyle I=4,\cdots ,n,}\hfill \end{array}\right.\end{array}$$

(16)

where ${\mathsf{\Phi }}_{im}^{\parallel }$ and ${\mathsf{\Phi }}_{\alpha m}^{\perp }$ are the phonon and phason stress function tensors, respectively. Here, ${ϵ}_{jkm}$ denotes the three-dimensional Levi–Civita tensor. Substituting Equation (15) into the left-hand side of the extended Hooke law (14), we obtain

$$\begin{array}{c}\hfill {ϵ}_{jkm}{\partial }_k{\mathsf{\Phi }}_{Im}=C_{IjKl}{\partial }_l{U}_K,\end{array}$$

(17)

which is nothing but the extended Hooke law (14) written in terms of $U_K$ and ${\mathsf{\Phi }}_{Im}$ as a partial differential equation of the first order.

3. Two-Dimensional Generalized Anisotropic Elasticity for Quasicrystals

We consider the framework of the generalized plane strain of quasicrystals. In general, the plane strain and antiplane strain fields do not decouple due to the anisotropy. If we choose Cartesian coordinates, then, in the generalized plane strain, all fields are independent of the variable $x_3$, and all derivatives with respect to $x_3$ vanish, ${\partial }_{3}f(x_1,x_2)=0$. Therefore, the extended displacement fields depend only on $x_1$ and $x_2$, $\mathit{x}\in {\mathbb{R}}^2$ but with the index in the hyperspace: $U_I(x_1,x_2)$, $I=1,\cdots ,n$ and thus ${\partial }_3{U}_I(x_1,x_2)=0$.

Consider a Cartesian coordinate system in the parallel space. Using a unit vector $\mathit{m}$ in the $x_1$-direction and a unit vector $\mathit{n}$ in the $x_2$-direction ($\mathit{m}\equiv {\mathit{e}}_1={(1,0,0)}^{\mathrm{T}}$, $\mathit{n}\equiv {\mathit{e}}_2={(0,1,0)}^{\mathrm{T}}$) and the notation

$$\begin{array}{c}\hfill {\left(ab\right)}_{IK}=a_j{C}_{IjKl}{b}_l,\end{array}$$

(18)

which is an $n\times n$ matrix in the hyperspace with the property

$$\begin{array}{c}\hfill {\left(ab\right)}_{IK}={\left(ba\right)}_{KI},\end{array}$$

(19)

or, alternatively,

$$\begin{array}{c}\hfill \left(ab\right)={\left(ba\right)}^{\mathrm{T}},\end{array}$$

(20)

which follows from the major symmetry of $C_{IjKl}$, Equation (11), the extended constitutive relation (14) reads for the generalized plane strain

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{I1}& ={\left(mm\right)}_{IK}{B}_{K1}+{\left(mn\right)}_{IK}{B}_{K2}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{I2}& ={\left(nm\right)}_{IK}{B}_{K1}+{\left(nn\right)}_{IK}{B}_{K2}\hfill \end{array}$$

(22)

with $I,K=1,\cdots ,n$. Here, the superscript T indicates transposition. In matrix form, Equations (21) and (22) become

$$\begin{array}{cc}\hfill \left(\begin{array}{c}{\mathsf{\Sigma }}_{I1}\\ {\mathsf{\Sigma }}_{I2}\end{array}\right)& =\left(\begin{array}{cc}{\left(mm\right)}_{IK}& {\left(mn\right)}_{IK}\\ {\left(nm\right)}_{IK}& {\left(nn\right)}_{IK}\end{array}\right)\left(\begin{array}{c}{B}_{K1}\\ B_{K2}\end{array}\right),\hfill \end{array}$$

(23)

where the constitutive tensor for the generalized plane strain is a symmetric $2n\times 2n$ matrix with four $n\times n$ blocks in the hyperspace

$$\begin{array}{c}\hfill \left(\begin{array}{cc}{\left(mm\right)}_{IK}& {\left(mn\right)}_{IK}\\ {\left(nm\right)}_{IK}& {\left(nn\right)}_{IK}\end{array}\right).\end{array}$$

(24)

The following holds: ${\left(nm\right)}_{IK}={\left(mn\right)}_{KI}$ or, alternatively, $\left(nm\right)={\left(mn\right)}^{\mathrm{T}}$.

For the generalized plane strain, the extended stress tensor can be written in terms of an extended stress function vector ${\mathsf{\Phi }}_{I3}\equiv {\mathsf{\Phi }}_I$, and Equation (15) reduces to

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{Ij}={ϵ}_{jk3}{\partial }_k{\mathsf{\Phi }}_{I3},\end{array}$$

(25)

which is valid in the absence of external forces. Then, it yields

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{I1}& ={\partial }_2{\mathsf{\Phi }}_I\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{I2}& =-{\partial }_1{\mathsf{\Phi }}_I.\hfill \end{array}$$

(27)

Substituting Equations (13), (26) and (27) into the extended Hooke law (21) and (22), we obtain

$$\begin{array}{cc}\hfill {\partial }_2{\mathsf{\Phi }}_I& ={\left(mm\right)}_{IK}{\partial }_1{U}_K+{\left(mn\right)}_{IK}{\partial }_2{U}_K\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill -{\partial }_1{\mathsf{\Phi }}_I& ={\left(nm\right)}_{IK}{\partial }_1{U}_K+{\left(nn\right)}_{IK}{\partial }_2{U}_K.\hfill \end{array}$$

(29)

Equations (28) and (29), which have the meaning of the extended Hooke law (14) written in terms of $U_K$ and ${\mathsf{\Phi }}_I$ for the generalized plane strain, are the two components of Equation (17) for the generalized plane strain with $j=1,2$.

Using the n-field vectors $\mathit{U}\equiv U_K$ and $\mathbf{\Phi }\equiv {\mathsf{\Phi }}_I$ in the hyperspace, the system of Equations (28) and (29) can be written in compact form

$$\begin{array}{cc}\hfill {\partial }_2\mathbf{\Phi }& =\left(mm\right){\partial }_1\mathit{U}+\left(mn\right){\partial }_2\mathit{U}\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill -{\partial }_1\mathbf{\Phi }& =\left(nm\right){\partial }_1\mathit{U}+\left(nn\right){\partial }_2\mathit{U}.\hfill \end{array}$$

(31)

By multiplying Equation (31) by ${\left(nn\right)}^{-1}$ and inserting the resulting ${\partial }_2\mathit{U}$ into Equation (30), it can be observed that the system of Equations (30) and (31) is equivalent to the following matrix partial differential equation of the first order

$$\begin{array}{c}\hfill \left[\mathit{I}{\partial }_2-\mathit{N}{\partial }_1\right]\left(\begin{array}{c}\mathit{U}(x_1,x_2)\\ \mathbf{\Phi }(x_1,x_2)\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right).\end{array}$$

(32)

This is the matrix differential equation for the generalized plane strain of quasicrystals. Here, we introduce the $2n$-vector of the extended displacement vector and the extended stress function vector for generalized plane strain

$$\begin{array}{c}\hfill \left(\begin{array}{c}\mathit{U}\\ \mathbf{\Phi }\end{array}\right)\equiv \left(\begin{array}{c}{U}_I\\ {\mathsf{\Phi }}_I\end{array}\right),I=1,\cdots ,n\end{array}$$

(33)

and the $2n\times 2n$ real matrix is defined by its $n\times n$ blocks in the hyperspace

$$\begin{array}{c}\hfill \mathit{N}=-\left(\begin{array}{cc}{\left(nn\right)}^{-1}\left(nm\right)& {\left(nn\right)}^{-1}\\ \left(mn\right){\left(nn\right)}^{-1}\left(nm\right)-\left(mm\right)& \left(mn\right){\left(nn\right)}^{-1}\end{array}\right).\end{array}$$

(34)

Here, $\mathit{I}$ is the $2n\times 2n$ identity matrix. The $2n\times 2n$ matrix $\mathit{N}$ is the fundamental elasticity matrix for quasicrystals depending on the elastic constants of quasicrystals. It is the generalization of the $6\times 6$ fundamental elasticity matrix of anisotropic elasticity (see [29,30]). The $2n\times 2n$ matrix $\mathit{N}$ is written in four $n\times n$ blocks. The northwest and southeast blocks of $\mathit{N}$ are transposes of each other, and the northeast and southwest blocks are symmetric. Note that the eigenvalue problem of the $2n\times 2n$ matrix $\mathit{N}$ given in Equation (34) leads to the generalized Stroh formalism for quasicrystals as given by Ding et al. [21] (see also [31]).

Now, we choose two orthogonal unit vectors $\mathit{m}$ and $\mathit{n}$ which are orthogonal to $\mathit{t}$ such that $(\mathit{m},\mathit{n},\mathit{t})$ forms a right-handed Cartesian basis in $E_{\parallel }^3$. This basis is rotated around $\mathit{t}$ by an angle $\varphi$ against another fixed $({\mathit{m}}_0,{\mathit{n}}_0,\mathit{t})$ basis in $E_{\parallel }^3$ such that

$$\begin{array}{cc}\hfill \left(\begin{array}{c}\mathit{m}\left(\varphi \right)\\ \mathit{n}\left(\varphi \right)\\ \mathit{t}\end{array}\right)& =\left(\begin{array}{ccc}cos\varphi & sin\varphi & 0\\ -sin\varphi & cos\varphi & 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}{\mathit{m}}_0\\ {\mathit{n}}_0\\ \mathit{t}\end{array}\right)\hfill \end{array}$$

(35)

as shown in Figure 1. It yields $\mathit{m}\equiv \mathit{m}\left(\varphi \right)$ and $\mathit{n}\equiv \mathit{n}\left(\varphi \right)$. Only the independent variable $x_j$ is transformed but not the dependent variables $U_I$ and ${\mathsf{\Phi }}_I$.

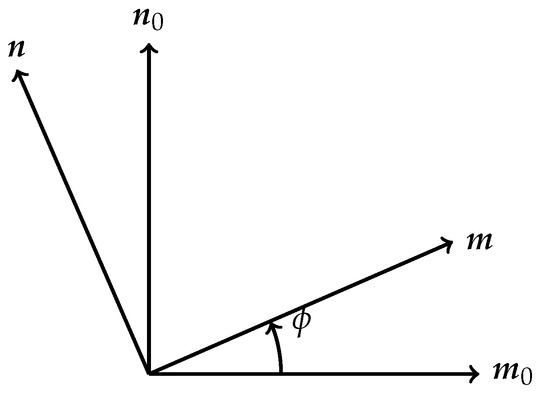
Figure 1. The unit vectors $\mathit{m}$ and $\mathit{n}$ are to be turned anticlockwise from ${\mathit{m}}_0$ and ${\mathit{n}}_0$ by an angle $\varphi$.

Using the relation

$$\begin{array}{c}\hfill {\partial }_l=m_l{\partial }_{1^{\prime }}+n_l{\partial }_{2^{\prime }},\end{array}$$

(36)

the extended elastic distortion tensor (13) becomes

$$\begin{array}{c}\hfill B_{Kl}=(m_l{\partial }_{1^{\prime }}+n_l{\partial }_{2^{\prime }})U_K,\end{array}$$

(37)

the extended constitutive relation (14) reads

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{Ij}=C_{IjKl}(m_l{\partial }_{1^{\prime }}+n_l{\partial }_{2^{\prime }})U_K\end{array}$$

(38)

and Equations (21) and (22) become

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}{m}_j& =m_j{C}_{IjKl}(m_l{\partial }_{1^{\prime }}+n_l{\partial }_{2^{\prime }})U_K\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}{n}_j& =n_j{C}_{IjKl}(m_l{\partial }_{1^{\prime }}+n_l{\partial }_{2^{\prime }})U_K.\hfill \end{array}$$

(40)

Moreover, Equations (25)–(27) become

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}& =(-n_j{\partial }_{1^{\prime }}+m_j{\partial }_{2^{\prime }}){\mathsf{\Phi }}_I\hfill \end{array}$$

(41)

and

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}{m}_j& ={\partial }_{2^{\prime }}{\mathsf{\Phi }}_I\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}{n}_j& =-{\partial }_{1^{\prime }}{\mathsf{\Phi }}_I.\hfill \end{array}$$

(43)

Substituting Equations (42) and (43) into Equations (39) and (40), it leads to

$$\begin{array}{cc}\hfill {\partial }_{2^{\prime }}{\mathsf{\Phi }}_I& ={\left(mm\right)}_{IK}{\partial }_{1^{\prime }}{U}_K+{\left(mn\right)}_{IK}{\partial }_{2^{\prime }}{U}_K\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill -{\partial }_{1^{\prime }}{\mathsf{\Phi }}_I& ={\left(nm\right)}_{IK}{\partial }_{1^{\prime }}{U}_K+{\left(nn\right)}_{IK}{\partial }_{2^{\prime }}{U}_K,\hfill \end{array}$$

(45)

which can be rewritten in the following form of the matrix partial differential equation of the first order in rotated coordinates

$$\begin{array}{c}\hfill \left[\mathit{I}{\partial }_{2^{\prime }}-\mathit{N}\left(\varphi \right){\partial }_{1^{\prime }}\right]\left(\begin{array}{c}\mathit{U}(x_{1^{\prime }},x_{2^{\prime }})\\ \mathbf{\Phi }(x_{1^{\prime }},x_{2^{\prime }})\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right).\end{array}$$

(46)

The $2n\times 2n$ matrix $\mathit{N}\left(\varphi \right)$ is defined by the contraction of the elastic constants with orthogonal unit vectors $\mathit{m}$ and $\mathit{n}$ according to ${\left(mm\right)}_{IK}=m_j{C}_{IjKl}{m}_l$, ${\left(mn\right)}_{IK}=m_j{C}_{IjKl}{n}_l$, etc. As mentioned above, the vectors $\mathit{m}\left(\varphi \right)$ and $\mathit{n}\left(\varphi \right)$ are turned against the ${\mathit{m}}_0$, ${\mathit{n}}_0$ coordinate system by an angle $\varphi$ (see Figure 1), so that $\mathit{N}$ depends on the angle $\varphi$

$$\begin{array}{c}\hfill \mathit{N}\left(\varphi \right)=-\left(\begin{array}{cc}{\left(nn\right)}^{-1}\left(nm\right)& {\left(nn\right)}^{-1}\\ \left(mn\right){\left(nn\right)}^{-1}\left(nm\right)-\left(mm\right)& \left(mn\right){\left(nn\right)}^{-1}\end{array}\right).\end{array}$$

(47)

Note that $\mathit{N}\left(0\right)\equiv \mathit{N}$ with $\mathit{m}\to {\mathit{m}}_0$ and $\mathit{n}\to {\mathit{n}}_0$. In polar coordinates $(r,\varphi )$, it yields $\mathit{m}\equiv {\mathit{e}}_r$ and $\mathit{n}\equiv {\mathit{e}}_{\varphi }$ (see Equation (35)) and ${\partial }_{1^{\prime }}={\partial }_r$ and ${\partial }_{2^{\prime }}=r^{-1}{\partial }_{\varphi }$, and the matrix partial differential equation of the first order (46) reduces to

$$\begin{array}{c}\hfill \left[\mathit{I}{\displaystyle \frac{1}{r}}{\partial }_{\varphi }-\mathit{N}\left(\varphi \right){\partial }_r\right]\left(\begin{array}{c}\mathit{U}(r,\varphi )\\ \mathbf{\Phi }(r,\varphi )\end{array}\right)=\left(\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right).\end{array}$$

(48)

This is the elementary matrix differential equation for the generalized plane strain of quasicrystals in the integral formalism.

4. Straight Dislocations and Line Forces in Quasicrystals

We consider a straight dislocation with extended Burgers vector $\mathit{b}$ and a line force with extended strength $\mathit{F}$ in a quasicrystal located at the origin of the coordinate system. The defect line runs along the axis $\mathit{t}$. The fields of the straight dislocation and line force are the extended displacement vector $\mathit{U}$ and the extended stress function vector $\mathbf{\Phi }$, the “sources” or “topological charges” are the extended Burgers vector $\mathit{b}$ and the extended line force strength $\mathit{F}$. In the integral formalism, the framework of multivalued fields can be used. In the framework of multivalued fields, the displacement vector of a straight dislocation and the stress function vector of a line force are multivalued fields. In field theory, the multivaluedness of fields is characteristic for topological defects (e.g., dislocations, monopoles, strings, and vortices), giving rise to a topological charge. Note that multivalued fields do not satisfy the Schwarz integrability conditions (see [33]).

In the hyperspace notation, the extended Burgers vector of a straight dislocation in quasicrystals is given by

$$\begin{array}{c}\hfill b_I=\left\{\begin{array}{cc}{\displaystyle b_i^{\parallel },}\hfill & {\displaystyle I=1,2,3,}\hfill \\ {\displaystyle b_{\alpha }^{\perp },}\hfill & {\displaystyle I=4,\cdots ,n,}\hfill \end{array}\right.\end{array}$$

(49)

where $b_i^{\parallel }$ is the phonon component, and $b_{\alpha }^{\perp }$ is the phason component of the extended Burgers vector, $b_I\in E_{\parallel }^3\oplus E_{\perp }^{(n-3)}$, and the extended body force vector of a line force in quasicrystals reads

$$\begin{array}{c}\hfill F_I=\left\{\begin{array}{cc}{\displaystyle F_i^{\parallel },}\hfill & {\displaystyle I=1,2,3,}\hfill \\ {\displaystyle F_{\alpha }^{\perp },}\hfill & {\displaystyle I=4,\cdots ,n,}\hfill \end{array}\right.\end{array}$$

(50)

where $F_i^{\parallel }$ and $F_{\alpha }^{\perp }$ are the strength of a phonon line force and the strength of a phason line force, $F_I\in E_{\parallel }^3\oplus E_{\perp }^{(n-3)}$, respectively.

The general solution of the matrix differential Equation (48) reads

$$\begin{array}{cc}\hfill \left(\begin{array}{c}\mathit{U}(r,\varphi )\\ \mathbf{\Phi }(r,\varphi )\end{array}\right)& =\left[\mathit{I}lnr+{\int }_0^{\varphi }\mathit{N}\left(\omega \right)\mathrm{d}\omega \right]\left(\begin{array}{c}\mathit{a}\\ \mathit{c}\end{array}\right)+\mathrm{const}\hfill \end{array}$$

(51)

with arbitrary vectors $\mathit{a}$ and $\mathit{c}$. The first and second parts in the solution (51) are the radial and angular parts. The constant term in Equation (51) gives a constant shift, which is irrelevant. From the closure condition of a line defect in quasicrystals

$$\begin{array}{c}\hfill \left(\begin{array}{c}\mathit{U}(r,2\pi )\\ \mathbf{\Phi }(r,2\pi )\end{array}\right)-\left(\begin{array}{c}\mathit{U}(r,0)\\ \mathbf{\Phi }(r,0)\end{array}\right)=\left(\begin{array}{c}\mathit{b}\\ -\mathit{F}\end{array}\right)\end{array}$$

(52)

and the relation

$$\begin{array}{c}\hfill \tilde{\mathit{N}}\left(2\pi \right)\tilde{\mathit{N}}\left(2\pi \right)=-\mathit{I}\end{array}$$

(53)

with

$$\begin{array}{c}\hfill \tilde{\mathit{N}}\left(\varphi \right)={\displaystyle \frac{1}{2\pi }}{\int }_0^{\varphi }\mathit{N}\left(\omega \right)\mathrm{d}\omega ,\end{array}$$

(54)

we find

$$\begin{array}{c}\hfill \left(\begin{array}{c}\mathit{a}\\ \mathit{c}\end{array}\right)=-{\displaystyle \frac{1}{{\left(2\pi \right)}^2}}{\int }_0^{2\pi }\mathit{N}\left(\omega \right)\mathrm{d}\omega \left(\begin{array}{c}\mathit{b}\\ -\mathit{F}\end{array}\right).\end{array}$$

(55)

Substituting Equation (55) into Equation (51), the solution of a straight dislocation with extended Burgers vector $\mathit{b}$ and a line force with extended strength $\mathit{F}$ for any quasicrystal is given by

$$\begin{array}{cc}\hfill \left(\begin{array}{c}\mathit{U}(r,\varphi )\\ \mathbf{\Phi }(r,\varphi )\end{array}\right)& =-{\displaystyle \frac{1}{{\left(2\pi \right)}^2}}\left[\mathit{I}lnr+{\int }_0^{\varphi }\mathit{N}\left(\omega \right)\mathrm{d}\omega \right]{\int }_0^{2\pi }\mathit{N}\left(\omega \right)\mathrm{d}\omega \left(\begin{array}{c}\mathit{b}\\ -\mathit{F}\end{array}\right).\hfill \end{array}$$

(56)

Equation (56) is the $2n$-vector of the solution of the extended displacement vector $\mathit{U}$ and the extended stress function vector $\mathbf{\Phi }$ for a straight dislocation with extended Burgers vector $\mathit{b}$ and a line force with extended strength $\mathit{F}$ in a quasicrystal. Therefore, Equation (56) represents the $2n$-dimensional unification of the extended displacement vector of a straight dislocation and a line force, and the extended stress function vector of a straight dislocation and a line force in quasicrystals. Both complete integration from 0 to $2\pi$ and incomplete integration from 0 to $\varphi$ of $\mathit{N}\left(\omega \right)$ are needed in Equation (56). In the limit to anisotropic elasticity, Equation (56) reduces to the solution of a line defect in anisotropic elasticity given in [34,35,36,37] (see also [30,38]). Therefore, Equation (56) represents the straightforward generalization of the solution of line defects in anisotropic elasticity towards the generalized elasticity of line defects in quasicrystals.

Using Equation (54), the solution (56) can be written in rather compact form as (see also [30,38,39])

$$\begin{array}{cc}\hfill \left(\begin{array}{c}\mathit{U}(r,\varphi )\\ \mathbf{\Phi }(r,\varphi )\end{array}\right)& =-\left[{\displaystyle \frac{1}{2\pi }}\mathit{I}lnr+\tilde{\mathit{N}}\left(\varphi \right)\right]\tilde{\mathit{N}}\left(2\pi \right)\left(\begin{array}{c}\mathit{b}\\ -\mathit{F}\end{array}\right).\hfill \end{array}$$

(57)

It can be easily seen that the solution (57) has a straightforward decomposition into a radial and an angular part.

Introducing the $n\times n$ matrices $S_{IK}$, $Q_{IK}$ and $B_{IK}$, which are tensors of rank two in the hyperspace, as the $n\times n$ blocks of the $2n\times 2n$ matrix $\tilde{\mathit{N}}$, Equation (54), with the block structure (47)

$$\begin{array}{c}\hfill \tilde{\mathit{N}}\left(\varphi \right)=\left(\begin{array}{cc}\mathit{S}\left(\varphi \right)& \mathit{Q}\left(\varphi \right)\\ \mathit{B}\left(\varphi \right)& {\mathit{S}}^{\mathrm{T}}\left(\varphi \right)\end{array}\right)\end{array}$$

(58)

and

$$\begin{array}{cc}\hfill \mathit{Q}\left(\varphi \right)& =-{\displaystyle \frac{1}{2\pi }}{\int }_0^{\varphi }{\left(nn\right)}^{-1}\mathrm{d}\omega ,\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill \mathit{S}\left(\varphi \right)& =-{\displaystyle \frac{1}{2\pi }}{\int }_0^{\varphi }{\left(nn\right)}^{-1}\left(nm\right)\mathrm{d}\omega ,\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill {\mathit{S}}^{\mathrm{T}}\left(\varphi \right)& =-{\displaystyle \frac{1}{2\pi }}{\int }_0^{\varphi }\left(mn\right){\left(nn\right)}^{-1}\mathrm{d}\omega ,\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill \mathit{B}\left(\varphi \right)& =-{\displaystyle \frac{1}{2\pi }}{\int }_0^{\varphi }\left[\left(mn\right){\left(nn\right)}^{-1}\left(nm\right)-\left(mm\right)\right]\mathrm{d}\omega ,\hfill \end{array}$$

(62)

where $\mathit{S}$, $\mathit{Q}$, $\mathit{B}$ and ${\mathit{S}}^{\mathrm{T}}$ (transpose of $\mathit{S}$) are $n\times n$ matrices resulting from integrating the four blocks in $\mathit{N}$ (see Equations (47) and (54)). Following Hirth and Lothe [40] (see also [41]), we use here the “symmetric” definition of the matrix $\mathit{B}$ instead of the original one used in anisotropic elasticity with an additional factor $4\pi$ (see [24,29]).

Equation (57) can be decomposed into its four pieces, which are n-vectors in the n-dimensional hyperspace:

• The extended displacement vector of a straight dislocation with extended Burgers vector $b_I$

  $$\begin{array}{cc}\hfill U_K(r,\varphi )& =-b_I\left[{\displaystyle \frac{1}{2\pi }}{S}_{KI}\left(2\pi \right)lnr+Q_{KM}\left(\varphi \right)B_{MI}\left(2\pi \right)+S_{KM}\left(\varphi \right)S_{MI}\left(2\pi \right)\right].\hfill \end{array}$$

  (63)
• The extended displacement vector of a line force with extended strength $F_I$

  $$\begin{array}{cc}\hfill U_K(r,\varphi )& =F_I\left[{\displaystyle \frac{1}{2\pi }}{Q}_{KI}\left(2\pi \right)lnr+S_{KM}\left(\varphi \right)Q_{MI}\left(2\pi \right)+Q_{KM}\left(\varphi \right)S_{MI}^{\mathrm{T}}\left(2\pi \right)\right].\hfill \end{array}$$

  (64)
• The extended stress function vector of a straight dislocation with extended Burgers vector $b_K$

  $$\begin{array}{cc}\hfill {\mathsf{\Phi }}_I(r,\varphi )& =-b_K\left[{\displaystyle \frac{1}{2\pi }}{B}_{IK}\left(2\pi \right)lnr+B_{IM}\left(\varphi \right)S_{MK}\left(2\pi \right)+S_{IM}^{\mathrm{T}}\left(\varphi \right)B_{MK}\left(2\pi \right)\right].\hfill \end{array}$$

  (65)
• The extended stress function vector of a line force with extended strength $F_K$

  $$\begin{array}{cc}\hfill {\mathsf{\Phi }}_I(r,\varphi )& =F_K\left[{\displaystyle \frac{1}{2\pi }}{S}_{IK}^{\mathrm{T}}\left(2\pi \right)lnr+B_{IM}\left(\varphi \right)Q_{MK}\left(2\pi \right)+S_{IM}^{\mathrm{T}}\left(\varphi \right)S_{MK}^{\mathrm{T}}\left(2\pi \right)\right].\hfill \end{array}$$

  (66)

It is important to note that Equation (63) is in agreement with the integral expression of the extended displacement vector of a straight dislocation given by Ding et al. [21]. In the limit from quasicrystals to anisotropic elasticity, the extended displacement vector of a straight dislocation and a line force given in Equations (63) and (64) reduce to the displacement vector field of a straight dislocation and a line force given by Asaro et al. [25] (see also [35]) and the extended stress function vector of a straight dislocation and a line force given in Equations (65) and (66) reduce to the stress functions of a straight dislocation and a line force given by Asaro et al. [42].

Using ${\partial }_{1^{\prime }}={\partial }_r$ and ${\partial }_{2^{\prime }}=r^{-1}{\partial }_{\varphi }$, Equation (36) becomes

$$\begin{array}{c}\hfill {\partial }_l=m_l{\partial }_r+{\displaystyle \frac{1}{r}}{n}_l{\partial }_{\varphi },\end{array}$$

(67)

the extended elastic distortion tensor (37) reads

$$\begin{array}{c}\hfill B_{Kl}=\left(m_l{\partial }_r+{\displaystyle \frac{1}{r}}{n}_l{\partial }_{\varphi }\right)U_K\end{array}$$

(68)

and the extended stress tensor (41) reads

$$\begin{array}{c}\hfill {\mathsf{\Sigma }}_{Ij}=\left(-n_j{\partial }_r+{\displaystyle \frac{1}{r}}{m}_j{\partial }_{\varphi }\right){\mathsf{\Phi }}_I.\end{array}$$

(69)

Using Equations (63) and (68), the extended elastic distortion tensor of a straight dislocation with extended Burgers vector $b_I$ is given by

$$\begin{array}{cc}\hfill B_{Kl}& =-{\displaystyle \frac{b_I}{2\pi r}}\left[m_l{S}_{KI}\left(2\pi \right)-n_l{\left(nn\right)}_{KN}^{-1}\left(B_{NI}\left(2\pi \right)+{\left(nm\right)}_{NM}{S}_{MI}\left(2\pi \right)\right)\right].\hfill \end{array}$$

(70)

Using Equations (64) and (68), the extended elastic distortion tensor of a line force with extended strength $F_I$ is given by

$$\begin{array}{cc}\hfill B_{Kl}& ={\displaystyle \frac{F_I}{2\pi r}}\left[m_l{Q}_{KI}\left(2\pi \right)-n_l{\left(nn\right)}_{KN}^{-1}\left(S_{NI}^{\mathrm{T}}\left(2\pi \right)+{\left(nm\right)}_{NM}{Q}_{MI}\left(2\pi \right)\right)\right].\hfill \end{array}$$

(71)

Using Equations (65) and (69), the extended stress tensor of a straight dislocation with extended Burgers vector $b_K$ is given by

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}& ={\displaystyle \frac{b_K}{2\pi r}}[n_j{B}_{IK}\left(2\pi \right)+m_j{\left[\left(mn\right){\left(nn\right)}^{-1}\left(nm\right)-\left(mm\right)\right]}_{IM}{S}_{MK}\left(2\pi \right)\hfill \\ \hfill & +m_j{\left[\left(mn\right){\left(nn\right)}^{-1}\right]}_{IM}{B}_{MK}\left(2\pi \right)].\hfill \end{array}$$

(72)

Using Equations (66) and (69), the extended stress tensor of a line force with extended strength $F_K$ is given by

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}& =-{\displaystyle \frac{F_K}{2\pi r}}[n_j{S}_{IK}^{\mathrm{T}}\left(2\pi \right)+m_j{\left[\left(mn\right){\left(nn\right)}^{-1}\left(nm\right)-\left(mm\right)\right]}_{IM}{Q}_{MK}\left(2\pi \right)\hfill \\ \hfill & +m_j{\left[\left(mn\right){\left(nn\right)}^{-1}\right]}_{IM}{S}_{MK}^{\mathrm{T}}\left(2\pi \right)].\hfill \end{array}$$

(73)

Note that all $\varphi$-dependence is contained in $\mathit{m}$, $\mathit{n}$, and the matrices $\left(mm\right)$, $\left(mn\right)$, $\left(nm\right)$ and ${\left(nn\right)}^{-1}$. Furthermore, Equations (70)–(73) show the typical $1/r$-behavior of the elastic fields of line defects. It can be easily seen that the following consistency conditions are fulfilled for Equations (70) and (72) and for Equations (71) and (73) (see also [29])

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}{m}_j& =m_j{C}_{IjKl}{B}_{Kl}\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill {\mathsf{\Sigma }}_{Ij}{n}_j& =n_j{C}_{IjKl}{B}_{Kl}.\hfill \end{array}$$

(75)

Equation (70) is in agreement with the integral expression given by Ding et al. [21]. In the limit from quasicrystals to anisotropic elasticity, the extended displacement elastic distortion tensor of a straight dislocation and a line force given in Equations (70) and (71) reduce to the elastic distortion tensor of a straight dislocation and a line force given by Asaro et al. [25] (see also [29]).

Using the extended stress function vector of a straight dislocation (65) for $r=r_0/R$ and $\varphi =0$, the elastic self-energy of a straight dislocation per unit length reads

$$\begin{array}{cc}\hfill \mathcal{E}& ={\displaystyle \frac{1}{2}}{b}_I{\mathsf{\Phi }}_I(r_0/R,0)\hfill \\ \hfill & ={\displaystyle \frac{1}{4\pi }}{b}_I{B}_{IK}\left(2\pi \right)b_{K}ln(R/r_0),\hfill \end{array}$$

(76)

where $r_0$ and R are the inner and our cutoff radii. Equation (76) is in agreement with the expression given by Ding et al. [21].

Using the extended displacement vector of line force (66) for $r=r_0/R$ and $\varphi =0$, the elastic self-energy of a line force per unit length reads

$$\begin{array}{cc}\hfill \mathcal{E}& ={\displaystyle \frac{1}{2}}{F}_K{U}_K(r_0/R,0)\hfill \\ \hfill & =-{\displaystyle \frac{1}{4\pi }}{F}_I{Q}_{IK}\left(2\pi \right)F_{K}ln(R/r_0).\hfill \end{array}$$

(77)

In the limit from quasicrystals to anisotropic elasticity, the elastic self-energy of a straight dislocation (76) and the elastic self-energy of a line force (77) reduce to the expressions given by Bacon et al. [29].

The Peach–Koehler force between a straight dislocation with Burgers vector $b_I^{\left(A\right)}$ at position $(r,\varphi )$ in the stress field ${\mathsf{\Sigma }}_{Ij}^{\left(B\right)}$ produced by another dislocation located at the position $(0,0)$ is given by (see [20,32,43])

$$\begin{array}{cc}\hfill {\mathcal{F}}_l^{\mathrm{PK}\left(AB\right)}& ={ϵ}_{lj3}{b}_I^{\left(A\right)}{\mathsf{\Sigma }}_{Ij}^{\left(B\right)}\hfill \\ \hfill & ={ϵ}_{lj3}{\displaystyle \frac{b_I^{\left(A\right)}{b}_K^{\left(B\right)}}{2\pi r}}[n_j{B}_{IK}\left(2\pi \right)+m_j{\left[\left(mn\right){\left(nn\right)}^{-1}\left(nm\right)-\left(mm\right)\right]}_{IM}{S}_{MK}\left(2\pi \right)\hfill \\ \hfill & +m_j{\left[\left(mn\right){\left(nn\right)}^{-1}\right]}_{IM}{B}_{MK}\left(2\pi \right)],\hfill \end{array}$$

(78)

where the stress field ${\mathsf{\Sigma }}_{Ij}^{\left(B\right)}$ of the straight dislocation with Burgers vector $b_K^{\left(B\right)}$ is given in Equation (72).

The Cherepanov force between a line force with strength $F_K^{\left(A\right)}$ at position $(r,\varphi )$ in the elastic distortion field $B_{Kl}^{\left(B\right)}$ produced by another line force located the the position $(0,0)$ is given by (see [32,43])

$$\begin{array}{cc}\hfill {\mathcal{F}}_l^{\mathrm{C}\left(AB\right)}& =F_K^{\left(A\right)}{B}_{Kl}^{\left(B\right)}\hfill \\ \hfill & ={\displaystyle \frac{F_K^{\left(A\right)}{F}_I^{\left(B\right)}}{2\pi r}}\left[m_l{Q}_{KI}\left(2\pi \right)-n_l{\left(nn\right)}_{KN}^{-1}\left(S_{NI}^{\mathrm{T}}\left(2\pi \right)+{\left(nm\right)}_{NM}{Q}_{MI}\left(2\pi \right)\right)\right],\hfill \end{array}$$

(79)

where the elastic distortion $B_{Kl}^{\left(B\right)}$ of the line force with strength $F_I^{\left(B\right)}$ given in Equation (71).

5. Green Tensor in the Integral Formalism

In the framework of the integral formalism, the displacement field of a line force, Equation (64), gives the two-dimensional Green tensor for quasicrystals, namely

$$\begin{array}{c}\hfill U_K=G_{KI}{F}_I.\end{array}$$

(80)

Therefore, within the integral formalism, the two-dimensional Green tensor for generalized plane strain in quasicrystals reads

$$\begin{array}{cc}\hfill G_{KI}(r,\varphi )& ={\displaystyle \frac{1}{2\pi }}{Q}_{KI}\left(2\pi \right)lnr+S_{KM}\left(\varphi \right)Q_{MI}\left(2\pi \right)+Q_{KM}\left(\varphi \right)S_{MI}^{\mathrm{T}}\left(2\pi \right).\hfill \end{array}$$

(81)

Note that the Green tensor (81) possesses a straightforward decomposition into a radial part ($lnr$-term) and an angular part depending on $\varphi$. Such a decomposition is not so easily visible in the general form of the two-dimensional Green tensor using Fourier transform (see [44]).

6. Conclusions

The six-dimensional integral formalism of anisotropic elasticity has been extended to an eight-dimensional integral formalism for one-dimensional quasicrystals, a ten-dimensional integral formalism for two-dimensional quasicrystals and a twelve-dimensional integral formalism for three-dimensional quasicrystals. The extended integral formalism can be used for the computation of the elastic fields of line defects in any quasicrystal. Using the extended integral formalism, the elastic fields of straight dislocations and line forces in quasicrystals have been determined, which are suitable for the analytical and numerical modeling of line defects in quasicrystals. The elastic fields of a line defect in quasicrystals have a surprisingly simple and compact form in the integral formalism. Moreover, the two-dimensional Green tensor of quasicrystals has been derived in the framework of the integral formalism.

Exact analytical solutions require analytical expressions for the integrals in the integral formalism. In the general case, only numerical solutions are possible using numerical integration. For quasicrystals of high symmetry and with a symmetrical orientation of the defect line, the complexity is reduced, and analytical solutions become possible because the integrals in the integral formalism can be computed analytically which will be performed in forthcoming publications. In the case of the lower symmetry of quasicrystals and of the orientation of the line defect, numerical treatment is needed in the integral formalism.