Artificial Intelligence Modeling of Materials’ Bulk Chemical and Physical Properties
Abstract
1. Introduction
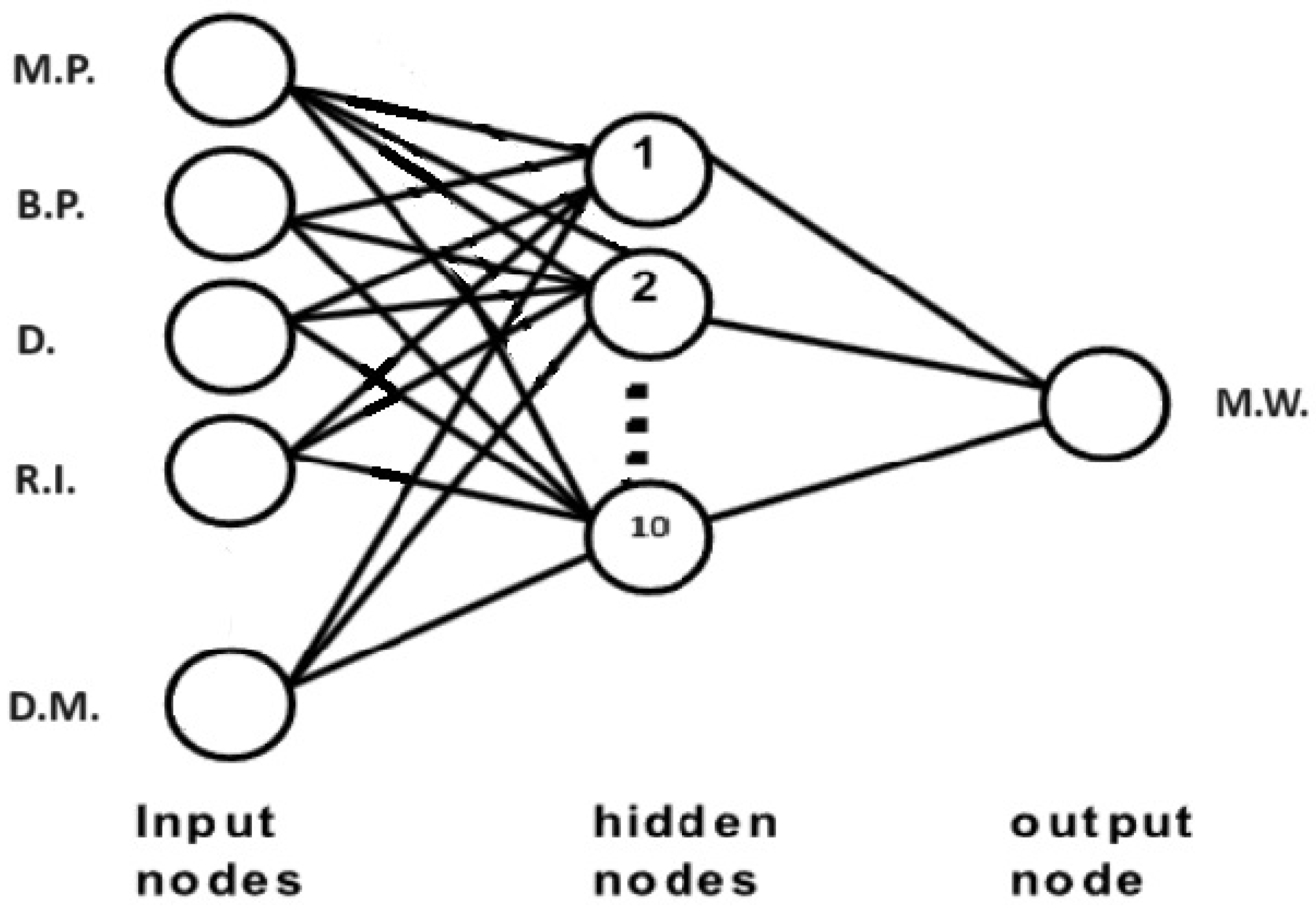
2. Artificial Intelligence
3. Methods
4. Results
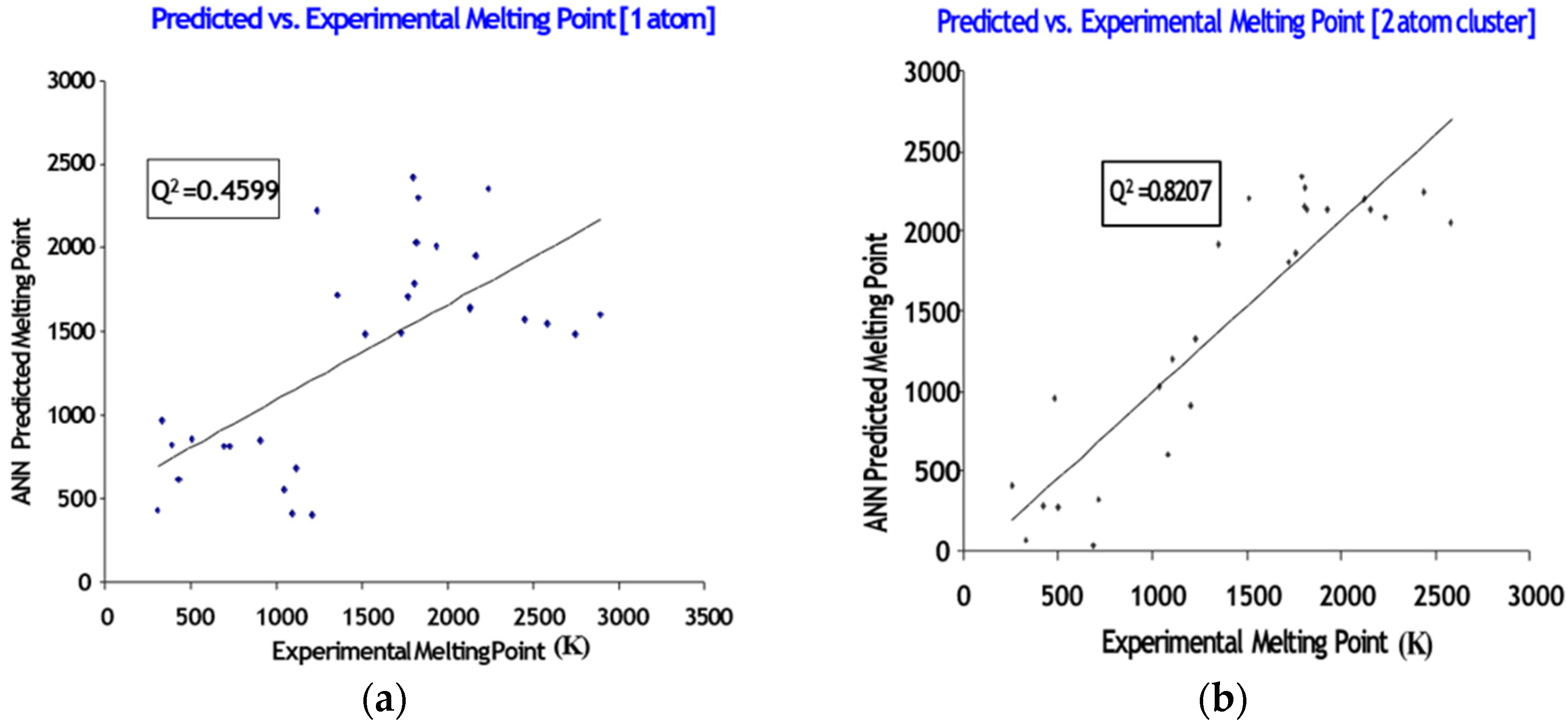
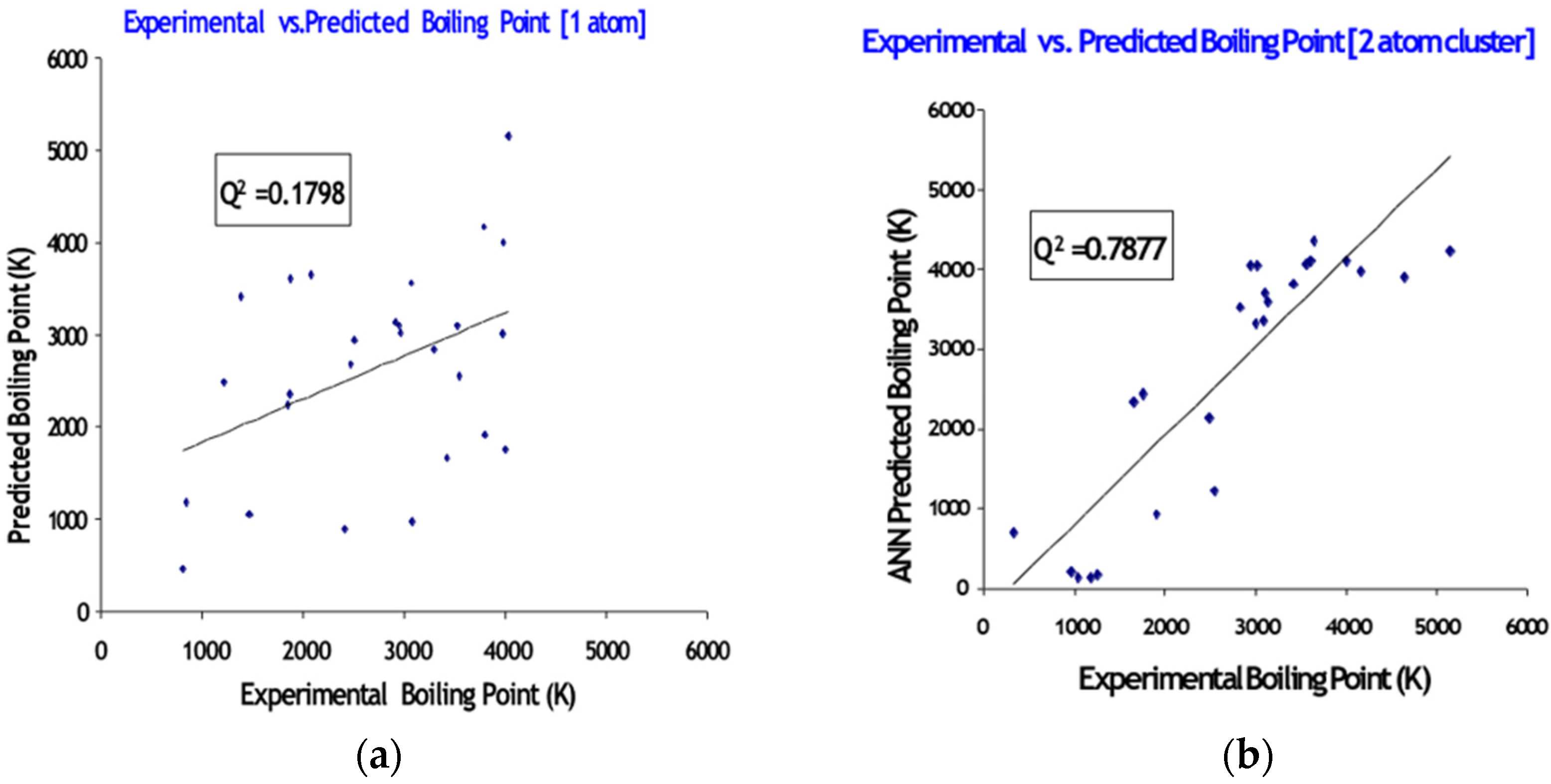
Atomic Systems
5. Summary
5.1. Atomic Systems
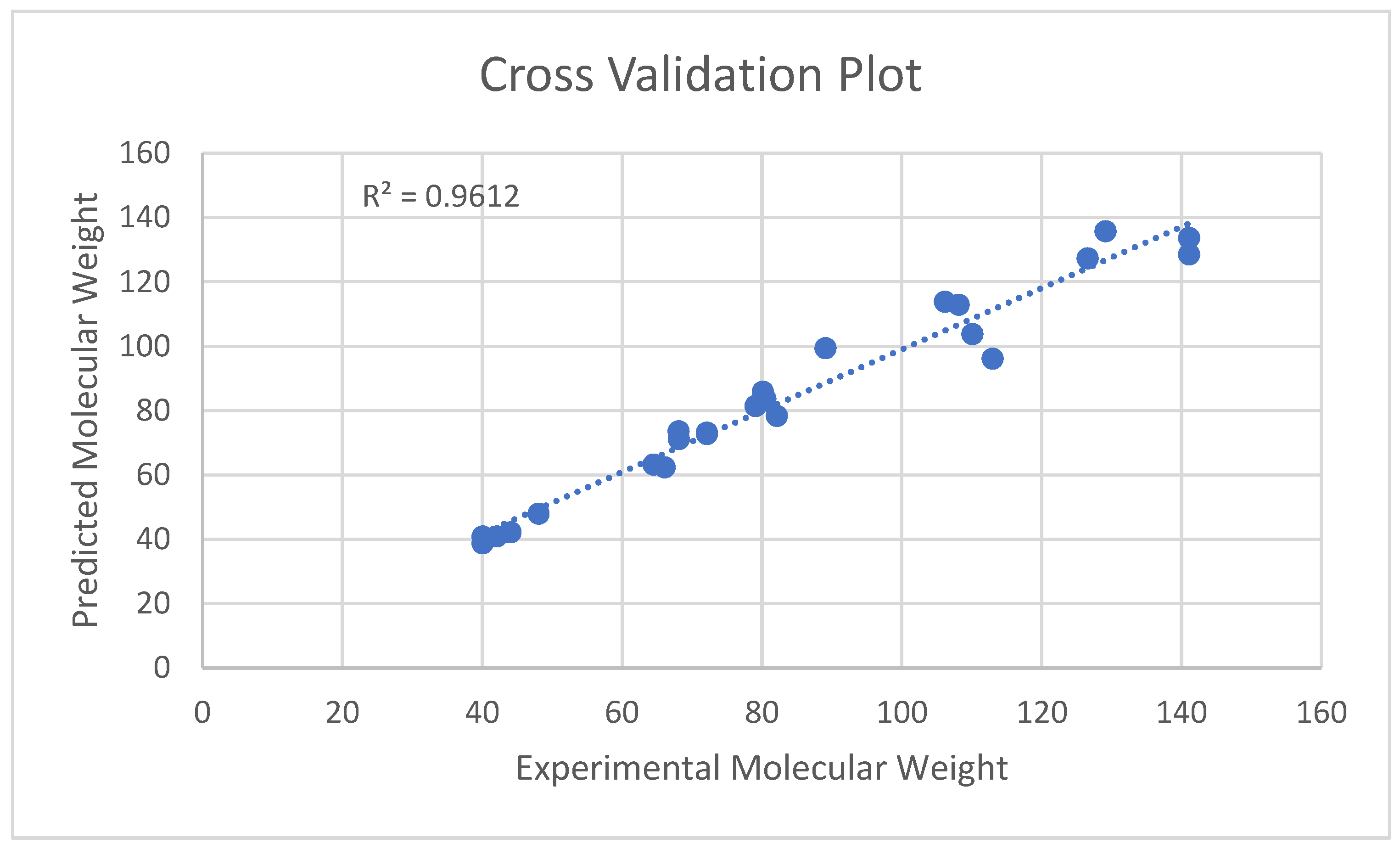
5.2. Molecular Systems
6. Results
Molecular Systems
7. Summary
Molecular Systems
Funding
Data Availability Statement
Conflicts of Interest
References
- Hyperchem, version 5.01; Hypercube, Inc.: Waterloo, ON, Canada, 1994. Available online: http://www.hypercubeusa.com/News/PressRelease/NewPolicyOct1997/tabid/397/Default.aspx (accessed on 29 August 2024).
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian, version 09; Gaussian, Inc.: Wallingford, CT, USA, 2009.
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Käser, S.; Vazquez-Salazar, L.I.; Meuwly, M.; Töpfer, K. Neural network potentials for chemistry: Concepts, applications and prospects. Digit. Discov. 2023, 2, 28–58. [Google Scholar] [CrossRef] [PubMed]
- Sumpter, B.G.; Getino, C.; Noid, D.W. Theory and Applications of Neural Computing in Chemical Science. Annu. Rev. Phys. Chem. 1994, 45, 439–481. [Google Scholar] [CrossRef]
- Shelton, R.; Baffes, P.T. Nets Back-Propagation; version 4.0; Software Technology Branch, NASA, Johnson Space Center: Houston, TX, USA, 1989. Available online: https://ntrs.nasa.gov/api/citations/19920012191/downloads/19920012191.pdf (accessed on 29 August 2024).
- Darsey, J.A.; Sumpter, B.G.; Noid, D.W. Correlating Physical Properties of Both Polymeric and Energetic Materials and their Organic Precursors of Polymers Using Artificial Neural Networks. Int. J. Smart Eng. Syst. Des. 2000, 2, 283–298. [Google Scholar]
- Tu, X.; Geesman, E.; Wang, K.; Compadre, C.; Buzatu, D.; Darsey, J. Prediction of the partition coefficient of dillapiol and its derivatives by use of molecular simulation and artificial neural networks. Chim. Oggi 2002, 10, 51–54. [Google Scholar]
- Lane, T.R.; Harris, J.; Urbina, F.; Ekins, S. Comparing LD50/LC50 Machine Learning Models for Multiple Species. J. Chem. Health Saf. 2023, 30, 83–97. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, N. A Systematic Approach for Developing Feed-Forward/Back-Propagating Neural Network Models for Predicting Bulk Chemical and Physical Properties of Transition Metals. Master’s Thesis, University of Arkansas at Little Rock, Little Rock, AR, USA, 2007. [Google Scholar]
- Baffer, P.T. NNETS Program; version 2.0; Johnson Space Center Report No. 23366; NASA: Houston, TX, USA, 1989.
- Soman, A. Application of Artificial Intelligence to Chemical Systems. Master’s Thesis, University of Arkansas at Little Rock, Little Rock, AR, USA, 1993. [Google Scholar]
- Lide, D.R. CRC Handbook CRC Handbook of Chemistry and Physics, 76th ed.; CRC Press: Cleveland, OH, USA, 1977. [Google Scholar]
- Eberhart, R.C.; Dobbins, R.W. Neural Network PC Tools. In A Practical Guide; Academic Press, Inc.: London, UK, 1990. [Google Scholar]
- Hert, J.; Krogh, A.; Palmer, R.G. Introduction to the Theory of Neural Computing; Addison-Wesley Publishing, Co.: Redwood City, CA, USA, 1991. [Google Scholar]
- Wasserman, P.D. Neural Computing Theory and Practice; Van Nostrand Reinhold: New York, NY, USA, 1989. [Google Scholar]
- Zurada, J.M. Introduction to Artificial Neural Systems; Weit Publishing Company: New York, NY, USA, 1992. [Google Scholar]
- Darsey, J.A.; Noid, D.W.; Wunderlich, B.; Tsoukalas, L. Neural-net extrapolations of heat capacities of polymers to low temperatures. Makromol. Chem. Rapid Commun. 1991, 12, 325. [Google Scholar] [CrossRef]


| No. | Compound Name | Mol. Weight (U) |
|---|---|---|
| 1 | Dichloro-fluoro-methane | 102.92 |
| 2 | Dibromo-methane | 173.85 |
| 3 | Nitro-methane | 61.04 |
| 4 | Pentachloro-ethane | 202.3 |
| 5 | Chloro-ethylene | 62.5 |
| 6 | Ethanal | 44.05 |
| 7 | Chloro-ethane | 64.52 |
| 8 | Fluoro-ethane | 48.06 |
| 9 | Iodo-ethane | 155.97 |
| 10 | Acetyl amine | 59.07 |
| 11 | Dimethyl sulfoxide | 78.13 |
| 12 | Dimethyl-amine | 45.09 |
| 13 | Propyne | 40.07 |
| 14 | 2-chloro-propene | 76.53 |
| 15 | Propene | 42.08 |
| 16 | 2,2-dichloro-propane | 112.99 |
| 17 | 1-propanol | 60.11 |
| 18 | Trimethyl-amine | 59.11 |
| 19 | Furan | 68.08 |
| 20 | Thiophene | 84.14 |
| 21 | 1,2-butadiene | 54.09 |
| 22 | Butanal | 72.12 |
| 23 | Cyclopentene | 68.13 |
| 24 | Pyridine | 79.10 |
| 25 | Bromo-benzene | 157.02 |
| 26 | Nitro-benzene | 123.11 |
| 27 | Phenol | 94.11 |
| 28 | p-chloro-toulene | 126.59 |
| 29 | Toulene | 92.15 |
| 30 | o-xylene | 106.17 |
| 31 | Dibutyl-ether | 130.23 |
| 32 | Quinoline | 129.16 |
| 33 | Isoquinoline | 129.16 |
| 34 | Phenyl-benzene | 154.21 |
| 35 | Tribromo-methane | 252.75 |
| 36 | Iodo-methane | 141.94 |
| 37 | Ethanethiol | 62.13 |
| 38 | Propanone | 58.08 |
| 39 | Butane | 58.13 |
| 40 | Dipropyl-ether | 102.18 |
| 41 | Fluoro-methane | 34.03 |
| 42 | 1,1-dichloro-ethane | 98.96 |
| 43 | 1,1-difluoro-ethane | 66.05 |
| 44 | 2-propanol | 60.11 |
| 45 | 1-nitro-propane | 89.09 |
| 46 | 2-chloro-propane | 78.54 |
| 47 | Aniline | 93.13 |
| 48 | Butanal | 72.12 |
| 49 | m-dichloro-benzene | 147.01 |
| 50 | m-fluoro-toulene | 110.13 |
| 51 | Ethane | 30.07 |
| 52 | Propadiene | 40.07 |
| 53 | Propene | 42.08 |
| 54 | Acetylene | 26.04 |
| 55 | 2-chloro-ethanol | 80.52 |
| 56 | 1,3-cyclohexadiene | 80.14 |
| 57 | 1-Hexyne | 82.15 |
| 58 | 1,4-dichloro-butane | 127.03 |
| 59 | Ethanoic acid | 60.05 |
| 60 | 1,3-dichloro-propane | 112.99 |
| 61 | 2-chloro-2-methyl-propane | 92.57 |
| 62 | m-chloro-nitrobenzene | 157.56 |
| 63 | p-chloro-nitrobenzene | 157.56 |
| 64 | 1,3-cyclopentadiene | 66.10 |
| 65 | 1,3-butadiene | 54.09 |
| 66 | 4-chloro-phenol | 128.56 |
| 67 | 1,3-cyclohexadiene | 80.14 |
| 68 | Phenyl-methanol | 108.15 |
| 69 | Acetophenone | 120.16 |
| 70 | p-fluoro-nitrobenzene | 141.10 |
| Compound Name | Experimental M.W. (U) | Predicted M.W. (U) |
|---|---|---|
| RUN 1: | ||
| Propene | 42.08 | 40.833 |
| Pyridine | 79.10 | 81.36 |
| Butanal | 72.12 | 73.10 |
| 1,3-cyclopentadiene | 66.10 | 62.32 |
| RUN 2: | ||
| Propyne | 40.07 | 40.85 |
| p-chloro-toulene | 126.59 | 127.3 |
| 1,3-cyclohexadiene | 80.14 | 85.82 |
| p-fluoro-nitrobenzene | 141.10 | 133.59 |
| RUN 3: | ||
| Chloro-ethane | 64.52 | 63.20 |
| Furan | 68.08 | 73.50 |
| Propadiene | 40.07 | 38.70 |
| Phenyl-methanol | 108.15 | 112.88 |
| RUN 4: | ||
| Fluoro-ethane | 48.06 | 47.90 |
| Cyclopentene | 68.13 | 71.11 |
| Isoquinoline | 129.16 | 135.72 |
| 1 Hexyne | 82.15 | 78.29 |
| RUN 5: | ||
| o-xylene | 106.17 | 113.8 |
| 1-nitro-propane | 89.09 | 99.35 |
| 1,3-dichloro-propane | 112.99 | 96.06 |
| p-fluoro-nitro-benzene | 141.10 | 128.5 |
| RUN 6: | ||
| Ethanal | 44.05 | 42.10 |
| Butanal | 72.12 | 72.70 |
| m-fluoro-toluene | 110.13 | 103.73 |
| 2-chloro-ethanol | 80.52 | 83.60 |
| No. | Compound Name | M.P. (°C) | B.P. (°C) | D (g/cc) | R.I. | D.M. (Debyes) |
|---|---|---|---|---|---|---|
| 1 | Dichloro-fluoro-methane | −135.0 | 9.0 | 1.405 9 | 1.3724 9 | 1.29 |
| 2 | Dibromo-methane | −52.55 | 97.0 | 2.4970 | 1.5420 90 | 1.43 |
| 3 | Nitro-methane | −28.50 | 100.8 | 1.1371 | 1.3817 20 | 3.46 |
| 4 | Pentachloro-ethane | −29.00 | 162.0 | 1.6796 | 1.5025 20 | 0.92 |
| 5 | Chloro-ethylene | −153.8 | −13.4 | 0.1906 | 1.3700 20 | 1.45 |
| 6 | Ethanal | −121.0 | 20.80 | 0.78 18 | 1.3316 20 | 2.69 |
| 7 | Chloro-ethane | −136.4 | 12.27 | 0.8978 | 1.3676 20 | 2.05 |
| 8 | Fluoro-ethane | −143.2 | −37.7 | 0.0022 | 1.2656 20 | 1.94 |
| 9 | Iodo-ethane | −108.0 | 72.30 | 1.9358 | 1.5133 20 | 1.91 |
| 10 | Acetyl amine | 82.30 | 221.2 | 0.99 85 | 1.4278 78 | 3.76 i |
| 11 | Dimethyl sulfoxide | 18.45 | 189.0 | 1.1014 | 1.4770 20 | 3.96 |
| 12 | Dimethyl-amine | −93.00 | 7.40 | 0.680 0 | 1.3500 17 | 1.03 |
| 13 | Propyne | −101.5 | −23.2 | 0.7 −50 | 1.386 −40 | 0.78 |
| 14 | 2-chloro-propene | −137.4 | 22.65 | 0.9017 | 1.3973 20 | 1.66 |
| 15 | Propene | −185.2 | −47.4 | 0.5193 | 1.357 −70 | 0.37 |
| 16 | 2,2-dichloro-propane | −33.80 | 69.30 | 1.1120 | 1.4148 20 | 2.27 |
| 17 | 1-propanol | −126.5 | 97.40 | 0.8035 | 1.3850 20 | 1.68 i |
| 18 | Trimethyl-amine | −117.2 | 2.87 | 0.671 0 | 1.3631 0 | 0.61 |
| 19 | Furan | −85.65 | 31.36 | 0.9514 | 1.4214 2 | 0.66 |
| 20 | Thiophene | −38.25 | 84.16 | 1.0649 | 1.5289 20 | 0.55 |
| 21 | 1,2-butadiene | −136.2 | 10.85 | 0.676 0 | 1.421 1.3 | 0.40 |
| 22 | Butanal | −99.00 | 75.70 | 0.8170 | 1.3843 20 | 2.72 i |
| 23 | Cyclopentene | −135.1 | 44.24 | 0.7720 | 1.4225 20 | 0.20 |
| 24 | Pyridine | −42.00 | 115.5 | 0.9819 | 1.5095 20 | 2.19 |
| 25 | Bromo-benzene | −30.82 | 156.0 | 1.4950 | 1.5597 20 | 1.70 |
| 26 | Nitro-benzene | 5.7 | 210.8 | 1.2037 | 1.5562 20 | 4.22 |
| 27 | Phenol | 43.0 | 70.86 | 1.0576 | 1.5418 41 | 1.45 |
| 28 | p-chloro-toulene | 7.5 | 162.0 | 1.0697 | 1.5150 20 | 2.21 |
| 29 | Toulene | −95.0 | 110.6 | 0.8669 | 1.4961 20 | 0.36 |
| 30 | o-xylene | −25.18 | 144.4 | 0.8802 | 1.5055 20 | 0.62 |
| 31 | Dibutyl-ether | −95.30 | 142.0 | 0.7689 | 1.3992 20 | 1.17 i |
| 32 | Quinoline | −15.60 | 238.1 | 1.0929 | 1.6268 20 | 2.29 |
| 33 | Isoquinoline | 26.50 | 243.3 | 1.0986 | 1.6148 20 | 2.73 |
| 34 | Phenyl-benzene | 71.00 | 255.9 | 0.8660 | 1.5880 77 | 0.00 |
| 35 | Tribromo-methane | 8.30 | 149.5 | 2.8899 | 1.5976 20 | 0.99 |
| 36 | Iodo-methane | −66.45 | 42.40 | 2.2790 | 1.5382 20 | 1.62 |
| 37 | Ethanethiol | −144.4 | 35.00 | 0.8391 | 1.4310 20 | 1.58 i |
| 38 | Propanone | −95.35 | 56.20 | 0.7899 | 1.3588 20 | 2.88 |
| 39 | Butane | −138.4 | −0.50 | 0.601 0 | 1.354 −19 | <0.05 |
| 40 | Dipropyl-ether | −122 | 91.00 | 0.7360 | 1.3809 20 | 1.21 i |
| 41 | Fluoro-methane | −141.8 | −78.4 | 0.8 −60 | 1.1727 20 | 1.85 |
| 42 | 1,1-dichloro-ethane | −16.98 | 57.28 | 1.1757 | 1.4164 20 | 2.06 |
| 43 | 1,1-difluoro-ethane | −117.0 | −24.7 | 0.9500 | 1.301 −72 | 2.07 |
| 44 | 2-propanol | −89.50 | 82.40 | 0.7855 | 1.3776 20 | 1.66 i |
| 45 | 1-nitro-propane | −108.0 | 130.5 | 1.01 24 | 1.4016 20 | 3.56 i |
| 46 | 2-chloro-propane | −117.2 | 35.74 | 0.8617 | 1.3777 20 | 2.17 |
| 47 | Aniline | −6.30 | 184.1 | 1.0217 | 1.5863 20 | 1.53 |
| 48 | Butanal | −99.0 | 75.7 | 0.8170 | 1.3843 20 | 2.72 i |
| 49 | m-dichloro-benzene | −24.7 | 173.0 | 1.2884 | 1.5459 20 | 1.72 |
| 50 | m-fluoro-toulene | −87.7 | 116.0 | 0.9986 | 1.4691 20 | 1.86 |
| 51 | Ethane | −183.3 | −88.6 | 0.5720 | 1.0377 0 | 0.00 |
| 52 | Propadiene | −136.0 | −34.5 | 1.7870 | 1.4168 | 0.00 |
| 53 | Propene | −185.3 | −47.4 | 0.5193 | 1.357 −70 | 0.37 |
| 54 | Acetylene | −80.8 | −84.0 | 0.6 −32 | 1.0005 0 | 0.00 |
| 55 | 2-chloro-ethanol | −67.5 | 128.0 | 1.2002 | 1.4419 20 | 1.78 i |
| 56 | 1,3-cyclohexadiene | −89.0 | 80.50 | 0.8405 | 1.4755 20 | 0.44 |
| 57 | 1-Hexyne | −131.9 | 71.30 | 0.7155 | 1.3989 20 | 0.83 i |
| 58 | 1,4-dichloro-butane | −37.3 | 153.9 | 1.1408 | 1.4542 20 | 2.22 i |
| 59 | Ethanoic acid | 16.604 | 117.9 | 1.0492 | 1.3716 20 | 1.74 |
| 60 | 1,3-dichloro-propane | −99.5 | 120.4 | 1.1878 | 1.4487 20 | 2.1 i |
| 61 | 2-chloro-2-methyl-propane | −25.4 | 52.0 | 0.8420 | 1.3857 20 | 2.13 |
| 62 | m-chloro-nitrobenzene | 24.00 | 235.0 | 1.34 50 | 1.5374 80 | 3.73 |
| 63 | p-chloro-nitrobenzene | 83.6 | 242.0 | 1.3 90 | 1.538 100 | 2.83 |
| 64 | 1,3-cyclopentadiene | −97.2 | 40.00 | 0.8021 | 1.4440 20 | 0.42 |
| 65 | 1,3-butadiene | −108.91 | −4.41 | 0.6211 | 1.429 −25 | 0.00 |
| 66 | 4-chloro-phenol | 43.20 | 219.8 | 1.27 40 | 1.5579 40 | 2.11 |
| 67 | 1,3-cyclohexadiene | −89.0 | 80.5 | 0.8405 | 1.4755 20 | 0.44 |
| 68 | Phenyl-methanol | −15.3 | 205.3 | 1.0419 | 1.5396 20 | 1.71 |
| 69 | Acetophenone | 20.5 | 202.0 | 1.0281 | 1.5372 20 | 3.02 |
| 70 | p-fluoro-nitrobenzene | 27.0 | 206.0 | 1.3300 | 1.5316 20 | 2.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darsey, J.A. Artificial Intelligence Modeling of Materials’ Bulk Chemical and Physical Properties. Crystals 2024, 14, 866. https://doi.org/10.3390/cryst14100866
Darsey JA. Artificial Intelligence Modeling of Materials’ Bulk Chemical and Physical Properties. Crystals. 2024; 14(10):866. https://doi.org/10.3390/cryst14100866
Chicago/Turabian StyleDarsey, Jerry A. 2024. "Artificial Intelligence Modeling of Materials’ Bulk Chemical and Physical Properties" Crystals 14, no. 10: 866. https://doi.org/10.3390/cryst14100866
APA StyleDarsey, J. A. (2024). Artificial Intelligence Modeling of Materials’ Bulk Chemical and Physical Properties. Crystals, 14(10), 866. https://doi.org/10.3390/cryst14100866






