Abstract
A series of solid acid compounds, representing the large family MmHn(AO4)(m + n)/2·yH2O (where M = K, Rb, Cs, NH4; AO4 = SO4, SeO4, HPO4, HAsO4), is characterized by high values of own proton conductivity, which arises as a result of a phase transition through the formation of a dynamically disordered hydrogen bond network. Such superprotonic phase transitions are observed, however, not for all compounds of the family and Rb3H(SO4)2 is one of them. The occurrence of superprotonic phase transitions has been experimentally demonstrated in the (KxRb1−x)3H(SO4)2 solid solutions through cation substitution. The high-temperature phases are unstable towards decomposition reaction, and their temperature range of existence is about 1–7 °C. The implementation of superprotonic transitions is discussed in terms of hydrogen bond lengths.
1. Introduction
The high proton conductivity of solid acids attracts attention in relation to using this phenomenon in various electrochemical devices, including fuel cells. The mechanism of high proton conductivity is a variation of the Grotthuss mechanism and is called the “Paddle-Wheel” mechanism [,], which is associated with the rotational disordering of polyanions and corresponds to a specific type of disorder in solid acids; the positions of hydrogen bonds in the crystal are dynamically disordered []. The disordering of hydrogen bonds occurs as a result of phase transitions in which the conductivity jumps by 3–5 orders of magnitude.
Solid acid compounds M3H(AO4)2 (M = Na, K, NH4, Rb; A = S, Se) are part of the superprotonic family and belong to monoclinic symmetry. Some of them undergo superprotonic phase transition (C2/c-Rm) upon heating at ambient pressure []. The crystal structure of the low-temperature monoclinic phase of M3H(SO4)2 crystals (M = K, Rb) is shown in Figure 1. The independent region of the elementary cell contains one AO4 tetrahedron and two non-equivalent M atoms, one of which is located in the special position M1 (4e) and another in the general position M2 (8f). The structure is characterized by an ordered system of hydrogen bonds that connect the SO4 tetrahedra. The structure of the superprotonic phase is similar to the low-temperature phase, but the hydrogen bond network is disordered [,].
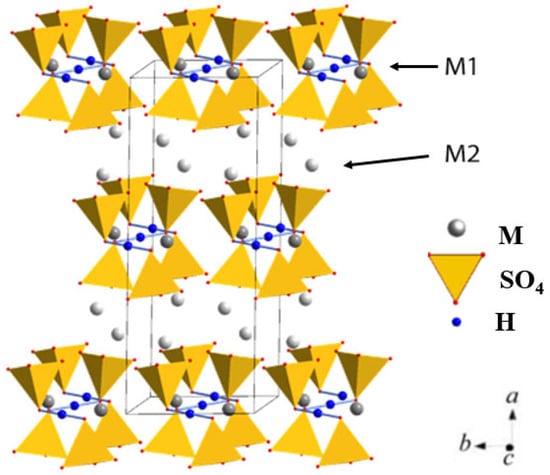
Figure 1.
Structure of the monoclinic phase M3H(SO4)2 (M = K, NH4, Rb; A = S, Se).
Phase transitions refer to classical first-order phase transitions, and the thermodynamics of these transitions are well described in terms of hydrogen bond disordering. At the transition to the trigonal Rm phase, one proton is disordering among three positions, and the oxygen atom of the oxoanion tetrahedron has a final occupancy of 1/3. The change in enthalpy during phase transitions for the M3H(AO4)2 group is in good agreement with the change in configurational entropy ΔS = R ln 3 (9.13) J/(mol·K) []. The range of existence of the trigonal phase for solid acid compounds, M3H(AO4)2, is different and is determined by the stability of the phases with respect to the dehydration reaction, which can be represented by the general scheme:
2M3H(SO4)2 ↔ M2S2O7 + 2M2SO4 + H2O,
Rb3H(SO4)2 is a member of the M3H(AO4)2 group, but the phase transition does not occur under normal pressure [] but is realized under pressure []. Another superprotonic compound, K3H(SO4)2, despite the fact that its structure is similar to other representatives of the M3H(SO4)2 group, exhibits anomalously slow kinetics of the superprotonic phase transition. To reveal a transition and correctly determine its temperature, the measurements must be carried out upon stepwise heating with long exposures at a constant temperature [,]. On the other hand, the influence of cationic substitution on the phase transition in K3H(SO4)2 was demonstrated. The phase transition kinetics radically changes due to the change in the system of hydrogen bonds [], whose formation involves additional ammonium protons. So, the purpose of the work was to investigate the influence of composition on the phase transitions in Rb3H(SO4)2 and K3H(SO4)2 crystals.
2. Materials and Methods
Rb2SO4 (high-purity grade, TU (Technical Requirements) no. 6-09-04-198-83), H2SO4 (special purity grade, 99.8%), and K2SO4 (reagent grade, TU no. 6-09-04-201-82) were used as initial agents. These agents were used without any additional purification.
The method of growing single crystals was similar to that described in reference []. The phase equilibria in the K2SO4–Rb2SO4–H2SO4–H2O system were studied by using the simultaneous parallel crystallization method.
A series of initial solutions in identical airtight vessels (crystallizers) with an altering ratio of initial dry components (~15 g) and a minimal amount of distilled water (~5 mL) were prepared. Subsequently, small amounts of water (1–5 mL) were added at a temperature slightly higher than the ambient temperature (50 °C). This process continued until saturated solutions, characterized by a minimal percentage of bottom sediment (no more than 3–5 salt crystals), were obtained. Then, the solutions were held for two days at a constant temperature. This exposure period is necessary to establish the dynamic interphase equilibria between a saturated solution and sediment in the crystallizer. Following this holding period, the temperature of the crystallizers was gradually lowered to the desired levels over several days. The crystals grown through this method ranged in size from 2 to 5 mm and could be easily separated from the solution through elutriation. Problems arose with solution compositions K: Rb = 1:1 and 4:6. These compositions are close to the phase boundary between M9H7(SO4)8·H2O and M2SO4 []. Therefore, obtaining high-quality single crystals for composition 1:1 proved to be unsuccessful, and for the 6:4 composition, only unit cell parameters were measured.
Cation compositions of the grown crystals were measured using energy-dispersive X-ray spectroscopy (Orbis EDAX, Pleasanton, USA) in conjunction with scanning electron microscopy. Measurements were conducted on fresh flat cleavage surfaces of single crystals by averaging the results from 5 experiments.
X-ray powder diffraction analysis (XRD) of grounded single crystals was performed at room temperature using a desktop X-ray diffractometer, Miniflex 600 (Rigaku, Japan) (CuKα radiation, continuous mode at a rate of 1.0–3.0 degrees/min, step size 0.01°, 2θ range 5–75°, static sample, ambient atmosphere). Unit cell parameters were calculated by means of Le Bail refinement (Jana 2006 []).
X-ray structural studies of the crystal, grown from a solution with a K: Rb ratio of 4:6, were conducted at room temperature using the XtaLAB Synergy-DW diffractometer (Rigaku, Tokyo, Japan) (MoKα).
Thermal properties of single- and polycrystalline samples were reviewed by the synchronous thermal analysis (thermogravimetry (TG) differential scanning calorimetry (DSC)) in the temperature range of 25–250 °C on the Netzsch STA 449 F1 instrument. Measurements were carried out under a flow of dry argon at heating rates of 1–5 K/min. The calculations were made in the Netzsch Proteus software Version 6.1.0. and the separation of peaks in the Netzsch Peak separation program. Calibration on heat was carried out on a sapphire single crystal.
Research on the electrical conductivity of single- and polycrystalline samples was conducted in the temperature range of 25–210 °C in air, using the impedance spectroscopy method within a frequency range of 1.0–3.0 × 107 Hz (Alpha-A impedance measurement system, Novocontrol, montabaur, Germany). Frequency-dependent impedance measurements were carried out during stepwise heating with temperature stabilization; the average temperature change rate was 0.07 K/min. Static bulk conductivity was calculated using equivalent circuit models obtained from the impedance spectra. Naturally faceting crystals (KxRb1-x)3H(SO4)2 possess a well-developed crystal plane (011). Therefore, single crystal samples with an orientation along the [100] axis were prepared by slightly polishing the crystal surface to form thin plates with characteristic linear dimensions of 5 mm and a thickness of 1 mm. Polycrystalline samples were obtained by grinding single crystals to a powder with the characteristic grain size of 5 μm and subsequently pressing (2 t/cm2) into tablets. The silver paste was used as electrodes.
Changes in the optical properties of single crystals upon heating were investigated within the temperature range of 25–210 °C. The samples under investigation were cut into optically transparent plates with parallel planes, allowing observations in the [100] direction. The samples were heated in the optical stage Linkam 420 (Linkam, London, UK), which was installed on a graduated rotating stage, enabling the measurement of optical activity angles. Observations were conducted in polarized light using parallel and crossed Nicols.
3. Results
Compositions of the samples and their relations to compositions of initial solutions are presented in Figure S1, as well as XRD patterns of all grown compositions in Figure S2.
The lattice parameters of the solid solutions, (KxRb1−x)3H(SO4)2, (where x = 0–1) were determined, and the data are summarized in Table A1.
The End members of the solid solutions K3H(SO4)2 and Rb3H(SO4)2 have the same symmetry (C2/c) but slightly different atomic coordinates; therefore, they are not isostructural. To determine the cell parameters of (KxRb1−x)3H(SO4)2, we used the initial lattice parameters of Rb3H(SO4)2 (ICSD #249556) for x = 0–0.64, and K3H(SO4)2 (ICSD #174401) for x = 0.66–1. Dependence of the unit cell parameters, Figure S3, and the volume of the elementary cell on the composition of the solid solution, (KxRb1−x)3H(SO4)2, Figure 2, demonstrates a break at structure changes around x ≈ 0.66. Within the structural type, the dependence on the composition is nearly linear and satisfies Vegard’s rule. Reliable data on the hydrogen bond lengths and the site occupancy of the M1 and M2 positions by potassium and rubidium cations are better obtained from structural studies of single crystals, which will be completely conducted in a separate study. In the present work, the structure was determined for one of the samples, occupancy positions were identified, and the hydrogen bond length was resolved based on single crystal X-ray diffraction (XRD) data. Complete experimental data and atomic coordinates are provided in Table A2 and Table A3, respectively. Cell parameters are in good agreement with the powder XRD data and have also been included in Figure S3 and Figure 2.
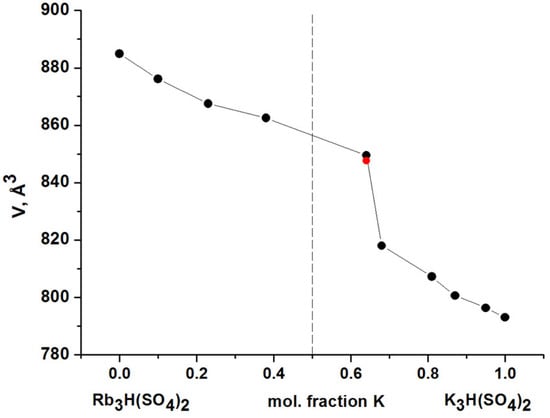
Figure 2.
Dependency of the volume of the elementary cell of solid solutions (KxRb1−x)3H(SO4)2 on composition. Red dot responds to the single crystal XRD data.
The results of the polycrystalline samples, (KxRb1−x)3H(SO4)2, thermal properties study are presented in Figure 3. The large endothermic effect in the temperature range of 180-210 °C and additional effect around 220 °C (x = 0.69–0.9) corresponds to the decomposition multistep process and are accompanied by a mass loss (Figure S4) of the sample at the temperature of the effect of about 0.5% by mass [,]. It is clearly seen that for compositions, x = 0.23–0.64, an additional endothermic peak appears.
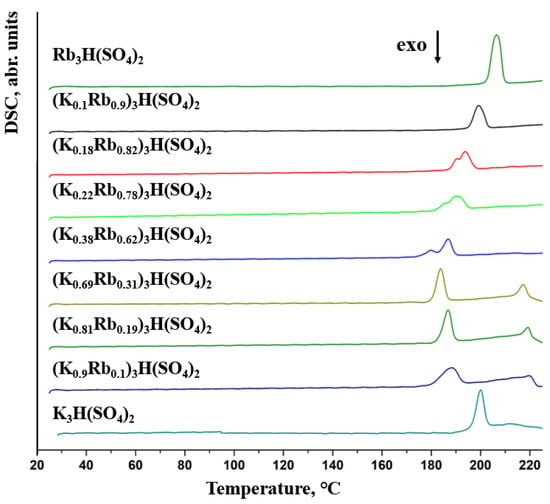
Figure 3.
DSC signal of the solid solutions (KxRb1−x)3H(SO4)2 powders, including pure compounds, at a heating rate of 1K/min.
The change in configurational entropy was calculated according to Equation (2)
where is the heat flow peak area and T is the extrapolated onset peak temperature. For additional peaks, the change in entropy is 7.8–9.8 J/(mol·K). Table 1 depends on composition, which is close to the theoretical value for a superprotonic phase transition (9.13 J/(mol·K)). Therefore, we suppose that these additional peaks correspond to a phase transition. It was also found that the additional peaks depend on the sample morphology and heating rate Figures S4–S6. This behavior is typical for anomalously slow kinetics of phase transition. In pure K3H(SO4)2 and solid solutions based on it, the phase transition does not manifest in DSC due to its slow kinetics []; therefore, only the decomposition reactions show thermal effects.

Table 1.
Temperatures of thermal effects for polycrystalline samples of solid solutions (KxRb1−x)3H(SO4)2 at a heating rate of 1 K/min, where Td is the decomposition temperature, Tonset tr is the extrapolated onset temperature of the phase transition, ΔStr is the change in configurational entropy during the phase transition.
In the conductivity study of the singe-crystalline samples with slow kinetics of phase transition, it is necessary to perform isothermal exposures for about 5–6 h in the transition temperature range []. These conditions significantly impede the experimental detection of the phase transition, making it preferable to investigate polycrystalline samples.
Examples of impedance spectra for low and high temperatures and fits are given in Figures S7–S10. Figure 4 presents the conductivity data of polycrystalline solid solutions (KxRb1−x)3H(SO4)2 x = 0–0.64 and single crystals, Figures S7 and S10. As mentioned in the experimental description, the average rate of stepwise heating was 0.07 K/min, which is an order of magnitude lower than the heating rate used in synchronous thermal analysis experiments. It turned out that the shape of the conductivity curve for solid solutions does not differ from the curve for decomposition in Rb3H(SO4)2, accompanied by a conductivity jump, and this behavior is reproducible in subsequent thermal cycles, Figure S7. A two-step conductivity jump was expected upon heating (Figure 5), so it could be attributed to the very narrow range of existence of the superprotonic phase. The two processes lead to conductivity growth: phase transition and solid phase decomposition. If they are not separated by temperature or are weakly separated, we can expect a behavior similar to Figure 4. However, it can be seen that the temperature range of conductivity jump widens with increasing potassium content and reaches about 13 °C for the composition x = 0.64. Such behavior can also be attributed to compositional inhomogeneity. Moreover, the conductivity of compositions x = 0.1 and 0.23 exhibits peculiarities in the temperature range of 170–190 °C, which could be associated with surface decomposition processes of the sample, as well as phase transitions. A similar behavior is observed for solid solutions with x = 0.81–1, Figure 5. For the pure K3H(SO4)2 sample, a phase transition occurs at 180 °C, and the conductivity jump at 188 °C corresponds to the decomposition process. The existence range of the superprotonic phase is narrow and is only 8 °C. In solid solutions, the conductivity plateau corresponding to the superprotonic phase disappears, and the magnitude of the conductivity jump becomes comparable to the jump in conductivity due to decomposition. Additionally, anomalies in conductivity appear at x = 0.87 and 0.81 in the temperature range of 170 °C to 190 °C, resembling conductivity plateaus similar to K3H(SO4)2. However, the conductivity jump is small, so attributing these anomalies to phase transitions is questionable and could be associated with surface decomposition reactions of the samples. Such temperature behavior indicates the loss of stability of the superprotonic phase (confirmed by weight loss Figure S4) in relation to the decomposition reaction under substitution. Thus, conductivity studies are unable to reliably establish the presence of phase transitions and determine their temperatures, except for the clearly manifesting phase transition in K3H(SO4)2.
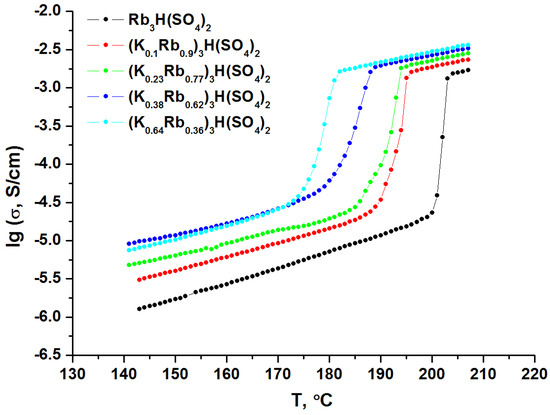
Figure 4.
Temperature dependencies of conductivity in solid solutions (KxRb1−x)3H(SO4)2, x = 0–0.64.
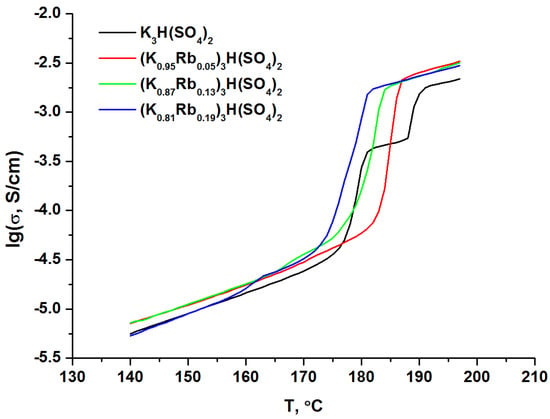
Figure 5.
Temperature dependence of conductivity in solid solutions (KxRb1−x)3H(SO4)2, x = 0.81–1.
Research on polarized light is well applicable to crystals of the M3H(SO4)2 group, allowing for direct observation of both decomposition processes and the movement of phase front boundaries during phase transitions.
The crystals are characterized by monoclinic symmetry, and as a result, domain structure extinction is observed at a 90° angle, corresponding to a two-fold axis. Observations are conducted in the [100] direction, and after the phase front passes, a three-fold axis is formed so single crystals become optically isotropic in this direction. The phase front boundary is clearly visible at the crossed Nicols observation. Microphotographs of single crystal samples (KxRb1−x)3H(SO4)2, where x = 0–0.64, are shown in Figure 6 and Figure S11.

Figure 6.
Microphotographs of single crystals (KxRb1−x)3H(SO4)2, x = 0–0.64 under polarized light in crossed Nicols at different temperatures. Temperature stabilization time was 15–30 min. The values of x are given next to the corresponding crystals.
It can be seen that the phase transition is present in all samples except for x = 0 and 0.1. The phase front moves from the edges of the sample towards the center, Figure 7, with its shape initially replicating the original sample shape and becoming more diffuse as it advances. In addition, the initial monoclinic phase breaks up into domains during the transition, indicating the presence of mechanical stresses in the crystal due to unit cell volume difference []. Furthermore, traces of decomposition, Figure 7 (187 °C), are visible on the sample surface in parallel Nicols, simultaneously with the phase front. The decomposition process and phase transition can, nevertheless, be distinguished by observing the transition at lower temperatures while increasing the exposure time, Figure 8. Prolonged exposure results in a complete phase transition, and upon subsequent cooling, a new domain structure emerges wherein the domains twin with respect to the lost symmetry element of the trigonal phase, the three-fold axis. Consequently, a system of domains with a two-fold axis is formed, with the domains themselves disoriented by 60° relative to each other. Figure 8 demonstrates the positions of extinction for different domains when rotated by 30°, and alignment between the positions of illumination and extinction is achieved when rotated by 60°. Thus, it is evident that the phase transition is reversible, exhibiting a temperature hysteresis of approximately 4 °C. We have determined a change in point symmetry during the phase transition as 2/m ↔ m and suppose that the change in space symmetry is similar to other representatives of the M3H(SO4)2 group (C2/c ↔ Rm).

Figure 7.
Single crystal (K0.23Rb0.77)3H(SO4)2 at different temperatures. The light background corresponds to parallel Nicols, black-crossed Nicols. The sample boundary is shown for clarity and the arrows indicate the path and current position of the phase front.

Figure 8.
Single crystal (K0.64Rb0.36)3H(SO4)2 at heating–cooling–heating thermal cycle. The light background corresponds to parallel Nicols and black-crossed Nicols; times of isothermal exposures are given next to the corresponding pictures.
A similar behavior is observed in crystals, x = 0.68–1, Figure 9. In the photos taken in crossed Nicols, the border of the phase front is visible; in parallel Nicols, the degradation of the samples is also evident, Figure S12. The transition temperatures were determined in the wake of the appearance of the isotropic phase at the edge of the samples. Therefore, the presence of a phase transition is confirmed for all crystals, x = 0.68–1.

Figure 9.
Microphotographs of single crystals (KxRb1−x)3H(SO4)2 x = 0.68–1 under polarized light in crossed Nicols at different temperatures. Temperature stabilization time was 20–45 min. The values of x are indicated next to the corresponding crystals.
4. Discussion
The study of properties of solid solutions conducted in this research is complicated by the following factors: slow kinetics of phase transition, a very narrow range of existence of the superprotonic phase, and the presence of a solid-state decomposition process with its own kinetics. To obtain reliable conclusions, it is necessary to separate the effects of these factors with respect to temperature, for example, by using different heating rates and varying the morphology of the samples. This was fully achieved only by polarized light single crystals observations and interpreting data from other research methods; moreover, the reversibility of the transition was shown. Taking into account the kinetics and peculiarities of the phase front movement (from the crystal surface towards its volume) in the crystal, it is logical to switch to polycrystalline samples. A decrease in the crystal size allows for increasing the fraction of the formed phase by upsizing the boundary area. However, the use of polycrystalline samples has significant drawback conditions for decomposition reaction and rapid degradation of samples are created for samples with a large surface. Nevertheless, the use of polycrystalline samples and low heating rates of 1 K/min allowed the detection of endothermic effects corresponding to phase transitions for (KxRb1−x)3H(SO4)2 x = 0.23–0.64 compositions. Such conditions are still not sufficient to detect phase transitions in solid solutions with a high potassium content, the kinetics of which are even slower. Reducing the rate to 0.07 K/min and using polycrystalline samples (KxRb1−x)3H(SO4)2, where x = 0.81–1, allows the observation of a transition in K3H(SO4)2 at conductivity studying, but even this slow rate is insufficient to observe transitions in single crystals and isothermal exposure for several hours is required. The effect of the heating rate on the temperature of phase transitions and the decomposition from DSC data, conductivity, and optical observations is shown in Figure 10. It is clearly visible that it can be roughly approximated by two linear dependencies with a break corresponding to the change in the structure type at x ≈ 0.66. It should be noted that the temperatures of the presumed phase transitions for compositions of x = 0 and 0.1 are higher than the decomposition temperatures. However, such transitions will be observed when the decomposition reaction is suppressed by applying an external pressure.
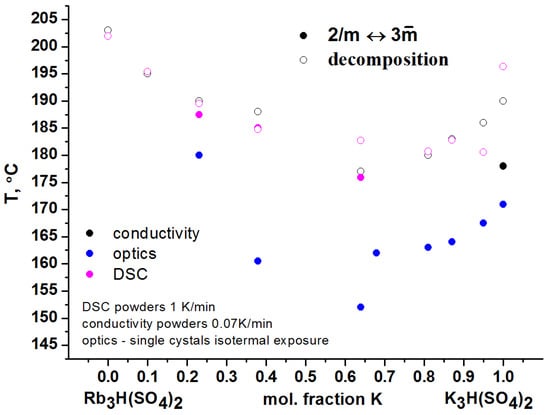
Figure 10.
The dependence of the phase transition temperature on the composition x of solid solutions (KxRb1−x)3H(SO4)2. Open symbols represent the decomposition process of compounds for which the phase transition was not detected.
Next, we considered the data obtained from the point of view of hydrogen bonds. The possible correlation between hydrogen bond length and temperature of the superprotonic phase transition in the group of crystals M3H(AO4)2 (M = Na, K, NH4, Rb; A = S, Se) was demonstrated in []. Based on this idea, we propose to use hydrogen bond length as a criterion for occurring phase transitions. Phase transitions and proton conductivity of the group, M3H(AO4)2, have been well studied up to the present, and the group itself is a model for such research. Known data on hydrogen bond lengths for structures near room temperature, superprotonic structures and phase transitions are given in Table 2. Similar lithium compounds are absent. We also have not found any structural data for Cs3H(SO4)2 and Na3H(SeO4)2. Attempts to crystallize these compositions failed, so we consider their existence to be doubtful.

Table 2.
Data on the lengths of hydrogen bonds in M3H(AO4)2 solid acids for low-temperature and high-temperature phases are presented, including X-ray experiment temperatures and phase transition temperatures.
Using the data of Table 1, crystallographic analysis [], and data on hydrogen bond formation energy [,], we constructed a diagram, Figure 11, showing the dependence of the hydrogen bond energy on the M3H(AO4)2 group for low-temperature and superprotonic phases. The diagram clearly shows the separation of all low-temperature phases into two regions relative to the phase transition, where the phase transition occurs and where the decomposition of the compound (Na, Rb) takes place (dotted line, Figure 11) []. Thus, the value of the bond length dO-O ≈ 2.49 Å at room temperature serves as a threshold for the implementation of the phase transition into the superprotonic phase. We suggest that the bond length in the superprotonic state could be considered as the criterion for achieving the phase transition when the rotational disorder of oxoanions begins. Accordingly, the bond lengths for these superprotonic Rm phases are shown in Figure 11. From Figure 11 and Table 1, it can be seen that for trigonal phases, the range of bond lengths is very narrow, with a maximum difference in transition temperatures of about 120 °C. This means that the phase transition occurs when the threshold bond length is reached, and the transition temperature, in this case, is a dependent parameter. We have evaluated the range of hydrogen bond lengths as dO-O ≈ 2.645–2.673 Å (dash lines in Figure 11) for the M3H(SO4)2 group (M = Na, K, NH4, Rb, Cs; A = S, Se), which includes the minimum energy of the hydrogen bond system at 2.669 Å (0.24 eV) (the intersection of the energy of hydrogen bond formation and the energy of proton on bond hopping) (Figure 11). Hydrogen bond length for the trigonal phase K3H(SeO4)2, only presented in one study [], although included in Table 1, is missing in Figure 11 and is considered to have a systematic error.
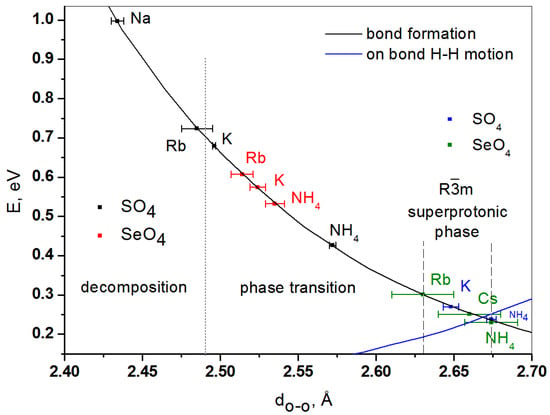
Figure 11.
The lengths and corresponding energies of hydrogen bond formation for the group M3H(AO4)2 (M = Na, K, NH4, Rb; A = S, Se). The dotted line represents boundary for hydrogen bond lengths near room temperature (black marks for sulfates and red marks for selenates), which divide the compositions relative to phase transition or decomposition. The two dashed lines represent the bond lengths for the superprotonic phases (blue marks for sulfates and green marks for selenates).
Consider the criterion of hydrogen bond length regarding the phase transition in Rb3H(SO4)2: the transition is not realized under normal pressure [] but is realized under pressure []. Thus, upon heating Rb3H(SO4)2, the elongation process of hydrogen bonding begins, but the threshold bond length is not reached, and a decomposition process occurs. Application of external pressure allows for suppression of the dehydration reaction (1) (according to Le Chatelier’s principle), the threshold bond length will be achieved, and a phase transition will occur. It should be noted that the application of pressure changes the threshold length of the hydrogen bond. The thermodynamic potential takes the form:
where G is Gibbs free energy, U is internal energy, T, S, P and V are temperature, entropy, pressure and volume, accordingly. The contribution of the pV term to the thermodynamic potential is small at pressures close to atmospheric. However, as the pressure increases, this contribution becomes significant and needs to be taken into account. It is evident that the volume, which is associated with the length of the hydrogen bond, dependence on pressure differs for the monoclinic and trigonal phases. So, the conditions for equalizing the potentials of the monoclinic and trigonal phases (phase transition conditions) will change when pressure is applied and correspond to a different threshold length for the hydrogen bond. Therefore, our assumptions about the role of hydrogen bond length in phase transitions are only valid for ambient pressure.
G = U − TS + pV,
Cationic/anionic substitution in this study was implemented to control the length of hydrogen bonds at room temperatures. Based on the values of hydrogen bond lengths for the end compositions of a series of solid solutions and the preservation of their structural type, it can be assumed that the hydrogen bond lengths are in the range between dO-O = 2.485(9) Å (Rb3H(SO4)2) and dO-O = 2.496(1) Å (K3H(SO4)2) at room temperature. This is confirmed by the structural studies of the crystal (K0.64Rb0.36)3H(SO4)2, where the hydrogen bond length was determined dO-O = 2.4957(11). The substitution of potassium leads to an increase in the hydrogen bond length, resulting in a phase transition upon heating. From this point of view, phase transitions in other solid solutions can also be interpreted. The introduction of about 5% at. ammonium into K3H(SO4)2 leads to an elongation of hydrogen bonds (dO-O = 2.496(1) Å → 2.549(8) Å) and anomalously slow kinetics of the phase transition becomes typical for superprotonic transitions []. The introduction of 57% at. leads to the occurrence of a disordered hydrogen bond network already at room temperature (dO-O = 3.2 Å RT) [].
The influence of the substitution of K with Rb is also peculiar. The weak dependence of the phase transition temperature for these compositions, Figure 11, should be considered from the perspective of the specific crystallographic sites, Figure 1, rather than the overall content of introduced rubidium. For (KxRb1−x)3H(SeO4)2 solid solutions, it has been shown that with the substitution of rubidium, it predominantly occupies the M2 sites between the layers of selenate tetrahedra []. Therefore, such a substitution has practically no effect on the hydrogen bond length and, as a consequence, weakly affects the phase transition temperature. We assume a similar uneven occupancy of crystallographic sites in (KxRb1−x)3H(SO4)2 solid solutions. Furthermore, the substitution also affects the conductivity of solid solutions in the monoclinic phase, depending on their composition. When potassium is replaced by rubidium, the conductivity increases, leading to a decrease in hydrogen bonding. Whereas, in the case of the Rb substitution, the conductivity remains almost unchanged, indicating the occupation of rubidium in the M2 position of the structure.
The question arises about the applicability of the threshold value of hydrogen bond length to other groups of superprotonics, such as the MHAO4 group. The hydrogen bond network of this group is complex and three-dimensional. For the best-known representative of the group CsHSO4, the determination of hydrogen bond lengths is a difficult task. The location of the heavy atoms could be determined precisely, but several models were proposed for oxygen and hydrogen atoms. As a result, the last published data on hydrogen bond lengths in the superprotonic phase were dO-O = 2.56 Å and 2.98 Å, but these data are given for a specific model []. For the CsHSeO4 crystal, dO-O = 3.35(1) Å and 3.50(1) Å were supposed to be the potential hydrogen bonds. These distances were calculated between the centers of thermal ellipsoids. However, the authors supposed that due to the strong librating movement of oxygen atoms, the momentary distances are much shorter, approximately 2.5 Å []. Thus, in the case of a complex three-dimensional hydrogen bond network in the MHAO4 group, the data on hydrogen bonds are not as unambiguous as for the M3H(AO4)2 group. Therefore, the conclusions drawn in this paper apply to the M3H(AO4)2 group, and the concept of using the hydrogen bond length as a criterion for phase transition requires further verification.
The idea of using hydrogen bond length as a criterion for phase transitions reveals experimental confirmation. This criterion can also be used to estimate the temperatures of phase transitions. By determining the thermal coefficient of hydrogen bond length change from the coefficient of crystal linear expansion in the [0kl] direction (for the group M3H(AO4)2), these data can be extrapolated to the critical bond length value and the temperature of the superprotonic phase transition can be estimated.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst13091401/s1, Figure S1. Dependence of the composition of single crystals of solid solutions (KxRb1−x)3H(SO4)2 on the composition of the initial solution; Figure S2. XRD patterns of the (KxRb1−x)3H(SO4)2 solid solutions at room temperature. Multiphase sample corresponds to K:Rb = 0.5 solution; Figure S3. Lattice parameters of the (KxRb1− x)3H(SO4)2 at room temperature. Red dot responds to the single crystal XRD data; Figure S4. DSC signal and weight loss of (KxRb1−x)3H(SO4)2 powders at heating rate 1K/min; Figure S5. DSC signal and weight loss of (KxRb1−x)3H(SO4)2 single crystals at heating rate 1K/min; Figure S6. DSC signal and weight loss of (KxRb1−x)3H(SO4)2 polycrystalline samples at heating rate 5K/min; Figure S7. Temperature dependencies of conductivity of the (K0.23Rb0.77)3H(SO4)2 single crystal in two subsequent heating-cooling cycles; Figure S8. (K0.23Rb0.77)3H(SO4)2 single crystal. (a) Nyquist plots and fits for different temperatures. The complete impedance spectrum is shown in the inset as well as equivalent circuit for fitting; (b) and (c) Bode plots and fits for different temperatures; Figure S9. (K0.23Rb0.77)3H(SO4)2 single crystal. (a) Nyquist plots and fits for different temperatures. The complete impedance spectrum is shown in the inset as well as equivalent circuit for fitting; (b) and (c) Bode plots and fits for different temperatures.; Figure S10. Conductivity of (KxRb1−x)3H(SO4)2 (x = 0–0.38) single crystals at stepwise heating, mean heating rate was 0.07K/min; Figure S11. Microphotographs of single crystals (KxRb1−x)3H(SO4)2, x = 0–0.64, under polarized light, crossed Nicols, at different temperatures. Temperature stabilization time was 15-30 min. The values of x are given next to the corresponding crystals; Figure S12. Microphotographs of single crystals (KxRb1−x)3H(SO4)2 x = 0.68–1 under polarized light. (Crossed Nicols—black background, parallel Nicols—light background). The pictures were taken for the same samples state. Trigonal phase and decomposition regions are marked by narrows.
Author Contributions
Conceptualization, V.V.G.; methodology, V.V.G.; investigation, V.V.G., V.A.K., I.S.T. and E.V.S.; writing—original draft preparation, V.V.G.; writing—review and editing, V.A.K. and I.S.T.; visualization, V.V.G. and I.S.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
This work was performed within the State Assignment of FSRC “Crystallography and Photonics” RAS.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Lattice parameters and cation compositions of (KxRb1 − x)3H(SO4)2 at room temperature.
Table A1.
Lattice parameters and cation compositions of (KxRb1 − x)3H(SO4)2 at room temperature.
| Composition (EDXS) | Rb3H(SO4)2 ICSD #249556 | (K0.1Rb0.9)3 | (K0.23Rb0.77)3 | (K0.38Rb0.62)3 | (K0.64Rb0.36)3 | (K0.68Rb0.32)3 | (K0.81Rb0.19)3 | (K0.87Rb0.13)3 | (K0.95Rb0.05)3 | K3H(SO4)2 ICSD #174401 |
|---|---|---|---|---|---|---|---|---|---|---|
| Sp.gr.; Z | C 1 2/c 1, 4 | C 1 2/c 1, 4 | C 1 2/c 1, 4 | C 1 2/c 1, 4 | C 1 2/c 1, 4 | C 1 2/c 1, 4 | C 1 2/c 1, 4 | C 1 2/c 1, 4 | C 1 2/c 1, 4 | C 1 2/c 1, 4 |
| a, Å | 15.1460(5) | 15.106(9) | 15.062(19) | 15.033(6) | 14.967(7) | 14.809(1) | 14.75(20) | 14.718(4) | 14.695(9) | 14.685(3) |
| b, Å | 5.8914(19) | 5.875(3) | 5.858(8) | 5.850(2) | 5.820(3) | 5.741(5) | 5.714(5) | 5.696(4) | 5.684(8) | 5.676(1) |
| c, Å | 10.1590(3) | 10.116(6) | 10.079(13) | 10.056(3) | 10.001(5) | 9.872(8) | 9.827(3) | 9.799(8) | 9.783(3) | 9.772(1) |
| β, ° | 102.540(6) | 102.62(17) | 102.69(4) | 102.75(2) | 102.82(5) | 102.96(7) | 102.98(7) | 103.00(6) | 103.00(9) | 103.2(1) |
| V, Å3 | 884.87 | 876.06(9) | 867.55(20) | 862.53(6) | 849.52(8) | 818.0(3) | 807.2(5) | 800.6(2) | 796.3(8) | 793.00 |

Table A2.
Main crystal data, characteristics of X-ray diffraction experiments, and the refinement parameters of the (K0.64Rb0.36)3H(SO4)2 structure.
Table A2.
Main crystal data, characteristics of X-ray diffraction experiments, and the refinement parameters of the (K0.64Rb0.36)3H(SO4)2 structure.
| Chemical Formula | (K0.64Rb0.36)3H(SO4)2 |
|---|---|
| T, K | 293 |
| Mr | 387.5 |
| Space group, Z | C2/c, 4 |
| a, Å | 14.957(1) |
| b, Å | 5.816(1) |
| c, Å | 9.993(2) |
| β, deg | 102.83(1) |
| V, Å | 847.59(3) |
| Dx, g/cm3 | 3.0369 |
| Crystal size, mm | 0.184 × 0.1 × 0.056 |
| Radiation; λ, Å | MoKα; λ = 0.71073 |
| μ, cm−1 | 10.784 |
| Diffractometer | XtaLAB Synergy-DW |
| Scan mode | ω |
| Absorption correction; Tmin, Tmax | Numerical over a multifaceted crystal model, Empirical using spherical harmonics; 0.891/1 |
| θmax, deg | 44.62 |
| Limiting h, k, l indices | −27/29 −11/11 −18/19 |
| No. of measured/independent/observed [I > 3σ(I)] reflections | 38006/3016/1875 |
| Rint | 0.0291 |
| Refinement method | Least-squares on F2 |
| Weighting scheme | 1/(σ2(I) + 0.0004 I2) |
| Number of parameters | 67 |
| Extinction correction, coefficient (isotropic type 2) | 0.1890 (130) |
| R1/wR2 | 0.0179/0.0383 |
| S | 1.10 |
| Δρmin/Δρmax, e/Å3 | −0.49/0.46 |
| Software | CrysAlisPro, Jana 2006 |

Table A3.
Coordinates (x/a, y/b, z/c), position, site occupancy (q), and equivalent isotropic parameters of thermal vibrations (Ueq, Å2) of the basic atoms in the structure at 293 K.
Table A3.
Coordinates (x/a, y/b, z/c), position, site occupancy (q), and equivalent isotropic parameters of thermal vibrations (Ueq, Å2) of the basic atoms in the structure at 293 K.
| Atoms | Position | q | x/a | y/b | z/c | Ueq |
|---|---|---|---|---|---|---|
| Rb1 | 4b | 0.2094(12) | 0.5 | 0.24504(3) | 0.75 | 0.02307(7) |
| K1 | 4b | 0.7906(12) | 0.5 | 0.24504(3) | 0.75 | 0.02307(7) |
| Rb2 | 8f | 0.7268(13) | 0.306546(7) | 0.23137(2) | 0.34832(1) | 0.02331(4) |
| K2 | 8f | 0.2732(13) | 0.306546(7) | 0.23137(2) | 0.34832(1) | 0.02331(4) |
| S1 | 8f | 1 | 0.61371(2) | 0.72578(3) | 0.96157(2) | 0.01767(6) |
| O1 | 8f | 1 | 0.51029(4) | 0.6832(1) | 0.94017(7) | 0.0302(2) |
| O2 | 8f | 1 | 0.65152(4) | 0.5293(1) | 0.90123(6) | 0.0253(2) |
| O3 | 8f | 1 | 0.65013(5) | 0.73765(9) | 1.10991(7) | 0.0250(2) |
| O4 | 8f | 1 | 0.62557(4) | 0.9406(1) | 0.89317(6) | 0.0279(2) |
| H1 | 8f | 0.5 | 0.4931(17) | 0.441(4) | 1.021(2) | 0.028(6) |
References
- Jansen, M. Volume Effect or Paddle-Wheel Mechanism—Fast Alkali-Metal Ionic Conduction in Solids with Rotationally Disordered Complex Anions. Angew. Chem. Int. Ed. Engl. 1991, 30, 1547–1558. [Google Scholar] [CrossRef]
- Merinov, B.V. Mechanism of Proton Transport in Compounds Having a Dynamically Disordered Hydrogen Bond Network. Solid State Ion. 1996, 84, 89–96. [Google Scholar] [CrossRef]
- Baranov, A.I. Crystals with Disordered Hydrogen-Bond Networks and Superprotonic Conductivity. Review. Crystallogr. Rep. 2003, 48, 1012–1037. [Google Scholar] [CrossRef]
- Makarova, I.P.; Chernaya, T.S.; Filaretov, A.A.; Vasil’Ev, A.L.; Verin, I.A.; Grebenev, V.V.; Dolbinina, V.V. Investigation of the Structural Conditionality for Changes in Physical Properties of K3H(SO4)2 Crystals. Crystallogr. Rep. 2010, 55, 393–403. [Google Scholar] [CrossRef]
- Magome, E.; Sawada, K.; Komukae, M. X-Ray Structure Analysis of Rb3H(SeO4)2 in the High-Temperature Phase. Ferroelectrics 2009, 378, 157–162. [Google Scholar] [CrossRef]
- Cowan, L.A.; Morcos, R.M.; Hatada, N.; Navrotsky, A.; Haile, S.M. High Temperature Properties of Rb3H(SO4)2 at Ambient Pressure: Absence of a Polymorphic, Superprotonic Transition. Solid State Ion. 2008, 179, 305–313. [Google Scholar] [CrossRef]
- Sinitsyn, V.V. Dinamical and Statistical Disorder in Condessed Matters at High Pressure. Doctoral Dissertation 2014, 1–327. [Google Scholar]
- Chen, R.H.; Chen, S.C.; Chen, T.M. High-Temperature Structural Phase Transition in Na3H(SO4)2 Crystal. Phase Transit. 1995, 53, 15–22. [Google Scholar] [CrossRef]
- Friese, K.; Aroyo, M.I.; Schwalowsky, L.; Adiwidjaja, G.; Bismayer, U. The Disordered High-Temperature Structure of (NH4)3H(SO4)2 and Its Relationship to the Room-Temperature Phase. J. Solid State Chem. 2002, 165, 136–147. [Google Scholar] [CrossRef]
- Komornikov, V.A.; Grebenev, V.V.; Timakov, I.S.; Ksenofontov, D.A.; Andreev, P.V.; Makarova, I.P.; Selezneva, E.V. Production of Complex Hydrosulphates in the K3H(SO4)2–Rb3H(SO4)2 Series: Part I. Crystallogr. Rep. 2019, 64, 479–483. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic computing system JANA2006: General FEATures. Z. Krist. 2014, 229, 345–352. [Google Scholar]
- Calum, R.C.; Haile, S.M. High-Temperature Phase Transitions in K3H(SO4)2. Solid State Ion. 2001, 145, 179–184. [Google Scholar]
- Matsuo, Y.; Hatori, J.; Nakashima, Y.; Ikehata, S. Superprotonic and Ferroelastic Phase Transition in K3H(SO4)2. Solid State Commun. 2004, 130, 269–274. [Google Scholar] [CrossRef]
- Sanghvi, S.; Haile, S.M. Crystal Structure, Conductivity, and Phase Stability of Cs3(H1.5PO4)2 under Controlled Humidity. Solid State Ion. 2020, 349, 115291. [Google Scholar] [CrossRef]
- Catti, M.; Ferraris, G.; Ivaldi, G. A Very Short, and Asymmetrical, Hydrogen Bond in the Structure of Na3H(SO4)2 and S–OH vs O–H...O Correlation. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1979, 35, 525–529. [Google Scholar] [CrossRef]
- Fortier, S.; Fraser, M.E.; Heyding, R.D. Structure of Trirubidium Hydrogenbis(Sulfate), Rb3H(SO4)2. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1985, 41, 1139–1141. [Google Scholar] [CrossRef]
- Pietraszko, A.; Łukaszewicz, K.; Augustyniak, M.A. Structure of Phase III of (NH4)3H(SeO4)2. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1992, 48, 2069–2071. [Google Scholar] [CrossRef]
- Lukaszewicz, K.; Pietraszko, A.; Augustyniak, M.A. Structure of (NH4)3H(SeO4)2 in High Temperature Phases I and II. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1993, 49, 430–433. [Google Scholar] [CrossRef]
- Ichikawa, M.; Sato, S.; Komukae, M.; Osaka, T. Structure of Ferroelastic K3H(SeO4)2. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1992, 48, 1569–1571. [Google Scholar] [CrossRef]
- Shikanai, F.; Tomiyasu, K.; Kiyanagi, R.; Yonemura, M.; Iwase, K.; Sulistyanintyas, D.; Wurnisha, T.; Mori, K.; Ishigaki, T.; Tsukushi, I.; et al. Neutron Powder Diffraction Study of Protonic Conductor K3H(SeO4)2. Ferroelectrics 2007, 347, 74–78. [Google Scholar] [CrossRef]
- Makarova, I.P.; Verin, I.A.; Shchagina, N.M. Crystal structure of rubidium hydroselenate Rb3H(SeO4)2. Kristallografiya 1986, 31, 178–180. [Google Scholar]
- Sonntag, R.; Melzer, R.; Knight, K.S.; Radaelli, P.G. Structural Study of the Proton Conductor Cs3H(SeO4)2 by High Resolution Neutron Powder Diffraction. Mater. Sci. Forum 1998, 278–281, 726–731. [Google Scholar] [CrossRef]
- Sonntag, R.; Melzer, R.; Knight, K.S. Determination of the Hydrogen Position in Cs3H(SeO4)2 at 483 K. Phys. B Condens. Matter 1997, 234–236, 89–91. [Google Scholar] [CrossRef]
- Sinitsyn, V.V.; Baranov, A.I.; Ponyatovsky, E.G.; Shuvalov, L.A. P-T-Phase Diagram of Superprotonic Conductor Rb3H(SeO4)2. Ferroelectrics 1995, 167, 67–72. [Google Scholar] [CrossRef]
- Lippincott, E.R.; Scheoeder, R. One-Dimensional Model of the Hydrogen Bond. J. Chem. Phys. 1955, 23, 1099–1106. [Google Scholar] [CrossRef]
- Yomosa, S.; Hasegawa, M. Valence Bond Study of the Hydrogen Bond. III. Formation and Migration of Ionic Defects in Water and Ice. J. Phys. Soc. Jpn. 1970, 29, 1329–1334. [Google Scholar] [CrossRef]
- Choudhury, R.R.; Chitra, R.; Selezneva, E.V.; Makarova, I.P. Effect of Cationic Substitution on the Double-Well Hydrogen-Bond Potential in [K1-x(NH4)x]3H(SO4)2 Proton Conductors: A Single-Crystal Neutron Diffraction Study. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2017, 73, 863–867. [Google Scholar] [CrossRef]
- Selezneva, E.V.; Makarova, I.P.; Malyshkina, I.A.; Gavrilova, N.D.; Grebenev, V.V.; Novik, V.K.; Komornikov, V.A. New Superprotonic Crystals with Dynamically Disordered Hydrogen Bonds: Cation Replacements as the Alternative to Temperature Increase. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2017, 73, 1105–1113. [Google Scholar] [CrossRef]
- Yi, D.; Sanghvi, S.; Kowalski, C.P.; Haile, S.M. Phase Behavior and Superionic Transport Characteristics of (MxRb1-x)3H(SeO4)2 (M = K or Cs) Solid Solutions. Chem. Mater. 2019, 31, 9807–9818. [Google Scholar] [CrossRef]
- Merinov, B.V. Localization of hydrogen atoms in protonic conductors with a dynamical disordered network of hydrogen bonds: Effect of anonalous manifestation of hydrogen atoms on electron-density maps. Crystallogr. Rep. 1997, 42, 906–917. [Google Scholar]
- Zakharov, M.A.; Troyanov, S.I.; Kemnitz, E. Superprotonic High Temperature Phase and Refinement of the Low Temperature Structure of CsHSeO4. Z. Krist. 2001, 216, 172–175. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).