Next Article in Journal
Effects of Different CO2 Concentrations and Degradation Media on Static Corrosion of Commercially Pure Zinc
Next Article in Special Issue
Laser Textured Superhydrophobic SiC Ceramic Surface and the Performance of Condensation Heat Transfer
Previous Article in Journal
Negative Thermal Expansion Caused by the Antiferroelectric Phase Transition in Lead-Free Perovskite Ceramics
Previous Article in Special Issue
Photocatalytic Azo Dye Degradation Using Graphite Carbon Nitride Photocatalyst and UV-A Irradiation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 13
Issue 5
10.3390/cryst13050752
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structure and Anharmonicity of α- and β-Sb2O3 at Low Temperature

by
Duncan H. Moseley
1,
Craig A. Bridges
1,
Luke L. Daemen
2,
Qiang Zhang
2,
Michael A. McGuire
1,
Ercan Cakmak
1 and
Raphaël P. Hermann
1,*
1
Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
2
Neutron Science Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
*
Author to whom correspondence should be addressed.
Crystals 2023, 13(5), 752; https://doi.org/10.3390/cryst13050752
Submission received: 14 March 2023 / Revised: 19 April 2023 / Accepted: 26 April 2023 / Published: 1 May 2023
(This article belongs to the Special Issue Recent Developments of Inorganic Crystalline Materials)
Browse Figures
Versions Notes

Abstract

:
Antimony oxides are important materials for catalysis and flame-retardant applications. The two most common phases, α -Sb2O3 (senarmontite) and β -Sb2O3 (valentinite), have been studied extensively. Specific focus has been placed recently on their lattice dynamics properties and how they relate to the α - β phase transformation and their potential anharmonicity. However, there has not been any direct investigation of anharmonicity in these systems, and a surprising lack of low-temperature structural information has prevented further study. Here, we report the powder neutron diffraction data of both phases of Sb2O3, as well as structural information. α -Sb2O3 behaved as expected, but β -Sb2O3 revealed a small region of zero thermal expansion along the c axis. Additionally, while the β phase matched well with reported atomic displacement parameters, the α phase displayed a marked deviation. This data will enable further investigations into these systems.

1. Introduction

Antimony is a toxic group 15 element mainly found in trace amounts in the Earth’s crust (0.2–0.5 ppm) as the mineral stibnite (Sb 2 S 3 ). Antimony oxides find many uses in industrial processes such as in flame retardants, polymerization catalysts, and as an additive in brake linings [1]. The oxide Sb 2 O 3 is found in several forms, including cubic senarmontite ( α -Sb 2 O 3 ) [1], orthorhombic valentinite ( β -Sb 2 O 3 ) [2], and the more recently discovered high-temperature and high-pressure phase, orthorhombic γ -Sb 2 O 3 [3]. As shown in Figure 1-Left, α -Sb 2 O 3 forms isolated cages of Sb 4 O 6 that are isomorphous to arsenolite (c-As 2 O 3 ) and finds use in catalysis [4,5], as an enamel opacifier [6,7] and as a fire retardant [8,9]. In contrast, β -Sb 2 O 3 forms a layer-chained ladder structure with the Sb and O atoms forming the side rails and another O forming the rungs; see Figure 1-Right. This compound is often found in Sb 2 O 3 -B 2 O 3 glasses to enhance nonlinear optical properties [10,11,12].
An interesting aspect of both structures is the presence of stereo-active electronic lone pairs, nonbonding electrons that can alter and stabilize chemical structures [13] such as α -Sb 2 O 3 , with its isolated cages and large void volume, that might otherwise adopt a structure similar to the long unbroken chain structure of Sb 2 S 3 . These lone pairs often create large, empty cavities in structures such as β -Sb 2 O 3 and the isomorphous ϵ -Bi 2 O 3 . This also leads to emergent properties such as low thermal conductivity [13,14] and catalytic activity [15]. A recent study of β -Sb 2 O 3 under high pressure revealed a potential new phase and indicated changes in the interactions between lone pairs at several critical points [16].
There is extensive work concerning the phase transformation of α -Sb 2 O 3 to β -Sb 2 O 3 [17,18,19,20,21,22,23,24,25,26,27]. However, we did not find any investigation of the lattice anharmonicity or of the lattice constants below room temperature in either the α or β phases. While α -Sb 2 O 3 is stable at ambient temperatures, the β phase is considered metastable, although it is stable for long periods of time [28]. A recent work that investigated the lattice dynamics and vibrational modes of both phases and their influence on the phase transformation that occurs around 570–606 K used Mössbauer spectroscopy, nuclear inelastic scattering, and inelastic neutron scattering [29]. This work confirmed the presence of a debated Sb-O-Sb wagging band in α -Sb 2 O 3 and also revealed that oxygen vibrational modes play an important role in the phase transition, as they contribute half of the reported phase transition entropy [30]. Additionally, the temperature dependence of the Mössbauer data raised an important question. In α -Sb 2 O 3 , the atomic displacement ( 〈 u 2 〉 ) matches what is expected from a harmonic model extrapolation from the Sb-specific phonon data. However, in β -Sb 2 O 3 , the Lamb-Mössbauer factor ( f L M ), which is directly related to the atomic displacement parameter, deviates from a harmonic model at low temperature, suggesting that the Sb displacement increases more slowly than expected for a harmonic solid at higher temperatures [29]. A potential culprit is the significant anharmonicity in this system. Considering the structure, such behavior can be rationalized: populating the vibrational modes of the rung oxygen atoms could lead to an overall contraction of the ladder structure (along the c axis). Another indication of structural modification comes from the quadrupole splitting and asymmetry parameters in the Mössbauer spectra which show signs of evolution with temperature, implying anisotropic thermal expansion, which might be expected for a low symmetry structure. Unfortunately, the lack of low temperature structural data makes it difficult to interpret these findings.
We thus obtained structural data for the α and β phases of Sb 2 O 3 for temperatures between 20 and 300 K, and analyzed the anisotropic thermal expansion. The ladder structure of β -Sb 2 O 3 does produce a zero or small negative thermal expansion along the c axis at low temperature, although it is not sufficient to cause a contraction of the total volume.

2. Materials and Methods

Powder of Sb 2 O 3 with 99.99% purity is commercially available from Sigma-Aldrich (St. Louis, MO, USA). Despite the chemical purity, the X-ray diffraction pattern of the commercial material showed a mixture of the α and β polymorphs; see Supplemental Figure S1. Therefore, pure samples of the α and β phases were prepared as follows.
To convert the commercial powder to the pure α phase, we loaded 2.5 g of the as-received material in a 23 mL Parr autoclave with a Teflon liner. For this hydrothermal route, 10 mL of a 2.5 M NaOH solution was added to the Teflon liner, and the resulting suspension was stirred briefly. The autoclave was then sealed and kept at 175 °C for 3 days in a convection oven. The material was removed from the autoclave and washed with large amounts of deionized H 2 O (Büchner funnel, vacuum filtration) until the filtrate was pH neutral. The recovered Sb 2 O 3 material was dried overnight at 40 °C in a vacuum oven. Its diffraction pattern showed pure α -Sb 2 O 3 . This synthesis was repeated several times to produce enough material for neutron diffraction; a portion of the sample was used to produce β -Sb 2 O 3 , as described below.
For β -Sb 2 O 3 , we compared two methods. First, a self-propagating metathesis reaction was used to produce β -Sb 2 O 3 [31]. A mixture of SbCl 3 and NaOH were ground in an agate mortar for 3 min, and the product was washed with water and then ethanol, which was followed by drying at 60 °C. Several reactions were conducted, and we note that a minor α -Sb 2 O 3 impurity was observed as a side product in some reactions. For the second method, approximately 6 g of α -Sb 2 O 3 produced by the hydrothermal route was placed in a vacuum-sealed quartz ampule (10 mm diameter, 60 mm long). The ampule was placed in a stainless steel crucible made with a piece of stainless steel tubing (12 mm diameter, 90 mm long) capped with Swagelok compression tube caps. This assembly was placed in a tube furnace at 625 °C overnight and then quenched in water. The same method was also used by heating commercial Sb 2 O 3 directly to 650 °C for several hours, which was followed by quenching in a bucket of ice water. The recovered material was pure β -Sb 2 O 3 for both of the latter routes. A very slight amount of preferred orientation was observed in the Rietveld-refined X-ray diffraction pattern. We used the water-quenched samples for the neutron diffraction measurements.
The phase purity of all samples was confirmed with XRD measurement using Cu K α radiation with a wavelength of 0.154 nm. Low-temperature X-ray diffraction data were collected using a Phoenix cryostat on a Panalytical X-pert Pro diffractometer.
For scanning electron microscopy (SEM), the samples were cold mounted in epoxy and polished using standard metallography techniques. The samples were then sputter coated with Au at 5 nm film thickness to increase conductivity. The SEM images and energy dispersive spectroscopy (EDS) maps were collected using a TESCAN Mira 3 FEG-SEM operated at 20 kV. An EDAX Octane Elect EDS detector was used for the EDS mapping.
The neutron diffraction data of α - and β -Sb 2 O 3 were obtained from 20 to 300 K at a wavelength centered at 0.8 Å using the time-of-flight (TOF) powder neutron diffractometer POWGEN at the Spallation Neutron Source (SNS) at Oak Ridge National Laboratory (ORNL), (Oak Ridge, TN, USA) [32,33]. Rietveld refinements were performed using Fullprof Suite [34].

3. Results

In order to assess the microstructure and homogeneity of the samples, we carried out scanning electron microscopy (SEM) measurements of both phases. SEM images are shown in Supplementary Figures S2 and S3 using secondary electron (SE) images. The main difference between the α and β powders is in their morphology, with α powders being more uniform and close to spherical and β powders being lamellar. While this may be dependent on how the samples were ground, it makes sense that the α phase does not form lamellar crystals, as it is more cubic and “molecular” in nature. EDS maps for the O and Sb elements are presented in Supplementary Figures S2 and S3, and were obtained using K and L lines, respectively. When overlaid on the SEM images, a uniform distribution of both elements can be observed. These images also reveal the average particle size to be about 2 × 2 μ m for the α phase. Pieces of the β phase are much less homogeneous in size and shape, visually ranging between 1 and 50 μ m on a side. No indication of particle-size broadening was found in the diffraction data, which is consistent with the particle sizes seen with SEM.
Powder neutron diffraction data were collected from 20 to 300 K on α - and β -Sb 2 O 3 ; see Figure 2 (Presented in q-space in Supplemental Figure S4) and Table 1. Rietveld refinements of the cubic α phase (space group F d 3 ¯ m ) revealed no anomalies in the thermal expansion of the lattice, as shown in Figure 3-Left and refinements of the orthorhombic β phase (space group P c c n ) revealed unusual behavior in the thermal expansion of the c parameter, as shown in Figure 4. For the α phase the linear thermal expansion coefficient can be extracted from the high-temperature values to give 1.49 (2) × 10 − 5 K − 1 . The relative positions of the Sb and O atoms both decrease by 0.2–0.3% within the unit cell from 20 to 300 K, as seen in Figure 5. This indicates that the size of the Sb 4 O 6 cages shrink slightly with increasing temperature, with Sb-Sb distances within the same cage decreasing, at the edge of the error bar, from 3.621(1) Å at 20 K to 3.619 (1) Å at 300 K. In contrast, the overall distance between Sb 4 O 6 units increases with temperature from 2.897(1) Å at 20 K to 2.916 (1) Å at 300 K, which provides ground for thermal expansion. Isotropic ( B i s o ) atomic displacement parameters (ADPs) yielded good refinements. Figure 3-Right indicates a clear increase with temperature for B i s o of both Sb and O, as expected for increasing thermal vibration-induced displacement. However, there is some deviation from the previously reported B i s o (dashed purple line in Figure 3-Right), derived from the temperature-dependent Mössbauer data [29].
The O-Sb-O and Sb-O-Sb bond angles were relatively constant across all temperatures at 95.94 (4)° and 131.4 (4)°, respectively. These compare well with the reported angles of 95.87 (5)° and 132.51 (7)°, respectively [35]. Previous work reported good fits with slightly anisotropic ADPs for Sb 2 O 3 and isostructural c-As 2 O 3 , although both had multiple negative values [36]. Using anisotropic ADPs was attempted with the current α phase but did not improve the refinement.
The ladder-like structure of β -Sb 2 O 3 is quite different from that of the α phase, which is comprised of spherical buckyball-like Sb 4 O 6 units. The β phase diffraction data was also fit well by isotropic ADPs (see Figure 4). In contrast, the refined c parameter exhibits a much smaller expansion, as well as a decrease from 5.40575 (7) Å to 5.40572 (7) Å upon increasing from 20 to 40 K. Since this decrease is within the error bar, and it can be viewed as a zero thermal expansion region along this axis. From the linear regions at higher temperatures, we can calculate the linear thermal expansion parameters ( α ) of 1.59 (1) × 10 − 5 , 1.29 (1) × 10 − 5 , and 9.2 (3) × 10 − 6 K − 1 for a, b, and c, respectively. As typical values for linear thermal expansion occur between 1 × 10 − 5 and 5 × 10 − 5 K − 1 , these values are not unusual although they are smaller than average. The difference in the expansion behavior of the a and b axes may be influenced by the weak interladder Sb-O bonds, preventing stronger expansion between the ladder structures. While the expansion is largest along the b axis, the relative change is smaller than along a but larger than along c, being only ∼0.3% from 20 to 300 K compared to ∼0.4% and ∼0.2% along a and c, respectively. In the a direction, bonding is essentially through lone electron pairs. and it is thus not surprising that the relative expansion along a is quite similar to that in α -Sb 2 O 3 (see Figure 1-Right).
We also measured temperature-dependent powder X-ray diffraction from 15 to 300 K with Cu K α radiation on β -Sb 2 O 3 . This seemed to confirm a zero thermal expansion along the c axis below 50 K; see Supplemental Figure S5. The lattice parameters are slightly different but within reason for differences between X-ray and neutron diffraction.
The isotropic ADPs ( B i s o ) range from 0.065(15) to 0.232(15) Å 2 at 20 K and gradually increase and converge with increasing temperatures. At 300 K, all three possess similar values of ∼0.84 Å 2 . The Sb B i s o compares well with the values extrapolated from the reported nuclear inelastic scattering (NIS) data in the harmonic approximation although there is some deviation below 40 K [29]. The extracted B i s o value from NIS at 35 K matches well with the values for Sb.
While isotropic ADPs provided a satisfactory refinement of the β -Sb 2 O 3 data, we also used anisotropic ADPs to determine if they provided a better model. When refining all anisotropic ADP values, only the β 11 values showed any appreciable temperature dependence; see Supplemental Figures S6 and S7. The β 11 values rose linearly with temperature, but all other β i j values hovered close to zero (ranging from −0.0041 to 0.0021 Å 2 across all temperatures), so they were fixed. Fixing these values did not significantly affect the β 11 values. The anisotropic fits provided a slightly better fit, with an average χ 2 value of 6.61 vs. 7.42 for the isotropic fits.
The atom positions exhibit consistent shifts with temperature; see Figure 5. The O1 atom constitute the rungs in the ladder structure, while the O2 makes up the side rails; see Figure 1. The O1 atom is symmetry locked in the X and Y directions at 0.25 fractional coordinates but has a minor shift in the Z direction. The Sb and O2 atoms shift slightly in the X and Z direction but show little change in the Y direction.
To obtain a better idea of how these atomic position shifts affect the Sb-O bonding, we calculated the bond valence sum (BVS) for the Sb atom in both phases. Although there is some disagreement as to the optimal set of bond valence parameters for Sb-O bonds, here we used the r 0 and b values reported by Sidey [37] of 1.927 and 0.446, respectively. However, these values are technically only valid for room temperature data and will overestimate the BVS at low temperature. Thus, we applied a simple correction based on the unit cell volume at each temperature [38]. Additionally, we used a coordination length limit of 3.5 Å [39,40], so 5 Sb-O bonds were included in calculation for the β phase. However, the BVS does not change significantly with temperature, hovering around 2.973(13) [2.996(12)] valence units (v.u.) when fit using isotropic [anisotropic] ADPs. In contrast, the BVS for the α phase (which included 6 bonds) gradually drops by ∼0.0085 v.u. from 3.0120(35) to 3.0035(41) with increasing temperature. The temperature dependence of the BVS in both phases is displayed in Supplemental Figure S8.
In the β phase, some slight changes in the bond angles occur with increasing temperature; see Supplemental Figure S9. The Sb-O1-Sb and Sb-O2-Sb bond angles gradually increase by approximately 0.5°and 0.3°, respectively, from 50 to 300 K. However, both angles show a slight decrease with increasing temperature from 20 K to 50 K of 0.07°and 0.14°, respectively. With anisotropic ADPs, both angles are slightly lower across all temperatures but still reasonably within the error bars. This initial decrease coincides with the region of zero thermal expansion in the c parameter, so this contraction of the bond angles might have limited the expansion in this direction.

4. Discussion

The disagreement with the reported B i s o data for the α phase raises questions. Below 150 K, the harmonic model based on the NIS data matches reasonably well but deviates more with increasing temperature. In fact, it is rather unexpected that the harmonic model would match so well with the β phase B i s o data because both phases have similar thermal expansion and hence anharmonicity. In Jafari et al., the α phase was fit well by the harmonic model extrapolated from the NIS data, but the β phase showed significant deviation below ∼100 K, which was attributed to anharmonicity in the system [29]. At this point, we do not have a clear explanation of the mismatch of B i s o in the α phase between the Mössbauer spectral data and neutron diffraction; however, a possible cause could be that Mössbauer spectroscopy measures the incoherent, Lamb-Mössbauer, displacement, whereas diffraction measures the pair-correlated, Debye-Waller, displacement.
Because α -Sb 2 O 3 possesses a similar structure to arsenolite (c-As 2 O 3 ), a comparison is warranted. α -Sb 2 O 3 is a slightly distorted structure compared to As 2 O 3 with angles of (O-As-O) 98.4 (2)°and (As-O-As) 128.7 (3)°, being slightly larger and smaller than those of α -Sb 2 O 3 , respectively [36,41]. Similarly, β -Sb 2 O 3 is isostructural with ϵ -Bi 2 O 3 . Here, the Bi-O1-Bi and Bi-O2-Bi bond angles are both slightly smaller than in β -Sb 2 O 3 at 122.13 (19)°and 111.31 (13)°, respectively. Reports of diffraction data of this phase use anisotropic ADPs [42,43]. Unfortunately, there is no published temperature-dependent diffraction data on ϵ -Bi 2 O 3 .
β -Sb 2 O 3 exhibits a higher density and is more structurally complex than is the α phase, which is one indicator that it may actually be the stable phase, whereas the α phase would be metastable. However, the β phase is more difficult to synthesize, so this question remains open. Sb 2 O 3 likely exists close to a phase boundary within the group 15 elements. Phases with discreet X 4 O 6 units (as for α -Sb 2 O 3 ) exist for P (although it is not a cubic phase) [44], As, and Sb, but not for Bi. Bi 2 O 3 does support a similar structure although it is a networked structure as opposed to discreet Bi 4 O 6 molecules, likely due to the less repulsive lone pairs [45]. β -Sb 2 O 3 has an isostructural phase for Bi. As supports structures that resemble the ladder of β -Sb 2 O 3 , but the side-rails are broken or severely distorted [46,47].

5. Conclusions

We analyzed the low temperature powder neutron diffraction data of both α and β -Sb 2 O 3 . We found isotropic ADPs to provide good fits for both phases in contrast to previously reported values. Anisotropic ADPs also gave a good fit for the β phase, revealing a significant β 11 value, and thus a pronounced atomic displacement along the a axis. However, while we sought out a possible negative thermal expansion in the β phase, we found only a small region of zero thermal expansion along the c axis.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst13050752/s1: Figure S1: Powder x-ray diffraction pattern of commercial Sb 2 O 3 ; Figure S2: SEM images of α -Sb 2 O 3 with EDS analysis for both O and Sb atoms; Figure S3: SEM images of β -Sb 2 O 3 with EDS analysis for both O and Sb atoms; Figure S4: Powder neutron diffractograms in q-space; Figure S5: Temperature-dependent lattice constants of β -Sb 2 O 3 from both powder neutron diffraction and powder X-ray diffraction; Figure S6: Temperature-dependent β -Sb 2 O 3 Rietveld refinement parameters using anisotropic ADPs; Figure S7: Temperature-dependent B 11 parameters of β -Sb 2 O 3 converted from the b11 values converted from the b 11 values; Figure S8: Temperature-dependent isotropic ADP values compared with displacement parameters extracted from NIS and Mössbauer spectroscopy; Figure S9: Comparison of temperature-dependent bond valence sum; Figure S10: Comparison of temperature-dependent bond angles in β -Sb 2 O 3 for both oxygen atoms refined with isotropic and anisotropic ADPs

Author Contributions

Conceptualization, R.P.H. and C.A.B.; formal analysis, D.H.M. and R.P.H.; investigation, R.P.H., Q.Z., M.A.M. and E.C.; data curation, D.H.M., resources, L.L.D.; writing—original draft preparation, D.H.M. and R.P.H.; visualization, D.H.M.; supervision, R.P.H.; project administration, R.P.H.; funding acquisition, R.P.H. All authors have read and agreed to the published version of the manuscript.

Funding

Neutron scattering work by D.H.M., C.A.B., and R.P.H. and the X-ray scattering work by M.A.M. were supported by the US Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES), Materials Sciences and Engineering Division. Samples were provided by L.L.D., supported by the US Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES), Neutron Scattering Division. A portion of this research (Diffraction at POWGEN, conducted with Q.Z.) used resources at the Spallation Neutron Source, supported by DOE, BES, Scientific User Facilities Division. We thank Jim Horenburg and Shaw Reeves for their assistance in SEM sample preparation.

Data Availability Statement

Neutron powder diffraction data are available upon reasonable request from the authors.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ADPatomic displacement parameter
BVSbond valence sum
NISnuclear inelastic scattering
TOFtime-of-flight
SEMscanning electron microscopy
SEsecondary electron
EDSenergy dispersive spectroscopy
SNSSpallation Neutron Source
ORNLOak Ridge National Laboratory

References

  1. Bozorth, R.M. The Crystal Structures Of The Cubic Forms Of Arsenious And Antimonious Oxides. J. Am. Chem. Soc. 1923, 45, 1621–1627. [Google Scholar] [CrossRef]
  2. Buerger, M.J.; Hendricks, S.B. The Crystal Structure of Valentinite (Orthorhombic Sb2O3). Z. Kristallogr. Cryst. Mater. 1938, 98, 1–30. [Google Scholar] [CrossRef]
  3. Orosel, D.; Dinnebier, R.E.; Blatov, V.A.; Jansen, M. Structure of a new high-pressure–high-temperature modification of antimony(III) oxide, γ-Sb2O3, from high-resolution synchrotron powder diffraction data. Acta. Crystallogr. B 2012, 68, 1–7. [Google Scholar] [CrossRef] [PubMed]
  4. Kokkalas, D.E.; Bikiaris, D.N.; Karayannidis, G.P. Effect of the Sb2O3 catalyst on the solid-state postpolycondensation of poly(ethylene terephthalate). J. Appl. Polym. Sci. 1995, 55, 787–791. [Google Scholar] [CrossRef]
  5. Venkateshwarlu, G.; Rajanna, K.C.; Saiprakash, P.K. Antimony Trioxide as an Efficient Lewis Acid Catalyst for the Synthesis of 5-Substituted 1H-Tetrazoles. Synth. Commun. 2009, 39, 426–432. [Google Scholar] [CrossRef]
  6. Shaw, J.B. Antimony oxide as an opacifier in cast iron enamels. J. Am. Chem. Soc. 1918, 1, 502–513. [Google Scholar] [CrossRef]
  7. Pavlish, A.E.; O’Bannon, L.S. An Investigation of Antimony Oxide as an Opacifier for Porcelain Enamels and Glass. Science 1952, 116, 196–200. [Google Scholar] [CrossRef]
  8. Naidu, B.; Pandey, M.; Sudarsan, V.; Vatsa, R.; Tewari, R. Photoluminescence and Raman spectroscopic investigations of morphology assisted effects in Sb2O3. Chem. Phys. Lett. 2009, 474, 180–184. [Google Scholar] [CrossRef]
  9. Liu, Y.; Wang, H.; Yang, K.; Yang, Y.; Ma, J.; Pan, K.; Wang, G.; Ren, F.; Pang, H. Enhanced Electrochemical Performance of Sb2O3 as an Anode for Lithium-Ion Batteries by a Stable Cross-Linked Binder. Appl. Sci. 2019, 9, 2677. [Google Scholar] [CrossRef]
  10. Hall, D.W.; Newhouse, M.A.; Borrelli, N.F.; Dumbaugh, W.H.; Weidman, D.L. Nonlinear optical susceptibilities of high-index glasses. Appl. Phys. Lett. 1989, 54, 1293–1295. [Google Scholar] [CrossRef]
  11. Chagraoui, A.; Yakine, I.; Tairi, A.; Moussaoui, A.; Talbi, M.; Naji, M. Glasses formation, characterization, and crystal-structure determination in the Bi2O3–Sb2O3–TeO2 system prepared in an air. J. Mater. Sci. 2011, 46, 5439–5446. [Google Scholar] [CrossRef]
  12. Petkova, P.; Soltani, M.T.; Petkov, S.; Tacheva, J.; Nedkov, V. Visible and far-infrared spectroscopic studies of Co-doped (80–x)Sb2O3–20Na2O–xWO3 glasses. Phys. Scr. 2012, T149, 014057. [Google Scholar] [CrossRef]
  13. Tolborg, K.; Gatti, C.; Iversen, B.B. Expression and interactions of stereochemically active lone pairs and their relation to structural distortions and thermal conductivity. IUCrJ 2020, 7, 480–489. [Google Scholar] [CrossRef] [PubMed]
  14. Nielsen, M.D.; Ozolins, V.; Heremans, J.P. Lone pair electrons minimize lattice thermal conductivity. Energy Environ. Sci. 2013, 6, 570–578. [Google Scholar] [CrossRef]
  15. Walsh, A.; Payne, D.J.; Egdell, R.G.; Watson, G.W. Stereochemistry of post-transition metal oxides: Revision of the classical lone pair model. Chem. Soc. Rev. 2011, 40, 4455–4463. [Google Scholar] [CrossRef] [PubMed]
  16. Sans, J.A.; Manjón, F.J.; Pereira, A.L.d.J.; Ruiz-Fuertes, J.; Popescu, C.; Muñoz, A.; Rodríguez-Hernández, P.; Pellicer-Porres, J.; Cuenca-Gotor, V.P.; Contreras-García, J.; et al. Unveiling the role of the lone electron pair in sesquioxides at high pressure: Compressibility of β-Sb2O3. Dalton Trans. 2021, 50, 5493–5505. [Google Scholar] [CrossRef] [PubMed]
  17. Orman, R.G. Phase Transitions in Antimony Oxides and Related Glasses. Ph.D. Thesis, University of Warwick, Coventry, UK, 2005. [Google Scholar]
  18. Orman, R.; Holland, D. Thermal phase transitions in antimony (III) oxides. J. Solid State Chem. 2007, 180, 2587–2596. [Google Scholar] [CrossRef]
  19. Roberts, E.J.; Fenwick, F. The antimony-antimony trioxide electrode and its use as a measure of acidity. J. Am. Chem. Soc. 1928, 50, 2125–2147. [Google Scholar] [CrossRef]
  20. Golunski, S.; Nevell, T.; Pope, M. Thermal stability and phase transitions of the oxides of antimony. Thermochim. Acta 1981, 51, 153–168. [Google Scholar] [CrossRef]
  21. Trofimov, V.; Sheinkman, A.; Kleshchev, G. Antimony pentoxide in the crystalline state. Izv. Vyssh. Uchebn. Zaved. Fiz. 1973, 3, 135–137. [Google Scholar] [CrossRef]
  22. White, W.; Dachille, F.; Roy, R. High-pressure polymorphism of As2O3 and Sb2O3. Z. Kristallogr. 1967, 125, 450–458. [Google Scholar] [CrossRef]
  23. Cody, C.A.; DiCarlo, L.; Darlington, R.K. Vibrational and thermal study of antimony oxides. Inorg. Chem. 1979, 18, 1572–1576. [Google Scholar] [CrossRef]
  24. Agrawal, Y.; Shashimohan, A.; Biswas, A. Studies on antimony oxides: Part I thermal analysis of Sb2O3 in air, nitrogen and argon. J. Therm. Anal. 1975, 7, 635–641. [Google Scholar] [CrossRef]
  25. Jones, S.; Fenerty, J.; Pearce, J. The enantiotropic phase transition of antimony(III) oxide. Thermochim. Acta 1987, 114, 61–66. [Google Scholar] [CrossRef]
  26. Centers, P.W. Sublimation-controlled oxidation of antimony trioxide. J. Solid State Chem. 1988, 72, 303–308. [Google Scholar] [CrossRef]
  27. Han, W.; Huang, P.; Li, L.; Wang, F.; Luo, P.; Liu, K.; Zhou, X.; Li, H.; Zhang, X.; Cui, Y.; et al. Two-dimensional inorganic molecular crystals. Nat. Commun. 2019, 10, 4728. [Google Scholar] [CrossRef]
  28. Gopalakrishnan, P.; Manohar, H. Kinetics and mechanism of the transformation in antimony trioxide from orthorhombic valentinite to cubic senarmontite. J. Solid State Chem. 1975, 15, 61–67. [Google Scholar] [CrossRef]
  29. Jafari, A.; Klobes, B.; Sergueev, I.; Moseley, D.H.; Manley, M.E.; Dronskowski, R.; Deringer, V.L.; Stoffel, R.P.; Bessas, D.; Chumakov, A.I.; et al. Phonon Spectroscopy in Antimony and Tellurium Oxides. J. Phys. Chem. A 2020, 124, 7869–7880. [Google Scholar] [CrossRef]
  30. Coughlin, J.P. Contributions to the data on theoretical metallurgy. XII. heats and free energies of formation of inorganic oxides. US Bur. Mines Bull. 1954, 542. [Google Scholar]
  31. Vuković, M.; Branković, Z.; Poleti, D.; Rečnik, A.; Branković, G. Novel simple methods for the synthesis of single-phase valentinite Sb2O3. J. Solgel Sci. Technol. 2014, 72, 527–533. [Google Scholar] [CrossRef]
  32. Huq, A.; Hodges, J.P.; Gourdon, O.; Heroux, L. Powgen: A third-generation highresolution high-throughput powder diffraction instrument at the Spallation Neutron Source. In Proceedings of the European Powder Diffraction Conference, Darmstadt, Germany, 27–30 August 2010; Oldenbourg Wissenschaftsverlag: München, Germany, 2011; pp. 127–136. [Google Scholar] [CrossRef]
  33. Huq, A.; Kirkham, M.; Peterson, P.F.; Hodges, J.P.; Whitfield, P.S.; Page, K.; Hugle, T.; Iverson, E.B.; Parizzi, A.; Rennich, G. POWGEN: Rebuild of a third-generation powder diffractometer at the Spallation Neutron Source. J. Appl. Crystallogr. 2019, 52, 1189–1201. [Google Scholar] [CrossRef] [PubMed]
  34. Rodriguez-Carvajal, J. Recent advances in magnetic-structure determination by neutron powder diffraction. Phys. B 1993, 192, 55–69. [Google Scholar] [CrossRef]
  35. Whitten, A.E.; Dittrich, B.; Spackman, M.A.; Turner, P.; Brown, T.C. Charge density analysis of two polymorphs of antimony(iii) oxide. Dalton Trans. 2004, 1, 23–29. [Google Scholar] [CrossRef]
  36. Pertlik, F. Strukturverfeinerung von Kubischem As2O3 (Arsenolith) mit Einkristalldaten. Czech. J. Phys. B 1978, 28, 170–176. [Google Scholar] [CrossRef]
  37. Sidey, V. On the accurate bond-valence parameters for the Sb3+/O2− ion pair. Acta Cryst. B 2010, 66, 307–314. [Google Scholar] [CrossRef] [PubMed]
  38. Bernert, A.; Chatterji, T.; Thalmeier, P.; Fulde, P. Structure determination, valence, and superexchange in the dimerized low temperature phase of α-NaV2O5. Eur. Phys. J. B 2001, 21, 535–546. [Google Scholar] [CrossRef]
  39. Locock, A.J.; Burns, P.C. Revised Tl(I)–O bond valence parameters and the structures of thallous dichromate and thallous uranyl phosphate hydrate. Z. Kristallogr. Cryst. Mater. 2004, 219, 259–266. [Google Scholar] [CrossRef]
  40. Mills, S.J.; Christy, A.G.; Chen, E.C.C.; Raudsepp, M. Revised values of the bond valence parameters for Sb(V)–O and Sb(III)–O. Z. Kristallog. 2009, 224, 423–431. [Google Scholar] [CrossRef]
  41. Ballirano, P.; Maras, A. Refinement of the crystal structure of arsenolite, As2O3. Z. Krist. 2002, 217, 177–178. [Google Scholar] [CrossRef]
  42. Cornei, N.; Tancret, N.; Abraham, F.; Mentré, O. New ϵ-Bi2O3 Metastable Polymorph. Inorg. Chem. 2006, 45, 4886–4888. [Google Scholar] [CrossRef]
  43. Kumada, N.; Kinomura, N. A New Allotropic Form of Bi2O3. Mat. Res. Soc. Symp. Proc. 1998, 547, 227–232. [Google Scholar] [CrossRef]
  44. Jansen, M.; Moebs, M. Structural investigations on solid tetraphosphorus hexaoxide. Inorg. Chem. 1984, 23, 4486–4488. [Google Scholar] [CrossRef]
  45. Zav’yalova, A.A.; Imamov, R.M. Special features of the crystal structure of bismuth oxides. J. Struct. Chem. 1973, 13, 811–814. [Google Scholar] [CrossRef]
  46. Guńka, P.A.; Dranka, M.; Hanfland, M.; Dziubek, K.F.; Katrusiak, A.; Zachara, J. Cascade of High-Pressure Transitions of Claudetite II and the First Polar Phase of Arsenic(III) Oxide. Cryst. Growth Des. 2015, 15, 3950–3954. [Google Scholar] [CrossRef]
  47. Guńka, P.A.; Hanfland, M.; Chen, Y.S.; Zachara, J. High-pressure and low-temperature structural study of claudetite I, a monoclinic layered As2O3 polymorph. CrystEngComm 2021, 23, 638–644. [Google Scholar] [CrossRef]
Crystals 13 00752 g001 550
Figure 1. Crystal structure of (Left) α - and (Middle) β -Sb 2 O 3 . The a-b plane of the β phase (Right) shows the space between the ladder structures.
Figure 1. Crystal structure of (Left) α - and (Middle) β -Sb 2 O 3 . The a-b plane of the β phase (Right) shows the space between the ladder structures.
Crystals 13 00752 g001
Crystals 13 00752 g002 550
Figure 2. (Red points) Powder neutron diffractograms of (Top) α and (Bottom) β -Sb 2 O 3 and (black curves) Rietveld fit at 20 K. The blue curves are the fitting residuals. R p values are 17.1 and 10.8 for α and β -Sb 2 O 3 , respectively.
Figure 2. (Red points) Powder neutron diffractograms of (Top) α and (Bottom) β -Sb 2 O 3 and (black curves) Rietveld fit at 20 K. The blue curves are the fitting residuals. R p values are 17.1 and 10.8 for α and β -Sb 2 O 3 , respectively.
Crystals 13 00752 g002
Crystals 13 00752 g003 550
Figure 3. Temperature-dependent lattice parameter (Right) and isotropic ADP values ( B i s o -Left) obtained from Rietveld refinements of α -Sb 2 O 3 . The lattice parameter is given in absolute values, and the adjacent axis indicates the relative change. The purple inverted triangle is the B i s o value extracted from Sb-specific NIS data, and the dashed purple line is the extrapolated Sb B i s o using the NIS data in the harmonic approximation [29]. Error bars are approximately the size of the data points.
Figure 3. Temperature-dependent lattice parameter (Right) and isotropic ADP values ( B i s o -Left) obtained from Rietveld refinements of α -Sb 2 O 3 . The lattice parameter is given in absolute values, and the adjacent axis indicates the relative change. The purple inverted triangle is the B i s o value extracted from Sb-specific NIS data, and the dashed purple line is the extrapolated Sb B i s o using the NIS data in the harmonic approximation [29]. Error bars are approximately the size of the data points.
Crystals 13 00752 g003
Crystals 13 00752 g004 550
Figure 4. Temperature-dependent lattice parameters (Left) and isotropic ADP values ( B i s o -Right) obtained from Rietveld refinements of β -Sb 2 O 3 . Lattice parameters are given in absolute values, and the adjacent axis indicates the relative change. Unless noted, error bars are approximately the size of the data points. The purple inverted triangle is the B i s o value extracted from Sb-specific NIS data, and the dashed purple line is the extrapolated Sb B i s o using the NIS data in the harmonic approximation [29].
Figure 4. Temperature-dependent lattice parameters (Left) and isotropic ADP values ( B i s o -Right) obtained from Rietveld refinements of β -Sb 2 O 3 . Lattice parameters are given in absolute values, and the adjacent axis indicates the relative change. Unless noted, error bars are approximately the size of the data points. The purple inverted triangle is the B i s o value extracted from Sb-specific NIS data, and the dashed purple line is the extrapolated Sb B i s o using the NIS data in the harmonic approximation [29].
Crystals 13 00752 g004
Crystals 13 00752 g005 550
Figure 5. Temperature-dependent atomic positions of (Top) α - and (Bottom) β -Sb 2 O 3 . Coordinates for Sb and O atoms are given in absolute coordinates of the corresponding axis.
Figure 5. Temperature-dependent atomic positions of (Top) α - and (Bottom) β -Sb 2 O 3 . Coordinates for Sb and O atoms are given in absolute coordinates of the corresponding axis.
Crystals 13 00752 g005
Table
Table 1. Cell parameters, atomic positions (in fractional coordinates), and isotropic atomic displacement parameters ( B i s o ) of α - and β -Sb 2 O 3 at (Top) 20 and (Bottom) 300 K.
Table 1. Cell parameters, atomic positions (in fractional coordinates), and isotropic atomic displacement parameters ( B i s o ) of α - and β -Sb 2 O 3 at (Top) 20 and (Bottom) 300 K.
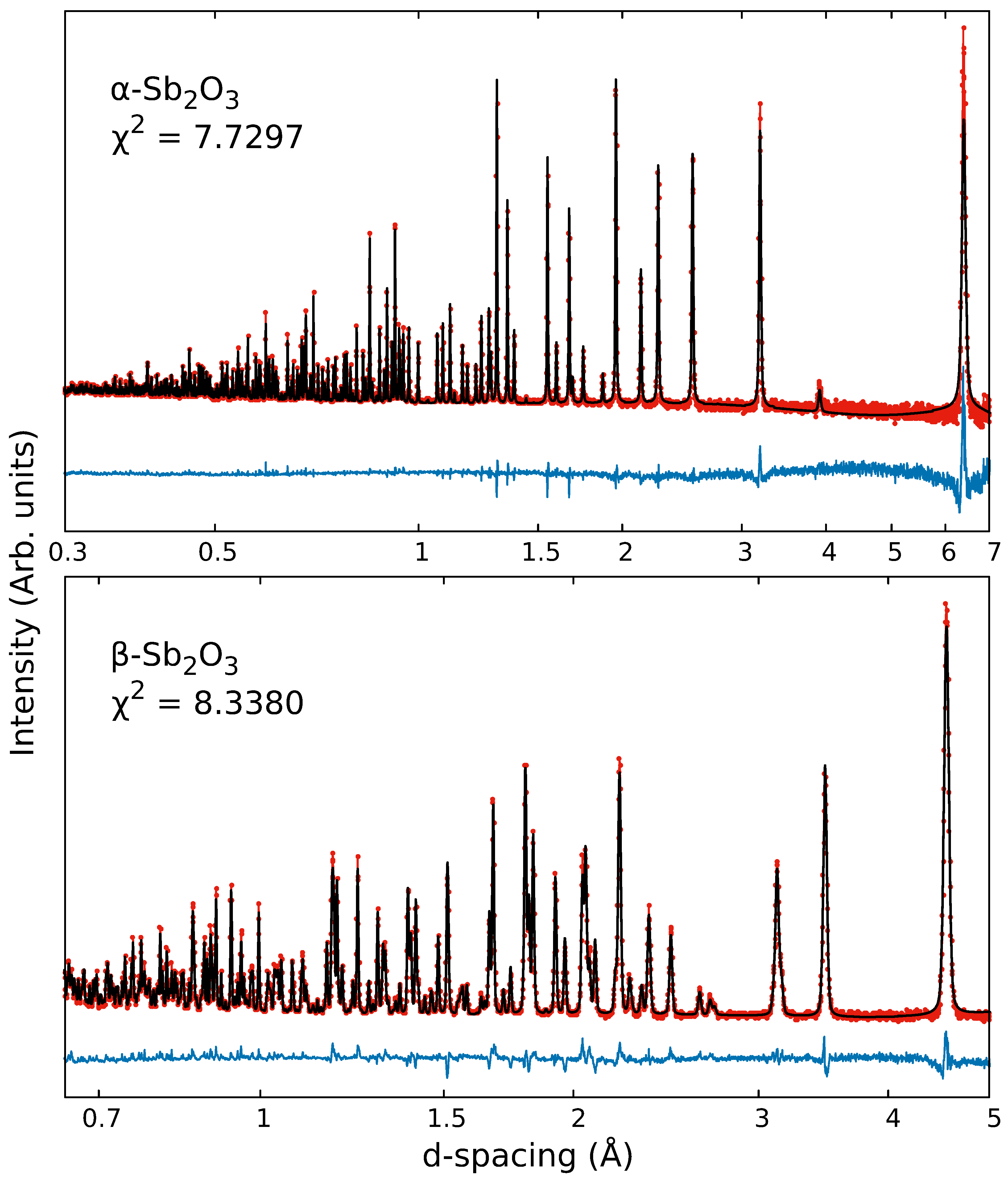
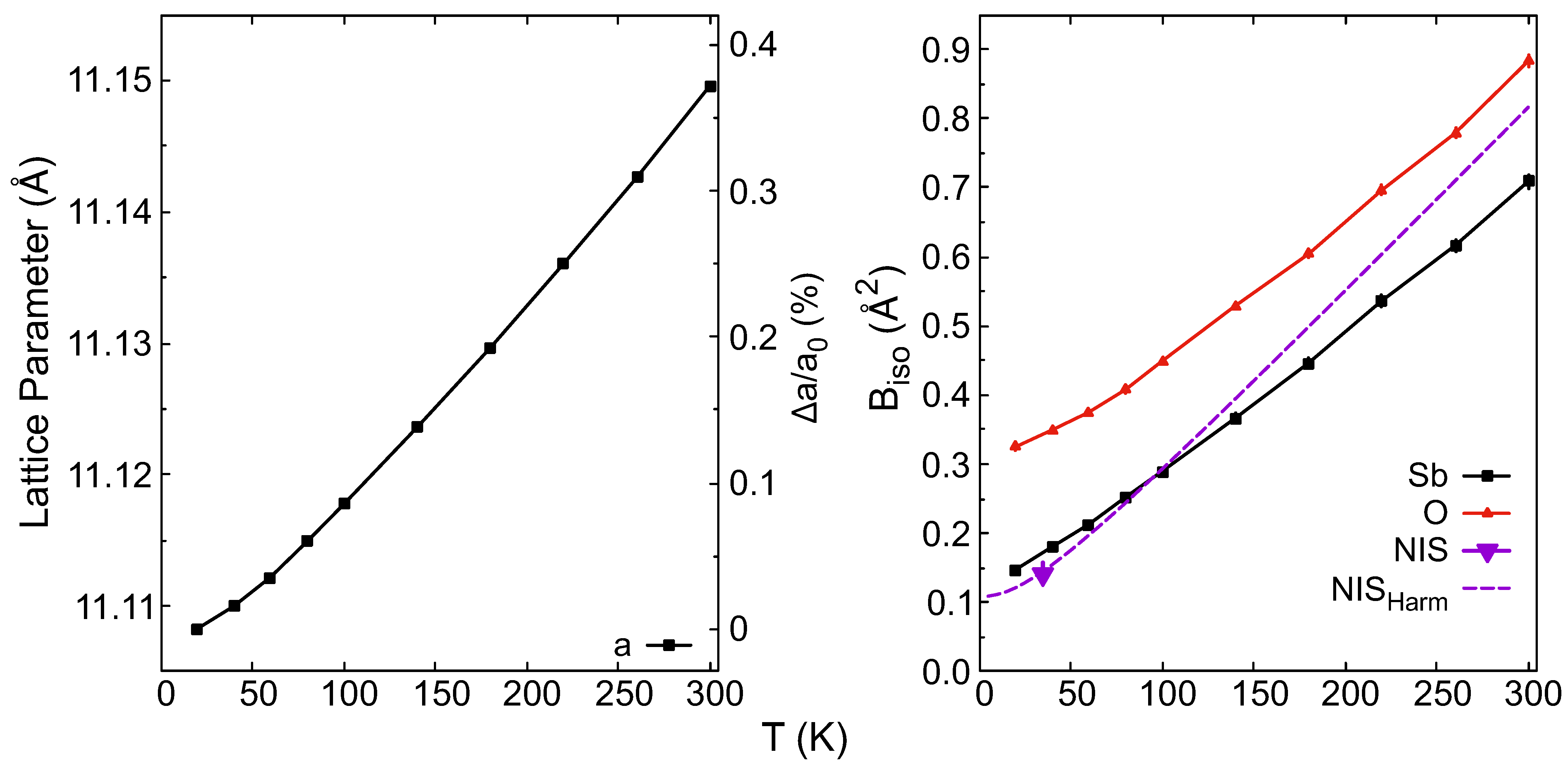
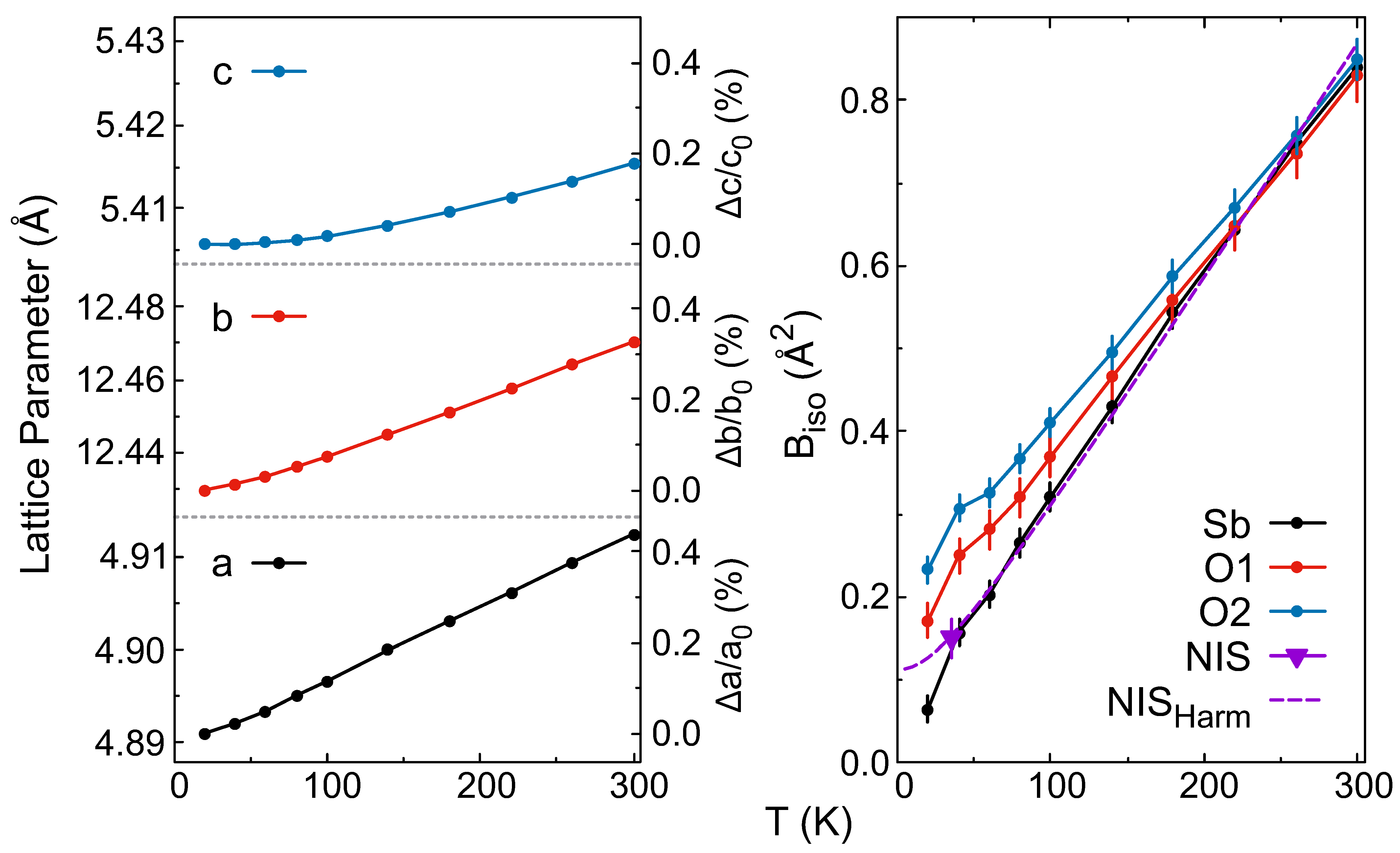
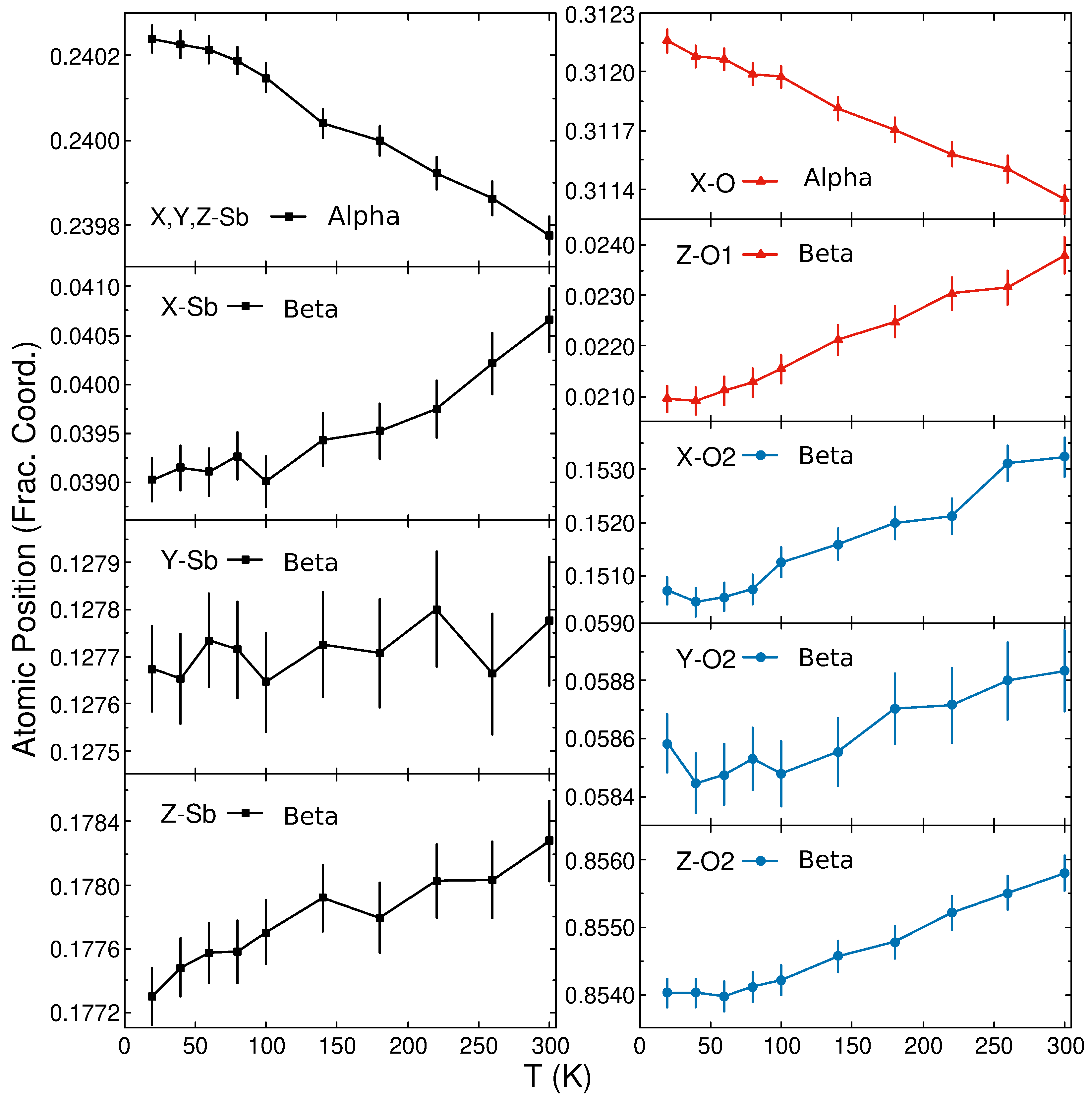
20 Ka (Å)b (Å)c (Å)V (Å3) Wyck.XYZ B iso (Å2)
α
F d 3 ¯ m 		11.108 (1)11.108 (1)11.108 (1)1370.685 (8)Sb32e0.2402 (1)0.5098 (1)0.0098 (1)0.159 (5)
O48f0.31216 (6)0.6250.1250.325 (4)
β
P c c n 		4.8910 (1)12.430 (1)5.4058 (1)328.637 (8)Sb8e0.0390 (2)0.1277 (1)0.1773 (2)0.064 (15)
O14c0.250.250.0210 (3)0.17 (2)
O28e0.1507 (3)0.0586 (1)0.8540 (2)0.232 (15)
300 K a (Å) b (Å) c (Å) V (Å3) Wyck. X Y Z B iso (Å2)
α
F d 3 ¯ m 		11.1496 (1)11.1496 (1)11.1496 (1)1386.039 (10)Sb32e0.2398 (1)0.5102 (1)0.01021 (1)0.709 (9)
O48f0.3114 (1)0.6250.1250.883 (8)
β
P c c n 		4.9125 (1)12.470 (1)5.4154 (1)331.75 (1)Sb8e0.0407 (3)0.1278 (1)0.1783 (3)0.839 (2)
O14c0.250.250.0238 (4)0.830 (3)
O28e0.1532 (4)0.0588 (1)0.8558 (3)0.849 (2)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Moseley, D.H.; Bridges, C.A.; Daemen, L.L.; Zhang, Q.; McGuire, M.A.; Cakmak, E.; Hermann, R.P. Structure and Anharmonicity of α- and β-Sb2O3 at Low Temperature. Crystals 2023, 13, 752. https://doi.org/10.3390/cryst13050752

AMA Style

Moseley DH, Bridges CA, Daemen LL, Zhang Q, McGuire MA, Cakmak E, Hermann RP. Structure and Anharmonicity of α- and β-Sb2O3 at Low Temperature. Crystals. 2023; 13(5):752. https://doi.org/10.3390/cryst13050752

Chicago/Turabian Style

Moseley, Duncan H., Craig A. Bridges, Luke L. Daemen, Qiang Zhang, Michael A. McGuire, Ercan Cakmak, and Raphaël P. Hermann. 2023. "Structure and Anharmonicity of α- and β-Sb2O3 at Low Temperature" Crystals 13, no. 5: 752. https://doi.org/10.3390/cryst13050752

APA Style

Moseley, D. H., Bridges, C. A., Daemen, L. L., Zhang, Q., McGuire, M. A., Cakmak, E., & Hermann, R. P. (2023). Structure and Anharmonicity of α- and β-Sb2O3 at Low Temperature. Crystals, 13(5), 752. https://doi.org/10.3390/cryst13050752

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop