Size Effect on the Thermal Conductivity of a Type-I Clathrate
Abstract
1. Introduction
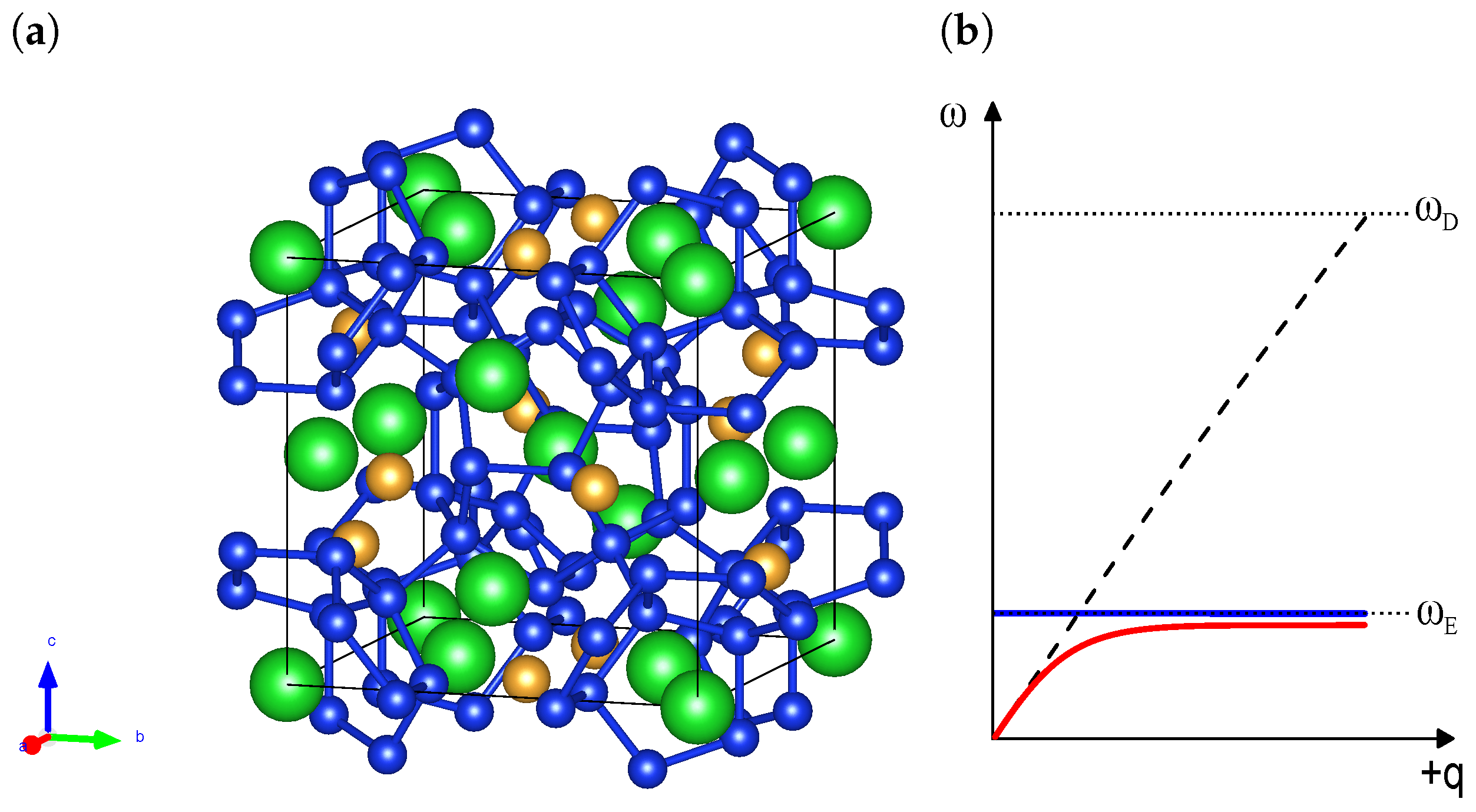
2. Materials and Methods
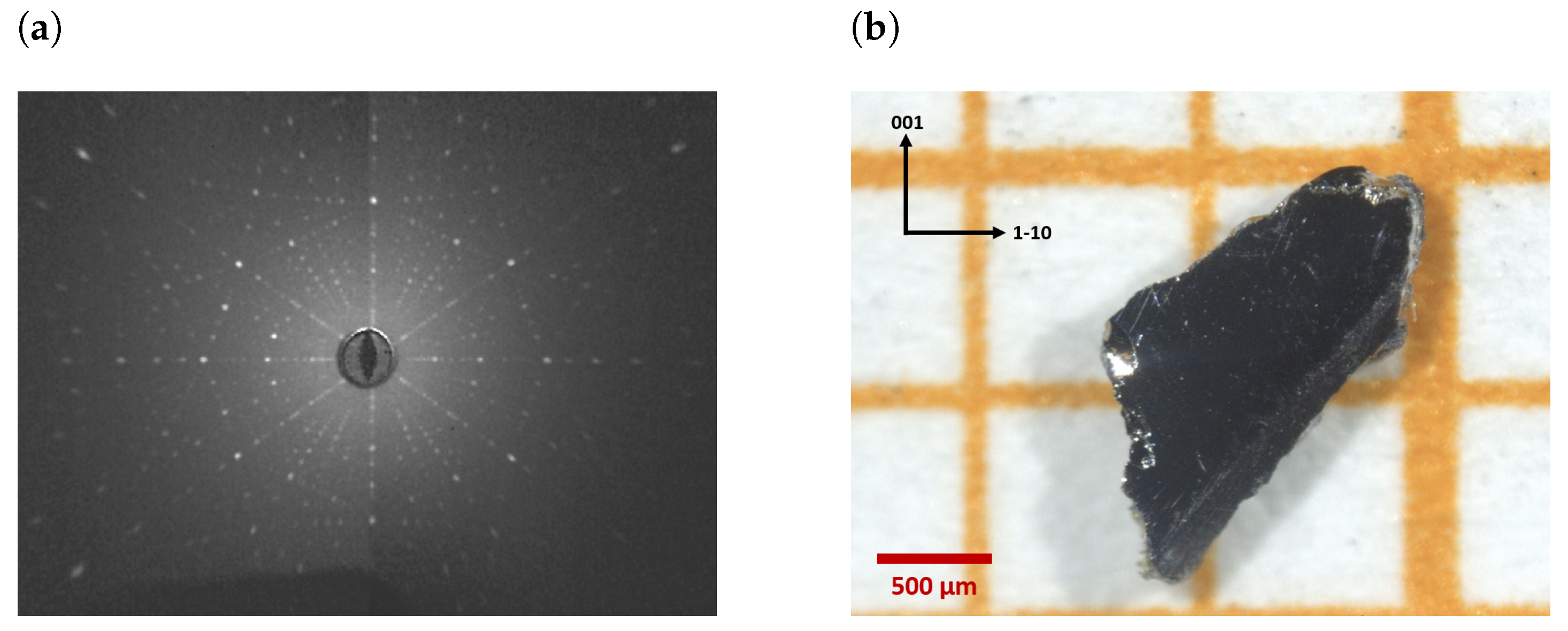
2.1. Samples
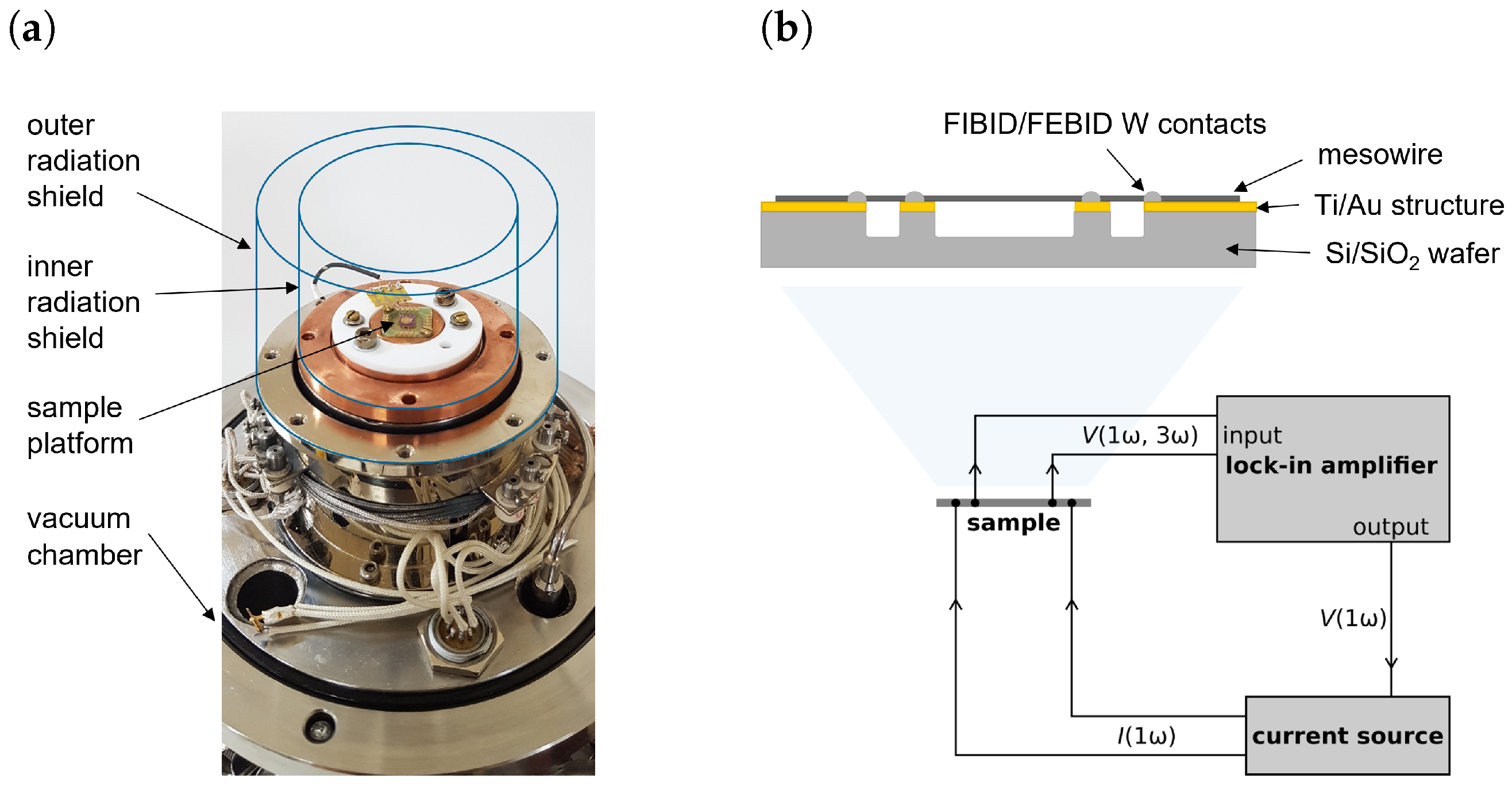
2.2. Nanofabrication Process
2.3. Measurement Method
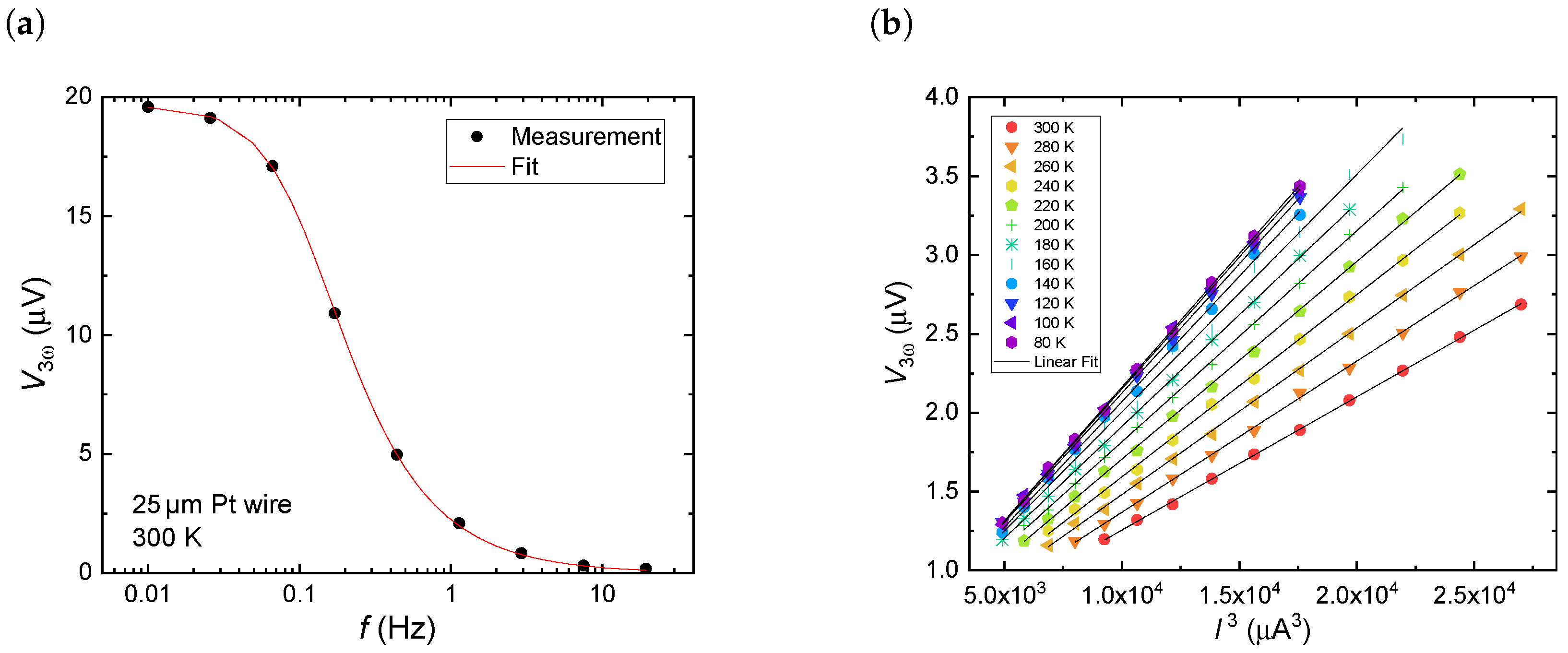
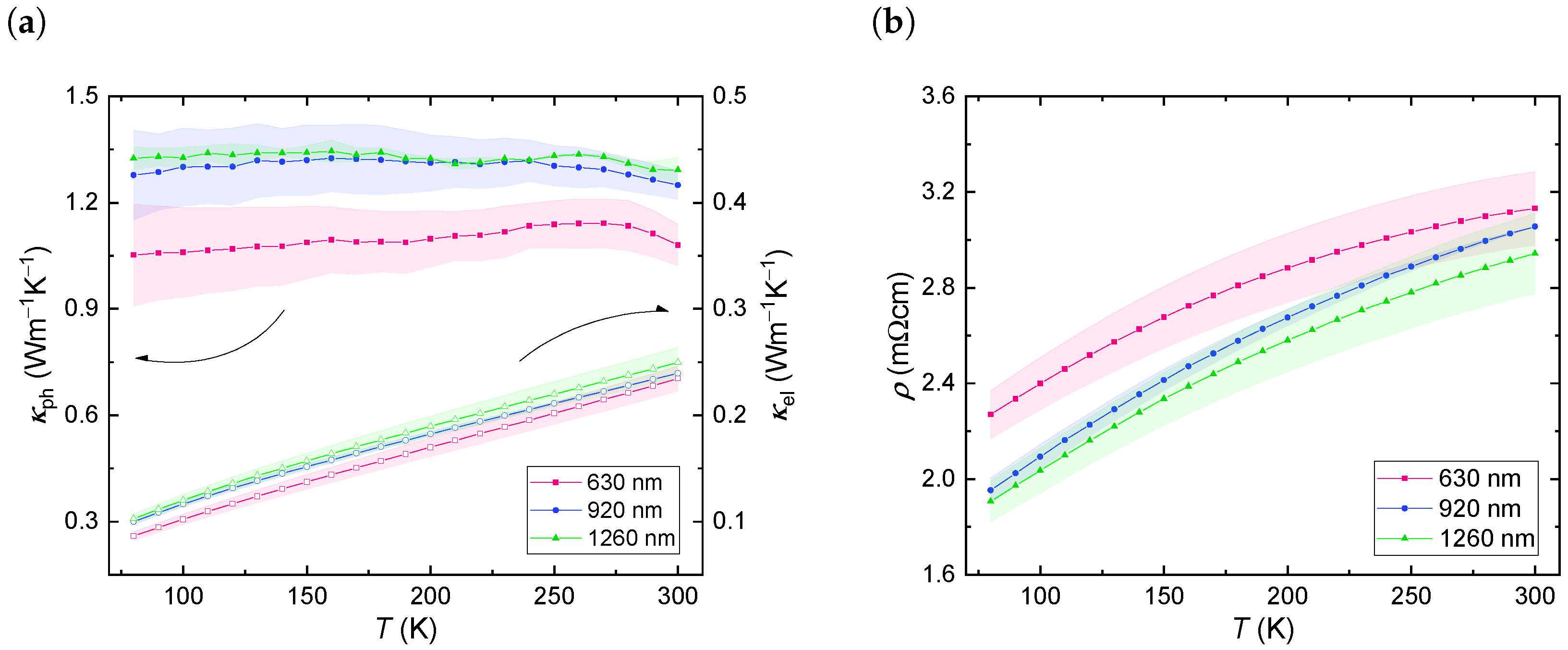
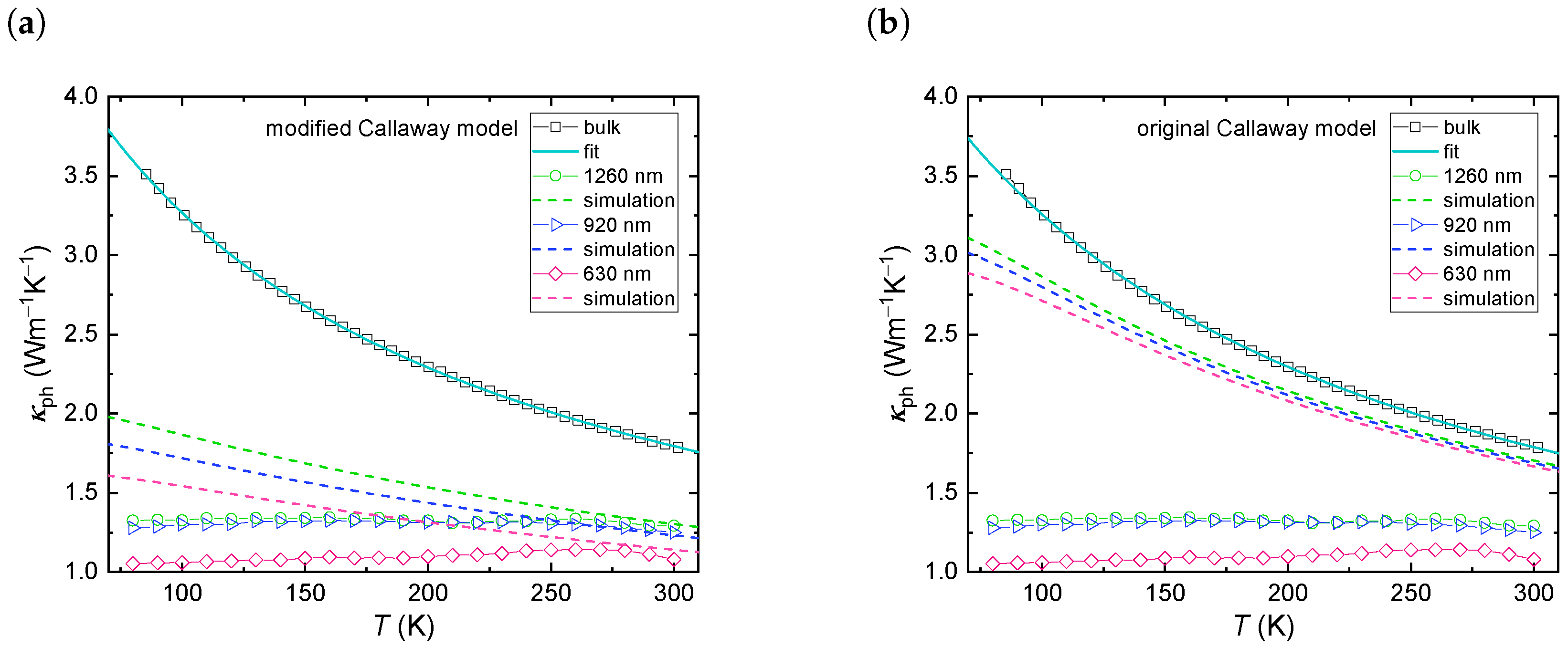
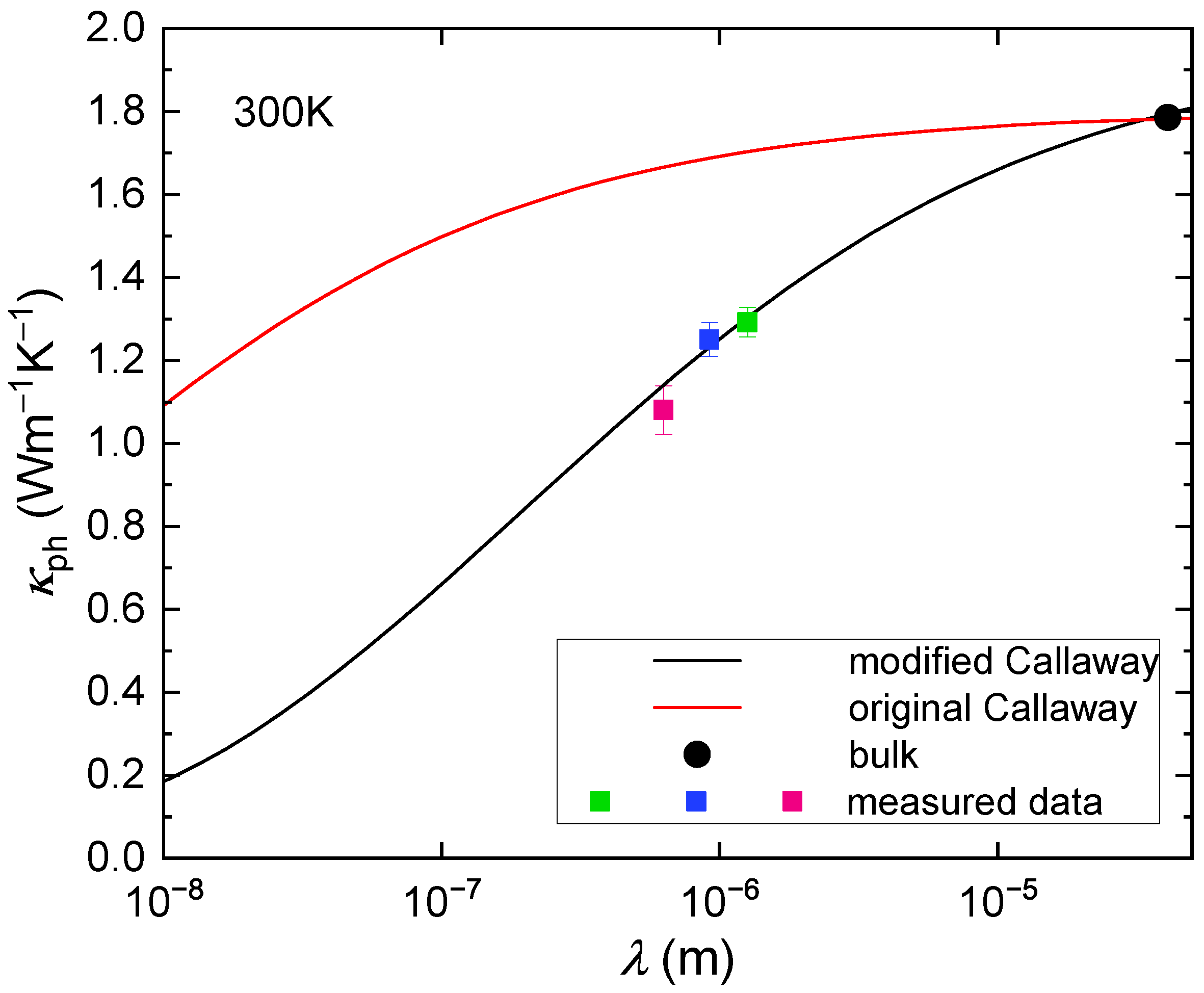
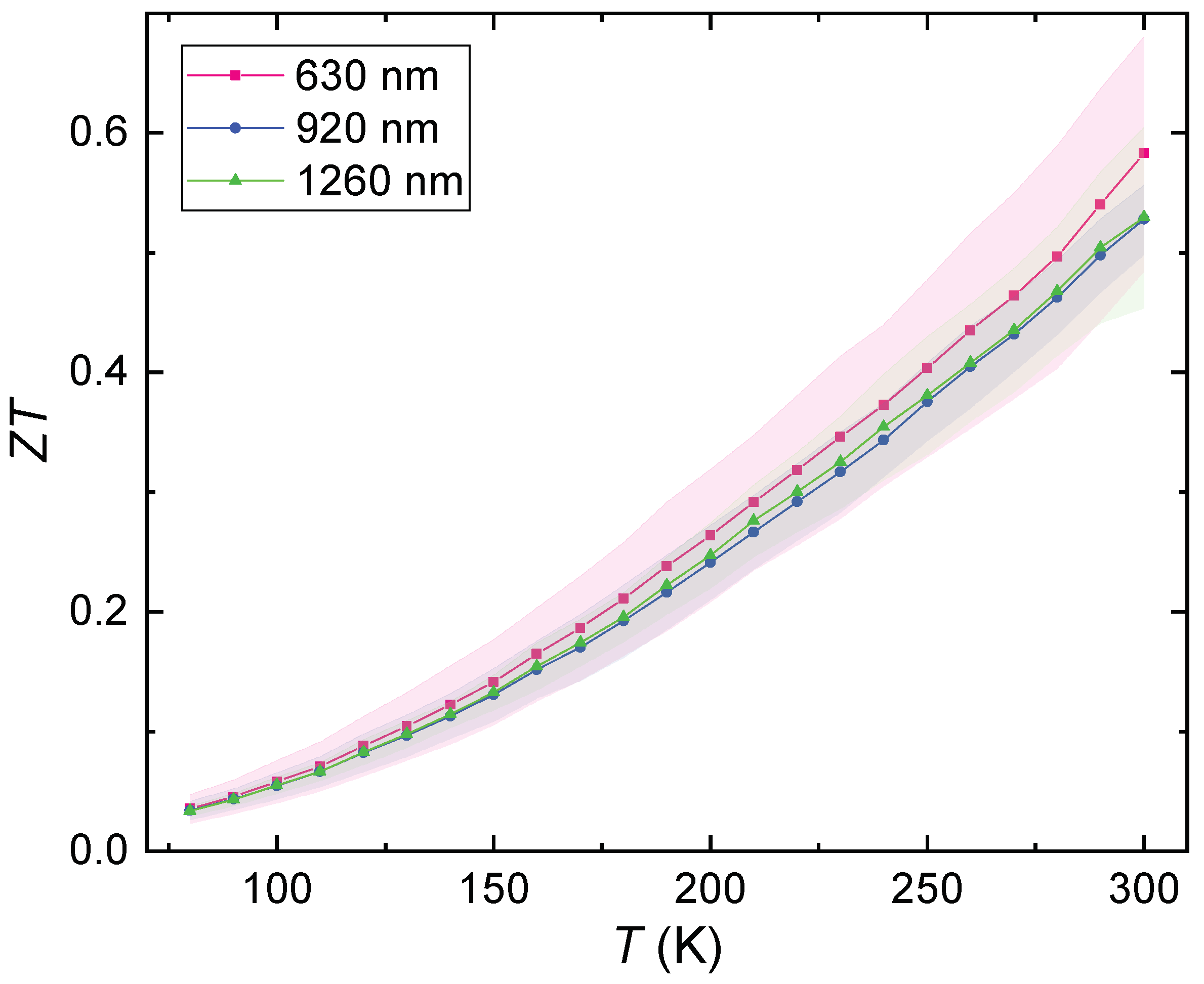
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. World Energy Outlook 2022; International Energy Agency: Paris, France, 2022. [Google Scholar]
- Dong, F.; Li, Y.; Gao, Y.; Zhu, J.; Qin, C.; Zhang, X. Energy transition and carbon neutrality: Exploring the nonlinear impact of renewable energy development on carbon emission efficiency in developed countries. Resour. Conserv. Recycl. 2022, 177, 106002. [Google Scholar] [CrossRef]
- Pourkiaei, S.M.; Ahmadi, M.H.; Sadeghzadeh, M.; Moosavi, S.; Pourfayaz, F.; Chen, L.; Pour Yazdi, M.A.; Kumar, R. Thermoelectric cooler and thermoelectric generator devices: A review of present and potential applications, modeling and materials. Energy 2019, 186, 115849. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Nolas, G.S.; Slack, G.A.; Schujman, S.B. Semiconductor clathrates: A phonon glass electron crystal material with potential for thermoelectric applications. Semiconduct. Semimet. 2001, 69, 255. [Google Scholar] [CrossRef]
- Paschen, S.; Carrillo-Cabrera, W.; Bentien, A.; Tran, V.H.; Baenitz, M.; Grin, Y.; Steglich, F. Structural, transport, magnetic, and thermal properties of Eu8Ga16Ge30. Phys. Rev. B 2001, 64, 214404. [Google Scholar] [CrossRef]
- Paschen, S.; Pacheco, V.; Bentien, A.; Sanchez, A.; Carrillo-Cabrera, W.; Baenitz, M.; Iversen, B.B.; Grin, Y.; Steglich, F. Are type-I clathrates Zintl phases and ‘phonon glasses and electron single crystals’? Phys. B Condens. Matter 2003, 328, 39. [Google Scholar] [CrossRef]
- Bentien, A.; Christensen, M.; Bryan, J.D.; Sanchez, A.; Paschen, S.; Steglich, F.; Stucky, G.D.; Iversen, B.B. Thermal conductivity of thermoelectric clathrates. Phys. Rev. B 2004, 69, 045107. [Google Scholar] [CrossRef]
- Takabatake, T.; Suekuni, K.; Nakayama, T.; Kaneshita, E. Phonon-glass electron-crystal thermoelectric clathrates: Experiments and theory. Rev. Mod. Phys. 2014, 86, 669. [Google Scholar] [CrossRef]
- Christensen, M.; Abrahamsen, A.B.; Christensen, N.B.; Juranyi, F.; Andersen, N.H.; Lefmann, K.; Andreasson, J.; Bahl, C.R.H.; Iversen, B.B. Avoided crossing of rattler modes in thermoelectric materials. Nat. Mater. 2008, 7, 811–815. [Google Scholar] [CrossRef]
- Euchner, H.; Pailhès, S.; Nguyen, L.T.K.; Assmus, W.; Ritter, F.; Haghighirad, A.; Grin, Y.; Paschen, S.; de Boissieu, M. Phononic filter effect of rattling phonons in the thermoelectric clathrate Ba8Ge40+xNi6−x. Phys. Rev. B 2012, 86, 224303. [Google Scholar] [CrossRef]
- Pailhès, S.; Euchner, H.; Giordano, V.M.; Debord, R.; Assy, A.; Gomès, S.; Bosak, A.; Machon, D.; Paschen, S.; de Boissieu, M. Localization of propagative phonons in a perfectly crystalline solid. Phys. Rev. Lett. 2014, 113, 025506. [Google Scholar] [CrossRef]
- Ikeda, M.S.; Euchner, H.; Yan, X.; Tomeš, P.; Prokofiev, A.; Prochaska, L.; Lientschnig, G.; Svagera, R.; Hartmann, S.; Gati, E.; et al. Kondo-like phonon scattering in thermoelectric clathrates. Nat. Commun. 2019, 10, 887. [Google Scholar] [CrossRef]
- Kaur, P.; Madsen, G.K.H.; Bera, C. Thermoelectric figure of merit and thermal conductivity of type-I clathrate alloy nanowires. MRS Commun. 2019, 9, 370–374. [Google Scholar] [CrossRef]
- Lu, L.; Yi, W.; Zhang, D.L. 3ω method for specific heat and thermal conductivity measurements. Rev. Sci. Instrum. 2001, 72, 2996–3003. [Google Scholar] [CrossRef]
- Yan, Y.; Tang, X.; Li, P.; Zhang, Q. Microstructure and thermoelectric transport properties of type-I clathrates Ba8Sb2Ga14Ge30 prepared by ultrarapid solidification process. J. Electron. Mater. 2009, 38, 1278–1281. [Google Scholar] [CrossRef]
- Tomeš, P.; Yan, X.; Kastner, R.; Svagera, R.; Waas, M.; Eilertsen, J.; Weidenkaff, A.; Paschen, S. Thermoelectric properties of meltspun Ba8Cu5(Si,Ge,Sn)41 clathrates. J. Alloys Compd. 2016, 654, 300–307. [Google Scholar] [CrossRef]
- Christian, R.; Ikeda, M.; Lientschnig, G.; Prochaska, L.; Prokofiev, A.; Tomeš, P.; Yan, X.; Zolriasatein, A.; Bernardi, J.; Schachinger, T.; et al. Nanostructured clathrates and clathrate-based nanocomposites. Phys. Status Solidi A 2016, 213, 784–801. [Google Scholar] [CrossRef]
- Zolriasatein, A.; Yan, X.; Bauer, E.; Rogl, P.; Shokuhfar, A.; Paschen, S. Influence of PCA on thermoelectric properties and hardness of nanostructured Ba–Cu–Si clathrates. Mater. Des. 2015, 87, 883–890. [Google Scholar] [CrossRef]
- Yan, X.; Falmbigl, M.; Rogl, G.; Grytsiv, A.; Prokofiev, A.; Bauer, E.; Rogl, P.; Zehetbauer, M.; Paschen, S. High-pressure torsion to improve thermoelectric efficiency of clathrates? J. Electron. Mater. 2013, 42, 1330–1334. [Google Scholar] [CrossRef]
- Sun, B.; Jia, X.; Zhao, J.; Li, Y.; Liu, H.; Ma, H. Effects of pressure on the microstructure and simultaneous optimization of the electrical and thermal transport properties of Yb0.5Ba7.5Ga16Ge30. Inorg. Chem. 2018, 57, 3323–3328. [Google Scholar] [CrossRef]
- Sun, B.; Zhao, J.; Li, Y.; Cao, L.; Yang, Y.; Fan, X.; Liu, X.; Wang, C.; Huang, X.; Wang, X.; et al. Effect of HPHT processing on structural and thermoelectric properties of low-cost type-I clathrate Ba8Cu6Si40. J. Phys. Chem. C 2020, 124, 9082–9088. [Google Scholar] [CrossRef]
- Yan, X.; Bauer, E.; Rogl, P.; Bernardi, J.; Prokofiev, A.; Paschen, S. Thermoelectric properties and stability of nanocomposites type-I clathrate Ba-Cu-Si with SiC. Z. Anorg. Allg. Chem. 2020, 646, 1055–1061. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Prokofiev, A.; Sidorenko, A.; Hradil, K.; Ikeda, M.; Svagera, R.; Waas, M.; Winkler, H.; Neumaier, K.; Paschen, S. Thermopower enhancement by encapsulating cerium in clathrate cages. Nat. Mater. 2013, 12, 1096–1101. [Google Scholar] [CrossRef]
- Candolfi, C.; Aydemir, U.; Baitinger, M.; Oeschler, N.; Steglich, F.; Grin, Y. High temperature thermoelectric properties of the type-I clathrate Ba8AuxSi46−x. J. Appl. Phys. 2012, 111, 043706. [Google Scholar] [CrossRef]
- Bhatta, R.P.; Annamalai, S.; Mohr, R.K.; Brandys, M.; Pegg, I.L.; Dutta, B. High temperature thermal conductivity of platinum microwire by 3ω method. Rev. Sci. Instrum. 2010, 81, 114904. [Google Scholar] [CrossRef]
- Choi, T.Y.; Poulikakos, D.; Tharian, J.; Sennhauser, U. Measurement of thermal conductivity of individual multiwalled carbon nanotubes by the 3ω method. Appl. Phys. Lett. 2005, 87, 013108. [Google Scholar] [CrossRef]
- Chien, C.H.; Lee, P.C.; Tsai, W.H.; Lin, C.H.; Lee, C.H.; Chen, Y.Y. In-situ observation of size and irradiation effects on thermoelectric properties of Bi-Sb-Te nanowire in FIB trimming. Sci. Rep. 2016, 6, 23672. [Google Scholar] [CrossRef]
- Li, L.; Jin, C.; Xu, S.; Yang, J.; Du, H.; Li, G. Thermal conductivity of a single Bi0.5Sb1.5Te3 single-crystalline nanowire. Nanotechnology 2014, 25, 415704. [Google Scholar] [CrossRef]
- Properties of solids. In CRC Handbook of Chemistry and Physics; David, R.L., Ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Callaway, J. Model for lattice thermal conductivity at low temperatures. Phys. Rev. 1959, 113, 1046–1051. [Google Scholar] [CrossRef]
- Klemens, P.G. Thermal conductivity and lattice vibrational modes. In Solid State Phys.; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1958; Volume 7, pp. 1–98. [Google Scholar] [CrossRef]
- Ikeda, M.S. Mechanism of the Thermal Conductivity of Type-I Clathrates. Ph.D. Thesis, TU Wien, Vienna, Austria, 2015. [Google Scholar]
- Muñoz Rojo, M.; Abad, B.; Manzano, C.V.; Torres, P.; Cartoixà, X.; Alvarez, F.X.; Martín Gonzalez, M. Thermal conductivity of Bi2Te3 nanowires: How size affects phonon scattering. Nanoscale 2017, 9, 6741–6747. [Google Scholar] [CrossRef] [PubMed]
- Dedi; Lee, P.-C.; Wei, P.-C.; Chen, Y.-Y. Thermoelectric characteristics of a single-crystalline topological insulator Bi2Se3 nanowire. Nanomaterials 2021, 11, 819. [Google Scholar] [CrossRef] [PubMed]
- Roh, J.W.; Jang, S.Y.; Kang, J.; Lee, S.; Noh, J.-S.; Kim, W.; Park, J.; Lee, W. Size-dependent thermal conductivity of individual single-crystalline PbTe nanowires. Appl. Phys. Lett. 2010, 96, 103101. [Google Scholar] [CrossRef]
- Liang, W.; Rabin, O.; Hochbaum, A.I.; Fardy, M.; Zhang, M.; Yang, P. Thermoelectric properties of p-type PbSe nanowires. Nano Res. 2009, 2, 394–399. [Google Scholar] [CrossRef]
- Swinkels, M.Y.; van Delft, M.R.; Oliveira, D.S.; Cavalli, A.; Zardo, I.; van der Heijden, R.W.; Bakkers, E.P.A.M. Diameter dependence of the thermal conductivity of InAs nanowires. Nanotechnology 2015, 26, 385401. [Google Scholar] [CrossRef]
- Boukai, A.I.; Bunimovich, Y.; Tahir-Kheli, J.; Yu, J.K.; Goddard Iii, W.A.; Heath, J.R. Silicon nanowires as efficient thermoelectric materials. Nature 2008, 451, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Ju, Y.S. Phonon heat transport in silicon nanostructures. Appl. Phys. Lett. 2005, 87, 153106. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lužnik, M.; Lientschnig, G.; Taupin, M.; Steiger-Thirsfeld, A.; Prokofiev, A.; Paschen, S. Size Effect on the Thermal Conductivity of a Type-I Clathrate. Crystals 2023, 13, 453. https://doi.org/10.3390/cryst13030453
Lužnik M, Lientschnig G, Taupin M, Steiger-Thirsfeld A, Prokofiev A, Paschen S. Size Effect on the Thermal Conductivity of a Type-I Clathrate. Crystals. 2023; 13(3):453. https://doi.org/10.3390/cryst13030453
Chicago/Turabian StyleLužnik, Monika, Günther Lientschnig, Mathieu Taupin, Andreas Steiger-Thirsfeld, Andrey Prokofiev, and Silke Paschen. 2023. "Size Effect on the Thermal Conductivity of a Type-I Clathrate" Crystals 13, no. 3: 453. https://doi.org/10.3390/cryst13030453
APA StyleLužnik, M., Lientschnig, G., Taupin, M., Steiger-Thirsfeld, A., Prokofiev, A., & Paschen, S. (2023). Size Effect on the Thermal Conductivity of a Type-I Clathrate. Crystals, 13(3), 453. https://doi.org/10.3390/cryst13030453





