Abstract
We study the elasto-optic behavior of stressed cubic crystals (all classes) and isotropic materials (like e.g., glasses). We obtain the explicit dependence of the refraction indices on the stress (either applied or residual), as well as a mild generalization of the Brewster law for cubic crystals. We show also that the optic indicatrix and the stress ellipsoid are coaxial only in the isotropic case. This theory allows the improvement of the measurement techniques, as photoelasticity, on cubic crystals and optically isotropic materials.
1. Introduction
The optic and elasto-optic behaviour of crystals and transparent media are well studied, starting from the pioneering works by Brewster [1], Born [2], Wolf [3], and Maxwell [4]. Based on those studies a number of photoelastic techniques have been developed, addressed to stress analysis and materials elastic properties investigation. Classically these methods are applied to and based on isotropic amorphous like materials. Perspex, glass, and other transparent non-crystalline materials belong to the class of substances to which studies have been addressed in number of different declinations for specific purposes. Transmitted photoelasticity, reflected method, scattered light techniques are some of the various methodologies based on the photoelastic theory for isotropic non-crystalline material [5,6]. This development is exploited, since years, in numbers of applications, spanning from mechanics to construction, from optics to electronics and it has acquired a renovated interest by the growing of the digital techniques for image processing [7,8,9]. Structural glasses, for buildings or cars, are evaluated by photoelastic techniques [10]: photoelasticity is one of the widest used experimental methods for validating the FEM simulations of stress distribution in mechanical parts; optical parts can be adjusted using photoelastic principles (e.g., optical modulation and retarders for surface measurements).
In optically isotropic materials the spherical shape of the optical indicatrix, describing the distribution of the dielectric impermeability (or refractive indexes) over the direction, is deformed by stress in an ellipsoid inducing a change in the optical behaviour. In this condition the light, crossing the specimen, is split in its ordinary and extraordinary components and get a phase delay; that is, birefringence. Fringes are produced by the relative phase delay acquired and observed via polariscopes. The analysis of the relative isochromate and isocline fringes allows to carry out information on load magnitude and direction, an instance which is particularly useful for the quality assessment and stress detection in amorphous isotropic media [5,11].
On the other hand, anisotropic crystalline materials exhibit a very different photoelastic behaviour. Their optic indicatrix is an ellipsoid even under stress free conditions, due to the anisotropy. The orientation and the shape of those ellipsoids are modified by the components and magnitude of the stress tensor, as described by the elasto-optic theory of the anisotropic crystals which was studied and developed since the last century [12,13,14]. The natural birefringence of these substances leads to a different approach for elasto-optic analysis and stress investigation. Recently, a tensorial algebra approach based on the dielectric impermeability, the piezo-optic tensor and the stress tensor has been developed for anisotropic crystals. The light acquires relative phase delay even in unstressed condition and, consequently, fringes are produced having a specific shape due to crystal specific symmetries; the modulation of these symmetries indicates the possible stress condition. Those studies are based on the analysis of the Bertin surfaces [15,16,17] which describes the loci of points where the ordinary and extraordinary light components get an iso-delay. The models developed allow to deepen the crystal knowledge in its elasto-optic characteristics and the assessment of the photoelastic constants (piezo-optic matrix) [18] allowing the internals stress measurements [19,20,21,22]. This theoretical effort paved the way to new measurements techniques such as laser conoscopy or sphenoscopy [23], thus allowing reliable and precise measurements techniques for the fast quality control and residual stress evaluation of these complex anisotropic materials [24,25,26,27].
However, also for some optically isotropic crystalline there is still a lack of knowledge of their elasto-optic characteristics: this large class of substances, which is represented by the cubic crystals, are fundamental in number of applications, from industrial to research ones. They are exploited as scintillators [28], in laser technology, as electro-optic and non-linear optics components for different purposes; in parallel with their excellent functional characteristics, which make them crucial in fields spanning from medicine, to aerospace, lasers and high energy physics [29], their production and life cycle manageability characteristics are quite interesting. In fact, the growth and the production process are less complex and critical with respect to the ones of the optically anisotropic crystals. All those mentioned properties lead to the large use of these interesting materials within a strategical context.
Despite their large use, the cubic crystalline materials elasto-optic properties where not extensively studied in their full extents. As a first approximation, they are considered as amorphous-like substances when a photoelastic inspection is required, an instance which is not only the rigorous way to proceed but which also leads to possible considerable error in the data interpretation or to a uninterpretable patterns.
In this paper we propose the elasto-optic study of both the isotropic cubic crystals and the isotropic amorphous ones, like glasses, starting from the tensorial approach of the stress-dependent dielectric impermeability tensor, as it was already done for the anisotropic crystals in previous papers.
The purpose of his paper is to give a new theoretical approach for a better comprehension of the elasto-optic behaviour of both cubic crystalline and amorphous isotropic media. This theory allows the improvement of the measurement techniques and measurements instrumentation, allowing further for the evaluation of the photoelastic parameters and the stress analysis for the quality control as well as for characterization of this complex class of materials. We also give some remarks about the extendibility of the Brewster law. Finally, we show that the principal stress directions coincide to the principal axes of the Optic Indicatrix (coaxiality) only for isotropic non-crystalline materials. The work allows for a fast interpretation of the photoelastic observations; it completes our previous application of the classical phtoelastic theory, including new results about the coaxiality between principal stress directions and optical indicatrix.
2. Materials and Methods
It is well known that the optical indicatrix Bxx = 1, where B is dielectric impermeability tensor, for an unstressed optically isotropic transparent material is a sphere [2], since the dielectric impermeability tensor is spherical:
B = no−2I,
An applied or residual stress T modifies the dielectric impermeability according to the Maxwell Equation:
where Π is the fourth-order piezo-optic tensor of the two optically isotropic point groups, namely the Cubic and Isotropic one, and no > 1 is the refraction index. Since the considered materials have a linear elastic behaviour, it makes sense to use the linear relations (2) which, from a mathematical point of view, holds true in the “small stress” regime. Such regime ranges, for brittle materials like crystals and glasses, over tens of MPa close to the ultimate tensile stress before the brittle fracture is reached and applies well to the cases we are treating. In the general case, besides some specific state of stress which leave the stressed crystal still optically isotropic and which were studied in details into [16], the tensor B(T) admits three eigencouples {(B1, u1), (B2, u2), (B3, u3)} and it becomes either optically uniaxial or biaxial (The stress which leaves an optically isotropic material still optically isotropic is the spherical (idrostatic) stress of the form T = σmI [16]).
B(T) = no−2I + Π[T],
Let (ξ,η,ζ) be the coordinates in the frame Σ{u1, u2, u3} of the eigenvectors of B(T), hence it makes sense, for biaxial and uniaxial materials to define the Bertin Surfaces [19,20]:
where , λ is the light wavelength of the polariscope, N is an integer that represent the fringe order, nmin and nmax are the minimum and maximum refraction indices and 2 is the angle between the optic axes, defined by:
which holds for B1 > B2 > B3 and vice-versa with see ref [15,19,20].
For optically uniaxial materials with B1 = B2, it is = 0 and (3) reduces to:
The importance of these surfaces is that it should be possible to observe the Cassini-like interference fringes, that is sections of the Bertin Surface with an observation plane, by the means of conoscopic observations [24,25,30]: indeed for e.g., = d the coordinate of an observation plane, from Equation (3) we get the family of curves, parameterized on d, N and H:
which by Equation (3) are even in their variable. Let a = |f(,0) = 0| and b = |f(0,) = 0|, then in [31] we introduced the ellipticity ratio or photoelastic constant C, a measurable parameter in a conoscopic fringe analysis:
By Equations (2)–(6) C may clearly depend on the applied stress and into [19,20] we generalized the definition by introducing the tensor of photoelastic constants Fσ such that:
Clearly, Equations (3)–(5) are undefined for optically isotropic materials and no conoscopic observation of interference fringes is possible in this case as defined before.
However, one can wonder what happens to e.g., an uniaxial Bertin surface when a monotonically increasing applied stress reduces B(T) to a spherical tensor, in order to figure out what happens to the observed interference fringes. This means that for isotropic materials with nmax = nmin:
in Equation (5). Now, let = d be the coordinate of an observation plane which is orthogonal to the optic axis , then the equation of the Cassini-like curves, for a given fringe order e.g., N = 1 and in polar coordinates r2 = reduces to:
r4 − H2r2 − d2H2 = 0,
If we solve for r then we obtain:
and hence the interference fringes growth monotonically to infinity when nmax − nmin0, thus disappearing progressively from the conoscopic field of observation.
Similar results can be obtained in the case of induced biaxiality with nmax − nmin0, in fact the parameters a and b introduced before, diverge with a similar law of (11).
A key point in any optical analysis is to arrive at an explicit relation for the dependence of the refraction indices in the stressed crystal in terms of the components of the piezo-optic tensor and of the stress tensor. However, since the relation between the eigenvalues of B(T) and the principal refraction indices nk, k = 1, 2, 3 is:
which is strongly non-linear in T, then within the same hypotheses of (2) we may arrive at the linearized relation:
In Equation (13) it is possible that the derivative of Bk with respect to T is not defined for T = 0, thus making the linearization impossible. A way to remove this inconvenience was proposed into [32], where precisely such a problem was addressed and completely solved in a general manner: however for who is not accustomed to the very formal algebraic treatment given therein, here we shall recover the same results in a different and more conventional way.
To finish this overview of the problems related to optically isotropic materials and crystals, we recall that for isotropic amorphous materials the Brewster law [1] relates the principal refraction index of B(T) to the principal values σk, k = 1, 2, 3 of T, namely:
where K depends on no and Π; the question in this case is if it is possible to extend, and to which extent, the Equation (14) to other crystallographic symmetry group. The answer was obtained in a definitive manner into [33] and here we shall show how the same results can be easily recovered within our present approach.
ni − nj = KB(σi − σj), i ≠ j, i,j = 1,2,3,
The frames we use in this work are the following: S {e1, e2, e3} with coordinates (x,y,z) which is the reference coincident with the crystallographic axes, and Σ {u1, u2, u3} with coordinates (ξ,η,ζ), we already introduced, and which is the reference frame for the Optic Indicatrix and Bertin surfaces.
In the following section we shall assume that all the observations are made along the direction spanned by e3 and accordingly we may observe only the effects of the plane stress Te3 = 0, since for the stress along the same direction, in absence of applied forces on the surfaces orthogonal to e3, we may assume zero mean value: therefore they are not detectable by the means of a conoscopic analysis since it takes the mean values on the optic path along the same direction. Accordingly, the components of such a plane stress in the frame S are:
Let (σ1, σ2, 0) be the principal stress of Equation (15) and U the frame of the corresponding eigenvectors which is rotated with respect to S by an angle α given by:
Then we shall also make use of the Mohr’s relations [34].
between the principal stress and the components of Equation (15).
3. Results
3.1. Cubic Crystals
3.1.1. Classes 23 and m3
In the frame S of Figure 1, the tensor B(T), for a plane stress is given by (2) with piezo-optic tensor [13,14]
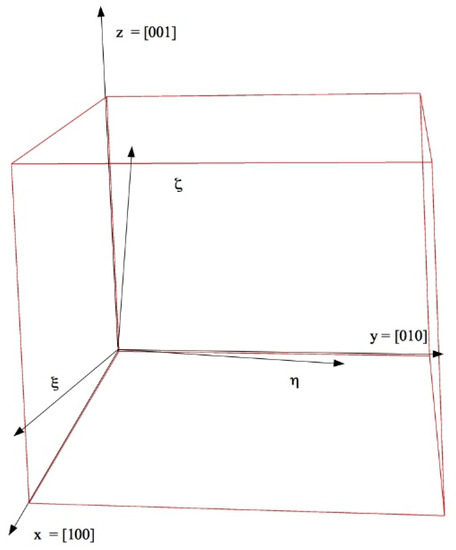
Figure 1.
The frame S is referred to the crystallographic axes of the cubic crystal with axes (a,a,a); the frame Σ corresponds to the principal axes of the Optic Indicatrix. In absence of stress, since the optical indicatrix is a sphere we may assume S = Σ.
Leads to, where for the sake of notation we write n0−2 = B0:
The eigenvalues of (19) are
where:
and eigenvectors
which means that the Σ is obtained from S by a rotation about the z = ζ axis which depends on T.
From (20) we have B1 > B2 but it is not possible to establish a-priori the complete ordering of the eigenvalues.
From (20) and (21), then:
and by a trivial application of (13) we see that, due to the presence of the term R as given in (21), the derivates of n1 and n2 blows up for T = 0.
Now, if we consider the rotation around the z-axis:
and since tan2γ can be estimated, in fact, the angle γ can be experimentally evaluated following the procedure described by Whalstrom [15].
Then from (24) we get:
By substituting (25) into (21) we have:
and then:
The relation (27), which depends on the measured parameter γ, can be successful linearized into:
When we evaluate the birefringence on the observation plane normal to e3 (we makes the same in the follow) ∆n = n1 − n2, from (28):
and by substituting (29) into (3.6) then we get:
By (17) relations (30) can be written in terms of the principal stress and of the angle α:
Finally is it possible to also write (29) as follows:
or by the means of (17):
where g1 and g2 depend on the Π components π13, π12, π11 and γ, meanwhile f1 and f2 depend also on the angles α.
Despite the complex cubic structure, the evaluation of both the ∆n and the rotation angle γ of the optic indicatrix axes around z allow the determination of the shear stress (30). The (31) shows ∆n as a function of principal stress difference as in the classical Brewster form.
3.1.2. Classes , 432, m3m
By following the previous procedure also for the cubic crystals of the classes , 432, m3m, since the piezo-optic tensor is given in this case by [13,14]:
then we obtain:
which yields, explicitly:
The eigenvalues of Equation (36) are:
with:
The corresponding eigenvectors are:
Also in this case there is a the rotation of the optic indicatrix around the z = ζ axis that is expressed by the angle γ, which can be experimentally evaluated by following Wahlstrom [15] as we remarked before. By a trivial calculation:
We define the difference ∆B as:
which in terms of the principal stresses (17) reads:
The angle α is the rotation of the principal stress frame, a parameter which is related to γ by Equation (40):
The angles α and γ coincide only when:
A condition which holds only for the material of the Isotropic symmetry group as shown in the follow.
In the general case, for cubic materials of these classes, the ratio:
determines the rotation of the principal stress frame U with respect to S so we can rewrite (42) by trivial transformations and using (43) as:
Equation (44) shows that ∆B is a linear function of the principal stress difference. When we turn our attention to ∆n in terms of the principal stress it is possible to linearize it to arrive at:
In this case, the experimental knowledge of ∆n, k, and the rotation angle γ allows for the calculation of the principal stress difference as in the classical Brewster law. Once determined the principal stress difference through the (45) it is possible also obtain the shear stress using also (43):
From (43) and (46) it is trivial to evaluate also the angle as (from (46)):
We remark that Equation (45) is a special instance of the Brewster law (see also [33]).
3.2. Isotropic Materials
The glass and plastic media composed by either random oriented micro-crystals or amorphous substance present the highest optic symmetry, and in this case the Π tensor is that of the Isotropic symmetry group [13,14]:
and in the case of plane stress (15) from (2) we have:
The eigenvalues of (49) are:
where:
The first part of Equation (50) can be written as (being in this case eigenvalue order indifferent):
In isotropic materials the principal directions of B(T) coincide with those of T [32]: indeed:
so K = 1 and by from Equation (15):
Hence U = Σ with α = γ and in this common frame we can write:
The γ angle represents the rotation of the index ellipsoid around z = ζ as usual [15].
Once again, from Equation (55) we obtain that B1 − B2 is a linear function of the principal stress difference:
and by linearization we trivially recover the Brewster Equation (14)
with:
Also in this case the shear can be calculated by means of Equation (57):
The ∆n21 (57) is proportional to the ∆B (56) in the same form of the Brewster law. Finally, the shear stress and the principal stress difference are valuable.
4. Conclusions
By starting from the stress-dependent dielectric impermeability tensor we gave a formal and abstract treatment of the stress-optic behaviour and the Brewster Law in cubic crystals and general isotropic media. In the small stress approximation, we linearized the refraction indices difference as a function of the stress in terms of the components of the piezo-optic tensor Π tensor and of the rotation angle γ of the optic indicatrix: we also extend, whenever it is possible, the Brewster law to cubic crystals.
These are fundamental aspects for a proper interpretation of the fringe patterns obtained via photoelastic investigation and for the evaluation of the stress via photoelastic measurements.
An additional interesting outcome of the work is that we demonstrated how the coaxiality of the optic indicatrix and the stress ellipsoid only in the case of isotropic materials. This is a crucial consideration to take into account for the experimental procedure and analysis.
Moreover, we showed that the Bertin surfaces as well as the Cassini-Like curves, are undefined in absence of stress, and in some limit case of linearized stress. In fact, for amorphous and cubic crystalline, the linearization of the related photoelastic parameters, as for instance the ellipticity ratio, may lead to undefined forms.
Author Contributions
Writing—original draft, D.R. and F.D.; Writing—review & editing, P.P.N. and L.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external founding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The research leading to these results is within the scope of CERN R&D Experiment 18 “Crystal Clear Collaboration” and the PANDA Collaboration at GSI-Darmstadt.
Conflicts of Interest
The authors declare no conflict of Interest.
References
- Brewster, D. Papers on Optics; Royal Society of London: London, UK, 1830. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 6th ed.; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Rastogi, P.K. Photomechanics; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Brcic, V. Photoelasticity in Theory and Practice: Course Held at the Department for Mechanics of Deformable Bodies. Springer: Udine, Italy, 1974.
- Dally, J.W.; Riley, W.F. Experimental Stress Analysis, 2nd ed.; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Aben, H.; Guillemet, C. Photoelasticity of Glass; Springer: Berlin/Heidelberg, Germany, 1993; Available online: https://books.google.it/books?hl=it&lr=&id=1VfrCAAAQBAJ&oi=fnd&pg=PA3&dq=H.+Aben+and+C.+Guillemet,+Photoelasticity+of+glass,+Springer+Verlag,+1993.&ots=saM2uglK67&sig=F_wATsfK2x3hkR2DD4mdLWcj61M#v=onepage&q&f=false (accessed on 12 November 2018).
- Castellini, P.; Stroppa, L.; Paone, N. Laser sheet scattered light method for industrial measurement of thickness residual stress distribution in flat tempered glass. Opt. Lasers Eng. 2012, 50, 787–795. [Google Scholar] [CrossRef]
- Ramesh, K.; Lewis, G. Digital Photoelasticity: Advanced Techniques and Applications. Appl. Mech. Rev. 2002, 55, B69–B71. [Google Scholar] [CrossRef]
- Ajovalasit, A.; Petrucci, G.; Scafidi, M. Review of RGB photoelasticity. Opt. Lasers Eng. 2015, 68, 58–73. [Google Scholar] [CrossRef] [Green Version]
- Hödemann, S.; Valdmann, A.; Anton, J.; Murata, T. Gradient scattered light method for non-destructive stress profile determination in chemically strengthened glass. J. Mater. Sci. 2016, 51, 5962–5978. [Google Scholar] [CrossRef]
- Frocht, M.M.; Leven, M.M. Photoelasticity: The Selected Scientific Papers of M.M. Frocht; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Sirotin, Y.I.; Shaskolskaya, M.P. Fundamentals of Crystal Physics; Mir Publishers: Moscow, Russia, 1982. [Google Scholar]
- Perelomova, N.V.; Tagieva, M.M. Problems in Crystal Physics with Solutions; Shaskol’skaya, M.P., Ed.; Mir Publishers: Moscow, Russia, 1983. [Google Scholar]
- Nye, J.F. Physical Properties of Crystals; Clarendon Press: Oxford, UK, 1985; Available online: https://global.oup.com/academic/product/physical-properties-of-crystals-9780198511656?cc=it&lang=en& (accessed on 23 October 2018).
- Wahlstrom, E.E. Optical Crystallography; Wiley: Hoboken, NJ, USA, 1969. [Google Scholar]
- Daví, F. On the Bertin surfaces of photoelastic crystals. J. Opt. Soc. Am. A 2015, 32, 2323–2337. [Google Scholar] [CrossRef] [PubMed]
- Rinaldi, D.; Pietroni, P.; Davì, F. Isochromate fringes simulation by Cassini-like curves for photoelastic analysis of birefringent crystals. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2009, 603, 294–300. [Google Scholar] [CrossRef]
- Mytsyk, B.G.; Demyanyshyn, N.M.; Solskii, I.M.; Sakharuk, O.M. Piezo- and elasto-optic coefficients for calcium tungstate crystals. Appl. Opt. 2016, 55, 9160–9165. [Google Scholar] [CrossRef] [PubMed]
- Rinaldi, D.; Daví, F.; Montalto, L. On the photoelastic constants for anisotropic stressed crystals. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2019, 947, 162782. [Google Scholar] [CrossRef]
- Rinaldi, D.; Daví, F.; Montalto, L. On the photoelastic constants and the Brewster law for stressed tetragonal crystals. Math. Methods Appl. Sci. 2018, 41, 3103–3116. [Google Scholar] [CrossRef]
- Natali, P.P.; Montalto, L.; Daví, F.; Mengucci, P.; Ciriaco, A.; Paone, N.; Rinaldi, D. Theoretical and experimental evaluation of piezo-optic parameters and photoelastic constant in tetragonal PWO. Appl. Opt. 2018, 57, 730–737. [Google Scholar] [CrossRef] [PubMed]
- Natali, P.; Montalto, L.; Scalise, L.; Davì, F.; Paone, N.; Rinaldi, D. Fringe modelling and Photoelastic stress Measurement method in tetragonal PWO observed in the plane normal to a crystallographic a-axis. J. Instrum. 2020, 15, P09037. [Google Scholar] [CrossRef]
- Montalto, L.; Rinaldi, D.; Scalise, L.; Paone, N.; Davì, F. Photoelastic sphenoscopic analysis of crystals. Rev. Sci. Instrum. 2016, 87, 15113. [Google Scholar] [CrossRef] [PubMed]
- Natali, P.P.; Montalto, L.; Rinaldi, D.; Davi, F.; Paone, N.; Scalise, L. Noninvasive Inspection of Anisotropic Crystals: Innovative Photoelasticity-Based Methods. IEEE Trans. Nucl. Sci. 2018, 65, 2203–2207. [Google Scholar] [CrossRef]
- Montalto, L.; Paone, N.; Rinaldi, D.; Scalise, L. Inspection of birefringent media by photoelasticity: From diffuse light polariscope to laser conoscopic technique. Opt. Eng. 2015, 54, 81210. [Google Scholar] [CrossRef]
- Montalto, L.; Scalise, L.; Rinaldi, D.; Paone, N. A Photoelasticity Measurement Set-Up for the Assessment of Residual Stresses in Scintillating Crystals. In Proceedings of the 3rd National Congress of Italian Mechanics Coordination, Naples, Italy, 30 June–1 July 2014; pp. 4–8. [Google Scholar]
- Montalto, L.; Natali, P.; Davi, F.; Mengucci, P.; Paone, N.; Rinaldi, D. Characterization of a defective PbWO4 crystal cut along the a-c crystallographic plane: Structural assessment and a novel photoelastic stress analysis. J. Instrum. 2017, 12, P12035. [Google Scholar] [CrossRef] [Green Version]
- Kamada, K.; Yanagida, T.; Endo, T.; Tsutumi, K.; Usuki, Y.; Nikl, M.; Fujimoto, Y.; Yoshikawa, A. 2-inch size single crystal growth and scintillation properties of new scintillator. In Proceedings of the IEEE Symposium on Nuclear Science (NSS/MIC), Valencia, Spain, 23–29 October 2011; pp. 1927–1929. [Google Scholar] [CrossRef]
- Atanov, N.; Baranov, V.; Budagov, J.; Cervelli, F.; Colao, F.; Cordelli, M.; Corradi, G.; Davydov, Y.; Di Falco, S.; Diociaiuti, E.; et al. The Mu2e undoped CsI crystal calorimeter. J. Instrum. 2018, 13, C02037. [Google Scholar] [CrossRef] [Green Version]
- Montalto, L.; Paone, N.; Scalise, L.; Rinaldi, D. A photoelastic measurement system for residual stress analysis in scintillating crystals by conoscopic imaging. Rev. Sci. Instrum. 2015, 86, 63102. [Google Scholar] [CrossRef] [PubMed]
- Ciriaco, A.; Davı, F.; Lebeau, M.; Majni, G.; Paone, N.; Pietroni, P.; Rinaldi, D. PWO photo-elastic parameter calibration by laser-based polariscope. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2007, 570, 55–60. [Google Scholar] [CrossRef]
- Daví, F. Exact and linearized refractive index stress-dependence in anisotropic photoelastic crystals. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190854. [Google Scholar] [CrossRef] [PubMed]
- Davì, F. On the generalization of the Brewster Law. Math. Mech. Complex Syst. 2020, 8, 29–46. [Google Scholar] [CrossRef]
- Sokolnikoff, I.S. Mathematical Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).