Next Article in Journal
Microtubules as One-Dimensional Crystals: Is Crystal-Like Structure the Key to the Information Processing of Living Systems?
Previous Article in Journal
Molecular Simulation of Crystallisation in External Electric Fields: A Review
Previous Article in Special Issue
Role of Strain Reversal in Microstructure and Texture of Pure Al during Non-Monotonic Simple Shear Straining
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 11
Issue 3
10.3390/cryst11030317
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Formation of Interstitial Dislocation Loops by Irradiation in Alpha-Iron under Strain: A Molecular Dynamics Study

by
Mohammad Bany Salman
1,†,
Mehmet Emin Kilic
2 and
Mosab Jaser Banisalman
3,*,†
1
Department of Civil Engineering, Incheon National University (INU), Incheon 22012, Korea
2
Department of Materials Science and Engineering, Yonsei University, Seoul 03722, Korea
3
Department of Nuclear Engineering, Seoul National University (SNU), Seoul 08826, Korea
*
Author to whom correspondence should be addressed.
†
Both authors contributed equally to this work.
Crystals 2021, 11(3), 317; https://doi.org/10.3390/cryst11030317
Submission received: 23 January 2021 / Revised: 14 March 2021 / Accepted: 17 March 2021 / Published: 23 March 2021
(This article belongs to the Special Issue Strain Reversal in Metals and Alloys: Origins and Consequences)
Browse Figures
Versions Notes

Abstract

:
The present work reports the formation of an interstitial dislocation loop with a lower primary knock-on atom (PKA) energy in alpha-iron under strain conditions by the use of molecular dynamics simulation. The study was conducted using a PKA energy of 1~10 keV and hydro-static strain from −1.4 to 1.6%. The application of 1.6% hydrostatic strain results in the formation of ½<111> dislocation loop with a low PKA of 3 keV. This result was associated with a threshold displacement energy decrement when moving from compression to tension strain, which resulted in more Frenkel pairs initiated at peak time. Furthermore, many of the initiated defects were energetically favorable by 2 eV in the form of the interstitial dislocation loop rather than a mono defect.

1. Introduction

Due to their remarkable physical properties, iron-based materials (ferritic phase) have been used for several applications [1] and are considered to be the main structural materials for use in next-generation nuclear reactors [2], where materials are exposed to several sources of radiation damage. Iron-based materials have been subjected to several studies about the radiation damage [3,4,5,6,7,8,9] considering a varying range of effects, such as temperature [10,11,12,13,14], application of strain, and impurity atoms additions [15].
The main sources of radiation coming from the energetic protons, neutrons, electrons, and ions that are likely to transfer energy to the primary knock-on atom (PKA) and thus initiates collision cascade events. One of the consequences of the collision cascade event is the produced defects that may accumulate to form voids, dislocations, and other clusters, causing rapid material deterioration [15,16]. Among the produced dislocation defects is the interstitial dislocation loop [16,17], which was observed at relatively high irradiation energies using transmission electron microscopy [18,19,20]. Experimentally, interstitial dislocation loops can be classified into two types: <100> and ½<111> Burgers vector, and ½<111> loops are commonly known to be dynamically stable [20].
Although it has been suggested that the highly mobile interstitial dislocation loops [21] may be generated directly from collision cascade events [18], we speculate that there is no direct observation for the formation probability of the interstitial dislocation loop processed under strain effect, either from experiments or from molecular dynamics (MD) simulations.
Several strain sources (local strains), such as void swelling induced by irradiation and solute segregation, are exerted on the structural materials inside fission reactors. Due to the volumetric expansion in one direction, the void-metal interactions could introduce strains as high as 5% [22,23]. The local strains could affect the number, type and shape of the defects created, thereby affecting the material characteristics. Of irradiated α-Fe, the number of survived vacancies or self-interstitial atoms (SIAs) can be referred to as Frenkel pairs (FPs). The minimum energy required to form an FP by the collision of atoms is defined as the threshold displacement energy (TDE). To evaluate the created FPs from compression to tension strain, it is necessary to accurately calculate the TDE. In MD, the TDE is usually defined as the average value of Ed,i, which is known as the threshold displacement energy for a structure in a specific direction, i, over a sufficient number of displacement directions. The average value is called Ed,avg. For theoretical quantification of the radiation damage, the Ed,avg is commonly used as a primary value for the Norgett–Robinson–Torrens (NRT) model [24]. Theoretically, the number of FPs generated under a cascade event is affected by Ed,avg, thus Ed,avg must be evaluated properly.
Using an atomistic model, we provide an insight into the probability of interstitial dislocation loop formation under strain, justifying the relationship between Ed,avg value, and the number of FP’s generated at relatively low PKA energies. We first evaluated the average free and strained TDE (as an indicator for the energy needed to form the FP’s). The four different deposition energies of PKA (namely, 1, 3, 6, and 10 keV) were then examined, and six strain magnitudes (i.e., −1.4, −0.8, −0.2, 0.4, 1.0, and 1.6%) were hydrostatically applied. We further studied the peak number and the number of survived FPs as well as the efficiency of the defect production during collision cascades.

2. Methods

2.1. Threshold Displacement Energy Calculation

The TDE for free-strain structure entails the average value of Ed,i over a set of i directions, i.e., Ed.avg; likewise, the average strained TDE is defined as E d , a v g s t r a i n e d . To evaluate Ed.avg accurately, we followed the recommended settings, which were reported in our previous work [25].
The classical MD is performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [26]. The interatomic interactions were applied using the embedded atom method (EAM) developed by Derlet et al. [27] and revised for recoil simulations by Björkas et al. [28] (DB).
The MD 8 × 8 × 12 supercells of the α-Fe are composed of 1536 atoms with periodic boundary conditions. First, each initial structure was optimized by the conjugate gradient energy minimization, which relaxes the position of ions to a low-energy configuration. After the energy minimization, the structures were equilibrated at a temperature of 30 K and pressure of 0 Pa. The system was subsequently subjected to hydrostatic or uniaxial strains from −1.4% to 1.6% with intervals of 0.6% (Figure 1), resulting in six different deformed structures for each strain type.
For each deformed structure, the uniaxial strain was applied along the [100] direction of the simulation cell. The structure was deformed in the x-direction at a deformation rate of 0.002 ps-1 up to the target strain under the NVT ensemble. The lateral borders are fixed in such a way that the lengths of the cells along the y-and z-direction remain unchanged for the side borders. Under hydrostatic conditions, the strains are applied to each side of the structures along the [100], [010], and [001] directions with the same amount of strain for each direction.
Recoil MD simulations were performed under the NVE ensemble, and for every single collision event, the simulations ran for 5 ps. The adaptive time step for the integration of Newton’s equations of motion was used. To evaluate the defect formation, we used the VORONOI package [29], as implemented in the LAMMPS code.
All collision events were activated by depositing energy onto a specifically centered atom picked up from each strained structure, where the atom is known as PKA. When introduced, the deposited energy of the collision event was converted to corresponding PKA velocity components (Vx, Vy, and Vz). Initially, the PKA deposition energy of the initiated cascade event started at 5 eV and then increased incrementally by 1 eV until defects were formed. Once a defect was detected, this energy was considered as the minimum strained Ed,i, i.e., E d , i s t r a i n e d . A systematic averaging of four E d , i s t r a i n e d of different simulation timings (0, 50, 100, and 150 fs) was applied. This averaging was conducted to overcome the deviation of the E d , i s t r a i n e d calculation that would be raised from the thermal vibration effect at 30 K [30]. For the evaluation of the directional effect, the (Ed,avg) of the 210 irreducible crystal directions (ICD) were evaluated for free-strained structure. The method for ICD directions preparation was reported previously [25,30]; however, the E d , a v g s t r a i n e d evaluation is conducted over 300 quasi-uniform directions.

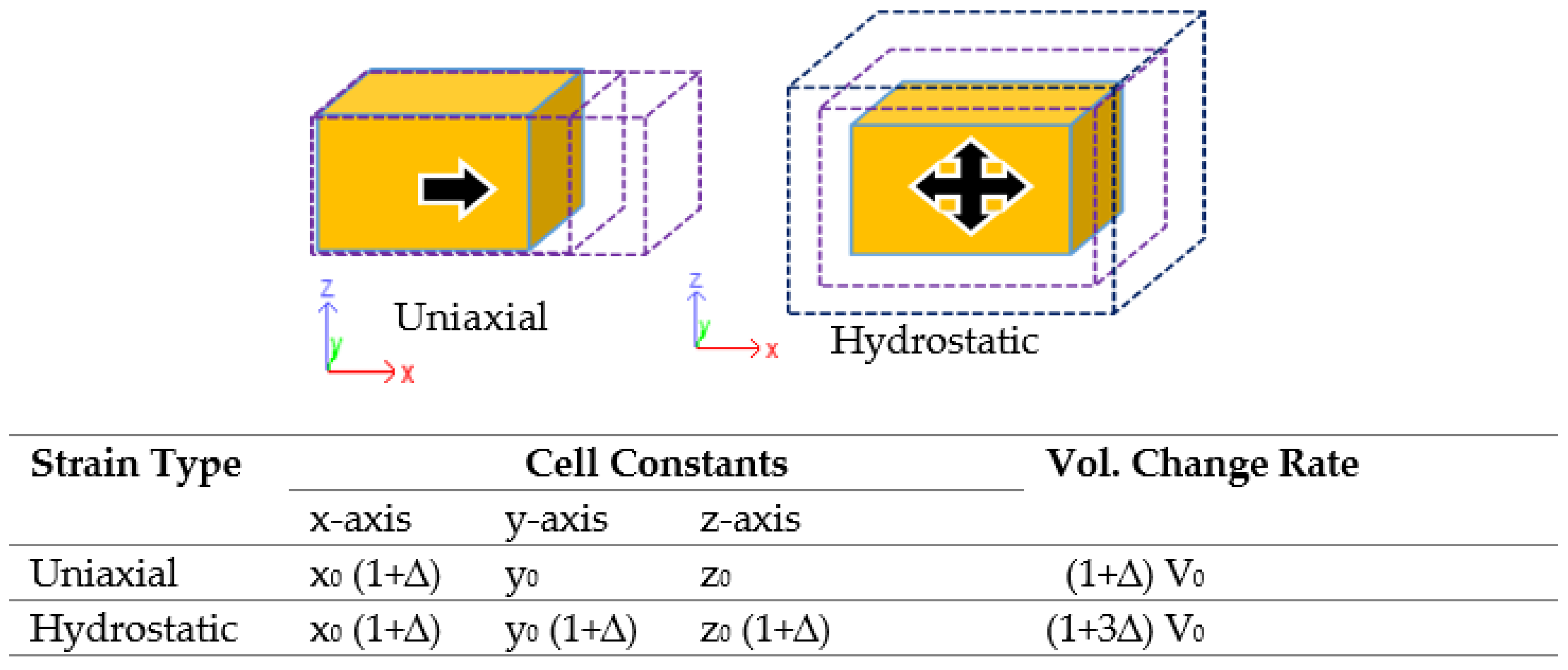
2.2. The Collision Cascades Evaluation under Strain

Similar calculation settings of 30 K and 0 Pa were applied, and the systems with 30 × 30 × 30, 45 × 45 × 45, 55 × 55 × 55, and 60 × 60 × 60 supercells, containing 54,000, 182,250, 332,750, and 432,000 α-Fe atoms, respectively, were constructed. The considered systems were confirmed to be sufficient to distribute the temperature of the system after the start of the collision event by 1, 3, 6, and 10 keV over <111>, <110>, <100>, and <321> collision directions and the average temperature was less than 200 K after the end of the simulation, while the displacement cascade was not in contact with the cell boundaries. Subsequently, the hydrostatic strain ranging between −1.4% and +1.6%, with an increasing step of 0.6%, resulted in six different structures. For every single collision event, the displacement evolution runs up to 20 ps in the canonical NVT ensemble, which was associated with the need for a longer time for higher PKA energies to reach stabilization compared to the lower PKA energies that could be stabilized in a shorter time. We confirmed that these settings are sufficient for the visualization and stabilization of the three main ballistics phases. The standard error of the mean (SEM) calculated as SEM = d x 0.5 , where d is the standard deviation of the average number of FPs values over four independent simulations of different collision event timings and x is the number of independent simulations. The dislocation extraction algorithm (DXA) of the Open Visualization Tool (OVITO) [31] was used to identify the probability of interstitial dislocation formation and to establish their types, lengths, and numbers from the created FP’s. It is to be noted that the electronic stopping was not considered in our MD simulation.

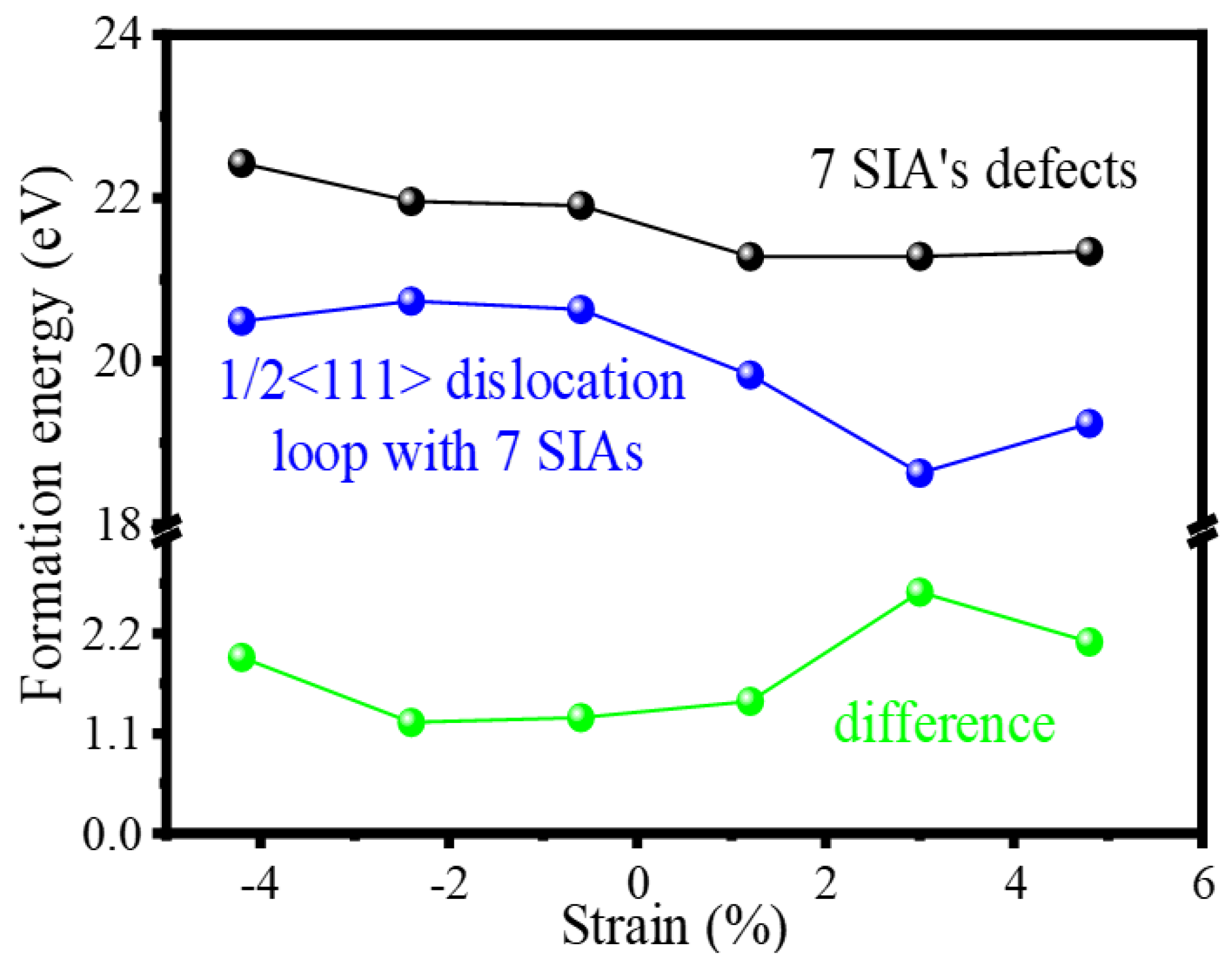
2.3. Calculation of Point Defects and Dislocation Formation Energies

The formation energies of seven single SIA defects (which did not interact with each other) were compared with the formation energy of the interstitial dislocation loop consists of 7-SIAs. For the dislocation loop, we extracted a pilot interstitial dislocation loop that formed at 10 keV after the end of the cascade simulation and then it was inserted into an intact structure. Subsequently, the strain was applied hydrostatically, and the dislocation loop formation energy was calculated.
The formation energy of defects (Ef) can be calculated as follows:
E f = E d f − E p e r f   N d f N p e r f .
where Edf and Eperf are the energy of the system with defects, and the energy of the intact structure without defects, respectively. The number of system atoms, including those with defects, is referred to as Ndf, and those of intact structures without defects are referred to as Nperf.

3. Results and Discussion

We aim to evaluate the interstitial dislocation loop formation under strain effects. The evaluation was conducted based on the number of FP’s formation under strain, and this can be directly linked with the changes of Ed under strain.

3.1. Evaluation and Validation of Free Strained Ed as Compared with DFT, MD and Theoretical Model Results

To validate the current MD-EAM potential model with density-functional theory (DFT) results, the formation and migration energies of vacancies and self-interstitials in various configurations are evaluated and compared with the DFT results from the literature (see Figure S1). The Ed,avg by DFT calculation is 32 eV [32], while with the current EAM MD potential, the value is 38.6 ± 2 eV. Thus, both results are comparably reasonable considering the MD error of calculation settings for Ed,avg. Although Ed<100>,MD and Ed<110>,MD are comparable with DFT results (Table S1 and Figure S2), the largest discrepancy between DFT and our EAM-MD was found for the close-packed <111> direction. The large discrepancy between DFT and MD of <111> would be related to the “focused collision sequence”. It is worthy to note that the reentry of atoms to the supercell image hardly affects the simulation result for displacement at the 30 K recoil simulation with non-cubic supercell (8 × 8 × 12) in which the Ed<111> = 43 eV. For cubic supercell, the 8 × 8 × 8 shows the low value (Ed<111> = 18.5 eV) even with a small number of system atoms compared with 16 × 16 × 16 that has Ed<111> = 36.25 eV (Table S2 and Figure S3). Nevertheless, the evaluated Ed,avg with non-cubic supercell converged faster, and the atom’s reentrant effect was not noticed for most of the 210 ICD directions (Figure S3). Therefore, the 8 × 8 × 12 system for Ed,avg evaluation was reasonable (Ed,avg = 38.6 eV ± 2 eV) when compared to DFT results (32 eV), even though the 8 × 8 × 8 systems resulted in smaller Ed,<111> value.
In comparison with other MD studies, Ed,min<100> of α-Fe ranges from 13 to 29 eV, which is comparable with our calculations [33]. We found that the current MD Ed,avg was around 3 eV lower than the previously reported value (Ed,avg 41.8 eV) [34]. This difference is due to the value of ΔEstep, which was used in both cases, where it is 1 eV in our study, while it was 5 eV in another study [34], which induces an error by 2 eV approximately. Although the value of Ed,avg obtained in the present work was slightly different from that of the ASTM standard (40 eV) [35], the used EAM potential model can still probably describe the interatomic interactions of recoils in contrast to other EAM potentials. For consistency, the entire calculations used the same EAM potential model.
In addition, experimentally, the current MD-study of Ed,min is only confirmed for <100> direction as Ed,min<100>,MD = 20 eV, and Ed,min<100>,EXP = 17 eV, but not for other directions due to the technical limitation in setting the <111> and <110> directions precisely [36].
This limitation is also expressed with the current MD-EAM potential model and the <100> direction of Ed,i has the most stable and the slowest deviation changes with angles up to 25° (Figure S4).
Furthermore, theoretically, using the Jan and Seeger equation, the Ed,avg is 23 eV [32,37]; however, the re-calculated Ed,avg for 210 ICD directions is 23.7 eV. The disadvantage of See- ger’s equation is the limitation of the evaluated Ed,i, which is dependent on the values of; Ed,<100> = 17 eV, Ed,<110> = 30 eV, and Ed,<111> = 20 eV, which were obtained experimentally [36]. From a technical standpoint, the values of Ed,<110> and Ed,<111> were not as accurate as of that Ed,<100>. Hence, the relation proposed by Jan and Seeger seems to be ineffective for estimating Ed,avg when compared with our MD results (see Figure S5). Thus, we presented an accurate method to evaluate Ed,avg, which is an important value to estimate the number of FPs formation under cascade events.

3.2. Evaluation of the Strain Effect on Ed,avg Value

The uniaxial and hydrostatic strained Ed,avg ( E d , a v g s t r a i n e d ) are shown in Figure 2a. The E d , a v g s t r a i n e d increases by moving from tension to compression for both uniaxial and hydrostatic strains, which is in harmony with the results reported in our previous work of bcc materials (W,Mo) [38] and in line with the results reported in Beeler’s work for Fe, which was hydrostatically strained by +2% [39]. The hydrostatic strain increases or decreases Ed,avg considerably in comparison with the uniaxial strain. As presented in Figure 2b, the uniaxial strain shows a minimal effect on changes the E d , a v g s t r a i n e d compared with the hydrostatic strain given that the amplitude of the strain is fixed. The proportional correlation between strain and defects is the correlation between defects and volume changes induced by strain [40], and such confirmation is shown in Figure 2b despite the strain type.
The displacement-direction and strain response correlation are shown in terms of threshold displacement energy change rate (TCR (%) = E d , i s t r a i n e d − E d , i 0 E d , i 0   ×   100 ), where ( E d , i 0 ) is the free strained Ed,i. TCR of 1.6% and −1.4% were obtained. The TCRs results in over 300 directions are shown in Figure S6. However, the general tendency is that TCRs become negative for tensile strain while becoming positive for compressive strain in most directions.
For a small strain on a solid, Hook’s law is applicable, and there are only three independent elastic constants, namely, C11, C12, and C44, for a cubic crystal. Furthermore, the bulk modulus B and tetragonal shear constant C’ are related to C11 and C12, i.e., B = 1/3(C11 + 2C12), C’ = ½(C11 − C12). The applied EAM interatomic potential shows a correct description of the elastic moduli of Fe. The values are 2.84 Å, 173.1 GPa, 121.9 GPa, and 52.5 GPa for lattice constant, B, C44, and C’, respectively [27]. The elastic stiffness constants described by the EAM potential are nicely confirmed with the DFT results [41], which in terms agrees well with the experiments values [42].

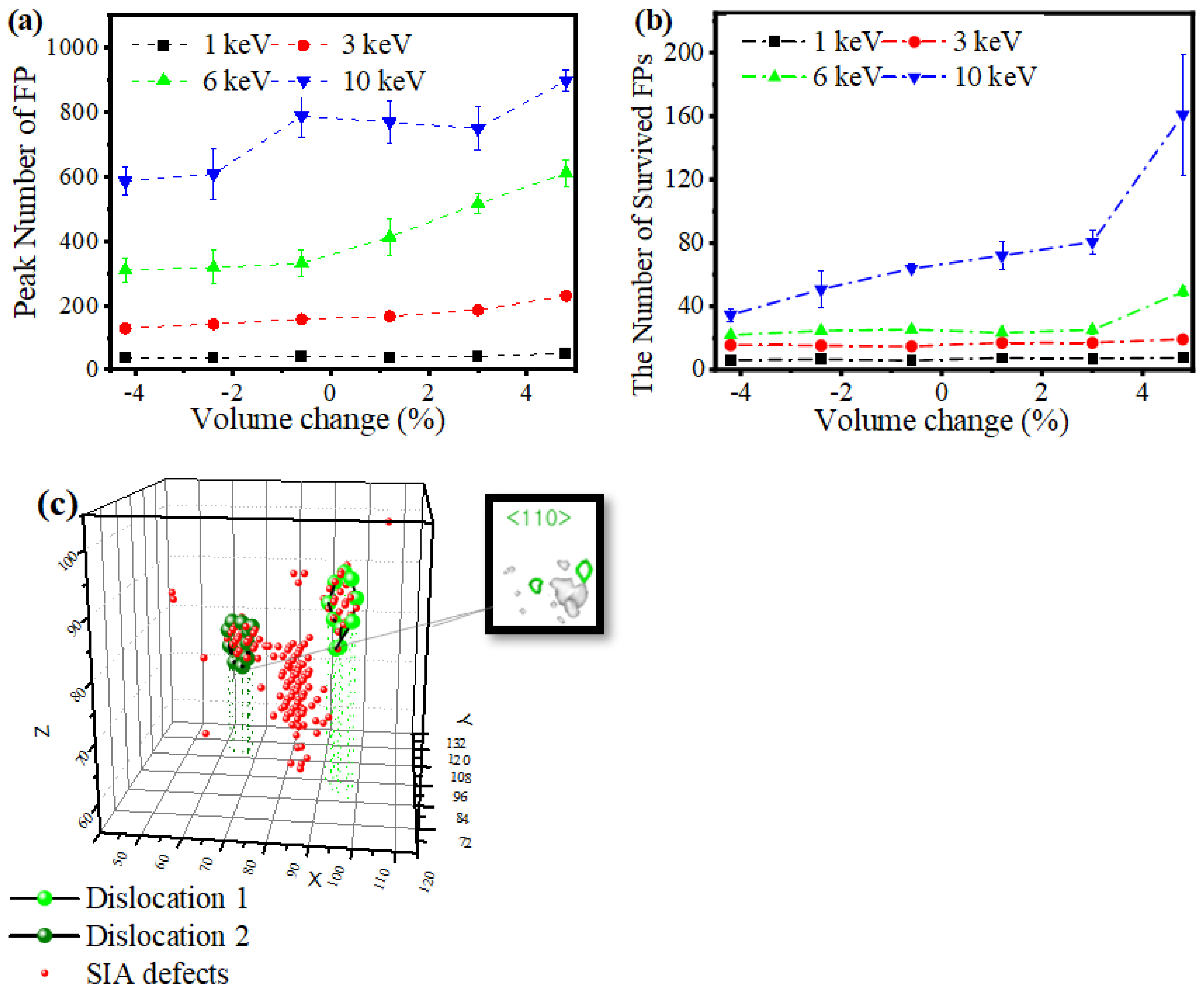
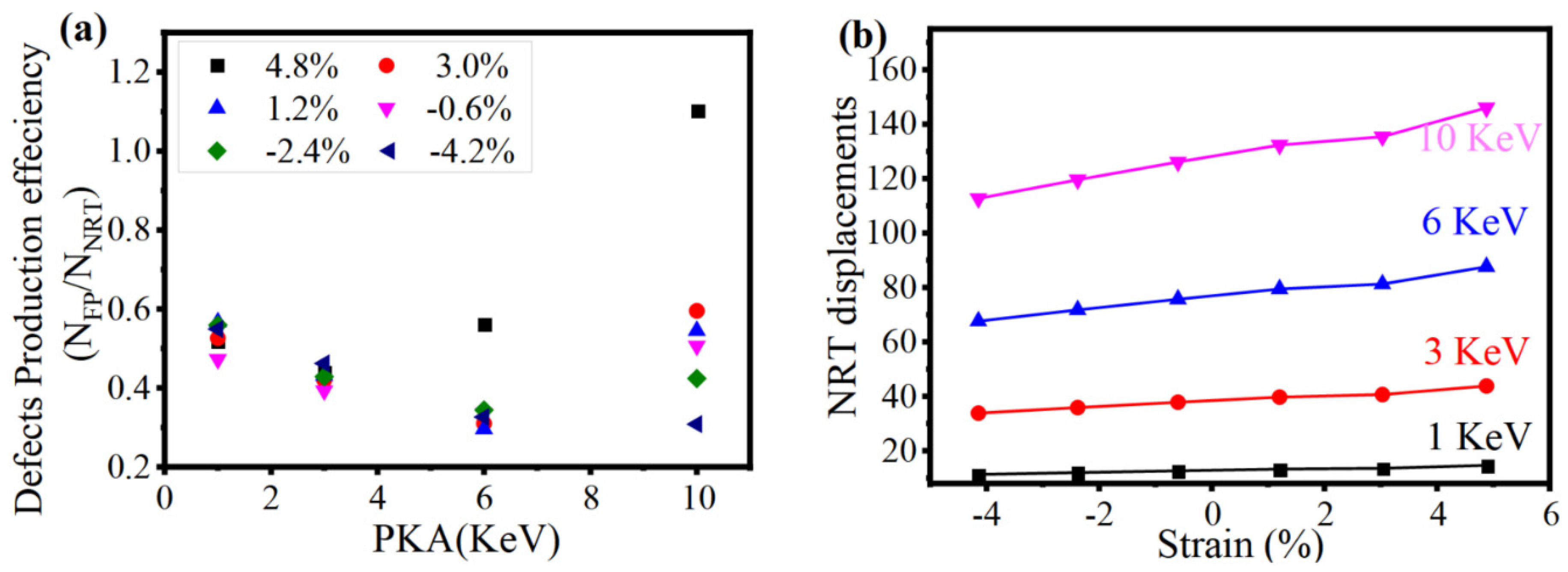
3.3. Strain Effect on Collision Cascade Event and FP Formation

The standard number of atomic displacements at free strain can also be theoretically estimated by NRT [24], which is expressed as follows:
NRT   displacement   =   0.8 E d e 2 E d
Here, Ede is the nuclear deposition energy, which is estimated to be substituted with the deposition collision energy carried by PKA for cascades. Furthermore, Ed was set to be ~39 eV according to our calculations in Section 3.1 and Section 3.2. Under compressed strains, the peak number of FPs occurred earlier, while under tensile strains, the peaks reached a great height and extended for a longer time (Figure 3). The peak time is one of the main ballistic phase specifications, and it is defined as the period between the initiations of the events until the maximum number of FPs formation is reached. However, most of the defects return to their original lattice locations during recombination time. The strain effects lead to different volume changes affecting the size of the displacement cascade that affect the number of created FPs [43].
During the cascade event, if the atomic recoil energy is lower than the Ed value, then the FPs will be recombined, and energy will be dissipated over the entire volume of atoms [16]. In contrast, the FP will be generated if the transferred recoil energy is ≥Ed. Because Ed tended to decrease from compression to tension, as described in Section 3.2, more FPs are generated with the tensile strain (Figure 3). Furthermore, if the tensile-strained structure is subjected to high PKA energy, the collided atoms rapidly move far away from the parent atoms, which reduces the chances of FPs recombination and results in a higher number of FPs. In comparison, once the structure is compressed, Ed increases, and atoms get closer to one another; hence the transferred energy equally distributes over a larger number of atoms, and more collisions occur without defect generation.

3.4. Effects of Strain on the Formation of Interstitial Dislocation Loop

The peak number of FPs under strain for various energies of PKA is plotted in Figure 4a. For simplicity, the average was taken for every four different PKA directions and four different timings at the center of the simulation cell; hence, each point of Figure 4 was averaged over 16 different individual simulations. The peak number of FPs increased when the tensile strain was applied. The SEM of each point is denoted by the error bars shown in Figure 4.
The number of survived FPs after equilibration time is paramount for estimating radiation damage effects. In Figure 4b, the number of survived FPs increased when the increasing tensile strain was applied, while the number of survived FPs decreased with compression strain. The number of survived FPs also increased for higher PKA energies. The number of survived FPs is comparable with the previous MD results conducted for iron at free strain conditions for 1 and 10 keV of PKA energies [11].
The nature of the cascade event and defect distribution after radiation damage is complex [44] and cannot be firmly explained for strain conditions because of the chaotic nature of the collision event. Hence, the prediction of the cascade evolution can be largely different due to its stochastic nature. Indeed, the 16 different sets of the simulation for each energy at a specific strain are averaged to minimize such complex nature. From these different simulation results, the chaos was naturally evident. At 10 keV with 4.8% of tensile strain, the unpredictable evolution of the primary damage has happened, as clearly shown in Figure 4a,b reveals that the defect generation significantly increased in nonlinear shape. Based on a deep analysis of the possible causes behind this sharp increase, we found that this was due to the interstitial dislocation loop formation at peak time. During the peak time, the interstitial dislocation loop formed as a result of interstitial accumulation in a more stable form than mono interstitial defects. Thus, the number of survived FPs reported in Figure 4a includes the number of FPs incorporated into interstitial dislocation loops.
Using the DXA algorithm of the OVITO code [31], we observed that several interstitial dislocation loops occurred at relatively low energies and high strains. The number of interstitial dislocation loops and lengths changed by the collision direction, timings, strain, and energy change. The interstitial dislocation loops are presented in Figure 4c, where the dislocation lines show that no embedded atoms interfere with the cluster point defects, and it is evident that the defects generated were of two types: mono-defects (vacancy/interstitials) and interstitial dislocation loops.
The dislocation occurrence probability among the 16 simulation sets is summarized in Table 1, and we found that only one type of interstitial dislocation loop was formed, which was ½<111>. The probability of ½<111> dislocation loops occurrence is 43% at 6 and 10 keV, while it is 0% at 1 keV. The formation energy of seven atoms length interstitial dislocation loop was compared to that of a seven-single SIA, wherein interstitial dislocation loop formation energy decreased by approximately 2 eV but increased at larger tensile strains (Figure 5). The 7-time formation energy of the <110> SIA dumbbell (single isolated <110>) (Figure S7) was also compared with the interstitial dislocation formation and showed a similar trend for energy formation behavior with Figure 5.
Herein, we confirm that the energy cutoff of interstitial loop observation is de- creased due to strain effects. Hence, we introduce the probability of ½<111> dislocation formation even at lower energies and lower atomic masses of PKA under high tensile strain values. Obviously, an increase in the PKA recoil energy under local tensile strains can augment the probability of the nucleation of several interstitial loops and different dislocation types.
Recently, C15 interstitial clusters were theoretically shown to be stable at small size in Fe bcc [41,42,43]; although a close investigation for C15 clusters was performed, the stability of this cluster could not be observed by the DD-BN EAM potential used in our study. However, C15 clusters exist with a low fraction (1–6%) at relatively high PKA energy [45], and ½<111> dislocation loops were also one of the stable clusters form. While of the current work, ½<111> dislocation loops were only observed at high tensile strain; hence, considering the formation of small size C15 cluster would not significantly affect our main conclusions. However, C15 clusters could be observed if another potential model of well-defined C15 clusters is used, and further info could be obtained.

3.5. Additional Analysis: Defect Production Efficiency under Strain

The defect production efficiency is defined as the ratio between the numbers of the theoretically evaluated FPs to those evaluated by MD. The defect production efficiency is defined as NFP/NNRT, as shown in Figure 6a, while Figure 6b is the deformed NRT dis- placements (i.e., the estimated number of FPs by the NRT theoretical model and the value of the Ed,j (∆V) -substituted form E d , a v g s t r a i n e d in Figure 2b). Figure 6a shows the defect production efficiency for strained conditions as a function of PKA energy; defect production efficiency showed similar trends for all strain conditions at 1 and 3 keV; this relation was disturbed at larger PKA energies (especially for 10 keV). In general, the defect production efficiency decreases as PKA increases (from 1~6 keV). However, for 10 keV and under larger tensile strains, the efficiency relation starts to increase. This is because the dislocation loop formation generates further defects, as clarified in Section 3.4 thereby, the efficiency increased again. This shows the sensitivity and complexity nature of the collision events and defect formation and confirms the inconsistency between the theoretical linear relation of the NRT model and the experimental results. Accordingly, the need for the NRT model development was recently suggested by Norland [46].

4. Conclusions

Application of strain reduces the PKA energy required to form an interstitial dislocation loop. Under high tensile strain, the ½<111> interstitial dislocation loop is formed at PKA energies as low as 3 keV. The reason behind this formation at lower PKA energies is due to the decrement of Ed when moving from compression to tension. Hence, more interstitials are likely to accumulate from the FPs at peak time. From the accumulated FPs, the formation energy of the interstitial dislocation loop becomes more stable with a 2 eV reduction compared with the mono interstitial formation energy under tensile strain. In addition, the formation energy of the interstitial dislocation loop, and E d , a v g s t r a i n e d can be directly used for theoretical models, such as evaluating defect formation by use of the NRT model, which can also be useful for multiscale modeling work.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4352/11/3/317/s1, Figure S1: a comparative study for the interstitial formation energies of current molecular dynamic study (MD) study potential model with the density functional theory (DFT) calculations at free strain, Figure S2: comparative study of the directional threshold displacement energy (Ed,i) of the current MD study with the DFT study, Figure S3: the system size and shape effect on the Ed,avg evaluation by MD, Figure S4: the angle deviation of Ed,i from the <100>, <110>, <111>, and <321> directions, Figure S5: (a) 210 ICD directions applied to generate 210 Ed,i by applying the Seeger theoretical model. (b) The Seeger and the MD differences for Ed,i calculation (ΔEd,I = Ed,i, theory of each value of 210 ICD − Ed,i, MD), Figure S6: The threshold displacement energy change rate (TCR) when structure deformed for 300 specific directions at 30 K. (a) is for uniaxial tensile strain and (b) is for uniaxial compression strain, Figure S7: the formation energy of ½<111> dislocation loop with 7 SIAs and as compared with single <110> defects x 7, Table S1: the comparison of the MD and DFT directional threshold displacement energy (Ed,i) ( i = <100>, <110> and <111>) and the average threshold displacement energy (Ed,avg) values referenced to the experiential results, Table S2: Ed,i values for <111> direction with several supercells in the 0 K recoil simulation.

Author Contributions

Conceptualization, M.B.S. and M.J.B.; methodology, M.B.S.; software, M.B.S.; validation, M.B.S., M.J.B.; formal analysis, M.B.S.; investigation, M.J.B.; resources, M.J.B.; data curation, M.J.B.; writing—original draft preparation, M.B.S.; M.E.K.; writing—review and editing, M.B.S.; M.E.K.; visualization, M.B.S.; M.E.K.; supervision, M.J.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kilic, M.E.; Alaei, S. Structural properties of β-Fe2O3 nanorods under compression and torsion: Molecular dynamics simulations. Curr. Appl. Phys. 2018, 18, 1352–1358. [Google Scholar] [CrossRef]
  2. Crocombette, J.-P.; Willaime, F. Ab Initio Electronic Structure Calculations for Nuclear Materials; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
  3. Stoller, R.E. Point defect survival and clustering fractions obtained from molecular dynamics simulations of high energy cascades. J. Nucl. Mater. 1996, 233-237, 999–1003. [Google Scholar] [CrossRef] [Green Version]
  4. Bacon, D.J.; Calder, A.F.; Harder, J.M.; Wooding, S.J. Computer simulation of low-energy displacement events in pure bcc and hcp metals. J. Nucl. Mater. 1993, 205, 52–58. [Google Scholar] [CrossRef]
  5. Gao, F.; Bacon, D.; Calder, A.; Flewitt, P.; Lewis, T. Computer simulation study of cascade overlap effects in α-iron. J. Nucl. Mater. 1996, 230, 47–56. [Google Scholar] [CrossRef]
  6. Gao, F.; Bacon, D.; Flewitt, P.; Lewis, T. A molecular dynamics study of temperature effects on defect production by displacement cascades in α-iron. J. Nucl. Mater. 1997, 249, 77–86. [Google Scholar] [CrossRef]
  7. Becquart, C.S.; Decker, K.M.; Domain, C.; Ruste, J.; Souffez, Y.; Turbatte, J.C.; Van Duysen, J.C. Massively parallel molecular dynamics simulations with EAM potentials. Radiat. Eff. Defects Solids 1997, 142, 9–21. [Google Scholar] [CrossRef]
  8. Stoller, R.E.; Greenwood, L.R. Subcascade formation in displacement cascade simulations: Implications for fusion reactor materials. J. Nucl. Mater. 1999, 271-272, 57–62. [Google Scholar] [CrossRef]
  9. Malerba, L. Molecular dynamics simulation of displacement cascades in α-Fe: A critical review. J. Nucl. Mater. 2006, 351, 28–38. [Google Scholar] [CrossRef]
  10. Phythian, W.; Stoller, R.; Foreman, A.; Calder, A.; Bacon, D. A comparison of displacement cascades in copper and iron by molecular dynamics and its application to microstructural evolution. J. Nucl. Mater. 1995, 223, 245–261. [Google Scholar] [CrossRef]
  11. Vascon, R.; Doan, N.V. Molecular dynamics simulations of displacement cascades in α-iron. Radiat. Eff. Defects Solids 1997, 141, 375–394. [Google Scholar] [CrossRef]
  12. Averback, R.; DE LA Rubia, T.D. Displacement Damage in Irradiated Metals and Semiconductors; Academic Press: Cambridge, MA, USA, 1997. [Google Scholar] [CrossRef]
  13. Soneda, N.; De La Rubia, T.D. Defect production, annealing kinetics and damage evolution in α-Fe: An atomic-scale computer simulation. Philos. Mag. A 1998, 78, 995–1019. [Google Scholar] [CrossRef]
  14. Robinson, M.; Marks, N.A.; Lumpkin, G.R. Sensitivity of the threshold displacement energy to temperature and time. Phys. Rev. B 2012, 86, 1–8. [Google Scholar] [CrossRef]
  15. Psakhie, S.G.; Zolnikov, K.P.; Kryzhevich, D.S.; Zheleznyakov, A.V.; Chernov, V.M. Evolution of atomic collision cascades in vanadium crystal with internal structure. Crystallogr. Rep. 2009, 54, 1002–1010. [Google Scholar] [CrossRef]
  16. Was, G.S. Fundamentals of Radiation Materials Science: Metals and Alloys; Springer: Heidelberg, Germany, 2016. [Google Scholar]
  17. R. Bullough Atomic Energy Research Establishment Harwell Berkshire England; Eyre, B.L.; Perrin, R.C. The Growth and Stability of Voids in Irradiated Metals. Nucl. Appl. Technol. 1970, 9, 346–355. [Google Scholar] [CrossRef]
  18. Masters, B.C. Dislocation loops in irradiated iron. Philos. Mag. 1965, 11, 881–893. [Google Scholar] [CrossRef]
  19. Dudarev, S.L.; Bullough, R.; Derlet, P.M. Effect of theα−γPhase Transition on the Stability of Dislocation Loops in bcc Iron. Phys. Rev. Lett. 2008, 100, 135503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Yao, Z.; Jenkins, M.; Hernández-Mayoral, M.; Kirk, M. The temperature dependence of heavy-ion damage in iron: A microstructural transition at elevated temperatures. Philos. Mag. 2010, 90, 4623–4634. [Google Scholar] [CrossRef]
  21. Arakawa, K.; Ono, K.; Isshiki, M.; Mimura, K.; Uchikoshi, M.; Mori, H. Observation of the One-Dimensional Diffusion of Nanometer-Sized Dislocation Loops. Science 2007, 318, 956–959. [Google Scholar] [CrossRef] [Green Version]
  22. Kaletta, D. The Role of Gases in Radiation Damage Patterns; Kernforschungszentrum Karlsruhe, Kaletta Institut für Material- und Festkörperforschung: Karlsruhe, Germany, 1979. [Google Scholar]
  23. Barrow, A.; Korinek, A.; Daymond, M. Evaluating zirconium–zirconium hydride interfacial strains by nano-beam electron diffraction. J. Nucl. Mater. 2013, 432, 366–370. [Google Scholar] [CrossRef]
  24. Norgett, M.; Robinson, M.; Torrens, I. A proposed method of calculating displacement dose rates. Nucl. Eng. Des. 1975, 33, 50–54. [Google Scholar] [CrossRef]
  25. Banisalman, M.J.; Park, S.; Oda, T. Evaluation of the threshold displacement energy in tungsten by molecular dynamics calculations. J. Nucl. Mater. 2017, 495, 277–284. [Google Scholar] [CrossRef]
  26. Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
  27. Dudarev, S.L.; Derlet, P.M. A ‘magnetic’ interatomic potential for molecular dynamics simulations. J. Phys. Condens. Matter 2005, 17, 7097–7118. [Google Scholar] [CrossRef]
  28. Björkas, C.; Nordlund, K.; Dudarev, S. Modelling radiation effects using the ab-initio based tungsten and vanadium potentials. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interactions Mater. Atoms. 2009, 267, 3204–3208. [Google Scholar] [CrossRef]
  29. Rycroft, C.H. VORO++: A three-dimensional Voronoi cell library in C++. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 041111. [Google Scholar] [CrossRef] [Green Version]
  30. Robinson, M.; Marks, N.A.; Whittle, K.R.; Lumpkin, G.R. Systematic calculation of threshold displacement energies: Case study in rutile. Phys. Rev. B 2012, 85, 104105. [Google Scholar] [CrossRef]
  31. Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 15012. [Google Scholar] [CrossRef]
  32. Olsson, P.; Becquart, C.S.; Domain, C. Ab initio threshold displacement energies in iron. Mater. Res. Lett. 2016, 4, 219–225. [Google Scholar] [CrossRef] [Green Version]
  33. Park, S.; Banisalman, M.J.; Oda, T. Characterization and quantification of numerical errors in threshold displacement energy calculated by molecular dynamics in bcc-Fe. Comput. Mater. Sci. 2019, 170, 109189. [Google Scholar] [CrossRef]
  34. Setyawan, W.; Selby, A.P.; Juslin, N.; Stoller, R.E.; Wirth, B.D.; Kurtz, R.J. Cascade morphology transition in bcc metals. J. Physics: Condens. Matter 2015, 27, 225402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Wechsler, M.S.; Lin, C.; Sommer, W.F.; Daemen, L.U.L.; Feguson, P.D. Standard Practice for Neutron Radiation Damage Simulation by Charged-Particle Irradiation; ASTM Stand E 521-96; ASTM International: West Conshohocken, PA, USA, 1996. [Google Scholar] [CrossRef]
  36. Maury, F.; Biget, M.; Vajda, P.; Lucasson, A.; Lucasson, P. Anisotropy of defect creation in electron-irradiated iron crystals. Phys. Rev. B 1976, 14, 5303–5313. [Google Scholar] [CrossRef]
  37. Jan, R.V.; Seeger, A. Zur Deutung der Tieftemperatur-Elektronenbestrahlung von Metallen. Phys. Status Solidi 1963, 3, 465–472. [Google Scholar] [CrossRef]
  38. Banisalman, M.J.; Oda, T. Atomistic simulation for strain effects on threshold displacement energies in refractory metals. Comput. Mater. Sci. 2019, 158, 346–352. [Google Scholar] [CrossRef]
  39. Beeler, B.; Asta, M.; Hosemann, P.; Grønbech-Jensen, N. Effect of strain and temperature on the threshold displacement energy in body-centered cubic iron. J. Nucl. Mater. 2016, 474, 113–119. [Google Scholar] [CrossRef] [Green Version]
  40. Beeler, B.; Asta, M.; Hosemann, P.; Grønbech-Jensen, N. Effects of applied strain on radiation damage generation in body-centered cubic iron. J. Nucl. Mater. 2015, 459, 159–165. [Google Scholar] [CrossRef] [Green Version]
  41. Wang, H.; Guo, G.-Y. Gradient-corrected density functional calculation of structural and magnetic properties of BCC, FCC and HCP Cr. J. Magn. Magn. Mater. 2000, 209, 98–99. [Google Scholar] [CrossRef]
  42. Kittel, C. Intro to Solid State Physics, 7th ed.; Wiley: New York, NY, USA, 1996. [Google Scholar]
  43. Wang, D.; Gao, N.; Wang, Z.; Gao, X.; He, W.; Cui, M.; Pang, L.; Zhu, Y. Effect of strain field on displacement cascade in tungsten studied by molecular dynamics simulation. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms. 2016, 384, 68–75. [Google Scholar] [CrossRef]
  44. Calder, A.; Bacon, D.; Barashev, A.; Osetsky, Y. On the origin of large interstitial clusters in displacement cascades. Philos. Mag. 2010, 90, 863–884. [Google Scholar] [CrossRef]
  45. Granberg, F.; Byggmästar, J.; Nordlund, K. Defect accumulation and evolution during prolonged irradiation of Fe and FeCr alloys. J. Nucl. Mater. 2020, 528, 151843. [Google Scholar] [CrossRef]
  46. Nordlund, K.; Zinkle, S.J.; Sand, A.E.; Granberg, F.; Averback, R.S.; Stoller, R.; Suzudo, T.; Malerba, L.; Banhart, F.; Weber, W.J.; et al. Improving atomic displacement and replacement calculations with physically realistic damage models. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef]
Crystals 11 00317 g001 550
Figure 1. Description of uniaxial and hydrostatic strain applications. The integrated table shows the variations in cell constants and volumes of free strained values (x0, y0, z0, V0) with a Δ of strain for each strain type.
Figure 1. Description of uniaxial and hydrostatic strain applications. The integrated table shows the variations in cell constants and volumes of free strained values (x0, y0, z0, V0) with a Δ of strain for each strain type.
Crystals 11 00317 g001
Crystals 11 00317 g002 550
Figure 2. (a) Uniaxial and a hydrostatic correlation between E d , a v g s t r a i n e d and strain changes in α-Fe. (b) Correlation between uniaxial and hydrostatic strain changes for E d , a v g s t r a i n e d as volume change. Every single point is the average value of over 300 quasi-uniform directions.
Figure 2. (a) Uniaxial and a hydrostatic correlation between E d , a v g s t r a i n e d and strain changes in α-Fe. (b) Correlation between uniaxial and hydrostatic strain changes for E d , a v g s t r a i n e d as volume change. Every single point is the average value of over 300 quasi-uniform directions.
Crystals 11 00317 g002
Crystals 11 00317 g003 550
Figure 3. The evolution of as Frenkel pairs (FPs) created during the displacement cascade of 10 keV as volume change. Each point is the average of overall direction and timing, i.e., 16 different samples. A similar thermal spike trend for all given PKA energies was noticed; hence the typical behavior of damage evolution over time was shown with 10 keV.
Figure 3. The evolution of as Frenkel pairs (FPs) created during the displacement cascade of 10 keV as volume change. Each point is the average of overall direction and timing, i.e., 16 different samples. A similar thermal spike trend for all given PKA energies was noticed; hence the typical behavior of damage evolution over time was shown with 10 keV.
Crystals 11 00317 g003
Crystals 11 00317 g004 550
Figure 4. (a) The peak number of FP under strain conditions for primary knock-on atom (PKA) energies (1, 3, 6, and 10) keV as a function of hydrostatic strain (b) number of survived FP after 20 ps, the black–box shows the ½<111> dislocation formation for <110> displacement collision direction at 10 keV. The error bar denotes the SEM over the selected samples (c) Analysis of the ½<111> dislocation configuration and defect formation.
Figure 4. (a) The peak number of FP under strain conditions for primary knock-on atom (PKA) energies (1, 3, 6, and 10) keV as a function of hydrostatic strain (b) number of survived FP after 20 ps, the black–box shows the ½<111> dislocation formation for <110> displacement collision direction at 10 keV. The error bar denotes the SEM over the selected samples (c) Analysis of the ½<111> dislocation configuration and defect formation.
Crystals 11 00317 g004
Crystals 11 00317 g005 550
Figure 5. The formation energy of 7 self-interstitial atoms (SIAs) defects as a function of compression and tensile strain is denoted in black. The formation energy of ½<111> dislocation loop with 7 SIAs is denoted in blue. The energy difference between 7 SIAs defects and ½<111> dislocation loop is denoted in green.
Figure 5. The formation energy of 7 self-interstitial atoms (SIAs) defects as a function of compression and tensile strain is denoted in black. The formation energy of ½<111> dislocation loop with 7 SIAs is denoted in blue. The energy difference between 7 SIAs defects and ½<111> dislocation loop is denoted in green.
Crystals 11 00317 g005
Crystals 11 00317 g006 550
Figure 6. (a) The defect production efficiency, which is defined as the ratio between the molecular dynamics (MD) and the Norgett–Robinson–Torrens (NRT) result for defect calculations. (b) Number of surviving Frenkel pairs for various PKA energies versus applied and hydrostatic strain from NRT model applications VNRT = 0.8 × Epka/2 Edj(∆V) [36].
Figure 6. (a) The defect production efficiency, which is defined as the ratio between the molecular dynamics (MD) and the Norgett–Robinson–Torrens (NRT) result for defect calculations. (b) Number of surviving Frenkel pairs for various PKA energies versus applied and hydrostatic strain from NRT model applications VNRT = 0.8 × Epka/2 Edj(∆V) [36].
Crystals 11 00317 g006
Table
Table 1. Dislocation occurrence probability (i.e., how many times dislocation appeared among the 16 different simulation sets). The only formed dislocation was ½<111> type.
Table 1. Dislocation occurrence probability (i.e., how many times dislocation appeared among the 16 different simulation sets). The only formed dislocation was ½<111> type.
PKA Energy (keV)Probability Occurrence of ½<111> Dislocation Loops among the 16 Sets at 4.8% of Volume Change
10
31/16
67/16
107/16
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Bany Salman, M.; Emin Kilic, M.; Jaser Banisalman, M. Formation of Interstitial Dislocation Loops by Irradiation in Alpha-Iron under Strain: A Molecular Dynamics Study. Crystals 2021, 11, 317. https://doi.org/10.3390/cryst11030317

AMA Style

Bany Salman M, Emin Kilic M, Jaser Banisalman M. Formation of Interstitial Dislocation Loops by Irradiation in Alpha-Iron under Strain: A Molecular Dynamics Study. Crystals. 2021; 11(3):317. https://doi.org/10.3390/cryst11030317

Chicago/Turabian Style

Bany Salman, Mohammad, Mehmet Emin Kilic, and Mosab Jaser Banisalman. 2021. "Formation of Interstitial Dislocation Loops by Irradiation in Alpha-Iron under Strain: A Molecular Dynamics Study" Crystals 11, no. 3: 317. https://doi.org/10.3390/cryst11030317

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop