Abstract
The Ce2Fe14B intermetallic, like Nd2Fe14B, has the tetragonal Nd2Fe14B-type structure (space group P42/mnm), in which Ce ions have a mixed-valence state characterized by the coexistence of trivalent 4f1 and tetravalent 4f0 electron states. Despite the fact that the saturation magnetization, magnetic anisotropy field, and Curie temperature of the Ce2Fe14B intermetallic are substantially lower than those of Nd2Fe14B and Pr2Fe14B, Ce2Fe14B retains the capacity of being able to be used in the manufacturing of rare-earth permanent magnets. Moreover, at low temperatures, the anisotropy field of Се2Fe14B is higher than that of Nd2Fe14B, and Се2Fe14B does not undergo the spin-reorientation transition. In this respect, studies of (Nd, Ce)-Fe-B alloys, which are intended for the improvement of the service characteristics-to-cost ratio, are very relevant. A model and algorithm for calculating the hysteresis loops of uniaxial hard magnetic materials with allowance for the K1 and K2 (K2 > 0 and K1 > 0 and K1 < 0) magnetic anisotropy constants were developed and allowed us to obtain data on their effect on the parameters of hysteresis loops for a wide temperature range (0–300 K). The simulation and analysis of hysteresis loops of the quasi-ternary intermetallics (Nd1−хСех)2Fe14B (х = 0–1) was performed. Results of the simulation indicate that the alloying of the Nd2Fe14B intermetallic with Ce to x = 0.94 (1) does not completely eliminate the negative effect of spin-reorientation phase transition on the residual magnetization of the (Nd1−хCeх)2Fe14B intermetallic and (2) slightly decreases the slope of magnetization reversal curve.
1. Introduction
In recent years, the low cost of Ce-containing Nd-Fe-B permanent magnets, in some areas being a potential alternative to those based on expensive rare-earth elements (Nd, Pr, Dy, Tb), has stimulated considerable research efforts [1,2].
Similar to the other R-Fe-B systems, the Ce-Fe-B system is characterized by the formation of the ternary intermetallic compound having a 2:14:1 stoichiometry and tetragonal Nd2Fe14B-type structure (space group P42/mnm) [3]. The unit cell contains four formula units comprising 68 atoms: there are six crystallographic iron sites (16k1, 16k2, 8j1, 8j2, 4c, 4e), two rare-earth metal sites (4f, 4g), and one boron site (4g). Table 1 shows the lattice parameters of the R2Fe14B compounds with R = Nd, Pr, and Ce and their principal magnetic characteristics. This shows that both the a and c lattice parameters of the Ce2Fe14B compound are slightly lower than those of the Nd2Fe14B and Pr2Fe14B compounds [4].

Table 1.
Saturation magnetization Is, magnetic anisotropy field HA, lattice parameters a and c, and Curie temperature TC of the R2Fe14B compounds with R = Ce, Pr, Nd at room temperature.
The anisotropy of the Nd2Fe14B compound is dominated by the rare-earth atoms that occupy two inequivalent sites, 4f and 4g, of the tetragonal structure [8,9]. One Nd site (g) strongly prefers the [001] direction at ambient temperature and dictates the macroscopic easy-axis direction. The other Nd site (f) (containing half of all the Nd atoms) reduces the intrinsic stability by favoring alignment along [110]-type directions (basal plane). The results indicate that coercivity may be enhanced by preferential chemical doping of Nd f sites. Nd2Fe14B is characterized by the uniaxial state at temperatures above the spin-reorientation temperature Tsr. Ce2Fe14B exhibits the uniaxial magnetic anisotropy over the whole temperature range of ferromagnetic ordering [10]. Its uniaxial anisotropy is higher than that of R2Fe14B with R =La, Lu, Y [10], but lower than that of Nd2Fe14B at temperatures substantially higher than the spin-reorientation temperature. It was predicted [11] that, theoretically, Ce atoms in the (Nd1−xCex)2Fe14B compounds occupy the 4g positions (large in volume); this is explained by atomic size effects. However according to [8], 4f position (smaller in volume) is preferred for the Ce atoms.
Taking into account the fact that Ce prefers 4f positions, the progressive substitution of Ce for Nd should decrease the easy magnetization axis (EMA) cone opening. Thus, the formation of a uniaxial state can occur even in the presence of a small amount of Nd in (Nd1−xCex)2Fe14B. At present, no experimental data confirming the assumption are available. In turn, when assuming that Ce atoms prefer 4g positions, it is possible to conclude that the cone opening will be smaller for low substitutions of Ce for Nd. Because of this, Tsr varies slightly for low Ce contents. A small change in Tsr for the Ce substitution to x = 0.3 was observed in [12]. According to the data from [8], the magnetocrystalline anisotropy of Nd2Fe14B remains when Ce substitutes for Nd up to 20%. The further increase in the Ce content decreases the uniaxial magnetic anisotropy energy.
The uniaxial anisotropy found in Ce2Fe14B is attributed mainly to the magnetism of Fe [8]. Alloying Ce on R-sites in (Nd1−xCex)2Fe14B barely affects the Fe moments. Nd magnetization changes orientation at x > 0.5, with a larger antiferromagnetic moment on 4f sites compared to 4g sites. Such a transition of the Nd magnetic state causes an overall reduction of the net magnetization of the cell, and is the reason for instability at higher percentage Ce [11]. The magnetic moment of rare-earth sublattice is mainly determined by Nd atoms. The temperature behavior of magnetization of R2Fe14B with R = Nd, Ce was studied in [12].
The metallurgical behavior, heat treatment conditions, fundamental characteristics, and magnetic properties of the Nd2Fe14B and Ce2Fe14B intermetallics differ substantially although the compounds have the same crystal structure. The existence of the CeFe2 phase determines the principal difference in the ternary Nd-Fe-B and Ce-Fe-B phase diagrams [3,13]. Cerium ions in the Ce2Fe14B intermetallic have a mixed-valence state, namely, the trivalent 4f1 and tetravalent 4f0 electron states coexist [14].
According to data from [15], the hysteretic properties of Nd-Ce-Fe-B magnets decrease as the Ce content increases. However, the squareness of the magnetization reversal curve remains high [16,17,18], and the magnetic characteristics remain adequate when the Ce content does not exceed 10%.
Usually, it is assumed that the decrease in the magnetic characteristics of Ce-containing Nd2Fe14B alloys is due to the lower magnetic properties of Ce2Fe14B as compared to those of Nd2Fe14B (see Table 1). However, according to data from [18,19], an anomalous increase in the coercive force was found by studying the effect of Ce substitution for Nd on the magnetic properties and microstructure of sintered magnets. Pathak et al. [20] reported that the substitution of 20% Ce for Nd in the ternary Nd2Fe14B alloy allowed the authors to reach a sufficiently high coercive force (Hci = 10 kOe), which exceeds that of Nd2Fe14B (Hci = 8.3 kOe).
Currently, the development of high-coercivity, high-performance permanent magnets operating in a wide temperature range, in particular at low and cryogenic temperatures, is of importance. Nd-Fe-B magnets are unsuitable for operation at such temperatures. The EMA of the Nd2Fe14B compound at 4.2 K is in the [110] plane and makes the angle θ ≈ 30° with the c axis. As the temperature increases, the transition to the collinear structure takes place at the spin-reorientation temperature Tsr = 135–138 K [21]. Below this temperature, the magnetic moment deviates from the c axis, the first magnetic anisotropy constant K1 passes zero and changes the sign from positive to negative, whereas the second magnetic anisotropy constant remains positive (K2 > 0). As a result, below Tsr, the experimental magnetization reversal curves in negative magnetic fields exhibit a bending, which increases with decreasing temperature. In this case, the residual magnetization and maximum energy product decrease abruptly.
At room temperature, the magnetic properties of Се2Fe14B are substantially lower than those of Nd2Fe14B, whereas, at cryogenic temperatures, the magnetic anisotropy field of Се2Fe14B is markedly higher than that of Nd2Fe14B. Moreover, it is of importance that Ce2Fe14B does not have a spin-reorientation transition. Thus, it is reasonable to expect that the partial substitution of Ce for Nd in the Nd2Fe14B compound can lead to the improvement of the hysteretic characteristics of permanent magnets based on the quasi-ternary (Nd, Ce)2Fe14B intermetallics.
Data on the effect of Ce substitution for Nd on the spin-reorientation transition temperature of the Nd2−xСеxFe14B single crystals are available in [22], where the evolution of the spin-reorientation temperature as a function of the Ce concentration up to x = 0.4 is considered. The spin-reorientation temperature decreases by only about 6% when Ce substitutes for 38% of Nd. It is shown that Tsr is suppressed much more rapidly for higher x. It is likely that the population of REM sites (4g or 4f) is responsible for the spin-reorientation [22].
Taking into account the absence of systematic data on this problem in the literature, the present study is aimed at the simulation of hysteretic properties of the (Nd1−xCex)2Fe14B intermetallics in order to determine the optimum alloyed compositions. The simulation and analysis of hysteresis loops of the (Nd1−xCex)2Fe14B (x = 0–1) compounds are performed for a temperature range of 0 to 300 K.
2. Algorithm and Model for Calculating the Hysteresis Loops of Hard Magnetic Materials with the Uniaxial Tetragonal Lattice
The resulting magnetization vector Is at each point of a crystalline ferromagnet is simultaneously oriented along certain crystallographic directions (EMAs). In order to rotate Is to another direction, magnetic field H should be applied along this direction, and work should be done. This work makes sense of the anisotropy energy Еа, which, for magnets with the uniaxial tetragonal lattice, is given by the expression:
where К1 and К2 are the first and second magnetic anisotropy constants, respectively, and φa is the angle made by the EMA and Is. The anisotropy constants are proportional to the work, which should be done to rotate the magnetization from the EMA direction to the hard magnetization axis direction.
To take into account the cooperative effect of magnetic anisotropy and magnetic field, we considered a single crystal in the form of a plain disk oriented along a certain crystallographic plane. When the magnetic field is applied along the plane, the magnetization is also within the plane. It is assumed that the magnetization of the body is uniform and domains are absent.
When applying magnetic field Н, the position of Is also determined by the magnetic field energy:
where φH is the angle made by the vectors. In the end, Is takes a position corresponding to the minimum summary energy:
In terms of the model and algorithm [23] (program Hysteresis developed by Associate Prof. V.L. Stolyarov) used for the simulation of magnetic hysteresis loops of (Nd1−xCex)2Fe14B intermetallics with the uniaxial tetragonal lattice, the following initial parameters are inputted: α is the angle made by an arbitrary plane and the X-axis [100] and the external magnetic field H is applied in this plane, θH is the angle made by the H field direction and Z-axis [001]. The following parameters are counted and outputted: θ is the angle made by the Z-axis [0001] and EMA, φa is the angle made by the EMA and Is; and angle φH.
Calculation of the position of the magnetization vector Is for an arbitrary vector H, at which the total energy is minimal (Equation (3)), allows us to calculate the projection of the magnetization on the field direction I = Isсos(φH) and to construct the magnetization curve I = I(Н).
3. Results and Discussion
3.1. Determination of Magnetic Anisotropy Constants, Normalized Ratio of Anisotropy Constants (K2/|K1|), and Angle of the EMA cone in Calculating Hysteresis Loops of the (Nd1−x Cex)2Fe14B Intermetallics with 0 ≤ x ≤1
Temperature dependences of the magnetic anisotropy constants K1 and K2 of Nd2Fe14B in a temperature range of 0–500 K are available in [24]. The sign of K1 alternates at the spin-reorientation transition temperature Tsr = 135 K. Below this temperature, the preferred direction of EMA begins to deviate from the c axis direction (Z-axis [001]) of the tetragonal crystal lattice, and the angle (θ) of the EMA cone for each temperature is given by the expression:
At 4.2 K, this angle reaches ~30° [24].
The temperature dependences of the magnetic anisotropy constant K1 and K2 of Ce2Fe14B in a temperature range of 0–300 K are available in [25]. Unlike the magnetic anisotropy constants of Nd2Fe14B, K1 and K2 of Ce2Fe14B remain positive within the 0–300 К temperature range. The absolute values of K1 and K2 of Ce2Fe14B are substantially lower than those of Nd2Fe14B.
To calculate the anisotropy constants of the quasi-ternary intermetallics (Nd1−xCex)2Fe14B with 0 ≤ x ≤1 at different temperatures, the literature data on the anisotropy constants of Nd2Fe14B and Ce2Fe14B and the following linear expressions were used:
The ratio of anisotropy constants К2 to К1 and the θ angle (made by the EMA and c axis) were calculated by the expressions:
at
at
The following composition ranges of (Nd1−xCex)2Fe14B were considered: (1) x = 0, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75; (2) x = 0.80, 0.85; 0.90, 0.91, 0.92 and (3) x = 0.93, 0.94, 0.95, 0.96, 0.97, 0.98, 0.99, 1.00.
The calculated temperature dependences of the magnetic anisotropy constants, their ratio, and temperature dependences of the θ angle for (Nd1−x Cex)2Fe14B with x = 0.05, 0.90, and 0.97 are given in Figure 1, as an example. The compositional dependences of the spin-reorientation temperature (TSR) of (Nd1−xCex)2Fe14B are given in Figure 2.
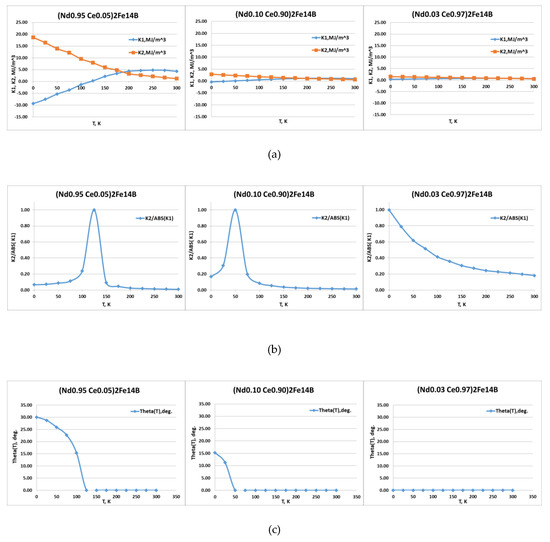
Figure 1.
Temperature dependences of the (a) К1 and К2 magnetic anisotropy constants, (b) normalized К2/|К1| ratio, and (c) θ angle for (Nd1−x Cex)2Fe14B with x = 0.05 (first composition range), 0.90 (second composition range), and 0.97 (third composition range).
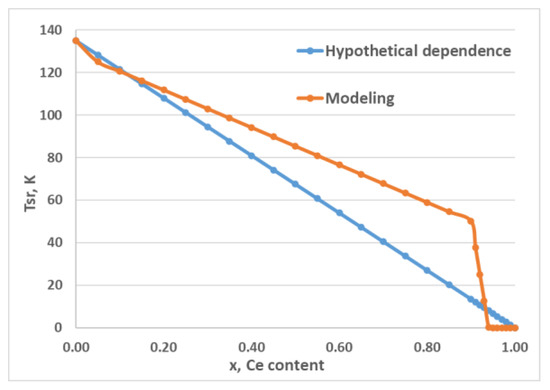
Figure 2.
Compositional dependences of spin-reorientation temperature (Tsr) of (Nd1−x Cex)2Fe14B: (blue) hypothetical (linear) trend and (red) results of simulation (this work).
It is seen from Figure 1 and Figure 2 that, as Ce substitutes for Nd in the range x = 0–0.75 (first composition range), the values of К1 and К2 constants decrease on average by ~75% and ~99%, respectively. The temperature corresponding to the maximum of the normalized К2/|К1| ratio decreases from 135 to 63 K. The temperature Tsr also decreases from 135 to 63 K. The highest value of the θ angle at 0 K decreases from 30.15° (x = 0) to 24.77° (x = 0.75).
As the Ce content in (Nd1−хCeх)2Fe14B increases in the range x = 0.80–0.92 (second composition range), the К1 and К2 values additionally decrease on average by ~61% and ~63%, respectively. In turn, the temperature corresponding to the maximum of normalized К2/|К1| ratio shifts from 59 to 25 K. The temperature Тsr also decreases from 59 to 25 K. The largest value of the θ angle at 0 K monotonically decreases from 23.12° (x = 0.80) to 11.03° (x = 0.92).
It is seen from the dependences given in Figure 1 and Figure 2 that, as the cerium content in the (Nd1−хCeх)2Fe14B intermetallic increases from x = 0.93 to x = 1.00, the anisotropy constant К2 additionally decreases by an average ~35%, whereas the К1 constant changes the sign from negative to positive. The Тsr temperature decreases from 13 to 0 K as the cerium content increases to x = 0.94. The temperature corresponding to the maximum of normalized К2/|К1| ratio also decreases from 13 to 0 K. The highest value of the θ angle at 0 K decreases from 7.34° to 0°(at x ≥ 0.94).
3.2. Simulation of Magnetization Curves and Hysteresis Loops of (Nd1−x Cex)2Fe14B with x = 0.00–1.00
The simulated hysteresis loops for (Nd1−x Cex)2Fe14B with x = 0–1.00 show that, as the applied magnetization reversing field reaches the coercive force Нc (at which the abrupt overturn of IS takes place), the decrease in the hysteresis loop squareness is observed; the “rounding” becomes more substantial as the temperature decreases. Below Тsr, the decrease starts in the positive fields. Figure 3 shows the temperature dependences of the normalized and unnormalized residual magnetization (Ir/Is and Ir) for the three composition ranges of the (Nd1−хCeх)2Fe14B compounds.
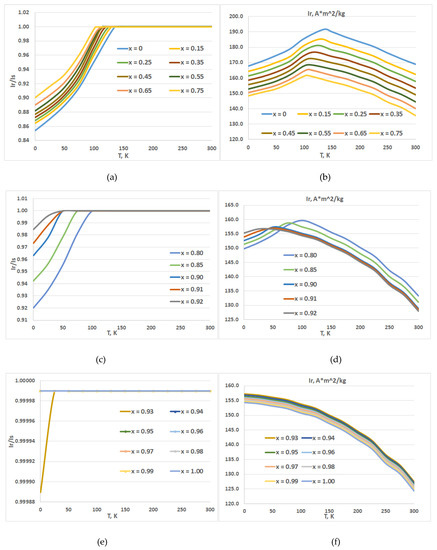
Figure 3.
Temperature dependences of the normalized and unnormalized residual magnetization (Ir/Is and Ir) of the (Nd1−хCeх)2Fe14B compounds with different x: (a) and (b) 0, 0.15, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75; (c) and (d) 0.80, 0.85, 0.90, 0.91, 0.92; (e) and (f) 0.93, 0.94, 0.95, 0.96, 0.97, 0.98, 0.99, 1.00.
For all quasi-ternary compositions, the Ir/Is ratio monotonically decreases with decreasing temperature. This is caused by the deviation of Is from the EMA in the applied magnetic field H and the transition to the EMA cone below Тsr. Only for the high-cerium contents (x ≥ 0.94), the Ir/Is ratio remains unchanged and equal to 0.9999 (<1.0000) for a certain temperature range.
For the composition range x = 0–0.75 (Figure 3a), as the temperature decreases from 300 K to Тsr(x), Ir/Is remains unchanged and equal to 0.9999 for all these compositions. This means that, after saturation, the magnetization remains parallel to the EMA and Z-axis as the external field decreases to zero. The monotonic progressive decrease in Ir/Is is observed simultaneously with decreasing temperature below Tsr(x) and Ce content x. For each Ce content x, the temperature dependences Ir(T, x) have the maximum value in the range of Тsr(x) (Figure 3b). The monotonic shift of the Ir maximum to low temperatures from Ir(T = 135 K, x = 0) =191.6 A m2/kg to Ir(T = 102 K, x = 0.75) = 161.5 A m2/kg correlates with a similar shift of the maximum of normalized K2/|K1| ratio and a decrease in Tsr(x) with increasing cerium content x (Figure 1 and Figure 2). The maximum in these dependences is related to the competition of two physical phenomena, such as the monotonic increase in the total magnetic moment of R2Fe14B intermetallics (where R = Nd or Ce) with decreasing temperature and the spin-reorientation below the Tsr temperature.
For the composition range x = 0.80–0.92 (Figure 3c), as the temperature decreases from 300 K to Тsr(x), Ir/Is remains equal to 0.9999 for all these compositions, i.e., the magnetization after saturation remains parallel to the EMA and Z-axis as the magnetizing field decreases to zero. The monotonic and progressive decrease in Ir/Is is observed with simultaneously decreasing temperature below Tsr(x) and Ce content x. For each Ce content x, the temperature dependences Ir(T, x) also have the maximum in the range of Тsr(x) (Figure 3d). The monotonic shift of the Ir maximum to the low temperature range from Ir(T = 100 K, x = 0.80) =159.6 A m2/kg to Ir(T = 25 K, x = 0.92) = 156.6 A m2/kg correlates with the similar shift of the normalized K2/|K1| ratio and a decrease in Tsr(x) with increasing cerium content x (Figure 1 and Figure 2). However, in this range of cerium concentrations, the temperature dependences of Ir overlap; the overlapping was not observed in the range x = 0–0.75 (Figure 3d). This interesting and anomalous change in Ir is also related to the “stronger” competition of a monotonic increase in the total magnetic moment of R2Fe14B intermetallics (where R = Nd or Ce) with decreasing temperature and the spin-reorientation below Tsr. Owing to the nature of the change in magnetic properties, the composition range x = 0.80–0.92 is intermediate between neodymium-based intermetallics and cerium-based intermetallics R2Fe14B.
Figure 3e shows the temperature dependences of the normalized residual magnetization for the third composition range of the (Nd1−хCeх)2Fe14B intermetallics with x = 0.93–1.00. As the temperature decreases from 300 K to 0 K, Ir/Is remains equal to 0.9999 for all alloys with x ≥ 0.94, i.e., after saturation, the magnetization remains parallel to the EMA and Z-axis as the magnetizing field decreases to zero. Only for the alloys with 0.93 ≤ x< 0.94, the monotonic and progressive decrease in Ir/Is is observed as the simultaneous decrease in temperature below Tsr(x) and decrease in the Ce concentration take place. As x increases from 0.94 to 1.00, the considered maximum of Ir shifts to zero and degenerates owing to the decreasing effect of the spin-reorientation. This effect also correlates with a similar shift of the normalized K2/|K1| ratio and a decrease in Tsr(x) with increasing cerium concentration x (Figure 1 and Figure 2).
The considered features of the change of the residual magnetization clearly manifest themselves in the concentration dependence at T = 0 K. Figure 4 shows that the composition range x = 0.80–0.92 is intermediate between neodymium-based intermetallics and cerium-based intermetallic R2Fe14B and is characterized by anomalous change in the residual magnetization.
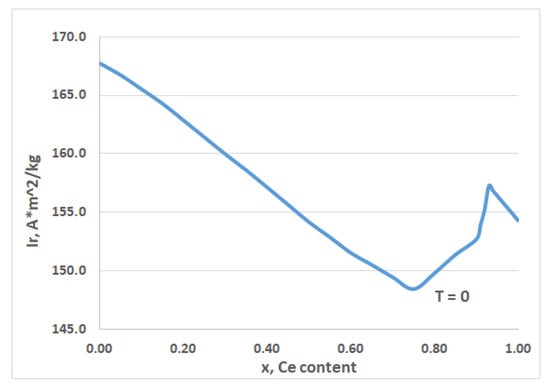
Figure 4.
Compositional dependence of the residual magnetization Ir for the (Nd1−хCeх)2Fe14B compounds at T = 0 K.
Figure 5 shows temperature dependences of the coercive force Нc of the (Nd1−хCeх)2Fe14B compounds with x = 0–1.00.
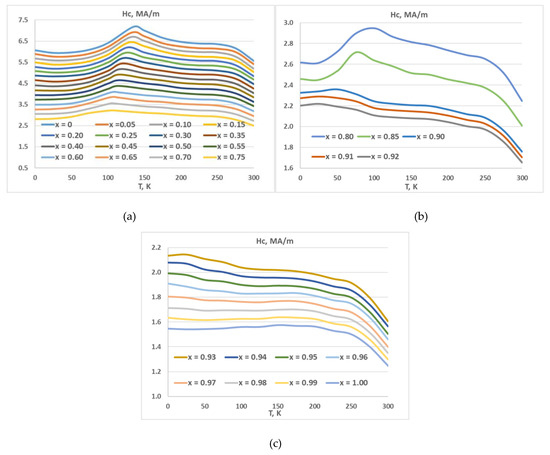
Figure 5.
Temperature dependences of the coercive force Нc of the (Nd1−хCeх)2Fe14B compounds with different x: (a) 0, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60, 0.65, 0.70, 0.75; (b) 0.80, 0.85, 0.90, 0.91, 0.92; and (c) 0.93, 0.94, 0.95, 0.96, 0.97, 0.98, 0.99, 1.00.
It is seen that, for each Ce content x = 0–0.75, the coercive force Нc reaches the maximum value in the range of Тsr(x) (Figure 5a). The monotonic shift of the Нc maximum to the low-temperature range from Нc(T = 135 K, x = 0) =7.2 MA/m to Нc(T = 102 K, x = 0.75) = 3.2 MA/m correlates with a similar shift of the maximum of normalized K2/|K1| ratio, shift of the maximum of Ir, and a decrease in Tsr(x) with increasing cerium concentration x (Figure 1 and Figure 3). The maximum in these dependences is related to the competition of two physical phenomena, such as the monotonic increase in the magnetic anisotropy field HA of R2Fe14B intermetallics (where R = Nd or Ce) with decreasing temperature and the spin-reorientation below Tsr, that facilitates the magnetization reversal process in an external magnetic field.
As is seen, for each Ce content x = 0.80–0.92 (Figure 5b), the coercive force Нc reaches the maximum value in a temperature range of Тsr(x). The monotonic shift of the Нc maximum to the low-temperature range from Нc(T = 100 K, x = 0.80) =2.9 MA/m to Нc(T = 25 K, x = 0.92) = 2.2 MA/m correlates with a similar shift of the maximum of the normalized K2/|K1| ratio, a shift of the maximum of IR, and a decrease in Tsr(x) with increasing cerium concentration x (Figure 1, Figure 2 and Figure 3).
For the compositions with x = 0.93–0.94 (Figure 5c), the maximum of Hc progressively shifts from 25 to ~10 K. For x > 0.94, the maximum shifts to 0 K and degenerates. This effect also correlates with a similar shift of the normalized K2/|K1| ratio, shift of the maximum of Ir, and a decrease in Tsr(x) with increasing cerium concentration x (Figure 1 and Figure 3).
4. Conclusions
The following are our conclusions, which are inferred based on the data obtained in simulating the magnetization reversal process of the (Nd1−хCeх)2Fe14B compounds with х = 0–1.00 and their hysteresis loops in a wide temperature range of 300 to 0 K.
1. The model and algorithm developed for simulating the hysteresis loops of ferromagnets allow us to obtain important data on the effect of uniaxial tetragonal lattice, magnetic anisotropy parameters, and temperature dependences of the magnetic anisotropy constants on the characteristics of hysteresis loops (anisotropy field, residual magnetization, the shape of the hysteresis loop, and coercive force) in a wide temperature range.
2. Results of the simulation indicate that alloying of Nd2Fe14B with cerium to its contents x = 0.94 (1) does not lead to the complete elimination of the negative effect of spin-reorientation phase transition on the residual magnetization of the (Nd1−х Ceх)2Fe14B compounds and (2) slightly decreases the slope of the magnetization curve and almost does not lead to the improvement of the squareness of the back of hysteresis loop.
3. The alloying of (Nd1−хCeх)2Fe14B with cerium to its contents x = 0.94 does not allow the temperature stability of hysteretic characteristics of (Nd1−хCeх)2Fe14B-based permanent magnets to be increased in order to ensure their operation at low temperatures without losing magnetic properties.
Author Contributions
Conceptualization, N.B.K. and A.G.S.; methodology and calculations M.V.Z.; formal analysis, Y.S.K. and J.Ć.; data curation, V.P.M.; visualization, N.A.D.; writing—original draft preparation, N.B.K. and M.V.Z.; writing—review and editing, N.B.K.; writing, K.S., M.K., and P.A.P.; project administration, G.S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Ministry of Science and Higher Education of the Russian Federation, agreement no. 05.604.21.0244, unique identification no RFMEFI60419X0244.
Acknowledgments
The authors thank Associate V.L. Stolyarov (National University of Science and Technology MISiS) for his assistance in the program Hysteresis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, Z.; Liu, W.; Zha, S.; Li, Y.; Wang, Y.; Zhang, D.; Yue, M.; Zhang, J.; Huang, X. Effects of Ce substitution on the microstructures and intrinsic magnetic properties of Nd–Fe–B alloy. J. Mag. Mag. Mater. 2015, 393, 551–554. [Google Scholar] [CrossRef]
- Zhao, L.; Li, C.; Hao, Z.; Liu, X.; Liao, X.; Zhang, J.; Su, K.; Li, L.; Yu, H.; Greneche, J.-M.; et al. Influences of element segregation on the magnetic properties in nanocrystalline Nd-Ce-Fe-B alloys. Mater. Charact. 2019, 148, 208–213. [Google Scholar] [CrossRef]
- Raghavan, V. The B-Ce-Fe (Boron-Cerium-Iron) System. In Phase Diagrams of Ternary Iron Alloys; Indian Institute of Metals: Kolkata, India, 1992; Volume 6A, pp. 297–300. [Google Scholar]
- Herbst, J.F. R2Fe14B materials: Intrinsic properties and technological aspects. Rev. Mod. Phys. 1991, 63, 819–898. [Google Scholar] [CrossRef]
- Hirosawa, S.; Matsuura, Y.; Yamamoto, H.; Fujimura, S.; Sagawa, M.; Sagawa, M.; Yamauchi, H. Magnetization and magnetic anisotropy of R2Fe14B measured on single crystals. J. Appl. Phys. 1986, 59, 873–879. [Google Scholar] [CrossRef]
- Fruchart, R.; L’Heritier, P.; Dalmas de Reotier, P.; Fruchart, D.; Wolfers, P.; Coey, J.M.D.; Ferreira, L.P.; Guillen, R.; Vulliet, P.; Yaouanc, A. Mossbauer spectroscopy of R2Fe14B. J. Phys. F Met. Phys. 1987, 17, 483–502. [Google Scholar] [CrossRef]
- Grössinger, R.; Sun, X.K.; Eibler, R.; Buschow, K.H.J.; Kirchmayr, H.R. Temperature dependences of anisotropy fields and initial susceptibilities in R2Fe14B compounds. J. Magn. Magn. Mater. 1986, 58, 55–60. [Google Scholar] [CrossRef]
- Haskel, D.; Lang, J.C.; Islam, Z.; Cady, A.; Srajer, G.; van Veenendaal, M.; Canfield, P.C. Atomic Origin of Magnetocrystalline Anisotropy in Nd2Fe14B. Phys. Rev. Lett. 2005, 95, 217207. [Google Scholar] [CrossRef]
- Colin, C.V.; Ito, M.; Yano, M.; Dempsey, N.M.; Suard, E.; Givord, D. Solid-solution stability and preferential site occupancy in (R-R′)2Fe14B compounds. Appl. Phys. Lett. 2016, 108, 242415. [Google Scholar] [CrossRef]
- Bolzoni, F.; Gavigan, J.P.; Givord, D.; Li, H.S.; Moze, O.; Pareti, L. 3d magnetism in R2Fe14B compounds. J. Magn. Magn. Mater. 1987, 66, 158. [Google Scholar] [CrossRef]
- Alam, A.; Khan, M.; McCallum, R.W.; Johnson, D.D. Site-preference and valency for rare-earth sites in (R-Ce)2Fe14B magnets. Appl. Phys. Lett. 2013, 102, 042402. [Google Scholar] [CrossRef]
- Abache, C.; Oesterreicher, J. Magnetic anisotropies and spin reorientations of R2Fe14B-type compounds. J. Appl. Phys. 1986, 60, 3671. [Google Scholar] [CrossRef]
- Hallemans, B.; Wollants, P.; Roos, J.R. Thermodynamic assessment of the Fe-Nd-B phase diagram. J. Phase Equilib. 1995, 16, 137–149. [Google Scholar] [CrossRef]
- Li, Z.B.; Shen, B.G.; Zhang, M.; Hu, F.X.; Sun, J.R. Substitution of Ce for Nd in preparing R2Fe14B nanocrystalline magnets. J. Alloy Compd. 2015, 628, 325–328. [Google Scholar] [CrossRef]
- Wang, J.; Liang, L.; Zhang, L.T.; Yano, M.; Terashima, K.; Kada, H.; Kato, S.; Kadono, T.; Imada, S.; Nakamura, T.; et al. Mixed-valence state of Ce and its individual atomic moments in Ce2Fe14B studied by soft X-ray magnetic circular dichroism. Intermetallics 2016, 69, 42–46. [Google Scholar] [CrossRef]
- Fan, X.; Ding, G.; Chen, K.; Guo, S.; You, C.; Chen, R.; Lee, D.; Yan, A. Whole process metallurgical behavior of the high-abundance rare-earth elements LRE (La, Ce and Y) and the magnetic performance of Nd0.75LRE0.25-Fe-B sintered magnets. Acta Mater. 2018, 154, 343–354. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhong, Z. Research and development of Ce-containing Nd2Fe14B-type alloys and permanent magnetic materials. J. Mater. Sci. Technol. 2017, 33, 1087–1096. [Google Scholar] [CrossRef]
- Pei, K.; Zhang, X.; Lin, M.; Yan, A.R. Effects of Ce-substitution on magnetic properties and microstructure of Nd–Pr–Fe–B melt-spun powders. J. Magn. Magn. Mater. 2016, 398, 96–100. [Google Scholar] [CrossRef]
- Yan, C.; Guo, S.; Chen, R.; Lee, D.; Yan, A. Effect of Ce on the Magnetic Properties and Microstructure of Sintered Didymium-Fe-B Magnets. IEEE Trans. Magn. 2014, 50, 2102605. [Google Scholar] [CrossRef]
- Pathak, A.K.; Gschneidner, K.A.; Khan, M.; McCallum, R.W.; Pecharsky, V.K. High performance Nd-Fe-B permanent magnets without critical elements. J. Alloys Compd. 2016, 668, 80–86. [Google Scholar] [CrossRef]
- Fuerst, C.D.; Herbst, J.F.; Sarrao, J.L.; Migliori, A. Resonant ultrasound measurements of elastic constants of melt-spun of R2Fe14B compounds (R=Ce, Pr, Nd, Er). J. Appl. Phys. 1994, 75, 6625–6627. [Google Scholar] [CrossRef]
- Susner, M.A.; Conner, B.S.; Saparov, B.I.; McGuire, M.A.; Crumlin, E.J.; Veith, G.M.; Cao, H.; Shanavas, K.V.; Parker, D.S.; Chakoumakos, B.C.; et al. Flux growth and characterization of Ce-substituted Nd2Fe14B single crystals. J. Mag. Mag. Mater. 2017, 434, 1–9. [Google Scholar] [CrossRef]
- Menushenkov, V.; Savchenko, A.; Stoliarov, V.; Zheleznyi, M.; Kolchugina, N.; Dormidontov, N.; Skotnicova, K.; Koshkidko, Y. Simulation of demagnetization reversal and hysteretic loops of (Nd, Pr)2Fe14B magnets at low temperatures. In Proceedings of 28-th International Conference on Metallurgy and Materials, Metal 2019, Brno, Czech Republic, 22–24 May 2019; Tanger Ltd.: Ostrava, Czech Republic, 2019; pp. 1621–1627. [Google Scholar]
- Jiang, S.; Li, H.; Xu, J.; Gao, R. Research on the origin of magneto-crystalline anisotropy in R2Fe14B compounds. J. Mag. Mag. Mater. 1994, 136, 294–300. [Google Scholar]
- Xu, W.G.; Liu, Y.L.; Ji, S.Q.; Chu, D.P.; Xu, Y.; Yang, G.L. Temperature dependence of the anisotropy constants K1 and K2 of R2Fe14B (R. = Ce, Pr, Gd). Acta Sin. 1986, 35, 1592–1597. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).