Abstract
The structural, electronic, and optical properties of inorganic CsPb(I1−xBrx)3 compounds were investigated using the full-potential linear augmented-plane wave (FP-LAPW) scheme with a generalized gradient approximation (GGA). Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) and modified Becke–Johnson GGA (mBJ-GGA) potentials were used to study the electronic and optical properties. The band gaps calculated using the mBJ-GGA method gave the best agreement with experimentally reported values. CsPb(I1−xBrx)3 compounds were wide and direct band gap semiconductors, with a band gap located at the M point. The spectral weight (SW) approach was used to unfold the band structure. By substituting iodide with bromide, an increase in the band gap energy (Eg) values of 0.30 and 0.55 eV, using PBE-GGA and mBJ-GGA potentials, respectively, was observed, whereas the optical property parameters, which were also investigated, demonstrated the reverse effect. The high absorption spectra in the ultraviolet−visible energy range demonstrated that CsPb(I1−xBrx)3 perovskite could be used in optical and optoelectronic devices by partly replacing iodide with bromide.
1. Introduction
Halide perovskite ABX3 has attracted increasing interest as a potential solar cell material because of its simple fabrication techniques and outstanding optoelectronic properties. ABX3 perovskite materials have a high absorption coefficient, appropriate band gap (Eg), and balanced electron and hole mobility [1,2,3,4,5,6]. In recent years, numerous researchers have focused on methylammonium lead trihalide perovskite (CH3NH3PbX3), metal halide perovskite (ABX3, A = Cs, Rb; B = Pb, Sn; X = Cl, Br, I), and CsPbI3, which have shown great potential [7,8].
Most of the researchers have studied the structural, electronic, and optical properties of CsPbX3 (X = Cl, Br, I) using the density functional theory (DFT) and the WIEN2k package [8,9,10,11]. The Eg tenability for CsPbX3 was studied experimentally [12], and the lattice modulation of Cs1−xRxPbBr3 (R = Li, Na, K, Rb, x = 0–1) was also investigated [13]. By doping the perovskite, the efficiency can be increased, as this can affect numerous electronic and optical properties [7]. The structural and electronic properties of all of the inorganic mixed-halide perovskites, CsPb(Br1−xIx)3 and CsPb(Cl1−xBrx)3, were investigated according to their halide composition using the Vienna ab initio simulation package (VASP) [14]. The accuracy of DFT calculations, i.e., how close they are to experimentally measured values, has been a concern for DFT calculations on perovskite since their recent introduction into solar cell and LED applications [15,16,17,18,19,20,21]. The accuracy of DFT calculations proved to be highly dependent on the exchange potential used in the calculations, such as local density approximation (LDA) [22], Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) [23], modified Becke–Johnson GGA (mBJ-GGA) [24,25], Green function for the wave equation approximation (GW) [26,27], and hybrid functionals (HF) [27,28]. The HF and GW potentials have shown higher accuracy of the calculated band gap [26,27,28], but these functionals were more computationally expensive than LDA or PBE-GGA. The calculated band gap using LDA or PBE-GGA potentials was strongly underestimated because these functions contain a self-interaction error [29,30]. For example, calculation of the Eg has varied greatly among many recent DFT reports, occasionally with considerable deviations from experimental values (band gap reported between 1.359–1.75 eV [8,9,31,32] compared to experimental values of ~1.791 eV [33,34] for CsPbI3 and 1.7–4.53 eV [1,8,10,35,36,37,38] compared to experimental values of ~2.3 eV [13,39,40,41,42,43,44] for CsPbBr3). However, very accurate measurements of the band gaps of semiconductors and insulators were obtained when an orbital-independent exchange-correlation potential, mBJ-GGA, was used. This depended solely on semilocal quantities and was competitive in accuracy with the expensive HF and GW methods [24,45]. The supercell calculations are usually performed to allow minor modification of the crystal structure by replacing one atom with another atom. The most successful approach, spectral weight (SW), which links the supercell band structure with the primitive basis representation, is based on a Bloch spectral density [46]. One of the main challenges of supercell electronic structure calculations is to recover the Bloch character of electronic eigenstates [46]. To our knowledge, there have been no studies so far for a spectral weight (SW) approach which can be used to unfold the band structure of inorganic perovskite compounds by fold2Bloch package [46]. The fold2Bloch package was used in the past to unfold the band structure for other compounds such as GaAsBi [47], group (III–V and II–VI) semiconductor solid solutions [46], and graphene [48].
In this study, a combination of CsPbI3 and CsPbBr3 was proposed to tune the electronic and optical properties, using the full-potential linear-augmented plane wave (FP-LAPW) method [49,50] within the framework of the DFT [22], as implemented in the WIEN2K code [51]. Here, an investigation into CsPb(I1−xBrx)3 (where x = 0.00, 0.25, 0.50, 0.75, 1.00) was performed to calculate the electronic and optical properties using PBE-GGA [23] and mBJ-GGA [24] methods. The structural properties were calculated using PBE-GGA potential. Unfolding the band structure of CsPb(I1−xBrx)3 compounds for a number of Br fractions was performed by calculating the Bloch SW, using the fold2Bloch package [46] implemented in WIEN2k, in order to observe how the electronic properties of these compounds develop [47]. The visualization for electronic and structural analysis (VESTA) program was used for atomic structure visualization [52].
2. Computational Method
The ground state properties of CsPb(I1−xBrx)3 were calculated by the FP-LAPW method [50] within the framework of the DFT [22,49], as implemented in the WIEN2K code [51]. The PBE-GGA and mBJ-GGA potentials were used to calculate the electronic properties of CsPb(I1−xBrx)3 perovskite [23,24]. To simulate CsPb(I1−xBrx)3 (x = 0.00, 0.25, 0.50, 0.75, 1.00), a 1 × 1 × 4 supercell with 20 atoms was used. For x = 0.25, three atoms of iodide were substituted with three atoms of bromide. For x = 0.50, six atoms of iodide were substituted with six atoms of bromide. For x = 0.75, nine atoms of iodide were substituted with nine atoms of bromide. For x = 1.00, twelve atoms of iodide were substituted with twelve atoms of bromide.
The muffin-tin radius RMT was chosen with no charge leakage from the core, and total energy convergence was ensured. The convergence of the basis set was controlled by the cutoff parameter, RMT·Kmax = 9, where Kmax is the largest reciprocal lattice vector used in the plane wave expansion within the interstitial region. The magnitude of the largest vector in the charge density Fourier expansion was Gmax = 12·(a.u)−1. The Brillouin zones were sampled with a 12 × 12 × 12 k-point mesh for the unit cell and a 15 × 15 × 3 k-point mesh for the supercell. The energy cutoff was chosen as −6.0 Ry, which defines the separation of the valence and core states. The charge convergence was selected as 0.0001e during the self-consistency cycles. The unfolded band structure of CsPb(I1−xBrx)3 compounds was determined by calculating the Bloch SW, using fold2Bloch package [46] implemented in WIEN2k, which is available from GitHub [46]. See the Supplementary Materials for more details about fold2Bloch package.
3. Results and Discussions
3.1. Structural Properties
The crystal structures of cubic CsPbX3 with the atomic positions of Cs at (0, 0, 0), Pb at (0.5, 0.5, 0.5), and X at (0.5, 0.5, 0) within the space group were evaluated through these calculations. The CsPb(I1−xBrx)3 semiconductor compounds were modeled at the selected compositions with ordered structures of periodically repeating supercells 1 × 1 × 4 with 20 atoms per unit cell for x = 0.00, 0.25, 0.50, 0.75, and 1.00, as shown in Figure 1. See the Supplementary Materials, Tables S1–S5 for more details.
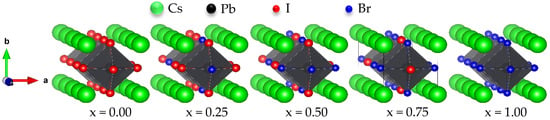
Figure 1.
Atomic structures of CsPb(I1−xBrx)3, with x = 0.00, 0.25, 0.50, 0.75, and 1.00 for the different mixed ratios of x.
The computed lattice parameters for cubic CsPbBr3, CsPbI3, and their compounds using PBE-GGA potential were in good agreement with previous experimental and theoretical values, as listed in Table 1. Figure 2 shows that the unit-cell volume varies linearly as a function of the ratio x, which is in agreement with Vegard’s law [14].

Table 1.
Calculated lattice constants (Å), bulk moduli B (GPa), and the pressure derivatives B’ using Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) potential compared with previous results.
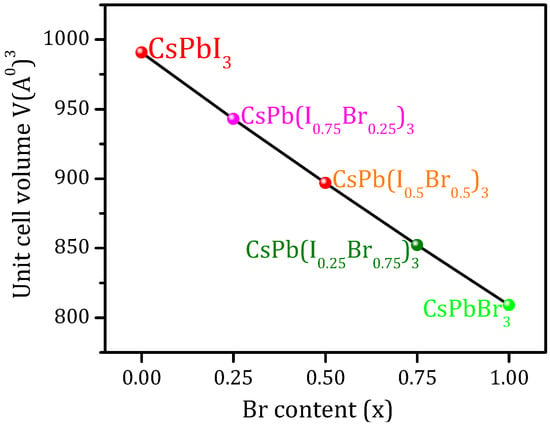
Figure 2.
The unit-cell volumes vary linearly as a function of Br content (x).
3.2. Electronic Properties
The electronic properties of CsPb(I1−xBrx)3 were studied by calculating the energy band structure. The folded band structure calculations at x = 0.00, 0.25, 0.50, 0.75, and 1.00 were performed using both PBE-GGA and mBJ-GGA methods. The calculated folded band structures along the wave vectors X, M, and Γ in the Brillouin zone, using mBJ-GGA potential, are shown in Figure 3a–e. In order to study the behavior of Eg with the composition x of Br, the variation of Eg versus the concentration obtained using the PBE-GGA and mBJ-GGA methods was calculated. Here, Eg increased with an increasing Br concentration, as shown in Figure 4. The folded band structures using PBE-GGA are available in the Supplementary Materials, Figure S1.
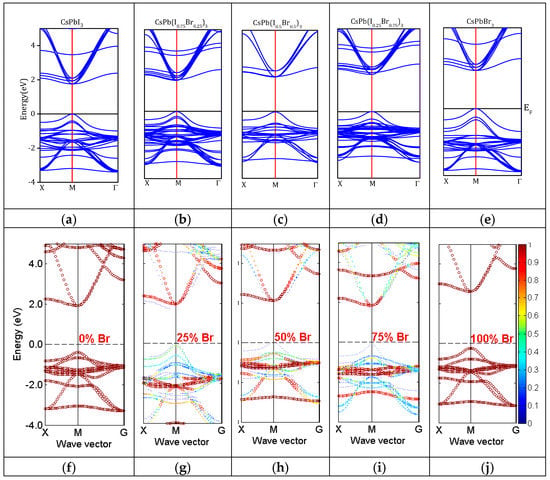
Figure 3.
(a–e) Calculated folded band structures of CsPbI3, CsPb(I0.75Br0.25)3, CsPb(I0.5Br0.5)3, CsPb(I0.25Br0.75)3, and CsPbBr3 using the (most accurate) modified Becke–Johnson generalized gradient approximation (mBJ-GGA) method. (f–j) Band structures obtained by the first-principle simulations equipped with fold2Bloch function at Br fractions of 0%, 25%, 50%, 75%, and 100% respectively. The color scale at the bottom right indicates the Bloch spectral weights.
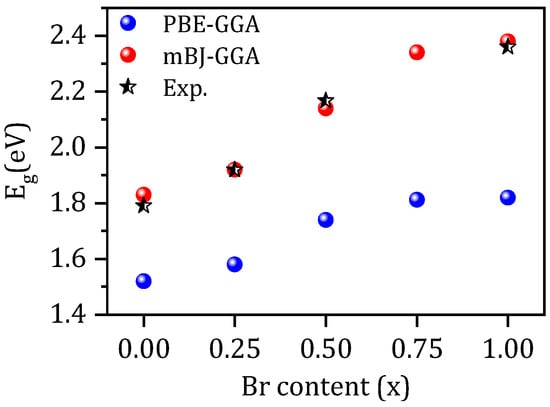
Figure 4.
Compositional dependence of the Eg calculated using the PBE-GGA and mBJ-GGA methods, compared with experimental values [12,13,33].
The substitution of bromide atoms at the iodide sites in the CsPbI3 compound provided a direct band gap character (M → M). The overall behavior of the folded band structures calculated by these two approximations was similar, except for the value of Eg, which was higher for the mBJ-GGA method, as listed in Table 2. The calculated Eg of CsPb(I1−xBrx)3, using the mBJ-GGA method, agreed with the experimental values, as listed in Table 2 and shown in Figure 4. Therefore, it could be concluded that the mBJ-GGA potential presents a good approach for calculating the electronic properties for a wide range of materials, such as wide-band-gap insulators, semiconductors, and three-dimensional transition-metal oxides, particularly their band gaps [24,45,59,60,61].

Table 2.
Calculated Eg (in eV) of CsPb(I1−xBrx)3 compared to the experimental and density functional theory (DFT) calculated values.
The folded band structure calculation for a 20-atom supercell of CsPb(I1−xBrx)3 represents a zone folding that hinders the analysis of the band structure of supercells, and the direct character of the folded band gap is obscured [46]. In order to recover the CsPb(I1−xBrx)3 band structure in its conventional Bloch representation, the SW approach was applied to unfold the electronic structure obtained from the framework of density functional theory, using the all-electron Wien2k package. The calculation of the SW is based on remapping the supercell reciprocal space with a mesh that is compatible with the translational symmetry of a primitive cell [46]. The unfolded band structure calculation for a 20-atom supercell 1 × 1 × 4 was calculated as shown in Figure 3f–j and can be directly compared to that in Figure 3a–e. The unfolded band structure for the pure supercell CsPbI3 is shown in Figure 3f. Due to the increases in the doping level of Br, the unfolded band structure becomes more obvious (Figure 3g–j). In another words, the colors in the conduction band minimum (CBM) and valence band maximum (VBM) change, which indicate the Bloch spectral weights as shown in the right axis of Figure 3. The SW is determined by both degeneracy and magnitude of the corresponding Bloch character [46,62,63,64].
3.3. Density of States
The total density of states (TDOS) and partial density of states (PDOS) based on the variable control approach were determined to further reveal the factors controlling the Eg trends. In order to study the effect of replacing iodide by bromide on Eg trend, the TDOS were calculated using PBE-GGA and mBJ-GGA methods shown in Figure 5a,b. The overall feature of the TDOS remains the same in CsPb(I1−xBrx)3 compounds. However, by increasing the concentration of x from 0.00 to 1.00, the edges of TDOS show upshifts. Figure 6 shows the calculated PDOS with various doping concentrations, using mBJ-GGA potential. For all concentrations, the Cs atom makes a negligible contribution to the valence band maximum (VBM) or conduction band minimum (CBM).
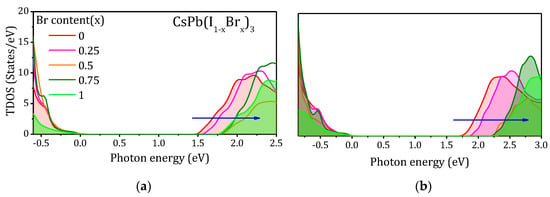
Figure 5.
Calculated total density of states (TDOS) of CsPb(I1−xBrx)3 with various doping concentrations by (a) PBE-GGA and (b) mBJ-GGA potentials where the valence band maximum (VBM) is shifted to 0 eV.
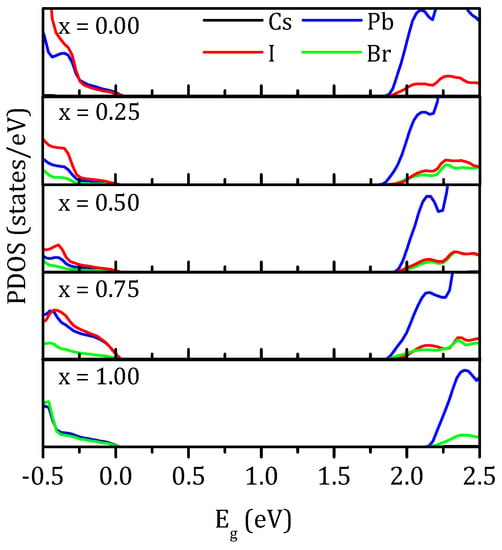
Figure 6.
Calculated partial density of states (PDOS) of CsPb(I1−xBrx)3 using the mBJ-GGA potential.
3.4. Optical Properties
The optical properties of a material, according to Maxwell’s equations, are based on characteristic constants of matter, such as the dielectric constant, magnetic permeability, and electrical conductivity, which are functions of the frequency (ω) of the incident photon [9].
The incident photon interacts with the constituent atoms, and subsequently, the dielectric function ε(ω) describes the optical response of a material. In Figure 7, the imaginary parts ε2(ω) of the calculated dielectric functions are shown using the results of the mBJ-GGA method. The optical parameters, including refraction, reflection, and absorption, can be derived from the real and imaginary parts of the dielectric function [9,69]. The complete response of a material to the disturbances caused by electromagnetic radiation is described by the complex dielectric function [57]. The imaginary part of the function ε2(ω) is related to the band structure and describes its absorptive behavior [57]. The critical (start) points in the spectra of ε2(ω) were at 1.79, 1.945, 2.11, 2.26, and 2.33 eV for CsPbI3, CsPb(I0.75Br0.25)3, CsPb(I0.5Br0.5)3, CsPb(I0.25Br0.75)3, and CsPbBr3, respectively, which are closely related to the band gaps of 1.78, 1.89, 2.21, 2.23, and 2.34 eV, respectively.
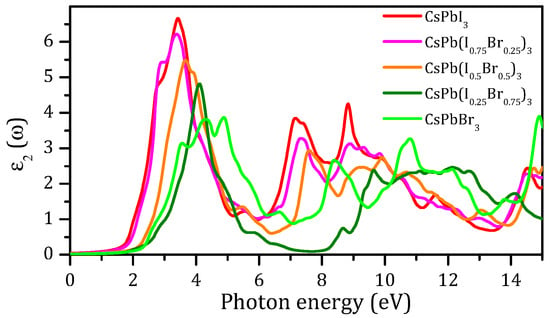
Figure 7.
Calculated ε2(ω) for CsPbI3, CsPb(I0.75Br0.25)3, CsPb(I0.5Br0.5)3, CsPb(I0.25Br0.75)3, and CsPbBr3 as a function of photon energy.
The optical conductivity spectra, σ(ω), shown in Figure 8a, demonstrate that optical conductance started at approximately 1.728, 1.864, 2.13, 2.48, and 2.54 eV for x = 0.00, 0.25, 0.50, 0.75, and 1.00, respectively; the σ(ω) values reached their maxima and then decreased with small variations [57,70]. Similar features were also observed for the absorption coefficients α(ω) (Figure 8b) and extinction coefficients k(ω) (Figure 8c). The wide absorption range suggests that these compounds could be used for various optical and optoelectronic devices in this range of the EM spectrum. Moreover, the absorption range could be tuned by varying the composition fraction with values for x between 0.00 and 1.00.
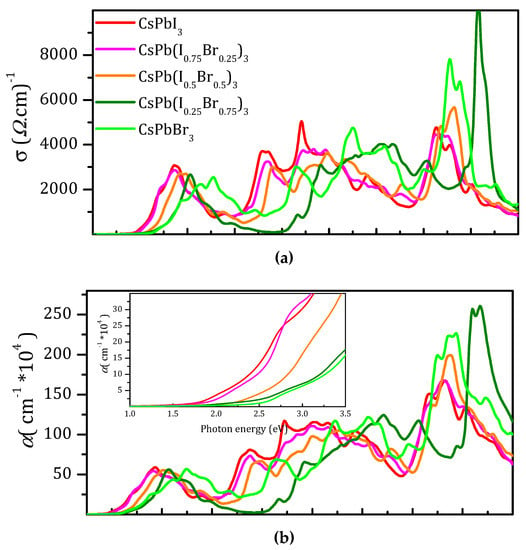
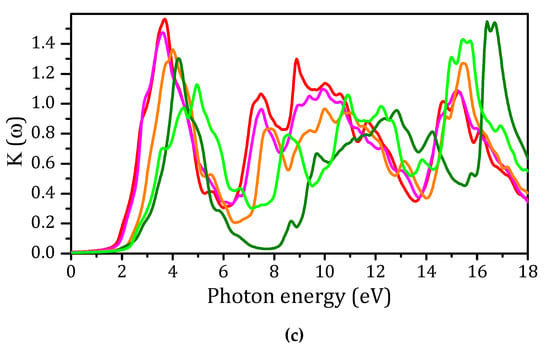
Figure 8.
Calculated optical conductivity σ(ω) (a), absorption coefficient α(ω) (inset: absorption spectra in the range from 1.0 to 3.5 eV) (b), and extinction coefficient k(ω) (c) as functions of photon energy for CsPbI3, CsPb(I0.75Br0.25)3, CsPb(I0.5Br0.5)3, CsPb(I0.25Br0.75)3, and CsPbBr3.
Figure 9a shows the variation of the real dielectric function ε1(ω) with energy. In this spectra, the zero frequency limit ε1(0) was the most important quantity that represented the electronic part of the static dielectric constant [57]. Here, ε1(ω) increased from the zero frequency limit to the maximum value and then decreased to below zero. The calculated ε1(0) is shown in Table 3. As seen in Table 3, ε1(0) decreased as x increased from 0.00 to 1.00, demonstrating an inverse relation between Br content (x) and ε1(0), see Figure 10.
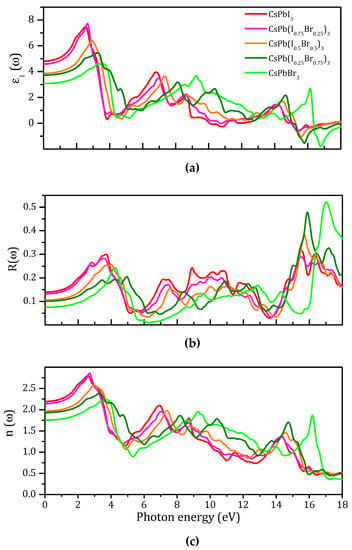
Figure 9.
Calculated ε1(ω) (a), R(ω) (b), and n(ω) (c) as a function of photon energy.

Table 3.
Calculated zero frequency limits of ε1(0), R(0), and n(0).
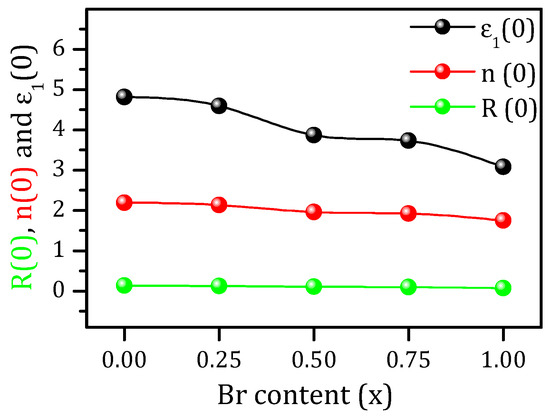
Figure 10.
Zero frequency limit of ε1(0), n(0), and R(0) vs. Br content (x).
The frequency-dependent reflectivity R(ω) for these compounds is shown in Figure 9b, while the zero frequency reflectivities are listed in Table 3. In addition, R(0) increased in a similar way to ε1(0) as the change of anion concentration x increases from 0.00 to 1.00. As Figure 9a,b shows, the maximum R(ω) occurred when ε1(ω) reached a negative value; thus, the material exhibited a dielectric behavior (ε1(ω) > 0); Below zero, the material demonstrated metallic properties (ε1(ω) < 0) [57,71]. The maximum range of R(ω) increased with the metallicity when ε1(ω) was negative [9]. The reflectivity R(w) was initially 14.1% and reached a maximum value of 31.3% for CsPbI3; for CsPb(I0.75Br0.25)3, R(ω) was initially 13.1% and increased to 28.7%; for CsPb(I0.5Br0.5)3, R(ω) was initially 10.7% and reached a maximum value of 38.5%; for CsPb(I0.25Br0.75)3, R(ω) was initially 7.6% and reached a maximum value of 52.2%; and for CsPbBr3, R(ω) was initially 10% and reached a maximum value of 47.9%. The maximum reflectivity peak decreased as x approached 1.00 [66]. The calculated R(0) is shown in Table 3 and Figure 10 which show that R(0) decreased as x increased from 0.00 to 1.00.
Figure 9c shows the refractive indices n(ω) as a function of the incident photon energy. The spectrum of n(ω) closely followed ε1(ω) [57,70]. From Figure 9c, n(ω) of the material increased with an increasing Br concentration in CsPbI3 from the zero frequency limits and reached the maximum values of 2.8, 2.85, 2.57, 2.234, and 2.38 for CsPbI3, CsPb(I0.75Br0.25)3, CsPb(I0.5Br0.5)3, CsPb(I0.25Br0.75)3, and CsPbBr3, respectively. After n(ω) reached the maximum value, it decreased to below unity in certain energy ranges; thus, the group velocity (Vg = c/n) of the incident radiation was greater than c [57,70]. The group velocity shifted to a negative domain, and the nature of the medium changed from linear to nonlinear or the material became superluminal for high energy photons [57,70]. The calculated n(0) is shown in Table 3, and Figure 10 shows that n(0) decreased as x increased from = 0.00 to 1.00.
4. Conclusions
The structural, electronic, and optical properties of CsPb(I1−xBrx)3 (x = 0.00, 0.25, 0.50, 0.75 and 1.00) were investigated using the FP-LAPW scheme within the framework of the GGA. The two exchange potentials, PBE-GGA and mBJ-GGA, were used to study the electronic and optical properties. In this study, a variation in the Eg values (1.83, 1.92, 2.14, 2.34, and 2.38 eV) was observed with the increasing concentration of Br atoms in the CsPb(I1−xBrx)3 compounds using the mBJ-GGA potential, while another variation in Eg values (1.52, 1.58, 1.74, 1.81, and 1.82 eV) was observed using the PBE-GGA potential. CsPb(I1−xBrx)3 compounds were found to be wide and direct band gap semiconductors with Eg located at the M-symmetry wave vector. The effects of the substitution of I by Br on the electronic structure were studied from first principles. By controlling the portion of Br, the unfolded band structure was obtained by both degeneracy and magnitude of the corresponding Bloch character, leading to color changes in CBM and VBM. The optical properties, such as the optical conductivities, absorption coefficients, real and imaginary parts of the dielectric functions, refractive indices, extinction coefficients, and reflectivities, were also calculated. The direct Eg and high absorption spectra of these compounds in the ultraviolet−visible energy range demonstrated that the perovskite could be used in optical and optoelectronic devices in this range of the spectrum by varying the level of x in the composition of the compound.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4352/10/5/342/s1, Tables S1–S5: Structural properties of CsPb(I1−xBrx)3 Perovskite, Figure S1: Calculated the band structures of CsPbI3, CsPb(I0.75Br0.25)3, CsPb(I0.5Br0.5)3, CsPb(I0.25Br0.75)3, and CsPbBr3 using the PBE-GGA method, fold2Bloch package.
Author Contributions
All authors have read and agreed to the published version of the manuscript. Conceptualization, H.M.G., Z.A.A., and A.S.A.; methodology, H.M.G. and Z.A.A.; software, H.M.G. and Z.A.A.; validation, Z.A.A., A.S.A. and S.M.H.Q.; formal analysis, H.M.G. and Z.A.A.; investigation, H.M.G., Z.A.A. and A.S.A.; data curation, H.M.G. and Z.A.A.; writing—original draft preparation, H.M.G.; writing—review and editing, Z.A.A., A.S.A., S.M.H.Q. and A.L.; supervision, A.S.A. and Z.A.A.; funding acquisition, A.S.A.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Deanship of scientific research at King Saud University for funding and supporting this research through the initiative of DSR Graduate Students Research Support (GSR).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mao, X.; Sun, L.; Wu, T.; Chu, T.; Deng, W.; Han, K. First-Principles Screening of All-Inorganic Lead-Free ABX3 Perovskites. J. Phys. Chem. C 2018, 122, 7670–7675. [Google Scholar] [CrossRef]
- Im, J.H.; Lee, C.R.; Lee, J.W.; Park, S.W.; Park, N.G. 6.5% Efficient Perovskite Quantum-Dot-Sensitized Solar Cell. Nanoscale 2011, 3, 4088–4093. [Google Scholar] [CrossRef]
- Gao, P.; Gratzel, M.; Nazeeruddin, M.K.; Online, V.A.; Gao, P.; Nazeeruddin, M.K. Environmental Science Organohalide lead perovskites for photovoltaic applications. Energy Environ. Sci. 2014, 7, 2448–2463. [Google Scholar] [CrossRef]
- Correa-Baena, J.P.; Abate, A.; Saliba, M.; Tress, W.; Jesper Jacobsson, T.; Grätzel, M.; Hagfeldt, A. The rapid evolution of highly efficient perovskite solar cells. Energy Environ. Sci. 2017, 10, 710–727. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, K. Organic-inorganic hybrid lead halide perovskites for optoelectronic and electronic applications. Chem. Soc. Rev. 2016, 45, 655–689. [Google Scholar] [CrossRef] [PubMed]
- Sum, T.C.; Mathews, N. Advancements in perovskite solar cells: Photophysics behind the photovoltaics. Energy Environ. Sci. 2014, 7, 2518–2534. [Google Scholar] [CrossRef]
- Eidsvåg, H.; Rasukkannu, M.; Vajeeston, P.; Velauthapillai, D. Bandgap engineering in CsSnxPb(1−x)I3 and their influence on light absorption. Mater. Lett. 2018, 218, 253–256. [Google Scholar] [CrossRef]
- Maqbool, M.; Rehman, G.; Ali, L.; Shafiq, M.; Iqbal, R.; Ahmad, R.; Khan, T.; Jalali-Asadabadi, S.; Maqbool, M.; Ahmad, I. Structural, electronic and optical properties of CsPbX3 (X = Cl, Br, I) for energy storage and hybrid solar cell applications. J. Alloys Compd. 2017, 705, 828–839. [Google Scholar]
- Afsari, M.; Boochani, A.; Hantezadeh, M. Electronic, optical and elastic properties of cubic perovskite CsPbI3: Using first principles study. Optik (Stuttg). 2016, 127, 11433–11443. [Google Scholar] [CrossRef]
- Jishi, R.A.; Ta, O.B.; Sharif, A.A. Modeling of lead halide perovskites for photovoltaic applications. J. Phys. Chem. C 2014, 118, 28344–28349. [Google Scholar] [CrossRef]
- Ilyas, B.M.; Elias, B.H. A theoretical study of perovskite CsXCl3 (X = Pb, Cd) within first principles calculations. Phys. B Condens. Matter 2017, 510, 60–73. [Google Scholar] [CrossRef]
- Moore, D.T.; Kamino, B.A.; Patel, J.B.; Miranda, L.; Johnston, M.B.; Parrott, E.S.; Haghighirad, A.A.; Hörantner, M.T.; Sutton, R.J.; Snaith, H.J.; et al. Bandgap-Tunable Cesium Lead Halide Perovskites with High Thermal Stability for Efficient Solar Cells. Adv. Energy Mater. 2016, 6, 1502458. [Google Scholar]
- Duan, J.; He, B.; Li, Y.; Tang, Q.; Zhao, Y.; Yuan, H. Lattice Modulation of Alkali Metal Cations Doped Cs1−xRxPbBr3 Halides for Inorganic Perovskite Solar Cells. Sol. RRL 2018, 2, 1800164. [Google Scholar]
- Chen, X.; Han, D.; Su, Y.; Zeng, Q.; Liu, L.; Shen, D. Structural and Electronic Properties of Inorganic Mixed Halide Perovskites. Phys. Status Solidi Rapid Res. Lett. 2018, 12, 1800193. [Google Scholar] [CrossRef]
- Shi, J.; Yun, S. First-Principles DFT Calculations for Perovskite Solar Cells. In Counter Electrodes for Dye—Sensitized and Perovskite Solar Cells, II; Yun, S., Hagfeldt, A., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2018; pp. 487–509. [Google Scholar]
- Umari, P.; Mosconi, E.; De Angelis, F. Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 Perovskites for Solar Cell Applications. Sci. Rep. 2014, 4, 4467. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Fu, L.; Yu, T.; Zhou, S.; Zhang, L.; Yin, L. Surface passivation engineering strategy to fully-inorganic cubic CsPbI3 perovskites for high-performance solar cells. Nat. Commun. 2018, 9, 1076. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, X.; Zhou, Y.; Jiang, Q.; Ye, Q.; Chu, Z.; Li, X.; Yang, X.; Yin, Z.; You, J. Solvent-controlled growth of inorganic perovskite films in dry environment for efficient and stable solar cells. Nat. Commun. 2018, 9, 2225. [Google Scholar] [CrossRef]
- Liu, C.; Hu, M.; Zhou, X.; Wu, J.; Zhang, L.; Kong, W.; Li, X.; Zhao, X.; Dai, S.; Xu, B.; et al. Efficiency and stability enhancement of perovskite solar cells by introducing CsPbI3 quantum dots as an interface engineering layer. NPG Asia Mater. 2018, 10, 552–561. [Google Scholar] [CrossRef]
- Wang, K.; Jin, Z.; Liang, L.; Bian, H.; Bai, D.; Wang, H.; Zhang, J.; Wang, Q.; Liu, S. All-inorganic cesium lead iodide perovskite solar cells with stabilized efficiency beyond 15%. Nat. Commun. 2018, 9, 4544. [Google Scholar] [CrossRef]
- Chen, M.; Ju, M.G.; Garces, H.F.; Carl, A.D.; Ono, L.K.; Hawash, Z.; Zhang, Y.; Shen, T.; Qi, Y.; Grimm, R.L.; et al. Highly stable and efficient all-inorganic lead-free perovskite solar cells with native-oxide passivation. Nat. Commun. 2019, 10, 16. [Google Scholar] [CrossRef]
- Kohn, W.; SHAM, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Tran, F.; Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef] [PubMed]
- Bylander, D.M.; Kleinman, L. Good semiconductor band gaps with a modified local-density approximation. Phys. Rev. B 1990, 41, 7868–7871. [Google Scholar] [CrossRef]
- Bechstedt, F.; Fuchs, F.; Kresse, G. Ab-initio theory of semiconductor band structures: New developments and progress. Phys. Status Solidi Basic Res. 2009, 246, 1877–1892. [Google Scholar] [CrossRef]
- Camargo-Martínez, J.A.; Baquero, R. The band gap problem: The accuracy of the wien2k code confronted. Rev. Mex. Fis. 2013, 59, 453–459. [Google Scholar]
- Heyd, J.; Peralta, J.E.; Scuseria, G.E.; Martin, R.L. Energy band gaps and lattice parameters evaluated with the Heyd-Scuseria-Ernzerhof screened hybrid functional. J. Chem. Phys. 2005, 123, 174101. [Google Scholar] [CrossRef]
- Koller, D.; Tran, F.; Blaha, P. Improving the modified Becke-Johnson exchange potential. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 85, 155109. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, R.; Xu, H.T.; Hong, F.; Xu, F.; Wang, L.J. Nature of the band gap of halide perovskites ABX3(A = CH3NH3, Cs; B = Sn, Pb; X = Cl, Br, I): First-principles calculations. Chinese Phys. B 2015, 24, 116302. [Google Scholar] [CrossRef]
- Ray, D.; Clark, C.; Pham, H.Q.; Borycz, J.; Holmes, R.J.; Aydil, E.S.; Gagliardi, L. Computational Study of Structural and Electronic Properties of Lead-Free CsMI3 Perovskites (M = Ge, Sn, Pb, Mg, Ca, Sr, and Ba). J. Phys. Chem. C 2018, 122, 7838–7848. [Google Scholar] [CrossRef]
- He, M.; Ding, L.; Liu, S.; Shao, G.; Zhang, Z.; Liang, X.; Xiang, W. Superior fluorescence and high stability of B-Si-Zn glasses based on Mn-doped CsPbBrxI3−x nanocrystals. J. Alloys Compd. 2019, 780, 318–325. [Google Scholar] [CrossRef]
- Eperon, G.E.; Stranks, S.D.; Menelaou, C.; Johnston, M.B.; Herz, L.M.; Snaith, H.J. Formamidinium lead trihalide: A broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 2014, 7, 982–988. [Google Scholar] [CrossRef]
- Castelli, I.E.; García-Lastra, J.M.; Thygesen, K.S.; Jacobsen, K.W. Bandgap calculations and trends of organometal halide perovskites. APL Mater. 2014, 2, 081514. [Google Scholar] [CrossRef]
- Goesten, M.G.; Hoffmann, R. Mirrors of Bonding in Metal Halide Perovskites. J. Am. Chem. Soc. 2018, 140, 12996–13010. [Google Scholar] [CrossRef] [PubMed]
- Kang, B.; Biswas, K. Exploring Polaronic, Excitonic Structures and Luminescence in Cs4PbBr6/CsPbBr3. J. Phys. Chem. Lett. 2018, 9, 830–836. [Google Scholar] [CrossRef] [PubMed]
- Wolf, C.; Lee, T.W. Exciton and lattice dynamics in low-temperature processable CsPbBr3 thin-films. Mater. Today Energy 2018, 7, 199–207. [Google Scholar] [CrossRef]
- Zhang, M.; Zheng, Z.; Fu, Q.; Chen, Z.; He, J.; Zhang, S.; Chen, C.; Luo, W. Synthesis and single crystal growth of perovskite semiconductor CsPbBr3. J. Cryst. Growth 2018, 484, 37–42. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Malliakas, C.D.; Peters, J.A.; Liu, Z.; Sebastian, M.; Im, J.; Chasapis, T.C.; Wibowo, A.C.; Chung, D.Y.; Freeman, A.J.; et al. Crystal growth of the perovskite semiconductor CsPbBr3: A new material for high-energy radiation detection. Cryst. Growth Des. 2013, 13, 2722–2727. [Google Scholar] [CrossRef]
- Yaffe, O.; Guo, Y.; Tan, L.Z.; Egger, D.A.; Hull, T.; Stoumpos, C.C.; Zheng, F.; Heinz, T.F.; Kronik, L.; Kanatzidis, M.G.; et al. The nature of dynamic disorder in lead halide perovskite crystals. In Physical Chemistry of Interfaces and Nanomaterials XV, SPIE Nanoscience + Engineering, 28 August–1 September 2016; Bakulin, A.A., Lovrincic, R., Banerji, N., Eds.; SPIE: San Diego, CA, USA, 2016; Volume 9923, p. 99231B. [Google Scholar]
- Akkerman, Q.A.; Motti, S.G.; Srimath Kandada, A.R.; Mosconi, E.; D’Innocenzo, V.; Bertoni, G.; Marras, S.; Kamino, B.A.; Miranda, L.; De Angelis, F.; et al. Solution Synthesis Approach to Colloidal Cesium Lead Halide Perovskite Nanoplatelets with Monolayer-Level Thickness Control. J. Am. Chem. Soc. 2016, 138, 1010–1016. [Google Scholar] [CrossRef] [PubMed]
- Paul, T.; Chatterjee, B.K.; Maiti, S.; Sarkar, S.; Besra, N.; Das, B.K.; Panigrahi, K.J.; Thakur, S.; Ghorai, U.K.; Chattopadhyay, K.K. Tunable cathodoluminescence over the entire visible window from all-inorganic perovskite CsPbX3 1D architecture. J. Mater. Chem. C 2018, 6, 3322–3333. [Google Scholar] [CrossRef]
- Liu, Z.; Peters, J.A.; Stoumpos, C.C.; Sebastian, M.; Wessels, B.W.; Im, J.; Freeman, A.J.; Kanatzidis, M.G. Heavy metal ternary halides for room-temperature X-ray and gamma-ray detection. In Hard X-ray Gamma-ray Neutron Detect. Phys. XV, Proceedings of SPIE—The International Society for Optical Engineering, 25–29 August 2013; Fiederle, M., Burger, A., Franks, L., James, R.B., Eds.; SPIE: San Diego, CA, USA, 2013; Volume 8852, p. 88520A. [Google Scholar]
- Koller, D.; Tran, F.; Blaha, P. Merits and limits of the modified Becke-Johnson exchange potential. Phys. Rev. B 2011, 83, 195134. [Google Scholar] [CrossRef]
- Rubel, O.; Bokhanchuk, A.; Ahmed, S.J.; Assmann, E. Unfolding the band structure of disordered solids: From bound states to high-mobility Kane fermions. Phys. Rev. B Condens. Matter Mater. Phys. 2014, 90, 115202. [Google Scholar] [CrossRef]
- Maspero, R.; Sweeney, S.J.; Florescu, M. Unfolding the band structure of GaAsBi. J. Phys. Condens. Matter 2017, 29, 075001. [Google Scholar] [CrossRef]
- Medeiros, P.V.C.; Stafström, S.; Björk, J. Effects of extrinsic and intrinsic perturbations on the electronic structure of graphene: Retaining an effective primitive cell band structure by band unfolding. Phys. Rev. B Condens. Matter Mater. Phys. 2014, 89, 041407. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 134, B864. [Google Scholar] [CrossRef]
- Nordström, L.; Madsen, G.K.H.; Blaha, P.; Schwarz, K.; Sjöstedt, E. Efficient linearization of the augmented plane-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 2001, 64, 195134. [Google Scholar]
- Blaha, P.; Schwarz, K.; Luitz, G.K.H.M.D.K.J.; Tran, R.L.F.; Marks, L.D. An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, 3rd-9501031st-ed.; Schwarz, K., Ed.; Vienna University of Technology: Vienna, Austria, 2019; Volume 2, ISBN 3-9501031-1-2. [Google Scholar]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Ghaithan, H.M.; Alahmed, Z.A.; Qaid, S.M.H.; Aldwayyan, A.S. First principle-based calculations of the optoelectronic features of 2 × 2 × 2 CsPb(I1−xBrx)3 perovskite. Superlattices Microstruct. 2020, 140, 106474. [Google Scholar] [CrossRef]
- Trots, D.M.; Myagkota, S.V. High-temperature structural evolution of caesium and rubidium triiodoplumbates. J. Phys. Chem. Solids 2008, 69, 2520–2526. [Google Scholar] [CrossRef]
- Eperon, G.E.; Paternò, G.M.; Sutton, R.J.; Zampetti, A.; Haghighirad, A.A.; Cacialli, F.; Snaith, H.J. Inorganic caesium lead iodide perovskite solar cells. J. Mater. Chem. A 2015, 3, 19688–19695. [Google Scholar] [CrossRef]
- Ghaithan, H.M.; Alahmed, Z.A.; Qaid, S.M.H.; Hezam, M.; Aldwayyan, A.S. Density Functional Study of Cubic, Tetragonal, and Orthorhombic CsPbBr3 Perovskite. ACS Omega 2020, 5, 7468–7480. [Google Scholar] [CrossRef] [PubMed]
- Murtaza, G.; Ahmad, I. First principle study of the structural and optoelectronic properties of cubic perovskites CsPbM3 (M = Cl, Br, I). Phys. B Condens. Matter 2011, 406, 3222–3229. [Google Scholar] [CrossRef]
- Sandor, E.; Wooster, W.A. Crystal Structure and Photoconductivity of Cæsium Plumbohalides. Nature 1958, 182, 1436. [Google Scholar]
- Dixit, H.; Saniz, R.; Cottenier, S.; Lamoen, D.; Partoens, B. Electronic structure of transparent oxides with the Tran-Blaha modified Becke-Johnson potential. J. Phys. Condens. Matter 2012, 24, 205503. [Google Scholar] [CrossRef]
- Fan, S.W.; Ding, L.J.; Yao, K.L. Electronic structure and ferromagnetism of boron doped bulk and surface CdSe: By generalized gradient approximation and generalized gradient approximation plus modified Becke and Johnson calculations. J. Appl. Phys. 2013, 114, 113905. [Google Scholar] [CrossRef]
- Traoré, B.; Bouder, G.; Lafargue-Dit-Hauret, W.; Rocquefelte, X.; Katan, C.; Tran, F.; Kepenekian, M. Efficient and accurate calculation of band gaps of halide perovskites with the Tran-Blaha modified Becke-Johnson potential. Phys. Rev. B 2019, 99, 035139. [Google Scholar] [CrossRef]
- Popescu, V.; Zunger, A. Effective band structure of random alloys. Phys. Rev. Lett. 2010, 104, 236403. [Google Scholar] [CrossRef]
- Popescu, V.; Zunger, A. Extracting E versus Effective band structure from supercell calculations on alloys and impurities. Phys. Rev. B Condens. Matter Mater. Phys. 2012, 85, 085201. [Google Scholar] [CrossRef]
- Chen, M.X.; Weinert, M. Revealing the substrate origin of the linear dispersion of Silicene/Ag(111). Nano Lett. 2014, 14, 5189–5193. [Google Scholar] [CrossRef] [PubMed]
- Lang, L.; Yang, J.H.; Liu, H.R.; Xiang, H.J.; Gong, X.G. First-principles study on the electronic and optical properties of cubic ABX3 halide perovskites. Phys. Lett. A 2014, 378, 290–293. [Google Scholar] [CrossRef]
- Heidrich, K.; Schäfer, W.; Schreiber, M.; Söchtig, J.; Trendel, G.; Treusch, J.; Grandke, T.; Stolz, H.J. Electronic structure, photoemission spectra, and vacuum-ultraviolet optical spectra of CsPbCl3 and CsPbBr3. Phys. Rev. B 1981, 24, 5642–5649. [Google Scholar] [CrossRef]
- Wang, K.; Yang, Q.; Duan, J.; Zhang, C.; Zhao, F.; Yu, H.; Hu, B. Spin-Polarized Electronic Transport through Ferromagnet/Organic–Inorganic Hybrid Perovskite Spinterfaces at Room Temperature. Adv. Mater. Interfaces 2019, 1, 1900718. [Google Scholar] [CrossRef]
- Qaid, S.M.H.; Al-Asbahi, B.A.; Ghaithan, H.M.; AlSalhi, M.S.; Al dwayyan, A.S. Optical and structural properties of CsPbBr3 perovskite quantum dots/PFO polymer composite thin films. J. Colloid Interface Sci. 2020, 563, 426–434. [Google Scholar] [CrossRef]
- Ghebouli, M.A.; Ghebouli, B.; Fatmi, M. First-principles calculations on structural, elastic, electronic, optical and thermal properties of CsPbCl3 perovskite. Phys. B Condens. Matter 2011, 406, 1837–1843. [Google Scholar] [CrossRef]
- Amin, B.; Ahmad, I.; Maqbool, M.; Goumri-Said, S.; Ahmad, R. Ab initio study of the bandgap engineering of Al1−xGaxN for optoelectronic applications. J. Appl. Phys. 2011, 109, 023109. [Google Scholar] [CrossRef]
- Xu, B.; Li, X.; Sun, J.; Yi, L. Electronic structure, ferroelectricity and optical properties of CaBi2Ta2O9. Eur. Phys. J. B 2008, 66, 483–487. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).