Abstract
Overconfidence is a well-established behavioral bias that involves the overestimation of one’s own capabilities. We introduce a model in which managers and agents exert effort in a joint production, after the manager decides on the allocation of the tasks. A rational manager tends to reduce their own effort by delegating the critical task to the agent more often than in an efficient task allocation. In contrast, an overconfident manager engages in responsibility hoarding, i.e., is likely to delegate a critical task less often to the agent than a rational manager. In fact, a manager with a sufficiently high ability and a moderate degree of overconfidence increases the total welfare by refusing to delegate critical tasks and by exerting more effort than a rational manager. Finally, we derive the conditions under which the responsibility hoarding can persist in an organization, showing that the bias survives as long as the overconfident manager can rationalize the observed output by underestimating the ability of the agent.
Mayer’s reluctance to delegate became a sticking point, too. She insisted on personally approving every hire. One executive complained to a friend that Mayer spent as much time deliberating Yahoo’s parking policies as she did strategizing over the sale of its Alibaba stock.(Carlson, 2014, New York Times Magazine, 12 December 2014)
1. Introduction
The reluctance to delegate, i.e., responsibility hoarding (we use the terms as synonyms), seems so pervasive in management that strong negative language is often used in management training literature warning managers and students of management to avoid the habit. Some authors, for example, include the reluctance to delegate in the list of “fatal business errors” (Muehlhausen, 2008), as one of the “deadly sins of management” (Morrissey, 2014), or among the “habits of highly ineffective managers” (James, 2011, 2012). In spite of the ubiquitous warnings, management journalists report evidence for the reluctance to delegate responsibility even in the behavior of a number of star CEOs such as Marissa Mayer, Carly Fiorina, Jack Welch, and quite a number of others.1
In the academic literature to date, the reluctance to delegate mainly contributes to two rational effects. Prendergast (1995) introduces a model of responsibility hoarding where a manager with discretion over the task assignment refuses to delegate some tasks to the agent, because taking on these tasks adds to the manager’s future income from the training on-the-job. Hence, the reluctance to delegate is a rational response to the increased payoffs from job experience in this model. In fact, there are numerous jobs that neatly fit into this framework, including surgeons, pilots, lawyers, and many other job in which greater experience sharply adds to productivity. However, there are also many jobs that do not share this feature. For example, managers are generally not considered to be more experienced because they performed many of the tasks by themselves. In contrast, efficient task delegation is usually considered as one of the central job requirements of managers.
A second phenomenon that is connected to the reluctance to delegate tasks is a manager’s preference for payoff autonomy and authority. Owens et al. (2014) show in a series of laboratory experiments that subjects seeking to reduce the influence of others on their earnings are often willing to pay to make their decisions autonomously. Bartling et al. (2014) present an experimental approach to measure the intrinsic value of autonomous decision making. In a different set of experiments, Fehr et al. (2013) show that subjects are also willing to pay for the right to decide on others’ payoffs, thus exhibiting an intrinsic value of exerting power over others. As in Prendergast’s model, these models also assume that managers make rational decisions based on rational expectations. The difference is that managers in these models entertain non-standard preferences for payoff autonomy or authority that drive the reluctance to delegate tasks, whereas the responsibility hoarding of the managers in Prendergast’s model is driven by the future monetary returns from the investment in their own human capital.
In this study, we suggest a completely different explanation for the reluctance to delegate, i.e., of responsibility hoarding. In our model managers are also assumed to maximize their expected utility, but they are boundedly rational in their expectations. More precisely, we assume that managers may be overconfident concerning their own capabilities. Since overconfident managers tend to believe that they can outperform agents in critical tasks, they may refuse to delegate the critical tasks even when delegation would increase their own expected payoff. Hence, our approach is fundamentally different from the other approaches, because managers in our model—much as is in the well-established literature on “behavioral CEOs” (Malmendier & Tate, 2015)—objectively harm themselves by refusing to delegate. If there is sufficient feedback over time, they may be able to reduce their overconfidence and learn to delegate more often. However, as we demonstrate in this study, correcting wrong beliefs on the quality of their own performance may be stalled by incomplete information on the agent’s ability. In fact, for some combinations of parameters in our model, we show that even the long-run feedback on previous outcomes will not drive managers away from overconfidence and their responsibility hoarding.2
To investigate the effect of overconfidence on task allocation and organizational performance, we introduce a model in which a manager and an agent can exert effort in a joint production. The production requires two distinct tasks with unequal impact on the output. The allocation of the tasks is at the discretion of the manager, who decides whether to perform the critical task (i.e., the task with the higher impact on the output) himself or to delegate the critical task to the agent. (We use male pronouns for the overconfident manager because males are generally found to exhibit a higher degree of overconfidence than females (see, e.g., Barber & Odean, 2001; Bengtsson et al., 2005; Correll, 2001)).
We show that an overconfident manager tends to hoard responsibility, i.e., to assign the critical task more often to himself than a rational manager would. The reluctance to delegate takes place, even though it is individually suboptimal for the manager, who suffers from a higher cost of effort by performing the critical task instead of the other task.
We also show that, despite adding to the overconfident manager’s effort cost, the reluctance to delegate may actually increase the total welfare of the enterprise. As long as the overconfident manager’s self-perception bias is not too large, the total welfare effect can be positive, because the effort exerted by the overconfident manager is closer to the efficient welfare maximizing level than the effort provided by a rational manager. (Note that in task allocation settings, payoff maximizing managers generally reduce their own cost by providing effort below the welfare maximizing level). Hence, by overestimating his own productivity and exerting a correspondingly greater amount of effort, the overconfident manager typically engages in less free-riding than his rational counterpart.
Finally, we show that the responsibility hoarding can persist in an organization, as long as the overconfident manager can rationalize the overestimation of his own ability by underestimating the ability of the agent. The more leeway an overconfident manager has to rationalize the observed outcome without having to adapt his positively biased assessment of his own ability level, the more likely it is to observe persistent responsibility hoarding in an organization. We determine the conditions for persistent responsibility hoarding in our model without assuming that managers are biased in the way that they update information. Adding biased information processing to the model (see e.g., Brunnermeier & Parker, 2005; Mobius et al., 2022) will intuitively increase the range of parameter values for which the responsibility hoarding is a persistent bias.
2. Related Literature
Overconfidence, a core assumption of our model, is a well-established behavioral pattern that involves overestimating one’s own capabilities, especially in tasks with a partially stochastic outcome (Lichtenstein et al., 1982; Russo & Schoemaker, 1992; Soll, 1996; Svenson, 1981). Although the degree of overconfidence may vary with the type of task (Grieco & Hogarth, 2009), it is generally found to persist when individuals assess the probability of their own success, the relative standing of their performance compared to others (Klayman et al., 1999), or their prospective memory (Ericson, 2011).
The behavioral patterns of overconfidence and its effects, especially in the domain of financial decisions, have been studied extensively (see, e.g., Barber & Odean, 2000; Deaves et al., 2008; De Bondt & Thaler, 1996). Top management’s overconfidence has often been found to persist and to have a partially beneficial effect on the enterprise’s bottom line by affecting the relationship of the enterprise with its external stakeholders. This phenomenon is shown both for the management’s financial decision-making (see, e.g., Burkhard et al., 2023; Malmendier & Tate, 2005, 2008; Palomino & Sadrieh, 2011 or Kaplan et al., 2021) and for other aspects of decision-making (see, e.g., Phua et al., 2018 for creating stakeholder commitment, Lai et al., 2021 for enhancing labor investment efficiency, Chang & Hu, 2024 for strengthening the position in supply chain competition or Tondji, 2022 for providing advantages in the R&D competition). The internal effects of overconfidence on organizational performance, however, are not fully understood yet. In particular, the question of how a manager’s overconfidence affects the decision-making on task allocation within the organization has not been studied so far.
Most of the existing literature on overconfidence in managerial settings is focused on the exaggerated investment risks taken by overconfident managers. While Barber and Odean (2000) and Deaves et al. (2008) report excessive trading by overconfident traders, Camerer and Lovallo (1999) observe excessive market entries in an experimental setting. Kinari (2016) finds that overconfidence in asset markets remains stable, while optimism and pessimism vary strongly over time. Malmendier and Tate (2005) argue that managerial overconfidence leads to distortive investment behavior and demonstrate that data on CEO investments in the own company are in line with their overconfidence model. Hackbarth (2008) shows that overconfident managers tend to bias the capital structure of the firm towards higher debt levels. Similar results can be found in Ben-David et al. (2007) who show that companies with overconfident CFOs have a significantly different capital structure than other firms. Furthermore, Malmendier and Tate (2008) find that overconfident managers also tend to overpay in mergers and even initiate value-destroying ones. Interestingly, this bias is sometimes advantageous for the firm’s value. For instance, Palomino and Peyrache (2010) show that managerial overconfidence can be advantageous concerning financial decisions. They analyze a model in which overconfident portfolio managers, who share profits, may exhibit risk attitudes that are more in line with the investors’ risk attitude than rational risk-averse managers. Analyzing data of large publicly traded firms from 1980 to 1994, Galasso and Simcoe (2011) present evidence that overconfident CEOs have a significantly higher probability to initiate corporate innovation.
In a team production setting, Gervais and Goldstein (2007) study a firm with complementary production technology and show that the presence of an overconfident agent can increase the firm’s output because it helps the agents to coordinate on a high effort level and therefore overcome the free-rider problem. Furthermore, Santos-Pinto (2008) shows that firms can benefit from using interdependent incentive schemes when workers have wrong beliefs about their coworkers’ abilities. Regarding individual performance, Weinberg (2009) for instance shows that a moderate overestimation of one’s own ability can be advantageous compared to a correct assessment, because it allows the overconfident individuals to undertake more challenging tasks that raise their expected output and utility. Recent experimental findings by Sautmann (2013) support the notion that overconfident agents accept lower wage offers, while Santos-Pinto (2010) shows that firms using tournaments as incentives can achieve greater profits if agents have a positive self-image. Similarly, Ludwig et al. (2011) find that moderate overconfidence can improve the agent’s performance in a Tullock contest relative to an unbiased opponent. These results are supported by the recent experiment of Kinari et al. (2011), reporting a significant positive impact of overconfidence on productivity in tournaments. Furthermore, Englmaier (2011) argues that firms should hire overoptimistic managers to ensure the implementation of certain investment strategies in R&D tournaments.
Regarding the literature on the delegation of tasks in a principal-agent model, we are, to the best of our knowledge, the first to take overconfidence into account. Prendergast (1995) suggests a model where a manager has discretion over task assignments and may exhibit responsibility hoarding, i.e., may delegate less tasks to the agent than a rational manager would. The result is driven by the assumption that the manager can earn future rents from the on-the-job training that performing the additional tasks provides. This model of rational reluctance to delegate is especially useful when studying professions with extraordinary high requirements for job experience, e.g., surgeons, pilots, or lawyers. Note, however, that—as our analysis shows—even in such settings, any degree of rational responsibility hoarding may be amplified by the manager’s overconfidence.
3. Basic Model
Consider a joint production setting in which a manager and an agent can exert effort to generate a shared output. For simplicity, we assume that both the manager and the agent are risk neutral. The total output Y is a function of the outcomes and of the tasks 1 and 2, correspondingly. A crucial assumption is that the two tasks differ in their impact on the total output, where w.l.o.g. we assume that task 1 is the critical task, i.e., it tends to have higher impact on total output than the non-critical task 2. Using an additive production function, we introduce the parameter that measures the relative impact of task 1 compared to task 2. Hence, the total output Y is defined as:
The manager and the agent share the total output. Let denote the manager’s share of the total output. We assume that the effort levels as well as the output of both tasks are not observable by the firm. Only the total output Y is observable for all parties. Either player can be assigned to perform either task, where the task allocation is chosen by the manager at the outset of each period. The allocation must be complete and bijective, i.e., both tasks must be allocated and each must be allocated to a different player because no player can perform both tasks in the same period. The outcome of each task j is endogenous, depending on the true ability and the chosen effort of the player i performing the task:
Note that while the production function is additive, the two production factors (i.e., the manager’s and the agent’s work input) are not substitutes in production due to the restriction that each player can only complete one task. Hence, full production needs the effort of both actors.3
Furthermore, the individual effort cost is strictly convex:
To simplify the discussion, we distinguish between those task allocation choices, in which the critical task 1 is performed by the manager (non-delegation), and those, in which the critical task 1 is allocated to the agent (delegation). More formally, we define:
Definition 1.
A delegation choice is a task allocation in which the critical task 1 is allocated to the agent and the non-critical task 2 is allocated to the manager. In case of non-delegation, the critical task 1 is allocated to the manager, and the non-critical task 2 is carried out by the agent.
Definition 2.
A task allocation is individually optimal if it maximizes the manager’s utility.
Definition 3.
A task allocation is efficient if it maximizes the total welfare of all involved parties.
Following Gervais and Goldstein (2007), we avoid introducing additional distributional assumptions by characterizing an overconfident manager as someone who systematically overestimates his own ability by a fixed but unknown amount b:
Definition 4.
An overconfident manager has an overly optimistic perception of his own ability, i.e.,
where denotes the manager’s true ability and the parameter his self-perception bias or the degree of his overconfidence.
Finally, we use the definitions above to characterize responsibility hoarding.
Definition 5.
Responsibility hoarding occurs when a manager performs the critical task 1 himself, even though the delegation choice is individually optimal for him.
4. First-Best, Second-Best, and the Reluctance to Delegate
We start by investigating the efficient task allocation choice (efficient first-best case), then proceed to the delegation choices of a rational manager (individually optimal second-best case), and finally, compare the two benchmarks to the case of an overconfident manager (better than second-best). Comparing the three results, we first show that rational managers delegate the critical task more often than is efficient. Next, we show that overconfidence always leads to less delegation compared to an equilibrium with a rational manager. Finally, we prove that the manager’s biased self-perception may increase efficiency, because the responsibility hoarding can be beneficial for the total welfare of the involved parties, as long as the increase in the overconfident manager’s contribution to firm output over-compensates the loss due to his individually suboptimal delegation and effort choices.
4.1. Efficient Task Allocation with Equal Payoff Shares (First-Best Case)
Assume that the critical task 1 is carried out by the manager and task 2 is assigned to the agent. The outcomes of the two tasks are then given by
where the index nd denotes the case of non-delegation.
In the first-best case with equal costs and payoff shares, the total welfare of the involved parties is maximized by:
which leads to the first-best effort levels given by
Hence, the total welfare in case of non-delegation is equal to
Next, assume that the critical task 1 is assigned to the agent and task 2 is carried out by the manager. Now, the outcomes of both tasks are given by
where the index d denotes the case of delegation.
In this case, the welfare maximization problem becomes
which leads to the first-best effort levels described by
Hence, the total welfare in case of delegation is equal to
Proposition 1.
In the efficient task allocation with equal costs and payoff shares, the critical task should be allocated to the agent if and only if her ability is at least as high as the manager’s ability, i.e., Otherwise, the critical task should better be assigned to the manager.
Proof.
It is straightforward that maximizing the total welfare requires that the critical task (i.e., the task with a higher impact on the total output) to be carried out by the individual with the higher ability. □
Moreover, the positive welfare effect of delegation is that the greater the delegation, the greater the agent’s ability is. However, it is not obvious that the welfare maximizing task allocation will generally be implemented when the manager allocates the tasks.
4.2. Delegation Choices with Varying Payoff Shares (First-Best and Second-Best Cases)
In this section, we analyze the task allocation choice of a rational manager, maximizing his individual utility, given his varying share of the payoff (). Note that the decision of a rational manager to delegate the critical task does not only depend on the abilities of the two players as in the first-best case with equal payoffs but also on his share of the payoff. We show that the manager’s utility maximization is not generally efficient but only second-best. This is due to the rational manager’s incentive to reduce his own effort provision by delegating the critical task, if his share of the payoff is not high enough.
Our analysis of the rational manager’s decision has two parts. We start by analyzing the case in which he maximizes mutual welfare, i.e., the sum of the utilities of both players. We refer to the state reached by this decision as the efficient (first-best) outcome with varying payoff shares. Next, we analyze the case of a rational manager who maximizes their own utility only. We refer to the state reached by this decision as the individually optimal (second-best) outcome. For the sake of simplicity and tractability, we assume in both cases that the manager has perfect information on the agent’s ability.4
We start with the case of the rational manager seeking an efficient (first-best) outcome by maximizing the total utility that the manager and the agent can achieve together, given their abilities and and the distribution of payoffs and ().
In case the manager does not delegate, the outcomes of the two tasks are then given by (1), and mutual welfare is given by
The effort choices are given by
and
which leads to
Mutual welfare in the case of delegation is given by
and the optimal effort choices are
and
which leads to
It is optimal for a rational manager seeking an efficient (first-best) outcome to delegate if
Note that if , this leads to as in Proposition 1. However, if the manager receives a higher amount of the output than the agent, it may sometimes be efficient to allocate the task to the manager even though the agent has a higher ability. This is so, because the manager exerts greater effort, if his share of output is higher.
Now, we analyze the case of a rational manager who only optimizes his own utility, thus, achieving the individually optimal (second-best) outcome.
In the case of non-delegation, the manager’s utility is maximized with
which leads to his individually optimal effort level described by
Furthermore, the agent’s optimization is given by
and her individually optimal effort level is
Since we assume that the manager has perfect information about the agent’s ability, his utility is equal to
Next, assume that the manager delegates the critical task 1 to the agent and carries out task 2 himself. The outcomes of both tasks are given by (4).
In this case, the manager’s optimization problem is
with
as his individually optimal effort level.
For the agent, the optimization is given by
which leads to an individually optimal effort level of
Hence, the manager’s utility in case of delegation is equal to
Now, by comparing (19) and (22), the rational manager optimizing his own utility (second-best) chooses delegation if and only if
Note that there is a range of values (i.e., ) for which the manager delegates the critical task to the agent, even though his ability is strictly higher than the agent’s ability. This is due to the fact that in equilibrium, the critical task 1 is performed with higher levels of effort and, thus, with a higher effort cost than the other task. Hence, delegating the task may pay, because delegation reduces the manager’s effort cost more than it reduces the expected outcome of the critical task when it is performed by the agent with somewhat lower ability. As the rational manager cannot commit to the efficient task allocation, this may lead to inefficient job distributions and lower total welfare in equilibrium. However, once the agent’s ability falls below the threshold , the manager prefers to perform the critical task himself because the benefit from his own higher ability surpasses the higher effort cost. The manager’s delegation decision also depends on the distribution of the payoffs, i.e., on the value of the manager’s payoff share . Generally, it seems sensible to assume that the manager will at least receive half of the project’s proceeds, i.e., . Obviously, the agent should also have a positive share of the surplus, i.e., . It is straightforward to show that as increases in , the delegation is reduced both in the efficient (first-best) and the individually optimal (second-best) case, because the agent’s incentives to perform the critical task decline as the manager’s payoff share is increased.
Given our analyses so far, it seems clear that the manager’s allocation decision depends both on the relationship between the manager’s and the agent’s abilities, i.e., on the ratio /, and on the distribution of payoffs between them, i.e., on . Figure 1 shows the relationship between the ratio of abilities, the payoff distribution, and the manager’s delegation choice. The dotted horizontal line indicates that in the first-best setting with equal costs and payoff shares, the critical task should always be performed by the actor with the greater ability, i.e., by the manager for > and by the agent for < . In the other cases, as we have discussed above, the delegation choice depends both on the ratio of the abilities and on the distribution of payoffs. The rational manager maximizing mutual utilities (i.e., efficient (first-best) with varying ) delegates the critical task when the parameter combination lies under the solid curve, and the rational manager maximizing their own utility only (i.e., individually optimal (second-best)) delegates when the parameter combination lies under the wide-dashed curve. Clearly, for any given , the rational manager is less likely to delegate the critical task when making a first-best decision and more likely to delegate when making an individually optimal (second-best) decision.
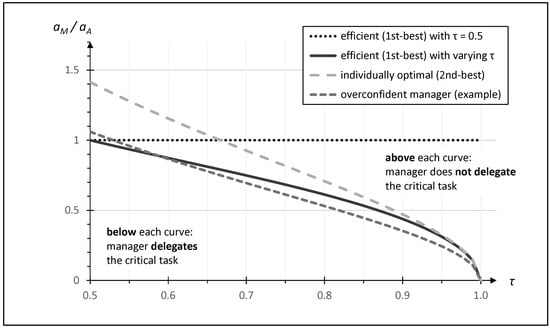
Figure 1.
Relationship between the ratio of abilities, the payoff distribution, and the manager’s delegation choice.
The intersection of the curve of individually optimal (second-best) allocations with / = 1 is also of some interest. Up to that point (i.e., at < 0.67), inefficient delegations occur, even though the agent has the lower ability to perform the critical task than the manager (i.e., / > 1). From the point on, inefficient delegations occur, where the agent has a higher ability than the manager (i.e., / < 1). Note that while these delegation choices are not first-best, they are individually optimal from the perspective of the utility-maximizing manager. In the next section, we analyze and discuss the individually non-optimal task allocation choices by overconfident managers that we refer to as responsibility hoarding. There we show that an overconfident manager may actually reduce his own utility due to excessive non-delegation, as represented by the dashed curve in Figure 1, depicting an example of an overconfident manager’s delegation choices.
4.3. Optimal Delegation Choice of an Overconfident Manager
In this section, we examine the task allocation choice of an overconfident manager, assuming that overconfidence leads to an overly optimistic perception of one’s own abilities. Recall that the self-perceived ability of an overconfident manager is given by
Given this slight modification of the model, we derive the equilibrium choices of the overconfident manager and the agent and compare these to the case with a rational manager. By substituting for and following the same procedure applied in the previous chapter, we derive the condition under which the overconfident manager chooses delegation:
Proposition 2.
With perfect information on the agent’s ability parameter , any positive self-perception bias leads to the responsibility hoarding by the overconfident manager, regardless of τ. In particular, the range of manager types choosing delegation is strictly decreasing in the managers’ degree of overconfidence b.
Proof.
By decreasing the right-hand side of the inequality, any positive self-perception bias b lowers the threshold for non-delegation, reducing the range of values for which delegation is chosen by the overconfident manager. Hence, it is obvious that an overconfident manager is more likely to hoard responsibility than a rational manager of the same true ability. In particular, the higher the self-perception bias b, the larger the range of ability values for which a rational manager delegates the critical task, but an overconfident manager will not, i.e., the greater the range of ability values in which the critical task is carried out by the manager. □
As we have shown in the last section, rational managers cannot commit to the efficient task allocation because they have an incentive to lower their own effort cost by delegating the critical task to the agent as long as the agent’s ability is sufficiently high. In contrast, overconfident managers overestimate their own ability, and therefore, allocate the critical task more often to themselves than rational managers. In particular, overconfident managers are more likely to hoard responsibility the larger their self-perception bias is. However, the task allocations chosen by overconfident managers may be closer to the efficient allocation than those of rational managers. Hence, overconfidence can be considered as a commitment device for managers to take more responsibilities and increase the efficiency of the job distribution, positively affecting the total welfare.
The dashed curve in Figure 1 displays the delegation choices of an overconfident manager. Note that the depicted curve is an example of a specific degree of overconfidence. The curve for a manager with higher overconfidence than in the example would lie to the left and for a less overconfident manager to the right of the displayed curve. None of the curves for overconfident managers, however, would lie to the right of the curve for the individually optimal (second-best) rational manager. Obviously, as overconfidence increases, the delegation area (to the bottom-left side of the curve) decreases and the non-delegation area (to the upper-right side of the curve) increases. Hence, for medium levels of overconfidence, the delegation choices of the overconfident manager are closer to those of the efficiency-seeking (first-best) rational manager than to those of the individually optimizing (second-best) rational manager. For high levels of overconfidence, the overconfident manager delegates the critical task even less often than the efficiency-seeking (first-best) rational manager does. This is why the dashed curve in Figure 1 (which represents a medium to high overconfidence example) partially lies to the left of the solid curve of the efficiency-seeking (first-best) rational manager.
4.4. Is Overconfidence Beneficial or Harmful?
As we have shown in the previous section, overconfidence may lead to less delegation and can, thus, improve the efficiency of the task allocations. Since an overconfident manager, in general, exerts more effort, the total output of the firm is often higher with an overconfident manager than with a rational manager. The higher effort level, however, also leads to a higher cost of effort provision for the overconfident manager. Hence, it is not clear whether the manager’s overconfidence is generally beneficial or harmful with regard to total welfare. In this section, we show that in many cases, including some in which the task allocation is not individually optimal for the manager, overconfidence is beneficial regarding the total welfare of the involved parties. Comparing the total welfare in equilibrium with a rational manager to that with an overconfident manager, we establish the following proposition:
Proposition 3.
If the manager’s self-perception bias b is on a moderate level relative to his true ability (i.e., ) and his true ability is sufficiently high (i.e., ) or sufficiently low (i.e., ), the total welfare of the involved parties in equilibrium is strictly higher with an overconfident manager than with a rational manager. For any ability value of the manager between those two thresholds (i.e., ), this result still holds if the manager’s true ability is at least as high as the agent’s true ability (i.e., ).
Proof.
See the Appendix A.1. □
This result has several interesting implications. First, note that the manager’s overconfidence is not generally harmful and can even be beneficial for the total welfare, if it is not too strong. On the one hand, the overconfident manager overestimates his own ability and, therefore, exerts more effort than the rational manager, irrespective of the task allocation. On the other hand, the overconfident manager also expects a higher total outcome when carrying out the critical task himself and thus is more likely than his rational counterpart to allocate the critical task to himself. This type of responsibility hoarding behavior is efficiency enhancing, if the manager is more able than the agent. Hence, overconfidence helps to reduce free-riding. Indeed, this positive incentive effect of manager overconfidence can even over-compensate the negative effect of individually suboptimal task allocation as long as the manager is at least as productive as the agent. Note that this finding is also in line with our result from the first-best case, stating that the delegation of the critical task is only efficient if the agent is more productive than the manager. In particular, the total welfare in equilibrium with an overconfident manager is closer to the efficient allocation than with a rational manager of the same true ability.
4.5. Optimal Degree of Overconfidence
As the manager’s overconfidence can be beneficial for total welfare, it is straightforward to proceed in our analysis with the determination of the optimal degree of overconfidence with respect to the total welfare. In this regard, we can show
Proposition 4.
The total welfare is highest if the manager’s self-perception bias (or degree of overconfidence) is equal to .
Proof.
See the Appendix A.2. □
Note that the positive welfare effect of overconfidence is strictly increasing in the manager’s true ability. Intuitively, the higher the manager’s true ability is, the less harmful his biased self-perception is, the more likely the responsibility hoarding may positively affect the total welfare. We summarize this result in the following corollary:
Corollary 1.
If a manager’s degree of overconfidence is equal to , his effort choice in equilibrium is exactly equal to the efficient effort level, both in the case of delegation and non-delegation.
Proof.
The results follows directly by substituting for b into the overconfident manager’s incentive conditions. □
5. Persistence of the Manager’s Overconfidence and the Underestimation of the Agent’s Ability
In the previous section, we have demonstrated that manager overconfidence can lead to less delegation, resulting in more efficient task allocations in a perfect information setting. The question that remains is whether the managers’ overconfidence and responsibility-hoarding behavior can persist over time, given imperfect information and feedback. If managers quickly learn to correct their overconfident assessment of their own ability, then overconfidence and responsibility hoarding will not persist. However, if the feedback from previous outcomes cannot be used to correct overconfidence, we can establish that the responsibility hoarding can be a persistent phenomenon with a sustained effect on organizational performance.
We derive the conditions under which overconfidence (and responsibility hoarding) can persist when managers have imperfect information on the agent’s ability and receive feedback only on previous performance. We restrict our analysis to the case where the manager only receives feedback on the total output of the firm (or the organizational unit). Obviously, persistence of overconfidence with more exact information, e.g., on all ability and effort parameters, would not be feasible. In the more realistic situation that we analyze, we assume that the agent’s ability parameter is her private information. More specifically, we assume that the manager uses an estimate of the agent’s ability parameter denoted by . Since, the feedback information is restricted to the total output, the overconfident manager faces one known parameter (his own effort level), two unknown parameters (the agent’s ability and effort level), and one parameter that he believes to know but actually does not (his own ability). Under these circumstances, we show that the overconfident manager may not be able to learn that his self-assessment is biased because he can construct a consistent model that explains the observed total outcome with an overestimated self ability parameter and an underestimated ability parameter for the agent.5 As long as the productivity of the agent can be underestimated sufficiently, the manager’s overconfidence can persist. We summarize this result in the following proposition:
Proposition 5.
If the agent’s true ability is not known to the manager and is sufficiently high, i.e., , the manager’s overconfidence persists because the manager rationalizes the observed outcome information by underestimating the agent’s ability. The higher the manager’s self-perception bias b is, the stronger the underestimation of the agent’s ability will be.
Proof.
See the Appendix A.3. □
A straightforward corollary to the proposition in this section is concerned with the limits of persistent overconfidence:
Corollary 2.
Manager overconfidence is persistent at some positive level iff .
The corollary simply points out that depending on the ability parameters there always might be some level of overconfidence that is persistent, as long as the agent’s ability is not zero. Intuitively, it is clear that overconfidence can only persist, as long as the overconfident manager has the possibility to underestimate the agent’s contribution to the observed total output, and thus, the ability of the agent. The range for the underestimation drops if the agent’s ability is decreased, leaving less and less room for persistently overconfident managers. If the agent’s ability is zero, she would not contribute at all to the total output, and persistent overconfidence would no longer be possible. However, note that the extreme case of zero ability has no empirical relevance because it describes a situation in which the agent cannot contribute to the output of the firm. Hence, the corollary shows that for any situation with empirical relevance, there is at least some level of persistent overconfidence, leading to some amount of persistent responsibility hoarding by overconfident managers.
6. Discussion
Using the results of the sections above, we discuss the range of optimal and persistent manager overconfidence and responsibility hoarding constellations in this section. The constellations are exhibited in Figure 2. It shows the four functions that determine the different outcome regions in the ability space. The manager’s ability is plotted on the horizontal, and the agent’s (possibly estimated) ability is plotted on the vertical axis.6
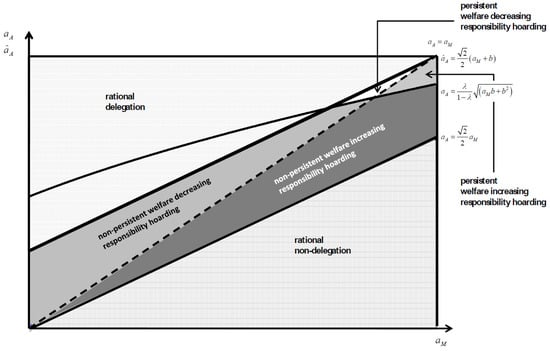
Figure 2.
Range of optimal and persistent overconfidence and responsibility-hoarding constellations depending on manager’s and agent’s abilities.
The dashed bisecting line depicts the function which separates the area of efficient delegation choices above the line from the area of efficient non-delegation choices below the line. The solid line running through the origin depicts the function and separates the area of individually optimal delegation (i.e., rational delegation) above the line from the area of individually optimal non-delegation (i.e., rational non-delegation) below the line. The area of individual optimal delegation is larger than the area of individual optimal non-delegation because—as we show in Section 3—as long as the agent’s ability is not too low, the rational manager prefers to avoid the high cost of effort associated with performing the critical task himself.
The solid line that intersects the vertical axis above the origin depicts the function and separates the area of delegation (the dotted area above the line) from the area of non-delegation (below the line) chosen by an overconfident manager. Note that in the dotted area, both the rational and the overconfident manager choose to delegate the critical task to the agent, while below the line running through the origin (the hatched area), both the rational and the overconfident manager choose to carry out the critical task themselves. The area enclosed by the functions and contains all ability constellations for the responsibility hoarding, in which the overconfident manager still assigns the critical task to himself but the rational manager does not.
The function separates the area of persistent (above) from the area of non-persistent manager overconfidence (below). Note that this separation is only valid in the area where the responsibility hoarding occurs, i.e., the area enclosed by the functions and . Our graph shows a large area of non-persistent (the shaded area and the dark gray area) and a relatively small area of persistent manager overconfidence with the responsibility hoarding by the overconfident manager (the white area and the white-dotted area). Intuitively, it seems clear that manager overconfidence has a lower chance to persist, if the manager carries out the critical task himself. The reason is that the overconfident manager always has more room to rationalize his overly optimistic self-perception by underestimating the agent’s contribution when the critical task is carried out by the agent.
The difference between the tasks concerning their impact on the firm outcome, i.e., the value of the parameter affects the location of the persistence curve (the function ) and, thus, the size of persistent overconfidence areas in the graph (the white area and the white-dotted area). The more important the critical task is, when compared to the other task (i.e., the higher ), the smaller are the areas of persistent overconfidence and responsibility hoarding. The more asymmetric a task constellation is, the more difficult it is for the overconfident manager to find a feasible set of parameters, in which the overestimation of the own ability can be compensated by underestimating the ability of the agent.
A similar but more subtle effect exists concerning the self-perception bias b. As b increases, the area of the responsibility hoarding obviously also increases. Note, however, that an increase in the level of overconfidence b also means that the persistence curve shifts upwards, reducing the area of persistent responsibility hoarding. Hence, more overconfident managers will tend to carry out the critical task more frequently but are also more likely to receive feedback that lets them revise their self-assessment and reduce their overconfidence.
Another implication of our analysis is that both the manager’s and the agent’s abilities must be relatively high to allow for persistent manager overconfidence. This is because the agent’s ability must be high enough to provide the relatively high degree of underestimation that persistence of overconfidence requires. Since persistent overconfidence of the manager is more likely to occur, when the ability levels of the two players are rather close to each other, the responsibility hoarding is most likely to be observed, when the overconfident manager’s true ability is close to the ability level of a high ability agent.
Finally, there are constellations of ability parameters for which manager overconfidence and responsibility hoarding have a sustained effect on the total welfare of all involved parties (the white area and the white-dotted area). However, persistent manager overconfidence and responsibility hoarding are welfare increasing only if the manager is indeed more able than the agent (the white-dotted area). This finding is in line with our results of the first-best case that the critical task should always be carried out by the more able individual due to its higher impact on total outcome.
Note that all discussed outcomes are structurally similar for any feasible value of the manager’s payoff share in . The size of the corresponding areas, however, vary in . Increasing leads to a higher incentive for both rational and overconfident managers to increase their own effort and to delegate the critical task less frequently. This reduces the range of responsibility hoarding outcomes.
7. Conclusions and Managerial Implications
We examine how managerial overconfidence influences organizational performance through task allocation decisions. We show that overconfident managers tend to hoard responsibility, assigning critical tasks to themselves more often than rational managers would. Although this behavior reduces the manager’s individual utility, it can increase overall firm output and welfare by inducing higher managerial effort, overconfidence partly offsets shirking by motivating managers to take on more responsibility and reduce inefficiencies in task delegation.
Our findings suggest that firms may not always avoid overconfident managers who resist delegation; in fact, moderate overconfidence can be beneficial in contexts where contracts cannot enforce efficient task allocation. This insight may help explain why leadership positions are disproportionately held by men, who generally display higher overconfidence. Moreover, firms can adjust management contracts to better align delegation incentives by tailoring payoffs according to a manager’s overconfidence level, improving organizational outcomes even under imperfect information.
We also identify conditions under which overconfidence and responsibility hoarding persist. High-ability agents, low accountability, and similar task values make it easier for managers to rationalize biased self-assessments, sustaining delegation reluctance. However, persistent hoarding may harm agent morale and increase turnover, which can weaken corrective feedback and entrench managerial biases further.
This dynamic helps explain why, despite near-universal managerial advice extolling delegation, many high-profile leaders remain reluctant to share responsibility. The business literature frequently cites refusal to delegate as a “fatal error” or “deadly sin” of leadership Muehlhausen (2008) and Morrissey (2014). Yet such behavior persists among even celebrated executives—such as Marissa Mayer at Yahoo!, Carly Fiorina at Hewlett-Packard, and Jack Welch at General Electric. Mayer was known for centralizing decision-making and tightly controlling strategic initiatives, including dozens of acquisitions, while maintaining limited engagement with broader teams. Fiorina likewise consolidated authority during the HP-Compaq merger, often punishing dissent and sidelining internal feedback. Welch, despite his reputation for performance-driven leadership, was also known for tightly controlling executive succession decisions and for installing layers of accountability that ultimately funneled major choices through his office. These patterns—reluctance to empower subordinates, belief in one’s unique strategic insight, and insulation from corrective input—are exactly the outcomes our model predicts when overconfidence interacts with unverifiable task allocation.
Our model provides an existence result demonstrating that overconfidence improves task allocation under specific assumptions. While stylized, the mechanism extends to more complex settings, such as when managers oversee multiple agents or tasks, or when discrete specialization matters, since tasks are indivisible and individuals differ in productivity. Although we abstract from other managerial decisions like investment choices, which may lessen the benefits of overconfidence, these extensions represent promising directions for future research. Additionally, exploring belief biases on both managers and agents could yield richer insights into optimal organizational design.
Beyond short-term efficiency gains, we emphasize the broader ethical and organizational implications. Overconfidence often masquerades as competence, especially in hierarchical environments where confidence signals leadership potential. This can lead organizations to reward overly certain individuals while overlooking more collaborative or self-aware candidates, resulting in repeated misallocation and underutilization of talent. Overconfident leaders’ unwillingness to delegate or recognize others’ strengths may stifle learning, collaboration, and employee development, ultimately harming culture and long-term performance.
Institutionally, reinforcing overconfidence raises concerns about fairness and accountability. Teams under overconfident leaders may face frustration and disengagement due to undervaluation and centralized decision-making. Over time, such environments discourage dissent, misinterpret risks, and insulate leadership from critical feedback, risks especially pronounced in high-stakes sectors like finance, health care, and public administration. Our findings carry important human resource implications. Organizations should implement evaluation systems that reward not just assertiveness but also effective delegation, team outcomes, and openness to feedback. Leadership development programs can benefit from integrating behavioral awareness training to help leaders recognize when confidence becomes counterproductive. Addressing these behavioral biases is vital to building equitable, adaptive, and ethically sound organizations.
Finally, the model is most relevant in knowledge-intensive, specialized environments—such as technology startups, consulting, R&D, and professional services—where task complexity and interdependence heighten the importance of accurate self-assessment and delegation. In contrast, routine or hierarchical organizations with formalized roles may experience fewer distortions from managerial overconfidence.
In sum, managerial overconfidence exhibits a dual nature: it can mitigate delegation inefficiencies and stimulate effort but also poses ethical and cultural risks. The persistence of delegation reluctance among high-visibility CEOs like Mayer, Fiorina, and Welch reinforces the idea that these behaviors are not mere personality quirks, but structural responses to environments where responsibility is hard to monitor and self-belief goes unchecked. Understanding and balancing these forces is crucial for both researchers and practitioners aiming to foster effective and responsible leadership.
Author Contributions
Conceptualization, formal analysis, and original draft preparation, P.N., A.S. and N.Z.; Review and editing, P.N. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
Petra Nieken gratefully acknowledges financial support by the Deutsche Forschungsgemeinschaft (DFG, grant SFB/TR 15). Abdolkarim Sadrieh gratefully acknowledges financial support by the Deutsche Forschungsgemeinschaft (DFG grant SA 1350/3-1) and of the Land Sachsen-Anhalt.
Data Availability Statement
This is a purely game-theoretic study that is based on mathematical proofs without empirical data.
Acknowledgments
We gratefully acknowledge discussions with participants of the PÖK 11 conference on a very early idea version of the paper. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1
Proof of Proposition 3.
First, we consider the case if . In this case, both a rational manager and an overconfident manager will choose non-delegation. This is also the individually optimal task allocation for the manager. The total welfare with a rational manager is equal to the sum of the utilities of the manager and agent, which is given by
With an overconfident manager, it is equal to
Comparing (A1) and (A3), it follows directly that the total welfare with an overconfident manager is strictly higher than with a rational manager if
Second, we consider the case if In this case, both a rational manager and an overconfident manager will choose delegation, which is also the individually optimal task allocation for the manager. The total welfare with a rational manager is given by
With an overconfident manager, total welfare is
Again, by comparing (A5) and (A7), the total welfare with an overconfident manager is strictly higher than with a rational manager if
Finally, we consider the non-trivial case, in which . In this case, a rational manager chooses to delegate the critical task to the agent, while an overconfident manager carries out the critical task himself.
Note that as long as the manager’s ability is at least as high as the agent’s, i.e., , and the manager’s degree of overconfidence is on a moderate level, i.e., , the total welfare with an overconfident manager is higher than with a rational manager. □
Appendix A.2
Proof of Proposition 4.
First, we consider the case , in which an overconfident manager chooses not to delegate the critical task. In this case, the total welfare is given by
By solving the following optimization problem
we obtain
Note that the second-order condition is automatically satisfied as is strictly concave in b. Furthermore, the constraint is also satisfied as long as Hence,
Second, we consider the case , in which an overconfident manager chooses to delegate the critical task. In this case, the total welfare is given by
Again, by solving the following optimization problem
we obtain
Note that the second-order condition is automatically satisfied as is strictly concave in b. Furthermore the constraint is also satisfied as long as Hence,
and the optimal degree of overconfidence is given . □
Appendix A.3
Proof of Proposition 5.
We prove the results by first analyzing the case of non-delegation and then the case of delegation. We derive the two conditions for sustained overconfidence. We then show that as long as the critical task contributes more to the total output than the other task, i.e., as long as , the condition stated in the proposition is binding for both delegation and non-delegation situations. Finally, we show that the higher the manager’s self-perception bias, the more the agent’s ability is underestimated.
- 1.
- Persistence of overconfidence in the case of non-delegation
Our essential assumption is that the manager will not revise his assessment of his own ability as long as he observes outcomes that can be rationalized by varying the two unknown parameters, i.e., the agent’s ability and effort level. As long as any observed outcome can be rationalized by the manager, overconfidence is persistent. In the following, we derive the sufficient condition for the persistence of overconfidence in the case of non-delegation.
Recall that the total output in the case of non-delegation is given by
If an overconfident manager observes this total output, he overestimates his own contribution and underestimates the agent’s contribution as follows:
This biased model (i.e., the overconfident rationalization of the observed output) is only feasible as long as the following condition holds:
Next, we check for the degree of underestimation of the agent’s contribution in the case of non-delegation. Let denote the underestimation of the agent’s ability. Since we can determine the level of underestimation by solving the following equation:
Since is higher than zero, we have established a positive underestimation of the agent’s ability that increases in the manager’s self-perception bias b.
- 2.
- Persistence of overconfidence in the case of delegation
Now, we derive the sufficient condition for the persistence of overconfidence in the case where the manager delegates the critical task to the agent. Recall that the total output in the case of delegation is
The overconfident manager rationalizes the observation of this output as follows
The overestimation of the own contribution (underestimation of the agent’s ability) is only feasible as long as the following condition holds:
Analogous to the non-delegation case, we check for the degree of underestimation of the agent’s contribution in case of delegation. Let denote the underestimation of the agent’s ability. Since we can determine the level of underestimation by solving the following equation:
Again, we find that is higher than zero, i.e., the overconfident manager underestimates the agent’s ability, and the underestimation increases in the manager’s self-perception bias b.
- 3.
- General conditions for both cases
Taking the results of the two parts together, we can show that for all cases in which the critical task contributes more to the total output than the other task, i.e., as long as , the condition for persistence in the first case (non-delegation) is generally more strict than in the first case:
Hence, if is true, then the condition also holds, allowing us to use the former as a general condition in the proposition. □
Notes
| 1 | See Carlson (2014) on Marissa Mayer, Burrows and Elgin (2005) on Carly Fiorina, James (2011) on Jack Welch, Vass (2012) on Raymond Miquel, and Garfield (2000) on Michel David-Weill. |
| 2 | While we do explore some long-run effects, the core focus of our analysis is on a static environment. In contrast, Prendergast (1995) focuses on a dynamic set-up with investment decisions under career concerns, putting the focus on learning dynamics. Our model is also in contrast to the setup in Bartling et al. (2014), in which overconfidence evolves over time, as agents endowed with decision rights gain confidence in their own choices. Thus, the very act of making choices boosts overconfidence by self-reinforcement, even if quality of decisions does not increase. The setting that is perhaps closest to our model is presented in Fehr et al. (2013). The study does not provide a formal model, but shows in a lab experiment that overconfidence can be socially beneficial in team settings, as it reduces free-riding and increases aggregate effort. While this finding is in line with our results, we focus on the delegation decision of managers whereas they focus on the effort provision of team members. |
| 3 | In this study, we focus on demonstrating and analyzing the existence of the effects of responsibility hoarding in a simple and transparent setting. Our preliminary assessment, however, indicates that our main findings are likely to also hold for other production function types. We leave the formal analyses of that claim for follow-up studies. |
| 4 | In fact, this assumption is not necessary. We could instead assume that the manager does not have perfect information, but only correct beliefs about the distribution of the agent’s ability. In that case, the rational manager, who is risk-neutral by assumption, simply uses the expected value of the agent’s ability for his decision. That alternative distributional assumption leaves our analysis and results unchanged. |
| 5 | Young (2002) shows that some games cannot be learned by rational players and demonstrates a class of learning environments in which convergence to equilibrium behavior fails to occur for any learning process, including the Bayesian updating of objectively correct priors. |
| 6 | We have fixed and to make a two-dimensional plot possible. |
References
- Barber, B. M., & Odean, T. (2000). Trading is hazardous to your wealth: The common stock investment performance of individual investors. Journal of Finance, 55, 773–806. [Google Scholar] [CrossRef]
- Barber, B. M., & Odean, T. (2001). Boys will be boys: Gender, overconfidence, and common stock investment. Quarterly Journal of Economics, 116, 261–292. [Google Scholar] [CrossRef]
- Bartling, B., Fehr, E., & Herz, H. (2014). The intrinsic value of decision rights. Econometrica, 82(6), 2005–2039. [Google Scholar] [CrossRef]
- Ben-David, I., Graham, J., & Harvey, C. (2007). Managerial overconfidence and corporate policies (NBER working paper 13711). NBER. [Google Scholar]
- Bengtsson, C., Persson, M., & Willenhag, P. (2005). Gender and overconfidence. Economics Letters, 86, 199–203. [Google Scholar] [CrossRef]
- Brunnermeier, M. K., & Parker, J. A. (2005). Optimal expectations. American Economic Review, 95(4), 1092–1118. [Google Scholar] [CrossRef]
- Burkhard, B., Sirén, C., van Essen, M., Grichnik, D., & Shepherd, D. A. (2023). Nothing ventured, nothing gained: A meta-analysis of CEO overconfidence, strategic risk taking, and performance. Journal of Management, 49(8), 2629–2666. [Google Scholar] [CrossRef]
- Burrows, P., & Elgin, B. (2005, March 14). The surprise player behind the coup at HP. Bloomberg Business. [Google Scholar]
- Camerer, C., & Lovallo, D. (1999). Overconfidence and excess entry: An experimental approach. American Economic Review, 89(1), 306–318. [Google Scholar] [CrossRef]
- Carlson, N. (2014, December 17). What happened when marissa mayer tried to be steve jobs. New York Times Magazine. [Google Scholar]
- Chang, J. J., & Hu, Z. J. (2024). The effect of overconfidence in a robust competing game. Kybernetes, 53(12), 5081–5119. [Google Scholar] [CrossRef]
- Correll, S. J. (2001). Gender and the career choice process: The role of biased self-assessments. American Journal of Sociology, 106, 1691–1730. [Google Scholar] [CrossRef]
- Deaves, R., Lüders, E., & Luo, G. (2008). An experimental test of the impact of overconfidence and gender on trading activity. Review of Finance, 13, 555–575. [Google Scholar] [CrossRef]
- De Bondt, W. F. M., & Thaler, R. H. (1996). Financial decision-making in markets and firms: A behavioral perspective. In Handbook in operations research and management science (Vol. 9). North Holland. [Google Scholar]
- Englmaier, F. (2011). Commitment in R&D tournaments via strategic delegation to overoptimistic managers. Managerial and Decision Economics, 32, 63–69. [Google Scholar]
- Ericson, K. M. M. (2011). Forgetting we forget: Overconfidence and memory. Journal of the European Economic Association, 9(1), 43–60. [Google Scholar] [CrossRef] [PubMed]
- Fehr, E., Herz, H., & Wilkening, T. (2013). The lure of authority: Motivation and incentive effects of power. American Economic Review, 103(4), 1325–1359. [Google Scholar] [CrossRef]
- Galasso, A., & Simcoe, T. S. (2011). CEO overconfidence and innovation. Management Science, 57, 1469–1484. [Google Scholar] [CrossRef]
- Garfield, A. (2000, November 2). Lazards clings to its glory years as vultures circle in the City. The Independent. [Google Scholar]
- Gervais, S., & Goldstein, I. (2007). The positive effects of biased self-perceptions in firms. Review of Finance, 11, 453–496. [Google Scholar] [CrossRef]
- Grieco, D., & Hogarth, R. M. (2009). Overconfidence in absolute and relative performance: The regression hypothesis and Bayesian updating. Journal of Economic Psychology, 30(5), 756–771. [Google Scholar] [CrossRef]
- Hackbarth, D. (2008). Managerial traits and capital structure decisions. Journal of Financial and Quantitative Analysis, 43, 843–881. [Google Scholar] [CrossRef]
- James, G. (2011, May 25). The 7 habits of highly ineffective managers. CBS News. [Google Scholar]
- James, G. (2012, March 6). 11 habits of highly ineffective managers. Inc. [Google Scholar]
- Kaplan, S. N., Sørensen, M., & Zakolyukina, A. A. (2021). What is CEO overconfidence? Evidence from executive assessments. Journal of Financial Economics, 145(2), 409–425. [Google Scholar] [CrossRef]
- Kinari, Y. (2016). Properties of expectation biases: Optimism and overconfidence. Journal of Behavioral and Experimental Finance, 10, 32–49. [Google Scholar] [CrossRef]
- Kinari, Y., Mizutani, N., Ohtake, F., & Okudaira, H. (2011). Overconfidence increases productivity (Vol. 814). Discussion Paper. Institute of Social and Economic Research—Osaka University. [Google Scholar]
- Klayman, J., Soll, J. B., Gonzalez-Vallejo, C., & Barlas, S. (1999). Overconfidence: It depends on how, what, and whom you ask. Organizational Behavior and Human Decision Processes, 79(3), 216–247. [Google Scholar] [CrossRef] [PubMed]
- Lai, S., Li, X., & Chan, K. C. (2021). CEO overconfidence and labor investment efficiency. North American Journal of Economics and Finance, 55, 101319. [Google Scholar] [CrossRef]
- Lichtenstein, S., Fischhoff, B., & Phillips, L. D. (1982). Calibration of probabilities: The state of the art to 1980. In D. Kahneman, P. Slovic, & A. Tversky (Eds.), Judgement under uncertainty: Heuristics and biases (pp. 306–334). Cambridge University Press. [Google Scholar]
- Ludwig, S., Wichardt, P. C., & Wickhorst, H. (2011). On the positive effects of overconfident self-perception in teams (Munich discussion paper No. 2011-11). Ludwig-Maximilians-Universität München. [Google Scholar]
- Malmendier, U., & Tate, G. (2005). CEO overconfidence and corporate investment. The Journal of Finance, 60, 2661–2700. [Google Scholar] [CrossRef]
- Malmendier, U., & Tate, G. (2008). Who makes acquisitions? CEO overconfidence and the market’s reaction. Journal of Financial Economics, 89(1), 20–43. [Google Scholar] [CrossRef]
- Malmendier, U., & Tate, G. (2015). Behavioral CEOs: The role of managerial overconfidence. Journal of Economic Perspectives, 29, 37–60. [Google Scholar] [CrossRef]
- Mobius, M. M., Niederle, M., Niehaus, P., & Rosenblat, T. S. (2022). Managing self-confidence: Theory and experimental evidence. Management Science, 68, 7793–8514. [Google Scholar] [CrossRef]
- Morrissey, C. (2014). The 7 deadly sins of leadership and how to overcome them in yourself and others. CreateSpace Independent Publishing Platform. [Google Scholar]
- Muehlhausen, J. (2008). The 51 fatal business errors and how to avoid them. Mulekick Publishing. [Google Scholar]
- Owens, D., Grossman, Z., & Fackler, R. (2014). The control premium: A preference for payoff autonomy. American Economic Journal: Microeconomics, 6(4), 138–161. [Google Scholar] [CrossRef]
- Palomino, F., & Peyrache, E. (2010). Psychological bias and gender wage gap. Journal of Economic Behavior & Organization, 76, 563–573. [Google Scholar] [CrossRef]
- Palomino, F., & Sadrieh, A. (2011). Overconfidence and delegated portfolio management. Journal of Financial Intermediation, 20(2), 159–177. [Google Scholar] [CrossRef]
- Phua, K., Tham, T. M., & Wei, C. (2018). Are overconfident CEOs better leaders? Evidence from stakeholder commitments. Journal of Financial Economics, 127, 519–545. [Google Scholar] [CrossRef]
- Prendergast, C. J. (1995). A theory of responsibility in organizations. Journal of Labor Economics, 13, 387–400. [Google Scholar] [CrossRef]
- Russo, J. E., & Schoemaker, P. J. H. (1992). Managing overconfidence. Sloan Management Review, 33, 7–17. [Google Scholar]
- Santos-Pinto, L. (2008). Positive self-image and incentives in organisations. The Economic Journal, 118, 1315–1332. [Google Scholar] [CrossRef]
- Santos-Pinto, L. (2010). Positive self-image in tournaments. International Economic Review, 51(2), 475–496. [Google Scholar] [CrossRef]
- Sautmann, A. (2013). Contracts for agents with biased beliefs: Some theory and an experiment. American Economic Journal: Microeconomics, 5(3), 124–156. [Google Scholar] [CrossRef][Green Version]
- Soll, J. B. (1996). Determinants of overconfidence and miscalibration: The roles of random error and ecological structure. Organizational Behavior and Human Decision Processes, 65, 117–137. [Google Scholar] [CrossRef]
- Svenson, O. (1981). Are we all less risky and more skillful than our fellow drivers? Acta Psychologica, 47, 143–148. [Google Scholar] [CrossRef]
- Tondji, J.-B. (2022). Overconfidence and welfare in a differentiated duopoly. Managerial Decision Econonmics, 43, 751–767. [Google Scholar] [CrossRef]
- Vass, S. (2012, June 3). I don’t retire. Herald Scotland. [Google Scholar]
- Weinberg, B. A. (2009). A model of overconfidence. Pacific Economic Review, 14(4), 502–515. [Google Scholar] [CrossRef]
- Young, H. P. (2002). Bounded rationality and learning. On the limits to rational learning. European Economic Review, 46, 791–799. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).