Abstract
Lower one- or two-dimensional coordination, or potential games, are popularly used to model interactive behavior, such as innovation diffusion and cultural evolution. Typically, this involves determining the “better” of competing solutions. However, examples have demonstrated that different measures of a “good” choice can lead to conflicting conclusions; a fact that reflects the history of game theory in equilibrium selection. This behavior is totally explained while extending the analysis to the full seven-dimensional class of potential games, which includes coordination games.
1. Introduction
When Schelling (1960) wrote Strategy of Conflict, it pivoted attention from zero-sum games to the more general behavior allowed by games with mutually beneficial outcomes (which was appropriate during this Cold War period) [1]. Specifically, Schelling made a case for coordination games, which Lewis (1969) used to discuss culture and convention [2]. This behavioral notion of mutually beneficial outcomes was further explored by Rosenthal (1973) with his development of the congestion game [3]. Monderer and Shapley (1996) built on the congestion game with “common interest” games; namely the potential games (which include coordination games) [4]. More recently, Young (2006, 2011) and Newton and Sercombe (2020) took this analysis a step further by modeling, with potential games, how populations on networks evolve from one convention to another [5,6,7]. The natural question in this work is to discover whether the status quo or an innovation will be accepted.
This issue of finding the “better outcome” (e.g., an innovation or the status quo), which is a theme of this paper, is a fundamental and general concern for game theory; answers require selecting a measure of comparison. A natural choice is to prefer those outcomes where the players receive larger payoffs. Rather than payoff dominance, another refinement of Nash equilibria offered by Harsanyi and Selton (1988) is risk dominance [8].1 The choice used by Young (2006, 2011) and later by Newton and Sercombe (2020) is to maximize social welfare. Still, other measures can be constructed [5,6,7].
With the social welfare measure, Young constructed a clever ad-hoc example where, although it is seemingly profitable to adopt the innovation, the innovation is worse than the status quo [5]. Young’s observation underscores the important need to understand when and why a model’s conclusions can change. This includes his concerns of identifying when and why a new cultural convention is “better”. Is there a boundary between the quality of innovations?
Conflicting conclusions must be anticipated because different measures emphasize different traits of games. Thus, answering the "better" question requires determining which aspects of a game a given measure ignores or accentuates. The approach used here to address this concern is new; it appeals to a recent decomposition (or coordinate system) created for the space of games [9,10,11,12] (in what follows, the [9,10,11] papers are designated by [JS1], and the book [12] by [JS2]). There are many ways to decompose games, where the emphases reflect different objectives. An early approach was to express a game in terms of its zero sum and identical play components, which plays a role in the more recent Kalai and Kalai bargaining solution [13]. Others include examining harmonic and potential games [14] and strategic behavior such as in [15,16]. While some overlap must be expected, the material in [JS1] and [JS2] appears to be the first to strictly separate and emphasize Nash and non-Nash structures.
Indeed, in [JS1], [JS2], and this paper, appropriate aspects of a game are used to extract all information, and only this information, needed for the game’s Nash structures; this is the game’s “Nash” component. Other coordinate directions (orthogonal to, and hence independent of the Nash structures) identify those features of a game that require interaction among the players, such as coordination, cooperation, externalities, and so forth. By isolating the attributes that induce behavior among players, these terms define the game’s “Behavioral” component. The final component, the kernel, is akin to adding the same value to each of a player’s payoffs. While this is a valuable variable with transferable assets, or to avoid having games with negative payoffs, it plays no role in the analysis of most settings. In [JS2], the [JS1] decomposition is extended to handle more player and strategies.2
One objective of this current paper is to develop a coordinate system that is more convenient to use with a wide variety of choices that include potential games (a later paper extends this to more players and strategies). An advantage of using these coordinates is that they intuitively organize the strategic and payoff structures of all games. This is achieved by extracting from each payoff entry the behavioral portions that capture ways in which players agree or disagree (e.g., in accepting or rejecting an innovation) and affect payoff values. Of interest is how this structure applies to all normal form games. When placing the emphasis on potential games, these coordinates cover their full seven-dimensional space, so they subsume the lower dimensional models in the literature.
By being a change of basis of the original decomposition, this system still highlights the unexpected facts that Nash equilibria and similar solution concepts (e.g., solution notions based on “best response” such as standard Quantal Response Equilibria) ignore nontrivial aspects of a game’s payoff structure; see [11]. In fact, this is the precise feature that answers certain concerns in the innovation diffusion literature. Young’s example [5], for instance, turns out to combine disagreement between two natural measures of "good" outcomes: one measure depends on unilateral deviations; the other aggregates the collective payoff. Newton and Sercombe re-parametrize Young’s model to further explore this disagreement [7]. As we show, Young’s example and the Newton and Sercombe arguments stem from a game’s tension between group cooperative behavior and individualistic forces.
Other contributions of this current paper are to
- describe the payoff structure of these games;
- characterize the full seven-dimensional space of potential games;
- analyze the behavioral tension between individual and cooperative forces in potential games;
- explain why different measures can reach different conclusions; and,
- relate the results to risk-dominance when possible.
The paper begins with an overview of the coordinate system for all normal form games. After identifying the source of all conflict with symmetric potential games, the full seven-dimensional class is described.
2. Overview of the Coordinate System
As standard with coordinate systems, the one developed for games in [JS1] can be adjusted to meet other needs. The choice given here [JS2] reflects central features of potential games.
Consider an arbitrary game (Table 1), where each agent’s strategies are labeled and (cells also will be denoted by TL (top-left), BR (bottom-right), etc.).

Table 1.
Arbitrary Game in Normal-Form.
A weakness of this representation is captured by the Table 2 game. Information about which strategy each player prefers, whether they do, or do not want to coordinate with the other player, and where to find group opportunities is packed into the entries. Yet, in general, this structure is not readily available from the Table 2 form.

Table 2.
An Example.
The coordinate system described here significantly demystifies a game by unpacking its valued behavioral information. This is done by decomposing a game into four orthogonal components, where each captures a specified essential trait: individual preference, individual coordinative pressures, pure externality (or Behavioral), and kernel components (see Table 3) (the orthogonality comment follows by identifying games with vectors). The original game is the sum of the four parts.

Table 3.
The Four Components of a Game.
To associate these components with behavioral traits of any game, the individual preference component identifies an agent’s inherent preference for strategy or . If , then agent i prefers strategy to independent of what the other agent plays. In turn, means that agent i’s individual preference is for strategy . The Table 2 values will turn out to be , which indicates that both players prefer (or TL).
The coordinative pressure component reflects a conforming stress a game imposes on agent j. Independent of the sign, a value rewards agent j a positive payoff by conforming with agent i’s preferred choice. Conversely, when , agent j’s payoff is improved by playing a strategy different than what agent i wants. With Table 2, while , so neither player is strategically supportive of personally reinforcing the other agent’s preferred choice.
The pure externality component represents consequences that an agent’s action imposes on the other agent.3 If agent i plays , for instance, then, independent of what agent j does, agent j receives an extra payoff! Acting alone, however, agent j is powerless to change this portion of the payoff. To see why this statement is true, should Column select L in Table 3c, then no matter what strategy Row chooses, this extra advantage remains . The sign of indicates which of agent i’s strategies contributes to, or detracts from, agent j’s payoff. In Table 2, the values convert TR into a potential group opportunity.
A subtle but important behavioral distinction is reflected by the and terms. The values capture whether, in seeking a personally preferred (Nash) outcome, an agent should, or should not, coordinate with the other agent’s preferred interests. In contrast, the values identify externalities and opportunities to encourage both to cooperate. For a supporting story, suppose the strategies are to take highway 1 or to drive to a desired location. A value indicates the first agent’s personal preference to avoid being on the same highway as the second. However, it should it be winter time, then the second agent, who always has a truck with a plow when driving on highway 1, creates a positive externality that can be captured with a value.
The final component is the kernel, which for Table 2 is . This can be treated as an inflationary term that adds the same value to each of the agent’s payoffs. Methods that compare payoffs cancel the kernel value, so, as in this paper, the kernel can be ignored.
It is important to point out that the individual and coordinative pressure components contain all information from a game that is needed to compute the Nash equilibrium and to analyze related strategic solution concepts [JS1]. To appreciate why this is so, recall that the Nash information relies on payoff comparisons with unilateral deviations. But with the pure externality and kernel components, all unilateral payoff differences equal zero, so they contain no Nash information. This also means that “best response” solutions and methods ignore, and are not affected by the wealth of a game’s information (for explicit examples, see [11]).
By involving eight orthogonal directions and independent variables, these components span the eight-dimensional space of all games. Consequently, any game can be expressed and analyzed in terms of these eight coordinates. The equations converting a game into this form are
For interpretations, is agent j’s average payoff, is agent j’s average payoff should the other agent play 1 minus the inflationary value, is half the difference of agent j’s average payoff if the other agent plays 1 and the average if the other agent plays , and is half the difference of the agent’s average TL, BR payoff, and average BL and TR payoff.
To illustrate the derivation of Equation (1), the value of the Table 4a game is computed. All that is needed is a standard vector analysis to find how much of game is in the coordinate direction, which is denoted by , where and . The sum of the squares of the entries (which in the following notation equals ) is so, according to vector analysis, . Here, is the sum of the products of corresponding entries from each cell. (Identifying a game’s payoffs with components of a vector in , is the scalar product of the vectors.) In this example, , so . Similarly, by defining a corresponding , the remaining values are and The Equation (1) expressions can be recovered in this manner.

Table 4.
Decomposing a game.
This decomposition simplifies the analysis by extracting the portion from each payoff that contributes to these different attributes of a game. Illustrating with Table 1, rather than handling each entry separately, behavior can be analyzed with the separated impact of the components. For instance, the entry is which, for Table 2, is
To connect this notation with [JS1], [JS2], a game’s Nash component, denoted by , is the sum of the individual preference and coordinative pressure components as given in Table 5.

Table 5.
The Nash component.
Principal facts about games follow.4 As a reminder, a game is a potential game if there exists a global payoff function that aggregates the unilateral incentive structure of the game. More precisely, the payoff difference obtained by an agent unilaterally deviating is reflected in the change of the potential function. Potential games are often called “common interest” games. Coordination games have pure strategy Nash equilibria precisely where the agents play the same strategy (i.e., the strategy profiles and ). On the other hand, anti-coordination games have pure strategy Nash equilibria when the agents play different strategies (i.e., the strategy profiles and ).
Theorem 1.
Generically (that is, all and entries are nonzero), the following hold for normal form games .
- 1.
- A cell is pure Nash if and only if all of the cell’s entries are positive.
- 2.
- is a potential game if and only if .
- 3.
- is a coordination game if and only if , and . If , then is an anti-coordination game.
- 4.
- All of the payoffs in a normal-form game, as in Table 3, can be expressed with the utility functions for agents 1 and 2 given by, respectively,where and represent the strategy choice (either or ) of agents 1 and 2,
- 5.
- A potential function for a game with components described in Table 3 can be transformed into
- 6.
- A potential game’s potential function is invariant to the pure externality and kernel components.
To explain certain comments, recall that a potential game has a potential function; if an agent changes a strategy, the change in the agent’s payoff equals the change in the potential function. To illustrate, suppose the first agent changes from strategy to , while agent 2 remains at According to Table 2, the change in the first agent’s payoff is
or for potential games. According to Equation (2), the change in the potential is the same value
Statement 1 is proved in [JS1]. To prove the second assertion, in (Chap. 2 of [JS2]) it is shown that game is a potential game if and only if it is orthogonal to the matching pennies game ; 5this orthogonality condition is . A direct computation shows that the individual preference, pure externality, and kernel components always satisfy this condition. The coordinative pressure component satisfies the condition if and only if .
Statement 4 is a direct computation. Statement 5 is a direct computation showing that changes in an agent’s strategy have the same change in the potential function as in the player’s payoff. Statement 6 follows, because (Equation (2)) does not have or values. A proof of the remaining statement 3 is in [JS2]. For intuition, the players in a coordination game coordinate their strategies, which is the defining feature of the coordinative pressure component. Thus, for to be a coordination game, the values must dominate the game’s Nash structure.
3. Disagreement in Potential Games
These coordinates lead to explanations why different behavioral measures can differ about which is the "better" outcome for certain games. This discussion is motivated by innovation diffusion, which is typically modeled by using coordination games with two equilibria, so a key step is to identify the preferred equilibria. A common choice is the risk-dominant pure Nash equilibria. In part, this is because these equilibria have been connected to the long-run behavior of dynamics, such as log-linear learning [18]. Because a coordination game is a potential game, the potential function’s global maximum is the risk-dominant equilibrium (Theorem 2).
However, as developed next, there are many games where a maximizing strategy for the potential function differs from the profile that maximizes social welfare. This difference is what allows agents to do “better” by using a profile other than the one leading to the risk-dominant equilibrium. Young [5,6] creates such an example using the utilitarian measure of social welfare, which sums all of the payoffs in a given strategy profile, and Newton and Sercombe [7] discuss similar ideas. A first concern is whether their examples are sufficiently isolated that they can be ignored, or whether they are so prevalent that they must be taken seriously. As we show, the second holds.
An explanation for what causes these conflicting conclusions emerges from the Table 2 decomposition and Theorem 1. A way to illustrate these results is to create any number of new, more complex examples. To do so, start with the fact (Theorem 2.5 in [JS2]) that with games and two Nash equilibria, a Nash cell is risk dominant over the other Nash cell if and only if the product of the values (see Table 4) of the first is larger than the product of the values of the second. (To handle some of our needs, this result is refined in Theorem 2.) Of significance is that, although the terms obviously affect payoff values, they play no role in this risk-adverse dominance analysis.
To illustrate, let (Theorems 1-2; to have a potential game) and (Theorem 1-3; to have a coordination game). This defines the Table 6a game where the TL Nash cell (with ) is risk dominant over the BR Nash cell (with ). There remain simple ways to modify this game that make the payoffs of any desired cell, say BR, more attractive than the risk dominant TL. All that is needed is to select values that increase the payoffs for the appropriate Table 3c cell; for the BR choice, this requires choosing negative values (Table 3c). Although these values never affect the risk-dominant analysis, they enhance each player’s BR payoff while reducing their TL payoffs. The choices define the Table 6b game where each player receives a significantly larger payoff from BR than from the risk dominant TL! In both games, the Nash and risk dominance structures remain unchanged.

Table 6.
Conflicting measures.
These coordinates make it possible to easily create a two-dimensional family of games with such properties. To do so, add Table 3c to the Table 6a game, and then select appropriate values to emphasize the payoffs of different cells. For instance, using Young’s welfare measure (the sum of a cell’s payoffs), no matter which cell is selected, suitable values exist to make that cell preferred to TL. It follows from the Table 3c structure, for instance, that a way to enhance the TR payoffs is to use and choices. Adding these values to the Table 6a game defines the TR cell values of and while the TL values are and . Thus, the sum of TR cell values dominates the sum of TL values if and only if
The coordinates also make it possible to compare other measures by mimicking the above approach. Games with payoff dominant strategies that differ from the risk adverse ones, for example, require appropriate values. To explain, if BR is risk dominant, then, as in the Equation (4) game (from Section 2.6.4 in [JS2]), the product of its values from BR in (first bimatrix on the right) is larger than the product of the TL values. This product condition ensures that the only way the payoff and risk dominant cells can differ is by introducing TL components; this is illustrated with in the second bimatrix in Equation (4). More generally and using just elementary algebra as in Equation (3), the regions (in the space of games) where the two concepts differ now can finally be determined.
For another measure, consider the 50–50 choice. This is where, absent any information about an opponent, it seems reasonable to assume there is a 50–50 chance the opponent will select one Nash cell over the other. This assumption suggests using an expected value analysis to identify which strategy a player should select. To discover what coordinate information this measure uses, if TL and BR are the two Nash cells, then for Row and this 50–50 assumption, the expected return from playing T is Similarly, the expected value of playing B is Consequently, an agent’s larger value completely determines the 50-50 choice. However, if the risk adverse cell of is not also payoff dominant, as true with the first bimatrix on the right in Equation (4), and if both players adopt the 50-50 measure, they will select a non-Nash outcome. Indeed, in Equation (4), BR is risk dominant, TL is payoff dominant, and BL, which is not a Nash cell (and Pareto inferior to both Nash cells), is the 50–50 choice. Again, elementary algebra of the Equation (3) form identifies the large region of games where this behavior can arise. (By using appropriate values, it is easy to create 50–50 outcomes that are disastrous.)
3.1. The Potential and Welfare Functions
Moving beyond examples, these coordinates can fully identify those games for which different measures agree or disagree, which is one of the objectives of this paper. The importance of this analysis is that it underscores our earlier comment that this conflict between the conclusions of measures is a fundamental concern that is suffered by a surprisingly large percentage of all games.
Our outcomes are described using maps of the space of games. The maps show where the potential and social welfare functions (e.g., the ones used by Young [5,6] and Newton and Sercombe [7]) agree, or disagree, on which is the "better" choice of two equilibria. Not only do these diagrams demonstrate the preponderance of this conflict, but they identify which behavior a specific game will experience. As an illustration, the dark regions of Figure 1 single out those potential games (so ), where and , which are without conflict; for games in the unshaded regions, different measures support different outcomes.
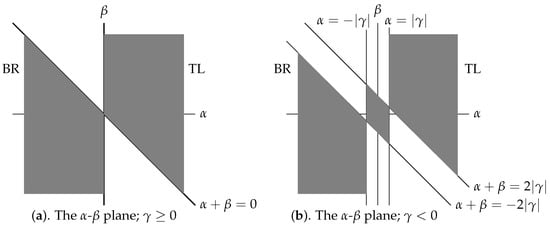
Figure 1.
Conflict and agreement with values.
Thanks to the coordinate system for games, the game theoretic analysis is surprisingly simple; it merely uses a slightly more abstract version of the Equation (3) analysis. To illustrate with the above 50-50 discussion, if the Nash cells are TL and BR, then are all positive (if the Nash cells are BL and TR, all of these entries are negative). Consequently, the two surfaces and separate which one of an agent’s values is larger. Even though the discussion applies to the four dimensional space of values, one can envision the huge wedges these surfaces define where the values force the 50–50 approach to select a non-Nash outcome.
A similar approach applies to all of the maps derived here. In Figure 1a, the dividing surface separating which Nash cell is selected by potential function outcomes is ; if , the game’s top Nash choice for the potential function is TL; if , the top Nash choice is BR. However, the social welfare conclusion is influenced by values, so it will turn out that the separating line between a social welfare function selecting TL or BR is the line. Above this line, TR is the preferred Nash choice; below it is BR. Given this legend, Figure 1a demonstrates those games for which the different measures agree or disagree about the top choices, and the magnitude of the problem. Stated simply, regions that emphasize behavioral terms place emphasis on payoff and social welfare dominant measures; regions that emphasize Nash strategic terms emphasize risk dominant measures.
Stated differently, difficulties in what follows do not reflect the game theory; the coordinate system handles all of these problems. Instead, all of the complications (there are some) reflect the geometric intricacy of the seven-dimensional space of potential games. Consequently, readers that are interested in applying this material to specific games should emphasize the maps and their legends (given in the associated theorems). Readers that are interested in the geometry of the space of potential functions will find the following technical analysis of value. However, first, a fundamental conclusion about potential games is derived.
3.2. A Basic “Risk Dominant” Theorem
The coordinates explicitly display a tension between what individuals can achieve on their own (Nash behavior) and with cooperative forces. With a focus on individualistic forces, the potential function is useful because its local maxima are pure Nash equilibria. Even more, as known, the potential’s global maximum is the risk dominant equilibrium. This fact is re-derived for potential games in a manner that now highlights the roles of a potential game’s coordinates.
Theorem 2.
For a potential game , its potential function has a global maximum at the strategy profile if and only if is ’s risk-dominant Nash equilibrium. With two Nash equilibria where one is risk dominant, is the risk dominant strategy if and only if the following inequalities hold
As shown in the proof, inequality c identifies the Nash cells; e.g., if , then , so the Nash cells are BL and TR. With two Nash cells, the inequality a identifies which one is a global maximum of the potential function. Similarly, inequality b requires to have a sufficiently large value to create two Nash cells. Of importance, Equation (5) does not include values!
To illustrate these inequalities, let and . By satisfying Equation (5b), there are two Nash cells. According to Equation (5c), , so , which positions the Nash cells at TL and BR. From Equation (5a), , or , so the risk dominant strategy is the BR cell. Conversely, to create an example where a desired cell, say TR, is risk dominant, the values require (Equation (5c)) and (Equation (5a)) Finally, select that satisfies Equation (5b); e.g., and suffice.
The Equation (5) inequalities lead to the following conclusion.
Corollary 1.
If a potential game has two pure Nash equilibria where one is risk dominant, then is a coordination game. If , the Nash cells are at TL and BR, where is a coordination game. If , the Nash cells are at BL and TR, where is an anti-coordination game.6
Proof of Corollary 1.
According to Theorem 2, the Corollary 1 hypothesis ensures that Equation (5) hold. With the b inequality, it follows from Theorem 1-3 that is a coordination game. In a game, pure Nash cells are diagonally opposite. If , it follows from Equation (5), c that the Nash strategies satisfy so the Nash cells are at TL (for ) and BR (for ), and that this is a coordination game. Similarly, if , then , so the Nash cells are at BL (for ) and TR (for ) to define an anti-coordination game. □
Proof of Theorem 2.
In a non-degenerate case (i.e., is not a constant function), P has a maximum, so there exists at least one pure Nash cell. If a game has a unique pure strategy Nash equilibrium, then, by default, it is risk-dominant and P’s unique maximum.
Assume there are two Nash cells; properties that the potential, P, must satisfy at a global maximum are derived. Pure Nash equilibria must be diametrically opposite in a normal form representation, so if has two pure strategy Nash equilibria where one is , then the other one is at . Consequently, if P has a global maximum at , then P has a local maximum at , so According to Equation (2), this inequality holds iff , which is inequality Equation (5)a.
The local maximum structure of requires that and Again, according to Equation (2), the first inequality is true if
or . Similarly, the second inequality is true iff Thus, for a potential game with two Nash cells, P has a global maximum at iff
The last inequality follows from the first one, which requires at least one of to be positive. Thus, the inequality follows from either the second or third inequality.
All that is needed to establish the equivalence of the Equation (6) inequalities and those of Equation (5) is that Equation (5b) is equivalent to the two middle inequalities of Equation (6). Equation (5b) implies the two middle inequalities of Equation (6) is immediate. In the opposite direction, the first Equation (6) inequality requires at least one of or to be positive. If it is , then because , this positive term requires the appropriate middle inequality of Equation (6) to be . If it holds for both terms, the proof is completed. If it holds for only one term, say , but , then the first Equation (6) inequality requires that , which completes the proof.
The second step requires showing that is a risk-dominant Nash equilibrium if Equation (5) holds. According to Harsanyi and Selten (1988), is a game’s risk-dominant Nash equilibrium if
which is This inequality reduces to
If , the Nash cells are at TL and BR, so both entries of these two Table 4 cells must be positive (Theorem 1-1). For the TL cell, this means that , while for the BR cell it requires Consequently, and : inequalities b and c of Equation (5) are satisfied. That inequality a of Equation (5) holds follows from and Equation (8).
A consequence of Theorem 2 is that the potential function can serve as a comparison measure of Nash outcomes. Other natural measures reflect the overall well-being of all agents, such as the utilitarian social welfare function that sums each strategy profile’s payoffs. To obtain precise conclusions, our results use this social welfare function. However, as indicated later, everything extends to several other measures.
3.3. Symmetric Games
Without question, it is difficult to understand the structures of a four-dimensional object, leave alone the seven-dimensions of the space of potential games. Thus, to underscore the ideas, we start with the simpler (but important) symmetric games (all symmetric games are potential games); doing so reduces the dimension of the space of games from seven to four (with the kernel). This is where and Ignoring the kernel term, the coordinates are given in Table 7.

Table 7.
Decomposition for a symmetric potential game.
To interpret Table 7, the Nash entries combine terms, where each agent prefers a particular strategy independent of what the other agent does (if , each agent prefers to play 1; if each agent prefers ) with terms that impose coordination pressures. That is, if , the game’s Nash structure inflicts a pressure on both agents to coordinate; if , the game’s joint pressure is for anti-coordination. With symmetric games, the payoffs for both agents agree at TL and at BR, so if one of these cells is social welfare top-ranked (the sum of the entries is larger than the sum of entries of any other cell), the cell also has the stronger property of being payoff dominant.
All symmetric games can be expressed with these four variables (Equation (1)). Ignoring , the remaining variables define a three-dimensional system. To tie all of this in with commonly used symmetric games, if BR is the sole Nash point, then the above defines a Prisoner’s Dilemma game if and , the second of which reduces to . Similarly, the Hawk–Dove game with Nash points at BL and TR, and “hawk” strategy as , has and for the Nash points, and to enhance the BR payoffs, so , , and A coordination game simply has (these inequalities allow the different games to easily be located in Figure 1 and elsewhere). As stated, because , it follows (Theorem 1-2) that all symmetric games are potential games with the potential function (Equation (2))
A computation (Table 7) proves that the social welfare function (the sum of a cell’s entries) is
Our goal is to identify those games for which the potential and social functions agree, or disagree, on the ordering of strategies. Here, the following results are useful.
Theorem 3.
A symmetric potential game satisfies
If , the potential function and the welfare function rankings of ’s four cells agree.
Both the potential and welfare functions are indifferent about the ranking of the BL and TR cells, denoted as . If one of these cells is a Nash cell for , then so is the other one, but neither is risk dominant.
Equation (11) explicitly demonstrates that values—the game’s behavioral or externality values—are solely responsible for all of the differences between how the potential and social welfare functions rank ’s cells.
Proof.
Adding and subtracting to Equation (10) leads to Equation (11). Thus, if , then so both functions have the same ranking of ’s four cells.
The BL and TR cells correspond, respectively, to and , where Thus, (Equation (11)), the , and P values for each of these cells is . As both measures have the same value for each cell, both have a tie ranking for the two cells denoted by .
The Nash entries of BL and TR are the same but in different order (Table 6a). Thus, if both entries of one of these cells are positive, then so are both entries of the other. This means that both are Nash cells (Theorem 1-1). The risk dominant assertion follows because inequality a of Equation (5) is not satisfied; it equals zero. Equivalently, P does not have a unique global maximum in this case. □
A Map of Games and Symmetries
A portion of a map that describes the structure of all games (Chapter 3, [JS2]) is expanded here to concentrate on the symmetric games. While variables require a three-dimensional space, the potential function does not depend on , so Figure 2a highlights the - plane. Treat the positive axis as coming out orthogonal to the page.
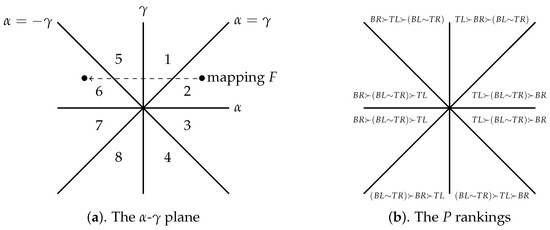
Figure 2.
The structures.
Changes in the potential game and P (Equation (9)) depend on and values, which suggests dividing the - plane into sectors where these terms have different signs. That is, divide the plane into eight regions (Figure 2a) with the lines , , , and . The first two lines represent changes in a game’s structure by varying the and signs. For instance, reversing the sign of changes which strategy the agents prefer; swapping the sign exchanges a game’s coordination, anti-coordination features. The other two lines are where certain payoffs (Table 6a) change sign, which affects the game’s Nash structure. The labelling of the regions follows:
A natural symmetry simplifies the analysis. In Table 6, interchanging each matrix’s rows and then columns creates an equivalent game, where the cell in the original becomes the cell in the image. This equivalent game is identified in Figure 2a with the mapping
Geometrically, F flips a point on the right (a symmetric potential game) about the axis to a point on the left (which corresponds to the described changing of rows and columns of the original game); e.g., in Figure 2a, the bullet in region 2 is flipped to the bullet in region 6. Similarly, the original value is flipped to the other side of the - plane. Consequently, anything stated about a strategy or cell for a game in region k holds for a strategy or cell of the corresponding game in region (). Thanks to this symmetry, by determining the P ranking of region k to the right of the axis, the P ranking of region is also known.
The following theorem describes each region’s P ranking. The reason the decomposition structure simplifies the analysis is that all of the comments about Nash cells follow directly from Table 6a. If, for instance, (region 1), then only cells TL and BR have all positive entries (Table 6a), so they are the only Nash cells. Similarly, if (region 4), only cells BL and TR have all positive entries, so they are the Nash cells (Theorem 1-1). Each cell’s P value is specified in matrix Table 8a, so the P ranking of the cells follows immediately. Region 2, for instance, has , so TL is P’s top-ranked cell. Whether BL is P-ranked over BR holds (Table 8a) iff , or , which is the case. This leads to P’s ranking of for all region 2 games (here, means A is ranked over B and means they are tied). Each cell’s ’s value (half the social welfare function), which comes from Equation (11), is given in Table 8b.

Table 8.
A symmetric potential game’s P and values.
Theorem 4.
The following hold for a symmetric potential game.
- 1.
- Region 1 has Nash equilibria at TL and BR, where TL is risk dominant. The P ranking of the cells is The region 5 P ranking is ; BR is risk dominant.
- 2.
- Regions 2 and 3 have a single Nash cell at TL, where, for each region, the P ranking of the cells is The P ranking in regions 6 and 7 is
- 3.
- Region 4 has Nash cells at BL and TR, where neither is risk dominant. The P ranking is The region 8 P ranking is
The content of this theorem is displayed in Figure 2b. Notice, with , the potential function has BR bottom ranked unless BR is a Nash cell. This makes sense; means (Table 3a) that both agents prefer a “” strategy, so they prefer T and L. In fact, with , the only way TL loses its top-ranked P status is with a sufficiently strong negative value (region 4 of Figure 2a). This also makes sense; a negative value (Table 3b) captures the game’s anti-coordination flavor, which, if strong enough, can crown BL and TR as Nash cells.
Similar comments hold for ; this is because TL and BR reverse roles in the P rankings (properties of F (Equation (12)). Thus, the P ranking of region 1 is so the P ranking of region 5 is Accordingly, for , P always bottom-ranks TL unless TL is a Nash cell, which reflects that is where the players have a preference for B and R.
The next theorem describes where the potential and social welfare function rankings agree or disagree. As its proof relies on Table 8b values, it is carried out in the same manner as for Theorem 4. Namely, to determine whether TL is ranked above BL or TR, it must be determined (Table 8b) whether , or whether . Next, according to (Table 8b), the social welfare function ranks BR above BL (or TR) iff , or . Thus, if , the social welfare ranking is
Theorem 5.
For a symmetric potential game with a coordinative flavor of , the social welfare function (Equation (10)) ranks the cells in the following manner:
- 1.
- If the ranking is and TL is payoff dominant,
- 2.
- if , the ranking is and TL is payoff dominant,
- 3.
- if , the ranking is and BR is payoff dominant, and
- 4.
- if , the ranking is where BR is payoff dominant.
For games with an anti-coordinative flavor of , the social welfare rankings are
- 5.
- if , the ranking is and TL is payoff dominant;
- 6.
- if , the ranking is ,
- 7.
- if , the ranking is and
- 8.
- if , the ranking is and BR is payoff dominant.
As with Theorem 4, this theorem ignores certain equalities, such as , but the social welfare ranking is the obvious choice. This equality captures the transition between parts 1 and 2, so its associated ranking is
A message of these theorems is to anticipate strong differences between the potential and social welfare rankings. Each game in region 1 of Figure 2a, for instance, has the unique P ranking of , so TL is P’s “best” cell. In contrast, each game in each region has four different social welfare rankings7 where most of them involve ranking conflicts! In region 1 of Figure 2a, for instance, an admissible social welfare ranking (Theorem 5-4) is , where the payoff dominant BR is treated as being significantly better than P’s top choice of TL.
The coordinates explicitly identify why these differences arise: The potential function ignores , while the values contribute to the social welfare rankings. By influencing a game’s payoffs and identifying (positive or negative) externalities that players can impose on each other, the values constitute important information about the game. To illustrate, Table 5 has two different symmetric games; they differ only in that the first game has with no externalities while the second has , which is a sizable externality favoring BR payoffs (Table 6b). Both of the games are in region 1 of Figure 2, so both have the same P ranking of (Theorem 4-1), where TL is judged the better of the two Nash cells. However, the social welfare ranking for the Table 5b game is , which disagrees with the P ranking by crowning BR as the superior cell. By examining this Table 5b game, which includes externality information, it would seem to be difficult to argue otherwise.
Viewed from this externality perspective, Theorem 5 makes excellent sense. It asserts that, with sufficiently large positive values, the social welfare function favors TL, which must be expected. The decomposition (Table 6b) requires to favor TL payoffs. Conversely, enhances the BR payoffs.
The potential and social welfare rankings can even reverse each other. According to Theorem 4-2, all games in region 2 of Figure 2a have a single Nash cell with the P ranking of This region requires , so the Table 9a example is constructed with . For this game, where , the P and social welfare rankings agree. To modify the game to obtain the reversed social welfare ranking of , where the non-Nash cell BR will be the social welfare function’s best choice, Theorem 5 describes precisely what to do; select values that satisfy . For Table 9, this means that The choice leads to the Table 9b game, where the social welfare ranking reverses that of the potential function. Again, it is difficult to argue against this game’s social welfare ranking.

Table 9.
Conflicting measures.
4. Conflict and Agreement
These negative conclusions, where potential and social welfare rankings disagree, can be overly refined for many purposes. Similar to an election, the interest may be in the winner rather than who is in second, third, or fourth place. Thus, an effective but cruder measure is to determine where potential and social welfare functions have the same top-ranked cell.
All of the conflict in potential and social welfare rankings are strictly caused by values, which suggests identifying those values that allow the same potential and social welfare preferred cell. It is encouraging how answers follow from and comparisons.
Corollary 2.
For symmetric games, the following hold for :
- 1.
- The potential and social welfare functions have TL as the top-ranked and payoff dominant cell for and (shaded Figure 1a region on the right).
- 2.
- If and (unshaded region region on the right of Figure 1a), then BR is the social welfare top-ranked and payoff dominant cell, but the top-ranked P cell is .
- 3.
- If and (shaded Figure 1a region on the left), both functions have the BR cell top-ranked. BR also is the payoff dominant cell.
- 4.
- If and (unshaded region on the left of Figure 1a), TL is the social welfare top-ranked and payoff dominant cell, while the P top-ranked cell is .
The content of this corollary serves as a legend for the Figure 1a map; the shaded regions are where both measures have the same top-ranked cell. A simple way to interpret this figure is that for all games to the right of the axis (), P’s top-ranked cell is TL, while to the left it is BR. In contrast, above the slanted line, the social welfare’s top-ranked cell is TL, while below it is BR. Thus, in the unshaded regions, one measure has BR top-ranked, while the other has TL.
This corollary and Figure 1a show that if the value (indicating a preference of the agents for T and L or B and R) is not overly hindered by the externality forces (e.g., if and ) then the potential and social welfare functions share the same top ranked cell. But should conflict arise between these two fundamental variables, where the and values favor cells in opposite directions, disagreement arises between the choices of the top ranked P and social welfare cells.
Proof.
The proof follows directly from Table 8. With P’s top-ranked cell is TL for (to the right of the Figure 1a axis), and BR for (Table 8a). According to Table 8b, the social welfare’s top-ranked cell is TL iff , or iff ; this is the region above the Figure 1a slanted line. The same computation shows that the social welfare’s top-ranked cell is BR for the region below the slanted line. This completes the proof. □
Everything becomes slightly more complicated with . The reason is that this anti-coordination factor permits BL and TR to become Nash cells. This characteristic is manifested in Figure 1b, where the Figure 1a and lines are separated into strips.
The content of the next corollary is captured by Figure 1b, where the potential and social welfare’s top-ranked cells agree in the three shaded regions. To interpret Figure 1b, P’s top-ranked cell is BR for all games to the left of the vertical strip (), cells BL and TR (or ) in the vertical strip (), and cell TL to the right of the vertical strip (). Similarly, the social welfare’s top-ranked cell is BR below the slanted strip, in the slanted strip, and TL above the slanted strip. As , the width of the strips shrink and Figure 1b merges into Figure 1a.
Corollary 3.
For symmetric potential games, the following hold for :
- 1.
- The top-ranked P cell is TL iff (the Figure 1b region to the right of the vertical line). In this region, the social welfare ranking is TL (to agree with P) for (shaded region on the right of Figure 1b), but conflicts with P’s choice with the social welfare top-ranking of if (the portion of the strip below the shaded region on the right of Figure 1b), and with the top-ranked BR for (the unshaded region below the strip on the right of Figure 1b).
- 2.
- For (the vertical strip of Figure 1b), both BL and TR are P’s top-ranked cells with the ranking . In this strip, the social welfare function has the same ranking only if (the shaded trapezoid). Outside of this region in the strip, the social welfare top-ranked cell differs from P’s choice by being TL for (above the trapezoid) and BR for (below the trapezoid).
- 3.
- The top-ranked cell for P is BR for (to the left of the vertical strip). The social welfare function’s top-ranked cell also is BR for (shaded Figure 1b region on the left). However, in this region, the social welfare function has BL and TR top ranked, or , for (the portion of the slanted strip above the shaded region) and TL top ranked for (above the slanted strip).
Proof.
The proof follows directly from Table 8. With , it follows from Table 8a that P’s top-ranked cell is TL if it is preferred to either BL or TR, which is if or if . This is the Figure 1b region to the right of the vertical line. Similarly, P’s top-ranked cell is BR if , or if ; this is the region to the left of the vertical line. The same computation shows that in the vertical strip , P’s top-ranked cells are the two Nash cells BL and TR, where P’s ranking is .
Using the same approach with Table 8b, it follows that the social welfare’s top-ranked cell is TL if it has a higher score than BL or TR, which is if , or if This is the region above the slanted line. Similarly, the social welfare top ranked cells are for , which is the slanted strip (which expanded the Figure 1a slanting line), and BR for , which is the region below the slanting strip. This completes the proof. □
4.1. Changing
The cause of conflict between potential and social welfare rankings now is clear; the first ignores values while the second depends upon them. However, a feature of the previous section is that if TL or BR ended up being the social welfare top-ranked cell, it also was the payoff dominant cell. This property is a direct consequence of the symmetric game structure where the behavioral terms (Table 6b) always favored one of these two cells.
To recognize the many other possibilities, change the structure from to . This affects Table 6b by changing the sign of player 2’s entries, so the game’s externality features now emphasize either BL or TR. The social welfare function becomes
A reason for considering this case is that any can be uniquely expressed as
Thus, combining Figure 1 with the impact of ( captures the general complexity.
Because the decomposition isolates appropriate variables for each measure, Table 8 is the main tool to derive the Figure 3 results. In this new setting, Table 8 is replaced with Table 10, where part a restates the potential function values for each cell and b gives half of the social welfare function’s values.
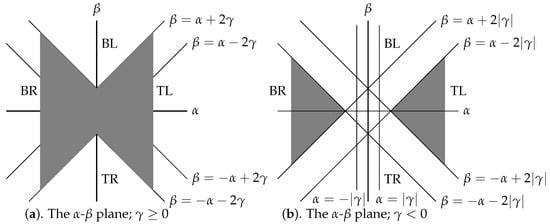
Figure 3.
More conflict and agreement with values.

Table 10.
A quasi-symmetric potential game’s P and values, with .
As with Figure 1a, if then P’s top-ranked cell is TL for and BR for The same holds for Figure 3a. According to Table 10b, the social welfare function ranks TL over BL if , or if . In Fig. Figure 3a, this is the region below the slanted line. Similarly, the social welfare function ranks TL over TR if , or , which is the Figure 3a region above the line. P’s top ranked cell is BR if , which is the Figure 3a region to the left of the axis. A similar analysis shows that the social welfare function ranks BR above TR if , or the region above the Figure 3a line. Finally, this function ranks BR above BL if , which is the region below the line.
Consequently, agreement between the two measure’s top-ranked cell is in Figure 3a shaded regions, where BR is the common choice to the left of the axis and TL is for the region to the left. Conflict occurs in the unshaded region where BL is the welfare’s top-cell on the top and TR is for the region below. Again, these outcomes capture the structure where, now, positive values emphasize the BL cell and negative values enhance the TR entries. Contrary to Figure 1a, the upper unshaded region now is where BL, rather than TL, is the welfare function’s top-ranked cell.
Consistent with Figure 1b, the situation becomes more complicated with the anti-coordination Again, P’s top ranked cell is BR to the left of the vertical strip, in the strip, and TR to the right of the strip. Similar algebraic comparisons show that the social welfare’s top-ranked cell is BL in the upper unshaded region of Figure 3b, including the portion of the axis. Similarly, TR is the welfare function’s top-ranked cell in the lower unshaded region. Consequently, the two large shaded regions are where agreement occurs (going from left to right, BR, TL).
With the Table 6a Nash structure, outcomes for all possible values can be computed from Figure 1 and Figure 3. To illustrate with , it follows from that BR is P’s top-ranked cell. The information for the welfare function comes from Equation (14) where To find half of the welfare functions value, substitute in Table 8b, substitute in Equation (13b), and add the values. It already follows from plotting these values in Figure 1b and Figure 3b that the outcome is either TL or BL.
4.2. Changing
The general setting for a potential game involves variables . This suggests mimicking what was done with by carrying out an analysis using ; this is simple, but not necessary. The reason is that most needed information about P’s top-ranked cell comes from Equation (5). As this expression shows, with appropriate choices of , , and , any cell can be selected to be P’s risk-dominant, top-ranked choice, any admissible pair of cells can be Nash cells, where a designated one is risk dominant, and any cell can be selected to be the sole Nash cell. Finding how the behavioral terms (the values) can change which cell is the welfare function’s top-ranked cell has been reduced to elementary algebra.
All that is needed to obtain answers is to have a generalized form of Table 8 and Table 10, which is given in Table 11. The Table 11a values come from the general form of the potential function in Equation (2). The Table 11b values for the welfare function come from a direct computation of its equation

Table 11.
A potential game’s P and w values.
In the manner employed above, Theorem 6 is a sample of results. Here, use Equation (5) to determine the potential function structure, and Theorem 6 to compare social welfare (and ) values.
Theorem 6.
The social welfare function (Equation (15)) is maximized at TL if and only if and , where and denotes the agent who is not i. The welfare function is maximized at TR if and only if , and . The welfare function is maximized at BL if and only if , and . Finally, the welfare function is maximized at BR if and only if and , for .
5. Discussion
Questions regarding the various measures for game theory have proved to be difficult to analyze. There is an excellent reason for this complexity; answers must depend upon the particular payoffs of a game, but it was not clear what portions of each payoff contribute to which aspects of a game. As such, a surprising and welcomed property of the coordinate system is how it identifies how all of a game’s entries interact; the coordinates precisely dissect and extract from each payoff entry its contribution to the different attributes of a game.
Support for these comments come from equations such as Equation (9) for the potential function and Equation (10) for the welfare function. The different signs of and coefficients, for instance, nicely capture the complexity of a standard approach; it indicates there exists a twisting of certain portions of the payoff entries that are needed to carry out an analysis. The decomposition’s separation of which parts of a payoff entry affect Nash structures and which affect payoff and externality factors explain why different measures of a game can have different conclusions. What illustrates the power of doing so is how the discovery and proofs of many subtle results now reduce to elementary algebraic computations.
Our analysis described how and why differences can arise among potential function, payoff dominance, and social welfare conclusions about games. Everything extends more generally. As the decomposition demonstrates, expect methods, learning approaches, and measures that emphasize “best response”, comparisons of individual payoff differences, and obtaining Nash equilibria to ignore behavioral terms. Should the objective be to identify properties of Nash structures, doing so simplifies the analysis by eliminating the redundant (for a Nash analysis) variables. However, by not including terms, it must be expected that answers from these approaches about games will differ from those measures that capture the value of payoffs, such as the social welfare function and payoff dominance. They must; the two different classes of measures depend upon different information about the games.
Author Contributions
Conceptualization, all authors; investigation, all authors; methodology, all authors; supervision, all authors; validation, all authors; writing-original draft, all authors; writing-review and editing, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Our thanks for useful comments from two referees and an editor.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schelling, T.C. The Strategy of Conflict; Oxford University Press: New York, NY, USA, 1960. [Google Scholar]
- Lewis, D.K. Convention: A Philosophical Study; Harvard University Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Rosenthal, R.W. A class of games possessing pure-strategy Nash equilibria. Int. J. Game Theory 1973, 2, 65–67. [Google Scholar] [CrossRef]
- Monderer, D.; Shapley, L.S. Potential games. Games Econ. Behav. 1996, 14, 124–143. [Google Scholar] [CrossRef]
- Young, P. The Diffusion of Innovations in Social Networks. In The Economy as an Evolving Complex System; Oxford University Press: New York, NY, USA, 2006; Volume III, pp. 267–281. [Google Scholar]
- Young, P. The dynamics of social innovation. Proc. Natl. Acad. Sci. USA 2011, 108, 21285–21291. [Google Scholar] [CrossRef] [PubMed]
- Newton, J.; Sercombe, D. Agency, potential and contagion. Games Econ. Behav. 2020, 119, 79–97. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Selten, R. A General Theory of Equilibrium Selection in Games; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Jessie, D.T.; Saari, D.G. Cooperation in n-player repeated games. In The Mathematics of Decisions, Elections, and Games; American Mathematical Society: Providence, RI, USA, 2014; pp. 189–206. [Google Scholar]
- Jessie, D.T.; Saari, D.G. Strategic and Behavioral Decomposition of Games; IMBS Technical Report 15-05; University of California: Irvine, CA, USA, 2015. [Google Scholar]
- Jessie, D.T.; Saari, D.G. From the Luce Choice Axiom to the Quantal Response Equilibrium. J. Math. Psychol. 2016, 75, 1–9. [Google Scholar] [CrossRef]
- Jessie, D.T.; Saari, D.G. Coordinate Systems for Games: Simplifying the “Me” vs. “We” Interactions; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Kalai, A.; Kalai, E. Cooperation in strategic games revisited. Q. J. Econ. 2013, 128, 917–966. [Google Scholar] [CrossRef][Green Version]
- Candogan, O.; Menache, I.; Ozdaglar, A.; Parrilo, P. Flows and Decompositions of Games: Harmonic and Potential Games. Math. Oper. Res. 2011, 36, 474–503. [Google Scholar] [CrossRef]
- Abdou, J.; Pnevmatikos, N.; Scarsini, M.; Venel, X. Decomposition of Games: Some Strategic Considerations. arXiv 2019, arXiv:1901.06048. [Google Scholar]
- Hwang, S.-H.; Rey-Bellet, L. Strategic Decompositions of Normal Form Games: Zero-sum Games and Potential Games. Games Econ. Behav. 2020, 122, 370–390. [Google Scholar] [CrossRef]
- Jessie, D.T.; Kendall, R. Decomposing Models of Bounded Rationality; Technical Report, IMBS Technical Reports, 15-06; MBS: Irvine, CA, USA, 2015. [Google Scholar]
- Blume, L.E. The Statistical Mechanics of Strategic Interaction. Games Econ. Behav. 1993, 5, 387–424. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sandholm, W.H. Stable Games and their Dynamics. J. Econ. Theory 2009, 144, 1665–1693. [Google Scholar] [CrossRef]
| 1. | A payoff dominant Nash cell is where each agent does at least as well as in any other Nash cell, and at least one does better. A risk-dominant Nash cell is less costly should coordination be mistakenly expected; see Section 3.1. |
| 2. | Experimental work has been done by Jessie and Kendall [17] by building on the decomposition in [JS1]. More precisely and as given in this paper, the separation aspect of the decomposition permits constructing large classes of games with an identical Nash component (or, the strategic component), but with wildly different externalities components (or, the behavioral component). As they showed, the choice of the behavioral term influenced an agent’s selection. Section 2 discusses these components. |
| 3. | This is the behavioral component in [JS1]. |
| 4. | All of these results extend to games. |
| 5. | This makes sense; “matching pennies” is antithetical (orthogonal) to the cooperative spirit of potential games. The space of matching pennies is the harmonic component discussed in [14]. |
| 6. | As pointed out by a referee, the case where appears to be related to the notion of self-defeating externalities, making the potential game in this case a stable game, as defined in [19]. |
| 7. | If ties, such as or are included, there are seven distinct social welfare rankings for each game in each Figure 2a region. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).