MacHa: Multi-Aspect Controllable Text Generation Based on a Hamiltonian System
Abstract
1. Introduction
2. Related Work
2.1. Multi-Faceted Controllable Text Generation
2.2. Hamilton System
- (1)
- We define an energy model based on the Hamilton function, placing it within the latent space and embedding multiple constraints into this energy field: kinetic energy governsthe fluency, naturalness, and diversity of generated text, while potential energy guides the target topic and emotional orientation, thereby coordinating the differences between various attributes during text generation.
- (2)
- During the final sampling phase, we employ an RL-based sampling method that leverages a reinforcement learning mechanism to dynamically adjust the sampling policy within complex decision processes, effectively eliminating the need for intricate search during decoding.
- (3)
- We evaluate the proposed MacHa framework on multi-aspect controllable text generation tasks and observe substantial improvements over current baselines, confirming the effectiveness of MacHa.
3. Method
3.1. Definition of Multi-Aspect Controlled Text Generation
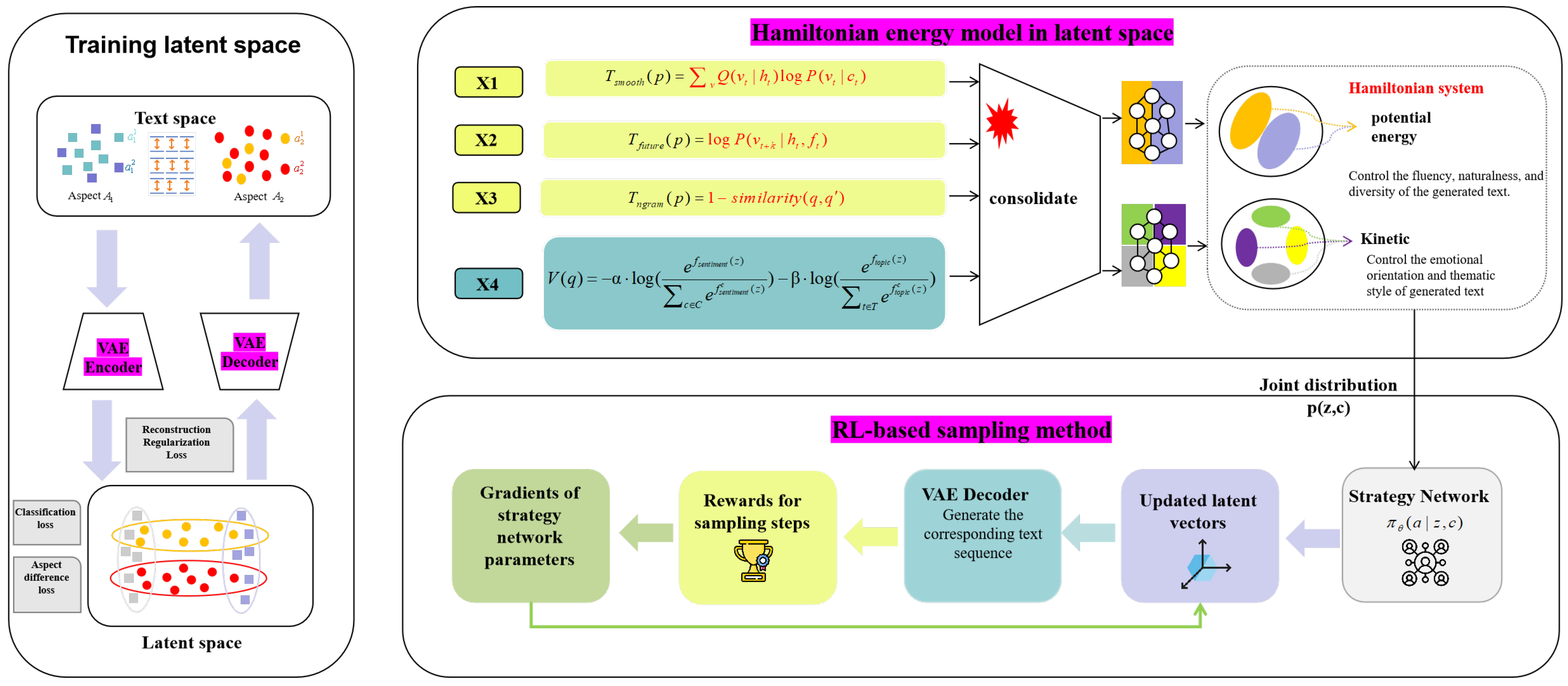
3.2. Train a Latent Space
3.3. Hamiltonian Energy Model
3.4. RL-Based Sampling Method
3.5. Theoretical Analysis of the Hamilton Energy Model
3.6. Property Decoupling Mechanism in Cartesian Coordinate Systems
3.7. Correlation Mapping Between Energy and Text Attributes
4. Experiment
4.1. Dataset
4.2. Experimental Environment and Parameter Settings
4.3. Baseline Method
4.4. Evaluation Criteria
4.5. Comparison of Experimental Results and Analysis
4.6. Ablation Analysis
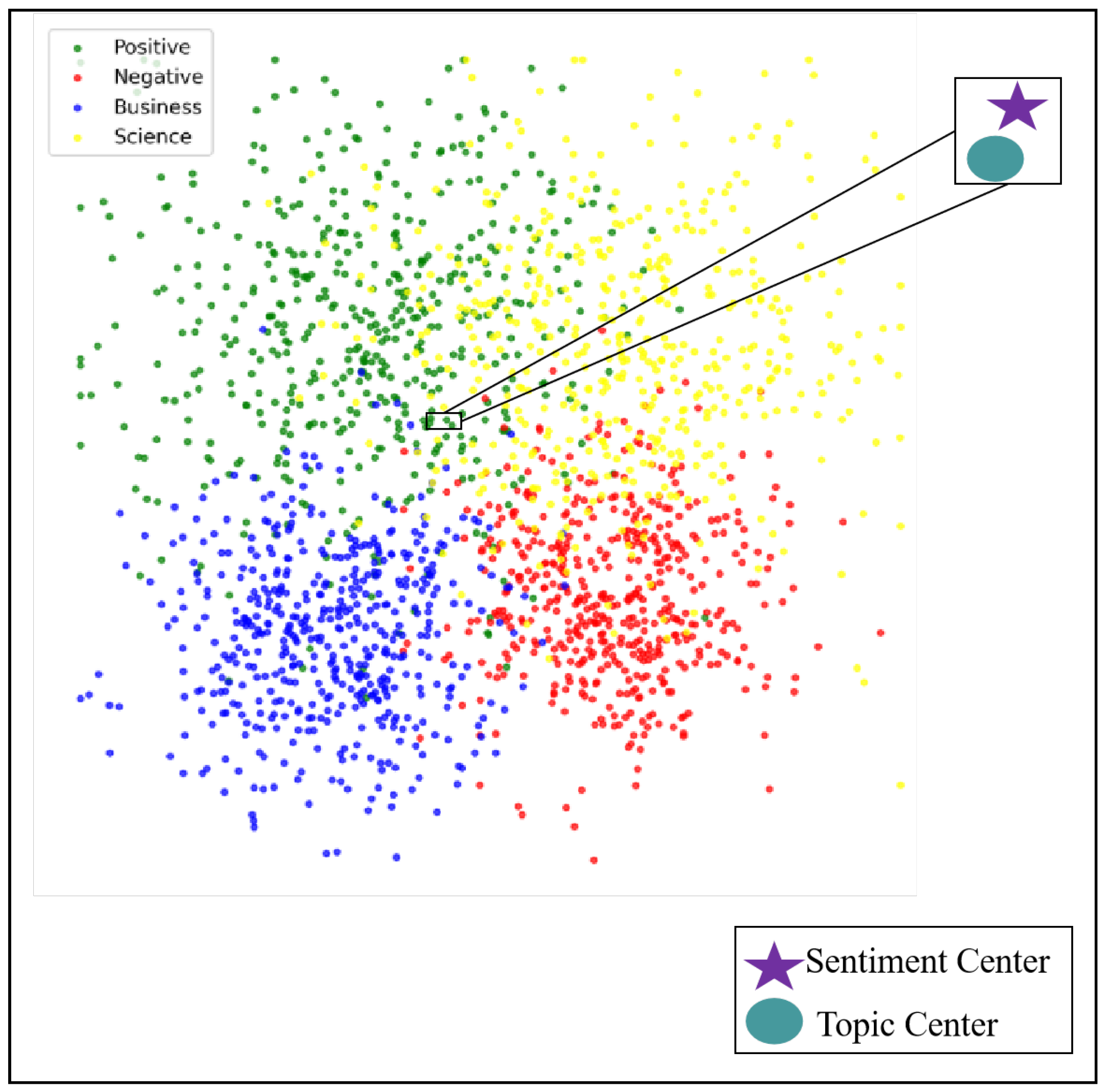
4.7. Visualization of Potential Space
4.8. Verification of Explainability Based on Causal Inference Methods
5. Summary and Conclusions
5.1. Limitations
5.2. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pei, J.; Yang, K.; Klein, D. PREADD: Prefix-adaptive decoding for controlled text generation. arXiv 2023, arXiv:2307.03214. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, T.; Shing, M.; Sawada, K.; Okumura, M. Focused prefix tuning for controllable text generation. J. Nat. Lang. Process. 2024, 31, 250–265. [Google Scholar] [CrossRef]
- Kumar, S.; Malmi, E.; Severyn, A.; Tsvetkov, Y. Controlled text generation as continuous optimization with multiple constraints. Adv. Neural Inf. Process. Syst. 2021, 34, 14542–14554. [Google Scholar]
- Huang, X.; Liu, Z.; Li, P.; Li, T.; Sun, M.; Liu, Y. An extensible plug-and-play method for multi-aspect controllable text generation. arXiv 2022, arXiv:2212.09387. [Google Scholar]
- Becker, J.; Wahle, J.P.; Gipp, B.; Ruas, T. Text generation: A systematic literature review of tasks, evaluation, and challenges. arXiv 2024, arXiv:2405.15604. [Google Scholar] [CrossRef]
- Xie, Z. Neural text generation: A practical guide. arXiv 2017, arXiv:1711.09534. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, Y.; Du, Z.; Ding, M.; Qian, Y.; Yang, Z.; Tang, J. GPT understands, too. AI Open 2024, 5, 208–215. [Google Scholar] [CrossRef]
- Zhu, C.; Liu, Y.; Lyu, C.; Yang, X.; Chen, G.; Wang, L.; Luo, W.; Zhang, K. Towards Lightweight, Adaptive and Attribute-Aware Multi-Aspect Controllable Text Generation with Large Language Models. arXiv 2025, arXiv:2502.13474. [Google Scholar]
- Konen, K.; Jentzsch, S.; Diallo, D.; Schütt, P.; Bensch, O.; Baff, R.E.; Opitz, D.; Hecking, T. Style vectors for steering generative large language model. arXiv 2024, arXiv:2402.01618. [Google Scholar] [CrossRef]
- Liu, S.; Ye, H.; Xing, L.; Zou, J. In-context vectors: Making in context learning more effective and controllable through latent space steering. arXiv 2023, arXiv:2311.06668. [Google Scholar]
- Krause, B.; Gotmare, A.D.; McCann, B.; Keskar, N.S.; Joty, S.; Socher, R.; Rajani, N.F. Gedi: Generative discriminator guided sequence generation. arXiv 2020, arXiv:2009.06367. [Google Scholar] [CrossRef]
- Yang, K.; Klein, D. FUDGE: Controlled text generation with future discriminators. arXiv 2021, arXiv:2104.05218. [Google Scholar] [CrossRef]
- Sitdikov, A.; Balagansky, N.; Gavrilov, D.; Markov, A. Classifiers are better experts for controllable text generation. arXiv 2022, arXiv:2205.07276. [Google Scholar] [CrossRef]
- Mudgal, S.; Lee, J.; Ganapathy, H.; Li, Y.; Wang, T.; Huang, Y.; Chen, Z.; Cheng, H.T.; Collins, M.; Strohman, T.; et al. Controlled decoding from language models. arXiv 2023, arXiv:2310.17022. [Google Scholar]
- Zhong, Q.; Ding, L.; Liu, J.; Du, B.; Tao, D. ROSE doesn’t do that: Boosting the safety of instruction-tuned large language models with reverse prompt contrastive decoding. arXiv 2024, arXiv:2402.11889. [Google Scholar]
- Choi, D.; Kim, J.; Gim, M.; Lee, J.; Kang, J. DeepClair: Utilizing Market Forecasts for Effective Portfolio Selection. In Proceedings of the 33rd ACM International Conference on Information and Knowledge Management, Boise, ID, USA, 21–25 October 2024; pp. 4414–4422. [Google Scholar]
- Maas, A.; Daly, R.E.; Pham, P.T.; Huang, D.; Ng, A.Y.; Potts, C. Learning word vectors for sentiment analysis. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, Portland, OR, USA, 19–24 June 2011; pp. 142–150. [Google Scholar]
- Zhang, X.; Zhao, J.; LeCun, Y. Character-level convolutional networks for text classification. Adv. Neural Inf. Process. Syst. 2015, 28, 649–657. [Google Scholar]
- Ajwani, R.D.; Zhu, Z.; Rose, J.; Rudzicz, F. Plug and Play with Prompts: A Prompt Tuning Approach for Controlling Text Generation. arXiv 2024, arXiv:2404.05143. [Google Scholar] [CrossRef]
- Li, W.; Wei, W.; Xu, K.; Xie, W.; Chen, D.; Cheng, Y. Reinforcement learning with token-level feedback for controllable text generation. arXiv 2024, arXiv:2403.11558. [Google Scholar] [CrossRef]
- He, X. Parallel refinements for lexically constrained text generation with bart. arXiv 2021, arXiv:2109.12487. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.; Li, C.; Ao, X.; He, Q. Controlling large language models through concept activation vectors. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 25851–25859. [Google Scholar]
- Liu, Y.; Liu, X.; Zhu, X.; Hu, W. Multi-aspect controllable text generation with disentangled counterfactual augmentation. arXiv 2024, arXiv:2405.19958. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, D.; Umrawal, A.K. JAM: Controllable and Responsible Text Generation via Causal Reasoning and Latent Vector Manipulation. arXiv 2025, arXiv:2502.20684. [Google Scholar] [CrossRef]
- Chen, Z.; Feng, M.; Yan, J.; Zha, H. Learning neural Hamiltonian dynamics: A methodological overview. arXiv 2022, arXiv:2203.00128. [Google Scholar] [CrossRef]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Lee, D.D.; Pham, P.; Largman, Y.; Ng, A. Advances in neural information processing systems 22. Tech. Rep. 2009. [Google Scholar]
- Zhang, J.; Zhu, Q.; Lin, W. Learning hamiltonian neural koopman operator and simultaneously sustaining and discovering conservation laws. Phys. Rev. Res. 2024, 6, L012031. [Google Scholar] [CrossRef]
- Ding, H.; Pang, L.; Wei, Z.; Shen, H.; Cheng, X.; Chua, T.S. Maclasa: Multi-aspect controllable text generation via efficient sampling from compact latent space. arXiv 2023, arXiv:2305.12785. [Google Scholar]
- Gu, Y.; Feng, X.; Ma, S.; Zhang, L.; Gong, H.; Qin, B. A distributional lens for multi-aspect controllable text generation. arXiv 2022, arXiv:2210.02889. [Google Scholar] [CrossRef]
- De Smet, L.; Sansone, E.; Zuidberg Dos Martires, P. Differentiable sampling of categorical distributions using the catlog-derivative trick. Adv. Neural Inf. Process. Syst. 2023, 36, 30416–30428. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Dathathri, S.; Madotto, A.; Lan, J.; Hung, J.; Frank, E.; Molino, P.; Yosinski, J.; Liu, R. Plug and play language models: A simple approach to controlled text generation. arXiv 2019, arXiv:1912.02164. [Google Scholar]
- Liu, A.; Sap, M.; Lu, X.; Swayamdipta, S.; Bhagavatula, C.; Smith, N.A.; Choi, Y. DExperts: Decoding-time controlled text generation with experts and anti-experts. arXiv 2021, arXiv:2105.03023. [Google Scholar] [CrossRef]
- Hallinan, S.; Liu, A.; Choi, Y.; Sap, M. Detoxifying text with marco: Controllable revision with experts and anti-experts. arXiv 2022, arXiv:2212.10543. [Google Scholar]
- Mireshghallah, F.; Goyal, K.; Berg-Kirkpatrick, T. Mix and match: Learning-free controllable text generation using energy language models. arXiv 2022, arXiv:2203.13299. [Google Scholar] [CrossRef]
- Qian, J.; Dong, L.; Shen, Y.; Wei, F.; Chen, W. Controllable natural language generation with contrastive prefixes. arXiv 2022, arXiv:2202.13257. [Google Scholar] [CrossRef]
- Liu, G.; Feng, Z.; Gao, Y.; Yang, Z.; Liang, X.; Bao, J.; He, X.; Cui, S.; Li, Z.; Hu, Z. Composable text controls in latent space with ODEs. arXiv 2022, arXiv:2208.00638. [Google Scholar]
- Liu, Z.; Lin, W.; Shi, Y.; Zhao, J. A robustly optimized BERT pre-training approach with post-training. In Proceedings of the China National Conference on Chinese Computational Linguistics, Hohhot, China, 13–15 August 2021; pp. 471–484. [Google Scholar]
- Maaten, L.v.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
| Method | Correctness (%) Senti and Topic ↑ | Text Fluency PPL ↓ | Diversity Dist-1 ↑ | Diversity Dist-2 ↑ | Efficiency Time (s) |
|---|---|---|---|---|---|
| PPLM | 18.14 ± 0.45 | 25.59 ± 1.09 | 0.23 | 0.64 | 40.56 |
| DEXPERTS | 23.93 ± 1.11 | 38.70 ± 2.51 | 0.23 | 0.70 | 0.64 |
| MaRCo | 27.81 ± 1.94 | 18.87 ± 1.85 | 0.18 | 0.58 | 0.40 |
| Mix and Match | 50.17 ± 2.07 | 68.72 ± 0.97 | 0.36 | 0.84 | 164.60 |
| Contrastive | 53.02 ± 1.52 | 52.56 ± 11.97 | 0.22 | 0.71 | 0.59 |
| LatentOps | 44.41 ± 5.72 | 26.11 ± 1.46 | 0.16 | 0.55 | 0.10 |
| Distribution | 49.79 ± 1.99 | 12.48 ± 0.52 | 0.08 | 0.28 | 0.04 |
| MacLaSa | 59.18 ± 0.18 | 28.19 ± 1.26 | 0.16 | 0.60 | 0.10 |
| MacHa | 63.59 ± 2.64 | 27.76 ± 2.31 | 0.28 | 0.74 | 0.05 |
| w/o | 49.32 ± 8.81 | 28.53 ± 1.43 | 0.20 | 0.68 | 0.05 |
| w/o | 53.97 ± 4.25 | 27.37 ± 1.28 | 0.25 | 0.73 | 0.05 |
| w/o | 55.28 ± 3.49 | 29.65 ± 0.77 | 0.22 | 0.71 | 0.05 |
| Method | Correctness (%) ↑ | Text Quality PPL ↓ | Diversity Distinct-1 ↑ | Diversity Distinct-2 ↑ | Senti and Topic AccT ↑ |
|---|---|---|---|---|---|
| PPLM | Positive-Word | 20.36 ± 1.69 | 25.47 ± 1.70 | 0.23 | 0.64 |
| Positive-Sport | 16.53 ± 1.13 | 25.78 ± 1.30 | 0.23 | 0.63 | |
| Positive-Business | 25.24 ± 2.96 | 26.66 ± 1.66 | 0.24 | 0.64 | |
| Positive-Sci/Tech | 61.73 ± 0.66 | 25.06 ± 1.53 | 0.24 | 0.66 | |
| Negative-Word | 3.87 ± 1.99 | 25.27 ± 1.23 | 0.23 | 0.64 | |
| Negative-Sport | 2.27 ± 0.57 | 25.96 ± 1.54 | 0.23 | 0.63 | |
| Negative-Business | 1.78 ± 1.26 | 26.11 ± 1.20 | 0.23 | 0.64 | |
| Negative-Sci/Tech | 13.29 ± 1.82 | 24.40 ± 1.11 | 0.24 | 0.66 | |
| Average | 18.14 ± 0.45 | 25.59 ± 1.09 | 0.23 | 0.64 | |
| DEXPERTS | Positive-Word | 34.22 ± 4.24 | 37.36 ± 3.46 | 0.24 | 0.72 |
| Positive-Sport | 8.40 ± 2.66 | 37.36 ± 3.46 | 0.24 | 0.72 | |
| Positive-Business | 10.98 ± 1.67 | 37.36 ± 3.46 | 0.24 | 0.72 | |
| Positive-Sci/Tech | 45.02 ± 4.31 | 37.36 ± 3.46 | 0.24 | 0.72 | |
| Negative-Word | 9.47 ± 2.68 | 40.03 ± 2.35 | 0.21 | 0.68 | |
| Negative-Sport | 8.17 ± 2.27 | 40.03 ± 2.35 | 0.21 | 0.68 | |
| Negative-Business | 10.98 ± 1.50 | 40.03 ± 2.35 | 0.21 | 0.68 | |
| Negative-Sci/Tech | 63.64 ± 8.73 | 40.03 ± 2.35 | 0.21 | 0.68 | |
| Average | 23.93 ± 1.11 | 38.70 ± 2.51 | 0.23 | 0.70 | |
| MaRCo | Positive-Word | 36.22 ± 8.04 | 17.13 ± 1.51 | 0.18 | 0.57 |
| Positive-Sport | 37.11 ± 25.23 | 18.16 ± 1.47 | 0.17 | 0.55 | |
| Positive-Business | 38.89 ± 8.34 | 19.43 ± 2.13 | 0.19 | 0.59 | |
| Positive-Sci/Tech | 50.00 ± 5.21 | 17.91 ± 1.39 | 0.18 | 0.57 | |
| Negative-Word | 8.22 ± 4.91 | 18.79 ± 1.88 | 0.19 | 0.59 | |
| Negative-Sport | 10.89 ± 0.38 | 19.94 ± 2.85 | 0.17 | 0.57 | |
| Negative-Business | 22.89 ± 20.07 | 20.51 ± 2.45 | 0.19 | 0.59 | |
| Negative-Sci/Tech | 18.22 ± 5.39 | 19.06 ± 1.91 | 0.18 | 0.59 | |
| Average | 27.81 ± 1.94 | 18.87 ± 1.85 | 0.18 | 0.58 | |
| Mix and Match | Positive-Word | 58.89 ± 0.83 | 61.27 ± 15.74 | 0.36 | 0.84 |
| Positive-Sport | 70.31 ± 5.55 | 66.58 ± 8.74 | 0.35 | 0.84 | |
| Positive-Business | 39.78 ± 1.66 | 65.89 ± 14.35 | 0.35 | 0.84 | |
| Positive-Sci/Tech | 65.33 ± 2.49 | 69.07 ± 12.27 | 0.36 | 0.84 | |
| Negative-Word | 41.55 ± 1.66 | 69.49 ± 15.52 | 0.35 | 0.84 | |
| Negative-Sport | 47.33 ± 8.13 | 72.72 ± 8.87 | 0.36 | 0.84 | |
| Negative-Business | 31.56 ± 5.15 | 71.61 ± 15.14 | 0.35 | 0.84 | |
| Negative-Sci/Tech | 58.00 ± 4.75 | 73.08 ± 9.81 | 0.37 | 0.84 | |
| Average | 50.17 ± 2.07 | 68.72 ± 11.97 | 0.36 | 0.84 | |
| Contrastive | Positive-Word | 67.87 ± 1.13 | 48.15 ± 15.74 | 0.23 | 0.72 |
| Positive-Sport | 70.31 ± 5.55 | 52.36 ± 8.74 | 0.21 | 0.70 | |
| Positive-Business | 53.16 ± 5.00 | 56.13 ± 14.35 | 0.22 | 0.72 | |
| Positive-Sci/Tech | 51.96 ± 3.09 | 45.03 ± 12.27 | 0.23 | 0.71 | |
| Negative-Word | 40.94 ± 4.26 | 51.27 ± 15.52 | 0.22 | 0.70 | |
| Negative-Sport | 40.71 ± 10.65 | 59.77 ± 8.87 | 0.21 | 0.71 | |
| Negative-Business | 48.84 ± 6.95 | 61.91 ± 15.14 | 0.20 | 0.70 | |
| Negative-Sci/Tech | 50.40 ± 3.95 | 45.86 ± 9.81 | 0.23 | 0.71 | |
| Average | 53.02 ± 1.52 | 52.56 ± 11.97 | 0.22 | 0.71 | |
| LatenOps | Positive-Word | 57.96 ± 5.07 | 24.79 ± 3.34 | 0.17 | 0.56 |
| Positive-Sport | 63.47 ± 11.01 | 28.01 ± 1.80 | 0.16 | 0.55 | |
| Positive-Business | 61.73 ± 9.36 | 25.73 ± 1.84 | 0.14 | 0.52 | |
| Positive-Sci/Tech | 39.64 ± 22.07 | 26.49 ± 1.73 | 0.17 | 0.55 | |
| Negative-Word | 34.62 ± 1.59 | 24.98 ± 1.56 | 0.16 | 0.55 | |
| Negative-Sport | 40.41 ± 9.72 | 25.14 ± 1.48 | 0.14 | 0.52 | |
| Negative-Business | 25.74 ± 2.41 | 27.30 ± 2.11 | 0.15 | 0.54 | |
| Negative-Sci/Tech | 31.56 ± 2.53 | 26.49 ± 0.99 | 0.16 | 0.57 | |
| Average | 44.41 ± 5.72 | 26.11 ± 1.46 | 0.16 | 0.55 | |
| Distribution | Positive-Word | 37.42 ± 4.38 | 13.34 ± 0.13 | 0.09 | 0.30 |
| Positive-Sport | 71.60 ± 4.39 | 14.67 ± 0.53 | 0.09 | 0.29 | |
| Positive-Business | 72.80 ± 6.45 | 11.23 ± 1.00 | 0.07 | 0.25 | |
| Positive-Sci/Tech | 72.80 ± 11.07 | 12.41 ± 0.64 | 0.08 | 0.28 | |
| Negative-Word | 46.80 ± 10.89 | 11.89 ± 1.12 | 0.07 | 0.28 | |
| Negative-Sport | 35.91 ± 7.84 | 12.99 ± 0.57 | 0.08 | 0.28 | |
| Negative-Business | 26.09 ± 5.60 | 11.03 ± 0.11 | 0.07 | 0.25 | |
| Negative-Sci/Tech | 34.86 ± 6.25 | 12.25 ± 0.93 | 0.08 | 0.27 | |
| Average | 49.79 ± 1.99 | 12.48 ± 0.52 | 0.08 | 0.28 | |
| MacLaSa | Positive-Word | 59.47 ± 6.66 | 26.26 ± 0.20 | 0.19 | 0.65 |
| Positive-Sport | 87.93 ± 4.20 | 28.69 ± 1.78 | 0.16 | 0.57 | |
| Positive-Business | 82.87 ± 3.27 | 27.67 ± 1.55 | 0.15 | 0.57 | |
| Positive-Sci/Tech | 76.34 ± 0.46 | 28.77 ± 2.03 | 0.16 | 0.60 | |
| Negative-Word | 56.54 ± 1.47 | 26.28 ± 1.26 | 0.16 | 0.59 | |
| Negative-Sport | 38.00 ± 2.67 | 32.23 ± 0.20 | 0.17 | 0.61 | |
| Negative-Business | 31.40 ± 4.07 | 29.06 ± 1.12 | 0.15 | 0.59 | |
| Negative-Sci/Tech | 44.74 ± 0.34 | 31.95 ± 0.48 | 0.17 | 0.62 | |
| Average | 59.18 ± 0.81 | 28.19 ± 1.26 | 0.16 | 0.60 | |
| MacHa | Positive-Word | 64.87 ± 1.96 | 25.83 ± 0.39 | 0.27 | 0.74 |
| Positive-Sport | 89.16 ± 2.86 | 27.63 ± 2.96 | 0.27 | 0.75 | |
| Positive-Business | 83.61 ± 1.57 | 26.50 ± 0.45 | 0.30 | 0.77 | |
| Positive-Sci/Tech | 88.29 ± 4.51 | 25.37 ± 2.57 | 0.28 | 0.73 | |
| Negative-Word | 58.49 ± 0.97 | 25.49 ± 0.63 | 0.28 | 0.72 | |
| Negative-Sport | 41.27 ± 1.39 | 31.58 ± 1.67 | 0.28 | 0.73 | |
| Negative-Business | 32.55 ± 0.87 | 28.81 ± 1.21 | 0.29 | 0.76 | |
| Negative-Sci/Tech | 50.53 ± 2.38 | 30.92 ± 1.64 | 0.27 | 0.74 | |
| Average | 63.59 ± 2.64 | 27.76 ± 2.31 | 0.28 | 0.74 |
| Method | Correctness | Text Fluency | Efficiency |
|---|---|---|---|
| PPLM | 1.96 | 2.67 | 2.54 |
| DEXPERTS | 1.98 | 2.38 | 1.88 |
| MaRCo | 2.08 | 2.78 | 2.65 |
| Mix and Match | 1.21 | 1.38 | 2.13 |
| Contrastive | 2.04 | 2.29 | 2.38 |
| LatentOps | 2.21 | 2.21 | 2.38 |
| Distribution | 2.67 | 2.67 | 2.63 |
| MacLaSa | 3.54 | 3.25 | 2.96 |
| MacHa | 4.02 | 3.86 | 3.25 |
| Method | Correctness (Senti and Topic) ↑ | Text Quality (PPL) ↓ |
|---|---|---|
| Random | 16.58 | 33.57 |
| LD | 31.47 | 10.46 |
| ODE | 59.23 | 28.91 |
| RL | 72.86 | 25.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Lin, M.; Wang, Y. MacHa: Multi-Aspect Controllable Text Generation Based on a Hamiltonian System. Computers 2025, 14, 503. https://doi.org/10.3390/computers14120503
Xu D, Lin M, Wang Y. MacHa: Multi-Aspect Controllable Text Generation Based on a Hamiltonian System. Computers. 2025; 14(12):503. https://doi.org/10.3390/computers14120503
Chicago/Turabian StyleXu, Delong, Min Lin, and Yurong Wang. 2025. "MacHa: Multi-Aspect Controllable Text Generation Based on a Hamiltonian System" Computers 14, no. 12: 503. https://doi.org/10.3390/computers14120503
APA StyleXu, D., Lin, M., & Wang, Y. (2025). MacHa: Multi-Aspect Controllable Text Generation Based on a Hamiltonian System. Computers, 14(12), 503. https://doi.org/10.3390/computers14120503





