Abstract
This paper explores the performance of ChatGPT and GeoGebra Discovery when dealing with automatic geometric reasoning and discovery. The emergence of Large Language Models has attracted considerable attention in mathematics, among other fields where intelligence should be present. We revisit a couple of elementary Euclidean geometry theorems discussed in the birth of Artificial Intelligence and a non-trivial inequality concerning triangles. GeoGebra succeeds in proving all these selected examples, while ChatGPT fails in one case. Our thesis is that both GeoGebra and ChatGPT could be used as complementary systems, where the natural language abilities of ChatGPT and the certified computer algebra methods in GeoGebra Discovery can cooperate in order to obtain sound and—more relevant—interesting results.
1. Introduction
Since the birth of Artificial Intelligence (AI), special attention has been given to mathematics as a suitable field for testing related systems and programs. One of the earliest computer programs in automatic mathematical reasoning, if not the first, was The Logic Theorist [1]. This program proved 38 out of the 52 theorems in Chapter 2 of the Russell and Whitehead’s Principia Mathematica [2], returning shorter proofs for some theorems. Regarding automatic geometry reasoning, H. Gelernter presented, back in 1959, at a UNESCO meeting in Paris, the first geometry-theorem-proving machine [3]. And, one year later, he described in this way its performance [4]:
In early spring, 1959, an IBM 704 computer, with the assistance of a program comprising some 20,000 individual instructions, proved its first theorem in elementary Euclidean plane geometry. Since that time, the geometry theorem-proving machine (a particular state configuration of the IBM 704 specified by the afore-mentioned machine code) has found solutions to a large number of problems taken from high school textbooks and final examinations in plane geometry …the theorem-proving program relies upon heuristic methods to restrain it from generating proof sequences that do not have a high a priori probability of leading to a proof for the theorem in question …At this stage in its development, the geometry machine was capable of producing proofs that were quite impressive…Three years ago, the dominant opinion was that the geometry machine would not exist today. And today, hardly an expert will contest the assertion that machines will be proving interesting theorems in number theory three years hence….
Sixty (not three!) years later, interest in AI tools for dealing with mathematical issues seems to be exploding. See, for instance, the general reflection in [5] or the more recent and specific papers [6,7,8] addressing such different topics as solving mathematical olympiad problems with AlphaGeometry, a neural language model, or using ChatGPT [9], a chatbot tool, to prepare lesson plans in primary school mathematics courses. In particular, the general availability of Large Language Models (LLMs) has facilitated their dissemination and exploration in different contexts. Thus, the suitability and accuracy of one of these LLMs, for example, through the widely known, LLM-based, ChatGPT chatbot, released at the end of 2022, has been rapidly tested in several fields of knowledge (e.g., see [10] for references). Regarding mathematics, the main point of attention we observe in the scientific literature is on teaching and learning issues; see, for instance, [8,11,12].
Here, continuing with the approach we started in [10], we focus on describing—through two traditional Euclidean geometry problems historically related to the AI context and a challenging problem from the American Mathematical Monthly—the performance of the automated geometric reasoning and discovery tools we implemented in GeoGebra Discovery, comparing it with ChatGPT’s automated answers on the same examples and reflecting on the potential cooperation of GeoGebra Discovery with AI bots. This goal is different from, and complementary to, the one in [10] that focused such a comparison on loci computation (e.g., envelopes of curves).
Let us remark that a similar goal, the comparison of and potential cooperation between AlphaGeometry and a computer algebra tool such as Xcas/Giac (remarking that Giac, see https://www-fourier.ujf-grenoble.fr/~parisse/giac.html, accessed on 22 July 2024, is also the computer algebra system implemented in GeoGebra and GeoGebra Discovery), was quite recently performed and described in [7], concluding that both approaches are not yet fully automatized, requiring human concourse (translation by the authors from the original text in French):
It is then essential here to parameterize the problem to make the calculations efficient, otherwise with Olympiad problems, the calculations quickly become impractical. This is where the intelligence of the human being comes in, guiding the calculations with the help of a few rules cited below. We could perhaps replace this step with artificial intelligence, with probably significantly less power required, but for the moment AIs do not seem to be coupled with efficient formal calculation engines.
…AlphaGeometry (AG) is more automated than Xcas, but not completely yet. Xcas solves almost twice as many Olympiad problems. Some problems are probably out of reach for the current version of AG because they require prior calculation to perform a construction, AG does not seem capable of reasoning about an approximate figure, unlike a human being in synthetic geometry or Xcas who can calculate in analytical geometry. AG provides a certificate (the details of the proof steps) which allows a human being to verify (if the number of steps is not too large), the calculations of Xcas are on the other hand often too technical to be verified at the main (therefore, closed source software should not be used to provide a proof in analytical geometry).
To achieve our goal of exemplifying the benefits of the cooperation of two fully automated but fundamentally different tools for dealing with geometry statements, we will describe here both the performance of GeoGebra Discovery and ChatGPT on the selected examples, as well as the singular features, recently included in GeoGebra Discovery reasoning tools, which provide enhanced information (certificates and grades of difficulty) and facilitate the exploration by the user, in an algorithmic but still not fully automatic way, of some involved geometric situations. We consider that these features are relevant (to understand, to conjecture, to generalize…) when addressing a geometry statement with the complementary help of ChatGPT and GeoGebra Discovery.
GeoGebra (http://www.geogebra.org, accessed on 22 July 2024) is a freely available educational software with over 100 million users in the world (data confirmed by GeoGebra’s CEO, personal communication, June 2024), operative over smartphones, tablets, and computers or just accessible through a web page. It includes computer algebra and dynamic geometry features and can also be used as a versatile numerical and statistical calculator. Concerning automated reasoning features, let us highlight that GeoGebra is capable of automatically finding an equality relation between two given geometric objects in a construction (i.e., of discovering, as the output of the command, a thesis involving such elements and holding under the set of hypotheses describing the geometric construction), of checking the truth/failure of a user-conjectured property (using the Prove or the ProveDetails commands), or finding—through the LocusEquation command—missing hypotheses for a given relation to hold true.
GeoGebra Discovery (see https://kovzol.github.io/geogebra-discovery/, accessed on 22 July 2024, for further details) is a fork version of GeoGebra that enlarges GeoGebra reasoning tools by including new features. It is available through several offline releases for different OS (Mac, Windows, Linux, RaspberryPi; see https://github.com/kovzol/geogebra/releases, accessed on 22 July 2024) as well as an online version (see https://www.autgeo.online/geogebra-discovery/, accessed on 22 July 2024). GeoGebra Discovery is able to find the relation between two given geometric objects in a construction, including, in the case of lengths, the discovery of relations that are not of equality: obtaining algebraic number ratios, or inequality relations, through comparison. It is also capable of checking the truth/failure of a conjectured (by the user) relation involving inequalities and of discovering automatically all possible relations of a certain kind (co-circularity, parallelism, perpendicularity, etc.) among the elements of a construction involving a chosen element or all elements of a construction.
In what follows, we will devote the next two sections to addressing two theorems from the early days of AI: namely, those considered back in 1959 in [4], analyzing the performance of ChatGPT and GeoGebra Discovery for solving them. Thus, in Section 2, we show how the theorem in Appendix 1 of [4] (labeled as Theorem 1 in what follows) is easily solved—in the case of ChatGPT, if formulated closely to the statement in [4]—with both tools, providing an adequate context to describe in detail the performance and the algorithmic approach of the novel command ShowProof from GeoGebra Discovery, which provides the user with a proof certificate (that can be verified through any Computer Algebra software, or by hand) and the proposal of an estimation of the difficulty of the statement. The section ends by remarking on some differences in the behavior of ChatGPT if the statement is formulated differently; for instance, if the input hypotheses are described just through an image, referring the reader to Appendix A in this article for further details.
Section 3 deals with the theorem in Appendix 2 of [4], labeled as Theorem 2 in what follows. In Appendix 2, after describing the six premises and the thesis of this theorem, the “Geometry Machine” declares “I Am Stuck, Elapsed Time = 8.12 Minutes” ([4], p. 148). Then, in the same Appendix 2, some auxiliary elements (points and segments) are introduced, and a couple of new premises involving such elements are added, yielding the “Geometry Machine” to be able to solve the problem in about 30 min. Again, both ChatGPT and GeoGebra Discovery are able to confirm the truth of the statement (although Appendix A shows, again, the problematic answers of ChatGPT if the statement is introduced with a different formulation). It is remarkable to mention here some singular features of GeoGebra Discovery concerning this statement:
- The automatic completion of the given set of hypotheses without requiring the formulation of the thesis;
- A warning sign suggesting the user to consider “exporting the CAS view as Maple, Mathematica…to the clipboard” to explore the inherent difficulties to deal with through the implemented complex algebraic geometry algorithms with statements involving lengths of segments.
As in the previous theorem, we will profit from the special behavior that GeoGebra Discovery exhibits in this statement to introduce the required (but not yet fully implemented, see Appendix B and Appendix C for the related computations, performed by us on Maple https://www.maplesoft.com, accessed on 22 July 2024)) algorithmic issues dealing with such difficulties (concepts of “True on Parts” [13] or of the “Minimal Extended Polynomial” (MEP) [14]).
Section 4 addresses, both with ChatGPT and GeoGebra Discovery, the proof of an inequality proposed in the Problem Section of the American Mathematical Monthly [15]: “If are the side lengths of a triangle with inradius r, then the following inequality holds: ”. We will show that ChatGPT fails at proving this inequality, while GeoGebra Discovery succeeds. But the relevant contribution of this section is the use of GeoGebra Discovery to verify some of the intermediate statements introduced by ChatGPT towards solving this problem.
Finally, we describe, in the Conclusions, the lessons learned from the experience of proving the above-mentioned Theorems 1 and 2 with current automated methods from two very diverse methodologies. And we argue—through the last example, the proof of a highly non-trivial triangle inequality—about the potential relevance of establishing cooperation, for an enhanced understanding of geometry statements, between ChatGPT and GeoGebra Discovery. Of course, the basic idea of confirming the truth of a statement, providing a kind of (e.g., algebraic) proof, etc., to complement/confirm/refute ChatGPT answers could as well be exemplified through other geometry-theorem-proving programs (e.g., JGEX (https://github.com/yezheng1981/Java-Geometry-Expert, accessed on 22 July 2024), or Open Geometry Theorem Prover (https://github.com/opengeometryprover, accessed on 22 July 2024)), each with different advantages and disadvantages regarding GeoGebra Discovery, but it is out of the scope of this article to perform such a comparative study.
2. Revisiting Gelernter et al. Theorem 1
The theorem was originally stated as follows:
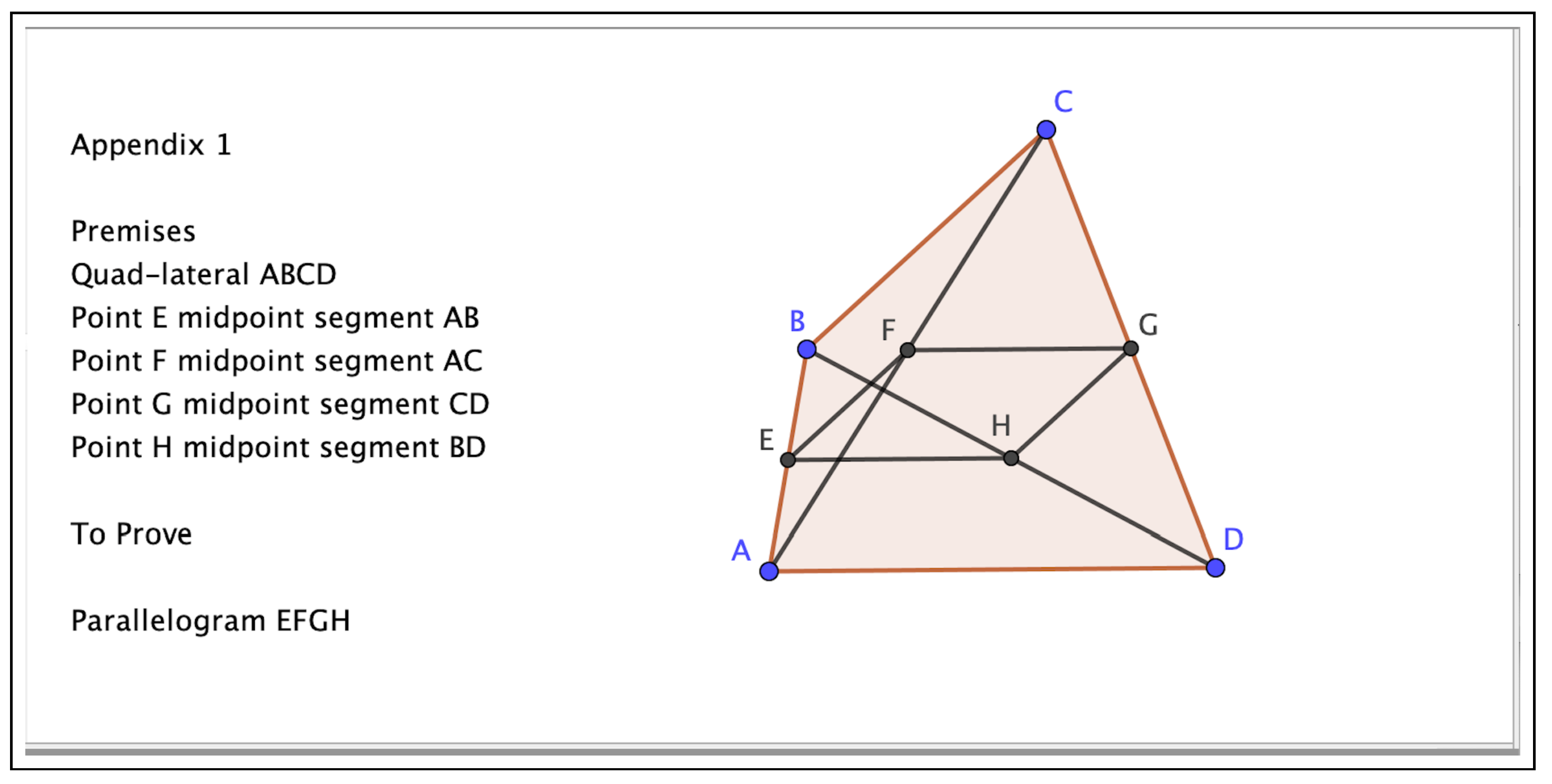
- PremisesQuad-lateral ABCDPoint E midpoint segment ABPoint F midpoint segment ACPoint G midpoint segment CDPoint H midpoint segment BDTo ProveParallelogram EFGHand was successfully proven by Gelernter et al., in 1.03 min, more than sixty years ago. See Figure 1. We will use ChatGPT and GeoGebra Discovery to prove it, both being successful.
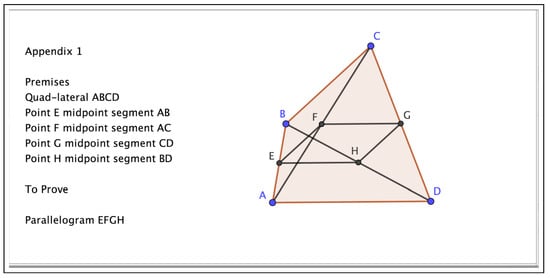
Figure 1.
Statement of Theorem 1 (taken from [4]).
Figure 1.
Statement of Theorem 1 (taken from [4]).
2.1. Gelernter et al. Theorem 1: ChatGPT
Concerning ChatGPT, with the input “Let be a quadrilateral and , and H be the midpoints of , and , respectively. Prove that is a parallelogram”, very close to Gelernter et al.’s formulation, the chatbot gives the following answer:
To prove that quadrilateral is a parallelogram, we need to show that both pairs of opposite sides of are parallel. We will use the midpoint theorem, which states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long.
1. Consider triangle :
E and H and are the midpoints of and respectively. By the midpoint theorem, the line segment is parallel to and .
2. Consider triangle :
F and G are the midpoints of and respectively. By the midpoint theorem, the line segment is parallel to and .
Since and are both parallel to and have the same length ( ), it follows that and .
3. Consider triangle :
E and F are the midpoints of and respectively. By the midpoint theorem, the line segment is parallel to and .
4. Consider triangle :
H and G are the midpoints of and respectively. By the midpoint theorem, the line segment is parallel to and .
Since and are both parallel to and have the same length (), it follows that and .
Therefore, we have shown that and with and . This means that has both pairs of opposite sides parallel and equal in length, which is the definition of a parallelogram.
Hence, is a parallelogram.
Let us remark that the synthetic proof given by the chatbot, and based on the well-known midpoint theorem, is correct. In Appendix A, we included ChatGPT answers to the same Theorem 1 when we introduced it through two very different prompts: first, via a completely descriptive geometry statement (without labeling points), and second, formulating the premises of the statement just graphically through an image of the geometric configuration. For both formulations, ChatGPT provides a proof using vectors between points in the construction to check parallelism and vector congruency. The reasoning sequences are correct for both prompts; but, in the second case, when the input is an image, ChatGPT fails in the interpretation of the configuration, as it begins the proof by considering, as the vertices of the sought quadrilateral, the midpoints of the four sides instead of the midpoints of two opposite sides and the midpoints of the diagonals, the correct ones, as displayed in the figure.
2.2. Gelernter et al. Theorem 1: GeoGebra Discovery
On the other hand, GeoGebra Discovery also proves that is a parallelogram by checking the parallelism of lines and and of and . Let us describe here the verification of the parallelism of and since the other one is similar.
First, we remark that, with GeoGebra Discovery, after writing
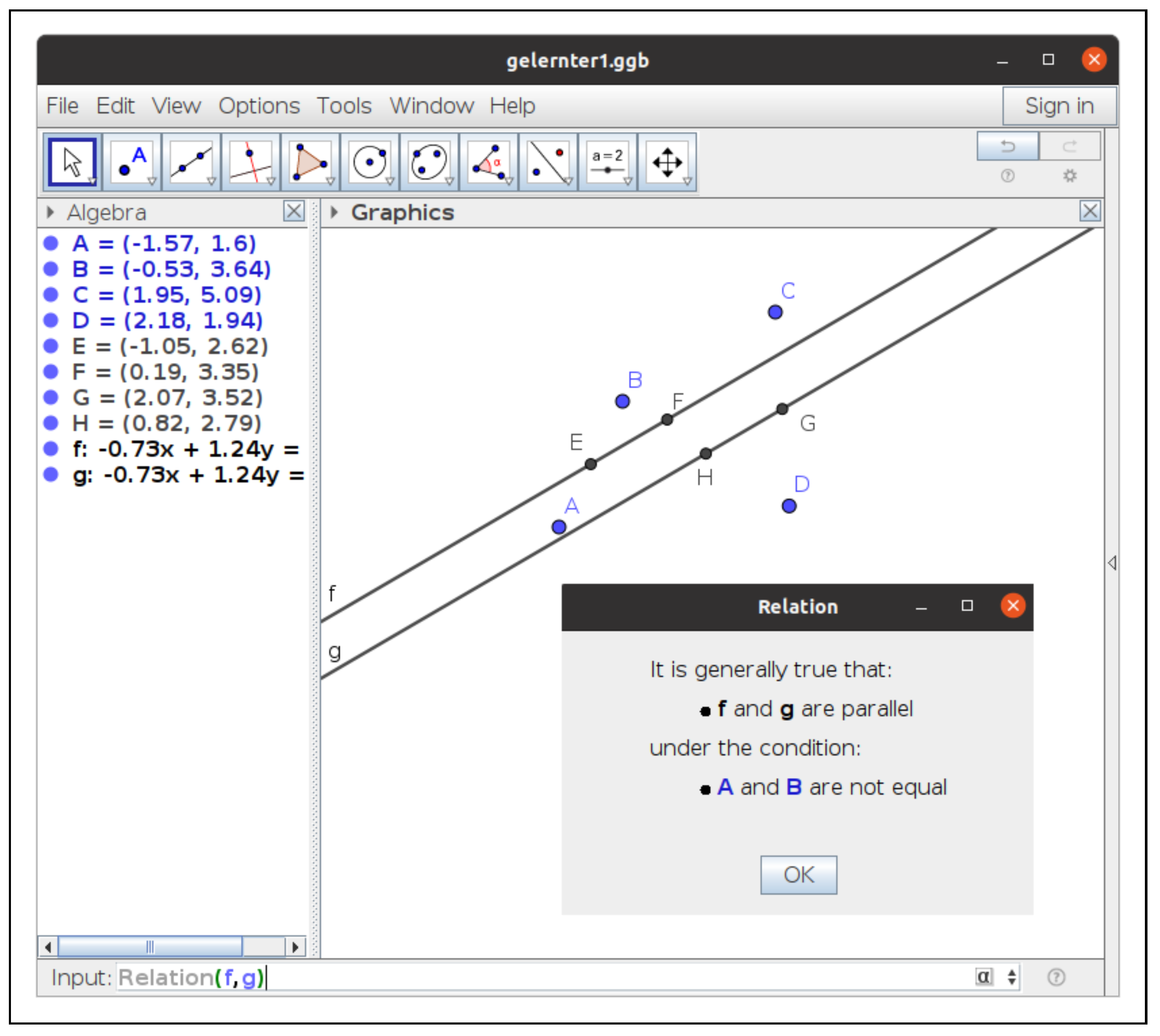
- Execute({"A = (-1.57, 1.6)", "B = (-.53, 3.64)", "C = (1.95, 5.09)","D = (2.18, 1.44)", "E = Midpoint(A, B)", "F = Midpoint(A, C)","G = Midpoint(C, D)", "H = Midpoint(B, D)", "f = Line(E, F)","g = Line(G, H)"})in the input bar, we do not even need to state the thesis (i.e., that are parallel). Indeed, we can ask GeoGebra Discovery to find out what the Relation between the lines and is. The system replies immediately that the two lines are numerically parallel. Then, clicking on the More… icon, we obtain the formal answer that both lines are parallel (Figure 2).
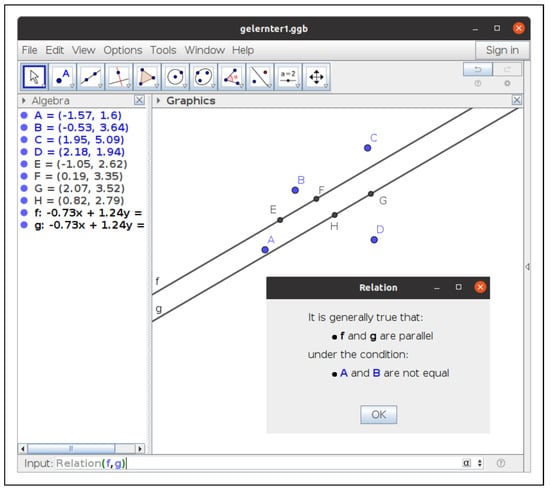
Figure 2.
Using Relation to check the parallelism of lines and .
Figure 2.
Using Relation to check the parallelism of lines and .
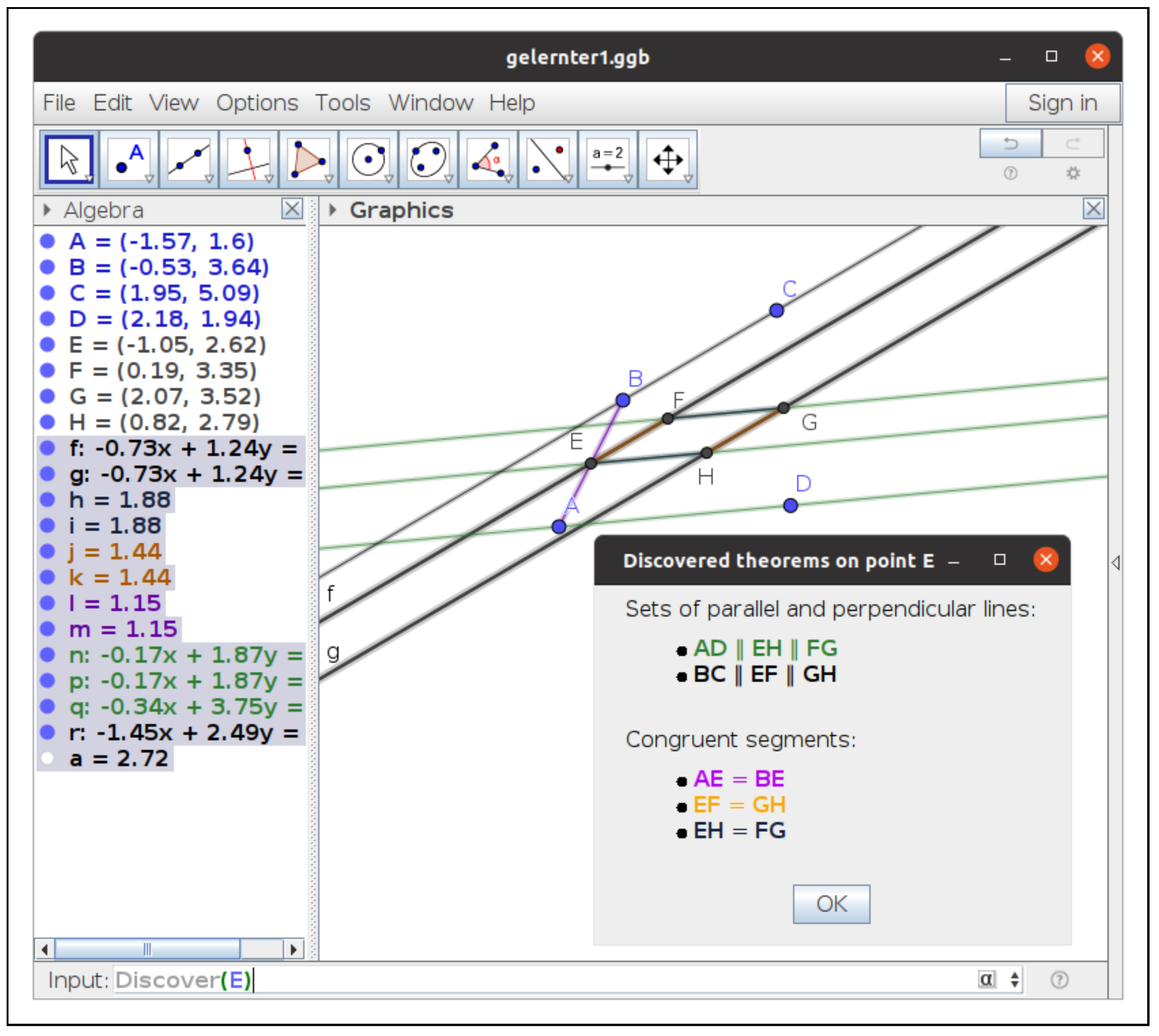
Another option for GeoGebra Discovery to address this statement is just to ask to Discover properties (formally) holding on geometric objects involving a point, say E. The answer, in Figure 3, shows the automatic finding of the parallelism of and ; thus, we conclude that the polygon is a parallelogram.
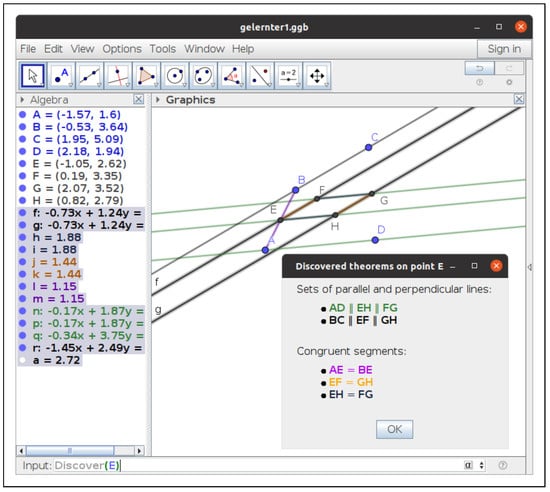
Figure 3.
Discovering properties on E to conclude that is a parallelogram.
Finally, GeoGebra Discovery, through the ShowProof command [16], provides the steps of the algebraic proof by contradiction using computer algebra methods; that is, collecting the different equations that represent each of the hypotheses and the negation of the thesis, namely f and g are not parallel, and then showing that one is a combination of these equations, multiplied by some polynomials that we call syzygies, see [16] for details and references. Thus, the negation of the thesis yields an absurdity, and the statement holds by contradiction.
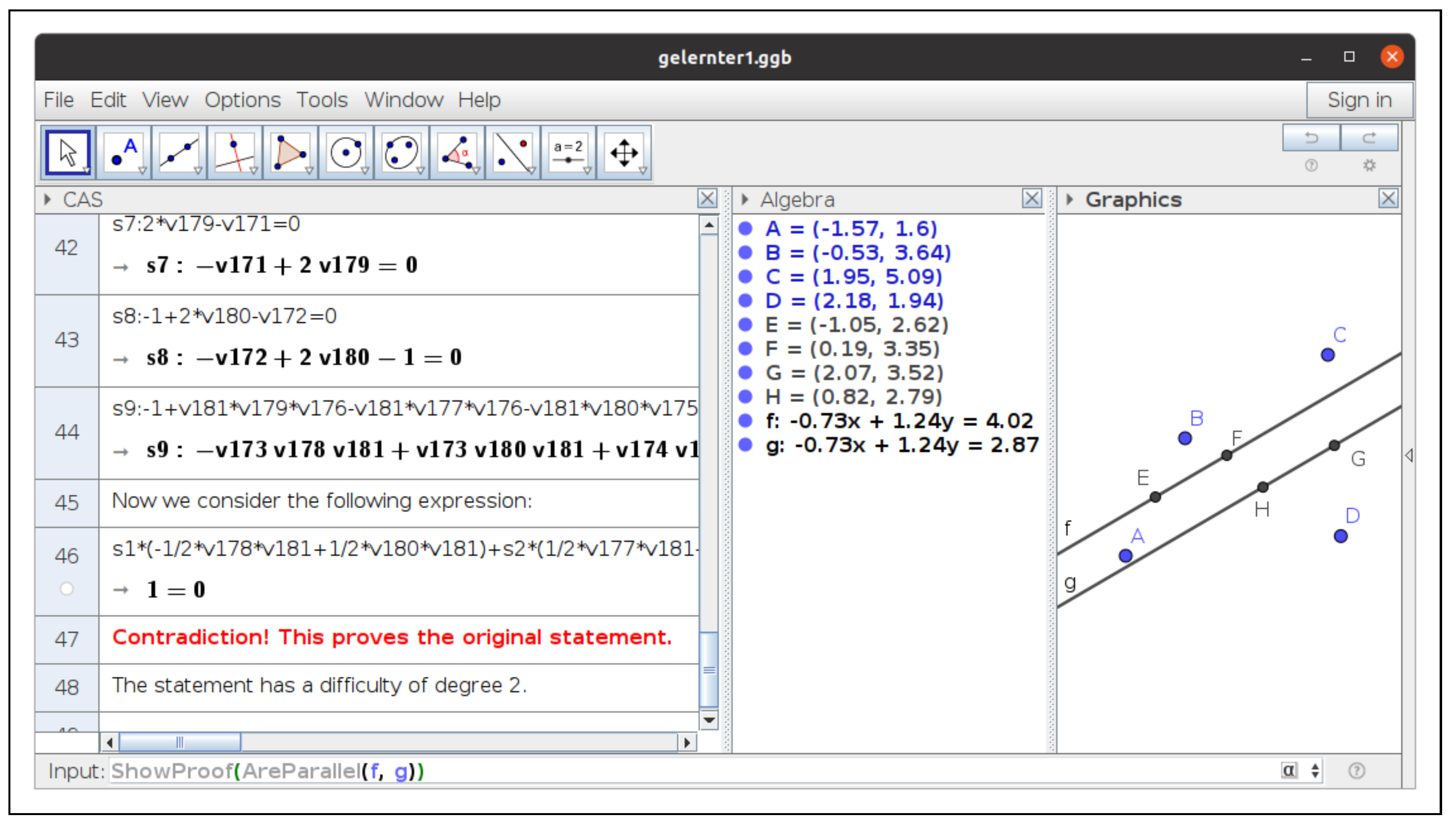
Moreover, GeoGebra Discovery internally computes the degrees of the syzygies and finds that the maximum degree is two, grading—following the definition introduced in [16]—in this way the complexity of the statement, considering such a degree as a kind of measure of the difficulty of expressing that one is a combination of the hypotheses and the negation of the thesis. See Figure 4 and the following verbatim reproduction of the output of the ShowProof command for this particular statement.
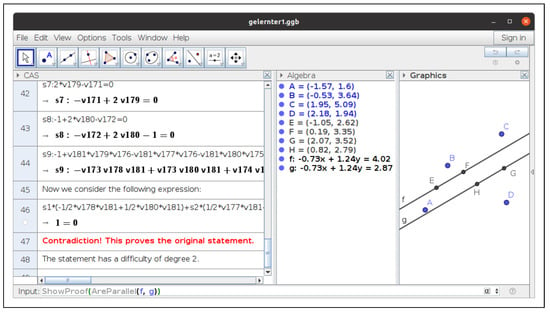
Figure 4.
Final steps of ShowProof when proving the parallelism of and .
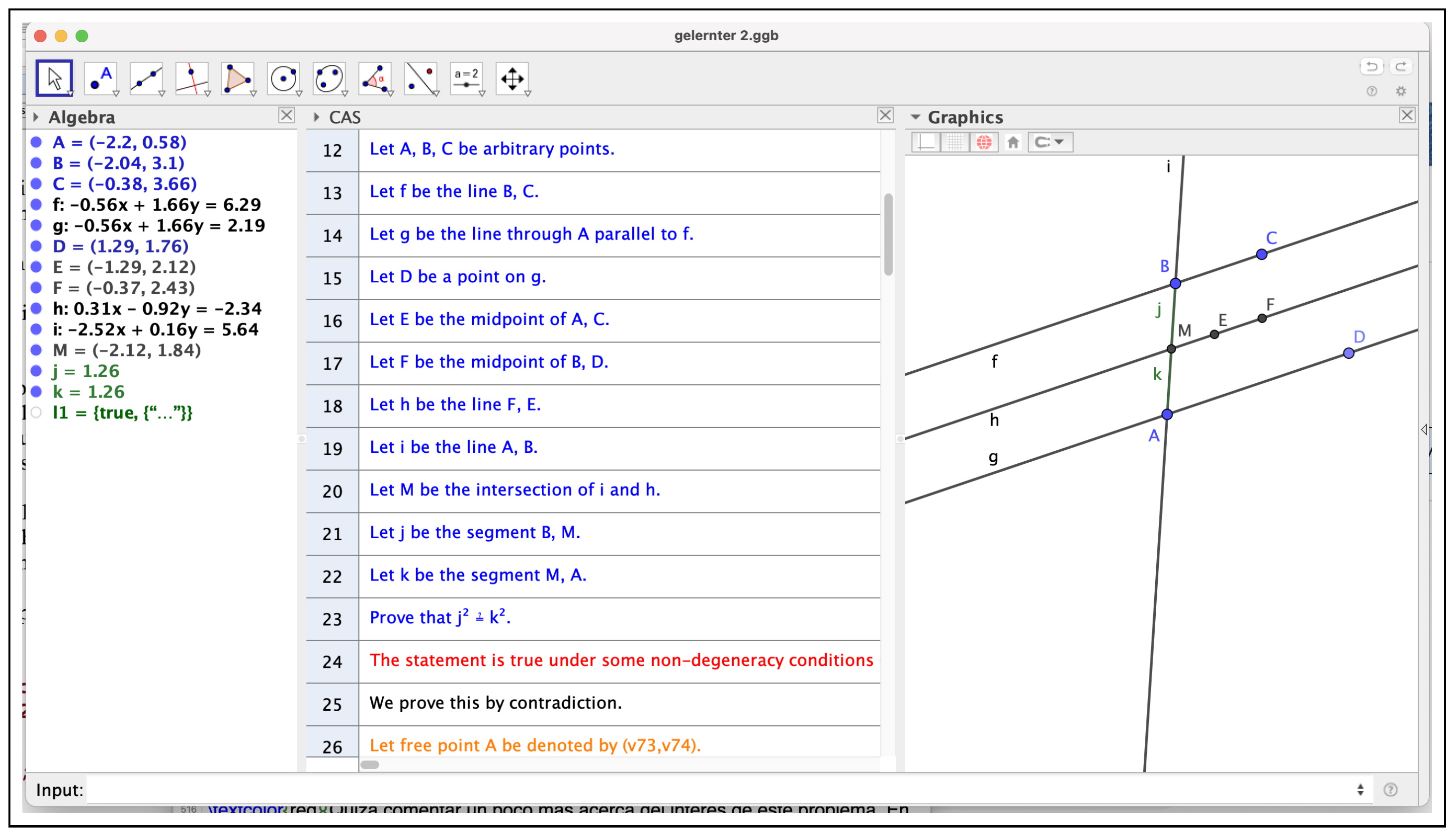
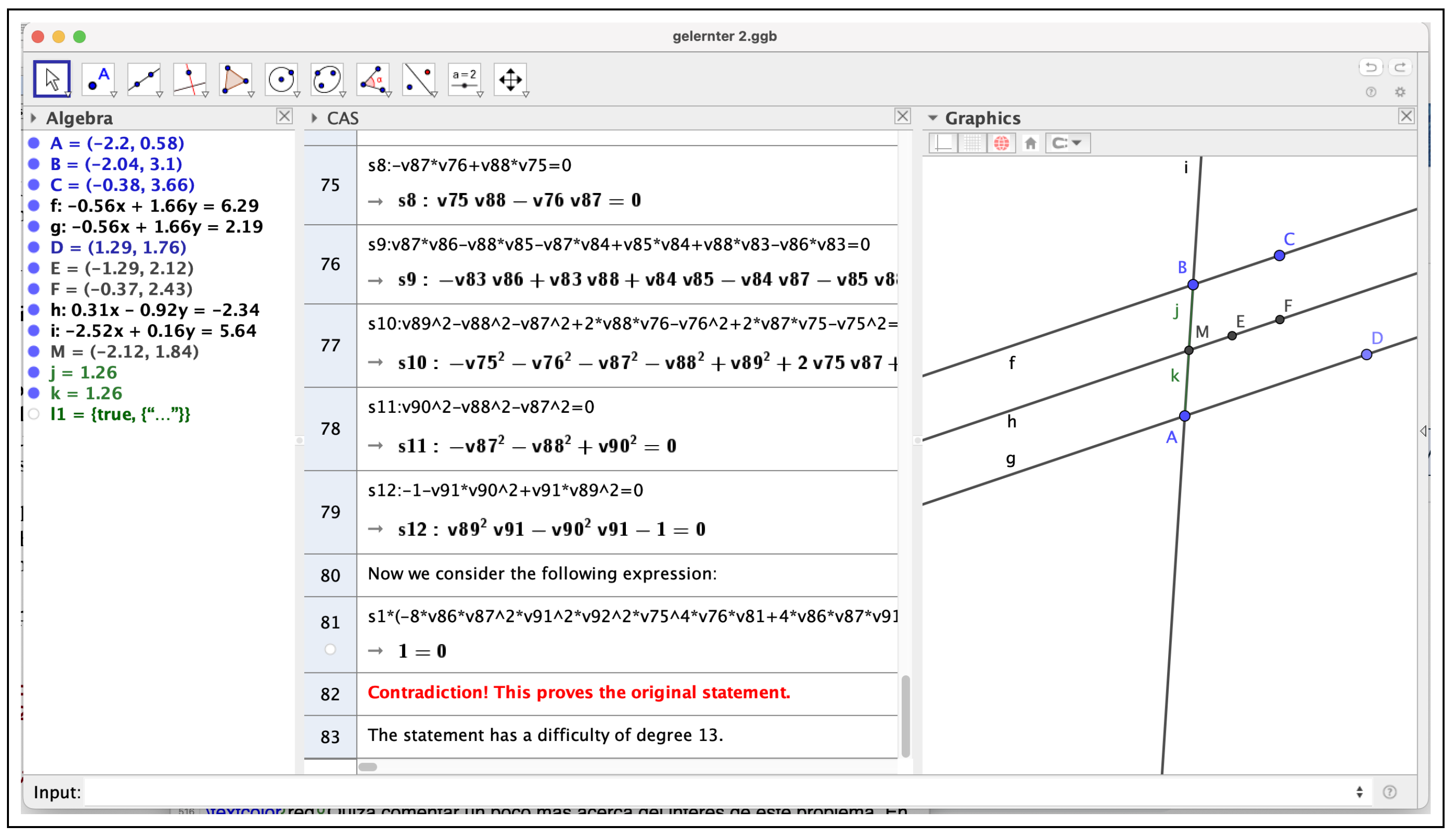
- # Let A, B, C, D be arbitrary points.# Let E be the midpoint of A, B.# Let F be the midpoint of A, C.# Let G be the midpoint of C, D.# Let H be the midpoint of B, D.# Let f be the line E, F.# Let h be the line G, H.# Prove that AreParallel(f, h).# The statement is true under some non-degeneracy conditions (see below).# We prove this by contradiction.# Let free point A be denoted by (v1,v2).# Let free point B be denoted by (v3,v4).# Let free point C be denoted by (v5,v6).# Let free point D be denoted by (v7,v8).# Considering definition E = Midpoint[A, B]:# Let dependent point E be denoted by (v9,v10).e1:=(2 * v9) - v3 - v1 = 0;e2:=(2 * v10) - v4 - v2 = 0;# Considering definition F = Midpoint[A, C]:# Let dependent point F be denoted by (v11,v12).e3:=(2 * v11) - v5 - v1 = 0;e4:=(2 * v12) - v6 - v2 = 0;# Considering definition G = Midpoint[C, D]:# Let dependent point G be denoted by (v13,v14).e5:=(2 * v13) - v7 - v5 = 0;e6:=(2 * v14) - v8 - v6 = 0;# Considering definition H = Midpoint[B, D]:# Let dependent point H be denoted by (v15,v16).e7:=(2 * v15) - v7 - v3 = 0;e8:=(2 * v16) - v8 - v4 = 0;# Thesis reductio ad absurdum (denied statement):e9:=-1 - ((v17 * v15) * v12) + ((v17 * v13) * v12) +((v17 * v16) * v11) - ((v17 * v14) * v11) + ((v17 * v15) * v10)- ((v17 * v13) * v10) - ((v17 * v16) * v9) + ((v17 * v14) * v9) = 0;# Without loss of generality, some coordinates can be fixed:{v1 = 0, v2 = 0, v3 = 0, v4 = 1};# All hypotheses and the negated thesis after substitutions:s1:=(2 * v9) = 0;s2:=-1 + (2 * v10) = 0;s3:=(2 * v11) - v5 = 0;s4:=(2 * v12) - v6 = 0;s5:=(2 * v13) - v7 - v5 = 0;s6:=(2 * v14) - v8 - v6 = 0;s7:=(2 * v15) - v7 = 0;s8:=-1 + (2 * v16) - v8 = 0;s9:=-1 - ((v17 * v15) * v12) + ((v17 * v13) * v12) + ((v17 * v16) * v11)- ((v17 * v14) * v11) + ((v17 * v15) * v10) - ((v17 * v13) * v10)- ((v17 * v16) * v9) + ((v17 * v14) * v9) = 0;# Now we consider the following expression:(s1 * (((1 / 2 * v14) * v17) - ((1 / 2 * v16) * v17))) +(s2 * (((-1 / 2 * v13) * v17) + ((1 / 2 * v15) * v17))) +(s3 * (((-1 / 2 * v14) * v17) + ((1 / 2 * v16) * v17))) +(s4 * (((1 / 2 * v13) * v17) - ((1 / 2 * v15) * v17))) +(s5 * (((1 / 4 * v17) * v6) - (1 / 4 * v17))) +(s6 * ((-1 / 4 * v17) * v5)) + (s7 * (((-1 / 4 * v17) * v6) +(1 / 4 * v17))) + (s8 * ((1 / 4 * v17) * v5)) + (s9 * (-1));# Contradiction! This proves the original statement.# The statement has a difficulty of degree 2.
Let us succinctly explain the different items in this reproduction of the GeoGebra Discovery CAS view. Notice, first of all, that equation above expresses, using the “dummy variable” , that vectors and are parallel. Indeed, this parallelism can be expressed (following the notation of the ShowProof output) as . And it is easy to check that is exactly the equation , i.e., 1 minus times the expanded form of the left term of the thesis equation.
Next, the ShowProof output shows the result of fixing, in order to simplify the computations, the free points . This does not affect the general validity of the considered statement since the fact that lines are parallel is kept through any rotation, translation, and homothecy, which takes any given to . The new collection of hypotheses equations, after replacing , are , while represents, again, the negation of the thesis . Let us remark that is equal to since it is not affected by the specialization of .
The last expression in the ShowProof output is the key to estimate, following our definition [16], the “difficulty” of the statement. Roughly speaking, GeoGebra Discovery verifies the (“geometric”, i.e., the thesis vanishes over all points ) truth of the statement by proving that ; that is, . Indeed, it is well known that this is equivalent to having a power of in the , which is equivalent, by Hilbert’s Nullstellensatz, to the geometric truth of the statement. Now, the verification of is equivalent to having as the Gröbner basis of the ideal for whatever monomial order. In general, Giac, GeoGebra Discovery’s internal CAS [17], performs the computation of the corresponding Gröbner basis, keeping a record of the expression of the elements in the obtained basis in terms of the given generators (here: ). Finally, Giac obtains this expression for one:
- 1= (s1 * (((1 / 2 * v14) * v17) - ((1 / 2 * v16) * v17))) +(s2 * (((-1 / 2 * v13) * v17) + ((1 / 2 * v15) * v17))) +(s3 * (((-1 / 2 * v14) * v17) + ((1 / 2 * v16) * v17))) +(s4 * (((1 / 2 * v13) * v17) - ((1 / 2 * v15) * v17))) +(s5 * (((1 / 4 * v17) * v6) - (1 / 4 * v17))) +(s6 * ((-1 / 4 * v17) * v5)) + (s7 * (((-1 / 4 * v17) * v6) +(1 / 4 * v17))) + (s8 * ((1 / 4 * v17) * v5)) + (s9 * (-1));
Thus, according to our definition, since only polynomials of degree at most two are involved in the expression of one in terms of , we could estimate the complexity of the statement (the relation hypotheses/thesis) as bounded by two.
A final remark: in this particular case, it holds that the thesis is not only geometrically true over the hypotheses’ variety but also algebraically true, i.e., the thesis itself belongs to the ideal of the hypotheses . In this case, we could (but GeoGebra Discovery does not, to be able to deal quickly with more involved situations) directly find the expression of the thesis in terms of the generators of the ideal hypotheses by first computing a Gröbner basis, expressing each element of the basis in terms of the generators, and then computing the Normal Form of the thesis (i.e., 0) and the representation of the in terms of the G-basis. Finally, combining both expressions, obtaining
that is,
and the complexity will be one, the degree of the polynomials that multiply the hypotheses’ equations. This difference, i.e., complexity 1 with the direct proof and complexity 2 in the proof by contradiction, is not relevant and is due, in part, to the inclusion of the “dummy variable” in the latter approach. Let us remark that most classical, elementary theorems (e.g., Pythagoras, Intersection of Medians, Intersection of Heights, etc.) obtain grades 1 or 2 by GeoGebra Discovery; a partial formulation of the nine-point circle theorem obtains complexity four; and some recent Austrian mathematics olympiad problem was graded with number 10 by our algorithm, see [18].
3. Revisiting Gelernter et al. Theorem 2
The theorem in Appendix 2 of [4] is stated as follows:
- PremisesQuad-lateral ABCDSegment BC parallel segment ADPoint E midpoint segment ACPoint F midpoint segment BDPrecedes MEFPrecedes AMBTo ProveSegment MB equals segment MAAs declared in Appendix 2, the system states, after 8.12 min, “I Am Stuck”. And the same Appendix mentions that, after manually adding a point K (see Figure 5) and completing the premises withPrecedes CFKCollinear AKDthe theorem was successfully proven, in those days, with an elapsed time of 30.68 min. Notice that Precedes means the involved points are “collinear in that order.” ([4], p. 157, last line).
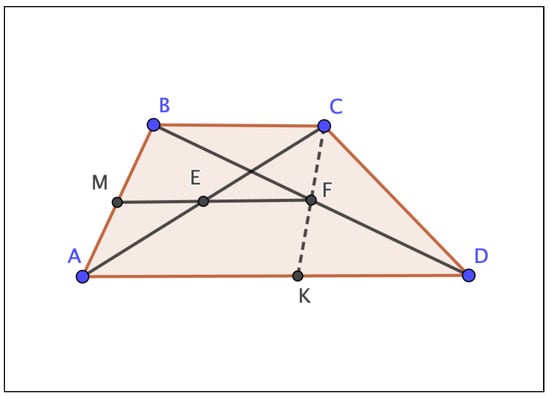
Figure 5.
Theorem 2 from Appendix 2 in [4], with an extra point K.
Figure 5.
Theorem 2 from Appendix 2 in [4], with an extra point K.
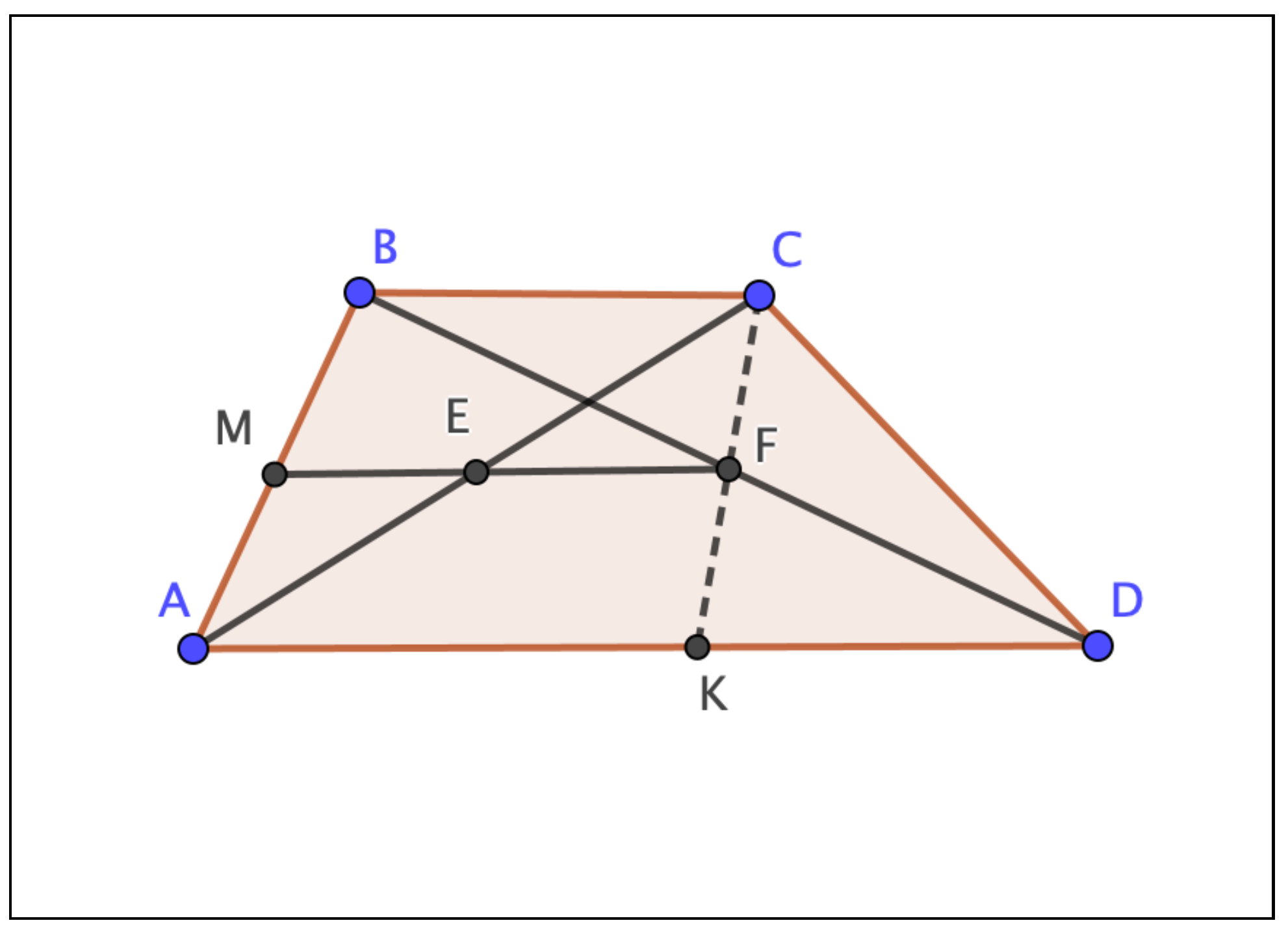
As in the precedent section, next we describe how both ChatGPT and GeoGebra Discovery succeed in proving the theorem.
3.1. Gelernter et al. Theorem 2: ChatGPT
ChatGPT, after entering the question “Let and D be a trapezoid with vertices given in clockwise manner, parallel to , f the line through B and C, g the line through A parallel to f, E the midpoint of , F the midpoint of , h the line through F and E, i the line through A and B, and M the intersection point of i and h. Prove that segment equals segment ”, outputs the following answer:
To prove that segment BM equals segment MA in the given configuration of a trapezoid ABCD where AD‖BC, follow these steps:
Trapezoid Configuration: Given trapezoid ABCD with AD‖BC and vertices in a clockwise manner. Line f passes through points B and C. Line g passes through point A and is parallel to f, hence g‖BC.
Midpoints: E is the midpoint of AC, so AE = EC. F is the midpoint of BD, so BF = FD.
Constructing Lines: Line h passes through points E and F. Line i passes through points A and B.
Intersection Point: Let M be the intersection point of lines h and i.
Properties and Symmetry: Since AD‖BC, and E and F are midpoints, line h (through E and F) behaves as a midsegment of trapezoid ABCD.
Key Property of Midsegment: The line segment joining the midpoints of the non-parallel sides of a trapezoid (line h) is parallel to the bases (AD and BC) and its length is half the sum of the lengths of the bases.
Geometric Analysis: Since h is the midsegment, it is parallel to AD and BC and divides the trapezoid into smaller sections that reflect the symmetry of the figure. Lines h and g are both parallel to BC (and thus to each other), and line i is the transversal through A and B.
Using the Midpoints E and F: Midpoint E of AC and midpoint F of BD create symmetry about the center of the trapezoid.
Intersection and Equal Segments: Since h connects the midpoints and i intersects h at M, by properties of trapezoids and midsegments, M divides AB such that BM = MA.
Detailed Symmetry Argument: Consider triangles ΔABE and ΔBDF. Line EF (the midsegment) maintains parallelism with the bases and equality in segment distances. The intersection M by nature of midpoint lines and parallel properties guarantees M lies equidistantly between A and B.
Conclusion: Since M divides AB symmetrically: BM = MA
Therefore, the segment BM equals segment MA. This synthetic proof confirms the equality of the segments based on the midpoint theorem and properties of trapezoids.
As in the previous example, we included in Appendix A the ChatGPT session when rephrasing Theorem 2, first in a completely textual way and then including just an image. Here, analytic proofs are given by taking suitable coordinates for points in the configuration. As in the previous statement, the proof for the first prompt is correct, but not for the second one. Indeed, in this case, ChatGPT proves nothing: the chosen parallel sides in the proof are different from those in the picture, i.e., it is declared that AB‖CD (similar issue as the one in Problem 1 with a figural prompt), which makes it impossible to follow the thesis because then line can not intersect line ; but, furthermore, ChatGPT continues taking M as the midpoint of in order to prove that M is the midpoint of !
3.2. Gelernter et al. Theorem 2: GeoGebra Discovery
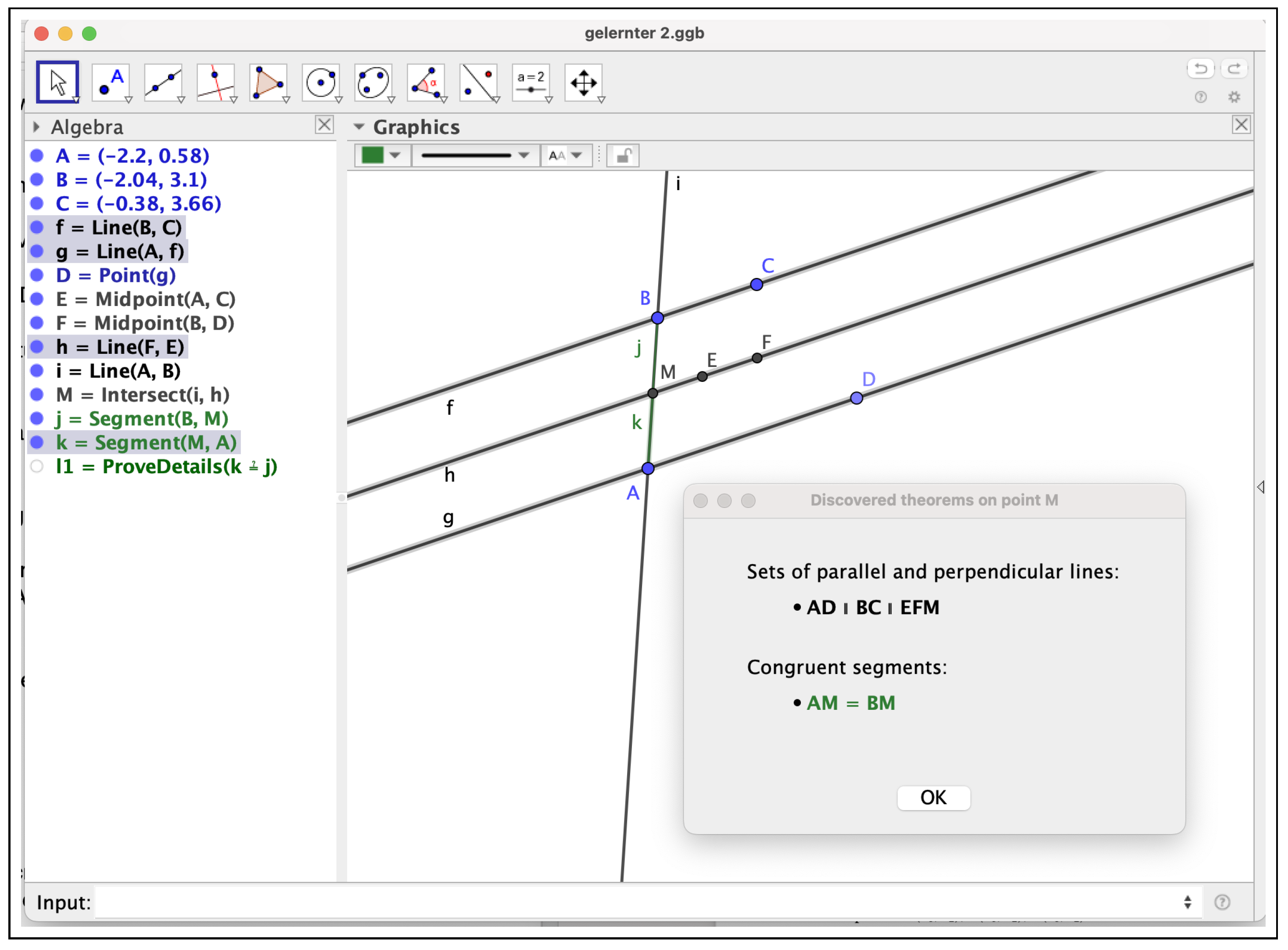
Similarly, GeoGebra Discovery declares the truth of the theorem by using, for example, ProveDetails(k==j). Note that, again, it would not be necessary to know the thesis about the equality of these two segment lengths because, in the given construction, after introducing the command Discover (M), a list of properties involving point M, including the sought thesis stating that segment and are congruent, could be obtained. Figure 6 displays both the results of the Discover(M) and of the ProveDetails(k==j) commands.
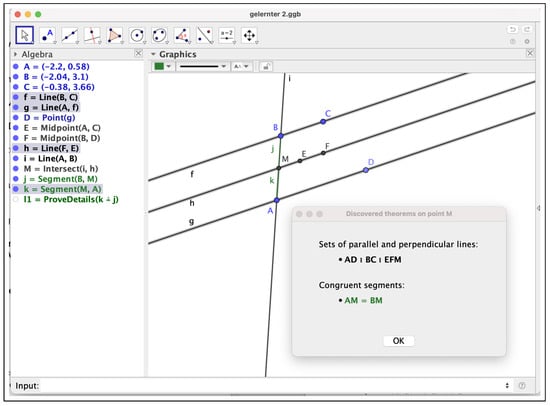
Figure 6.
GeoGebra Discovery discovers, and verifies, the equality of segments .
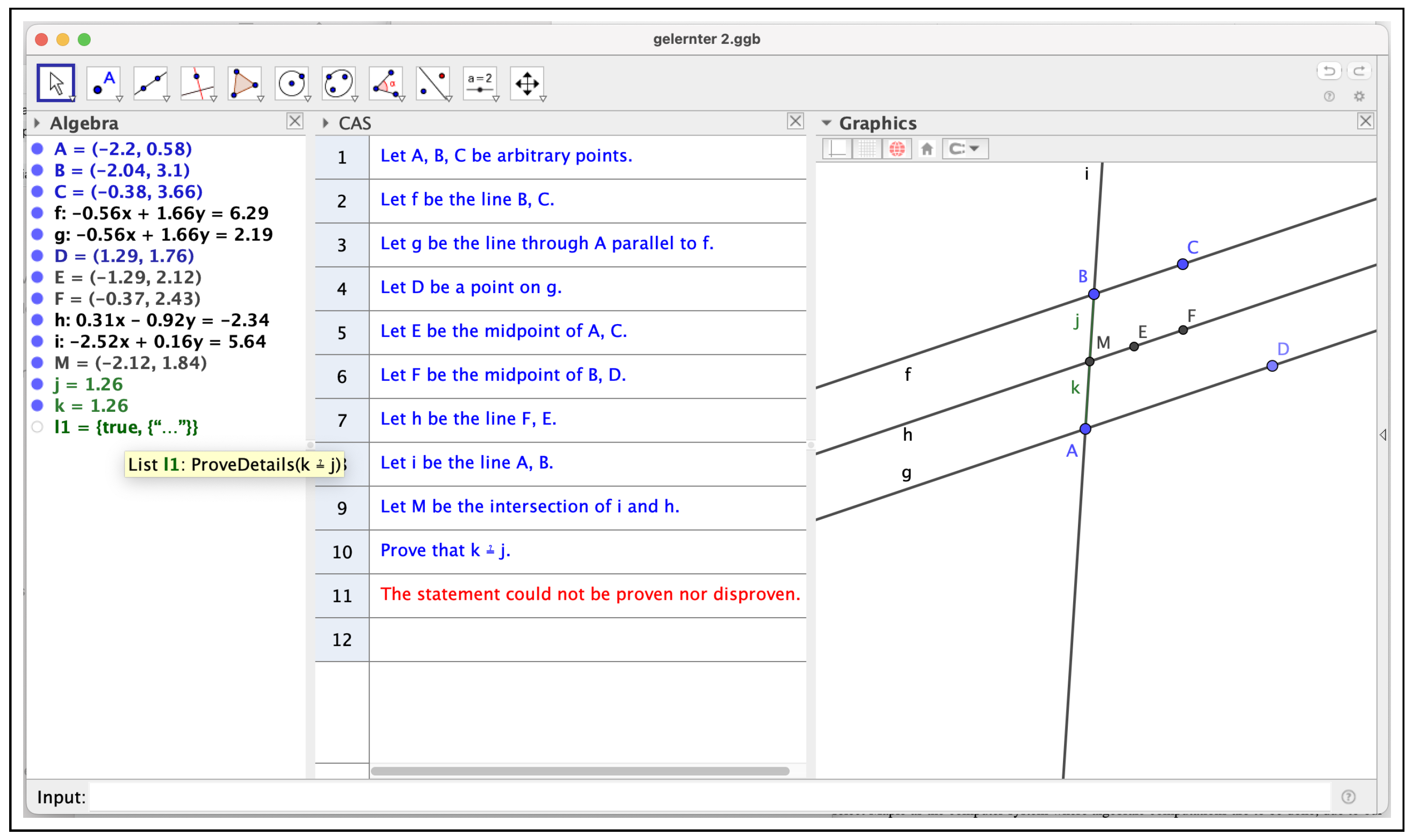
Nevertheless, things are not simple. When GeoGebra Discovery is asked to give a proof via the ShowProof command, it declares that the statement could not be proven or disproven (an answer that should be regarded as a modern counterpart to the “I am stuck” comment concerning the proof of this theorem in the article of Gelernter et al. [4]). See Figure 7, which exhibits two contradictory messages: “The statement could not be proven nor disproven” and if ProveDetails(k==j) is entered.
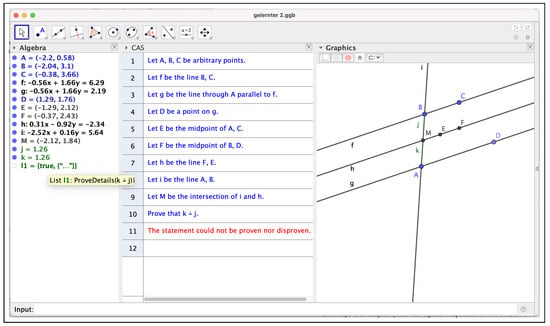
Figure 7.
GeoGebra Discovery declares that it can neither prove nor disprove the equality of segments .
Clarifying this strange behavior requires reference to some subtle computational complex algebraic geometry algorithms that are behind the scenes:
- The notion of “True on Parts” [13], which labels statements that are true on some non-degenerate prime components of the hypotheses’ variety but are also false on some others;
- The notion of the Minimal Extended Polynomial (MEP) [14] to deal with statements involving variables that are defined through square powers (like the distance between two points or the length of a segment).
3.2.1. True on Parts
Roughly speaking (referring the reader to the above-mentioned references for details), let us say that the algebraic translation of the steps of a geometric construction might give rise to some unexpected (by the user) prime components of the hypotheses’ variety where the statement does not hold while being true on the “expected” components.
This fact (i.e., being “True on Parts”) can be verified through two different algorithms: one, performing a prime, or primary, decomposition of the hypotheses’ variety, and then applying the automated proving methods to each of the components. Two, performing the elimination of all variables that are not free in the construction over the ideal of the hypotheses plus the negation of the thesis and over the ideal of the hypotheses plus the thesis. If the output in both cases is 0, it means that there are prime components where the free variables are independent, which do not have an open set (Zariski topology) where the thesis holds, and that there are also such components that have an open set where the thesis holds (hence, over all the component).
GeoGebra Discovery implements the second option as it is computationally more efficient than having to compute the prime/primary decomposition. As a negative counterpart, when declaring “True on Parts”, GeoGebra Discovery is not able to specify the components where the statement is true or is false, leaving the user without further geometric information to understand more deeply what is going on. Thus, in order to realize the situation of Theorem 2, we will have to perform the computations by ourselves. We will conduct them through the Maple CAS ( https://www.maplesoft.com, accessed 22 July 2024); see Appendix B for details.
As in the previous section, we might be interested in grading the complexity of the statement. Here, obtaining such a grade could involve, perhaps, the introduction of a measure associated with the relation between the given hypotheses and the new hypotheses—the ones describing the components where the theorem holds true. What could be a reasonable proposal of a complexity measure for statements that are partially true and thus transformed into a new statement if we know the complexity of B to be ? To ask an even simpler question: what could be a sound definition of the complexity of checking that is a factor of ? We could say it is one since we only need to multiply times , a degree one polynomial. Likewise, what could be a measure of the complexity of testing that the generators of a given ideal generate a prime component of the hypotheses’ ideal H? Remark: we are not talking about the complexity of computing the components but of having a sort of proof certificate that the computation is correct. This is, surely, work for the future, involving both computer algebra and automated reasoning.
3.2.2. Minimal Extended Polynomial
It is easy to conclude, from the computations described in Appendix B concerning this “True on Parts” statement, that it seems more reasonable—in order to apply the very well-performing complex algebraic geometry algorithms implemented in GeoGebra Discovery—to change the thesis of the previous theorem from to as this wider thesis generally holds in the components of the hypotheses’ variety. Understanding how to go from to (of course, in much more general situations) is precisely the computation of the Minimal Extended Polynomial (MEP) of , the smallest multiple with only even powers of the variables ; see [14] for details.
Here, we just want to show that, indeed, keeping the same hypotheses of Theorem 2 and considering now the thesis , we obtain a generally true statement that can be computed by the elimination of all variables except the free one on the ideal of the hypotheses and the negation of the new thesis with the “dummy” variable t, i.e., . See Appendix C for the output of this elimination and its interpretation. This is already achieved (but not detailed) by GeoGebra Discovery, see Figure 8 and Figure 9, depicting the output of the ShowProof computations, similar to those described in the previous section. But let us remark on the high complexity, 13, of this MEP variant of Theorem 2 in [4]. More precisely, this measure refers to the complexity of Theorem 2, but after adding certain non-degeneracy hypotheses and extending the thesis to include the case .
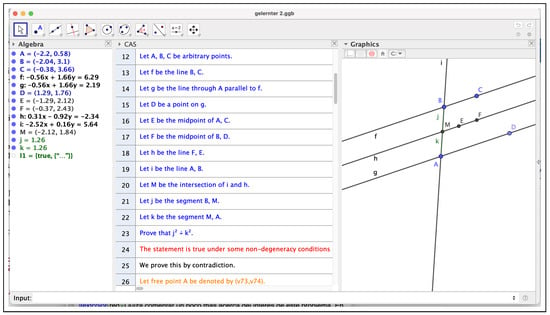
Figure 8.
GeoGebra Discovery verifies the truth of .
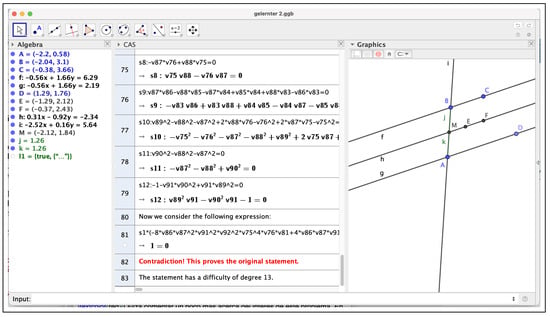
Figure 9.
GeoGebra Discovery estimates the complexity of the MEP variant of Theorem 2.
Again, it is still pending work to propose a reasonable measure of the complexity of statements that involve computing and adding non-degeneracy conditions. For instance, should we add, to rank the initial statement, to the grade obtained for the final statement, the complexity of checking that the found non-degeneracy conditions belong to the ideal of the hypotheses and the negation of the thesis?
4. AMM Problem 11984
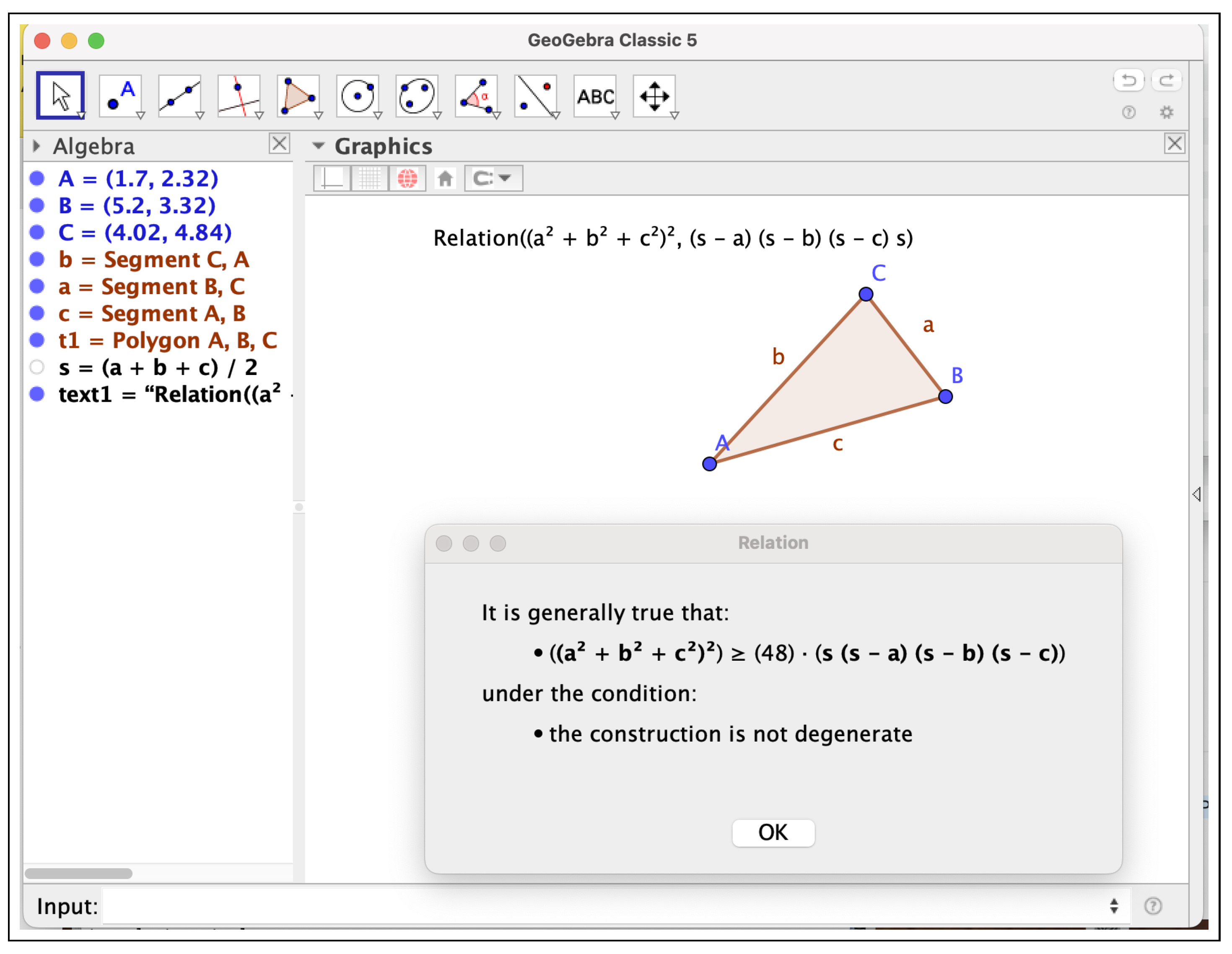
As a final comparison of the performance of ChatGPT and GeoGebra Discovery, let us consider, following the trend to test AI performance in mathematical problems of recognized difficulty (e.g., problems from mathematics olympiads), as mentioned in the Introduction, the proof of an inequality that was proposed in the challenging Problem Section of the American Mathematical Monthly [15]: “If are the side lengths of a triangle with inradius r, then the following inequality holds: ”.
In order to prove this inequality, the GeoGebra Discovery version must be v5.0.641.0-2024Apr03 or above. Furthermore, it should be executed with the options
- singularws=enable:true,remoteurl:http\://prover-test.geogebra.org/~kovzol/singularws-dev/andtimeout:3000---prover=timeout:3000.For reproducibility issues, let us mention that the construction can be introduced into the GeoGebra input bar asExecute({"A = (-.86, -.08)", "B = (6.92, .18)", "C = (5.54, 3.94)","Polygon(A, B, C)", "IncircleCenter(A, B, C)", "PerpendicularLine(D, c)","Intersect(f, c)", "r = Segment(D, E)", "Prove( a^6 +b^6 +c^6 >= 5184r^6)"})GeoGebra Discovery succeeds in proving the inequality, as shown in Figure 10. Moreover, using the ProveDetails command the system returns{true, {‘‘AreCollinear(A,B,C)’’, ‘‘AreEqual(A,B)’’}}meaning that the inequality is true except for certain degenerate configurations, such as the collinearity of the three vertices. Notice that, in the case of inequalities (and, more generally, real algebraic geometry statements), the GeoGebra Discovery command ShowProof is still not able to provide a proof certificate (a non-trivial, theoretically still not clear task), only some steps. See Figure 11, Figure 12 and Figure 13.
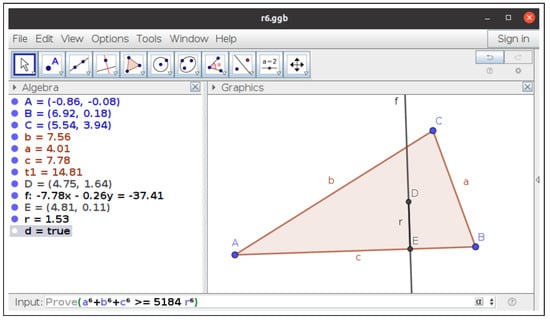
Figure 10.
GeoGebra Discovery confirms that the inequality: holds.
Figure 10.
GeoGebra Discovery confirms that the inequality: holds.
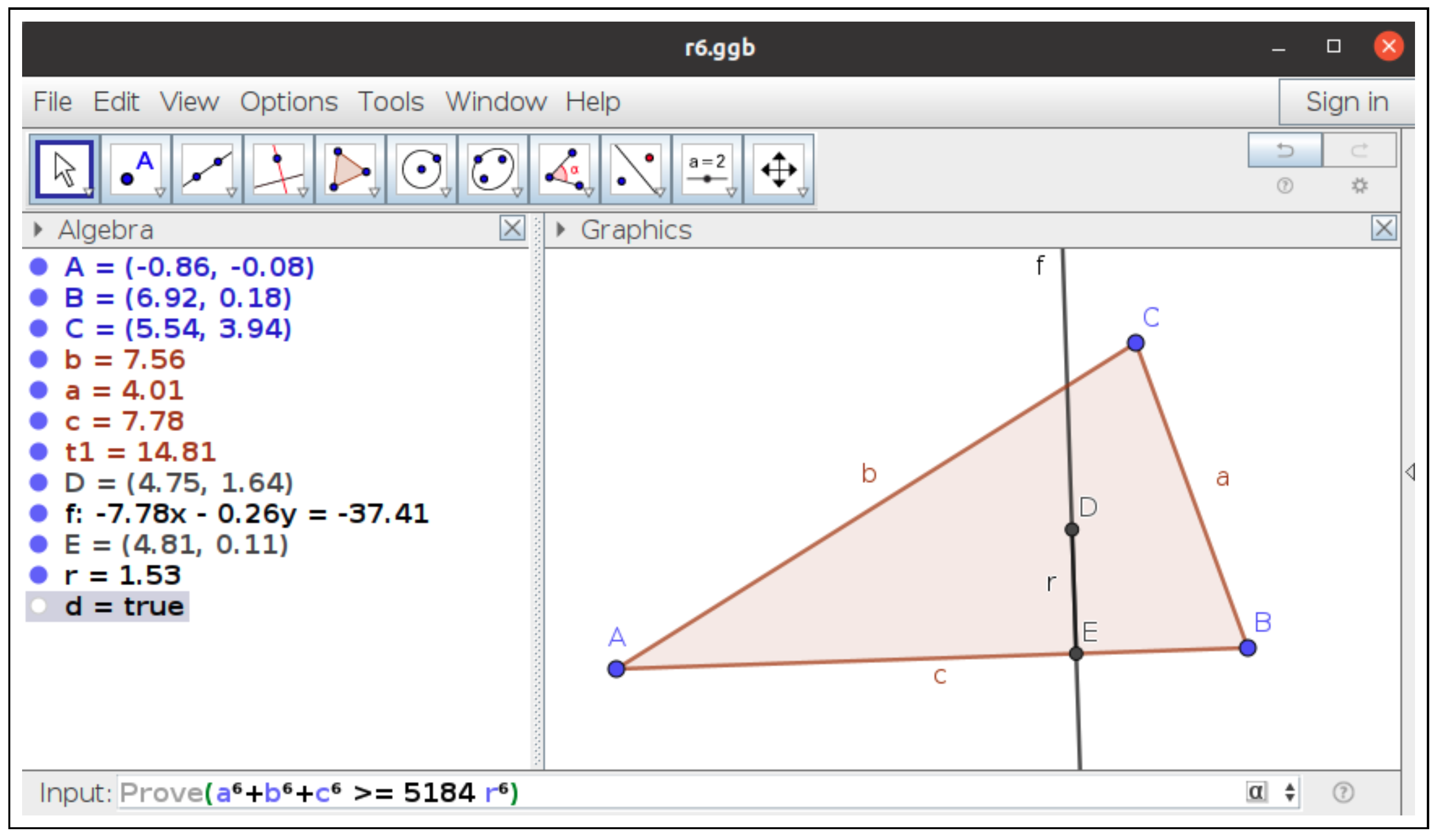
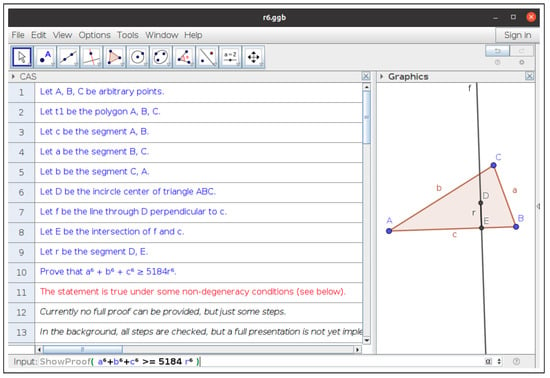
Figure 11.
Viewing proof of the inequality through ShowProof. Initial steps.
Figure 11.
Viewing proof of the inequality through ShowProof. Initial steps.
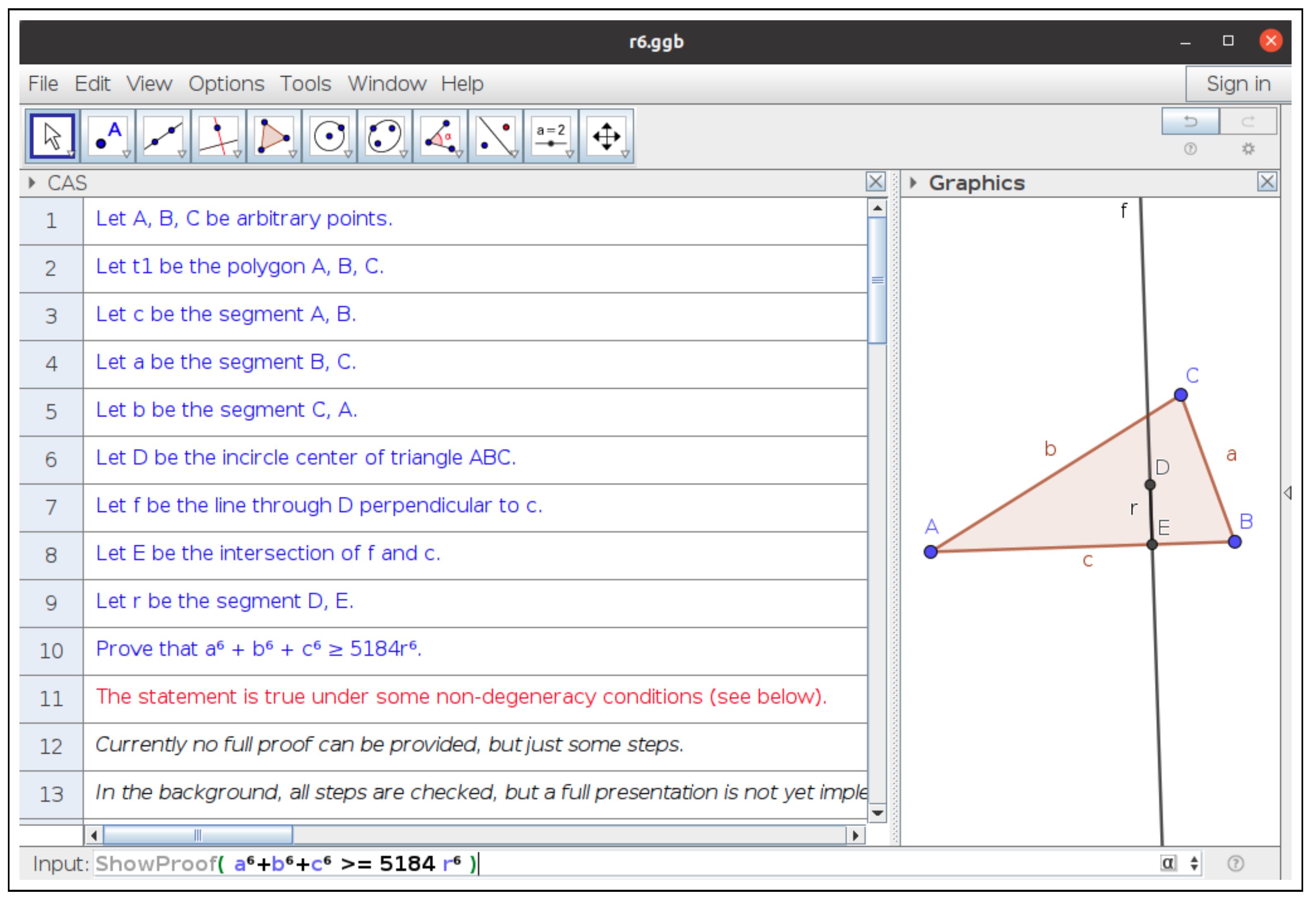
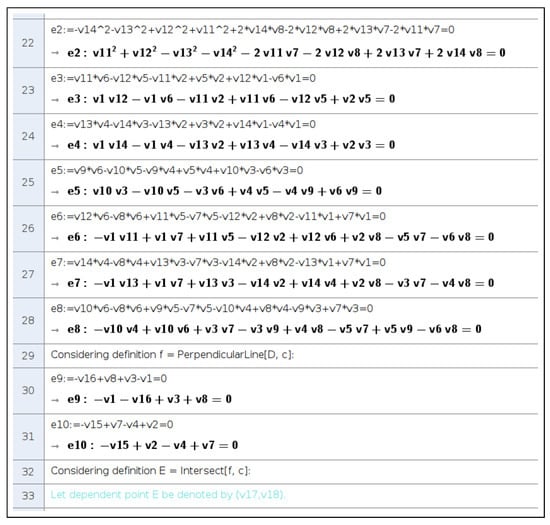
Figure 12.
Viewing proof of the inequality through ShowProof. Intermediate steps.
Figure 12.
Viewing proof of the inequality through ShowProof. Intermediate steps.
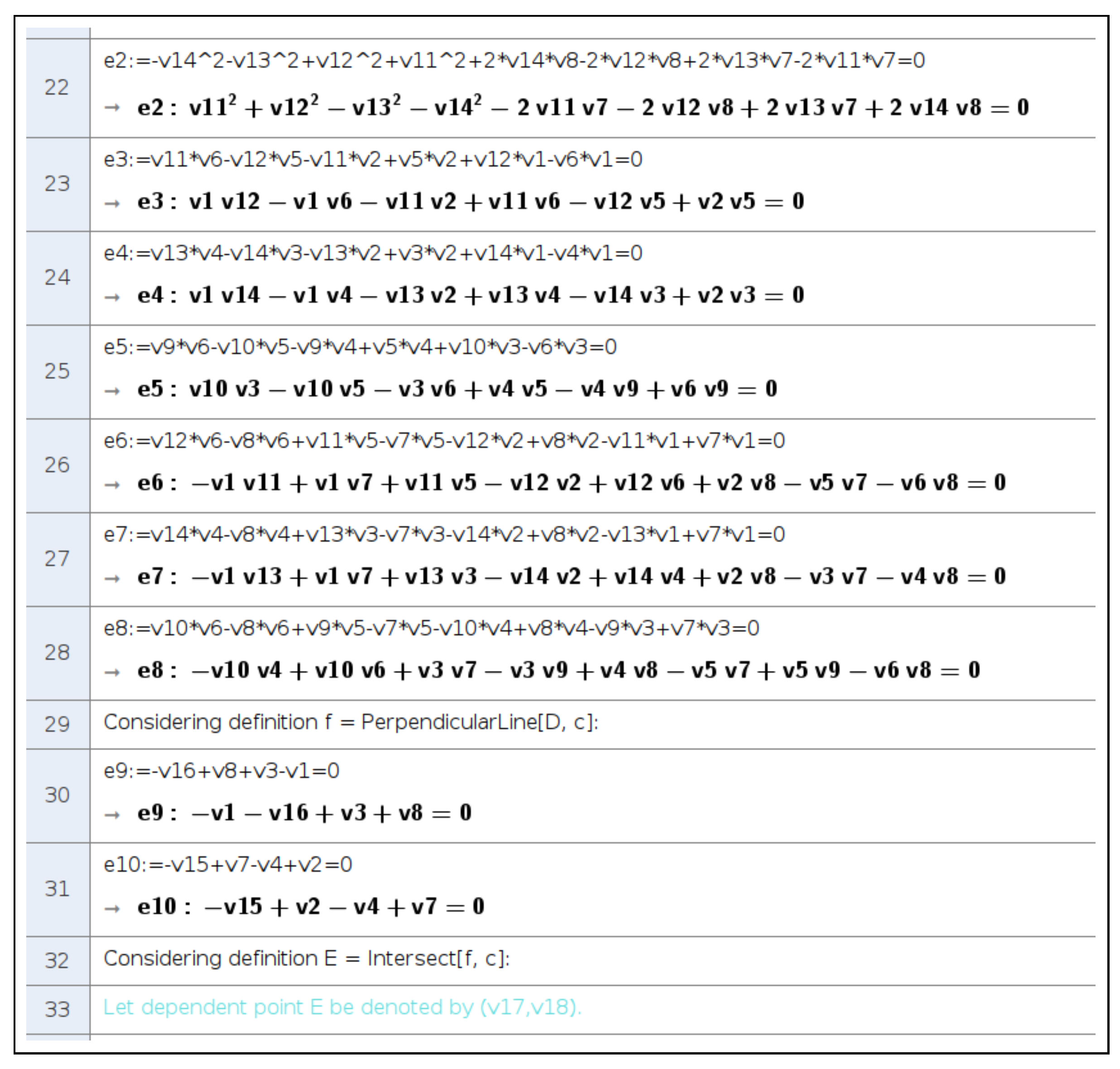
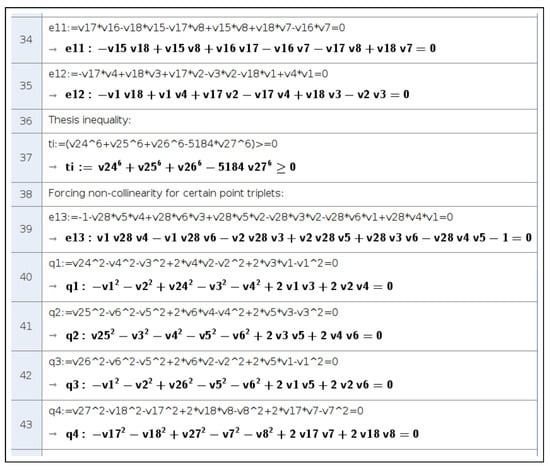
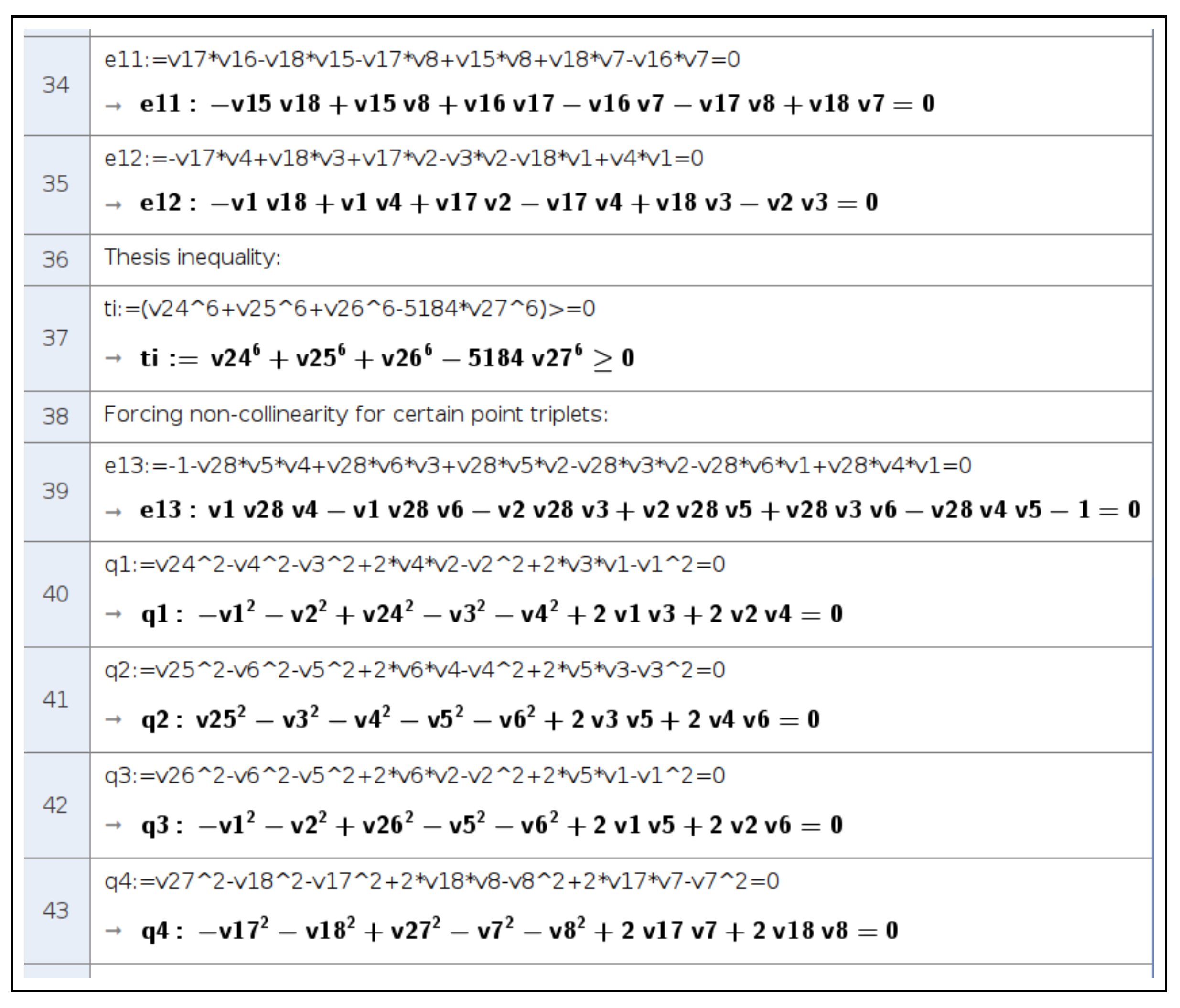
Figure 13.
Viewing proof of the inequality through ShowProof. Final steps.
Figure 13.
Viewing proof of the inequality through ShowProof. Final steps.
On the other hand, attempting to obtain a human-readable proof of the same inequality, we use ChatGPT, which “pretends” to succeed in proving the inequality (see Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18). What is relevant here is that the user can test each of the ChatGPT steps through GeoGebra, so assuring or denying the correctness of the proof. For instance, in Figure 14, Weitzenböck’s inequality (, where A is the area of the triangle) is used by ChatGPT as one of the arguments for proving Problem 11984. If a reader of the proof is unaware of this inequality, the user could check it in GeoGebra, confirming that this inequality holds. Thus, Figure 19 displays the quite impressive performance of GeoGebra Discovery, which not only automatically verifies the truth of this inequality but also “discovers” this inequality (in an equivalent formulation) if asked about the relation between and , where s is the semi-perimeter. Notice that GeoGebra Discovery does not have a command to express the area A of a triangle, and thus the user must introduce its definition, for example, as shown in Figure 15, using Heron’s formula.

Figure 14.
ChatGPT proof of the inequality (1/5).

Figure 15.
ChatGPT proof of the inequality (2/5).

Figure 16.
ChatGPT proof of the inequality (3/5).

Figure 17.
ChatGPT proof of the inequality (4/5).

Figure 18.
ChatGPT proof of the inequality (5/5).
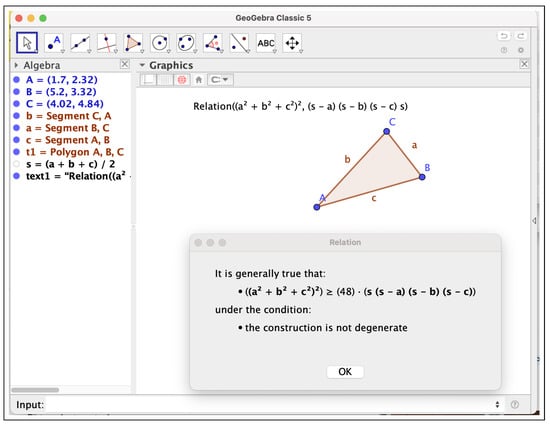
Figure 19.
GeoGebra discovers (and verifies) Weitzenböck’s inequality, included by ChatGPT in the proof of AMM Problem 11984 [15].
An anonymous reader of an early version of this paper noted that, in his/her attempt of proving the inequality using ChatGPT, the chatbot claimed that , thus returning a wrong proof. Likewise, here, the top equality in Figure 15,
is obviously false, as a straightforward computation of the right side of this expression shows it is equal to and not to . Notice that, in the same Figure, the next substitution is also wrong: the inequality mentioned in this substitution should supposedly be the one in the last line of Figure 14:
not the one displayed here: . And, in general, the rest of the proof by ChatGPT is not reliable at all.
5. Conclusions
It is relevant to remark that all the features of GeoGebra Discovery that we exemplified in the previous sections are accomplished through the internal execution of computer algebra algorithms, which implies both the formal validity of the obtained results (a relevant property that is essential in our comparison with the performance of A.I. tools addressing the same tasks) and the difference in methodology with other automated provers that use formal reasoning, such as GeoCoq ( https://geocoq.github.io/GeoCoq/, accessed 22 July 2024), and output high-level proofs in the same style as in high school [19].
Now, concerning the validity of the use of automated deduction methods through algebraic geometry tools, let us quote [20], where it is stated that
The arithmetization of geometry paves the way for the use of algebraic automated deduction methods in synthetic geometry. Indeed, without a back-translation from algebra to geometry, algebraic methods only prove theorems about polynomials and not geometric statements. However, thanks to the arithmetization of geometry, the proven statements correspond to theorems of any model of Tarski’s Euclidean geometry axioms.
Thus, a first conclusion, concerning the comparison of ChatGPT and GeoGebra Discovery in the three examples we described, is that GeoGebra Discovery offers mathematical reliability and performs well even for complicated statements (see [18]) but does not output human-like explanations: just proof certificates, through the recent ShowProof command, and an estimation of the difficulty of the statement. Both features still require being theoretically developed in different contexts: when there is an automated completion of a statement by means of non-degeneracy conditions, when dealing with statements that are just “True on Parts”, or with statements that involve real algebraic geometry issues (such as dealing with lengths or inequalities). Moreover, even considering just statements that do not involve any of these issues, the performance of ShowProof and its associated complexity measure deserve to be tested—and their output compared with human intuition—in a large number of examples of different kinds, and that could be relevant in the educational context.
On the other hand, we showed that ChatGPT’s performance depends on the prompt input, as it could be relevant to the previous training of the chatbot. Thus, for Gelernter et al. Theorems 1 and 2 (as shown in Section 2 and Section 3), when the input is a textual copy of a previous statement, ChatGPT performed very well at presenting correct and readable proofs. But this is not the case for other formulations of the same statements (see Appendix A and Appendix B). ChatGPT also fails when dealing with the AMM Problem 11984, as described in Section 4. Indeed, ChatGPT states on its webpage that it can commit errors and recommends checking the provided information. One could say that it is generally plausible but not reliable.
It is perhaps interesting to remark that, despite the very different approach for different technological tools (Gelernter “Geometry Machine”, ChatGPT, and GeoGebra Discovery) for dealing with geometry statements, their performance in the three considered examples shows some common features. Thus, Theorem 1 is easy for both ChatGPT and GeoGebra, while Theorem 2 required us to add some extra hypotheses to the input of the “Geometry Machine” and to “understand” the subtleties of the “True on Parts” and “Minimal Extended Polynomial” issues involved in the proof of this statement through GeoGebra Discovery. This is related to the fact that the statement is, actually, a statement that requires using signs (for segment lengths), and thus it is deeply (and formally: see [20]) related to real computational algebraic geometry, well known to be much more demanding than complex geometry—although GeoGebra Discovery implements some tricks to avoid getting fully in the real algebraic geometry realm when possible. The same reflection applies to the case of the AMM Problem 11984, a pure real geometry statement, where ChatGPT fails and where GeoGebra Discovery requires using some optional features.
In view of this set of coincidences, we consider it would be quite useful, in the context of Euclidean geometry statements, to develop close cooperation between chatbots and GeoGebra Discovery, where the latter controls the validity of the steps of the proof described by the bot and offers the possibility to the human user, through the proof certificate, of verifying by other, different computational tools, the correction of the decisions of ChatGPT.
In conclusion, we think we provided arguments to support the potential of our cooperation proposal: the mixing of the natural language abilities of a chatbot with the recently extended features of GeoGebra Discovery, providing
- A rigorous checking of the mathematical truth of a given statement, drawn in the dynamic geometry window of this program;
- The availability of the corresponding algebraic translation for analyzing and obtaining, through a CAS, further insight about its geometry, which could be quite relevant in special cases (e.g., “True on Parts” and “Minimal Euclidean Polynomials”), as it would provide a kind of automated completion of the initial statement;
- The production of proof certificates;
- The estimation of the difficulty of geometric theorems.
A final reflection: we think that, in this context of elementary geometry, the final goal is not just to prove, but to learn more. And we consider that by merging both ChatGPT and, very specially, the GeoGebra Discovery output, even when it is not conclusive enough, we are naturally encouraged to learn more.
Author Contributions
Conceptualization, F.B., T.R. and M.P.V.; methodology, F.B., T.R. and M.P.V.; software, F.B., T.R. and M.P.V.; validation, F.B., T.R. and M.P.V.; investigation, F.B., T.R. and M.P.V.; writing—original draft preparation, F.B., T.R. and M.P.V.; writing—review and editing, F.B., T.R. and M.P.V. All authors have read and agreed to the published version of the manuscript.
Funding
The second and third authors are partially supported by a “Mathematical Visualization: Foundations, Algorithms and Applications” grant (PID2020-113192GB-I00) from the Spanish MICINN.
Data Availability Statement
All data were contained in main text.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
In this appendix, we show the performance of ChatGPT when we rephrase the input by some equivalent (to the ones exhibited in Section 2.1 and Section 3.1) statements from Gelernter et al. [4] Theorem 1 and Theorem 2. First, we ask ChatGPT for a proof when the prompt includes just a purely descriptive geometry statement, even without labeling points. Then, for both Theorem 1 and Theorem 2, we describe the performance of ChatGPT when the prompt is just an image of the geometric configuration, and we ask it to prove the thesis.
Appendix A.1. Gelernter et al. Theorem 1: ChatGPT Performance for Alternative Formulations
Appendix A.1.1. Descriptive Statement Prompt

Yes, we can prove this statement using vector geometry. Let’s consider a quadrilateral and denote the midpoints of , , , and as E, F, G, and H respectively.
1. Midpoints of Opposite Sides:
2. Midpoints of Diagonals:
We need to prove that forms a parallelogram.
Step-by-Step Proof:
Step 1: Define the Points Using Vectors
Step 2: Find Midpoints Using Vectors
Step 3: Calculate Vectors of the Sides of Quadrilateral
Notice that:
Since and are equal, is parallel and equal in length to .
Notice that:
Since and are equal, is parallel and equal in length to .
Conclusion: Both pairs of opposite sides and , and are equal and parallel. Therefore, the quadrilateral is a parallelogram.
This completes the proof.
Appendix A.1.2. Figural Prompt
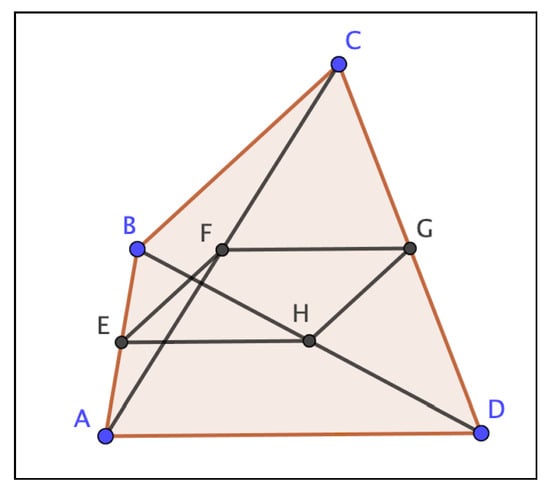
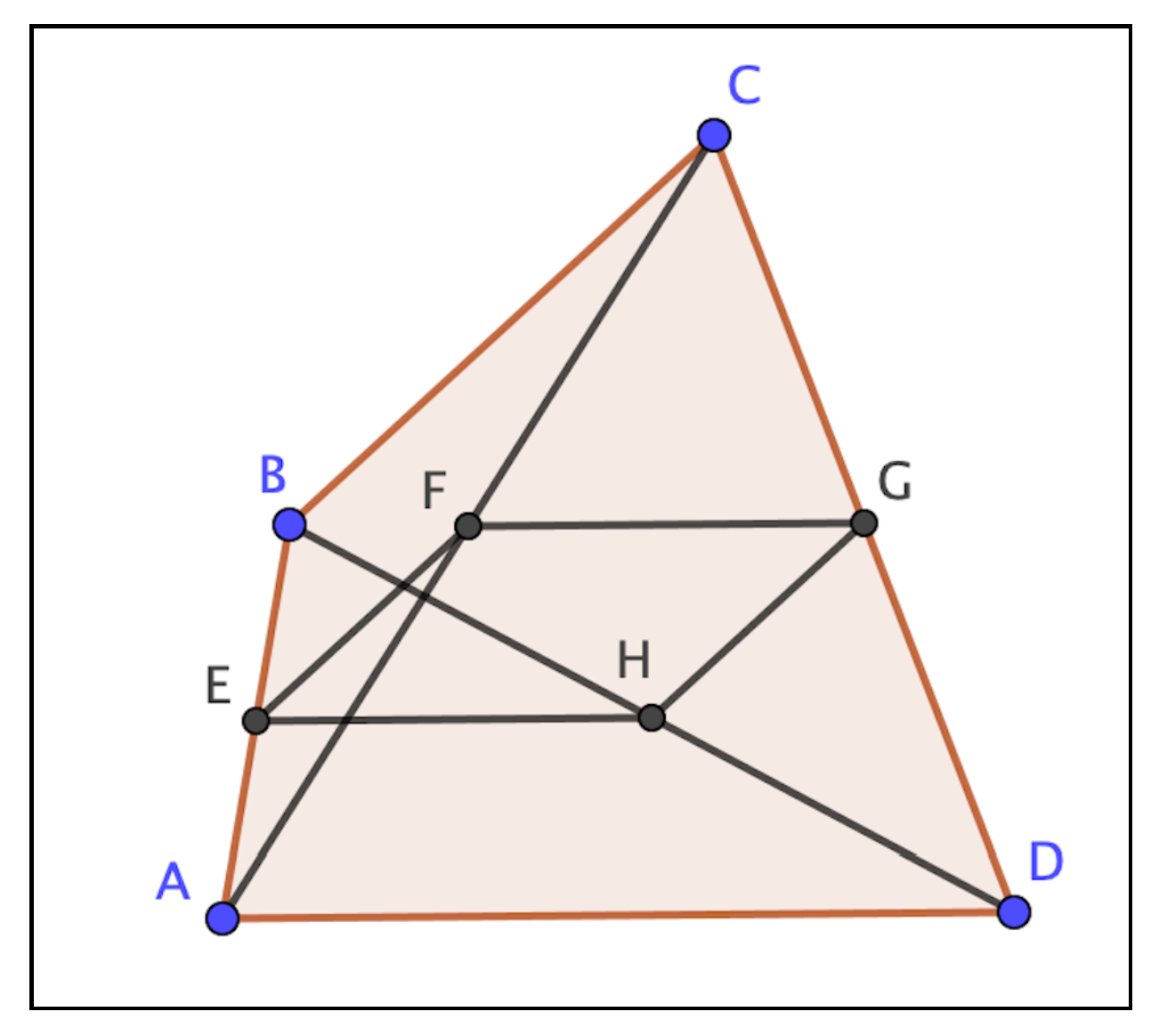
Figure A1.
Image describing context of Theorem 1.
Figure A1.
Image describing context of Theorem 1.
The image below reproduces exactly the beginning of the output of ChatGPT when asked, after introducing as input the Figure A1 describing Theorem 1, the literal question “Consider the following figure. Prove that EFGH is a parallelogram”.
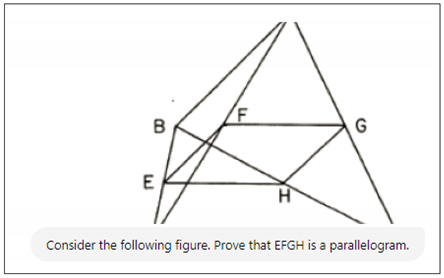
Notice that, although the above output image does not fully reproduce the introduced figure, by clicking over the geometric construction, the user can verify that ChatGPT answers handles the complete figure. What follows is the textual reproduction of ChatGPT reply:
To prove that EFGH is a parallelogram in the given figure, we’ll use the properties of midpoints and vectors as previously outlined. Let’s identify and label the points clearly from the image:
Step-by-Step Proof:
Step 1: Define the Points Using Vectors
Let’s assign position vectors to points A, B, C, and D as , , , and respectively.
Step 2: Find Midpoints Using Vectors
Step 3: Calculate Vectors of the Sides of Quadrilateral
Notice that:
Since and are equal in magnitude and direction, is parallel to and equal in length to .
Notice that:
Since and are equal in magnitude and direction, is parallel to and equal in length to .
Conclusion: Both pairs of opposite sides and , and are equal in length and parallel. Therefore, quadrilateral is a parallelogram.
Appendix A.2. Gelernter et al. Theorem 2: ChatGPT Performance for Alternative Formulations

Appendix A.2.1. Descriptive Statement Prompt
To prove the given statement about a trapezoid, we’ll consider a trapezoid with and as the parallel sides (). Let the non-parallel sides be and .
We need to prove that the line passing through the midpoints of the diagonals and intersects the non-parallel sides and at their midpoints.
Here is the proof:
1. Identify the Midpoints of the Diagonals: Let E be the midpoint of diagonal and F be the midpoint of diagonal .
2. Coordinate Geometry Setup: Place the trapezoid in a coordinate system with , , , and .
3. Find Coordinates of the Midpoints E and F:
The coordinates of midpoint E of diagonal are:
The coordinates of midpoint F of diagonal are:
4. Equation of Line through E and F:
The slope m of the line passing through points E and F is:
Therefore, the line through E and F is horizontal, given by .
5. Midpoints of Non-Parallel Sides:
The midpoint G of (where and ) is:
The midpoint H of (where and ) is:
6. Verify Intersection Points:
Since both midpoints G and H lie on the horizontal line , which is the same as the line through E and F, the line through the midpoints of the diagonals intersects the non-parallel sides and at their midpoints G and H.
Therefore, we have proven that the line passing through the midpoints of the diagonals and intersects the non-parallel sides and at their respective midpoints.
Appendix A.2.2. Figural Prompt
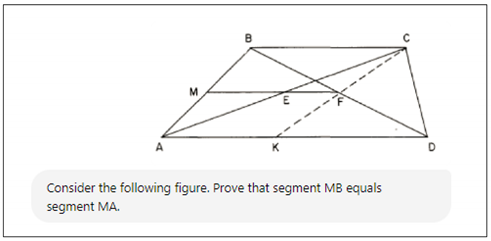
To prove that segment is equal to segment in the given trapezoid with , let’s use a combination of coordinate geometry and properties of midpoints in trapezoids. The key insight is to show that M is the midpoint of .
Step-by-Step Proof:
1. Identify the Key Points:
2. Find Coordinates of Midpoints M and K:
3. Equation of Line through M and K:
4. Prove :
This implies that, geometrically, if M is the midpoint of , then segments and are congruent as they are each half of .
Conclusion: In the given trapezoid , with and M being the midpoint of , we have . This is because M divides into two equal segments by definition, confirming that .
Appendix B
Maple computations describing the “True on Parts” issues involved in the automated proof by the algebraic geometry methods of Gelernter et al. Theorem 2 (see Section 3.2.1).
First, we introduce the following polynomials associated with the statement of the theorem:
- Free points:
- Line :
- Line through A parallel to :
- point on g:
- midpoint of :
- midpoint of :
- Line through :
- Line through :
- intersection of :
- Segment :
- Segment :
We will show that the thesis () in this example does vanish on some, but not all, non-degenerate components of the hypotheses’ variety, so the statement is true on some components and false on some others (see [13]).
To verify this, we compute the dimension of the ideal of the hypotheses, seven, and show that are seven free variables (as point D must be on a line parallel from A to ):
- Hypo:=<(d1-a1)*(c2-b2)-(d2-a2)*(c1-b1),2*e1-(a1+c1),2*e2-(a2+c2),2*f1-(b1+d1),2*f2-(b2+d2),(m1-f1)*(f2-e2)-(m2-f2)*(f1-e1),(m1-a1)*(a2-b2)-(m2-a2)*(a1-b1), j^2-(b1-m1)^2-(b2-m2)^2,k^2-(a1-m1)^2-(a2-m2)^2>:HilbertDimension(Hypo);7EliminationIdeal(Hypo, {a1,a2,b1,b2,c1,c2,d1});<0>
Adding to the hypotheses’ ideal, the thesis , or its negation, introducing the equation , using t as a “dummy” variable, we obtain in both cases that the elimination ideal over the ring of free variables is 0:
- EliminationIdeal(<(d1-a1)*(c2-b2)-(d2-a2)*(c1-b1),2*e1-(a1+c1),2*e2-(a2+c2),2*f1-(b1+d1),2*f2-(b2+d2),(m1-f1)*(f2-e2)-(m2-f2)*(f1-e1),(m1-a1)*(a2-b2)-(m2-a2)*(a1-b1), j^2-(b1-m1)^2-(b2-m2)^2,k^2-(a1-m1)^2-(a2-m2)^2, t*(j-k)-1>,{a1,a2,b1,b2,c1,c2,d1});<0>EliminationIdeal(<(d1-a1)*(c2-b2)-(d2-a2)*(c1-b1),2*e1-(a1+c1),2*e2-(a2+c2),2*f1-(b1+d1),2*f2-(b2+d2),(m1-f1)*(f2-e2)-(m2-f2)*(f1-e1),(m1-a1)*(a2-b2)-(m2-a2)*(a1-b1), j^2-(b1-m1)^2-(b2-m2)^2,k^2-(a1-m1)^2-(a2-m2)^2, (j-k)>,{a1,a2,b1,b2,c1,c2,d1});<0>
It is thus a “True on Parts” statement. Figure 7 already gives a hint about this fact since the answer to the ProveDetails(k==j) input is not able to include any non-degeneracy condition, which should have been expressed in the “…” of the output . Now, in order to understand more deeply the situation, we start by computing the decomposition of the hypotheses’ variety in irreducible components. The primary decomposition of the hypotheses’ ideal turns out to be too difficult to obtain, but the prime decomposition (which is enough, in geometric terms, to compute the irreducible components) is affordable, yielding 12 prime ideals, although it is too large to be displayed here in detail:
- PP:=PrimeDecomposition(Hypo);PP := <j + k, a1 + b1 - 2 m1, a2 + b2 - 2 m2, -2 e1 + a1 + c1, [...]
Next, we check which of these components are non-degenerate (i.e., not including any polynomial restriction involving the free variables of the construction):
- for i from 1 to 2 do HilbertDimension(PP[i]),EliminationIdeal(PP[i], {a1,a2,b1,b2,c1,c2,d1}) od;7, <0>7, <0>for i from 3 to 8 do HilbertDimension(PP[i]),EliminationIdeal(PP[i], {a1,a2,b1,b2,c1,c2,d1}) od;6, <b1 - a1, c1 - a1, d1 - a1>6, <b1 - a1, c1 - a1, d1 - a1>6, <b1 - a1, c1 - a1, d1 - a1>6, <b1 - a1, c1 - a1, d1 - a1>6, <c1 - b1, d1 - a1>6, <c1 - b1, d1 - a1>for i from 9 to 12 do HilbertDimension(PP[i]),EliminationIdeal(PP[i], {a1,a2,b1,b2,c1,c2,d1}) od;7, <b1 - a1 + d1 - c1>7, <b1 - a1 + d1 - c1>7, <-a1 b2 + a1 c2 + a2 b1 - a2 c1 - b1 c2 + c1 b2>7, <-a1 b2 + a1 c2 + a2 b1 - a2 c1 - b1 c2 + c1 b2>
So, only the first two are non-degenerate. The remaining components are either of dimension six or of dimension seven, but in all cases, they do not have as free variables, so they are degenerate as defined in [13].
Next, we observe that indeed is generally true, i.e., it vanishes over the irreducible variety corresponding to the second component and is not generally true on the first one. We check this, as in the previous section, by contradiction, showing that one belongs to the ideal of the second component plus the negation of the thesis and that the closure of the projection of the points of the first component, where the thesis fails, is the whole space of free points; that is, the thesis is false for almost all instances, belonging to this component, of the construction:
- for i from 1 to 2 do EliminationIdeal(PP[i]+<t*(j-k)-1>,{a1,a2,b1,b2,c1,c2,d1}) od;<0><1>
Likewise, we verify that is not generally false on the second component, and it is generally false on the first one, maybe holding true if we add the requirement , which, from the real point of view, means imposing that , so it is a non-interesting requirement:
- for i from 1 to 2 do EliminationIdeal(PP[i]+<(j-k)>,{a1,a2,b1,b2,c1,c2,d1}) od;<a1^2 - 2a1b1 + a2^2 - 2a2b2 + b1^2 + b2^2><0>
Since these two components have such relevant—and diverse—behaviors, we might be interested in knowing about their generators:
- PP[1]:=<j + k, a1 + b1 - 2*m1, a2 + b2 - 2*m2, -2*e1 + a1 + c1, -2*e2 + a2+ c2, d1 - 2*f1 - a1 + 2*m1, 2*m2 - a2 - 2*f2 + d2, -e1*f2 + e1*m2 +e2*f1 - e2*m1 - f1*m2 + f2*m1, -a1^2 + 2*a1*m1 - a2^2 + 2*a2*m2 +j^2 - m1^2 - m2^2>;PP[2]:=<k - j, a1 + b1 - 2*m1, a2 + b2 - 2*m2, -2*e1 + a1 + c1, -2*e2 + a2+ c2, d1 - 2*f1 - a1 + 2*m1, 2*m2 - a2 - 2*f2 + d2, -e1*f2 + e1*m2 +e2*f1 - e2*m1 - f1*m2 + f2*m1, -a1^2 + 2*a1*m1 - a2^2 + 2*a2*m2 +j^2 - m1^2 - m2^2>noticing that both components have the same generators, except the first one; that is, in the first component and in the second. This information gives us a sound explanation about the “true on parts” issue here: the first component implies that , so the two segments have opposite lengths, which is impossible from the real point of view…But let us recall that we are working—as it is much more efficient and “a fortiori” fully reliable in the real setting—on the complex algebraic geometry context, and our definition of is through a square root, so both variables can take positive and negative values.
A final reflection. As in the previous section, we might be interested in grading the complexity of the statement that is true, namely . Indeed, here it is immediate to conclude that the thesis is already one of the hypotheses and one of the generators in , so the statement is of complexity 0, and it is trivial (as is always the case when the conclusion is one of the hypotheses). But this does not mean that the original Theorem 2 in [4] should be classified as difficulty 0, because in order to derive from Theorem 2 the new, true, statement , we have to perform a (non-trivial) prime decomposition.
Appendix C
Computations related to the Minimal Extended Polynomial thesis of Theorem 2 (Section 3.2.2):
- EliminationIdeal(<(d1-a1)*(c2-b2)-(d2-a2)*(c1-b1),2*e1-(a1+c1),2*e2-(a2+c2),2*f1-(b1+d1),2*f2-(b2+d2),(m1-f1)*(f2-e2)-(m2-f2)*(f1-e1),(m1-a1)*(a2-b2)-(m2-a2)*(a1-b1), j^2-(b1-m1)^2-(b2-m2)^2,k^2-(a1-m1)^2-(a2-m2)^2,t*(j^2-k^2)-1>,{a1,a2,b1,b2,c1,c2,d1});<a1^2*b2 - a1^2*c2 - a1*a2*b1 + a1*a2*c1 - a1*b1*b2 + 2*a1*b1*c2 - a1*b2*d1- a1*c1*c2 + a1*c2*d1 + a2*b1^2 - 2*a2*b1*c1 + a2*b1*d1 + a2*c1^2 -a2*c1*d1 - b1^2*c2 + b1*b2*c1 + b1*c1*c2 - b1*c2*d1 - b2*c1^2 + b2*c1*d1>
The zeroes of this degree three elimination ideal (that should be avoided in order to have a true statement) are the union of the instances of the construction where the three initial points are aligned, and the instances where the first coordinates of E and F coincide, which include cases where is not defined and, thus, does not have to be equal to . After adding to the hypotheses the negation of these two degenerate cases, we obtain a geometrically true theorem.
References
- Newell, A.; Shaw, J.C.; Simon, H.A. Empirical explorations of the logic theory machine: A case study in heuristic. In Papers Presented at the February 26–28, 1957, Western Joint Computer Conference: Techniques for Reliability; Association for Computing Machinery: New York, NY, USA, 1957; pp. 218–230. [Google Scholar] [CrossRef]
- Whitehead, A.N.; Russell, B. Principia Mathematica, 2nd ed.; Cambridge University Press: Cambridge, UK, 1935; Volume 1. [Google Scholar]
- Gelernter, H. Realization of a geometry—Theorem proving machine. English, with English French, German, Russian, and Spanish summaries. Information processing. In International Conference on Information Processing, UNESCO, Paris 15–20 June 1959, UNESCO, Paris, R. Oldenbourg, Munich, and Butterworths, London, 1960; Cambridge University Press: Cambridge, UK, 2014; pp. 273–282. [Google Scholar]
- Gelernter, H.; Hansen, J.; Loveland, D. Empirical Explorations of the Geometry-Theorem Proving Machine. In Proceedings of the Western Joint IRE-AIEE-ACM Computer Conference, San Francisco, CA, USA, 3–5 May 1960; pp. 143–149. [Google Scholar] [CrossRef]
- Davies, A.; Veličković, P.; Buesing, L.; Blackwell, S.; Zheng, D.; Tomašev, N.; Tanburn, R.; Battaglia, P.; Blundell, C.; Juhász, A.; et al. Advancing mathematics by guiding human intuition with AI. Nature 2021, 600, 70–74. [Google Scholar] [CrossRef]
- Trinh, T.H.; Wu, Y.; Le, Q.V.; He, H.; Luong, T. Solving olympiad geometry without human demonstrations. Nature 2024, 625, 476–482. [Google Scholar] [CrossRef] [PubMed]
- Parisse, B. Géométrie et Olympiades: AI Google 23++ vs Xcas 40. 4 February 2024. Available online: https://www-fourier.ujf-grenoble.fr/~parisse/irem/alphageo.html#sec5 (accessed on 22 July 2024).
- Karaman, M.R.; Goksu, I. Are lesson plans created by ChatGPT more effective? An experimental study. Int. J. Technol. Educ. (IJTE) 2024, 7, 107–127. [Google Scholar] [CrossRef]
- OpenAI. ChatGPT: Optimizing Language Models for Dialogue. Available online: https://openai.com/blog/chatgpt (accessed on 22 July 2024).
- Botana, F.; Recio, T. Geometric Loci and ChatGPT: Caveat Emptor! Computation 2024, 12, 30. [Google Scholar] [CrossRef]
- Li, P.H.; Lee, H.Y.; Cheng, Y.P.; Starčič, A.I.; Huang, Y.M. Solving the self-regulated learning problem: Exploring the performance of ChatGPT in Mathematics. In International Conference on Innovative Technologies and Learning; ICITL 2023. Lecture Notes in Computer Science; Huang, Y.M., Rocha, T., Eds.; Springer: Cham, Switzerland, 2023; Volume 14099, pp. 77–86. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, L.M.; Moll-López, S.; Nuñez-Pérez, A.; Morán-Fernández, J.A.; Vega-Fleitas, E. ChatGPT challenges blended learning methodologies in engineering education: A case study in mathematics. Appl. Sci. 2023, 13, 6039. [Google Scholar] [CrossRef]
- Kovács, Z.; Recio, T.; Vélez, M.P. Detecting truth, just on parts. Rev. Matemática Complut. 2019, 32, 451–474. [Google Scholar] [CrossRef]
- Kovács, Z.; Recio, T.; Sólyom-Gecse, C. Rewriting input expressions in complex algebraic geometry provers. Ann. Math. Artif. Intell. 2019, 85, 73–87. [Google Scholar] [CrossRef]
- Edgar, G.A.; Ullman, D.H.; West, D.B. Problem 11984: Sum of Powers of the Sides of a Triangle. In Problems and Solutions. Am. Math. Mon. 2019, 126, 188. [Google Scholar] [CrossRef]
- Kovács, Z.; Recio, T.; Vélez, M.P. Showing Proofs, Assessing Difficulty with GeoGebra Discovery. In Electronic Proceedings in Theoretical Computer Science EPTCS, Proceedings of the 14th International Conference on Automated Deduction in Geometry, Belgrade, Serbia, 20–22 September 2023; Quaresma, P., Kovács, Z., Eds.; Open Publishing Association: Waterloo, Australia, 2024; Volume 398, pp. 43–52. [Google Scholar] [CrossRef]
- Kovács, Z.; Parisse, B. Giac and GeoGebra Improved Gröbner basis computations. In Computer Algebra and Polynomials: Applications of Algebra and Number Theory; Lecture Notes in Computer Science; Gutierrez, J., Schicho, J., Weimann, M., Eds.; Springer: Cham, Switzerland, 2015; Volume 8942, pp. 126–138. [Google Scholar] [CrossRef]
- Ariño-Morera, B.; Kovács, Z.; Recio, Z.T.; Tolmos, P. Solving with GeoGebra Discovery an Austrian Mathematics Olympiad problem: Lessons Learned. In Proceedings 14th International Conference on Automated Deduction in Geometry, Belgrade, Serbia, 20–22 September 2023, Electronic Proceedings in Theoretical Computer Science EPTCS; Quaresma, P., Kovács, Z., Eds.; Open Publishing Association: Waterloo, Australia, 2024; Volume 398, pp. 101–109. [Google Scholar] [CrossRef]
- Narboux, J. A Graphical User Interface for Formal Proofs in Geometry. J. Autom. Reason. 2007, 39, 161–180. [Google Scholar] [CrossRef]
- Boutry, P.; Braun, G.; Narboux, J. Formalization of the arithmetization of Euclidean plane geometry and applications. J. Symb. Comput. 2019, 90, 149–168. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).