Abstract
A zero-confirmation transaction is a transaction that has not yet been confirmed on the blockchain and is not yet part of the blockchain. The network propagates zero-confirmation transactions quickly, but they are not secured against double-spending attacks. In this study, the proposed method is used to secure zero-confirmation transactions by using the security hashing algorithm 512 in elliptic curve cryptography (ECDSA) instead of the security hashing algorithm 256. This is to generate a cryptographic identity to secure the transactions in zero-confirmation transactions instead of security hashing algorithm 256. The results show that SHA-512 is greater than SHA-256 in throughput. Additionally, SHA-512 offers better throughput performance than SHA-256 while also having a larger hash size. Results also show that SHA-512 is more secure than SHA-256.
1. Introduction
Bitcoin is a decentralized peer-to-peer (p2p) system that incorporates numerous concepts and technologies that form the fundamental basis of the digital currency ecosystem. Through the network, users are empowered to effectuate Bitcoin transactions for a wide range of purposes, such as purchasing and selling goods, transferring funds to individuals or entities, and extending credit. In essence, Bitcoin serves as a fully distributed system that facilitates a diverse range of financial transactions, which are similar in nature to those that can be performed using traditional currencies. To make the Bitcoin network more secure, Bitcoin technology has some features that are based on encryption and digital signatures. One of the most significant security concerns that digital currencies face is the phenomenon known as double-spending, which entails the utilization of a currency token multiple times. Physical currency is different from digital currency tokens in that the latter can be duplicated and used twice if security measures are not properly implemented, while the second type is hard to copy and it passes to the recipients’ hands once it has been spent [1].
The process of transferring value between Bitcoin wallets, which is captured and stored in the blockchain, is commonly referred to as a Bitcoin transaction. In order to prove mathematically that a transaction came from the wallet’s owner, a secret piece of information known as a secret key is used to sign it. The signature also prevents the alteration of the transaction by anybody once it has been issued. All transactions are transmitted into the network via a process called mining and typically begin to be approved within ten to twenty minutes. Transactions are identified as zero-confirmation transactions in the period between the broadcasting of the transaction and its inclusion. Because of this, the Bitcoin p2p network can accommodate several transactions with related outputs over that time period.
Upon reception of a transaction that employs an unspent output, a node’s standard protocol is to preserve the transaction in its native memory pool (mempool), while simultaneously discarding any incoming transactions that endeavor to exploit resources from the same source at any future point in time [2]. Although double-spending might be attempted, different nodes might get different transaction spending amounts from the same source. Let us consider an example where an attacker, denoted by A, generates two transactions, namely, tx1 and tx2, which both utilize the same output from a preceding transaction, referred to as tx0. B is provided with a set of products to purchase using transaction tx1, while the attacker is subsequently refunded the funds through transaction tx2. The attack is successful when A can persuade B to be certain that tx1 is the sole transaction taking money from tx0’s output, yet tx2 eventually ends up being included in a block. Figure 1 shows the aforesaid example. A block will only contain one double-spending transaction since Bitcoin prevents duplicate spending by design. However, if tx2 is included in a block, tx1 will be rejected, resulting in the successful execution of the double-spending attempt [3].
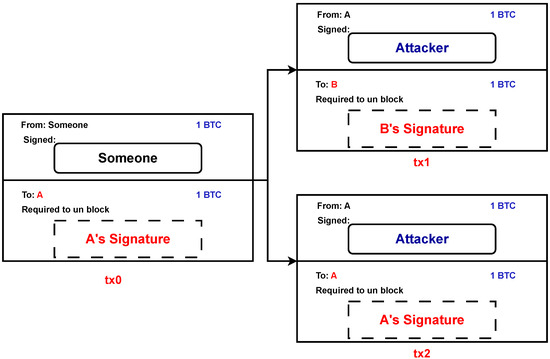
Figure 1.
Transactions that involve the practice of double-spending.
The Elliptic Curve Digital Signature Algorithm (ECDSA) is a cryptographic algorithm used for digital signatures, which is a key component of secure communication. In ECDSA, a public key and a private key are generated by the user. The public key is employed for the purpose of validating the authenticity of digital signatures, whereas the private key is utilized for generating digital signatures.
The generation of an ECDSA public key entails the derivation of a point on an elliptic curve via the utilization of a randomly selected base point on the same curve. This public key is obtained by multiplying the base point with the private key, resulting in a point on the curve that is utilized as the public key. Subsequently, this public key is typically shared with other users who want to verify digital signatures generated by the holder of the corresponding private key.
The security of the ECDSA relies on the computational challenge associated with solving the discrete logarithm problem, which involves the computation of the logarithm of a designated number within a finite field. The strength of the algorithm is directly related to the size of the key, so longer keys are generally considered more secure.
ECDSA is widely used in various applications, including secure communication, digital signature, and authentication. It is a popular choice for applications that require high security and low computational overhead, such as mobile devices and smart cards.
This article introduces a proposed enhancement aimed at addressing the problem of double-spending frequently observed in zero-confirmation transactions within the Bitcoin system. We use the ECDSA algorithm in our proposal to generate a crypto identity in order to make transactions more secure. Our solution makes a double-spending attack or even an attempt more difficult.
The present manuscript is arranged in the following manner: First, Section 2 offers an extensive review of the latest progress in the domain of double-spending avoidance within the Bitcoin landscape, coupled with a thorough examination of the cryptographic methodologies that are employed to establish the integrity of transactions. Section 3 presents the background of the digital signatures on Bitcoin, secure hash algorithms, and double-spending prevention mechanisms. Then, Section 4 provides implementation details and hash functions deployed in ESDSA. Section 5 describes preprocessing, padding the message, and parsing the message. Then, Section 6 presents the main results and the discussion. Finally, Section 7 provides the main conclusions and future work.
2. Related Work
The first study of double-spending attacks on Bitcoin transactions with zero confirmation was done by Karame et al. [4]. The researchers used certain rational hypotheses to demonstrate the high likelihood of an attacker’s double-spending attack succeeding without needing special computation or significant network overhead. Furthermore, they also showed the uselessness of the basic countermeasures to avoid these kinds of attacks (such as adding observers whose job it is to report back to the payee or delaying receiving the payment for a short period of time). In addition, the researchers proposed a modification to the Bitcoin protocol’s regulations wherein nodes would transmit double-spending transactions instead of discarding them. Companies such as GAP600 [5] implement the strategy of monitoring observers to give risk ratings for allowing zero-confirmation transactions.
Bamert et al. [6] suggested additional defenses against double-spending attacks that could lessen the risk that a seller would be duped, which required the connection of the seller to a sizable arbitrary sample of network nodes and the refusal of incoming connections. The seller assured that the assailant was unable to deliver the transaction straightaway to them or to recognize their neighbors by using such countermeasures. Additional research studies proved the possibility of this kind of attack, and that the attacker was capable of determining the seller’s neighbors and also coercing the seller into connecting solely to the attacker’s nodes [7,8,9].
Cristina et al. [2] analyzed the double-spending prevention mechanism. The authors outline a method for securing fast payments within Bitcoin. This mechanism decreased the danger of double-spending attacks in transactions with zero confirmation and discouraged attempts of double-spending through the creation of a distinct sort of outputs that compelled secret key revelation in the event of a double-spending endeavor. Any user could participate in the network as an observer and earn rewards for discovering double-spending trials.
Hashing is a term used to describe a cryptographic security method. Hash algorithms are used currently in many places in internet procedures and in several security applications. Nithya et al. [10] implemented the security hashing algorithms 256 and 512 and gave their performance results for speed, memory, and throughput.
Several major factors can be noted while examining the vulnerabilities of existing methods in the prevention of double-spending attacks. These include the following: (1) Transaction confirmation delays: Existing methods often rely on transaction confirmation mechanisms that introduce delays in the validation and inclusion of transactions in the blockchain. This delay provides an opportunity for malicious actors to execute double-spending attacks during the confirmation window, exploiting the time gap before the transaction is confirmed and added to the blockchain. (2) Transaction malleability: Some existing methods may not adequately address transaction malleability, which refers to the ability to modify certain components of a transaction without invalidating its overall structure. This can enable attackers to manipulate transaction details, such as transaction ID or signature, to create multiple versions of the same transaction and attempt double-spending attacks. (3) Consensus algorithm limitations: The consensus algorithm employed by the blockchain network can also introduce vulnerabilities. For example, if the network relies on a proof-of-work (PoW) consensus mechanism, there is a possibility of a 51% attack, where a malicious entity controls the majority of the network’s computational power. This control can be exploited to execute double-spending attacks by creating an alternative chain with conflicting transactions.
By highlighting these vulnerabilities, the paper can provide a comprehensive understanding of the limitations of existing methods in effectively mitigating double-spending attacks. This discussion sets the foundation for justifying the need for a stronger hashing algorithm such as SHA-512, which offers enhanced security features to address these vulnerabilities and strengthen the overall security of zero-confirmation transactions.
3. Background
3.1. Digital Signatures on Bitcoin
In the context of the Bitcoin network, the creation of digital signatures is accomplished through the implementation of the ECDSA. The ECDSA contains several parameters of the system: 1. An elliptic curve field and equation C. 2. An elliptic curve C generator . 3. A prime p that is related to the order of . For Bitcoin, these parameters’ values are known as secp256k1 [6]. Points on elliptic curves can be generated through the process of scalar multiplication, typically represented by the symbol ∗. Assuming a private key d and a predetermined set of parameters, the following is a definition of the ECDSA over the message m [2,11]:
- The message hash can be computed by employing a cryptographic hash function such as SHA-512: .
- Arbitrarily select an integer k in .
- .
- .
- .
- If either s or r is 0, go back to the initial step 1.
- Return .
There are several valid signatures that can be formed for the same message using the same secret key. The integer k is used to choose a particular signature from the list of valid signatures. There is a familiar flaw in ECDSA signatures that lets an assailant obtain the secret key if the signer employs the same secret key twice and two different messages are signed with it. Thus, k’s selection is crucial to the system’s security [12,13,14,15].
3.2. Secure Hash Algorithms
The existence of a Secure Hash Standard has been established, which outlines various secure hash algorithms such as SHA-1, SHA-224, SHA-256, and others. These algorithms have the characteristic of being iterative, employing one-way hash functions capable of processing a message digest. With the help of these algorithms, it is possible to determine the integrity of a message because any message changes will almost certainly produce a dissimilar message digest [10,16,17]. These hash algorithms’ fundamental characteristics are shown in Table 1.

Table 1.
Secure hash algorithm properties.
3.3. Prevention Mechanism
In the context of proposed double-spending prevention mechanisms, the user Alice seeks to utilize the double-spending prevention system. Alice is in possession of a key pair consisting of an ECDSA public key, denoted by PKa, and a corresponding private key, denoted by . The prevention mechanism for double-spending consists of two distinct phases, namely the initialization phase and the fast-payment phase. Preceding the actual payment transaction, the initialization phase is enacted, subsequently followed by the fast-payment phase, wherein the payment is executed.
3.3.1. Initialization Phase
This phase is a critical stage in many processes, particularly those involving secure communication and financial transactions. In the context of double-spending prevention mechanisms, the initialization phase is the initial step taken before a payment transaction is made.
During the initialization phase, the system is set up and configured to verify the authenticity of the payment transaction and prevent any potential double-spending. This may involve the generation of cryptographic keys, the establishment of secure communication channels, and the verification of the user’s identity and credentials.
During the initialization phase, Alice engages in a critical step that involves generating a funding transaction. This transaction’s goal is to make it easier for Alice to move a certain amount of money from one output that she controls to another output that she controls, which is a FR-P2PK output that is particular to her needs. Alice starts the procedure by picking a random integer, which is represented by the symbol k, as well as a public key, PKa, for which she already possesses the corresponding secret key, . This is done so that the transaction is easier to complete. After that, Alice builds the FR-P2PK output, and then she initiates the transfer of the intended cash to an output that she has control over. This process ensures that the necessary funds are available for the subsequent fast-payment phase, during which the actual payment transaction takes place (see Figure 2).
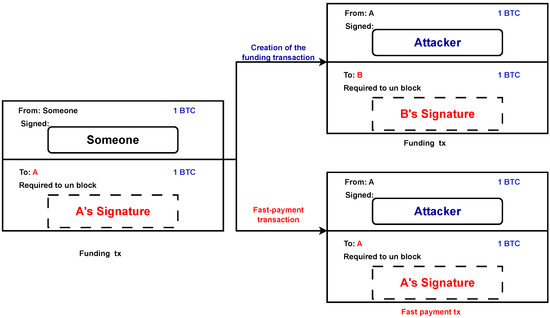
Figure 2.
Creation of the funding transaction and fast-payment transaction.
After the funding transaction is finalized, Alice proceeds to transmit the transaction to the network and patiently awaits confirmation, which serves as an indication that the initialization phase has concluded. It is important to note that a single-funding transaction has the potential to encompass numerous FR-P2PK outputs, each associated with a distinct public key. This feature allows Alice to employ the suggested preventive measure multiple times without having to execute the initialization phase prior to each fast payment, as long as there are sufficient funds in the FR-P2PK outputs. In the event that Alice exhausts her unspent FR-P2PK outputs, she may repeat the initialization phase to obtain additional funds. It is important to note that Alice maintains authority over all funds that are deposited through the funding transaction, and she has the authority to return them back to the standard output.
In a theoretical scenario, Alice has the intention of transferring a specific amount of bitcoins to a different person, Bob, at an unspecified time in the future. Given that Alice does not wish to await verification of the transaction and Bob is uncertain whether to authorize the transaction in the absence of such confirmation, both parties conclude that the utilization of the fast-payment phase is necessary for the successful implementation of the suggested double-spending prevention mechanism.
The initialization phase is critical to the success of the overall process, as it lays the foundation for the secure and efficient execution of the subsequent steps. If the initialization phase is not completed properly, it may result in errors, vulnerabilities, or security breaches that can compromise the integrity of the entire system.
3.3.2. Fast Payment
Alice utilizes the FR-P2PK output derived from the preceding funding transaction in order to generate a fast-payment transaction for the purpose of transferring funds to Bob. To authenticate her ownership of the corresponding private key () for the corresponding public key (), Alice, acting as the redeemer, needs to generate a valid signature as required by the input script for this transaction. Furthermore, the requirement of the input script is that Alice must provide a signature that has been generated utilizing a specified k value that she had chosen in the initialization phase, as depicted in Figure 2. After the fast-payment transaction is generated, Alice publishes it to the Bitcoin network.
Bob can authenticate the FR-P2PK script associated with the funding transaction’s output, which was used in the previous fast-payment transaction, after observing the fast-payment transaction in his mempool. If the authentication process is successful, Bob is aware that if Alice attempts to engage in any double-spending of the transaction, she is exposing herself to the potential loss of the bitcoins associated with that output.
To execute double-spending of a fast-payment transaction, Alice must generate a double-spending transaction utilizing the FR-P2PK output from the funding transaction, as depicted in Figure 3 within the context of a double-spending attempt scenario. This double-spending transaction requires a second signature to be included in it to be recognized as valid. The generation of this second signature involves the utilization of both and the k value that was initially selected during the initialization stage. Consequently, the creation of the double-spend transaction results in the existence of two distinct signatures that were generated using the same private key, , and identical r values. It is important to note that the signatures will differ due to the difference in signed content (i.e., the transactions). It is noteworthy that the aforementioned vulnerability in the ECDSA implies that the knowledge of two distinct signatures that were generated using the same private key with the same k value is sufficient to derive the private key that was utilized for signing purposes.
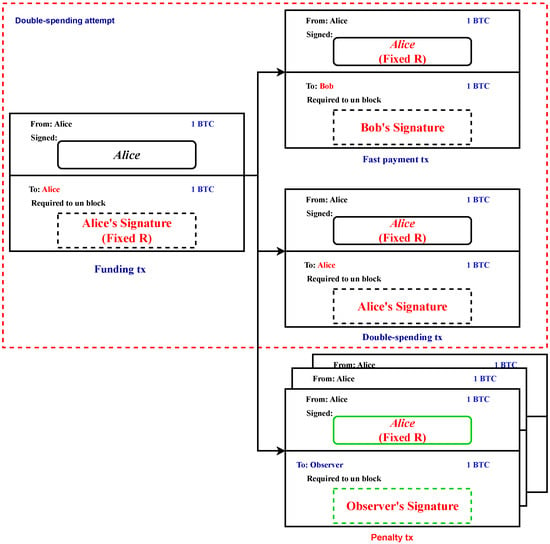
Figure 3.
Transactions involved in the scheme.
Therefore, in the case where Alice chooses to distribute the double-spend transaction, she faces the potential loss of her funds. The reason for this occurrence is that any entity with the ability to receive both the fast-payment transaction and the double-spending transaction can determine Alice’s secret key, denoted by , and subsequently create a third transaction known as the penalty transaction. The penalty transaction is specifically designed to utilize the funding transaction’s FR-P2PK output, while also being structured to transfer the corresponding bitcoins to the entity mentioned earlier. It is important to note that multiple entities may opt to undertake this strategy in parallel, leading to the creation of multiple penalty transactions, as illustrated in Figure 3.
Alice can prevent the creation of penalty transactions by ensuring that the fast-payment transaction is confirmed before attempting any double-spending of the associated output. Once the fast-payment transaction is confirmed, the output of the funding transaction that Alice spent in the fast-payment transaction becomes unspendable, and any attempt to create a double-spend transaction using the same output will be rejected by the network.
In addition, Alice can also prevent the creation of penalty transactions by not revealing the private key to any third party, and carefully managing the security of her computing and communication devices to prevent unauthorized access. It is important for Alice to maintain a high level of security to prevent any potential compromise of her private key, which could result in a loss of funds.
Furthermore, Alice can also opt to implement additional security measures, such as multisignature schemes or time-locked transactions, to further enhance the protection of her funds. By taking these precautions, Alice can ensure that her funds remain secure and that the risk of penalty transactions being created is minimized.
4. The Proposed Double-Spending Prevention Method
In this study, we suggest an approach that generates a crypto identity using elliptic curve cryptography. This methodology makes the transaction more secure and decreases the attempts of double-spending attacks using the security hashing algorithm 512.
Figure 4 shows that we have used the curve in the form of . An elliptic curve takes three integers to define a, b, and p. Then, from the equation, we generate the key pair (secret key and public key). After that, the digital signature lets the recipient of a message make sure that the message is genuine by the public key of the authenticator. Finally, we use SHA-512 and RIPEMD 160 hash functions to get our Bitcoin address.
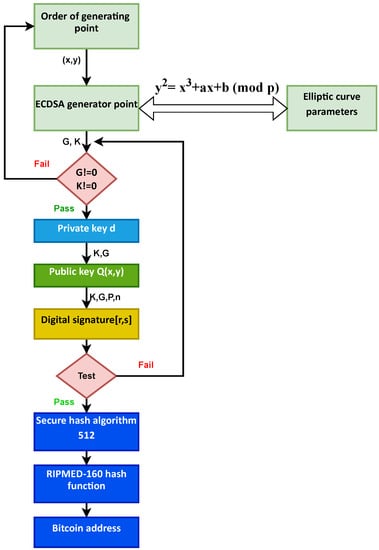
Figure 4.
Scheme of the proposed method.
5. Proposed Analyses
In the ECDSA, we propose utilizing the SHA-512 hash algorithm rather than the SHA-256 hash method to increase transaction security and reduce the possibility of double-spending attacks on a zero-confirmation transaction. First of all, the SHA-512 algorithm employs 6 logical operations, each of which operates on 64-bit words, which have the letters , and c as their symbols. A new 64-bit word is the output of each function.
In the secure hash algorithm requirements, the following operations are carried out: The rotate-right operation: It is represented as
represents the logical OR of the expressions for the right shift of a binary number by n bits and the left shift of x by bits .
The right-shift operation: The mathematical notation of it is
is a bitwise operation that shifts the bits of a binary number to the right by a specified number of positions.
Let x represent a word of length w bits, and let n be an integer satisfying the condition .
Second, it utilizes the exact same series of 80 constant 64-bit words, which is .
5.1. Preprocessing
Three steps make up the preprocessing: padding the message, MS, parsing the message into message blocks, and establishing the starting hash value, .
5.1.1. Padding the Message
By using padding, depending on the algorithm, it is ensured that the padded message is a multiple of 512 or 1024 bits. Assume that l bits is the length of the message MS in bits. Add the bit “1” to the message’s end, followed by k zero bits, where the smallest non-negative solution to the equation is k.
5.1.2. Parsing the Message
The message must be partitioned into a series of N blocks, each consisting of m bits, in addition to the inclusion of padding. In the SHA-512 algorithm, the message and its padding are divided into a series of N blocks, each consisting of 1024 bits. These blocks are denoted by .
5.1.3. Setting the Initial Hash Value ()
The initialization value needs to be specified prior to beginning the hash computation for each of the secure hash algorithms. The size of the message digest determines the word’s size and number in .
5.1.4. SHA-512 Hash Computation
The message schedule consists of a sequence of words denoted by . The set of eight operational variables is denoted by , and z. The hash value words are denoted by . These words represent the initial hash value, , which is replaced by each subsequent intermediate hash value, , until reaching the final hash value, . The SHA-512 algorithm also utilizes two temporary variables, denoted by and [17]. The following stages from Algorithm 1 are used to sequentially process each message block, .
| Algorithm 1 SHA-256 Hash Computation |
|
After iteratively executing steps 1 through 4 for a total of N iterations, the resulting 512-bit message digest of the message, denoted by MS, is .
6. Experimental Results
The experimental setup involved utilizing Google Colab, a cloud-based platform known as Google Colaboratory, designed for executing Python code. In this study, we utilized the Jupyter Notebook within Google Colab to create, digitally sign, and broadcast a Bitcoin transaction using Python. Within the Google Colab environment, popular libraries for data science and machine learning, including cryptographic libraries for SHA-512 and SHA-256, are generally available. By leveraging the capabilities of Google Colab, we executed the experimental setup, enabling the evaluation and comparison of SHA-512 and SHA-256 in a controlled and reproducible manner.
The virtual machines in Google Colab run on Linux-based operating systems and come with a preconfigured software environment. The CPUs used in these virtual machines are sourced from different providers, such as Intel or AMD. The memory capacity in Google Colab virtual machines is dynamically allocated based on the selected runtime type and available resources. Different runtime types offer varying memory capacities, typically ranging from around 12 GB to 25 GB. The virtual machines in Google Colab also provide access to GPUs, particularly NVIDIA Tesla GPUs such as Tesla K80, Tesla T4, or Tesla P100. It is important to note that GPU availability is not guaranteed for every session and may depend on resource availability.
In this section, the results of security hashing algorithms SHA-256 and SHA-512 are discussed. Numerous factors are important when using hash algorithms (security, speed, and purpose of use). There have not been enough studies conducted to determine the algorithm’s speed throughput and memory used of the hash algorithm. To determine the performance, these parameters were used. Additionally, here, different text file input sizes were used to determine the performance. Each algorithm received text files ranging in size from 877 kb to 21,854 kb as input. Results for speed, throughput and memory usage were provided by the simulation [18]. In Table 2, SHA-512 and SHA-256 execution times are compared. From this, SHA-512 had the largest execution time.

Table 2.
Execution time of SHA-256 and SHA-512 in millisecond.
Table 2 shows the execution time in milliseconds for the SHA-256 and SHA-512 hashing algorithms on text files of different sizes, ranging from 877 KB to 21,854 KB. The table is divided into three columns: the first column lists the size of the text file in kilobytes, while the second and third columns show the execution time for SHA-256 and SHA-512, respectively, in milliseconds.
The table shows that as the size of the text file increases, the execution time for both algorithms also increases. However, the execution time for SHA-512 is consistently larger than that of SHA-256 for all file sizes. For example, for a file size of 877 KB, SHA-256 takes 55.478 milliseconds to execute, while SHA-512 takes 153.072 milliseconds. Similarly, for a file size of 21,854 KB, SHA-256 takes 932.596 milliseconds to execute, while SHA-512 takes 1817.312 milliseconds. Moreover, the table shows that the execution time for SHA-256 and SHA-512 depends on the size of the text file being hashed, with larger files taking longer to hash. Additionally, the table highlights the difference in execution time between SHA-256 and SHA-512, with SHA-512 taking significantly longer to execute for all file sizes.
Table 3 shows the throughput of the SHA-256 and SHA-512 hashing algorithms in bits per second, for text files of different sizes ranging from 877 KB to 21,854 KB. The table has three columns: the first column lists the size of the text file in kilobytes, and the second and third columns show the throughput of SHA-256 and SHA-512, respectively, in bits per second.

Table 3.
Throughput of SHA-256 and SHA-512 (bits per second).
The results show that the throughput of both algorithms decreases as the size of the text file increases. For example, for a file size of 877 KB, SHA-256 achieves a throughput of 64.81 bits per second, while SHA-512 achieves a throughput of 178.84 bits per second. Similarly, for a file size of 21,854 KB, SHA-256 achieves a throughput of 43.698 bits per second, while SHA-512 achieves a throughput of 85.153 bits per second.
Furthermore, the results show that SHA-512 achieves a higher throughput than SHA-256 for all file sizes. For example, for a file size of 877 KB, SHA-512 achieves a throughput that is almost three times higher than that of SHA-256. This suggests that SHA-512 may be a better choice for applications that require a high throughput, even though it may take longer to execute than SHA-256.
The results of Table 4 show the memory used in kilobytes by the SHA-256 and SHA-512 hashing algorithms for text files of different sizes ranging from 877 KB to 21,854 KB. The table has three columns: the first column lists the size of the text file in kilobytes, and the second and third columns show the amount of memory used by SHA-256 and SHA-512, respectively, also in kilobytes.

Table 4.
Memory used by SHA-256 and SHA-512 (kilobytes).
The results indicate that both algorithms use the same amount of memory for all file sizes. Specifically, SHA-256 and SHA-512 use 184 KB and 192 KB of memory, respectively, for all file sizes tested. This suggests that memory usage may not be a significant factor in choosing between these two algorithms, since they use similar amounts of memory.
Throughput is a key metric of the performance discovery of an algorithm. It is called the rate of data transfer whose unit is bits per second. Table 3 shows that SHA-512 has the highest throughput and the longest output length. Another factor that affects how well an algorithm performs is the amount of processing space it requires. Calculations of the memory used for hash algorithms were performed and showed that SHA256 and SHA-512 algorithms used the same space to compute a hash, regardless of the size of the file (as shown in Table 4). If a space of 190 kb was taken for an 877 kb file, the same space would be used for the file size, 21,854. Consequently, SHA-512 is more secure than SHA-256 when we use it in the Elliptic Curve Digital Signature Algorithm (ECDSA) to prevent double-spending-attack on zero-confirmation transactions.
There were some limitations and constraints for this study from using Google Colab for experiments: (1) Resource limitations: Google Colab provides limited computational resources, including CPU, RAM, and GPU. This can impact the scale and complexity of experiments, especially when dealing with large datasets or computationally intensive operations. (2) Session timeouts: Google Colab sessions have a time limit of approximately 12 h. If the experiment exceeds that time limit, the session is terminated, and the data may be lost. (3) Storage limitations: Google Colab provides limited storage space for files and datasets.
6.1. The Results of the Elliptic Curve Digital Signature Algorithm
The primary aim of the study is to develop a novel cryptographic identity, specifically in the form of a private–public key pair. In contrast to the widely used RSA encryption, Bitcoin employs elliptic curve cryptography (ECC) as a means of ensuring the security of its transactions. Based on the previous results, it is clear that SHA-512 provides a higher level of security compared to SHA-256 in mitigating double-spending attacks on zero-confirmation transactions. Thus, the ECDSA utilizes the SHA-512 hash algorithm to enhance transaction security and mitigate the risk of double-spending attacks on zero-confirmation transactions. Section 6.1.1 provide a comprehensive explanation of the main steps involved in generating a key pair, which includes both a public and private key. Additionally, Section 6.1.2 explains the steps of creating a transaction, establishing a Bitcoin identity, and generating a unique transaction ID.
6.1.1. Create a Key Pair
The ECDSA system utilizes elliptic curves, which are mathematical structures of relatively low dimensionality that may be defined using only three integers. The mathematical expression that defines these curves can be denoted as . Within the domain of Bitcoin, the coefficients are assigned specific numerical values, namely , and 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,908,834,671,663. Consequently, the curve may be expressed as .
A generator point is added to the curve, representing an “initial point” along the trajectory of the curve that has been previously generated. This point serves as the starting point for the random traversal through the curve. The coordinates of the generator point in the context of are specified as x and y, as shown in Table 5. The generator point is commonly denoted by the symbol “G”. In addition, the variable “n” is assigned the numerical value of 115,792,089,237,316,195,423,570,985,008,687,907,852,837,564,279,074,904,382,605,163,141,518,161,494,337, which corresponds to the order of the generator point “G”. The subsequent notion that is taught pertains to the private key, which is referred to as the “secret key” from this point forward. A random integer is generated, according to the condition that it must be more than or equal to 1 and less than n . The secret key is determined to be 10,052,413,588,762,591,598,988,360,171,631,676,119,543,660.

Table 5.
Secret key, public key, and the generator point.
The public key is derived as a result of performing many additions of the generator point to itself, a number of times equal to the private key. This process can be mathematically expressed as public_key = secret_key * G = (repeated secret key times). The symbols ’+’ and ’∗’ are used to represent an addition and multiplication, respectively. the generator point G is defined as a tuple , which represents a point on the curve as illustrated in Table 5, while the secret key is represented as an integer. This generator point ultimately produces a public key in the form of another tuple , which also represents a point on the curve. To verify that the public key is on the curve, it is necessary to evaluate the equation: .
The combination of the private key and the public key is used to generate the cryptographic identity. This is when we derive the corresponding Bitcoin wallet address. In particular, the wallet address is more than just a representation of the public key; rather, it comes from deterministic derivation methods, which include further features such as an integrated checksum. However, before beginning the address-generating process, specific hash functions must be defined. In this regard, Bitcoin implements the well-known SHA-512 algorithm in conjunction with RIPEMD-160. These hash functions serve as integral components of the subsequent steps in this cryptographic framework.
The SHA512 hashing algorithm works by first receiving a byte message, which is then padded before being partitioned into segments. These segments are then subjected to a complex “bit mixer”, as explained in Section 3, which consists of complex bit shifts and binary operations performed in a manner that generate a deterministic, fixed-size, supposedly stochastic digest from variable-length source messages, achieving a noninvertible scrambling. Furthermore, generating an alternative message that hashes to a predefined digest becomes computationally impossible.
In the world of Bitcoin, SHA512 is widely used to generate hashes. Its paramount significance lies in Bitcoin’s proof-of-work mechanism, where the objective is to modify the transaction block until the collective hash of the entire structure reaches a sufficiently low numerical value (when the digest’s bytes are interpreted as a numerical value). Because of SHA512’s advantageous features, this undertaking demands a brute force approach. Consequently, the ASICs engineered for efficient mining are carefully optimized hardware implementations of the exact chain of computations described above. Bitcoin address = “mjGbJc4xVRVbLvEf82Phr52PPkmhhsZQEg”.
The Bitcoin elliptic curve is used to construct the crypto identity, which consists of a secret key (a random integer) known only to us and a public key derived from the secret key by a scalar multiplication of the generating point. Two hash functions (SHA512 and RIPEMD160) are used to obtain the related Bitcoin address that we can share with others for requesting funds. Table 6 summarizes the three important parameters of the first Bitcoin identity.

Table 6.
The important parameters of the first Bitcoin identity.
6.1.2. Create a Transaction
The transaction is created by sending the specified quantity of Bitcoin from the first address generated (which is “mjGbJc4xVRVbLvEf82Phr52PPkmhhsZQEg”) to the second wallet. The second wallet, known as the “target”, is produced in the manner illustrated in Table 7. The table summarizes the three important parameters of the second Bitcoin identity. Thus, the purpose is to transfer some BTC from “mjGbJc4xVRVbLvEf82Phr52PPkmhhsZQEg” to “mw2PK9MGnUg5Gbh2mAtHoPFVh4Tbtkhemq”.

Table 7.
The important parameters of the second Bitcoin identity.
First, since we created these identities from scratch, the first wallet has no bitcoin. We can request BTC utilizing one of multiple faucets to transmit bitcoins to our source address “mjGbJc4xVRVbLvEf82Phr52PPkmhhsZQEg”. The blockchain explorer shows that the first wallet received 0.001 BTC after a few minutes. Every transaction created has its own unique id/hash. In this instance, the transaction ID for the faucet is “46325085c89fb98a4b7ce955f09e1ddc86d8dad3dfdcba46b4d36b”. This is just an SHA512 double hash of the transaction data structure. In addition, the serialized size of this transaction was 249 bytes. Bitcoin frequently substitutes double SHA512 hashes for a single SHA512 hash for the purpose of increased security. This is done to compensate for a few limitations imposed by using only one round of SHA512.
7. Conclusions
Hashing algorithms SHA-256 and SHA-512 were implemented on the .Net platform. The results displayed that SHA-512 had the greatest throughput, the largest hash size, and the best throughput performance. SHA-512 took a larger space for the process than SHA-256, and SHA-512 had the largest execution time. This research studied the performance of SHA-256 and SHA-512 and proved that SHA-512 was more secure than SHA-256. SHA-512 was used in elliptic curve cryptography to generate a cryptographic identity to secure transactions in zero-confirmation transactions. Future research on SHA-256 and SHA-512 will focus on identifying and analyzing the hash algorithm’s attacks and strengthening these two hashing algorithms to offer better security. This will include a complete investigation of vulnerabilities and weaknesses to develop effective strategies for fortifying their security properties. Efforts can be directed towards strengthening SHA-256 and SHA-512 by exploring algorithm modifications, optimizing mathematical operations, and incorporating additional rounds to bolster their resistance against attacks. Furthermore, future research will evaluate the performance and scalability of SHA-256 and SHA-512 in diverse computing environments, spanning resource-constrained devices and high-performance computing systems. This evaluation will include looking at how well they work on different platforms and identifying optimization techniques to enhance throughput and computational efficiency. The aim is to ensure the reliability, robustness, and cryptographic strength of SHA-256 and SHA-512 in the face of evolving security threats.
Author Contributions
Conceptualization, H.H. and A.R.A.; methodology, I.G.; software, A.R.A.; validation, I.G., H.A.-K. and A.F.E.; formal analysis, H.H.; investigation, A.E.; resources, A.E.; data curation, A.R.A.; writing—original draft preparation, H.A.-K.; writing—review and editing, I.G.; visualization, A.R.A.; supervision, A.R.A.; project administration, H.A.-K.; funding acquisition, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data has been present in the main text.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Karame, G.O.; Androulaki, E.; Capkun, S. Double-spending fast payments in bitcoin. In Proceedings of the 2012 ACM Conference on Computer and Communications Security, Raleigh North, CA, USA, 16–18 October 2012; ACM: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Pérez-Solà, C.; Delgado-Segura, S.; Navarro-Arribas, G.; Herrera-Joancomartí, J. Double-spending prevention for Bitcoin zero-confirmation transactions. Int. J. Inf. Secur. 2018, 18, 451–463. [Google Scholar] [CrossRef]
- Delgado-Segura, S.; Pérez-Solà, C.; Herrera-Joancomartí, J.; Navarro-Arribas, G. Bitcoin private key locked transactions. Inf. Process. Lett. 2018, 140, 37–41. [Google Scholar] [CrossRef]
- Karame, G.O.; Androulaki, E.; Roeschlin, M.; Gervais, A.; Čapkun, S. Misbehavior in Bitcoin. Acm Trans. Inf. Syst. Secur. 2015, 18, 1–32. [Google Scholar] [CrossRef]
- Crockett, M. Digital preservation handbook, 2nd Edition. Arch. Rec. 2019, 41, 92–95. [Google Scholar] [CrossRef]
- Bamert, T.; Decker, C.; Elsen, L.; Wattenhofer, R.; Welten, S. Have a snack, pay with Bitcoins. In Proceedings of the IEEE P2P 2013 Proceedings, Trento, Italy, 9–11 September 2013; IEEE: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Biryukov, A.; Khovratovich, D.; Pustogarov, I. Deanonymisation of Clients in Bitcoin P2P Network. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014; ACM: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Felten, E.W.; Kroll, J.A. Help Wanted on Internet Security. Sci. Am. 2014, 311, 14. [Google Scholar] [CrossRef] [PubMed]
- Conti, M.; Kumar, E.S.; Lal, C.; Ruj, S. A Survey on Security and Privacy Issues of Bitcoin. IEEE Commun. Surv. Tutor. 2018, 20, 3416–3452. [Google Scholar] [CrossRef]
- Nithya, B.; Sripriya, P. Cryptographic Hash Algorithms Performance Finding using .Net Simulation. Int. J. Comput. Algorithm 2016, 5, 79–83. [Google Scholar] [CrossRef]
- Paar, C.; Pelzl, J. Understanding Cryptography; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Cai, Z. A Study on Parameters Generation of Elliptic Curve Cryptosystem over Finite Fields. Ph.D. Thesis, The University of Hong Kong, Hong Kong, China, 2001. [Google Scholar] [CrossRef]
- Turner, S.; Brown, D. Elliptic Curve Private Key Structure; Technical Report; IETF: Fremont, CA, USA, 2010. [Google Scholar] [CrossRef]
- Goyal, J.; Ahmed, M.; Gopalani, D. Empirical Study of Standard Elliptic Curve Domain Parameters for IoT Devices. In Proceedings of the 2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Kuala Lumpur, Malaysia, 12–13 June 2021; IEEE: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Moody, D. Recommendations for Discrete Logarithm-Based Cryptography; Technical Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. [Google Scholar] [CrossRef]
- Pornin, T. Deterministic Usage of the Digital Signature Algorithm (DSA) and Elliptic Curve Digital Signature Algorithm (ECDSA); Technical Report; RFC Editor: San Francisco, CA, USA, 2013. [Google Scholar] [CrossRef]
- Dang, Q.H. Secure Hash Standard; Technical Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar] [CrossRef]
- Gupta, D.N.; Kumar, R. Sponge based Lightweight Cryptographic Hash Functions for IoT Applications. In Proceedings of the 2021 International Conference on Intelligent Technologies (CONIT), Karnataka, India, 25–27 June 2021; IEEE: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).