Abstract
This paper utilizes convex optimization to implement a day-ahead scheduling strategy for operating a photovoltaic distribution static compensator (PV-STATCOM) in medium-voltage distribution networks. The nonlinear non-convex programming model of the day-ahead scheduling strategy is transformed into a convex optimization model using the second-order cone programming approach in the complex domain. The main goal of efficiently operating PV-STATCOMs in distribution networks is to dynamically compensate for the active and reactive power generated by renewable energy resources such as photovoltaic plants. This is achieved by controlling power electronic converters, usually voltage source converters, to manage reactive power with lagging or leading power factors. Numerical simulations were conducted to analyze the effects of different power factors on the IEEE 33- and 69-bus systems. The simulations considered operations with a unity power factor (active power injection only), a zero power factor (reactive power injection only), and a variable power factor (active and reactive power injections). The results demonstrated the benefits of dynamic, active and reactive power compensation in reducing grid power losses, voltage profile deviations, and energy purchasing costs at the substation terminals. These simulations were conducted using the CVX tool and the Gurobi solver in the MATLAB programming environment.
1. Introduction
Sustainable development is a global concern due to the harmful effects of global warming, which is mainly caused by fossil energy sources in the transportation and electricity sectors [1,2]. In the case of transportation, in recent years, the transition from fossil fuel-based methods to electrical mobility has become a reality as more and more electric vehicles (EVs) are seen on all roads worldwide [3,4]. However, this change must be coordinated with electricity production, given that the growing demand for power to charge EV batteries must be met by renewable and clean energy systems in order to effectively reduce the CO footprint in the atmosphere [5,6]. Otherwise, if electrical systems continue using fossil fuels, atmospheric pollution by greenhouse gas emissions will only move its focus from transportation systems to energy production without any real mitigation [7]. One of the most promising alternatives to effectively reduce the CO footprint is the massive integration of renewable energy resources in electrical networks at any voltage level, typically in the form of wind and solar power technologies, as they are mature and require reduced investment and operating costs while offering a wide array of possibilities regarding scalability from low- to high-voltage levels [8,9].
Electrical networks, especially distribution systems, have undergone a massive integration of distributed energy resources [10,11], which, even though they contribute to the sustainable development goals, pose significant challenges for utility companies and regulatory entities, since their operation requires new methodologies and remunerations [12,13]. The latter is needed to ensure the economic feasibility of renewable energy projects and guarantee quality, security, reliability, and efficiency in the electricity service for all end users [14].
Electrical distribution networks are one of the main links in the electricity service chain, as they directly connect large-scale power systems located at substations with medium- and low-voltage consumers in rural or urban areas [15]. These grids were initially designed while considering the end users’ passive behavior. Here, the energy flow typically goes from the primary substations to the consumers in an unidirectional way [16]. However, the massive integration of renewable energy resources has transformed these passive grids into active networks [17], which poses new challenges for their planning, operation, coordination, and control [18].
Considering the new paradigm of active distribution networks, this research seeks to study a class of distributed energy resources that can be connected to these grids, which is known as a photovoltaic distribution static compensator (PV-STATCOM) [19,20,21] and can compensate active and reactive power in electrical networks in order to improve technical, economic, and environmental indices [14,22,23]. The main characteristic of PV-STATCOMs is that they combine the use of clean energy sources to reduce CO emissions and fossil fuel energy production costs while improving grid efficiency (i.e., power loss reductions and voltage profile improvements).
To design efficient operation methodologies for PV-STATCOMs, it is necessary to deal with the solution of the exact nonlinear programming model that represents their operation for a given period, which typically corresponds to a day-ahead scheduling scenario [24]. However, the solution of this exact model is not an easy task due to its non-convexities [25,26]. Therefore, this research aims to propose a new convex optimization model in order to determine the day-ahead dispatch of multiple PV-STATCOMs interconnected with medium-voltage distribution networks while considering technical and economic objective functions.
The effective integration, operation, and control of PV-STATCOMs in electrical grids (transmission and distribution networks) have been widely explored in recent years. Some of the latest advances in this research area are discussed below.
The authors of [19] presented the application of the hunter-prey-based algorithm to determine the optimal location and sizing of PV-STATCOMs in electrical distribution networks, aiming to minimize the total grid power losses and improve the grid voltage profiles. Classical IEEE 33- and 69-bus grids were used for numerical validations, which included a comparative analysis with the particle swarm optimizer, the golden search optimizer, the differential evolution approach, and the artificial rabbits algorithm, among others. Numerical results showed that the energy losses were reduced by more than 57%, and voltage profiles were improved by more than 42% in both test feeders.
In [27], the authors proposed using PV-STATCOMs in medium-voltage distribution networks while considering a day-ahead operation scenario to improve grid voltage regulation and correct the power factor of a particular load application. The Bluewater Power Corporation in Sarnia, Canada, was used to validate the PV-STATCOM concept, considering dynamic active and reactive power compensation in a 10 kW PV system installed in its network.
The work by [28] enhanced the operation of an electrical distribution network under steady-state and fault conditions. In the steady-state scenario, the voltage profile was optimally regulated using dynamic active and reactive power compensation. In contrast, for the faulted operation, possible over-voltages caused by asymmetrical faults were mitigated. A 10 MW PV generation system connected to a utility company in Ontario, Canada, was simulated in the PSCAD software in order to confirm the new possible ancillary services provided by PV-STATCOMs with satisfactory numerical validations.
In [29], the authors proposed the optimal installation and sizing of PV-STATCOMs in medium-voltage distribution networks to provide ancillary services. The artificial rabbits optimization algorithm was employed as an optimization technique. Here, the objective was to reduce the total grid power losses and improve the voltage profile performance. The IEEE 33-bus grid was used for numerical validation, and a comparison of the results with those of the differential evolution and the golden search algorithms demonstrated the effectiveness of the proposed optimization approach. The authors of this research reported a reduction of about 54.36% in daily energy losses and improvements of about 43.29% in the voltage profiles’ behavior.
The study by [30] presented a multi-objective analysis considering PV-STATCOMs in transmission networks. The main goals were to simultaneously minimize the active and reactive power losses, improve grid voltage profiles, and reduce the total energy production costs. The IEEE 30-bus network was used as a test feeder. As a solution methodology, a combination of the optimal power flow formulation and the particle swarm optimization technique was implemented.
Additionally, optimization methodologies for the efficient integration of PV-STATCOMs in electrical networks include the gorilla troop optimizer [31], the gray wolf optimizer [32], the modified bat algorithm [33], the modified ant lion optimizer [34], and the fuzzy-lightning search algorithm [35], among others.
Table 1 summarizes the main contributions made regarding PV-STATCOMs in electrical distribution networks in recent years.

Table 1.
Summary of literature reports on PV-STATCOMs.
The main characteristic highlighted by the above-presented literature review (see Table 1) is that most optimization algorithms belong to the family of combinatorial optimization (i.e., metaheuristics). In addition, most objective functions focus on minimizing the total grid energy losses and improving voltage profiles. This work found that more research is required concerning the efficient day-ahead scheduling of PV-STATCOM applications for distribution grids, especially in the case of convex optimization, since no works were found on this topic, which constitutes a research opportunity to which this document aims to contribute.
In light of the above, the main contributions of this research are summarized below:
- i.
- The convex reformulation of the problem regarding the efficient operation of PV-STATCOMs in medium-voltage distribution networks via second-order cone programming in the complex variable domain. The product between two complex voltages was transformed using its hyperbolic equivalent, which allowed relaxing it as a convex cone equivalent formulation.
- ii.
- The evaluation of four different simulation scenarios, including a benchmark case without PV-STATCOM penetration and cases with unity, zero, and variable power factors. These simulations were conducted in the IEEE 33- and 69-bus grids while considering three possible objective functions: the minimization of grid energy losses, grid energy purchasing costs, and average voltage deviation. The results showed the positive effects of dynamically scheduling active and reactive power injections in PV-STATCOMs in order to improve technical or economic grid indices.
In the scope of this research, it is essential to mention that: (i) the active and reactive power demand curves, as well as the solar generation availability, correspond to inputs of our research, which were provided by the distribution company in the area of influence of the electrical distribution grid under analysis; and (ii) a previous planning stage defined the sizes and locations of the PV-STATCOMs (this research only focuses on their efficient daily operation while considering different simulation scenarios).
This work is structured as follows. Section 2 presents the general nonlinear programming formulation for the problem regarding the efficient operation of PV-STATCOMs in electrical distribution networks using a complex-domain representation. Section 3 defines the general convexification approach in the complex domain using the hyperbolic equivalent of the product between two variables, which allows obtaining a second-order cone equivalent formulation for the studied problem. Section 4 shows the main characteristics of the IEEE 33- and 69-bus grids and the characterization of the PV-STATCOMs (i.e., their sizes and locations). Section 5 presents the main numerical results obtained while considering four different simulation cases (i.e., operation with unity, zero, and variable power factors in the PV-STATCOMs, in addition to a benchmark case where the PV-STATCOMs were off). Finally, Section 6 describes the main concluding remarks derived from this work, as well as some possible future works.
2. General Formulation
The problem regarding the optimal operation of PV-STATCOMs in medium-voltage distribution networks while considering a day-ahead scheduling scenario is associated with an adequate active and reactive power compensation aiming to minimize the expected grid power losses, voltage profile deviations, and energy purchasing costs at the terminals of the substation bus [20]. This optimization problem can be formulated using a nonlinear programming model in the complex variable domain. Each of the objective functions and constraints are listed below.
2.1. Possible Objective Functions
The efficient operation of PV-STATCOMs in electrical distribution networks can be addressed with different objective functions. These can include technical, economic, and environmental indices [19].
2.1.1. Energy Losses Minimization
Minimizing the expected energy losses in a daily operation scenario is one of the most typical problems in electrical distribution networks, that is, when multiple distributed energy resources must be optimally coordinated. The objective function regarding energy losses minimization is defined in Equation (1).
where is the expected value of the daily energy losses; and correspond to the voltage values in the complex domain (i.e., magnitudes and angles) at nodes k and m in period h; is the complex value of the admittance matrix that relates nodes k and m; denotes the period of analysis, which is typically one hour or fractions of one; and represents the complex conjugate operation of the argument. Note that defines the set containing all the network nodes, and is associated with the number of periods under analysis.
2.1.2. Voltage Profile Improvement
One of the distribution companies’ main interests is supplying electricity to all end users while ensuring efficiency, reliability, quality, and security [36]. To this effect, improving voltage profiles is common practice [32]. This objective function is defined in Equation (2).
where H and N are the cardinalities (number of elements) of the sets and , respectively; and is the nominal operating voltage at node k.
2.1.3. Energy Purchasing Costs
For distribution companies, one of the main issues with the multiple integration/operation of distributed energy resources (including PV-STATCOMs) is the minimization of the energy purchasing costs at the terminals of the substation bus, which corresponds to the energy bought in the spot market to provide electricity to all end users in medium- and low-voltage networks. This objective function is defined in Equation (3).
where represents the energy purchasing costs at the terminals of the substation bus; is the complex power injection at the substation connected at node k in period h, and represents the average value of the energy purchased in these terminals.
2.2. Set of Constraints
Multiple operating constraints must be observed while efficiently operating distributed energy resources in electrical distribution networks. These include the active and reactive power balance, device capabilities, and voltage regulations. Each one of these constraints is presented below.
Equation (4) defines the complex power equilibrium for each network node and period.
where represents the complex power generation of the PV-STATCOM connected at node k in period h, and denotes the apparent power consumption of the constant power load connected at node k in period h.
To ensure the correct operation of the conventional power source (i.e., the substation bus), its nominal capacities can not exceed the transformer capabilities, as defined by inequality constraint Equation (5). In addition, constraint Equation (6) is added to ensure that no active power is transferred from the distribution grid to the power system at the terminals of the substation bus.
where represents the maximum power transference capacities at the terminals of the substation bus.
For the efficient operation of PV-STATCOM devices, constraints regarding active and reactive power injection are imposed, as the nominal power transference capacities of the power electronic converter that interfaces these systems with the distribution grid must be ensured in every period. Constraints Equations (7) and (8) are therefore defined.
where represents the nominal power transference capacity of the converter associated with the PV-STATCOM system connected at node k, and represents the expected solar power availability at node k for each period. This parameter provides a projection based on the expected weather conditions for a day-ahead operation.
Finally, the voltage profile must be maintained between two permissible regulation bounds due to regulatory policies applicable to medium-voltage distribution networks. This operating constraint is defined in Equation (9).
where and represent the minimum and maximum voltage regulation bounds.
2.3. Model Characterization
The main characteristics of the general optimization model defined from Equations (1)–(9) are the following:
- i.
- The objective function defined in Equation (1) is a nonlinear function of the voltage magnitudes in all the network nodes and periods. However, it has a convex structure [37].
- ii.
- The objective function in Equation (2) is a nonlinear non-convex function due to the embedded structure of two -norms [32].
- iii.
- The objective function defined in Equation (3) exhibits a linear structure, which implies that it is a convex-concave function [38].
- iv.
- The power balance constraint in Equation (4) corresponds to the main complication regarding the optimal operation of PV-STATCOM systems in distribution grids, as it implies the product between two complex variables, which are non-convex due to the equality imposition [39].
- v.
Note that, in order to obtain an equivalent convex optimization model that represents the problem under study, it is necessary to obtain an approximation of the objective function Equation (2) and the power balance constraint in Equation (4). In the next section, the convex approximation approach is presented.
3. Convexification Proposal
This research proposes a conic approximation aimed at obtaining a convex approximation of the nonlinear programming model Equations (1)–(8). The main idea of conic programming is to approximate some hyperbolic constraints into equivalent cones [40], which allows reaching a second-order cone programming equivalent that represents the studied problem [41].
To obtain the convex equivalent, the following auxiliary variables are defined:
Note that Equation (10) is multiplied on both sides by . Thus, the following set of results is reached:
where the right-hand side of Equation (13) can be transformed using the hyperbolic equivalent of the product between two real variables, as defined in Equation (15).
It is worth mentioning that constraint Equation (14) is still non-convex, as the only set of solutions is contained in the circle that fulfills the equality condition. However, as recommended by the authors of [39], this constraint can be convexified by relaxing the equality condition to a lower, equal one, as presented below.
Now, considering definitions in Equations (10)–(12), the nonlinear optimization model Equations (1)–(11) can be represented as a second-order cone approximated model:
Objective functions:
Subject to:
where is a constant parameter that defines the voltage magnitude at the substation as a real constant.
Note that, as previously mentioned, the approximation of the objective function Equation (2) regarding the average voltage deviation of the system is non-convex due to the presence of two embedded norms. Therefore, in Equation (17), a convex approximation of this function is proposed. To illustrate the convexification effect, consider a system with two voltage variables and one period ( and ), which implies that Equation (2) takes the form and Equation (17) can be defined as . Figure 1 shows the 3D plot of both functions. The scale was exaggerated to show that is non-convex and is convex.
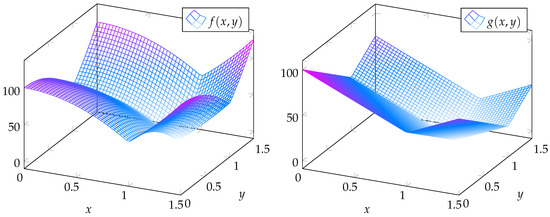
Figure 1.
Example of the non-convex function and its convex approximation .
It is worth mentioning that the range of application of the convex approximation for the voltage deviation function Equation (2) using the approximation in Equation (17) lies between the minimum and maximum voltage regulation bounds, which, in medium-voltage networks, implies that variables x and y will be contained within the interval between and of the nominal voltage, i.e., and using the per-unit representation.
A flowchart of the day-ahead scheduling of PV-STATCOMs using the proposed convex model is illustrated in Algorithm 1.
| Algorithm 1: SOC relaxation for day-ahead scheduling of PV-STATCOMs. |
 |
4. Test Feeders
To validate the effectiveness of the day-ahead optimization model to operate PV-STATCOM systems in medium-voltage distribution networks, conventional grids of this type were used, i.e., the IEEE 33- and 69-bus systems. The electrical configuration of these networks and their electrical parameters are presented in Figure 2 and Figure 3 and Table 2 and Table 3, respectively. The main characteristics of these test feeders are the following: (i) the voltage supplied at the terminals of the substation is 12.66 kV, and (ii) both networks exhibit a radial structure.
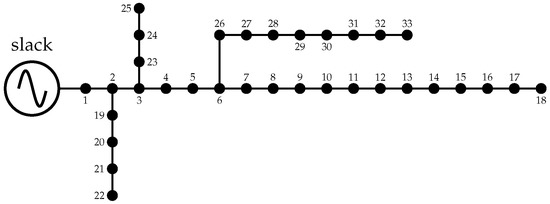
Figure 2.
Electrical configuration of the IEEE 33-bus test system.
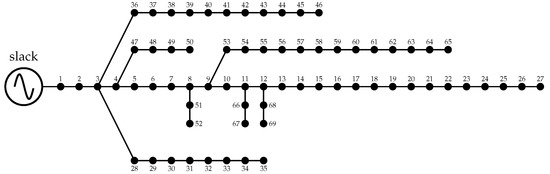
Figure 3.
Electrical configuration of the IEEE 69-bus test system.

Table 2.
Electrical parameters of the IEEE 33-bus grid.

Table 3.
Electrical parameters of the IEEE 69-bus grid.
To determine the electrical behavior of the networks in a day-ahead operation environment, the active and reactive power demand curves, as well as the solar availability curve, are depicted in Figure 4 [24].
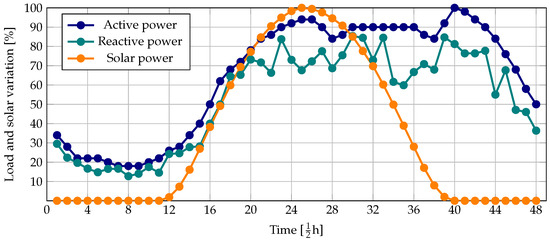
Figure 4.
Active and reactive power and solar availability curves.
The following aspects were considered for the numerical simulations carried out in the IEEE 33- and 69-bus grids.
- i.
- The average cost of the energy purchasing costs at the terminals of the substation (i.e., ) was assigned as USD/kWh . Note that H is equal to 48 periods (see Figure 1), which means that h and N is 33 or 69 depending on the test feeder under analysis.
- ii.
- The locations of the PV-STATCOMs in the IEEE 33-bus grid were nodes 13, 24, and 30, with sizes of 800 kW, 1090 kW, and 1050 kW, respectively.
- iii.
- The locations of the PV-STATCOMs in the IEEE 69-bus grid were nodes 17, 50, and 61, with sizes of 510 kW, 720 kW, and 1810 kW, respectively.
- iv.
- The voltage regulation bounds (i.e., and ) were set between and of the nominal voltage, which is 12,660 V for both test feeders.
Note that the information regarding the nominal sizes of the PV systems was obtained from [42], and these were set as the nominal rates for operating the PV-STATCOMs. In addition, the voltage relation bounds for the IEEE 33- and 69-bus grids were set as .
5. Computational Validation
The proposed day-ahead scheduling model to operate PV-STATCOMs in medium-voltage distribution networks via second-order cone programming (see optimization model Equations (16)–(26)) was implemented in the Yalmip toolbox [43], using the Gurobi solver [44] of the MATLAB 2021a interface. A Dell Inspiron 15 7000 Series (Intel Quad-Core i7-7700HQ @2.80 GHz) PC with 16 GB RAM and 64-bit Windows 10 Home Single Language was used to carry out the simulations. The following scenarios were considered in order to validate the effectiveness of the proposed solution methodology.
- i.
- S1: each objective function was evaluated considering that the PV-STATCOM systems were disconnected from the main grid. This simulation scenario corresponds to the benchmark case.
- ii.
- S2: each objective function was minimized considering that the PV-STATCOM systems operated with a zero power factor, i.e., they could not inject active power.
- iii.
- S3: each objective function was minimized considering that the PV-STATCOM systems operated with a unity power factor, i.e., they could not inject reactive power.
- iv.
- S4: each objective function was minimized considering that the PV-STATCOM operated with a variable power factor, which means that active and reactive power could be simultaneously injected.
It is worth mentioning that all the simulation scenarios have a variable power factor with regard to the load behavior, as the load curves depicted in Figure 4 cause the power factors to change at each load per period. However, in the simulation scenarios presented above, the variable power factor case only refers to when the PV-STATCOMs vary each active and reactive power output at each period as a function of the grid requirements.
5.1. Numerical Results in the IEEE 33-Bus Grid
Table 4 presents the numerical results of each simulation scenario in the IEEE 33-bus grid. Note that the percentages of improvement with respect to the benchmark case defined by S1 are included in parentheses.

Table 4.
Numerical results in the IEEE 33-bus grid for all the tested simulation cases.
These results show that:
- i.
- Using PV-STATCOMs with different power factors affects the reduction of energy losses and energy purchasing costs at the substation terminals. The reductions in energy losses for S2 to S4 were , , and with respect to the benchmark case. As for the energy purchasing costs at the terminals of the substation, the reductions for S2 to S4 were , , and , respectively.
- ii.
- As expected, the injection of reactive power in S2 shows that it is possible to reduce the power losses with respect to the benchmark case. However, the expected reductions in energy purchasing costs are minimal, as the main substation still supplies all of the energy consumed by constant power loads. In this scenario, the reduced energy losses were kWh/day, with an average cost of about USD/day . This value is the difference between the energy purchasing costs of S2 and S1.
- iii.
- In all the simulation scenarios where active and reactive power was injected, it was observed that the average voltage profile improved with respect to the benchmark case. However, it was noted that reactive power has a greater influence on the voltage profile. For example, in S2 and S4, the improvements were and , respectively, whereas, in the case of active power injection, this improvement was about .
To illustrate the positive effect of the efficient scheduling of PV-STATCOMs in distribution networks, the active power generation at the terminals of the substation bus is reported in Figure 5 for each simulation scenario.
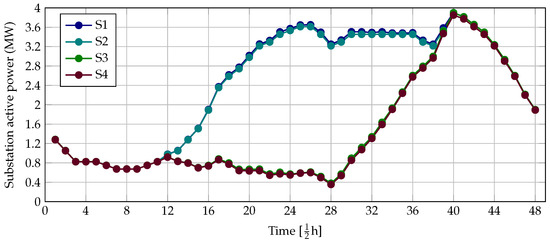
Figure 5.
Behavior regarding active power injection at the terminals of the substation bus for each simulation scenario in the IEEE 33-bus grid.
From the behavior of the energy generated at the substation terminals depicted in Figure 5, three prominent aspects can be highlighted. (i) The main effect of using PV-STATCOMs with unity or variable power factors (see the curve for S1 and compare it against the curves for S3 and S4) is that, at the terminals of the substation bus, the power generation is reduced as much as possible. From periods 12 to 40 (6:00 to 20:00), the power injection in the slack source is reduced. During these times, there is active power available in the PV-STATCOMs (Figure 4). (ii) As observed in Figure 5, the amount of renewable energy resources is not enough to cover all the electricity demand of the network; during all periods, conventional sources (substation) generate power to ensure the power equilibrium. (iii) The effect of reactive power on the total grid generation cost is minimal, as this allows reducing only some part of the total grid power losses, which results in a slight reduction of the total grid operating costs.
5.2. Numerical Results in the IEEE 69-Bus Grid
Table 5 presents the numerical results of each simulation scenario in the IEEE 69-bus grid. Note that the percentages of improvement with respect to the benchmark case defined by S1 are included in parentheses.

Table 5.
Numerical results in the IEEE 69-bus grid for all the tested simulation cases.
These results show that:
- i.
- The efficient operation of PV-STATCOMs in medium-voltage distribution networks has a positive effect on each one of the objective functions. In the case of the total grid energy losses, between S1 and S4, the total reduction was about . Meanwhile, in the case of the total grid operating costs at the terminals of the substation, this reduction was about . As for the voltage profile improvements, the best reductions were reported by the scenarios where reactive power was injected. Comparing S2 and S4 to S1, the improvements in the average voltage profile were about and , respectively.
- ii.
- The energy losses reduction observed when comparing S1 to S2 was kWh/day, which, considering the average cost of USD/kWh , corresponds to savings of dollars per day of operation, with the main characteristic that it is the exact difference between the energy purchasing costs at the terminals of the substation in both simulation cases. This confirms that the impact of using reactive power to reduce energy purchasing costs is only associated with the possible savings with regard to the total grid power losses.
- iii.
- The use of PV-STATCOMs while considering reactive power injection has a direct effect on the average voltage profile behavior (see S2 and S4) since, for both cases, the most significant improvements in this objective function were observed. These results confirm the direct relationship between voltage profiles and reactive power, which is due to the fact that PV-STATCOMs work as a variable reactive power source, injecting this type of power in the nodes where they are installed. This allows improving the lagging power factor at the terminals of the substation.
The active power generation at the terminals of the substation bus is reported in Figure 6 for each simulation scenario.
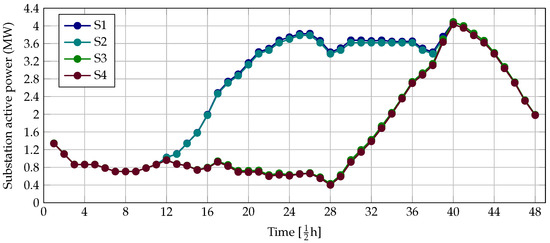
Figure 6.
Behavior regarding active power injection at the terminals of the substation bus for each simulation scenario in the IEEE 69-bus grid.
Figure 6 shows that: (i) the energy generation reduction at the terminals of the substation is directly related to the ability to inject active power with PV-STATCOMs (i.e., S2 and S4); (ii) the contribution of reactive power injection to the total grid operating costs is minimal since its contribution corresponds to the reduction of the total grid power losses, which is small when compared to the energy consumed by all the loads during a day of operation; and (iii) the available solar energy for day-ahead scheduling is not enough to replace the substation bus in any period, which is attributable to the initial sizes assigned for the IEEE 69-bus grid, which are small in comparison with the total demand.
5.3. Complementary Analysis
To illustrate the effect of the variable power factor in minimizing each objective function under analysis, the function was selected for g minimized in S2 to S4 for the IEEE 33-, and 69-bus grids. For the sake of compactness, all the active or reactive power in the PV-STATCOM systems was added in order to observe the cumulative effect of these variables as a function of the operation scenario, as can be seen in Figure 7.
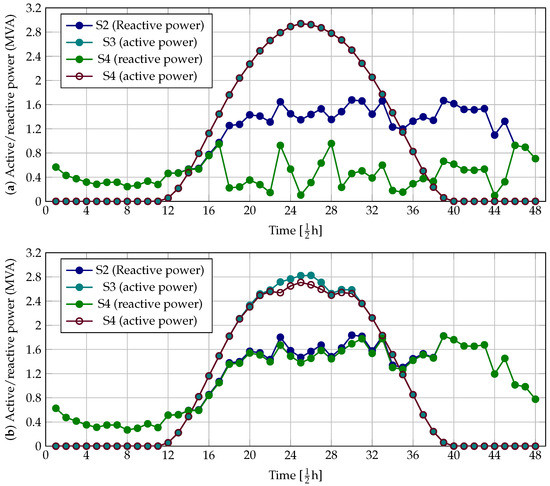
Figure 7.
Cumulative active and reactive power injections in scenarios 2 to 4: (a) IEEE 33-bus grid, and (b) IEEE 69-bus system.
The behavior of the active and reactive power injection in Figure 7 shows that:
- i.
- The amount of reactive power injections in the IEEE 33-bus grid exhibits essential variations in the IEEE 33-bus grid between periods 17 and 46, being higher in S2, as these reactive injections are required to minimize the power losses. However, in the case of S4, this reactive power injection is lower, which is attributable to the fact that active power injection in S4 allows for better energy losses reductions when compared to the zero power factor case (S2). Note that, in S3 and S4, the available active power is fully injected into the network. This may imply that the PV plants for the IEEE 33-bus grid have been subsized and higher active power injection capabilities may help with better objective function improvements.
- ii.
- The results for the IEEE 33-bus grid showed a more promising performance since the total active power injection capabilities for this system were about 3040 kW. However, the active power injection in S3 and S4 is about 2825 kW, which implies that a full capacity is not required to minimize the total grid energy losses. In addition, the reactive power behavior has similar, which means that the active and reactive power injections are complementary variables that allows for better objective function values when working simultaneously, i.e., when comparing S4 to S2 and S3.
The numerical results in Figure 7 suggest that more research is required to define the optimal sizes and location of PV-STATCOMs in medium-voltage distribution networks, which can be considered as an opportunity for future works.
6. Conclusions
An efficient day-ahead scheduling strategy for operating PV-STATCOMs in medium-voltage distribution networks via convex optimization was proposed in this study. The exact nonlinear programming model representing this problem was transformed using a second-order cone approximation in the complex domain. This approximation was performed by transforming the product of two complex variables into its equivalent hyperbolic representation, which was then relaxed to obtain a convex cone. Four simulation scenarios, including a benchmark case, were considered to test the impact of optimal PV-STATCOM scheduling on electrical networks. These scenarios assumed operations with unity, zero, and variable power factors. Numerical simulations in the IEEE 33- and 69-bus grids confirmed that:
- i.
- The use of PV-STATCOMs with zero or variable power factors had a significant impact on the average voltage profile behavior. For both test feeders, the expected improvements were greater than (IEEE 33-bus grid) and (IEEE 69-bus grid) when considering a zero power factor (as shown in S2). Furthermore, when a variable power factor was employed (S4), the improvements reached 80% and 67% for the each grid.
- ii.
- The most significant benefit of using variable active power injection with PV-STATCOMs was observed in the form of a substantial decrease in grid energy purchasing costs at the substation terminals. This reduction was achieved by injecting active power from renewable energy sources, which directly resulted in a decrease in the total power injection at the substation terminals. For both test grids in S3 and S4, the reductions in energy purchasing costs exceeded when PV-STATCOMs were optimally scheduled while considering both unity and variable power factors.
- iii.
- In the case of daily energy losses minimization, all operating scenarios exhibited significant reductions. For the IEEE 33-bus grid, the minimum and maximum reductions in the total grid power losses were between and (as could be seen in S2 and S4), whereas, for the IEEE 69-bus grid, these were and .
As a general conclusion based on the numerical results, using PV-STATCOMs with a zero power factor (i.e., purely dynamic reactive power compensation) is a suitable method for minimizing grid power losses or improving grid voltage profiles. However, in the case of energy purchasing costs minimization, the only contribution of this type of operation is associated with a reduction in the costs of energy losses, which is a small contribution when compared to the aggregated energy consumption costs in all of the demand nodes.
As for future work, the following studies can be conducted: (i) combining the efficient operation of PV-STATCOMs with battery energy storage systems in order to obtain an efficient scheduling methodology that allows providing active power in periods where renewable generation resources are not available; (ii) transforming the proposed second-order cone optimization model into a mixed-integer convex equivalent for simultaneously determining the daily scheduling and optimal placement and sizing of PV-STATCOMs; and (iii) comparing the proposed convex methodology against combinatorial approaches or semi-definite programming models in meshed distribution networks.
Author Contributions
Conceptualization, methodology, software, and writing (review and editing): O.D.M., O.D.F.-C. and W.G.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received support from the Ibero-American Science and Technology Development Program (CYTED) through thematic network 723RT0150, Red para la integración a gran escala de energías renovables en sistemas eléctricos (RIBIERSE-CYTED). This research was also supported by project no. 6-23-7, titled Desarrollo de una metodología para la compensación óptima de potencia reactiva en sistemas eléctricos de distribución from at Universidad Tecnológica de Pereira.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing does not apply to this article.
Acknowledgments
To God, who opens the doors of scientific knowledge and enlightens us to achieve our goals.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Value of the daily energy losses (W). | |
| Value of voltage deviation (%). | |
| Energy purchasing costs at the terminals of the substation bus ($). | |
| Nominal voltage at the substation terminal (V). | |
| Nominal operating voltage at node k (V). | |
| s | Superscripts associated with the substations. |
| Superscripts associated with the PV-STATCOMs. | |
| d | Superscripts associated with the demands. |
| Subscripts associated with nodes. | |
| h | Subscripts associated with period or time. |
| Complex conjugate operation of the argument. | |
| Part real of argument. | |
| Magnitude of the argument. | |
| Euclidean norm of the argument. | |
| Average value of the energy purchased ($/kWh). | |
| Complex value of the admittance matrix that relates nodes k and m (S). | |
| Period of analysis h (h). | |
| , | Minimum and maximum voltage allowed at node k (V). |
| Maximum power injection capacities at substation (VA). | |
| Nominal power transference capacity of the PV-STATCOM system at node k (VA). | |
| Nominal active power available of the PV-STATCOM system at node k (VA). | |
| Set that contains all periods under analysis. | |
| Set that contains all nodes in the network. | |
| Complex power generation at substation at node k and time h (VA). | |
| Complex power generation of the PV-STATCOM at node k and time h (VA). | |
| CComplex power demanded at node k and time h (VA). | |
| Complex value of the nodal voltage at node k and time h (V). | |
| Complex value of the nodal voltage at node m and time h (V). | |
| Complex value of the product between voltages at nodes k and m and time h (V). | |
| Square voltage at node k and time h (V). |
References
- Churchill, S.A.; Inekwe, J.; Ivanovski, K.; Smyth, R. Transport infrastructure and CO2 emissions in the OECD over the long run. Transp. Res. Part D Transp. Environ. 2021, 95, 102857. [Google Scholar] [CrossRef]
- Peng, G.; Xiang, Y. CO2 emission coupled power generation mix evolution: A system dynamics approach. Energy Rep. 2022, 8, 597–604. [Google Scholar] [CrossRef]
- Barreto, R.; Faria, P.; Vale, Z. Electric Mobility: An Overview of the Main Aspects Related to the Smart Grid. Electronics 2022, 11, 1311. [Google Scholar] [CrossRef]
- Kubik, A. Impact of the Use of Electric Scooters from Shared Mobility Systems on the Users. Smart Cities 2022, 5, 1079–1091. [Google Scholar] [CrossRef]
- Piazza, G.; Bracco, S.; Delfino, F.; Somma, M.D.; Graditi, G. Impact of electric mobility on the design of renewable energy collective self-consumers. Sustain. Energy Grids Netw. 2023, 33, 100963. [Google Scholar] [CrossRef]
- Babonneau, F.; Chotard, D.; Haurie, A. Assessing electric mobility and renewable energy synergy in a small New Caledonia Island community. Int. J. Green Energy 2023, 1–15. [Google Scholar] [CrossRef]
- Falfari, S.; Bianchi, G.M. Concerns on Full Electric Mobility and Future Electricity Demand in Italy. Energies 2023, 16, 1704. [Google Scholar] [CrossRef]
- Rakhshani, E.; Rouzbehi, K.; Sánchez, A.J.; Tobar, A.C.; Pouresmaeil, E. Integration of Large Scale PV-Based Generation into Power Systems: A Survey. Energies 2019, 12, 1425. [Google Scholar] [CrossRef]
- de Almeida, P.M.; Barbosa, P.G.; Duque, C.A.; Ribeiro, P.F. Grid connection considerations for the integration of PV and wind sources. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R. Integration of renewable distributed generators into the distribution system: A review. IET Renew. Power Gener. 2016, 10, 873–884. [Google Scholar] [CrossRef]
- Erdiwansyah; Mahidin; Husin, H.; Nasaruddin; Zaki, M.; Muhibbuddin. A critical review of the integration of renewable energy sources with various technologies. Prot. Control Mod. Power Syst. 2021, 6, 3. [Google Scholar] [CrossRef]
- European Union Institute. Regulatory Menu for Integration of Renewables; Publications Office: Luxembourg, 2022. [CrossRef]
- Karimi-Arpanahi, S.; Jooshaki, M.; Moeini-Aghtaie, M.; Abbaspour, A.; Fotuhi-Firuzabad, M. Incorporating flexibility requirements into distribution system expansion planning studies based on regulatory policies. Int. J. Electr. Power Energy Syst. 2020, 118, 105769. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Rosales-Muñoz, A.A.; Cortés-Caicedo, B.; Montoya, O.D.; Andrade, F. Optimal Operation of PV Sources in DC Grids for Improving Technical, Economical, and Environmental Conditions by Using Vortex Search Algorithm and a Matrix Hourly Power Flow. Mathematics 2022, 11, 93. [Google Scholar] [CrossRef]
- Al-Jaafreh, M.A.; Mokryani, G. Planning and operation of LV distribution networks: A comprehensive review. IET Energy Syst. Integr. 2019, 1, 133–146. [Google Scholar] [CrossRef]
- Lakshmi, S.; Ganguly, S. Transition of Power Distribution System Planning from Passive to Active Networks: A State-of-the-Art Review and a New Proposal. In Sustainable Energy Technology and Policies; Springer: Singapore, 2017; pp. 87–117. [Google Scholar] [CrossRef]
- Siano, P.; Rigatos, G.; Piccolo, A. Active Distribution Networks and Smart Grids: Optimal Allocation of Wind Turbines by Using Hybrid GA and Multi-Period OPF. In Atlantis Computational Intelligence Systems; Atlantis Press: Paris, France, 2012; pp. 579–599. [Google Scholar] [CrossRef]
- Azizivahed, A.; Gholami, K.; Li, L.; Zhang, J. Accurate optimal power flow for active distribution networks via floating tangent surface. Electr. Power Syst. Res. 2023, 217, 109167. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Ginidi, A.; Elsayed, A.M.; Al-Gahtani, S.F. Optimal Allocation of PV-STATCOM Devices in Distribution Systems for Energy Losses Minimization and Voltage Profile Improvement via Hunter-Prey-Based Algorithm. Energies 2023, 16, 2790. [Google Scholar] [CrossRef]
- Varma, R.K.; Siavashi, E.M. PV-STATCOM: A New Smart Inverter for Voltage Control in Distribution Systems. IEEE Trans. Sustain. Energy 2018, 9, 1681–1691. [Google Scholar] [CrossRef]
- Lachovicz, F.J.; Fernandes, T.S.P.; Junior, J.A.V. Impacts of PV-STATCOM Reactive Power Dispatch in the Allocation of Capacitors Bank and Voltage Regulators on Active Distribution Networks. J. Control Autom. Electr. Syst. 2023, 34, 796–807. [Google Scholar] [CrossRef]
- Ali, M.B.; Kazmi, S.A.A.; Khan, Z.A.; Altamimi, A.; Alghassab, M.A.; Alojaiman, B. Voltage Profile Improvement by Integrating Renewable Resources with Utility Grid. Energies 2022, 15, 8561. [Google Scholar] [CrossRef]
- Sadiq, R.; Wang, Z.; Chung, C.; Zhou, C.; Wang, C. A review of STATCOM control for stability enhancement of power systems with wind/PV penetration: Existing research and future scope. Int. Trans. Electr. Energy Syst. 2021, 31, e13079. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W. Dynamic active and reactive power compensation in distribution networks with batteries: A day-ahead economic dispatch approach. Comput. Electr. Eng. 2020, 85, 106710. [Google Scholar] [CrossRef]
- Liu, F.; Mo, Q.; Yang, Y.; Li, P.; Wang, S.; Xu, Y. A nonlinear model-based dynamic optimal scheduling of a grid-connected integrated energy system. Energy 2022, 243, 123115. [Google Scholar] [CrossRef]
- Cruz-De-Jesús, E.; Martínez-Ramos, J.L.; Marano-Marcolini, A. Optimal Scheduling of Controllable Resources in Energy Communities: An Overview of the Optimization Approaches. Energies 2022, 16, 101. [Google Scholar] [CrossRef]
- Varma, R.K.; Das, B.; Axente, I.; Vanderheide, T. Optimal 24-hr utilization of a PV solar system as STATCOM (PV-STATCOM) in a distribution network. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar] [CrossRef]
- Varma, R.K.; Siavashi, E.M. Enhancement of Solar Farm Connectivity With Smart PV Inverter PV-STATCOM. IEEE Trans. Sustain. Energy 2019, 10, 1161–1171. [Google Scholar] [CrossRef]
- Elshahed, M.; Tolba, M.A.; El-Rifaie, A.M.; Ginidi, A.; Shaheen, A.; Mohamed, S.A. An Artificial Rabbits’ Optimization to Allocate PVSTATCOM for Ancillary Service Provision in Distribution Systems. Mathematics 2023, 11, 339. [Google Scholar] [CrossRef]
- Kumar, P.; Bohre, A.K. Optimal allocation of Hybrid Solar-PV with STATCOM based on Multi-objective Functions using combined OPF-PSO Method. SSRN Electron. J. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Amin, A.; Ebeed, M.; Nasrat, L.; Aly, M.; Ahmed, E.M.; Mohamed, E.A.; Alnuman, H.H.; Hamed, A.M.A.E. Techno-Economic Evaluation of Optimal Integration of PV Based DG with DSTATCOM Functionality with Solar Irradiance and Loading Variations. Mathematics 2022, 10, 2543. [Google Scholar] [CrossRef]
- Mahmoud, K.; Abdel-Nasser, M.; Lehtonen, M.; Hussein, M.M. Optimal Voltage Regulation Scheme for PV-Rich Distribution Systems Interconnected with D-STATCOM. Electr. Power Compon. Syst. 2020, 48, 2130–2143. [Google Scholar] [CrossRef]
- Thangaraj, Y. Integration of Solar and Wind Based DGs with DSTATCOM in Distribution Systems using Modified Bat Algorithm. Gazi Univ. J. Sci. 2019, 32, 895–912. [Google Scholar] [CrossRef]
- Oda, E.S.; Hamed, A.M.A.E.; Ali, A.; Elbaset, A.A.; Sattar, M.A.E.; Ebeed, M. Stochastic Optimal Planning of Distribution System Considering Integrated Photovoltaic-Based DG and DSTATCOM Under Uncertainties of Loads and Solar Irradiance. IEEE Access 2021, 9, 26541–26555. [Google Scholar] [CrossRef]
- Isha, G.; Jagatheeswari, P. Optimal allocation of DSTATCOM and PV array in distribution system employing fuzzy-lightning search algorithm. Automatika 2021, 62, 339–352. [Google Scholar] [CrossRef]
- Saastamoinen, A.; Kuosmanen, T. Quality frontier of electricity distribution: Supply security, best practices, and underground cabling in Finland. Energy Econ. 2016, 53, 281–292. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garces, A.; Gil-González, W. Minimization of the distribution operating costs with D-STATCOMS: A mixed-integer conic model. Electr. Power Syst. Res. 2022, 212, 108346. [Google Scholar] [CrossRef]
- Jakšetić, J. One Concave-Convex Inequality and Its Consequences. Mathematics 2021, 9, 1639. [Google Scholar] [CrossRef]
- Farivar, M.; Low, S.H. Branch Flow Model: Relaxations and Convexification—Part I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Zohrizadeh, F.; Josz, C.; Jin, M.; Madani, R.; Lavaei, J.; Sojoudi, S. A survey on conic relaxations of optimal power flow problem. Eur. J. Oper. Res. 2020, 287, 391–409. [Google Scholar] [CrossRef]
- Yuan, Z.; Hesamzadeh, M.R. Second-order cone AC optimal power flow: Convex relaxations and feasible solutions. J. Mod. Power Syst. Clean Energy 2018, 7, 268–280. [Google Scholar] [CrossRef]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar] [CrossRef]
- Löfberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual: Gurobi Web Page; Gurobi Optimization, LLC.: Beaverton, OR, USA, 2022; Available online: https://www.gurobi.com/documentation/current/refman/index.html (accessed on 16 July 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).