Abstract
The dispersion of the fundamental super mode confined along the boundary between a multilayer metal-insulator (MMI) stack and a dielectric coating is theoretically analyzed and compared to the dispersion of surface waves on a single metal-insulator (MI) boundary. Based on the classical Kretschmann setup, the MMI system is experimentally tested as an anisotropic material to exhibit plasmonic behavior and a candidate of “metametal” to engineer the preset surface plasmon frequency of conventional metals for optical sensing applications. The conditions to obtain artificial surface plasmon frequency are thoroughly studied, and the tuning of surface plasmon frequency is verified by electromagnetic modeling and experiments. The design rules drawn in this paper would bring important insights into applications such as optical lithography, nano-sensing and imaging.
1. Introduction
The multilayer metal-insulator (MMI) stack system (also termed as metal-dielectric composite or MDC) has been widely used as an optically-anisotropic composite [1,2,3], utilized for imaging [4,5,6,7,8], optical lithography [9] and subwavelength sensing/detecting [10]. One of the most attractive features of this stratified medium is its ability to engineer the dispersion of engaged electromagnetic waves, and to tune the frequency range where interesting optical phenomena could occur. As a fundamental form of 2D periodic structure, the optical property of MMI stack has been extensively studied [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] and both rigorous formalism and approximation approach have been developed. Based on a rigorous transfer-matrix method (TMM) [10], the transmittance and reflectance of any incident beams at any layer can be accurately obtained. The effective medium theory (EMT) [13,14], on the contrary, has been applied to approximate the macroscopic behavior of the MMI system as a uniform anisotropic material, and offers more control than TMM towards a demand-oriented design procedure, while important corrections related to non-local effect [17,18] has been made.
As a promising approach towards deep subwavelength optics, plasmonics have attracted great research interests for optical sensing and imaging in recent years. However, plasmonic materials are generally scarce in variety plus the working frequency is limited because of the preset plasma frequency of each plasmonic metal. This problem is worse off in optical frequency, as almost no substitutions (mostly doped semiconductor compounds) can be chosen to replace the overwhelmingly used metals such as aluminum (for DUV), silver and gold (for visible and NIR) due to high loss. It would therefore be significant for optical sensing or imaging applications to explore stratified medium as a plasmonic material or “metametal” and understand how its plasmonic features could be controlled, so as to broaden the frequency window for imaging or sensing applications [2,10]. As one of the most important prototype for plasmonic sensing, Kretschmann configuration can accurately pick off the surface wave’s resonant point at metal-dielectric half-plane by exciting the fundamental TM surface mode on the boundary [2,16]. In this paper, we investigate this surface mode thoroughly and manage to highlight the background (host) material as an important factor, which is rarely noticed in prior art. Specifically, we outline explicit design rules for shifting surface plasmon frequency to not only lower [10], but also higher, for optical sensing. We have then experimentally verified the tuning of surface plasmon frequency in optical frequency based on Kretschmann setup. The conclusions would bring important insights into plasmonic applications from optical lithography to nano-sensing and imaging.
2. Theoretical Analysis and its Comparison with Finite-Difference Time-Domain (FDTD) Modeling
Starting from the anisotropy of MMI structure, the effective permittivity tensor is obtained as [4]
 (1)
(1) where η is the filling ratio of the layer thickness defined by η = d2/d1, and the axes are setup in Figure 1(a). In the following derivation, we treat ε1 as the insulator and ε2 as the metal. Regarded as a single anisotropic medium, it can be placed next to the semi-space of a dielectric material (εd) and form a boundary as host of surface waves. Assuming a fundamental TM-polarized surface wave (super mode) propagating along this boundary and applying proper boundary conditions, the MMI-insulator boundary supports a propagation surface mode with the dispersion relation obtained as
 (2)
(2) To ensure this wave is confined to the boundary, an additional condition is applied as εx < 0, or
 (3)
(3) When η approaches infinite as the MMI gradually becomes a uniform metal layer, Equation (2) can be simplified to
 (4)
(4) which is exactly the well-known dispersion relation for a metal-insulator (MI) boundary. When ω approaches zero, the dispersion curve overlaps with
 (5)
(5) which is the lightline of the dielectric coating.
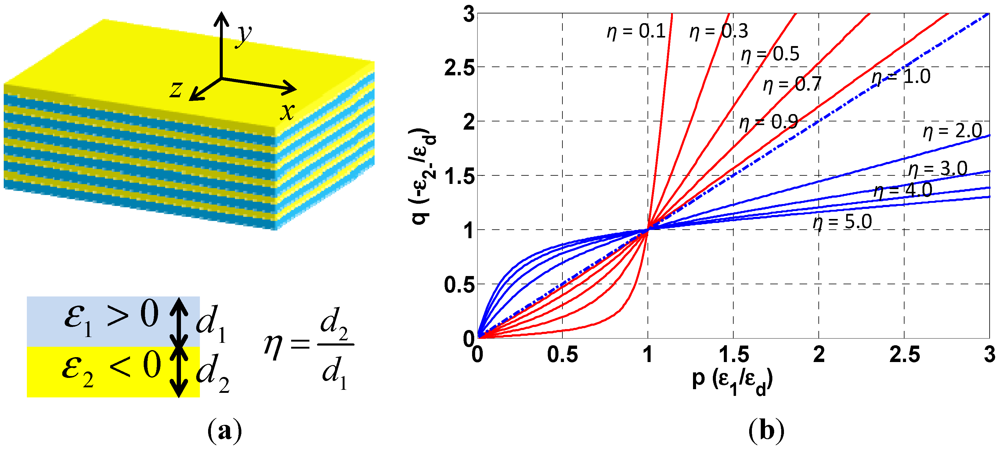
Figure 1.
(a) The multilayer metal-insulator (MMI) scheme and definitions of parameters;(b) The q vs. p curve used to analyze different conditions for tuning effective surface plasmon frequency with a semi-space dielectrics εd.
The similarity of the dispersion between MMI-insulator and MI-insulator structure revealed in Equations (4) and (5) gives a possibility to develop a concept of effective surface plasmon frequency (ESPF), especially when MMI is placed inside (or neighbored to) a dielectric semi-space to act just like a uniform metal (metametal). Firstly, we try to derive the value of the ESPF of MMI structure. Similar to the case of MI-insulator, the surface plasmon resonance (SPR) happens at the pole of the β-ω relation described in Equation (2). The poles of Equation (2) can be analytically obtained after solving a quadratic equation of ε2. The solution can be expressed by εd, ε1 and the filling ratio η, as
 (6)
(6) while the positive root should be discarded based on the preconditions εx < 0 applied in the related section of Equation (3). Based on Equation (1), at least one of the two materials in the multilayered medium needs to have negative permittivity to make εx < 0. The negative root from Equation 6 gives the largest dielectric constant the metametal could reach at
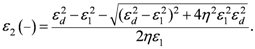 (7)
(7) To study the plasmonic property of the metametal, it is convenient to start from the Drude model of the filling metal 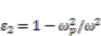 , when ωp is the plasmonic frequency of the filling metal. Here a characteristic frequency for the metametal can be defined as equal to ESPF (
, when ωp is the plasmonic frequency of the filling metal. Here a characteristic frequency for the metametal can be defined as equal to ESPF ( 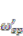 ), which yields
), which yields 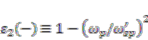 . This is analogy to the definition of surface plasmon frequency defined by
. This is analogy to the definition of surface plasmon frequency defined by 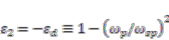 , in while εd describes the dielectric half space. It would be interesting to study the relation between
, in while εd describes the dielectric half space. It would be interesting to study the relation between 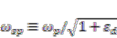 and
and 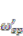 then, as for the latter, there are many parameters that can be controlled even if the same metal is used in the system. Based on the definition above, the relation between
then, as for the latter, there are many parameters that can be controlled even if the same metal is used in the system. Based on the definition above, the relation between 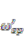 and
and 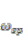 can be easily appreciated by the ratio of ε2(–) and εd. For simplicity, we introduced a new term p = ε1/εd, and another term q for the ratio of ε2(–) and –εd. From Equation (7), the factor q can be expressed by p and η as
can be easily appreciated by the ratio of ε2(–) and εd. For simplicity, we introduced a new term p = ε1/εd, and another term q for the ratio of ε2(–) and –εd. From Equation (7), the factor q can be expressed by p and η as
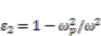 , when ωp is the plasmonic frequency of the filling metal. Here a characteristic frequency for the metametal can be defined as equal to ESPF (
, when ωp is the plasmonic frequency of the filling metal. Here a characteristic frequency for the metametal can be defined as equal to ESPF ( 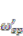 ), which yields
), which yields 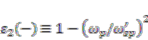 . This is analogy to the definition of surface plasmon frequency defined by
. This is analogy to the definition of surface plasmon frequency defined by 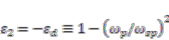 , in while εd describes the dielectric half space. It would be interesting to study the relation between
, in while εd describes the dielectric half space. It would be interesting to study the relation between 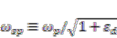 and
and 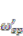 then, as for the latter, there are many parameters that can be controlled even if the same metal is used in the system. Based on the definition above, the relation between
then, as for the latter, there are many parameters that can be controlled even if the same metal is used in the system. Based on the definition above, the relation between 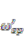 and
and 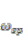 can be easily appreciated by the ratio of ε2(–) and εd. For simplicity, we introduced a new term p = ε1/εd, and another term q for the ratio of ε2(–) and –εd. From Equation (7), the factor q can be expressed by p and η as
can be easily appreciated by the ratio of ε2(–) and εd. For simplicity, we introduced a new term p = ε1/εd, and another term q for the ratio of ε2(–) and –εd. From Equation (7), the factor q can be expressed by p and η as (8)
(8) Figure 1(b) shows how q varies with different η and p. Again, the factor q is a direct indication of the relation between 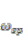 and
and 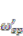 since
since
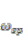 and
and 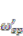 since
since  (9)
(9) The observation indicates that the ratio q does change with both p and η as expected. More importantly, q can change from less than unity to larger than unity. From Equation (9), it is clear that 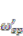 can also be shifted higher or lower than
can also be shifted higher or lower than 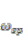 with different values of p and η. The limitation shown in Equation (3) adds another upper cut-off frequency and this value can be smaller than ESPF when η is smaller than 1, which should also be taken into account while exploiting the tunability of MMI system.
with different values of p and η. The limitation shown in Equation (3) adds another upper cut-off frequency and this value can be smaller than ESPF when η is smaller than 1, which should also be taken into account while exploiting the tunability of MMI system.
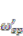 can also be shifted higher or lower than
can also be shifted higher or lower than 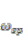 with different values of p and η. The limitation shown in Equation (3) adds another upper cut-off frequency and this value can be smaller than ESPF when η is smaller than 1, which should also be taken into account while exploiting the tunability of MMI system.
with different values of p and η. The limitation shown in Equation (3) adds another upper cut-off frequency and this value can be smaller than ESPF when η is smaller than 1, which should also be taken into account while exploiting the tunability of MMI system. When p is larger than 1 (which means the insulator used in MMI has higher index than the background material), q is usually larger than 1. From Equation (9), the ESPF 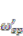 will usually be smaller than the conventional surface plasma frequency
will usually be smaller than the conventional surface plasma frequency 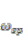 for all possible filling ratio η. This can usually be understood as a result of smaller electron density because of the existence of dielectric filling. Note that when p = 1, the ESPF remains the same to conventional surface plasma frequency regardless of the filling ratio η. On the other hand, the ESPF
for all possible filling ratio η. This can usually be understood as a result of smaller electron density because of the existence of dielectric filling. Note that when p = 1, the ESPF remains the same to conventional surface plasma frequency regardless of the filling ratio η. On the other hand, the ESPF 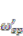 can be shifted higher and even close to
can be shifted higher and even close to 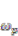 when η is small and p < 1, which means the tuning of surface plasma frequency can theoretically overcome the upper cut-off frequency for any fundamental TM mode supported on a single MI boundary.
when η is small and p < 1, which means the tuning of surface plasma frequency can theoretically overcome the upper cut-off frequency for any fundamental TM mode supported on a single MI boundary.
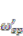 will usually be smaller than the conventional surface plasma frequency
will usually be smaller than the conventional surface plasma frequency 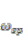 for all possible filling ratio η. This can usually be understood as a result of smaller electron density because of the existence of dielectric filling. Note that when p = 1, the ESPF remains the same to conventional surface plasma frequency regardless of the filling ratio η. On the other hand, the ESPF
for all possible filling ratio η. This can usually be understood as a result of smaller electron density because of the existence of dielectric filling. Note that when p = 1, the ESPF remains the same to conventional surface plasma frequency regardless of the filling ratio η. On the other hand, the ESPF 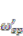 can be shifted higher and even close to
can be shifted higher and even close to 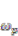 when η is small and p < 1, which means the tuning of surface plasma frequency can theoretically overcome the upper cut-off frequency for any fundamental TM mode supported on a single MI boundary.
when η is small and p < 1, which means the tuning of surface plasma frequency can theoretically overcome the upper cut-off frequency for any fundamental TM mode supported on a single MI boundary.This case (p < 1) highlights an especially interesting property of MMI stack, as the “diluting” of electron density by mixing metals with dielectrics does not sufficiently lead to a decreased surface plasmon frequency. When a low-index filling material has applied its relaxation on the electron oscillation of a pure metal to form a MMI stack, a high-index coating (or substrate εd) will not be able to decrease the free electron oscillation down to 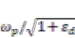 , as the “under-relaxed” MMI has somehow averaged or compensated for the relaxation taking place along the substrate boundary. This observation introduces new perspectives into spoof plasmonics, as an essential supplement to the conventional concept such as effective free electron density.
, as the “under-relaxed” MMI has somehow averaged or compensated for the relaxation taking place along the substrate boundary. This observation introduces new perspectives into spoof plasmonics, as an essential supplement to the conventional concept such as effective free electron density.
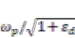 , as the “under-relaxed” MMI has somehow averaged or compensated for the relaxation taking place along the substrate boundary. This observation introduces new perspectives into spoof plasmonics, as an essential supplement to the conventional concept such as effective free electron density.
, as the “under-relaxed” MMI has somehow averaged or compensated for the relaxation taking place along the substrate boundary. This observation introduces new perspectives into spoof plasmonics, as an essential supplement to the conventional concept such as effective free electron density.To verify the existence of this super resonance mode and better explain the tuning of effective surface plasmon frequency (ESPF), we introduce a specific case for an identical substrate material under uniform gold and two types of MMIs. In Figure 2, both MMI structures (and the uniform gold as reference) use the same substrate with εd = 2.5 (which can be regarded as a polymer-based photoresist). We then apply gold-SiO2 (ε = 2.1 for SiO2 at 633 nm) and gold-Al2O3 (ε = 3.15 for Al2O3 at 633 nm) multilayer stacks respectively to this substrate. It is obvious that the filling insulators have been chosen to make sure the ratio p = εinsulator/εd can be less than unity for one case, and larger than unity for the other. Using the Equation (2) and the mode matching condition, we predicted the shifts of ESPF and SPR angle towards different directions (prism np = 2.6). In Figure 2(a), the ESPF (upper cut-off for the TM band) is below and above the preset surface plasmon frequency for gold-SiO2 and gold-Al2O3 case respectively.
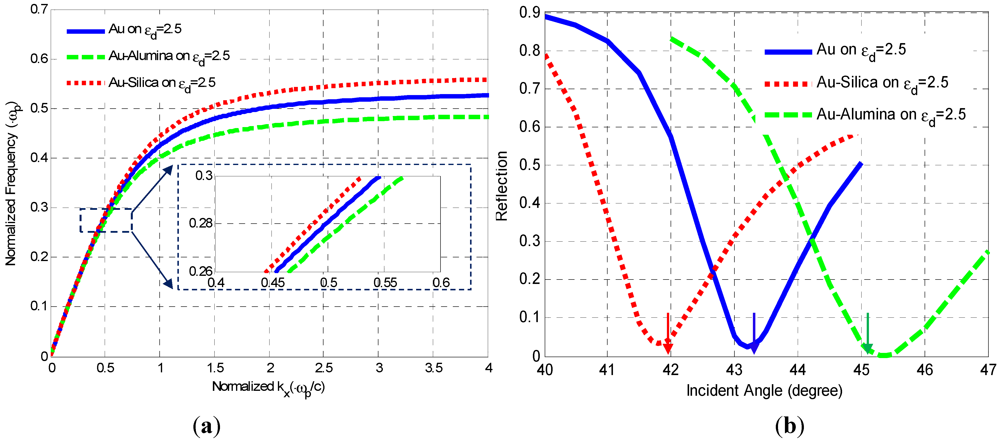
Figure 2.
(a) The analytical dispersion curves calculated by effective medium theory. The upper cut-off frequencies are treated as the effective surface plasmon frequencies (ESPFs) for two MMI cases. Near 633 nm, the shift of wave vectors are shown in the inset for uniform gold (blue), gold-Al2O3 MMI (green) and gold-SiO2 MMI (red); (b) FDTD simulation for the shift of surface plasmon resonance (SPR) angles based on uniform gold (blue), gold-Al2O3 MMI (green) and gold-SiO2 MMI (red). All three curves are on top of the same ε = 2.5 substrate. The small arrows mark the calculated angles based on mode matching.
The FDTD modeling of these 3 structures under a Kretschmann setup is shown in Figure 2(b). MMI stacks are defined as 10 nm gold (ε = −11.84 + j1.24) plus 10nm insulator for 5 cycles, and the shifts of SPR angle apparently go to opposite directions for different p value, verifying the theoretical calculations above. The simulated angles match well with the analytical results marked by small arrows (Figure 2(b)). The insets of Figure 2(a) also imply that under the light source of the same frequency, MMI stack can host a surface wave with a different wave vector as well as the mode size, which can be useful for optical lithography [9]. Although in the theoretical analysis above we have limited the discussion to real propagation constant, we find that the general conclusion can still be applied even to visible spectrum when the ohmic loss from metal is moderate.
3. Numerical and Experimental Demonstration
To verify the tuning of surface plasma frequency, we have modeled a Kretschmann prism-coupling process (Figure 3) for 633-nm light engaging a uniform gold film and an MMI gold-alumina stack (both cases have 50-nm total thickness of metal) using FDTD Solutions of Lumerical [20]. Previous effort [16] has successfully demonstrated the existence of complex modes supported by MMI systems, while here we focus on the link between the tunability of surface waves and the p parameter. Here we try to launch incident beams from a dielectric prism (np = 2.6) to excite the surface waves when the plasmons are neighbored to silicon dioxide (n = 1.45) or silicon nitride (n = 2.01). The dielectric constants of gold (ε = −11.84 + j1.24) and alumina (n = 1.776) are fitted data from [21] and [22] respectively. According to momentum matching condition for SPR, the incident angle can be calculated theoretically as
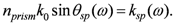 (10)
(10) 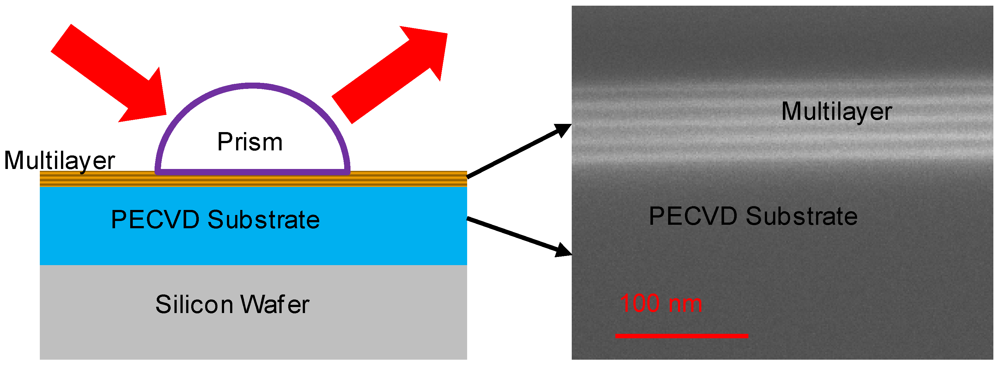
Figure 3.
Experimental setup for studying multilayer metal-insulator stacks and the cross-sectional view of the fabricated multilayer sample (SEM). Each individual layer is 10 nm and there are 10 layers (5 pairs) in total.
Note that for Kretschmann setup and the calculation from Equation (10), the mode of greatest interest here is the confined fundamental TM mode. Although MMI could support more complex modes [12,16,17,18], the analysis in last section is sufficient to predict the sharpest resonance point of bounded SPP waves under this condition. As the original surface plasmon frequencies are shifted lower (silicon dioxide substrate, Figure 4(a)) and higher (silicon nitride substrate, Figure 4(b)), the k-vectors are shifted larger and smaller accordingly. The variation of the incident angle for minimum reflection can then be used to observe the tuning of surface plasmon frequency. Based on Equation 10, we have theoretically calculated the resonant angle shift from 38° to 40° for silicon oxide substrate, and from 73° to 64° for silicon nitride substrate. The Figure 4(a,b) show the FDTD simulated reflection (left axis) versus incident angle, in which the tuning from uniform metal (solid red) to MMI (dashed blue) is clearly visible. Here the gold single layer has a total thickness of 50 nm, and the gold-alumina stack consists of 5 cycles of 10-nm gold plus 10-nm alumina for a total gold thickness of 50 nm. The multilayer region is meshed by 1 nm grid. The excitation angles shift from 38° to 41° for tuning down (silicon dioxide substrate, Figure 4(a)), and 71° to 61° for tuning up (silicon nitride substrate, Figure 4(b)), which match well with the theoretical predictions performed above.
Measured reflected power from a Kretschmann setup with a ZnSe (n = 2.6) hemispherical prism are collected by an optical power meter from multiple samples illuminated by a collimated TM-polarized He-Ne laser beam (Figure 3, left). The SiO2 and Si3N4 substrates are deposited via plasma-enhanced chemical vapor deposition (PECVD), while the gold single-layer and gold-alumina multilayer are deposited via e-beam evaporation (Figure 3, right). The thickness of deposition is kept identical to the simulations performed above. The red crosses and the blue triangles in Figure 4 (right axis) denote the results of gold single layer and gold-alumina multilayer respectively. The observed SPR angles shift from 39° to 40° for silicon dioxide substrate, and 68° to 65° for silicon nitride substrate. The shift direction of SPR agrees with the major conclusion regarding the refractive index relation between the substrate and the filling dielectric film. The discrepancy between the exact observed SPR angle and the calculation might be caused by fabrication disorder and the variation of dielectric constants compared to fitted data, but the disagreement of the effective indexes of super modes between the measured and calculated values are all below 2.5% level.
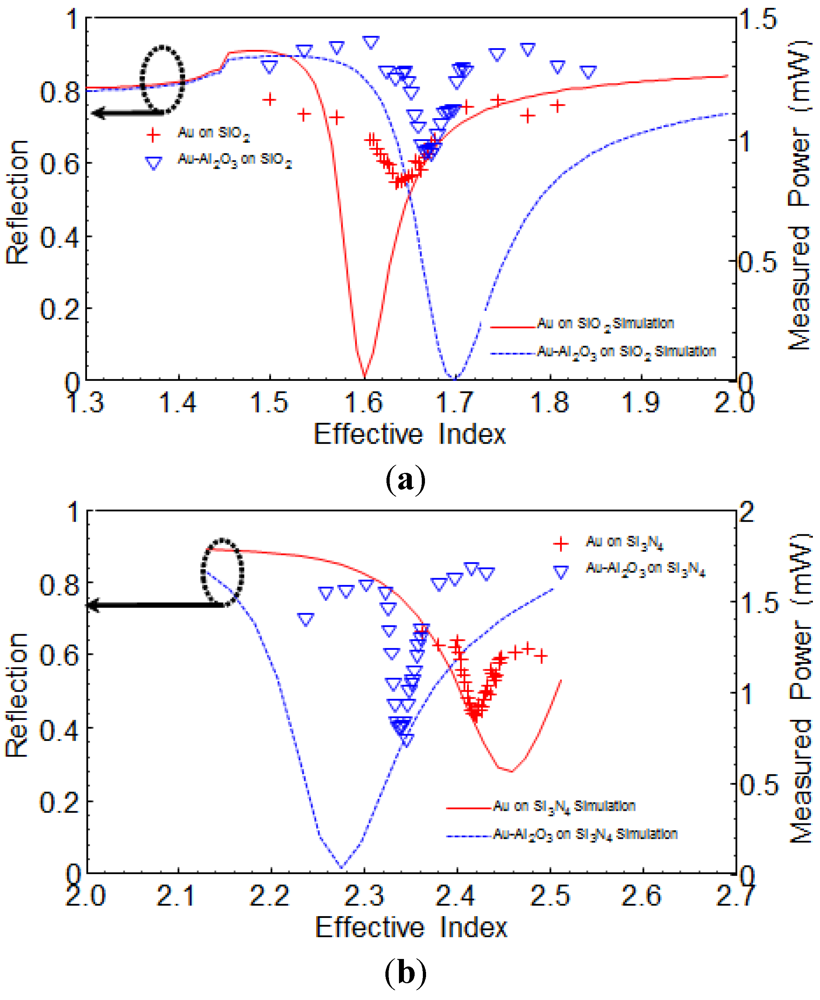
Figure 4.
Numerical and experimental results of reflection vs. effective index for (a) increased ESPF with SiO2 substrate and (b) decreased ESPF with Si3N4 substrate. Red and blue lines describe the simulation results for single-layer and multilayer respectively. Red crosses and blue triangles denote the measured results.
The results shown in Figure 4 not only verify the analytical basis of last section for optical sensing based on SPR, but also suggest possibilities of using MMI stack to achieve manageable mode size and wider frequency range for plasmonics applications. Specifically, as the surface plasma frequency is tuned down, the dispersion curve “flattens” faster in MMI case and therefore at the same frequency of incident light, the propagation constant is increased and smaller wavelength of surface waves can be created which is impossible using uniform metal. On the other hand, by tuning up the ESPF it is possible to broaden the frequency range of surface waves.
As an example, in Figure 4(a,b), we use the design rules mentioned above to illustrate how the increased ESPF allows super surface modes at frequency beyond the conventional surface plasmon frequency. In this modeling we use normalized frequency and length unit. We set the background material as εd = 2.5, and the MMI system consists of 20 pairs of thin layers (ε1 = 1.25 and ε2 = −1.8) for a filling ratio η = 3. If a Drude metal is used here, the working frequency will locate at approximate 0.6 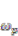 , larger than the conventional cutoff of
, larger than the conventional cutoff of 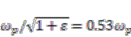 . For uniform metal at this frequency, there will be no surface waves supported at the boundary (Figure 5(a)). With the tuning of ESPF from MMI, however, the working frequency can now exceed 0.58
. For uniform metal at this frequency, there will be no surface waves supported at the boundary (Figure 5(a)). With the tuning of ESPF from MMI, however, the working frequency can now exceed 0.58 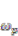 . Here we use COMSOL [22] to simulate the propagation of the super surface mode (Figure 5(b)), showing the subwavelength confinement of the engineered super surface mode bounded and propagated along. Note that in this simulation, the thickness of each repeated unit is 0.04 λ0 (d2 = 0.03 λ0, η = d2/d1 = 3), and the EMT theory could well approximate the behavior of the super surface mode. The mesh-size is small enough to resolve the finest layer d1.
. Here we use COMSOL [22] to simulate the propagation of the super surface mode (Figure 5(b)), showing the subwavelength confinement of the engineered super surface mode bounded and propagated along. Note that in this simulation, the thickness of each repeated unit is 0.04 λ0 (d2 = 0.03 λ0, η = d2/d1 = 3), and the EMT theory could well approximate the behavior of the super surface mode. The mesh-size is small enough to resolve the finest layer d1.
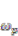 , larger than the conventional cutoff of
, larger than the conventional cutoff of 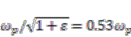 . For uniform metal at this frequency, there will be no surface waves supported at the boundary (Figure 5(a)). With the tuning of ESPF from MMI, however, the working frequency can now exceed 0.58
. For uniform metal at this frequency, there will be no surface waves supported at the boundary (Figure 5(a)). With the tuning of ESPF from MMI, however, the working frequency can now exceed 0.58  . Here we use COMSOL [22] to simulate the propagation of the super surface mode (Figure 5(b)), showing the subwavelength confinement of the engineered super surface mode bounded and propagated along. Note that in this simulation, the thickness of each repeated unit is 0.04 λ0 (d2 = 0.03 λ0, η = d2/d1 = 3), and the EMT theory could well approximate the behavior of the super surface mode. The mesh-size is small enough to resolve the finest layer d1.
. Here we use COMSOL [22] to simulate the propagation of the super surface mode (Figure 5(b)), showing the subwavelength confinement of the engineered super surface mode bounded and propagated along. Note that in this simulation, the thickness of each repeated unit is 0.04 λ0 (d2 = 0.03 λ0, η = d2/d1 = 3), and the EMT theory could well approximate the behavior of the super surface mode. The mesh-size is small enough to resolve the finest layer d1.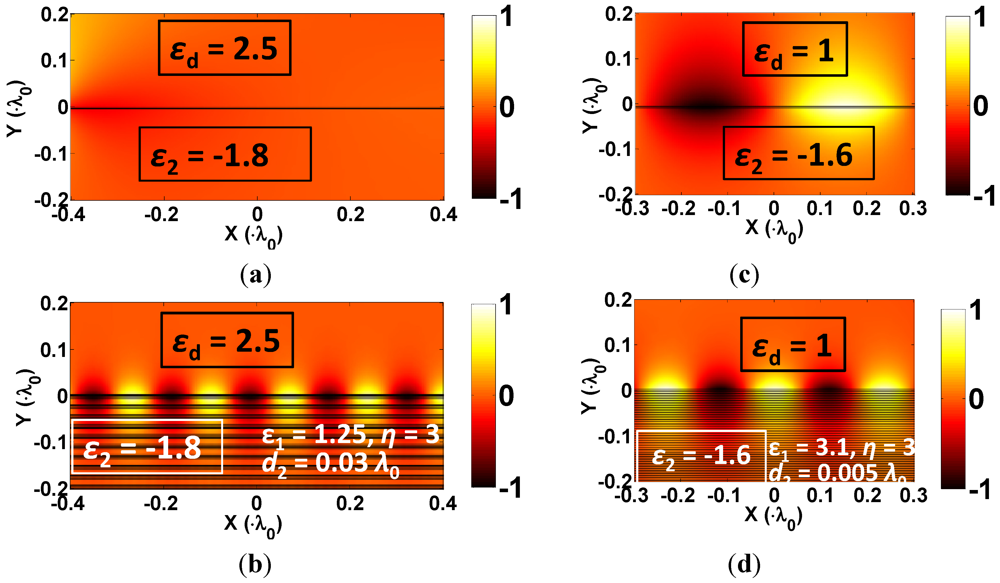
Figure 5.
H field distribution for: (a) No propagation of bounded surface modes above surface plasmon frequency; (b) Bounded surface wave with subwavelength mode profile beyond the conventional cutoff frequency defined in (a); (c) Bounded surface wave propagated on a single metal-insulator interface; (d) Bounded surface wave on a MMI-insulator boundary with shorter wavelength and manageable mode size compared to (c).
Figure 5(c,d) gives another pair of illustration for mode size engineering with multilayer stack. Here the background material is εd = 1.0, and the MMI system consists of 35 pairs of thin layers (ε1 = 3.1 and ε2 = −1.6) for a filling ratio η = 3. According to the design rule, a low-index coating will decrease the ESPF as well as the wavelength of the super surface wave. The metal-insulator boundary shown in Figure 5(c) supports the fundamental TM surface wave for a wavelength of 0.61 λ0, as can also be calculated from Equation 4. When the uniform metal is replaced by “metametal”, the dispersion curve will bend faster away from lightline (Figure 2(b)). Therefore, a larger wave vector plus a decreased wavelength (0.26 λ0) is expected. According to the dispersion relation, this trend will also shrink the length of the exponential tail in the dielectric side, as can be clearly seen comparing the H field distribution in the εd = 1.0 region of Figure 5(c,d). We have also observed the variation of wavelength relative to the thickness of each repeated unit, as have been mentioned in [5,17,18], which indicates the limit of EMT and a general preference of using thin layers to match EMT’s prediction given by Equation (2).
4. Summary
We have theoretically and experimentally investigated the MMI stack as a plasmonic metametal and studied its capability of supporting surface waves and engineering surface plasmon frequency. The analysis proposes a concept of effective surface plasma frequency that can be effectively controlled, and provides new insight into using MMI stacks to accomplish deep subwavelength imaging and artificial dispersion of electromagnetic waves. The outlined design rules would empower researchers to excite confined surface waves more freely from a limited pool of plasmonic materials for optical lithography and subwavelength imaging, and to envision and demonstrate novel detecting/sensing scheme.
Acknowledgments
This material is based upon work supported in part by the US Army under Award No. W911NF-10-1-0153 and the National Science Foundation under Award No. ECCS-1057381. Acknowledgement is made to the Donors of the American Chemical Society Petroleum Research Fund for partial support of this research.
References
- Smith, D.R.; Schurig, D. Electromagnetic wave propagation in media with indefinite permittivity and permeability tensors. Phys. Rev. Lett. 2003, 90, 077405. [Google Scholar] [CrossRef]
- Shi, Z.; Piredda, G.; Liapis, A.C.; Nelson, M.A.; Novotny, L.; Boyd, R.W. Surface-plasmon polaritons on metal-dielectric nanocomposite films. Opt. Lett. 2009, 34, 3535–3537. [Google Scholar] [CrossRef]
- Beruete, M.; Navarro-Cía, M.; Sorolla, M. Strong lateral displacement in polarization anisotropic extraordinary transmission metamaterial. New J. Phys. 2010, 12, 063037. [Google Scholar] [CrossRef]
- Nielsen, R.; Thoreson, M.; Chen, W.; Kristensen, A.; Hvam, J.; Shalaev, V.; Boltasseva, A. Toward superlensing with metal-dielectric composites and multilayers. Appl. Phys. B: Lasers Opt. 2010, 100, 93–100. [Google Scholar] [CrossRef]
- Wood, B.; Pendry, J.B.; Tsai, D.P. Directed subwavelength imaging using a layered metal-dielectric system. Phys. Rev. B 2006, 74, 115116:1–115116:8. [Google Scholar]
- Webb, K.J.; Yang, M. Subwavelength imaging with a multilayer silver film structure. Opt. Lett. 2006, 31, 2130–2132. [Google Scholar] [CrossRef]
- Jacob, Z.; Alekseyev, L.V.; Narimanov, E. Optical hyperlens: Far-field imaging beyond the diffraction limit. Opt. Express 2006, 14, 8247–8256. [Google Scholar] [CrossRef]
- Liu, Z.; Lee, H.; Xiong, Y.; Sun, C.; Zhang, X. Far-Field optical hyperlens magnifying Sub-Diffraction-limited objects. Science 2007, 315, 1686. [Google Scholar] [CrossRef]
- Xiong, Y.; Liu, Z.; Sun, C.; Zhang, X. Two-Dimensional imaging by Far-Field superlens at visible wavelengths. Nano Lett. 2007, 7, 3360–3365. [Google Scholar] [CrossRef]
- Gan, C.H.; Lalanne, P. Well-confined surface plasmon polaritons for sensing applications in the near-infrared. Opt. Lett. 2010, 35, 610–612. [Google Scholar] [CrossRef]
- Kawakami, S. Light propagation along periodic metal-dielectric layers. Appl. Opt. 1983, 22, 2426–2428. [Google Scholar] [CrossRef]
- Davis, T. Surface plasmon modes in multi-layer thin-films. Opt. Commun. 2008, 282, 135–140. [Google Scholar] [CrossRef]
- Salen, B.E.A.; Teich, M.C. Fundamentals of Photonics, 2nd ed; Wiley-Interscience: Hoboken, NJ, USA, 2007; pp. 246–264. [Google Scholar]
- Kildishev, A.V.; Cai, W.; Chettiar, U.K.; Yuan, H.-K.; Sarychev, A.K.; Drachev, V.P.; Shalaev, V.M. Negative refractive index in optics of metal-dielectric composites. J. Opt. Soc. Am. B 2006, 23, 423–433. [Google Scholar]
- Bergman, D. The dielectric constant of a composite material—A problem in classical physics. Phys. Rep. 1978, 43, 377–407. [Google Scholar] [CrossRef]
- Avrutsky, I.; Salakhutdinov, I.; Elser, J.; Podolskiy, V.A. Highly confined optical modes in nanoscale metal-dielectric multilayers. Phys. Rev. B 2007, 75, 241402:1–241402:4. [Google Scholar]
- Elser, J.; Govyadinov, A.A.; Avrutsky, I.; Salakhutdinov, I.; Podolskiy, V.A. Plasmonic nanolayer composites: Coupled plasmon polaritons, effective-medium response, and subdiffraction light manipulation. J. Nanomater. 2007, 7. [Google Scholar]
- Elser, J.; Podolskiy, V.A.; Salakhutdinov, I.; Avrutsky, I. Nonlocal effects in effective-medium response of nanolayered metamaterials. Appl. Phys. Lett. 2007, 90, 191109:1–191109:3. [Google Scholar]
- Nam, S.H.; Ulin-Avila, E.; Bartal, G.; Zhang, X. Deep subwavelength surface modes in metal-dielectric metamaterials. Opt. Lett. 2010, 35, 1847–1849. [Google Scholar] [CrossRef]
- FDTD Solutions 7.5. Available online: http://www.lumerical.com (accessed on 11 January 2012).
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids, 3rd ed; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- COMSOL Multiphysics 3.3. Available online: http://www.comsol.com (accessed on 11 January 2012).
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).