Electromechanical Characteristics Analysis of Magnetic Shield on Superconducting Magnetic Levitation Train
Abstract
1. Introduction
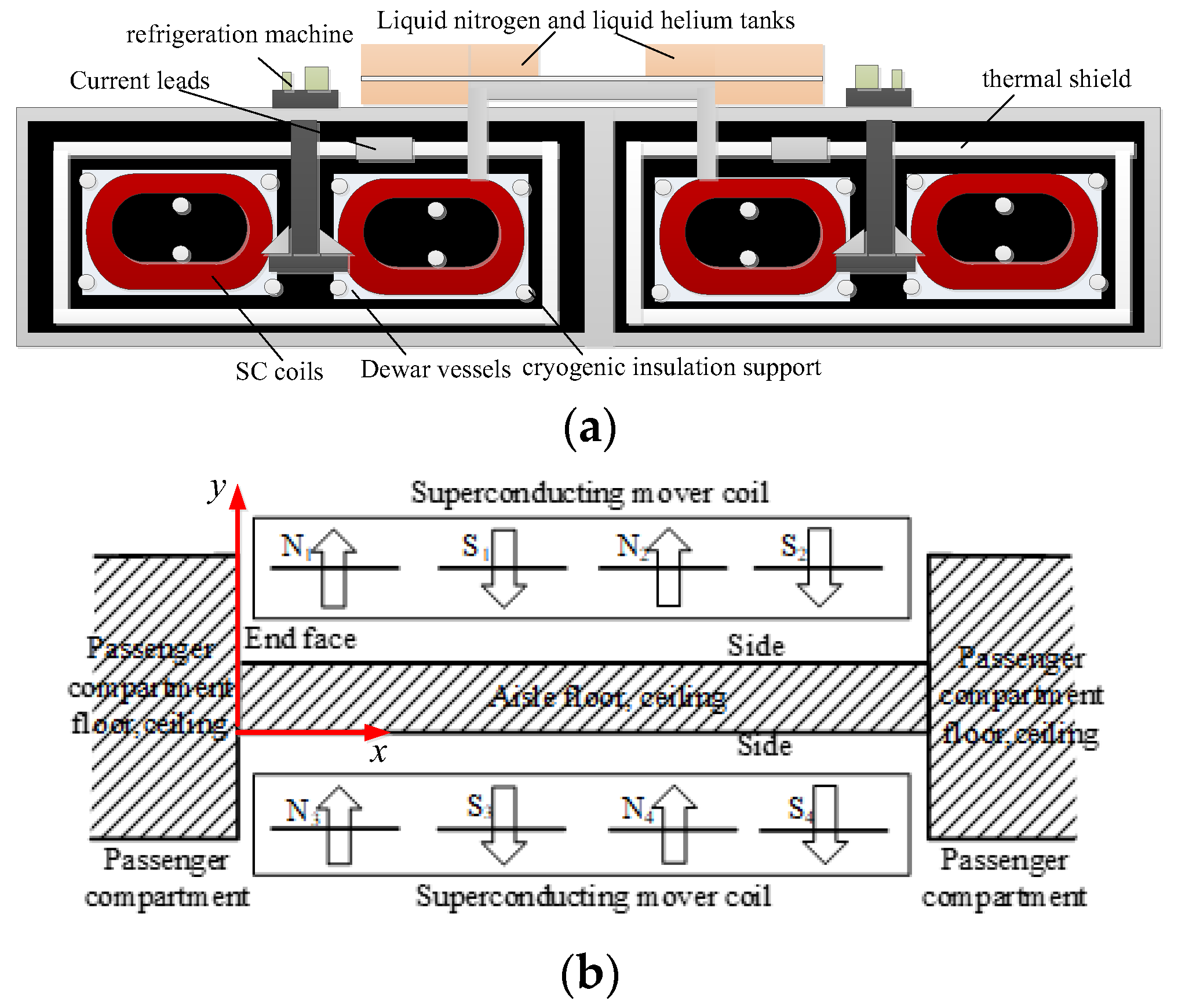
2. The SC Coils and Magnetic Shield Structure
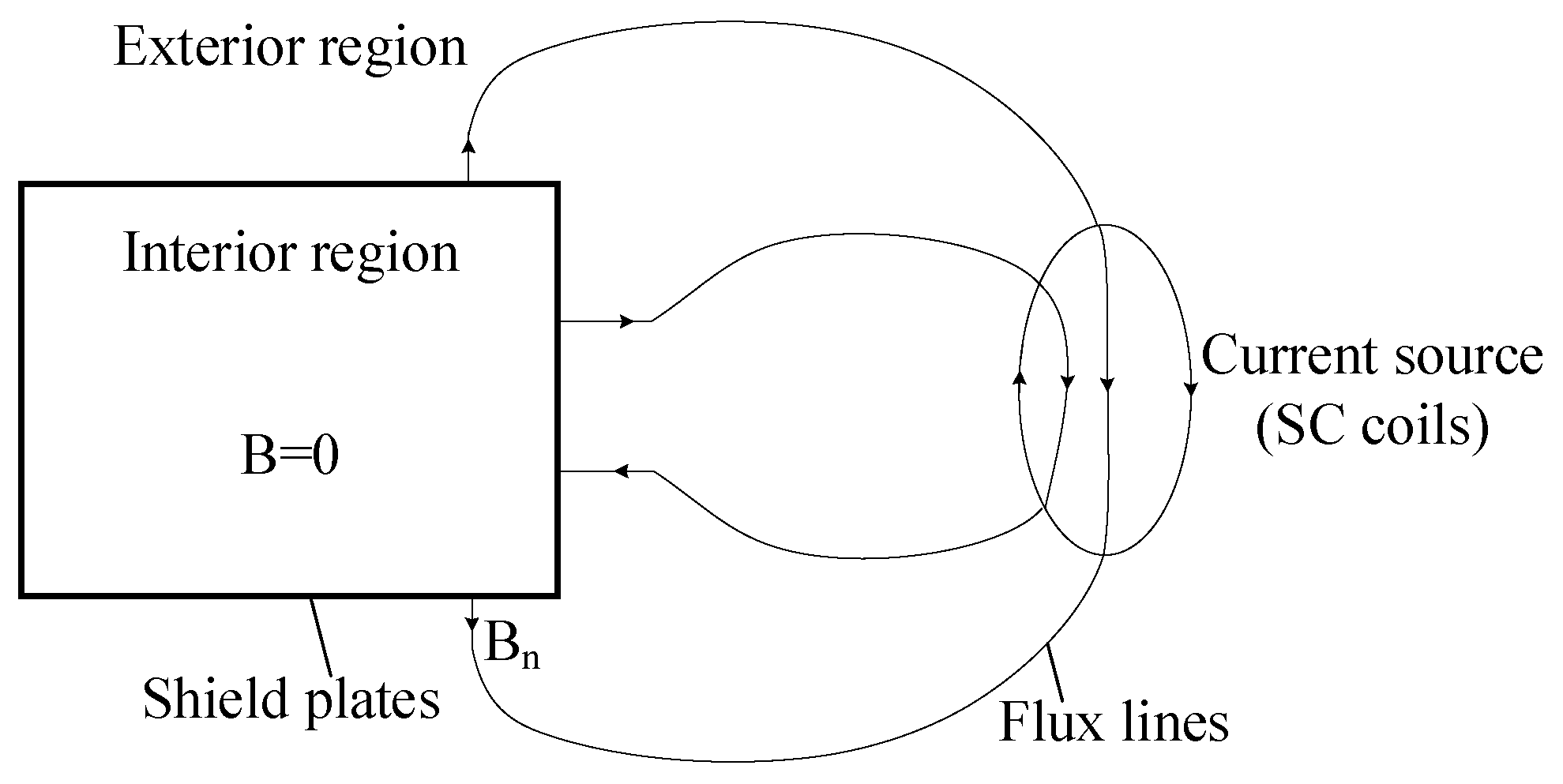
3. The Optimization of Maglev SC Coils
- (1)
- The magnetic permeability of the magnetic shielding plate is infinite
- (2)
- The internal area that needs to be shielded is completely covered by a magnetic shielding plate
- (3)
- The magnetic shielding plate cannot carry magnetic flux higher than the saturation magnetic flux density Bs
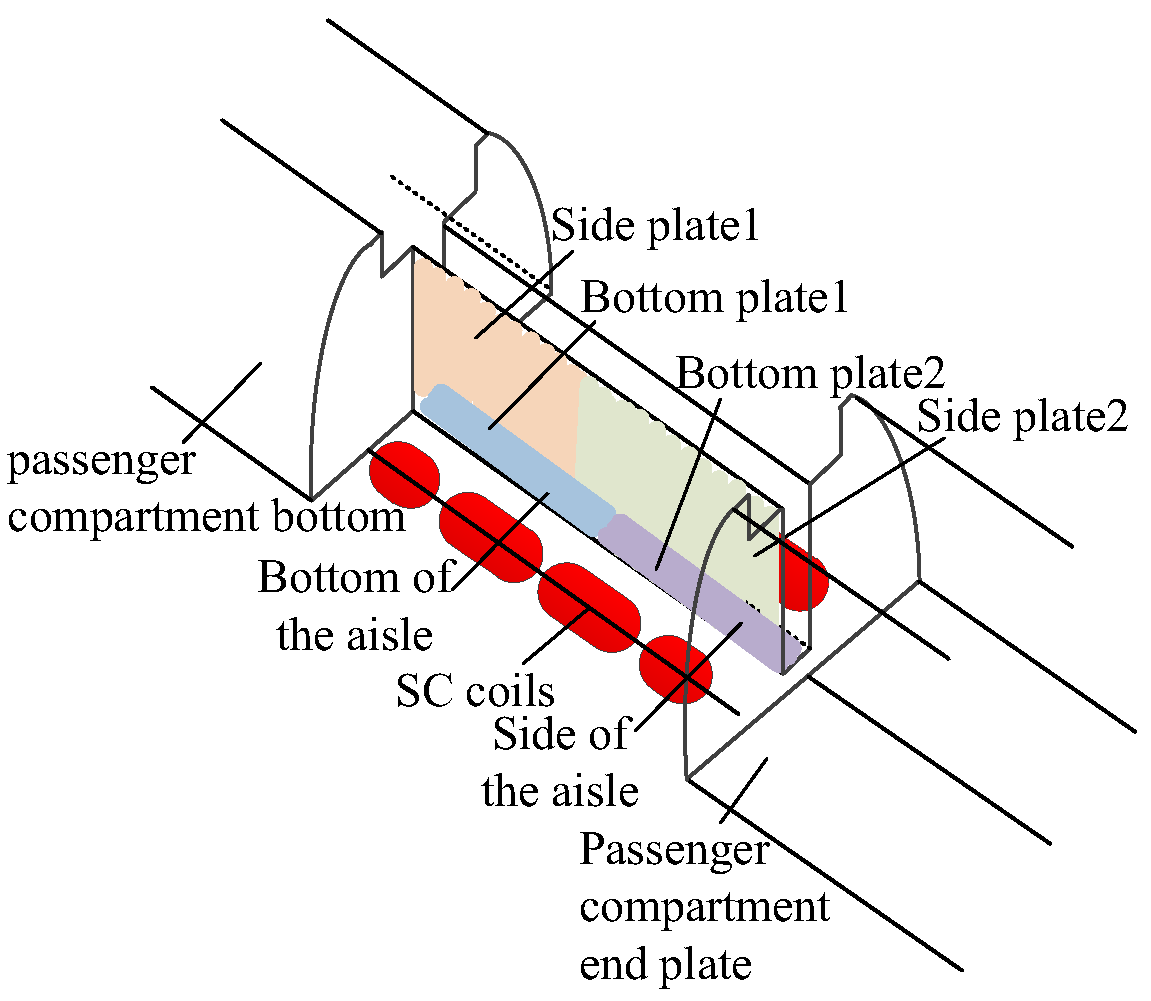
4. Design and Analysis of Magnetic Shielding
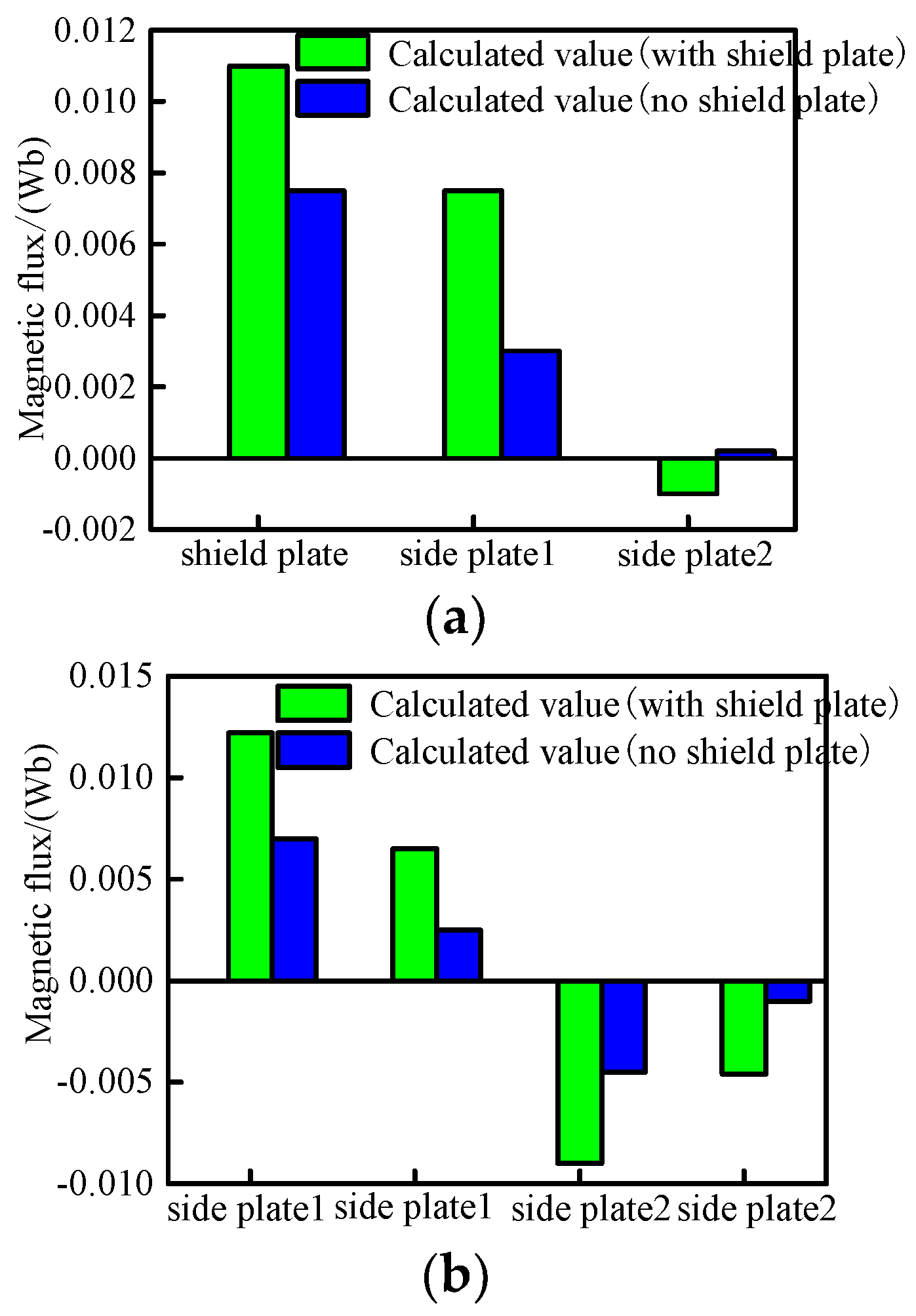
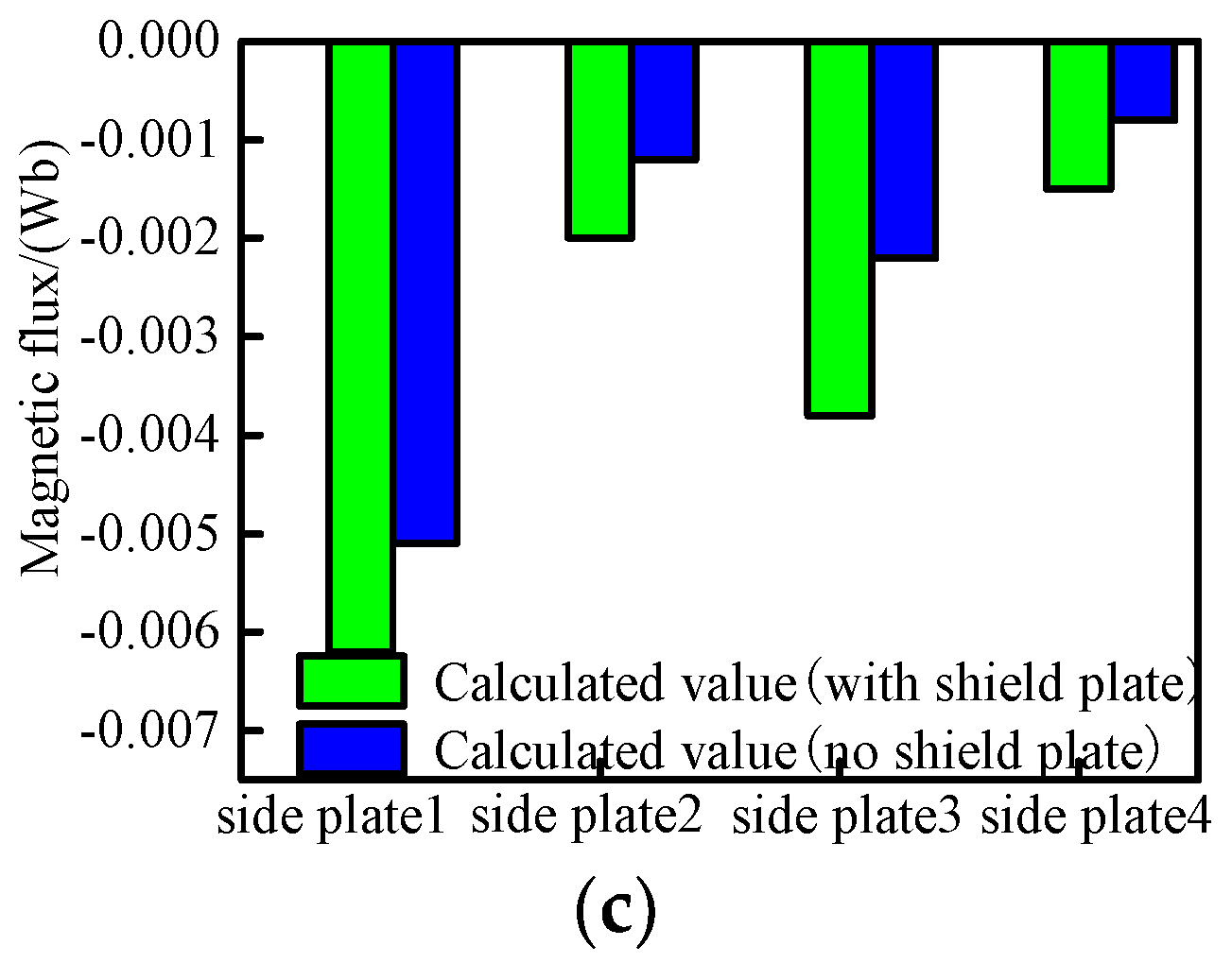
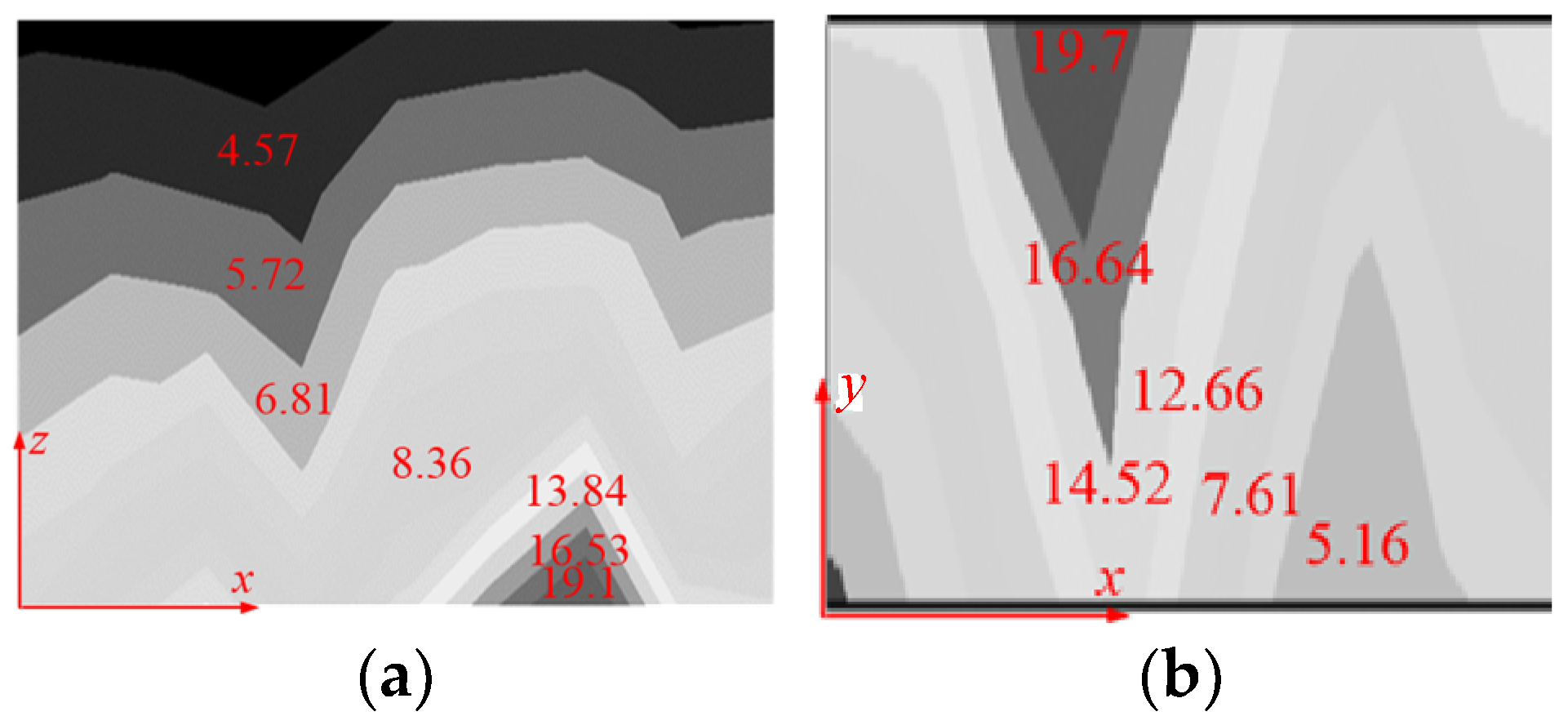
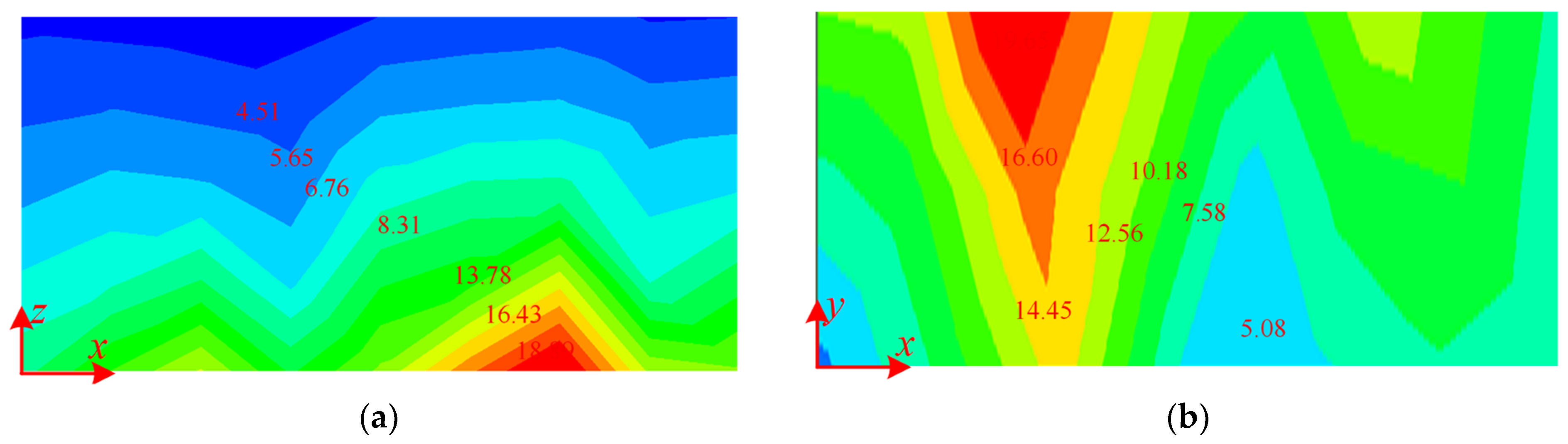
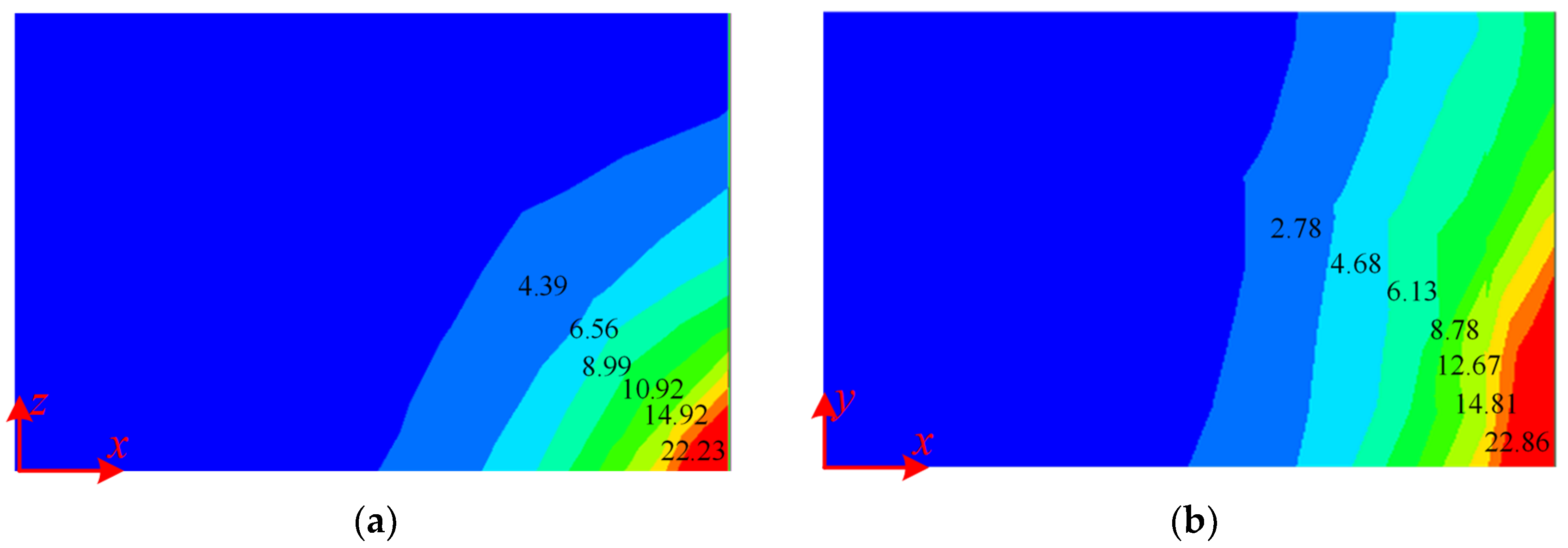
4.1. The Calculation Analysis of Magnetic Flux at the Aisle and the Guest Room
4.2. The Calculation Analysis of Magnetic Flux Density at Aisle and Guest Room
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boldea, I. Linear Electric Machines, Drives, and Maglevs Handbook; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Bernstein, P.; Noudem, J. Superconducting magnetic levitation: Principle, materials, physics and models. Supercond. Sci. Technol. 2020, 33, 033001. [Google Scholar] [CrossRef]
- Igarashi, M.; Nakao, H.; Terai, M.; Kuriyama, T.; Hanai, S.; Yamashita, T. Persistent current HTS magnet cooled by cryocooler (1)—Project overview. IEEE Trans. Appl. Supercond. 2005, 15, 1469–1472. [Google Scholar] [CrossRef]
- Shen, B.; Fu, L.; Geng, J.; Zhang, X.; Zhang, H.; Dong, Q.; Li, C.; Li, J.; Coombs, T.A. Coombs Design and simulation of superconducting Lorentz force electrical impedance tomography (LFEIT). Phys. C Supercond. Appl. 2016, 524, 5–12. [Google Scholar] [CrossRef]
- Gong, T.; Ma, G.; Qian, H.; Liu, K.; Liu, K.; Wang, C.; Zhao, Z.; Zhao, Z. Electromagnetic investigation of a high-temperature superconducting linear synchronous motor for high-speed railway. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Zhao, Z.; Ma, G.; Luo, J.; Li, J.; Su, Z.; Liu, K. Modeling and characteristic analysis of air-cored linear synchronous motors with racetrack coils for electrodynamic suspension train. IEEE Trans. Transp. Electrif. 2022, 8, 1828–1838. [Google Scholar] [CrossRef]
- Ge, Q.; Kou, B.; Zhang, H.; Du, X.; Wang, M. Harmonic magnetic field analysis method and modeling of double-sided air-cored superconducting linear synchronous motor for EDS train. IEEE Trans. Ind. Electron. 2023, 70, 1717–1728. [Google Scholar] [CrossRef]
- Subcommand, A. Adaptive neural network control of electromagnetic suspension system. Int. J. Robot. Autom. 2014, 29, 2206–3728. [Google Scholar] [CrossRef]
- Huang, H.; Deng, Z.; Li, H.; Zhu, H.; Shi, H.; Zheng, J. Numerical simulation of dynamic electromagnetic characteristics of superconducting electrodynamic suspension (EDS) train. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Song, M.; Zhou, D.; Yu, P.; Zhao, Y.; Wang, Y.; Tan, Y.; Li, J. Analytical calculation and experimental verification of superconducting electrodynamic suspension system using null-flux ground coils. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14978–14989. [Google Scholar] [CrossRef]
- Albicini, F.; Andriollo, M.; Martinelli, G.; Morini, A. General expressions of propulsion force in EDS-MAGLEY transport systems with superconducting coils. IEEE Trans. Appl. Supercond. 1993, 3, 425–429. [Google Scholar] [CrossRef]
- Chung, Y.D.; Lee, C.Y.; Kim, D.W.; Kang, H.; Park, Y.G.; Yoon, Y.S. Conceptual design and operating characteristics of multi-resonance antennas in the wireless power charging system for superconducting MAGLEV train. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Matsue, H.; Suzuki, E.; Nemoto, K.; Kurihara, M.; Okino, T.; Murai, T.; Yamamoto, T.; Watanabe, H. Heat load caused by electromagnetic vibration of superconducting magnet combined with linear generator. IEEE Trans. Appl. Supercond. 2000, 10, 913–916. [Google Scholar] [CrossRef]
- Fujie, J. An advanced arrangement of the combined propulsion, levitation and guidance system of superconducting maglev. IEEE Trans. Magn. 1999, 35, 4049–4051. [Google Scholar] [CrossRef]
- Ohashi, S. Effect of the active damper coils of the superconducting magnetically levitated bogie in case of acceleration. IEEE Trans. Magn. 2008, 44, 4163–4166. [Google Scholar] [CrossRef]
- He, J.L.; Coffey, H. Magnetic damping forces in figure-eight-shaped null-flux coil suspension Systems. IEEE Trans. Magn. 1997, 33, 4230–4232. [Google Scholar]
- Oh, J.M.; Bang, T.K.; Jang, G.H.; Lee, J.I.; Haran, K.S.; Cho, H.W. Simplex optimization of shield coil geometry for increasing magnetic shielding performance of air-core superconducting generator. J. Phys. Conf. Ser. 2020, 1590, 012054. [Google Scholar] [CrossRef]
- Andriollo, M.; Martinelli, G.; Morini, A.; Scuttari, A. Minimization of the induced current effects in the shields of SC coils in EDS-MAGLEV trains. IEEE Trans. Appl. Supercond. 1995, 5, 604–609. [Google Scholar] [CrossRef]
- Kvitkovic, J.; Patel, S.; Pamidi, S. Magnetic shielding characteristics of hybrid high-temperature superconductor ferromagnetic material multilayer shields. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Sugouchi, R.; Komiya, M.; Miura, S.; Iwakuma, M.; Yoshida, K.; Sasayama, T.; Yoshida, T.; Yamamoto, K.; Sasamori, Y.; Honda, H.; et al. Conceptual design and electromagnetic analysis of 2 MW fully superconducting synchronous motors with superconducting magnetic shields for turbo-electric propulsion system. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Jin, Y.; Li, L.; Pan, D.; Song, K.; Lou, S.; Zou, Z.; Sun, Z. Analysis and design of a uniform magnetic field coil with a magnetic shield based on an improved analytical model. IEEE Trans. Ind. Electron. 2022, 69, 3068–3077. [Google Scholar] [CrossRef]
- Iwasa, Y. Magnetic shielding for magnetically levitated trains. Proc. IEEE 1973, 61, 598–603. [Google Scholar] [CrossRef]
- Takashi, S.; Naoto, T.; Toshiki, H.; Ken, N. A Design of Magnetic Shielding for a Superconducting Magnetically Levitated Train. Electr. Eng. Jpn. 1998, 124, 42–54. [Google Scholar] [CrossRef]



| SC Coils | Value |
|---|---|
| Number of coils | 8 |
| Polar distance (m) | 1.35 |
| Coil length (m) | 1.07 |
| Coil width (m) | 0.50 |
| Turns | 1400 |
| SC Coils | Value |
|---|---|
| Number of coils | 8 |
| Polar distance (m) | 1.05/1.5 |
| Coil length (m) | 0.8/1.25 |
| Coil width (m) | 0.50 |
| Turns | 2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Zhang, L.; Tao, R.; Wang, P. Electromechanical Characteristics Analysis of Magnetic Shield on Superconducting Magnetic Levitation Train. Micromachines 2025, 16, 1248. https://doi.org/10.3390/mi16111248
Hu M, Zhang L, Tao R, Wang P. Electromechanical Characteristics Analysis of Magnetic Shield on Superconducting Magnetic Levitation Train. Micromachines. 2025; 16(11):1248. https://doi.org/10.3390/mi16111248
Chicago/Turabian StyleHu, Mingyuan, Lei Zhang, Ran Tao, and Ping Wang. 2025. "Electromechanical Characteristics Analysis of Magnetic Shield on Superconducting Magnetic Levitation Train" Micromachines 16, no. 11: 1248. https://doi.org/10.3390/mi16111248
APA StyleHu, M., Zhang, L., Tao, R., & Wang, P. (2025). Electromechanical Characteristics Analysis of Magnetic Shield on Superconducting Magnetic Levitation Train. Micromachines, 16(11), 1248. https://doi.org/10.3390/mi16111248







